初二期中复习最短路径+角平分线+全等三角形综合
- 格式:doc
- 大小:326.12 KB
- 文档页数:13

综合滚动练习:等腰三角形与全等、垂直平分线、角平分线的综合【知识点过关】1.等腰三角形,两条相等,两个相等;等边三角形三条边,三个角,每个角都是 .2.等腰三角形、、重合,也称为“三线合一”.3.于一条线段,并且这条线段的直线,叫做这条线段的垂直平分线.4.线段的垂直平分线上的点到这条线段两端点的 .5.角平分线上的点到这个角的两边的 .【当堂检测】1.如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列结论不一定成立的是()A.AD=BDB.BD=CDC.∠1=∠2D.∠B=∠C2.如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是 .第1题第2题第3题3.如图,在△ABC中,AC的垂直平分线分别交AC,BC于E,D两点.若EC=4,△ABC的周长为23,则△ABD的周长为 .4.如图,点B,C分别在∠MAN的两条边上,∠NBC与∠MCB的平分线交于点P,且PE⊥AM于点E.若PE=6cm,则点P到AN的距离为 .5.如图,在△ABC中,AB=AC,点D是AB的中点,且DE⊥AB交AB、AC于点D、E.(1)若∠A=40°,求∠CBE的度数;(2)若△BCE的周长为8cm,AB=5cm,求BC的长.【当堂训练】1.如果等腰三角形的周长为16,其一边长为4,那么它的底边为 .2.已知AD是等边△ABC的高,BE是AC边的中线,AD与BE交于点F,则∠AFE= .3.在等腰三角形ABC中,腰AB是中垂线与腰AC所在直线相交成的锐角为50°,则底角B的大小为 .4.如图,∠C=90°,∠BAD=∠CAD,若AB=14,BC=11,BD=7,则△ABD的面积是 .5.如图,在△ABC中,AB=AC,∠C=30°,D是BC的中点,DE⊥AB于点E,BC=12.(1)求∠1的度数. (2)求∠CDE的度数.6.如图,在△ABC中,AD⊥BC于点D,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠BAE=40°,求∠C的度数.(2)若△ABC周长为13cm,AC=6cm,求DC长.【选做】感知:如图①,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC(不需要说明理由);探究:如图②,AD平分∠BAC,∠B+∠C=180°,∠B<90°,试说明:DB=DC;应用:如图③,在四边形ABCD中,AD平分∠BAC,∠B=45°,∠C=135°,DE⊥AB,且BE=a,则AB-AC= (用含a的代数式表示).。

八年级数学中的最短路径问题,通常涉及到几何图形中的点、线、面等元素,需要利用一些基本的几何知识和数学原理来求解。
以下是一些常见的最短路径题型及其解题方法:1.两点之间的最短距离:题型描述:在平面上给定两点A和B,求A到B的最短距离。
解题方法:直接连接A和B,线段AB的长度即为最短距离。
2.点到直线的最短距离:题型描述:在平面上给定一点P和一条直线l,求P到l的最短距离。
解题方法:作点P到直线l的垂线,垂足为Q,则PQ的长度即为最短距离。
3.直线到直线的最短距离:题型描述:在平面上给定两条直线l1和l2,求l1到l2的最短距离。
解题方法:如果l1和l2平行,则它们之间的距离即为最短距离;如果l1和l2不平行,则作l1到l2的垂线,垂足所在的线段即为最短4.点到圆的最短距离:题型描述:在平面上给定一点P和一个圆O,求P到圆O的最短距离。
解题方法:如果点P在圆O内,则最短距离为P到圆心的距离减去圆的半径;如果点P在圆O外,则最短距离为P到圆心的距离;如果点P在圆O上,则最短距离为0。
5.圆到圆的最短距离:题型描述:在平面上给定两个圆O1和O2,求O1到O2的最短距离。
解题方法:如果两圆外离,则它们之间的最短距离为两圆的半径之和;如果两圆外切,则它们之间的最短距离为两圆的半径之差;如果两圆相交或内切,则它们之间的最短距离为0;如果两圆内含,则它们之间的最短距离为两圆的半径之差减去两圆半径之和的绝对值。
6.多边形内的最短路径:题型描述:在一个多边形内给定两个点A和B,求A到B的最短解题方法:通常需要将多边形划分为多个三角形,然后利用三角形内的最短路径(即连接两点的线段)来求解。
7.立体几何中的最短路径:题型描述:在立体图形中给定两点A和B,求A到B的最短路径。
解题方法:通常需要将立体图形展开为平面图形,然后利用平面几何中的最短路径原理来求解。
在解决最短路径问题时,需要注意以下几点:准确理解题目要求,确定需要求的是哪两点之间的最短距离。


八年级数学期中考试知识点总结第十一章三角形一、知识框架:二、知识概念:1. 三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形. (选择题)2. 三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边. (选择题,填空题)3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.(钝角三角形三条高的交点在三角形外,直角三角形的三条高的交点在三角形上,锐角三角形的三条高在三角形内)(选择题,填空题)4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线 . (选择题,填空题)(三条中线的交点叫重心)5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线 . (选择题,填空题,解答题)(三角形三条角平分线的交点到三边距离相等)6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性 . (选择题)(例如自行车的三角形车架利用了三角形具有稳定性)7. 多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形. (选择题)8.多边形的内角:多边形相邻两边组成的角叫做它的内角 . (选择题,填空题)9. 多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角. (选择题,填空题)10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线 .(选择题,填空题)11. 正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形. (选择题,填空题)12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用1多边形覆盖平面,(选择题,填空题)13.公式与性质:⑴三角形的内角和:三角形的内角和为180°(选择题,填空题)⑵三角形外角的性质:(选择题,填空题)性质 1:三角形的一个外角等于和它不相邻的两个内角的和.性质 2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n 边形的内角和等于(n2) ·180°(选择题,填空题,解答题)⑷多边形的外角和:多边形的外角和为360° . (选择题,填空题,解答题)⑸多边形对角线的条数:①从n 边形的一个顶点出发可以引(n3) 条对角( n 2) 个三角形.②n边形共有n( n 3)条对角线.(选择题,填空题) 2第十二章全等三角形一、知识框架:二、知识概念:1.基本定义:(选择题,填空题)⑴全等形:能够完全重合的两个图形叫做全等形 . ⑵全等三角形:能够完全重合的两个三角形叫做全等三角形 . ⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点 . ⑷对应边:全等三角形中互相重合的边叫做对应边 . ⑸对应角:全等三角形中互相重合的角叫做对应角 .2.基本性质:(选择题,填空题)⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性 .2⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:(选择题,填空题,解答题)⑴边边边( SSS):三边对应相等的两个三角形全等.⑵边角边( SAS ):两边和它们的夹角对应相等的两个三角形全等.⑶角边角( ASA ):两角和它们的夹边对应相等的两个三角形全等.⑷角角边( AAS ):两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边( HL ):斜边和一条直角边对应相等的两个直角三角形全等 .4.角平分线:⑴画法:(解答题)⑵性质定理:角平分线上的点到角的两边的距离相等 . (选择题,填空题,解答题)⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上. (解答题)(三角形三条角平分线的交点到三边距离相等)5.证明的基本方法:(解答题)⑴明确命题中的已知和求证 . (包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证 . ⑶经过分析,找出由已知推出求证的途径,写出证明过程 .第十三章轴对称一、知识框架:二、知识概念:1.基本概念:(选择题、解答题)⑴轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形 .3⑵两个图形成轴对称:把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称 . ⑶线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线 .⑷等腰三角形:有两条边相等的三角形叫做等腰三角形 . 相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角 .⑸等边三角形:三条边都相等的三角形叫做等边三角形.2.基本性质:⑴对称的性质:(选择题)①不管是轴对称图形还是两个图形关于某条直线对称,对称轴都是任何一对对应点所连线段的垂直平分线 .②对称的图形都全等 .⑵线段垂直平分线的性质:(解答题)①线段垂直平分线上的点与这条线段两个端点的距离相等.②与一条线段两个端点距离相等的点在这条线段的垂直平分线上.⑶关于坐标轴对称的点的坐标性质:(选择题、填空题)①点 P (x, y)关于 x 轴对称的点的坐标为P ' (x,y) .②点 P (x, y)关于 y 轴对称的点的坐标为P " (x, y) .⑷等腰三角形的性质:(解答题)①等腰三角形两腰相等 .②等腰三角形两底角相等(等边对等角).③等腰三角形的顶角角平分线、底边上的中线,底边上的高相互重合.④等腰三角形是轴对称图形,对称轴是三线合一(1条).⑸等边三角形的性质:(解答题)①等边三角形三边都相等.②等边三角形三个内角都相等,都等于60°③等边三角形每条边上都存在三线合一.④等边三角形是轴对称图形,对称轴是三线合一(3条).3.基本判定:(解答题)⑴等腰三角形的判定:4①有两条边相等的三角形是等腰三角形.②如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) .⑵等边三角形的判定:①三条边都相等的三角形是等边三角形.②三个角都相等的三角形是等边三角形.③有一个角是60°的等腰三角形是等边三角形.5。
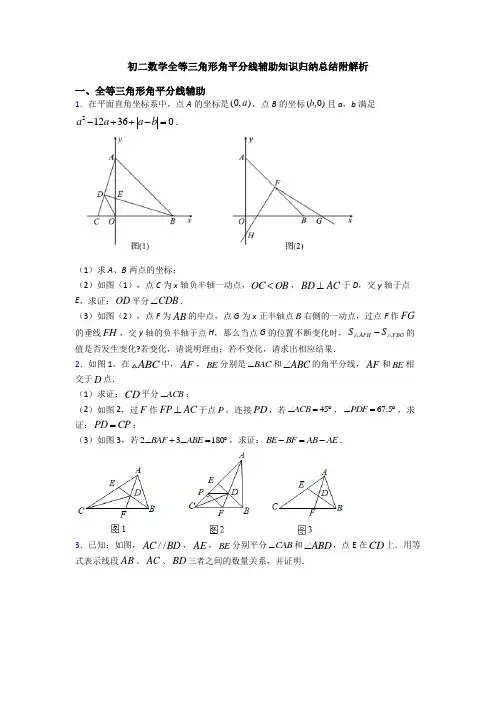
初二数学全等三角形角平分线辅助知识归纳总结附解析一、全等三角形角平分线辅助1.在平面直角坐标系中,点A 的坐标是(0,)a ,点B 的坐标(,0)b 且a ,b 满足212360a a a b -++-=.(1)求A 、B 两点的坐标;(2)如图(1),点C 为x 轴负半轴一动点,OC OB <,BD AC ⊥于D ,交y 轴于点E ,求证:OD 平分CDB ∠.(3)如图(2),点F 为AB 的中点,点G 为x 正半轴点B 右侧的一动点,过点F 作FG 的垂线FH ,交y 轴的负半轴于点H ,那么当点G 的位置不断变化时,AFH FBG S S -△△的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.2.如图1,在ABC 中,AF ,BE 分别是BAC ∠和ABC ∠的角平分线,AF 和BE 相交于D 点.(1)求证:CD 平分ACB ∠;(2)如图2,过F 作FP AC ⊥于点P ,连接PD ,若45ACB ∠=︒,67.5PDF ∠=︒,求证:PD CP =;(3)如图3,若23180BAF ABE ∠+∠=︒,求证:BE BF AB AE -=-.3.已知:如图,//AC BD ,AE ,BE 分别平分CAB ∠和ABD ∠,点E 在CD 上.用等式表示线段AB 、AC 、BD 三者之间的数量关系,并证明.4.如图,在ABC 中,AB AC =,100A ∠=︒,BD 是ABC ∠的平分线,延长BD 至点E ,DE AD =,试求ECA ∠的度数.5.如图,∠D =∠C =90°,点E 是DC 的中点,AE 平分∠DAB ,∠DEA =28°,求∠ABE 的大小.6.如图,在梯形ABCD 中,AD ∥BC ,AE 平分∠BAD ,BE 平分∠ABC ,且AE 、BE 交CD 于点E .试说明AD =AB ﹣BC 的理由.7.如图,已知等腰直角三角形ABC 中,AB =AC ,∠BAC =90°,BF 平分∠ABC ,CD ⊥BD 交BF 的延长线于点D ,试说明:BF =2CD .8.阅读下面材料:小明遇到这样一个问题:如图一,△ABC 中,∠A=90°,AB=AC ,BD 平分∠ABC ,猜想线段AD 与DC 数量关系.小明发现可以用下面方法解决问题:作DE ⊥BC 交BC 于点E :(1)根据阅读材料可得AD 与DC 的数量关系为__________.(2)如图二,△ABC 中,∠A=120°,AB=AC ,BD 平分∠ABC ,猜想线段AD 与DC 的数量关系,并证明你的猜想.(3)如图三,△ABC 中,∠A=100°,AB=AC ,BD 平分∠ABC ,猜想线段AD 与BD 、BC 的数量关系,并证明你的猜想.9.如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,AD+AB=2AE ,求证:∠ADC+∠B=180º10.如图,ABC ∆的外角ACD ∠的平分线CP 与内角ABC ∠的平分线BP 交于点P ,若40BPC ∠=︒,求CAP ∠的度数.【参考答案】***试卷处理标记,请不要删除一、全等三角形角平分线辅助1.(1)6(0)A ,,0(6)B ,;(2)证明见解析;(3)不变化,9AFH FBG S S -=.【分析】(1)由非负性可求a ,b 的值,即可求A 、B 两点的坐标; (2)过点O 作OM BD ⊥于M ,ON AC ⊥于N ,根据全等三角形的判定和性质解答即可;(3)由于点F 是等腰直角三角形AOB 的斜边的中点,所以连接OF ,得出OF =BF .∠BFO =∠GFH ,进而得出∠OFH =∠BFG ,利用等腰直角三角形和全等三角形的判定和性质以及三角形面积公式解答即可.【详解】解:(1)∵212360a a a b ++--=∴2(6)0a a b -+-=,∴600a a b -=⎧⎨-=⎩,即6a b ==. ∴6(0)A ,,0(6)B ,. (2)如图,过点O 作OM BD ⊥于M ,ON AC ⊥于N ,根据题意可知=90ACO CAO ∠+∠︒.∵BD AC ⊥,∴=90BCD CBE ∠+∠︒,∴=CAO CBE ∠∠.∵6(0)A ,,0(6)B ,, ∴OA =OB =6.在AOC △和BOE △中,90CAO EBO OA OB AOC BOE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴AOC BOE ASA ≅(). ∴OE OC =,AC BE = ,=AOC BOE SS . ∴1122AC ON BE OM =, ∴=OM ON ,∴点O 一定在∠CDB 的角平分线上,即OD 平分∠CDB .(3)如图,连接OF ,∵AOB 是等腰直角三角形且点F 为AB 的中点,∴OF AB ⊥,OF FB =,OF 平分∠AOB .∴90OFB OFH HFB ∠∠+∠︒==.又∵FG FH ⊥,∴90HFG BFG HFB ∠=∠+∠=︒,∴OFH BFG ∠∠=. ∵1452FOB AOB ∠=∠=︒, ∴4590135FOH FOB HOB ∠=∠+∠=︒+︒=︒.又∵180********FBG ABO ∠=︒-∠=︒︒=︒﹣,∴FOH FBG ∠=∠.在FOH △和FBG △中OFH BFG OF BF FOH FBG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴FOH FBG ASA ≅(). ∴FOH FBG S S =, ∴11116692224AFH FBG AFHFOH FOA AOB S S S S OA OB S S -====⨯=⨯⨯=﹣. 故不发生变化,且9AFH FBG S S -=.【点睛】本题为三角形综合题,考查非负数的性质,角平分线的判定,等腰直角三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,正确添加辅助线,构造全等三角形解决问题,属于中考压轴题.2.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)过D 点分别作三边的垂线,垂足分别为G 、H 、K ,根据角平分线的定义可证得DG=DH=DK ,从而根据角平分线的判定定理可证得结论;(2)作DS AC ⊥,DT BC ⊥,在AC 上取一点Q ,使QDP FDP ∠=∠,通过证明SQD TFD △≌△和QDP FDP △≌△得到22.5PDC PCD ∠=∠=︒,从而根据等角对等边判断即可;(3)延长AB 至M ,使BM BF =,连接FM ,通过证明AFC AFM △≌△得到AC AM =,再结合CE EB =即可得出结论.【详解】(1)证明:如图所示,过D 点分别作三边的垂线,垂足分别为G 、H 、K ,∵AF ,BE 分别是BAC ∠和ABC ∠的角平分线,∴DG DH DK ==,∴CD 平分ACB ∠;(2)证明:如图,作DS AC ⊥,DT BC ⊥,在AC 上取一点Q ,使QDP FDP ∠=∠. ∵CD 平分ACB ∠,∴DS DT =,∵67.5QDP FDP ∠=∠=︒,45ACB ∠=︒,∴13545180QDF ACB ∠+∠=︒+︒=︒,在四边形QDFC 中,180CQD DFC ∠+∠=︒,又∵180DFT DFC ∠+∠=︒,∴CQD DFT ∠=∠,在SQD 和TFD △中,90CQD DFT DS DT DSQ DTF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴SQD TFD △≌△,∴QD FD =,在QDP △和FDP 中QD FD QDP FDP DP DP =⎧⎪∠=∠⎨⎪=⎩∴QDP FDP △≌△,∴45QPD FPD ∠=∠=︒又∵QPD PCD PDC ∠=∠+∠,22.5PCD ∠=︒,∴22.5PDC PCD ∠=∠=︒,∴CP PD =;(3)证明:延长AB 至M ,使BMBF =,连接FM . ∵AF ,BE 分别是BAC ∠和ABC ∠的角平分线, ∴22180BAF ABE C ∠+∠+∠=︒,又∵23180BAF ABE ∠+∠=︒,∴C ABE CBE ∠=∠=∠,∴CE EB =,∵BM BF =,∴BFM BMF ABE CBE C ∠=∠=∠=∠=∠,在AFC △和AFM △中,C BMF CAF BAF AF AF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴AFC AFM △≌△,∴AC AM =,∴AE CE AB BM +=+,∴AE BE AB BF +=+,∴BE BF AB AE -=-.【点睛】本题考查角平分线的性质与判断,以及全等三角形的判定与性质,灵活结合角平分线的性质构造辅助线是解题关键.3.AB=AC+BD ,证明见详解.【分析】延长AE ,交BD 的延长线于点F ,先证明AB=BF ,进而证明△ACE ≌△FDE ,得到AC=DF ,问题得证.【详解】解:延长AE ,交BD 的延长线于点F ,∵//AC BD ,∴∠F=∠CAF ,∵AE 平分CAB ∠,∴∠CAF=∠BAF ,∴∠F=∠BAF ,∴AB=BF ,∵BE 平分ABF ∠,∴AE=EF ,∵∠F=∠CAF ,∠AEC=∠FED ,∴△ACE ≌△FDE ,∴AC=DF ,∴AB=BF=BD+DF=BD+AC .【点睛】本题考查了等腰三角形的判断与性质,全等三角形的判定与性质,根据题意添加辅助线构造等腰三角形和全等三角形是解题关键.4.40°【分析】在BC 上截取BF AB =,连接DF ,通过证明()ABD FBD SAS ≌,可得18080DFC A ︒∠=-∠=︒,再通过证明()DCE DCF SAS ≌,即可求得40ECA DCB ∠=∠=︒【详解】解:如图,在BC 上截取BF AB =,连接DF , BD 是ABC ∠的平分线,ABD FBD ∴∠=∠,在ABD △和FBD 中,,,,AB FB ABD FBD BD BD =⎧⎪∠=∠⎨⎪=⎩()ABD FBD SAS ∴△≌△,BFD A ∴∠=∠,AD DF =,∴DE=DF ,18080DFC A ∴∠=︒-∠=︒,又40ABC ACB ∠=∠=︒,60FDC ∴∠=︒,18060EDC ADB ABD A ∠=∠=︒-∠-∠=︒,EDC FDC ∴∠=∠,在DCE 和DCF 中,,,,DE DF EDC FDC DC DC =⎧⎪∠=∠⎨⎪=⎩()DCE DCF SAS ∴△≌△,故40ECA DCB ∠=∠=︒.【点睛】本题考查了全等三角形的问题,掌握全等三角形的性质以及判定定理是解题的关键. 5.28°【分析】过点E 作EF ⊥AB 于F ,根据角平分线上的点到角的两边距离相等可得DE=EF ,根据线段中点的定义可得DE=CE ,然后求出CE=EF ,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE 平分∠ABC ,即可求得∠ABE 的度数.【详解】如图,过点E 作EF ⊥AB 于F ,∵∠D=∠C=90°,AE 平分∠DAB ,DE=EF ,∵E 是DC 的中点,∴DE=CE ,∴CE=EF ,又∵∠C=90°,∴点E 在∠ABC 的平分线上,∴BE 平分∠ABC ,又∵AD ∥BC ,∴∠ABC+∠BAD=180°,∴∠AEB=90°,∴∠BEC=90°-∠AED=62°,∴Rt △BCE 中,∠CBE=28°,∴∠ABE=28°.【点睛】考查了平行线的性质与判定、角平分线上的点到角的两边距离相等的性质、到角的两边距离相等的点在角的平分线上的性质,解题关键是熟记各性质并作出辅助线.6.见解析【分析】在AB 上找到F 使得AF =AD ,易证△AEF ≌△AED ,可得AF =AD ,∠AFE =∠D ,根据平行线性质可证∠C =∠BFE ,即可证明△BEC ≌△BEF ,可得BF =BC ,即可解题.【详解】证明:在AB 上找到F 使得AF =AD ,∵AE 平分∠BAD ,∴∠EAD =∠EAF ,∵在△AEF 和△AED 中,AD AF EAD EAF AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AED ,(SAS )∴AF =AD ,∠AFE =∠D ,∵AD ∥BC ,∴∠D +∠C =180°,∵∠AFE +∠BFE =180°∴∠C =∠BFE ,∵BE 平分∠BAD ,∴∠FBE =∠C ,∵在△BEC 和△BEF 中,BFE C FBE CBE BE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEC ≌△BEF ,(AAS )∴BF =BC ,∵AB =AF +BF ,∴AB =AD +BC ,即AD =AB ﹣BC .【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AEF ≌△AED 和△BEC ≌△BEF 是解题的关键.7.见解析【分析】作BF 的中点E ,连接AE 、AD ,根据直角三角形得到性质就可以得出AE =BE =EF ,由BD 平分∠ABC 就可以得出∠ABE =∠DBC =22.5°,从而可以得出∠BAE =∠BAE =∠ACD =22.5°,∠AEF =45°,由∠BAC =90°,∠BDC =90°就可以得出A 、B 、C 、D 四点共圆,求出AD =DC ,证△ADC ≌△AEB 推出BE =CD ,从而得到结论.【详解】解:取BF 的中点E ,连接AE ,AD ,∵∠BAC =90°,∴AE =BE =EF ,∴∠ABD =∠BAE ,∵CD ⊥BD ,∴A ,B ,C ,D 四点共圆,∴∠DAC =∠DBC ,∵BF 平分∠ABC ,∴∠ABD =∠DBC ,∴∠DAC =∠BAE ,∴∠EAD =90°,∵AB =AC ,∴∠ABC =45°,∴∠ABD =∠DBC =22.5°,∴∠AED =45°,∴AE =AD ,在△ABE 与△ADC 中,ABE DAC BAE ACD AE AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ADC ,∴BE =CD ,∴BF =2CD .【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,直角三角形的性质,角平分线的性质,正确的作出辅助线是解题的关键.8.(1)CD=AD ;(2)CD=AD ;(3)BC=AD+BD.【解析】【分析】(1)由角平分线的性质可得AD=DE ,根据∠A=90°,AB=AC ,可得∠C=45°,由DE ⊥BC 可得△DEC 是等腰直角三角形,可得CD=DE ,进而可得答案;(2)在BC 上截取BE=AB ,连接DE ,利用SAS 可证明△ABD ≌△EBD ,可得AD=DE ,∠BED=∠A=120°,由等腰三角形的性质可得∠C=30°,利用三角形外角性质可得∠CDE=90°,利用含30°角的直角三角形的性质即可得答案;(3)在BC 上取一点E ,使BE=BD ,作DF ⊥BA 于F ,DG ⊥BC 于G ,由角平分线的性质就可以得出DF=DG ,利用AAS 可证明△DAF ≌△DEG ,可得 DA=DE ,利用外角性质可求出∠EDC=40°,进而可得DE=CE ,即可得出结论.【详解】(1)∵∠A=90°,BD 平分∠ABC ,DE ⊥BC ,∴DE=AD ,∵∠A=90°,AB=AC ,∴∠C=45°,∴△CDE 是等腰直角三角形,∴CD=DE=AD ,故答案为:CD=AD (2)如图,在BC 上截取BE=AB ,连接DE ,∵BD 平分∠ABC ,∴∠ABD=∠DBE ,在△ABD和△EBD中,,∴△ABD≌△EBD,∴DE=AD,∠BED=∠A=120°,∵AB=AC,∴∠C=∠ABC=30°,∴∠CDE=∠BED-∠C=90°,∴CD=DE=AD.(3)如图,在BC上取一点E,是BE=BD,作DF⊥BA于F,DG⊥BC于G,∴∠DFA=∠DGE=90°.∵BD平分∠ABC,DF⊥BA,DG⊥BC,∴DF=DG.∵∠BAC=100°,AB=AC,∴∠FAD=80°,∠ABC=∠C=40°,∴∠DBC=20°,∵BE=BD,∴∠BED=∠BDE=80°,∴∠FAD=∠BED.在△DAF和△DEG中,,∴△DAF≌△DEG(AAS),∴AD=ED.∵∠BED=∠C+∠EDC,∴80°=40+∠EDC,∴∠EDC=40°,∴∠EDC=∠C,∴DE=CE,∴AD=CE.∵BC=BE+CE,∴BC=BD+AD.【点睛】本题考查了等腰三角形的性质的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,解答时合理添加辅助线是解答本题的关键.9.见解析.【分析】延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件AD+AB=2AE可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠B=∠FDC,问题得证.【详解】证明:延长AD过C作CF垂直AD于F,∵AC平分∠BAD,∴∠FAC=∠EAC,∵CE⊥AB,CF⊥AD,∴∠AFC=∠AEC=90°,AC=AC,∴△AFC≌△AEC(AAS),∴AF=AE,CF=CE,∵AD+AB=2AE,又∵AD=AF−DF,AB=AE+BE,AF=AE,∴2AE=AE+BE+AE−DF,∴BE=DF,在△CDF和△CBE中,CF CECFD CEBDF BE⎧⎪∠∠⎨⎪⎩===,∴△CDF≌△CBE(SAS),∴∠B=∠FDC,∵∠ADC+∠FDC=180°,∴∠ADC+∠B=180º.【点睛】本题考查了全等三角形的判定与性质,解题的关键是牢记三角形全等的判定定理.10.50°【解析】【分析】根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP ,即可得出答案.【详解】延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD=x°,∵CP 平分∠ACD ,∴∠ACP=∠PCD=x°,PM=PN ,∵BP 平分∠ABC ,∴∠ABP=∠PBC ,PF=PN ,∴PF=PM ,∵∠BPC=40°,∴∠ABP=∠PBC=∠PCD-∠BPC=(x-40)°,∴∠BAC=∠ACD-∠ABC=2x°-(x°-40°)-(x°-40°)=80°,∴∠CAF=100°,在Rt △PFA 和Rt △PMA 中,PA PA PM PF =⎧⎨=⎩, ∴Rt △PFA ≌Rt △PMA(HL),∴∠CAP=∠FAP ,又∵∠CAP+∠PAF=∠CAF ,∴∠CAP =50°.【点睛】本题主要考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF 是解决问题的关键.。

第 7 讲全等三角形的综合、角均分线第一部分知识梳理知识点一:全等三角形的综合⑴ 平移全等型⑵ 对称全等型⑶ 旋转全等型知识点二:角均分线的性质⑴、角均分线上的点到角的两边的距离相等;⑵、到角的两边距离相等的点在角的均分线上.它们拥有互逆性.角均分线是天然的、波及对称的模型,一般状况下,有以下三种作协助线的方式:1.由角均分线上的一点向角的两边作垂线,2.过角均分线上的一点作角均分线的垂线,进而形成等腰三角形,3.OA OB ,这类对称的图形应用得也较为广泛,A A AO O O PP PBB B知识点三:角均分线的作法角均分线的作法(尺规作图)①以点 O 为圆心,随意长为半径画弧,交OA、OB 于 C、 D 两点;②分别以 C、 D 为圆心,大于 CD长为半径画弧,两弧交于点P;③过点 P 作射线 OP,射线 OP 即为所求.第二部分考点精讲精练考点 1、三角形全等综合1、全等三角形实质应用1、如图,要测量河两岸相对的两点A、B 间的距离,先在过 B 点的 AB 的垂线 L 上取两点 C、D,使 CD=BC,再在过 D 点的垂线上取点E,使 A、C、E 在一条直线上,ED=AB这时,测 ED的长就得 AB 得长,判断△ACB≌△ECD的原因是()A. SASB. ASAC. SSS D .AAS2、如图,小强利用全等三角形的知识测量池塘两头M 、 N 的距离,假如△ PQO≌△ NMO,则只需测出其长度的线段是(B)A. PO B.PQ C.MO D. MQ(1)(2)3、如图,工人师傅要在墙壁的 O 处用钻打孔,要使孔口从墙壁对面的点 B 处翻开,墙壁厚是 35cm,点 B 与点 O 的垂直距离 AB 长是 20cm,在点 O 处作向来线平行于地面,在直线上截取 OC=35cm,过 C作 OC的垂线,在垂线上截取 CD=20cm,连结 OD,而后,沿着 D0 的方向打孔,结果钻头正好从点 B 处打出.这是什么道理?4、1805 年,法军在拿破仑的带领下与德军在莱茵河边激战.德军在莱茵河北岸Q处,以下图,因不知河宽,法军大炮很难对准敌营.聪慧的拿破仑站在南岸的点 O 处,调整好自己的帽子,使视野恰巧擦着帽舌边沿看到对面德国军营Q 处,而后他一步一步退后,向来退到自己的视野恰巧落在他刚才站立的点0 处,让士兵测量他所站立地点 B 与 0 点的距离,并命令依据这个距离炮轰德军.试问:法军能命中目标吗?请说明原因.用帽舌边沿视野法还能够如何测量,也能测出河岸两边的距离吗?5、某校七年级学生到野外活动,为测量一池塘两头A, B 的距离,甲、乙、丙三位同学分别设计出以下几种方案:甲:如图①,先在平川取一个可直接抵达A,B 的点 C,再连结 AC,BC,并分别延伸 AC至 D,BC至 E,使 DC=AC,EC=BC,最后测出 DE的长即为 A,B 的距离.乙:如图②,先过点 B 作 AB 的垂线 BF,再在 BF 上取 C,D 两点,使 BC=CD,接着过点 D 作 BD 的垂线 DE,交 AC的延伸线于点 E,则测出 DE的长即为 A,B 的距离.丙:如图③,过点 B 作 BD⊥AB,再由点 D 观察,在 AB 的延伸线上取一点 C,使∠BDC=∠BDA,这时只需测出 BC的长即为 A,B 的距离.(1)以上三位同学所设计的方案,可行的有 ______;(2)请你选择一可行的方案,谈谈它可行的原因.2、证两次全等有关问题1、已知 : 如图 ,AB=AE,BC=ED,∠B= ∠E,AF⊥CD,F 为垂足 , 求证 :CF=DF.2、已知:如图, AB=CD,BC=DA,AE=CF.求证: BF=DE.3、如图, AB=AD, BC=DE,且 BA⊥AC,DA⊥AE,你能证明 AM=AN 吗?3、探究两线段的关系问题1、以下图,已知 AE⊥AB,AF⊥ AC,AE=AB,AF=AC. 求证:( 1)EC=BF;(2)EC⊥BF.2、已知:如图,△ABC中, AD⊥BC于 D,E 是 AD 上一点, BE的延伸线交 AC 于 F,若 BD=AD, DE=DC。

专题07最短路径问题两条线段之和1.如图,点A 、B 在直线l 的同一侧.(1)如图①,在直线l 上找一点P ,使得PA PB (尺规作图,保留作图痕迹)(2)如图②,请借助三角尺和刻度尺在直线l 上找一点Q ,使得QA QB 最短.【答案】(1)见解析(2)见解析【分析】(1)连接AB ,作AB 的垂直平分线,与直线l 交于点P ;(2)利用工具作出点A 关于直线l 的垂线并延长,使得1AC A C ,连接1A B ,与直线l 交于点Q .【详解】(1)解:如图,点P 即为所求;(2)如图,点Q 即为所求.【点睛】本题考查了垂直平分线的作法和性质,最短路径问题,解题的关键是理解知识点,掌握相应的作图方法.2.如图,在ABC 中,AB 的垂直平分线EF 分别交AB AC 、边于点E 、F ,点K 为EF 上一动点,则BK CK 的最小值是以下哪条线段的长度()A .EFB .ABC .ACD .BC【答案】C 【分析】连接AK ,根据线段垂直平分线的性质得到AK BK ,求得BK CK AK CK ,得到AK CK 的最小值BK CK 的最小值,于是得到当AK CK AC 时,AK CK 的值最小,即BK CK 的值最小,即可得到结论.【详解】解:连接AK ,EF ∵是线段AB 的垂直平分线,AK BK ,BK CK AK CK ,AK CK 的最小值BK CK 的最小值,AK CK AC ∵,当AK CK AC 时,AK CK 的值最小,即BK CK 的值最小,BK CK 的最小值是线段AC 的长度,故选:C .【点睛】本题考查的是轴对称 最短路线问题,线段垂直平分线的性质,三角形的三边关系,熟知线段垂直平分线的性质是解答此题的关键.3.如图,在ACD 中,AB =AC =7,AD =8.3,点E 在AD 上,CE =CB ,CF 平分∠BCE 交AD 于点F .点P 是线段CF 上一动点,则EP +AP 的最小值为()A .6B .7C .7.5D .8.3【答案】B 【分析】连接BP ,由ECP BCP ≌得BP EP ,EP AP BP AP +,根据BP AP AB 知,当点P 在线段AB 上时,EP AP +的最小值是AB ,问题得解.【详解】解:连接BP ,CF ∵平分BCE 交AD 于点F ,ECP BCPCE CB ∵,CP CP ,ECP BCP SAS ≌,BP EP ,EP AP BP AP ∵+且BP AP AB ,当点P 在线段AB 上时,EP AP +的最小值是AB ,7AB ∵,EP AP +的最小值为7.故选:B【点睛】本题考查了轴对称图形的性质,两点之间线段最短,其中准确作出点关于对称轴对称的对称点是解题的关键.4.如图,ABC 的面积是2150cm ,最长边30cm AB ,AD 平分BAC ,点M ,N 分别是AD ,AC 上的动点,则CM MN 的最小值为cm .【答案】10【分析】过点C 作CE AB 于点E ,交AD 于点M ,过点M 作MN AC 于N ,则CE 的长即为CM MN 的最小值,再根据三角形的面积公式求出CE 的长即可.【详解】解:过点C 作CE AB 于点E ,交AD 于点M ,过点M 作MN AC 于N ,AD ∵平分BAC ,CE AB 于点E ,MN AC 于N ,ME MN ,CE CM ME CM MN ,根据垂线段最短可知,CE 的长即为CM MN 的最小值,∵ABC 的面积是2150cm ,最长边30cm AB ,1301502CE ,10CE ,即CM MN 的最小值为10.故答案为:10.【点睛】本题考查轴对称——最短路径问题,关键是根据垂线段最短将CM MN 的最小值转化为CE .5.如图,在等腰ABC 中,AB AC ,7BC ,作AD BC 于点D ,12AD AB,点E 为AC 边上的中点,点P 为BC 上一动点,则PA PE 的最小值为.【答案】72【分析】作点A 关于BC 的对称点A ,延长AD 至A ,使AD A D ,连接A E ,交BC 于P ,此时PA PE 的值最小,就是A E 的长,证明A E CD 即可.【详解】解:作点A 关于BC 的对称点A ,延长AD 至A ,使AD A D ,连接A E ,交BC 于P ,此时PA PE 的值最小,就是A E 的长,∵AB AC ,7BC ,AD BC ,72BD CD ,∵12AD AB ,30B ,60BAD CAD ,∵AD A D ,AA C 是等边三角形,∵点E 为AC 边上的中点,A E AC ,72A E CD ,即PA PE 的最小值为72,故答案为:72.【点睛】本题考查了轴对称,最短路径问题和直角三角形的性质,解题的关键是根据轴对称的性质作出对称点,掌握线段垂直平分线的性质和等边三角形的性质与判定的灵活运用.6.如图,等边ABC 和等边A B C △的边长都是4,点B C B ,,在同一条直线上,点P 在线段A C 上,则AP BP 的最小值为.【答案】8【分析】连接PE ,根据ABC 和A B C △都是边长为4的等边三角形,证明ACP B CP △≌△,可得AP B P ,所以AP BP BP B P ,进而可得当点P 与点C 重合时,AP BP 的值最小,正好等于BB 的长,即可求解.【详解】解:如图,连接PB ,∵ABC 和A B C △都是边长为4的等边三角形,∴60AC B C ACB A CB ,,∴60ACA ,∴ACA A CB ,在ACP △和B CP △中,AC B C ACA A CB CP CP,∴ SAS ACP B CP △≌△,∴AP B P ,∴AP BP BP B P ,∴当点P 与点C 重合时,点A 与点B 关于A C 对称,AP BP 的值最小,正好等于BB 的长,∴AP BP 的最小值为448 ,故答案为:8.【点睛】本题考查了轴对称—最短路线问题、全等三角形的判定和性质和等边三角形的性质,灵活运用所学知识求解是解决本题的关键.周长之和7.如图,等腰三角形ABC 的底边BC 长为4,面积是16,腰AC 的垂直平分线EF 分别交AC ,AB 边于E ,F 点,若点D 为BC 边的中点,点M 为线段EF 上一动点,则CDM V 周长的最小值为()A .12B .8C .10D .20【答案】C【分析】连接AD ,由于ABC 是等腰三角形,点D 是BC 边的中点,故AD BC ,再根据三角形的面积公式求出AD 的长,再根据EF 是线段AC 的垂直平分线可知,点C 关于直线EF 的对称点为点A ,故AD 的长为CM MD 的最小值,由此即可得出结论.【详解】解:连接AD ,∵ABC 是等腰三角形,点D 是BC 边的中点,∴AD BC ,122CD BC,∴1141622ABC S BC AD AD △,解得8AD ,∵EF 是线段AC 的垂直平分线,∴点C 关于直线EF 的对称点为点A ,∴AD 的长为CM MD 的最小值,∴CDM V 周长的最小值为8210CM MD CD AD CD .故选:C .【点睛】本题考查的是轴对称——最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.8.如图,边长为a 的等边ABC 中,BF 是AC 上中线且BF b ,点D 在BF 上,连接AD ,在AD 的右侧作等边ADE V ,连接EF ,则AEF △周长的最小值是()A .1223a b B .12a b C .12a +b D .32a 【答案】B【分析】由题意等边三角形性质和全等三角形判定得出 SAS BAD CAE ≌△△,进而作点A 关于直线CE 的对称点M ,连接FM 交CE 于E ,此时AE FE 的值最小,最后依据AEF △周长的最小值AF FE AE AF FM 求值即可得出答案.【详解】解:如图,∵ABC ADE △,△都是等边三角形,∴60AB AC a AD AE BAC DAE ABC,,∴BAD CAE∴SAS BAD CAE ≌△△∴ABD ACE∵12AF CF a BF b ,∴30ABD CBD ACE BF AC,∴点E 在射线CE 上运动(30ACE ),作点A 关于直线CE 的对称点M ,连接FM 交CE 于E ,此时AE FE 的值最小,∵60CA CM ACM,∴ACM △是等边三角形,∴AM AC∵BF AC∴FM BF b∴AEF △周长的最小值12AF FE AE AF FM a b.故选:B .【点睛】本题考查轴对称最短路径问题和等边三角形的性质和判定以及全等三角形的判定和性质等知识,解题的关键是利用轴对称性质得出AE FE 的值最小.角度问题9.如图,在五边形ABCDE 中,120BAE ,90B E ,AB BC ,AE DE ,在BC 、DE 上分别找到一点M 、N ,使得AMN 的周长最小,则AMN ANM +的度数为()A .100B .110C .120D .130【答案】C 【分析】根据要使AMN 的周长最小,即利用点的对称,让三角形的三边在同一直线上,A 关于BC和ED 的对称点'A ,''A ,即可得出''''60A A HAA ,进而得出 '''+2AMN ANM A A 即可得出答案.【详解】解:作A 关于BC 和ED 的对称点'A ,''A ,连接'A ,''A ,交BC 于M ,交ED 于N ,则'A ,''A 即为AMN 的周长最小值.作EA 延长线AH ,∵120BAE ,∴'60HAA ,∴''''60A A HAA ,∵''A MAA ,''A NAE ,且''A MAA AMN ,''A NAE ANM ,∴ '''''''+2260120A MAA NAE A AMN ANM A A ,故选:C .【点睛】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M ,N 的位置是解题关键.110.如图,22AOB ,点M ,N 分别是边OA ,OB 上的定点,点P ,Q 分别是边OA ,OB 上的动点,记MQP ,OPN ,当MQ QP PN 最小时,则α与β的数量关系为.【答案】44【分析】作M 关于OB 的对称点M ,N 关于OA 的对称点N ,连接M N 交OA 于P ,交OB 于Q ,则MQ QP PN 最小,易知OQM OQM NQP ,OPQ APN APN ,根据三角形的外角的性质和平角的定义即可得到结论.【详解】解:如图,作M 关于OB 的对称点M ,N 关于OA 的对称点N ,连接M N 交OA 于P ,交OB 于Q ,则MQ QP PN 最小,∴OQM OQM NQP ,OPQ APN APN ,∴ 111802218022PQN AOB MPQ ,∴44 ,故答案为:44 .【点睛】本题考查轴对称—最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题.11.如图,在Rt ABC △中,90ACB ,AC BC ,点C 在直线MN 上,30BCN ,点P 为MN 上一动点,连接AP ,BP .当AP BP 的值最小时,CBP 的度数为度.【答案】15【分析】如图,作B 关于MN 的对称点D ,连接,,AD BD CD ,AP BP 的值最小,则MN 交AD 于P ,由轴对称易证CBP CDP ,结合30BCN 证得BCD △是等边三角形,可得AC CD ,结合已知根据等腰三角形性质可求出CDP ,即可解决问题.【详解】如图,作B 关于MN 的对称点D ,连接,,AD BD CD ,AP BP ∵的值最小,则MN 交AD 于P ,由轴对称可知:CB CD ,PB PD ,,,CBD CDB PBD PDB CBP CDP ,30BCN ∵,260BCD BCN ,BCD △是等边三角形,AC BC ∵,AC CD ,CAD CDA ,90ACB ∵,60BCD ,1180152CAD CDA ACB BCD ,15CBP CDP ,故答案为:15.【点睛】本题考查等边三角形判定和性质、轴对称的性质、最短路径问题、等腰三角形的性质;熟练掌握相关性质的联系与运用,会利用最短路径解决最值问题是解答的关键.12.如图,在三角形ABC 中,50BAC ,AB AC ,BD AC 于D ,M ,N 分别是线段BD ,BC 上的动点,BM CN ,当AM AN 最小时,MAD .【答案】12.5【分析】在BC 下方作CNA ,使CNA BMA ≌,连接AA ,则AM AN 最小值为AA ,此时A 、N 、A 三点在同一直线上,推出18010537.52A AC A,所以37.5BAM ,即可得到5037.512.5MAD BAC BAM .【详解】解:在BC 下方作CNA ,使CNA BMA ≌,连接AA .则NCA MBA ,AM A N .∴AM AN A N AN AA ,即AM AN 最小值为AA ,此时A 、N 、A 三点在同一直线上.∵50BAC ,AB AC ,∴65ACB ABC ,∵BD AC ,∴905040ABD ,∴40NCA ,∴6540105ACA ,∴18010537.52A AC A ,∴37.5BAM ,∴5037.512.5MAD BAC BAM ,故答案为:12.5 .【点睛】本题考查了最短路线问题以及等腰三角形的性质的运用,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.13.如图,点(,0),(0,)A a B b ,且a ,b 满足2(1)|22|0a b .若P 为x 轴上异于原点O 和点A 的一个动点,连接PB ,以线段PB 为边构造等腰直角BPE (P 为顶点),连接AE .(1)如图1,直接写出点A 的坐标为___________,点B 的坐标为___________;(2)如图2,当点P 在点O ,A 之间时,连接BE ,AE ,证明BA AE ;(3)如图3,点P 在x 轴上运动过程中,若AE 所在直线与y 轴交于点F ,请直接写出F 点的坐标为___________,当OE BE 的值最小时,请直接写出此时OE 与BE 之间的数量关系___________.【答案】(1)(1,0),(0,1)(2)见解析(3)(0,1) ,2 BE OE【分析】(1)根据非负数的性质得到1a ,1b ,得到1OA ,1OB ,于是得到结果;(2)过点E 作EH x 轴于H ,证明(AAS)BOP PHE △≌△,由全等三角形的性质得出1OB PH OA ,OP EH ,由等腰直角三角形的性质得出45OAB ,证出90EAB ,则可得出结论;(3)由直角三角形的性质证出1OA OF ,则可得出(0,1)F ;取点(1,1)G ,连接FG ,OG ,O 与G 关于直线AF 对称,连接BG 交AF 于E ,连接OE ,则OE EG ,根据三角形的面积关系可得出2 BE OE .【详解】(1)解:2(1)|22|0a b ∵,10a ,220b ,1a ,1b ,(1,0)A 、(0,1)B ,故答案为:(1,0),(0,1);(2)证明:过点E 作EH x 轴于H ,BPE ∵ 是等腰直角三角形,BP PE ,90BPE ,90BPO EPH ,90OBP BPO ∵,OBP EPH ,又90BOP PHE ∵,(AAS)BOP PHE △≌△,1OB PH OA ,OP EH ,OP PA PA AH ,OP AH ,EH AH ,又90AHE ∵,45HAE ,OA OB ∵,90AOB ,45OAB ,90EAB ,BA AE ;(3)BA AE ∵,90BAF ,OA OB ∵,45BAO ,45OAF \Ð=°,90AOF ∵,45OAF OFA ,1OA OF ,(0,1)F ;取点(1,1)G ,连接FG ,OG ,(0,1)F ∵,45OFA AFG ,O 与G 关于直线AF 对称,连接BG 交AF 于E ,连接OE ,则OE EG ,此时OE BE 最小,OE BE EG BE BG ,E ∵到FB ,FG 的距离相等,2BF ,1FG ,2BFE GFE S S △△,2BE EG ,2BE OE .故答案为:(0,1) ,2 BE OE .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,坐标与图形的性质,,等腰直角三角形的判定与性质,三角形的面积等知识点,正确的作出辅助线是解题的关键.14.如图,在Rt ABC △中,90ACB ,60A ,4AC ,CD 平分ACB ,交边AB 于点D ,点E 是边AB 的中点.点P 为边CB 上的一个动点.(1)AE ______,ACD ______度;(2)当四边形ACPD 为轴对称图形时,求CP 的长;(3)若CPD △是等腰三角形,求CPD 的度数;(4)若点M 在线段CD 上,连接MP 、ME ,直接写出MP ME 的值最小时CP 的长度.【答案】(1)4;45(2)4(3)90 或45 或67.5(4)2【分析】(1)根据题意可得30B ,则28AB AC ,即可求得AE 的长,再根据CD 平分ACB ,即可求得ACD 的度数;(2)根据轴对称图形的性质可得答案;(3)根据题意可得45PCD ,分三种情况:PC PD ,DP DC ,CP CD ,再结合三角形内角和定理即可求解;(4)过点M 作MP BC ,点P 关于CD 的对称点P ,根据题意可得PCM P CM ,CM CM ,根据AAS ,可得PCM P CM ≌,则PM P M ,CP CP ,因此MP ME MP ME EP ,以此得点E ,M ,P 三点共线时,MP ME 的值最小,此时EP BC ∥,最后根据解含30度角的直角三角形即可得到结果.【详解】(1)解:∵90ACB ,60A ,18030B ACB C ,28AB AC ,∵点E 是边AB 的中点,142AE AB ∵CD 平分ACB ,1452ACD ACB ,故答案为:4;45.(2)∵四边形ACPD 为轴对称图形,CD 平分ACB ,∴对称轴为直线CD ,∴4CP CA .(3)∵CD 平分ACB ,90ACB ,∴45PCD .当PC PD 时,45PDC PCD ,∴180454590CPD ;当DP DC 时,45CPD PCD ;当CP CD 时, 18045267.5CPD CDP .综上所述,CPD 的度数为90 或45 或67.5 .(4)如图,点M 在CD 上,且MP BC ,作点P 关于CD 的对称点P ,MP BC ∵,MP AC ,∵CD 平分ACB ,PCM P CM ,在PCM △和P CM 中,MPC MP C PCM P CM CM CM, (AAS)PCM P CM ≌PM P M ,CP CPMP ME MP ME EP ∵,当点E ,M ,P 三点共线时,MP ME 的值最小,又∵根据垂线段最短,当EP AC 时,EP 有最小值, EP BC ∥,30AEP B ,90AP E ACB 4AE ∵,122AP AE ,2CP CP AC AP .【点睛】本题主要考查轴对称——最短路径问题,全等三角形的判定与性质,等腰三角形的性质,含30度角的直角三角形,角平分线的性质,本题综合性较强,作出辅助线,找到最短路径是解题关键.。

最新人教版数学八年级上册最短路径问题最短路径问题求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求。
例如,在图中,点A、B分别在直线l异侧,需要在直线l上找一个点C,使得CA + CB最小,此时点C是直线l与AB的交点。
类似地,求直线同侧的两点与直线上一点所连线段的和最小的问题,只需找到其中一个点关于这条直线的对称点,连接对称点与另一个点,与该直线的交点即为所求。
例如,在图中,点A、B分别在直线l同侧,需要在直线l上找一个点C,使得CA + CB最小,此时先作点B关于直线l的对称点B',则点C是直线l与AB'的交点。
为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C',连接AC'、BC'、B'C',证明AC + CB < AC' +C'B。
具体证明过程可参考下图:在解决距离最短问题时,可以运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长。
无论题目如何变化,核心思路都是直线同旁有两点,这两点到直线上某点的距离和最小。
因此,所有作法都相同。
需要注意的是,在利用轴对称解决最值问题时,应注意题目要求,根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法。
在解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,以免导致答案不符合要求。
另外,利用平移也可以确定最短路径选址。
具体做法是,在地图上选定起点和终点,将地图平移到起点与终点连线的中点处,然后在平移后的地图上连接起点和终点,最短路径即为连接线段。
选址问题的关键在于将多条线段转化为一条线段。
如果两个点在一条直线的同侧,那么过这两个点的直线与原直线的交点处构成的线段的差最大;如果两个点在一条直线的异侧,那么过这两个点的直线与原直线的交点处构成的线段的和最小。
这些问题都可以通过三角形的三边关系来解释,通常可以选择其中一个点的对称点来解决最大值或最小值的情况。

初二数学期中复习要点
初二数学期中复习要点
全等三角形有如下性质:
(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;
(3)全等三角形的对应中线、对应角平分线、对应高相等;(4)全等三角形的面积相等,周长相等.
判定两个三角形全等的依据:
(1)边边边公理(SSS):三条边对应相等的'两个三角形全等
(2)边角边公理(SAS):两边及其夹角对应相等的两个三角形全等;
(3)角边角公理(ASA):两角及其夹边对应相等的两个三角形全等;
(4)(角边角公理的推论(AAS):两角和其中一角的对边对应相等的两个三角形全等;
(5)斜边、直角边公理(HL):斜边和一直角边对应相等的两个三角形全等.
全等三角形对应边对应角找法:
①、对应角所对的边是对应边;对应边所对的角是对应角。
②、公共边是对应边;公共角(对顶角)是对应角。
③、相等的边是对应边;相等的是对应角。
④、最大(小)边与最大(小)边是对应边;最大(小)角与最大(小)角是对应角。
⑤、对应角所夹的边是对应边;对应边所夹的角是对应角。

第十一章:全等三角形复习一全等三角形1、什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?能够完全重合的两个三角形叫做全等三角形。
一个三角形经过平移、翻折、旋转可以得到它的全等形。
2、全等三角形有哪些性质?(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3、一般三角形全等的条件(包括直角三角形):(1)定义(重合)法;(2)SSS:三边对应相等的两个三角形全等;(3)SAS:两边和它们的夹角对应相等两个三角形全等;(4)ASA:两角和它们的夹边对应相等的两个三角形全等;(5)AAS:两角和其中一角的对边对应相等的两个三角形全等。
解题常用后面四种方法。
直角三角形全等特有的条件:HL(斜边和一条直角边对应相等的两个直角三角形全等)。
4、证明两个三角形全等的基本思路:(1)已知两边:a、找第三边(SSS);b、找夹角(SAS);c、找是否有直角(HL)。
(2)已知一边一角:①已知一边和他的邻角:a、找这边的另一个邻角(ASA);b、找这个角的另一个边(SAS);c、找这边的对角 (AAS)。
②已知两角:a、找两角的夹边(ASA);b、找夹边外的任意边(AAS)。
二角平分线1、角平分线的性质:角的平分线上的点到角的两边的距离相等。
2、角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上。
用法1:∵ QD⊥OA,QE⊥OB 用法2:∵ QD⊥OA,QE⊥OB,QD=QE。
∴点Q在∠AOB的平分线上。
∴点Q在∠AOB的平分线上∴ QD=QE3、总结提高:学习全等三角形应注意以下几个问题(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4)时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”。
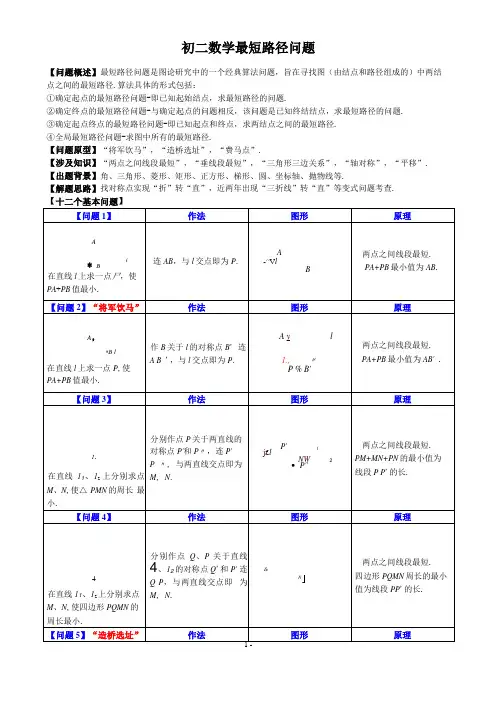
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】A・*B l在直线l上求一点P,使|PA—PB|的值最大. 作直线AB,与直线l的交点即为P.--^^lP三角形任意两边之差小于第三边.pA^i - PB W AB.|PA- PB|的最大值一AB .【问题11]作法图形原理Al■B在直线l上求一点P,使|PA—PB|的值最大. 作B关于l的对称点B' 作直线A B"与l交点即为P.—r^lB三角形任意两边之差小于第三边.pA^i - PB\ W AB ;|PA—PB| 最大值一AB【问题12]“费马点”作法图形原理A zAB C△ ABC中每一内角都小于120°,在4ABC内求一点P,使PA+PB+PC值最小. 所求点为“费马点”,即满足N APB =N BPC =NAPC =120° .以AB、AC 为边向外作等边^ ABD、△ACE,连CD、BE相交于P,点P即为所求.D"一B C两点之间线段最短.PA+PB+PC最小值一CD.【精品练习】1.如图所示,正方形ABCD的面积为12,八ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点尸,使PD+PE的和最小,则这个最小值为()A. 2V3B.2V16C. 3D. v162.如图,在边长为2的菱形ABCD中,N ABC=60°, 交于点E、F,则△ CEF的周长的最小值为()A. 2B. 2t3C. 2 + J3D. 4若将^ACD绕点A旋转,当AC、AD,分别与BC、CD3.四边形ABCD 中,N B =/D = 90°,N C =70°,在BC 、CD 上分别找一点M 、乂使^ AMN 的周长最小时,上的动点,则BM +MN 的最小值是5 .如图,Rt △ ABC 中,N C =90°,N B = 30°, AB = 6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合),且ED =AE ,则线段AE 的取值范围是6 .如图,N AOB = 30°,点M 、N 分别在边OA 、OB 上,且OM =1, ON =3,点P 、Q 分别在边OB 、OA 上, 则MP +PQ + QN 的最小值是.(注”勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt △ ABC 中,N C =90°,则有 AC 2 + BC 2 = AB 2 )7 .如图,三角形"BC 中,N OAB =N AOB = 15°,点B 在%轴的正半轴,坐标为B (6<3 , 0).OC 平分N AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是/AMN +N ANM 的度数为( A . 120°B . 130°)C . 110°D . 140°4.如图,在锐角^ABC 中,AB = 4v2 ,N BAC =45°,N BAC 的平分线交BC 于点D , M 、N 分别是AD 和AB8.已知A (2, 4)、B (4, 2). C在y轴上,D在%轴上,则四边形ABCD的周长最小值为此时C、D两点的坐标分别为9.已知A (1, 1)、B (4, 2).(1)P为%轴上一动点,求PA+PB的最小值和此时P点的坐标;(2)P为%轴上一动点,求|PA PB|的值最大时P点的坐标;(3)CD为%轴上一条动线段,D在C点右边且CD =1,求当AC + CD+DB的最小值和此时C点的坐标;10.点C为N AOB内一点.(1)在OA求作点D, OB上求作点E,使△ CDE的周长最小,请画出图形;(2)在(1)的条件下,若N AOB = 30°, OC =10,求4CDE周长的最小值和此时N DCE的度数.如图①,△ ABD 和^ACE 均为等边三角形,BE 、CE 交于凡连AF ,求证:AF +BF + CF = CD ;在^ABC 中,N ABC =30°, AB = 6, BC =8,N A ,N C 均小于 120°,求作一点尸,使 PA+PB+PC 的12.荆州护城河在CC '处直角转弯,河宽相等,从A 处到达B 处,需经过两座桥DD '、EE ',护城河及两桥 都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,11. (1) (2) 值最小, 试求出最小值并说明理由.图①。
八年级期中数学易考知识点在八年级数学的学习中,期中考试是至关重要的一环。
对于学生来说,熟练掌握数学易考知识点是取得好成绩的关键。
下面就让我们来看看八年级期中数学易考知识点有哪些。
一、代数部分1.一元一次方程与解法一元一次方程,顾名思义就是只有一个未知数的一次方程式。
解一元一次方程的基本步骤是先系数化,再移项,最后化简,得到未知数的值。
2.二元一次方程组与解法二元一次方程组也是我们常见的方程,就是由两个未知数和两个方程构成的方程组。
常见的解法有代入法、消元法和图解法等。
3.整式及其加减乘除整式是由项按照一定的规则聚合得到的代数式,整式的加减乘除运算是我们必须掌握的知识点之一。
其中,乘法的运算法则需要我们熟练掌握并且能够熟练运用。
二、几何部分1.全等三角形的判定全等三角形是指两个三角形的对应边和对应角相等。
常用的判定方法有SSS、SAS、ASA和AAS等。
2.相似三角形的判定相似三角形是指两个三角形的对应角相等,但是对应的边长不一样。
常用的判定方法有AA、SAS和SAA。
3.角平分线定理角平分线定理是与三角形有关的一个定理,这个定理指的是三角形内一条角平分线所分割的两个角的大小之比等于与这条角平分线相关的两边的长度之比。
三、立体几何部分1.棱柱体、棱锥体和圆柱体的计算对于常见的立体几何形体,比如棱柱体、棱锥体和圆柱体等,我们需要熟练掌握它们的面积和体积的计算方法。
2.表面积和体积的计算表面积和体积是我们在学习立体几何中常见的计算内容。
要求学生掌握基本的公式,并且能够巧妙应用,灵活计算。
以上就是八年级期中数学易考知识点的部分内容,希望同学们能够认真学习并且做好相关的练习题,早日掌握这些知识点,取得更好的成绩。
初中数学几何综合大题压轴讲义——最短路径、线段最值先上整篇目录:
一、最短路径
在初中的平面几何中,有一类求最短路径的问题,比较常见的类型可以称为“将军饮马”问题。
这类题在题型上比较典型,一般是求线段和(通常是两条线段,少见三条线段)的最小值。
在解决问题的方法上也是比较典型,即通过对称,借助”两点之间,线段最短”解决问题。
经典问题再现
详细解答过程
对于求线段和最小值的问题,通常都是借助对称来完成的,不同的是,如果是求两条线段的最小值,一般可以通过作一次对称解决;如果是求三条线段和的最小值,通常需要作两次对称才可以解决。
作对称的目的,是要把所求线段的最值转化为两点之间的距离。
与垂线段的结合:
垂线段最短
练习
二、线段最值
在众多的中考试题类型当中,有一类题目是求某一条线段的最值。
实际上,初中阶段有关最值的题目类型比较单一。
比较常见的解题思路之一是构造函数,利用函数求最值;解题思路之二是直线外一点到
直线上所有点的连线中,垂线段最短;还有一种解题思路是构遺三角形,利用第三条边与另外两条边的数量关系确定最值。
这一节,我们主要来研究后者。
全等三角形章末复习整理知识点1、全等三角形的概念与性质1、能够的两个三角形叫做全等三角形。
2、全等三角形的对应边,对应角。
全等三角形对应边上的、、相等。
全等三角形的周长,面积。
知识点2、全等三角形的判定1、三边的两个三角形全等,简写成“边边边”或“SSS”。
2、两边和它们的对应相等的两个三角形全等,简写成“边角边”或“SAS”。
3、两角和它们的对应相等的两个三角形全等。
简写为“角边角”或“ASA”4、两角和其中一角的对应相等的两个三角形全等。
简称“角角边”或“AAS”。
5、斜边和对应相等的两个直角三角形全等。
简写成“斜边直角边”或“HL”。
方法指引:知识点3、角平分线的性质1、角平分线上的点到角的两边的距离。
2、角的内部到角的两边的距离相等的点在上。
二、基本题型1、如图,∠DAB=∠EAC=65°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是___.第1题图第2题图第3题图第4题图2、如图,在平面直角坐标系中,有一块含450角的直角三角板如图放置,其中∠ACB=90°,AC=BC点C的坐标为(-2,0),点A的坐标为(1,4),则点B的坐标为.3、如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45∘角的直角三角板如图放置,顶点A. B. C 恰好分别落在三条直线上,则△ABC的面积为___.4、如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动。
若当△BPD与△CQP全等时,则点Q运动速度可能为___厘米/秒。
5、已知如图,在△ABC中,AB=2AC,AD是∠BAC的角平分线,且AD=BD.求证:∠ADB=2∠ADC.6、如图,在△ABC中,∠ACB=90°,AC=BC,AD是角平分线,BE⊥AD交AD的延长线于点E,求证:AD=2BE.7、如图,△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=5,AC=3,求AD的取值范围.8、如图.AB=AE,AB⊥AE,AD=AC.AD⊥AC,点M为BC的中点,求证:DE=2AM.9、如图,AD为△ABC的中线,E为AD上一点,BE=AC,BE的延长线交AC于F,FG⊥AD于G.求证:AG=EG.10、如图,D为CE的中点,F为AD上一点,且EF=AC.求证:∠DFE=∠DAC.11、(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120∘,∠B=∠ADC=90∘.E,F分别是BC,CD上的点,且∠EAF=60∘,请探究图中线段BE,EF,FD之间的数量关系是什么?小明探究此问题的方法是:延长FD到点G,使DG=BE,连结AG.先证明△ABE≌△ADG,得AE=AG;再由条件可得∠EAF=∠GAF,证明△AEF≌△AGF,进而可得线段BE,EF,FD之间的数量关系是___.(2)拓展应用:如图2,在四边形ABCD中,AB=AD,∠B+∠D=180∘.E,F分别是BC,CD上的点,且∠EAF=12∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由。
初二数学全等三角形角平分线辅助知识点-+典型题及解析一、全等三角形角平分线辅助1.已知:如图,//AC BD ,AE ,BE 分别平分CAB ∠和ABD ∠,点E 在CD 上.用等式表示线段AB 、AC 、BD 三者之间的数量关系,并证明.2.在ABC 中,60A ∠=︒,BD ,CE 是ABC 的两条角平分线,且BD ,CE 交于点F .(1)如图1,用等式表示BE ,BC ,CD 这三条线段之间的数量关系,并证明你的结论;小东通过观察、实验,提出猜想:BE CD BC +=.他发现先在BC 上截取BM ,使BM BE =,连接FM ,再利用三角形全等的判定和性质证明CM CD =即可. ①下面是小东证明该猜想的部分思路,请补充完整:ⅰ)在BC 上截取BM ,使BM BE =,连接FM ,则可以证明BEF 与 全等,判定它们全等的依据是 ;ⅱ)由60A ∠=︒,BD ,CE 是ABC 的两条角平分线,可以得出EFB ∠= °; ②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想BE CD BC +=的过程. (2)如图2,若40ABC ∠=︒ ,求证:BF CA =.3.如图,矩形ABCD 中,AB=4,AD=3,∠A 的角平分线交边CD 于点E .点P 从点A 出发沿射线AE 以每秒2个单位长度的速度运动,Q 为AP 的中点,过点Q 作QH ⊥AB 于点H ,在射线AE 的下方作平行四边形PQHM (点M 在点H 的右侧),设P 点运动时间为t 秒.(1)直接写出AQH 的面积(用含t 的代数式表示).(2)当点M 落在BC 边上时,求t 的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的t 的值;若不存在请说明理由(不能添加辅助线). 4.阅读资料,解决问题.人教版《数学九年级(下册)》的30页有这样一个思考问题:问题:如图,在ABC △中,DE BC ∥交AB ,AC 于点D ,E ,如果通过“相似的定义”证明ADE ABC △△∽?分析:根据“两直线平行,同位角相等”容易得出三对对应角分别相等,再根据“平行线分线段成比例”的基本事实,容易得出AD AE AB AC =,所以这个问题的核心时如何证明“DE AE BC AC =”. 证明思路:过点E 作EF AB ∥交BC 于点F ,构造平行四边形BDEF ,得到DE BF =,从而将比例式中的DE ,BC 转化为共线的两条线段BF ,BC ,同时也构造了基本图形“”,得到BF AE BC AC=,从而得证.解决问题:(1)①类比资料中的证明思路,请你证明“三角形内角平分线定理”.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.已知:如图1,ABC △中,AD 是角平分线.求证:AB BD AC DC=.②运用“三角形内角平分线定理”填空:已知:如图2,ABC △中,AD 是角平分线,7AB =,4AC =,6BC =,则BD =__________.(2)我们知道,如果两个三角形有相同的高或者相等的高,那么它们面积的比就等于底的比.请你通过研究ABD △和ACD 面积的比来证明三角形内角平分线定理.已知:如图3,ABC △中,AD 是角平分线.求证:AB BD AC DC=.5.如图,在ABC 中,AB AC =,100A ∠=︒,BD 是ABC ∠的平分线,延长BD 至点E ,DE AD =,试求ECA ∠的度数.6.如图1,点A 是直线MN 上一点,点B 是直线PQ 上一点,且MN//PQ .NAB ∠和ABQ ∠的平分线交于点C .(1)求证:BC AC ⊥;(2)过点C 作直线交MN 于点D (不与点A 重合),交PQ 于点E,①若点D 在点A 的右侧,如图2,求证:AD BE AB +=;②若点D 在点A 的左侧,则线段AD 、BE 、AB 有何数量关系?直接写出结论,不说理由.7.如图,已知BC 是⊙O 的弦,A 是⊙O 外一点,△ABC 为正三角形,D 为BC 的中点,M 为⊙O 上一点.(1)若AB 是⊙O 的切线,求∠BMC ;(2)在(1)的条件下,若E ,F 分别是AB ,AC 上的两个动点,且∠EDF =120︒,⊙O 的半径为2,试问BE +CF 的值是否为定值?若是,求出这个定值;若不是,请说明理由. 8.如图所示,在ABC ∆中,=60ACB ∠,,AE BD 是ABC ∆的角平分线,,AE BD 交于点G ,求证:GD GE =.9.如图,在ABC ∆中,AB AC >,AD 平分BAC ∠交BC 于D ,求证:AB AC BD CD ->-.10.如图,已知:在△ABC 中,AD 平分∠BAC ,AB=AD ,CE ⊥AD ,交AD 的延长线于E.求证:AB+AC=2AE.【参考答案】***试卷处理标记,请不要删除一、全等三角形角平分线辅助1.AB=AC+BD ,证明见详解.【分析】延长AE ,交BD 的延长线于点F ,先证明AB=BF ,进而证明△ACE ≌△FDE ,得到AC=DF ,问题得证.【详解】解:延长AE ,交BD 的延长线于点F ,∵//AC BD ,∴∠F=∠CAF ,∵AE 平分CAB ∠,∴∠CAF=∠BAF ,∴∠F=∠BAF ,∴AB=BF ,∵BE 平分ABF ∠,∴AE=EF ,∵∠F=∠CAF ,∠AEC=∠FED ,∴△ACE ≌△FDE ,∴AC=DF ,∴AB=BF=BD+DF=BD+AC .【点睛】本题考查了等腰三角形的判断与性质,全等三角形的判定与性质,根据题意添加辅助线构造等腰三角形和全等三角形是解题关键.2.(1)①ⅰ)△BMF ,边角边;ⅱ)60;②详见解析;(2)详见解析【分析】(1)先得出结论;①利用三角形内角和求出∠ABC+∠ACB=120°,进而得出∠FBC+∠FCB=60°,得出∠BFC=120°,即可得出结论;②利用角平分线得出∠EBF=∠MBF ,进而得出△BEF ≌△BMF ,求出∠BFM ,即可判断出∠CFM=∠CFD ,即可判断出△FCM ≌△FCD ,即可得出结论;(2)先求出相关角的度数,进而判断出BG=CE ,进而判断出△BGF ≌△CEA ,即可得出结论.【详解】(1)BC CD BE =+①如图1,在BC 上取一点M ,使BM BE =,ⅰ)BD 是ABC ∠的平分线,EBF MBF ∴∠=∠, 在BEF ∆和BMF ∆中,BE BM EBF MBF BF BF =⎧⎪∠=∠⎨⎪=⎩,()BEF BMF SAS ∴∆≅∆;ⅱ)BD ,CE 是ABC ∆的两条角平分线,12FBC ABC ∴∠=∠,12BCF ACB ∠=∠, 在ABC ∆中,180A ABC ACB ∠+∠+∠=︒,60A ∠=︒,180120ABC ACB A ∴∠+∠=︒-∠=︒,1180()180()1202BFC CBF BCF ABC ACB ∴∠=︒-∠+∠=︒-∠+∠=︒,18012060EFB ∴∠=︒-︒=︒;故答案为:ⅰ)ΔBMF ,SAS ;ⅱ)60;②由①知,60BFE ∠=︒,BEF BMF ∆≅∆,60CFD BFE ∴∠=∠=︒,∵BEF BMF ∆≅∆,60BFE BFM ∴∠=∠=︒,60CFM BFC BFM ∴∠=∠-∠=︒,60CFM CFD ∴∠=∠=︒, CE 是ACB ∠的平分线,FCM FCD ∴∠=∠,在FCM ∆和FCD ∆中,CFM CFD CF CF FCM FCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()FCM FCD ASA ∴∆≅∆,CM CD ∴=,BC CM BM CD BE ∴=+=+;(2)如图2,在ABC ∆中,60A ∠=︒,40ABC ∠=︒,80ACB ∴∠=︒, BD ,CE 是ABC ∆的两条角平分线,1202ABD CBD ABC ∴∠=∠=∠=︒,1402BCE ACE ACB ∠=∠=∠=︒, 80AEC ABC BCE ∴∠=∠+∠=︒,ABC BCE ∠=∠,BE CE ∴=,在ABC ∆的边AB 左侧作20ABG ∠=︒,交CE 的延长线于G ,40FBG ABD ABG ACE ∴∠=∠+∠=︒=∠.80AEC ∠=︒,80BEG ∴∠=︒,18080G ABG BEG BEG AEC ∴∠=︒-∠-∠=︒=∠=∠,BG BE ∴=,BG CE ∴=,在BGF ∆和CEA ∆中,4080FBG ACE BG CE BGF AEC ∠=∠=︒⎧⎪=⎨⎪∠=∠=︒⎩,BGF CEA ∴∆≅∆,BF AC ∴=.【点睛】此题是三角形综合题,主要考查了角平分线的定义,三角形内角和定理,全等三角形的判定和性质,解本题的关键是(1)判断出CFM CFD ∠=∠,(2)作出辅助线,判断出BG CE =.3.(1)214t ;(2)22t =3)存在,如图2(见解析),当AHQ HBM ≅时,22t =3(见解析),当ADE AHE ≅时,32t =4(见解析),当EGQ HBF ≅时,722t =【分析】(1)先根据线段中点的定义可得12AQ AP =,再根据矩形的性质、角平分线的定义可得45HAQ ∠=︒,从而可得AQH 是等腰直角三角形,然后根据等腰直角三角形的性质可得AH 的长,最后根据等腰直角三角形的面积公式即可得;(2)先根据平行四边形的性质可得//HQ MP ,从而可得//HQ BP ,再根据三角形中位线定理可得HQ 是ABP △的中位线,从而可得122AH AB ==,然后与(1)所求的22AH =建立等式求解即可得; (3)分①当点H 是AB 的中点时,AHQ HBM ≅;②当点Q 与点E 重合时,ADE AHE ≅;③当EG HB =时,EGQ HBF ≅三种情况,分别求解即可得.【详解】(1)由题意得:2AP t =,点Q 为AP 的中点,12AQ AP t ∴==, 四边形ABCD 是矩形,90B D BAD ∴∠=∠=∠=︒,AE ∵是BAD ∠的角平分线, 1452HAQ DAE BAD ∴∠=∠=∠=︒, QH AB ⊥,AQH ∴是等腰直角三角形,2222AH HQ AQ t ∴===, 则AQH 的面积为21124AH HQ t ⋅=; (2)如图1,四边形PQHM 是平行四边形, //HQ MP ∴,点M 在BC 边上,//HQ BP ∴,点Q 为AP 的中点,HQ ∴是ABP △的中位线,122AH BH AB ∴===, 由(1)知,22AH t =, 则222t =, 解得22t =;(3)由题意,有以下三种情况:①如图2,当点H 是AB 的中点时,则AH HB =,四边形PQHM 是平行四边形, //HM PQ ∴,HAQ BHM ∴∠=∠,在AHQ 和HBM △中,90HAQ BHM AH HB AHQ HBM ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,()AHQ HBM ASA ∴≅,由(2)可知,此时22t =;②如图3,当点Q 与点E 重合时,在ADE 和AHE 中,9045D AHE DAE HAE AE AE ∠=∠=︒⎧⎪∠=∠=︒⎨⎪=⎩,()ADE AHE AAS ∴≅,3AD AH ∴==,则232t =, 解得32t =;③如图4,当EG HB =时,四边形ABCD 是矩形,四边形PQHM 是平行四边形,//,//CD AB HM PQ ∴,,90GEQ HAQ BHF EGQ AHQ B ∴∠=∠=∠∠=∠=︒=∠,在EGQ 和HBF 中,GEQ BHF EG HB EGQ B ∠=∠⎧⎪=⎨⎪∠=∠⎩,()EGQ HBF ASA ∴≅, 2,42AH t AB ==, 242HB AB AH t ∴=-=-, 在Rt ADE △中,45,3DAE AD ∠=︒=,Rt ADE ∴是等腰直角三角形,232AE AD ==,32EQ AQ AE t ∴=-=-,在Rt GEQ 中,45GEQ HAQ ∠=∠=︒,Rt GEQ ∴是等腰直角三角形,22622t EG EQ -==, 则由EG HB =得:262422t t -=-, 解得722t =;综上,如图2,当AHQ HBM ≅时,22t =;如图3,当ADE AHE ≅时,32t =4,当EGQ HBF ≅时,722t =【点睛】 本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点,较难的是题(3),依据题意,正确分三种情况讨论并画出图形是解题关键.4.(1)①证明见解析②4211 (2)证明见解析 【解析】【分析】(1)①如图过点C 作AB 的平行线交AD 的延长线于点E ,然后说明ADB EDC △∽△,利用相似三角形的性质即可完成证明;②设BD x =,然后利用(1)的结论和已知条件即可完成解答; (2)过点D 作AB ,AC 的垂线,垂足为M 、N ,过点A 作BC 的垂线,垂足为H ;先利用角平分线定理说明DM DN =,然后再利用等面积法得到11:::22ABD ADC S S AB MD AC DN AB AC =⋅⨯=△△和11:::22ABD ADC S S BD AH OC AH BD DC =⋅⋅=△△,从而得到::AB AC BD DC =,即AB BD AC DC=. 【详解】(1)①证明:过点C 作AB 的平行线交AD 的延长线于点E ,∴1E ∠=∠,又∵AD 平分BAC ∠,∵12∠=∠,∴2E ∠=∠,∴AC CE =,又∵34∠=∠,∴ADB EDC △∽△,∴AB BD CE DC =, ∴AB BD AC DC=. ②设BD x =,∴6DC x =-,又∵AB BD AC DC =, ∴746x x=-, ∴4427x x =-,∴1142x =,42x 11=.(2)过点D 作AB ,AC 的垂线,垂足为M 、N ,过点A 作BC 的垂线,垂足为H ,∵AD 为BAC ∠的角分线,∴DM DN =,11:::22ABD ADC S S AB MD AC DN AB AC =⋅⨯=△△, 又∵11:::22ABD ADC S S BD AH OC AH BD DC =⋅⋅=△△, ∴::AB AC BD DC =,∴AB BD AC DC=. 【点睛】 本题主要考查了相似三角形的知识,其中运用等面积法、相似三角形的性质和证明、做辅助线均是解答本题的关键.5.40°【分析】在BC 上截取BF AB =,连接DF ,通过证明()ABD FBD SAS ≌,可得18080DFC A ︒∠=-∠=︒,再通过证明()DCE DCF SAS ≌,即可求得40ECA DCB ∠=∠=︒【详解】解:如图,在BC 上截取BF AB =,连接DF ,BD 是ABC ∠的平分线,ABD FBD ∴∠=∠,在ABD △和FBD 中,,,,AB FB ABD FBD BD BD =⎧⎪∠=∠⎨⎪=⎩()ABD FBD SAS ∴△≌△,BFD A ∴∠=∠,AD DF =,∴DE=DF ,18080DFC A ∴∠=︒-∠=︒,又40ABC ACB ∠=∠=︒,60FDC ∴∠=︒,18060EDC ADB ABD A ∠=∠=︒-∠-∠=︒,EDC FDC ∴∠=∠,在DCE 和DCF 中,,,,DE DF EDC FDC DC DC =⎧⎪∠=∠⎨⎪=⎩()DCE DCF SAS ∴△≌△,故40ECA DCB ∠=∠=︒.【点睛】本题考查了全等三角形的问题,掌握全等三角形的性质以及判定定理是解题的关键. 6.(1)见解析;(2)见解析;(3)BE AD AB =+【分析】(1) 由平行线性质可得∠NAB+∠ABQ=180°,再由角平分线定义可得11,22∠=∠∠=∠BAC NAB CBA ABQ ,再利用三角形内角和定理即可得∠C=90°,即可证明BC ⊥AC;(2) ①延长AC 交PQ 点F ,先证明AC=FC,再证明△ACD ≌△FCE,即可得AD+BE=AB; ②方法与①相同.【详解】解:(1)∵MN ∥PQ∴∠NAB+∠ABQ=180°∵AC 平分∠NAB ,BC 平分∠ABQ ∴11,22∠=∠∠=∠BAC NAB CBA ABQ∴∠BAC+∠ABC=12180⨯︒=90°在△ABC中,∵∠BAC+∠ABC+∠C=180°∴∠C=180°- (∠BAC+∠ABC) =180°-90°=90°∴BC⊥AC;(2)①延长AC交PQ于点F∵BC⊥AC∴∠ACB=∠FCB=90°∵BC平分∠ABF∴∠ABC=∠FBC∴BC=BC∴△ABC≌△FBC∴AC=CF,AB=BF∵MN∥BQ∴∠DAC=∠EFC∵∠ACD=∠FCE∴△ACD≌△FCE∴AD=EF∴AB=BF=BE+EF=BE+AD即:AB=AD+BE②线段AD,BE,AB数量关系是:AD+AB=BE 如图3,延长AC交PQ点F,∵MN//PQ .∴∠AFB=∠FAN ,∠DAC=∠EFC∵AC 平分∠NAB∴∠BAF=∠FAN∴∠BAF=∠AFB∴AB=FB∵BC ⊥AC∴C 是AF 的中点∴AC=FC在△ACD 与△FCE 中DAC EFC AC FCACD FCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ACD FCE ASA ≅∴AD=EF∵AB=FB=BE-EF∴AD+AB=BE【点睛】本题考查了平行线性质,全等三角形性质判定,等腰三角形性质等,解题关键正确添加辅助线构造全等三角形.7.(1)60°;(2)BE+CF 的值是定值,BE+CF=3. 【分析】(1)连接BO ,由AB 是切线可以得到∠ABO 的度数,由△ABC 为等边三角形,得到∠OBC 的度数,然后得到∠BOC ,根据圆心角与圆周角的关系得到∠BMC 的度数.(2)作DH ⊥AB 于H ,DN ⊥AC 于N ,连结AD ,OD ,如图2,根据等边三角形三角形的性质得AD 平分∠BAC ,∠BAC=60°,则利用角平分线性质得DH=DN ,根据四边形内角和得∠HDN=120°,由于∠EDF=120°,所以∠HDE=∠NDF ,接着证明△DHE ≌△DNF 得到HE=NF ,于是BE+CF=BH+CN ,再计算出BH=12BD ,CN=12DC ,则BE+CF=12BC ,于是可判断BE+CF 的值是定值,为等边△ABC 边长的一半,再计算BC 的长即可.【详解】(1)解:如图,连接BO ,∵AB是圆的切线,∴∠ABO=90°,∵△ABC是等边三角形,∴∠ABC=60°,∴∠CBO=90°-60°=30°,∵BO=CO,∴∠BCO=∠CBO=30°,∴∠BOC=120°,∴∠BMC=1BOC602∠=︒(2)解:BE+CF的值是为定值.理由:作DH⊥AB于H,DN⊥AC于N,连结AD,OD,如图2,∵△ABC为正三角形,D为BC的中点,∴AD平分∠BAC,∠BAC=60°,∴DH=DN,∠HDN=120°,∵∠EDF=120°,∴∠HDE=∠NDF,在△DHE和△DNF中,∴DHE DNFDH DNHDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DHE≌△DNF,∴HE=NF,∴BE+CF=BH-EH+CN+NF=BH+CN,在Rt△DHB中,∵∠DBH=60°,∴BH=12BD,同理可得CN=12 OC,∴BE+CF=12DB+12DC=12BC , ∵BD=3,∴BC=23,∴BE+CF=3,∴BE+CF 的值是定值,为:3.【点睛】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等边三角形的性质.8.详见解析 【解析】【分析】在AB 上截AF AD =,连接FG ,根据角平分线的性质、结合三角形内角和定理可得AGD=120AGB ∠︒∠=︒60,,证明ADG AFG ∆∆≌,得GD=GF ,AGD AGF ∠=∠=60°,可证得BGF BGE ∆∆≌,即可得GF=GE=GD.【详解】证明:在AB 上截AF AD =,连接FG ,∵AE 平分∠BAC ,∴∠EAC=∠EAB ,又∵AG=AG ,∴ADG AFG ∆∆≌,GD GF ∴=,AGD AGF ∠=∠ ,∵60ACB ∠=︒,AE,BD 是ΔABC 的角平分线,∴()111802211802120AGB CAB CBA CAB CBA ∠=︒-∠-∠=︒-∠+∠=︒, ∴60AGD AGF BGF BGE ∠=∠=∠=∠=︒,∵BGF BGE BG BG GBF GBE ∠=∠⎧⎪=⎨⎪∠=∠⎩()BGF BGE ASA ∴∆∆≌,∴GF GE = ,∴GD=GE.【点睛】本题考查角平分线的性质、全等三角形的判定和性质,作辅助线是解题的关键. 9.详见解析【解析】【分析】可以在AB 上截取AE=AC ,构造三角形全等,再结合三角形三边关系可证得结论.【详解】在AB 上截取AE=AC ,则BE=AB-AC ,在△AED 和△ACD 中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△AED ≌△ACD(SAS),∴DE=DC ,在△BDE 中,BD-DE <BE(三角形两边之差小于第三边),∴BE>BD-CD ,即AB-AC>BD-CD.【点睛】本题考查了全等三角形的判定与性质,三角形三边关系,构造三角形全等是解题的关键. 10.详见解析【分析】延长AE 到M ,使ME=AE ,连接CM ,求出AC=CM ,求出DM=MC ,即可得出答案.【详解】延长AE 到M ,使ME=AE ,连接CM ,则AM=2AE ,∵CE ⊥AE ,∴AC=CM,∴∠M=∠CAD=∠DAB,∴AB∥MC,∴∠B=∠MCD,∵AB=AD,∴∠B=∠ADB,∵∠ADB=∠MDC,∴∠MCD=∠MDC,∴MC=MD,∴AM=2AE=AD+MD=AB+AC,即AB+AC=2AE.【点睛】本题考查了平行线的性质和判定,线段垂直平分线性质,等腰三角形的性质和判定的应用,解此题的关键是推出DE=EC,有一定的难度.。
(一)最短路径
知识点:“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。
“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
一、两点在一条直线异侧
例:已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
(根据:两点之间线段最短.)
二、两点在一条直线同侧
例:图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
三、一点在两相交直线内部
例1:已知:如图A是锐角∠MON内部任意一点,在∠MON的两边OM,
ON上各取一点B,C,组成三角形,使三角形周长最小.
例2:如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造
在何处才能使从A到B的路径AMNB最短?(假设河的两岸是平行的直
线,桥要与河垂直)
A·
B
M
N
E
例3:某班举行晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
例4:如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的
最短路线。
四、综合应用
例1:如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,问如何恰当地架桥可使ADD′E′EB的路程最短?
例2:
A O
B
E
N
C
M
A
O
B
D
·C H
F
D
(二)角平分线性质判定
1、角平分线的性质定理:
注意两点:(1)角平分线上的点到角两边的距离相等(2)一对全等三角形
经典例题透析
类型一:角平分线性质的应用
1、如图,△ABC中,∠C=90°,AD平分∠BAC,点D在BC上,且BC=24,CD:DB=3:5
求:D到AB的距离。
思路点拨:点到直线的距离是经过该点作直线的垂线,该点与垂足之间线段的长度。
举一反三:
【变式】如图,∠ACB=90°,BD平分∠ABC交AC于D,DE⊥AB于E,ED的延长线交BC的延长线于F.
求证:AE=CF
类型二:角平分线的判定
2、已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF。
求证:AF为∠BAC的平分线。
思路点拨:由已知条件与待求证的结论,应想到角平分线的判定定理。
总结升华:应用角平分线定理及逆定理时不要遗漏了“垂直”的条件。
如果遗漏了说明没有认识到“垂直”条件在证明结论的必要性。
举一反三:
【变式】如图,已知AB=AC,AD=AE,DB与CE相交于O
(1) 若DB⊥AC,CE⊥AB,D,E为垂足,试判断点O的位置及OE与OD的大小关系,并证明你的结论。
(2) 若D,E不是垂足,是否有同样的结论?并证明你的结论。
类型三、角平分线的综合应用
一、已知角平分线,构造三角形
例题:如图所示,在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于F。
求证:
1
()
2
BE AC AB
=-
二、已知一个点到角的一边的距离,过这个点作另一边的垂线段
如图所示,∠1=∠2,P为BN上的一点,并且PD⊥BC于D,AB+BC=2BD。
求证:∠BAP+∠BCP=180°。
2
1
F
E
D C
B
A
B C E ,,在同一条直线上,连结CD . (彩图为提示)
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); (2)证明:CD ⊥BE
[变形3]、如图2,在△ABC 中,高AD 与BE 相交于点H ,且AD=BD ,
问△BHD ≌△ACD ,为什么?
[变形4]:如图3, 已知ED ⊥AB ,EF ⊥BC ,BD =EF ,问BM =ME 吗?说明理由。
图2
A
B
C
E H D
图2
A
C B
E
D
图1
A
C B
E
D
B。