配对样本t检验的定义与前提条件

配对t检验的应用条件配对t检验的应用条件一、什么是配对t检验？配对t检验是一种常用的假设检验方法，它可以通过比较两组相关样本的均值差异来判断这两组样本是否存在显著差异。

在实际应用中，常常需要比较同一组个体在不同时间或不同条件下的测量值，此时就可以采用配对t检验来进行分析。

二、何时适合使用配对t检验？1. 样本数据为连续型变量：配对t检验只适用于连续型变量，不能应用于分类变量或顺序变量。

2. 样本数据为成对数据：配对t检验要求样本数据为成对数据，即每个个体都有两次测量值或两种处理条件。

3. 数据符合正态分布：配对t检验要求样本数据符合正态分布，否则会影响结果的准确性。

4. 数据方差相等：如果两组样本方差不相等，则需要进行修正后再进行分析。

三、如何进行配对t检验？1. 收集样本数据并计算均值和标准差；2. 计算每个个体的差值（第二次测量值减去第一次测量值）；3. 计算所有个体差值的平均值和标准差；4. 计算t值并查找t分布表确定p值；5. 判断p值是否小于显著性水平（通常为0.05），若小于则拒绝原假设，认为两组样本存在显著差异。

四、实际应用中的例子以下是一个实际应用中的例子，展示了配对t检验的具体步骤和结果。

1. 实验目的：比较同一组学生在两次考试中的成绩是否有显著差异。

2. 实验设计：选择一组30名学生，在第一次考试后1个月进行第二次考试，并记录两次考试成绩。

3. 数据处理：（1）计算每个学生的成绩差值；（2）计算所有学生成绩差值的平均值和标准差；（3）计算t值：t = (x1 - x2) / (s / √n)，其中x1为第一次考试平均分，x2为第二次考试平均分，s为样本标准差，n为样本容量；（4）查找t分布表确定p值。

4. 结果分析：（1）计算得到所有学生成绩差值的平均数为5分，标准差为3分；（2）根据计算公式得到t值为3.33；（3）查找t分布表可得p值小于0.01，显著性水平为0.05，因此可以拒绝原假设，认为两次考试成绩存在显著差异。

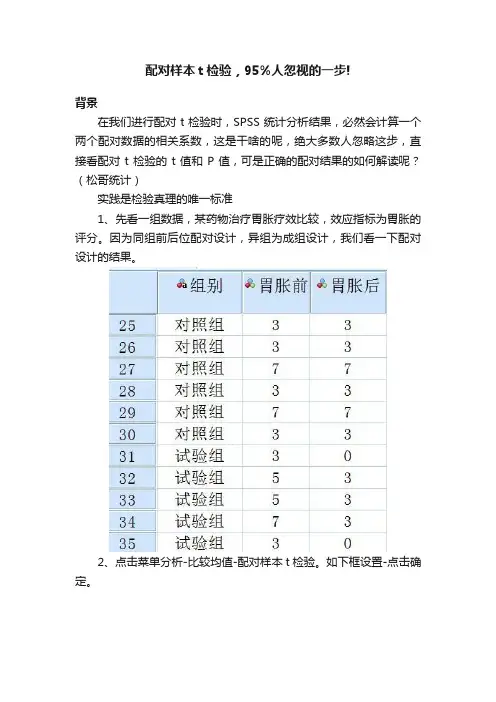
配对样本t检验，95%人忽视的一步!背景在我们进行配对t检验时，SPSS统计分析结果，必然会计算一个两个配对数据的相关系数，这是干啥的呢，绝大多数人忽略这步，直接看配对t检验的t值和P值，可是正确的配对结果的如何解读呢？（松哥统计）实践是检验真理的唯一标准1、先看一组数据，某药物治疗胃胀疗效比较，效应指标为胃胀的评分。

因为同组前后位配对设计，异组为成组设计，我们看一下配对设计的结果。

2、点击菜单分析-比较均值-配对样本t检验。

如下框设置-点击确定。

3、结果解读（三步法）3.1第一步：获取胃胀前与胃胀后的三个核心统计量（样本量、均数和标准差）。

产生主观意识：本例胃胀前均数4.37，胃胀治疗后均数2.65，可能治疗有效，但这种疗效可能是抽样误差所致，因此需要进行检验。

知识连接配对设计是一种配对后两组数据相互关联的设计，也就是说配对后数据如果不相关，那就失去了配对设计t检验的前提条件，因此，很多软件进行配对设计时，会检验数据是否存在相关性。

3.2结果解读第二步：检查配对前后数据的相关性，本例相关系数r=0.520，P=0.000<>3.3结果解读第三步：配对t检验结果，发现t=8.121，对应的P=0.000<>大同小异），本例小于0.05，因此小异，有差异。

即治疗前后胃胀评分差异有统计学意义。

在结合前后的均数，可以得出治疗后胃胀评分下降，该药有效。

松哥统计说配对样本t检验的相关系数检验，确实很多人忽视，甚至一些供研究生用的统计教材都用错了。

下图（中间部分）为某教材中部分，分析认为配对组相关系数r=0.075>0，就配对成功。

个人认为确实不太妥当，至少2点。

一为：只看r值大小，不看r值的P值，本例虽然r=0.075>0，但后面的P=838>0.05。

意思是前面的r=0.075可能是有抽样误差导致，并不是匹配的结果。

二为：忽视r值的专业意义，本例r=0.075是一份非常小的值，微弱微弱，几乎无相关性。

配对t检验的应用条件一、引言配对t检验是一种常见的假设检验方法，它用于比较两个相关样本的均值差异。

在实际应用中，我们经常需要分析某个变量在不同条件下的差异，并判断这种差异是否具有统计学意义。

配对t检验正是为了解决这一问题而设计的。

本文将详细介绍配对t检验的应用条件以及使用方法，帮助读者更好地理解和运用该方法。

二、什么是配对t检验配对t检验，也称为相关t检验或重复测量t检验，是一种用于比较两个相关样本的均值差异的统计方法。

它适用于两个相关样本之间的配对观测，例如同一组人在不同时间点的测量结果，同一组人在不同处理条件下的观测结果等。

通过配对t检验，我们可以判断两个相关样本均值之间是否存在显著差异，从而对比较结果进行科学推断。

三、配对t检验的应用条件配对t检验适用于满足以下条件的数据：1. 样本间相关配对t检验要求两个样本之间存在相关性，即两个样本中的观测值是配对的。

例如，在临床实验中，同一组病人在治疗前后的观测结果；在心理学研究中，同一组被试在不同条件下的反应时间等。

只有满足样本间相关的条件，才能使用配对t检验进行分析。

2. 观测值之间独立配对t检验要求样本中的观测值之间相互独立。

这意味着样本中的每个观测值在配对时是独立的，互不影响。

例如，在治疗前后的观测中，相邻观测值之间不能有依赖关系，每个观测值的测量结果都是相互独立的。

3. 观测值近似正态分布配对t检验要求样本中的观测值近似满足正态分布。

在实际应用中，通常通过样本量的大小来判断观测值的分布是否近似正态分布。

当样本量较大时，配对t检验对观测值的分布偏离正态分布的程度较为宽容。

因此，在使用配对t检验时，我们需要对数据的分布进行适当的检验。

4. 观测值之间方差相等配对t检验要求样本中的观测值之间具有相等的方差。

这是因为配对t检验的基本原理是通过比较两个样本的均值差异来进行假设检验，如果两个样本的方差差异较大，那么均值差异可能受到方差差异的干扰。

一般情况下，我们通过方差齐性检验来判断样本的方差是否相等。

三种t检验的应用条件t检验是统计学中一种常用的假设检验方法，被广泛应用于各个领域的研究中。

t检验根据数据的不同特征和研究目的的不同，可以分为三种类型的应用条件，分别是单样本t检验、独立样本t检验和配对样本t检验。

一、单样本t检验单样本t检验是指对一个样本进行假设检验，用于检验样本的平均值是否与一个已知的常数有显著差异。

单样本t检验的应用条件如下：1. 样本数据应符合正态分布，即样本数据呈现出钟形曲线的分布形态。

2. 样本数据应是随机抽样的，即样本中每个个体都有同等概率被抽取到。

3. 样本数据应是独立的，即样本中每个个体之间的差异是相互独立的。

4. 样本数据应是连续性的，即样本数据是数值型数据，而非分类变量。

二、独立样本t检验独立样本t检验是指对两个独立的样本进行假设检验，用于检验两个样本之间的平均值是否存在显著性差异。

独立样本t检验的应用条件如下：1. 两个样本的数据应符合正态分布，即两个样本的数据分布形态应呈现出钟形曲线。

2. 两个样本的数据应是独立的，即两个样本中的个体之间没有相互影响。

3. 两个样本的数据应是连续性的，即两个样本的数据是数值型数据，而非分类变量。

4. 两个样本的方差应相等，即两个样本的方差应该相近。

三、配对样本t检验配对样本t检验是指对同一组个体在两个不同时间点或不同条件下的数据进行假设检验，用于检验两组数据之间的平均值是否存在显著性差异。

配对样本t检验的应用条件如下：1. 两组数据应是配对的，即两组数据应该来自同一组个体，且每个个体在两个时间点或不同条件下的数据是相互对应的。

2. 两组数据应符合正态分布，即两组数据的分布形态应呈现出钟形曲线。

3. 两组数据应是连续性的，即两组数据是数值型数据，而非分类变量。

4. 两组数据的差值应符合正态分布，即两组数据的差值应呈现出钟形曲线的分布形态。

t检验是一种非常有用的假设检验方法，但在应用时需要根据数据的特征和研究目的的不同，选择适当的t检验类型，并遵循相应的应用条件，以保证检验结果的准确性和可靠性。

t检验的假设条件
（1）单样本的t检验要求资料服从正态分布。

（2）配对t检验要求差值服从正态分布。

（3）两样本的t检验要求两组数据服均从正态分布，切两样本的方差相等，尤其对小样本。

（4）假设检验的结论不能绝对化。

通过假设检验作出的检验推断具有概率性，有可能发生两类错误。

拒绝H O时犯I型错误，接受H O时间犯II型错误。

（5）假设检验和区间估计的区别。

假设检验用于推断质的不同的两个总体或多个总体参数
是否不等。

可信区间估计是用于说明量的大小，推断总体参数的范围。

可信区间可以回答假设检验的问题。

在判断两个或多个总体参数是否不相等时，假设检验与区间估计是完全等价的。

t检验的原理方法选择和应用条件一、t检验的原理t检验是一种统计分析方法，用于比较两个样本均值是否存在显著差异。

其原理基于样本数据的均值和标准差，以及样本大小。

通过计算t值，可以判断两个样本之间的差异是否显著。

二、t检验的方法选择根据研究问题和实验设计的不同，可以选择不同的t检验方法。

以下是常见的t检验方法：1.单样本t检验：用于比较一个样本的均值与已知的总体均值之间是否存在显著差异。

适用于总体标准差未知的情况。

2.独立样本t检验：用于比较两个独立样本的均值是否存在显著差异。

适用于两个样本之间相互独立、总体标准差未知的情况。

3.配对样本t检验：用于比较同一组样本在不同条件下的均值是否存在显著差异。

适用于两个样本之间存在相关性、总体标准差未知的情况。

根据研究目的和数据特点，可以选择适合的t检验方法进行分析。

三、t检验的应用条件为了保证t检验结果的准确性和可靠性，在应用t检验时需要满足一定的条件。

以下是t检验的应用条件：1.样本数据近似正态分布：t检验建立在样本数据近似正态分布的基础上，如果样本数据不满足正态分布，可能会导致结果不准确。

2.样本独立性：当进行独立样本t检验时，两个样本应该是互相独立的，即两个样本之间没有相关性。

否则，会导致结果不准确。

3.总体标准差未知：t检验假设总体标准差未知，当已知总体标准差时，可以使用z检验进行分析。

如果以上条件都满足，就可以使用t检验进行统计分析。

四、使用t检验的注意事项在应用t检验时需要注意以下几点：1.样本大小：样本大小直接影响t检验的准确性和可靠性，通常样本大小越大，结果越准确。

2.显著性水平：在进行参数估计时，需要设置显著性水平，常见的显著性水平包括0.05和0.01，选择适合的显著性水平可以得到更可靠的结论。

3.效应大小：在比较两个样本均值时，需要考虑效应大小。

如果效应较小，样本大小可能需要更大才能得到显著的结果。

通过合理选择t检验的方法、满足应用条件，并注意上述注意事项，可以更加准确地进行数据分析和结论推断。

配对样本t检验原理在统计学中，配对样本t检验是一种用于比较两个相关样本均值是否有显著差异的方法。

它是t检验的一种特殊形式，适用于两个样本之间存在相关性的情况。

本文将介绍配对样本t检验的原理、应用场景、计算方法以及结果解释。

原理配对样本t检验的原理基于两个相关样本之间的差异。

在配对样本t 检验中，我们比较的是两个相关样本的均值差异是否显著。

这种方法适用于两个样本之间存在相关性的情况，例如同一组人在不同时间点的测量结果、同一组人在不同条件下的测量结果等。

应用场景配对样本t检验适用于以下场景：1.同一组人在不同时间点的测量结果比较。

例如，我们想比较同一组人在某项任务上的成绩在两个不同时间点的差异。

我们可以使用配对样本t检验来比较这两个时间点的成绩是否有显著差异。

2.同一组人在不同条件下的测量结果比较。

例如，我们想比较同一组人在不同条件下的反应时间。

我们可以使用配对样本t检验来比较这两个条件下的反应时间是否有显著差异。

计算方法配对样本t检验的计算方法与独立样本t检验类似，但需要考虑两个样本之间的相关性。

具体计算步骤如下：1.计算两个样本的差值。

2.计算差值的平均值和标准差。

3.计算t值。

t值的计算公式为：t = (差值的平均值 - 零假设的差值) / (标准差 / 样本大小的平方根)其中，零假设的差值为0，表示两个样本的均值相等。

4.计算p值。

p值表示在零假设成立的情况下，观察到t值或更极端的概率。

p值越小，说明差异越显著。

结果解释在配对样本t检验中，我们需要关注t值和p值。

如果t值大于临界值，说明两个样本的均值差异显著；如果p值小于显著性水平（通常为0.05），则拒绝零假设，认为两个样本的均值差异显著。

例如，我们进行了一项实验，比较同一组人在不同条件下的反应时间。

我们得到了以下结果：差值的平均值：10ms标准差：5ms样本大小：20t值：4.0p值：0.001在这种情况下，t值大于临界值，说明两个样本的均值差异显著。

T检验分为三种方法
T检验是一种常见的统计推断方法，它用于比较两个样本之间的差异。

T检验分为三种方法：独立样本T检验、配对样本T检验和单样本T检验。

下面将对这三种方法进行介绍。

1.独立样本T检验：
独立样本T检验用于比较两个不相关的样本之间的均值差异。

要进行
独立样本T检验，首先需要收集两个独立的样本数据，然后根据这些数据
计算出两个样本的均值和方差。

T检验的原假设是这两个样本的均值相等，备择假设是这两个样本的均值不相等。

根据计算的T值和自由度，可以计
算出P值，从而判断原假设是否成立。

2.配对样本T检验：
配对样本T检验用于比较同一个样本在不同条件下的均值差异。

配对
样本T检验适用于两种情况：一是两个样本是相关的，例如同一个受试者
在不同时间点的数据；二是两个样本是配对的，例如同一组受试者在不同
条件下的数据。

在配对样本T检验中，计算的T值和自由度与独立样本T
检验类似，根据P值判断原假设是否成立。

3.单样本T检验：
单样本T检验用于判断一个样本的均值是否与一个已知的总体均值相等。

在单样本T检验中，收集一个样本的数据，计算样本的均值和标准差。

T检验的原假设是样本的均值等于总体的均值，备择假设是样本的均值不
等于总体的均值。

根据计算的T值和自由度，计算P值，从而判断原假设
是否成立。

总的来说，T检验是一种常用的统计方法，可以用于比较两个样本均值是否有差异，并判断这种差异是否显著。

根据实际问题的需求，可以选择独立样本T检验、配对样本T检验或单样本T检验来进行分析。

配对样本t检验的应用条件
配对样本t检验的应用条件主要包括以下几点：
1. 两组样本必须是连续型数据类型，且存在配对关系。

2. 数据应满足独立性，各观察值之间不能相互影响。

3. 数据应满足正态性，各个样本均应来自于正态分布的总体。

4. 数据应满足方差齐性，各个样本所在总体的方差应相等。

如果数据不满足正态分布或方差不齐时，可以考虑使用非参数检验。

同时，当样本量n<30时，数据为正态分布时，可以使用配对t检验；当数据不满足正态分布时，可以考虑使用对数转换、平方根变换、倒数变换、平方根反正弦变换等变量变换方法将数据变为正态或接近正态分布，再进行配对t检验。

另外，当样本量n<30时，样本总体标准差已知时，也可使用配对z检验；当n≥30时，可以使用配对t检验，也可使用配对z检验。

请注意，以上内容仅供参考，如需准确信息，建议查阅统计学相关书籍或咨询专业统计学家。

配对t检验应用条件
配对t检验是一种常用的统计方法，它用于比较两组相关的数据的均值是否有显著差异。

在使用配对t检验时，需要满足以下几个条件：
1. 数据类型：配对t检验适用于连续型的数据。

例如，可以使用配对t检验比较同一个人在不同时间点的体重变化，或者比较同一个实验组在不同处理条件下的成绩变化。

如果数据是分类型的，如喜欢与不喜欢，则不能使用配对t检验。

2. 数据的配对：配对t检验要求数据是配对的，也就是每个观测值都要与另一个相关的观测值相对应。

例如，可以比较参与同一个训练课程的学生在训练前后的体重变化，其中每个学生的体重都有相应的配对观测。

3. 数据的正态性：配对t检验要求数据服从正态分布。

在样本量较大（通常大于30）时，正态分布假设通常可以得到满足。

在样本量较小的情况下，可以使用正态性检验（如Shapiro-Wilk检验）来验证数据的正态性。

4. 数据的独立性：配对t检验要求数据是独立采样的，即每个观测值的取值不会受到其他观测值的影响。

这意味着，每组的观测值应该是随机选择的，并且每个观测值之间应该是相互独立的。

如果以上条件得到满足，我们可以使用配对t检验来判断两组相关数据的均值是否存在显著差异。

在进行统计分析时，我们需要计算配对观测值的差异值，并对这些差异值进行假设检验，以得出最终的结论。

总之，配对t检验适用于对同一组观测值在不同条件下的比较，并且需要满足数据类型为连续型、数据配对、数据正态性和数据独立性这几个条件。

这一方法可以帮助我们判断两组数据的均值是否有显著差异，对于科学研究和实证分析具有重要的意义。

使用配对t检验的限制条件使用配对t检验的限制条件引言：在统计学中，配对t检验是一种用于比较两个相关配对样本之间差异的假设检验方法。

这种方法广泛应用于医学、心理学、教育等领域，在确定相关变量之间是否存在显著差异时非常有效。

然而，使用配对t 检验时，我们必须注意一些限制条件，以确保分析的准确性和可靠性。

本文将介绍配对t检验的限制条件，并探讨在使用该方法时需要考虑的关键要点。

一、简要介绍配对t检验在开始探讨配对t检验的限制条件之前，先简要回顾一下它的基本原理。

配对t检验用于比较两个相关配对样本之间的均值差异。

与独立样本的t检验相比，配对t检验更适用于两个样本存在一定相关性的情况，例如同一组人在不同时间条件下的观测结果。

在进行配对t检验时，首先我们需要确定一个原假设（H0）和一个备择假设（H1）。

原假设通常是指两个样本的均值之间没有显著差异，而备择假设则是指两个样本的均值之间存在显著差异。

根据样本数据计算出t值，并根据t值和自由度确定关键值。

我们将计算得到的t值与关键值进行比较，以决定是否接受或拒绝原假设。

二、限制条件尽管配对t检验是一种强大而有用的统计方法，但我们在使用它时必须考虑以下限制条件：1. 样本之间的相关性：配对t检验适用于两个相关样本的比较。

确保在进行分析之前，我们已经建立了合理的相关性，并且样本之间的相关性是显著的。

如果样本之间的相关性不显著，那么使用配对t检验可能得不到准确的结果。

2. 正态性假设：配对t检验依赖于正态性假设，即样本数据应符合正态分布。

如果数据不符合正态分布，将会影响配对t检验的准确性。

为验证正态性假设，可以使用正态性检验方法，如Shapiro-Wilk检验或Kolmogorov-Smirnov检验。

3. 样本的独立性：配对t检验要求样本之间的观测值是独立的。

这意味着在进行配对t检验时，样本之间的观测值不能相互影响或依赖。

如果样本之间的观测值不独立，配对t检验的结果将失去准确性。

1、两配对样本T检验2、单因素方差分析3、多因素方差分析一、两配对样本T 检验定义 :两配对样本T 检验就是根据样本数据对样本来自得两配对总体得均值就是否有显著性差异进行推断。

一般用于同一研究对象(或两配对对象 )分别给予两种不同处理得效果比较 ,以及同一研究对象 (或两配对对象 )处理前后得效果比较。

两配对样本 T 检验得前提要求如下 :两个样本应就是配对得。

在应用领域中,主要得配对资料包括 :具有年龄、性别、体重、病况等非处理因素相同或相似者。

首先两个样本得观察数目相同 ,其次两样本得观察值顺序不能随意改变。

样本来自得两个总体应服从正态分布二、配对样本 t 检验得基本实现思路设总体服从正太分布,总体服从正太分布,分别从这两个总体中抽取样与,且两样本相互配对。

要求检验就是否有显著差异。

第一步 ,引进一个新得随机变量对应得样本值为,其中 ,这样 ,检验得问题就转化为单样本t 检验问题。

即转化为检验Y 得均值就是否与0 有显著差异。

第二步 ,建立零假设第三步 ,构造 t 统计量第四步 ,SPSS自动计算 t 值与对应得 P 值第五步 ,作出推断 :若 P 值<显著水平 ,则拒绝零假设即认为两总体均值存在显著差异若P 值>显著水平 ,则不能拒绝零假设 ,即认为两总体均值不存在显著差异三、 SPSS配对样本 t 检验得操作步骤例题 :研究一个班同学在参加了暑期数学、化学培训班后,学习成绩就是否有显著变化。

数据如表3所示。

1、操作步骤 :首先打开 SPSS软件1、1 输入数据点击 : 文件 -----打开文本数据 (D)-----选择需要编辑得数据 -----打开图 1 (这个就是已经导入数据得截图)在这里首先需要确定导入得数据就是符合两配对样本T 检验得前提得。

1、2 找到配对样本T 检验得位置点击 : 菜单栏得分析按钮 ----选择比较均值 -----配对样本 T 检验 (如图2 )图 21、3 将数据对应导入配对样本T 检验得选项框图1、31 导入前得图像如图3图 31、32 导入后得图像如图4图 4在此选项中需要设置“选项”得值为95%图 5选择选项完成后 ,点击“继续” ,接下来执行下面步骤 :图 6点击确定生成我们需要得表格:图 7表 1 成对样本统计量均值N标准差均值得标准误数学 172、941820、 1574、 751对 1数学 284、781810、 3392、 437化学 181、831815、 2403、 592对 2化学 289、44188、 1831、 929该表 1 给出了本实验对样本得一些统计量。

t检验的条件t检验是一种用于检验两个样本均值是否存在显著差异的统计方法。

在进行t检验之前，需要满足以下条件：一、独立性独立性是指两个样本之间相互独立，即一个样本的观测值不会影响另一个样本的观测值。

如果两个样本之间存在相关关系，则不能使用t检验。

二、正态性正态性是指每个样本的数据符合正态分布。

正态分布是一种钟形曲线，具有对称性和峰度（峰度越大表示数据分布越集中）。

如果数据不符合正态分布，则不能使用t检验。

三、方差齐性方差齐性是指两个样本的方差相等。

如果两个样本的方差不相等，则不能使用简单t检验，而需要使用修正后的Welch t检验或Mann-Whitney U检验。

四、随机抽样随机抽样是指从总体中随机地选择样本，使得每个总体单位有相同的概率被选入到样本中。

如果没有进行随机抽样，则不能保证结果具有代表性和可靠性。

五、连续变量t检验只适用于连续变量，即可以用数字来表示的变量。

如果变量是分类变量或有序变量，则不能使用t检验。

六、样本容量样本容量应当足够大，以确保结果的可靠性。

通常来说，每个样本的容量应当大于30。

如果样本容量太小，则可能无法满足正态性和方差齐性的条件。

七、两个样本的大小相等如果两个样本的大小相等，则可以使用简单t检验。

如果两个样本的大小不相等，则需要使用Welch t检验或Mann-Whitney U检验。

总结：t检验是一种常用的统计方法，用于比较两个样本均值是否存在显著差异。

在进行t检验之前，需要满足独立性、正态性、方差齐性、随机抽样、连续变量、样本容量和两个样本大小相等这七个条件。

只有满足这些条件，才能保证t检验结果具有代表性和可靠性。