空间向量的坐标运算

空间向量的坐标与运算空间向量是向量的一种特殊形式，用于表示空间中的位置和方向。

在三维空间中，我们可以用三个坐标轴来表示空间向量的三个分量，分别是x、y和z轴的坐标。

通过对空间向量的坐标进行运算，我们可以进行各种有趣的空间几何计算。

首先，我们来看一下空间向量的表示。

一个三维向量可以表示为(Vx, Vy, Vz)，其中Vx、Vy和Vz分别是向量在x、y和z轴上的坐标。

如果我们在空间中有两点A(x1, y1, z1)和B(x2, y2, z2)，我们可以通过这两点的坐标求出空间向量AB的坐标。

坐标运算是对空间向量的坐标进行运算。

常用的坐标运算有加法、减法、数量乘法和点乘。

首先，让我们来看一下向量的加法和减法。

如果有两个向量A(x1,y1, z1)和B(x2, y2, z2)，它们的坐标和分别是(x1+x2, y1+y2, z1+z2)。

也就是说，向量的坐标相加就是分别将对应坐标相加。

同样，向量的减法也是使用相同的方式。

接下来，我们来看一下向量的数量乘法。

向量的数量乘法是将向量的坐标分别乘以一个标量。

如果有一个向量A(x, y, z)和一个标量k，那么A乘以k的结果就是(kx, ky, kz)。

最后，我们来看一下向量的点乘。

向量的点乘也叫数量积，结果是一个标量。

如果有两个向量A(x1, y1, z1)和B(x2, y2, z2)，它们的点乘结果等于x1*x2 + y1*y2 + z1*z2。

点乘的结果可以用来判断两个向量之间的夹角、平行性等。

除了以上的基本运算外，我们还可以进行其他更复杂的运算，如叉乘、模长计算等。

叉乘是两个向量的乘积，结果是一个新的向量。

叉乘的结果正交于原来的两个向量，并且模长与原向量之积等于原向量之间的夹角的正弦值。

空间向量的坐标和运算在几何学、物理学等许多学科中都有广泛的应用。

通过对坐标的运算，我们可以计算两点之间的距离、判断两个向量之间的关系等。

在计算机图形学、计算机游戏等领域，也经常使用空间向量的坐标和运算来表示和处理三维图形。

空间向量的坐标表示与计算空间向量是三维空间中的一个重要概念，可以用来表示空间中的一个点或者空间中的两个点之间的位移向量。

为了方便计算和表示，我们可以使用坐标表示来描述和计算空间向量。

一、空间向量的坐标表示在三维坐标系中，可以使用三个坐标轴（通常是x轴、y轴、z轴）来表示一个空间向量的坐标。

这三个坐标轴是相互垂直的，构成一个直角坐标系。

对于一个空间向量v，可以使用v的起点在坐标原点的坐标表示来表示该向量。

假设v的坐标表示为(x, y, z)，其中x、y、z分别表示v在x轴、y轴、z轴上的坐标值。

例如，对于一个空间向量v，如果它的起点在坐标原点，终点的坐标分别为(3, 4, 5)，那么可以表示为v = (3, 4, 5)。

二、空间向量的计算1. 向量的加法空间向量的加法是指将两个向量相加得到一个新的向量。

假设有两个向量a和b，它们的坐标表示分别为(a1, a2, a3)和(b1, b2, b3)。

那么它们的和向量c的坐标表示为(c1, c2, c3)，其中c1 = a1 + b1，c2 = a2 + b2，c3 = a3 + b3。

+ b的坐标表示为(c1, c2, c3) = (1 + 4, 2 + 5, 3 + 6) = (5, 7, 9)。

2. 向量的减法空间向量的减法是指将一个向量减去另一个向量得到一个新的向量。

假设有两个向量a和b，它们的坐标表示分别为(a1, a2, a3)和(b1, b2, b3)。

那么它们的差向量c的坐标表示为(c1, c2, c3)，其中c1 = a1 - b1，c2 =a2 - b2，c3 = a3 - b3。

例如，对于向量a = (1, 2, 3)和向量b = (4, 5, 6)，它们的差向量c = a - b的坐标表示为(c1, c2, c3) = (1 - 4, 2 - 5, 3 - 6) = (-3, -3, -3)。

3. 向量的数量积空间向量的数量积是指将两个向量相乘得到一个标量（即一个数）。

空间向量的3种坐标运算洋葱数学摘要：1.空间向量的概念及坐标表示2.空间向量的加法运算3.空间向量的减法运算4.空间向量的数乘运算5.空间向量的坐标运算应用举例正文：一、空间向量的概念及坐标表示空间向量是指在三维空间中的有向线段，它可以用来表示空间中的物体和运动。

空间向量通常用有序的三元组(x, y, z) 来表示，其中x, y, z 分别代表向量在x, y, z 三个坐标轴上的分量。

二、空间向量的加法运算空间向量的加法是指将两个空间向量相加，得到一个新的空间向量。

空间向量的加法满足平行四边形法则，即两个向量的和等于以这两个向量为邻边的平行四边形的对角线。

设向量A = (x1, y1, z1) 和向量B = (x2, y2, z2)，则向量A 和向量B 的和为：A +B = (x1 + x2, y1 + y2, z1 + z2)三、空间向量的减法运算空间向量的减法是指将两个空间向量相减，得到一个新的空间向量。

空间向量的减法也满足平行四边形法则，即两个向量的差等于以这两个向量为邻边的平行四边形的对角线。

设向量A = (x1, y1, z1) 和向量B = (x2, y2, z2)，则向量A 和向量B 的差为：A -B = (x1 - x2, y1 - y2, z1 - z2)四、空间向量的数乘运算空间向量的数乘是指将一个向量与一个标量相乘，得到一个新的空间向量。

数乘运算满足分配律和结合律。

设向量A = (x, y, z) 和标量k，则向量A 与标量k 的乘积为：kA = (kx, ky, kz)五、空间向量的坐标运算应用举例假设有一个空间直角坐标系，原点为O，向量A = (2, 3, 4) 和向量B = (1, 2, 3)。

现在需要求解向量A 和向量B 的和、差以及向量A 与向量B 的数乘。

空间向量坐标运算空间向量是指在空间中有大小和方向的线段。

空间向量的坐标运算包括向量的加法、减法、数乘和内积。

下面将对这些运算进行详细介绍。

一、向量的加法设空间中有两个向量A和B，它们的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)。

向量的加法即将两个向量的对应分量相加得到一个新的向量C。

它的坐标为(Ax+Bx, Ay+By, Az+Bz)。

例如，设A = (1, 2, 3)和B = (4, 5, 6)，则A+B = (1+4, 2+5, 3+6) = (5, 7, 9)。

二、向量的减法向量的减法是指将一个向量减去另一个向量。

设向量A和B的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)，则向量A减去向量B的坐标为(Ax-Bx, Ay-By, Az-Bz)。

例如，设A = (1, 2, 3)和B = (4, 5, 6)，则A-B = (1-4, 2-5, 3-6) = (-3, -3, -3)。

三、向量的数乘向量的数乘是指一个向量乘以一个实数。

设向量A的坐标为(Ax, Ay, Az)，实数k，则向量A乘以实数k的坐标为(kAx, kAy, kAz)。

例如，设A = (1, 2, 3)，k = 2，则kA = (2*1, 2*2, 2*3) = (2, 4,6)。

四、向量的内积向量的内积又称为点乘，它是两个向量之间的一种运算。

设向量A和B的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)，则向量A与向量B的内积为Ax*Bx + Ay*By + Az*Bz。

例如，设A = (1, 2, 3)和B = (4, 5, 6)，则A·B = 1*4 + 2*5 +3*6 = 32。

向量的内积有以下几个性质：1. 交换律：A·B = B·A；2. 分配律：(A+B)·C = A·C + B·C；3. 数乘结合律：(kA)·B = k(A·B) = A·(kB)。

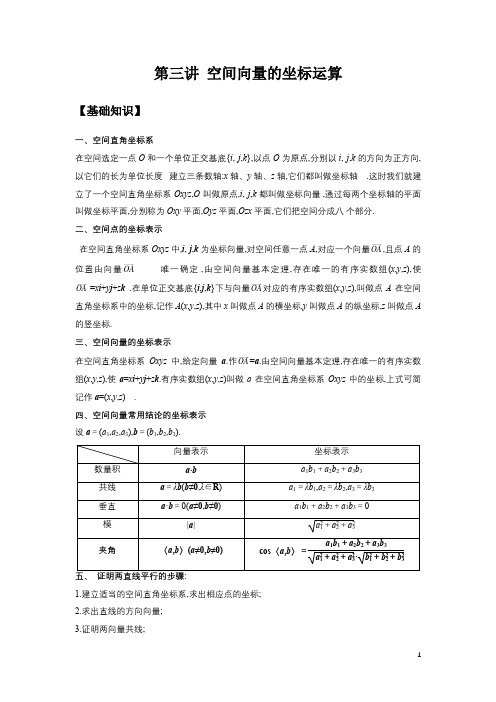
第三讲空间向量的坐标运算【基础知识】一、空间直角坐标系在空间选定一点O和一个单位正交基底{i, j,k},以点O为原点,分别以i, j,k的方向为正方向,以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i, j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面,它们把空间分成八个部分.二、空间点的坐标表示在空间直角坐标系Oxyz中,i, j,k为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位置由向量OA唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使OA=x i+y j+z k.在单位正交基底{i,j,k}下与向量OA对应的有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A 的竖坐标.三、空间向量的坐标表示在空间直角坐标系Oxyz中,给定向量a.作OA=a.由空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=x i+y j+z k.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,上式可简记作a=(x,y,z).四、空间向量常用结论的坐标表示设a＝(a1,a2,a3),b＝(b1,b2,b3).1.建立适当的空间直角坐标系,求出相应点的坐标;2.求出直线的方向向量;3.证明两向量共线;4.说明其中一个向量所在直线上的一点不在另一个向量所在的直线上,即表示方向向量的 有向线段不共线,即可得证. 六、证明两直线垂直的步骤:1.根据已知条件和图形特征,建立适当的空间直角坐标系,正确地写出各点的坐标;2.根据所求点的坐标求出两直线方向向量的坐标;3.计算两直线方向向量的数量积为0;4.由方向向量垂直得到两直线垂直. 七、求两异面直线夹角的步骤1.求异面直线a ,b 上的方向向量的坐标:a =(x 1,y 1,z 1),b =(x 2,y 2,z 2);2.利用公式cos<a ,b >= 求解;3.设异面直线a ,b 所成的角为θ,则cos θ=|cos<a ,b >|.【考点讲解】考点一：求点的坐标例1．已知空间点(3,1,4)P --，则点P 关于y 轴对称的点的坐标为（ ） A ．(3,1,4)--- B ．(3,1,4)-- C ．(3,1,4)-D ．(3,1,4)考点二：求向量的坐标例2．给定空间三个点()1,1,2A ､()3,7,1B -､()5,4,0C . (1)求以向量AB ､AC 为一组邻边的平行四边形的面积S ； (2)求与向量AB ､AC 都垂直的单位向量a .考点三：线性运算的坐标表示例3．已知向量()3,2,5a =-，()1,5,1b =-，则3a b -=（ ） A ．8,11(),14-B ．9,3(),15-C ．10,1(),16-D ．(0,13,2)考点四：数量积运算的坐标表示例4．（多选）已知空间向量()1,1,1a =，()1,0,2b =-，则下列正确的是（ ） A ．()0,1,3a b +=B ．3a =C ．2a b ⋅=D ．a <，4b π→>=考点五：求长度或距离例5．空间两点()1,2,3A 、()2,0,5B 之间的距离为______．考点六：求角度例6．已知()cos ,1,sin a αα=-，()sin ,1,cos b αα=-，则向量a b +与a b -的夹角为（ ） A ．90° B ．60°C ．30°D ．0°考点七：根据平行或垂直求参数的值例7.已知点(2,0,2)A -，(1,1,2)B -，(3,0,4)C -，设a AB =，b AC =． (1)求a ，b 夹角的余弦值．(2)若向量ka b +，2ka b -垂直，求k 的值． (3)若向量a b λ-，a b λ-平行，求λ的值．【课堂练习】1.已知向量(2,1,3),(,2,6)a b x →→=-=-，若a b →→⊥，则实数x 的值为（ ） A ．7B ．8C ．9D ．102.若向量()1,,0a λ=，(2,1,2)b =-且a 与b 的夹角余弦值为23，则实数λ等于（ ） A ．0B ．－43C ．0或－43D ．0或433.平行六面体1111ABCD A B C D -中，()()11,2,3,1,2,4AC C =-，则点1A 的坐标为（ ） A ．()0,4,7B ．()2,0,1-C ．()2,0,1-D ．()2,0,14. （多选）已知平面{}00P n P P α=⋅=，其中点0P 是平面α内的一定点，n 是平面α的一个法向量，若0P 坐标为()2,3,4，()1,1,1n =，则下列各点中在平面α内的是（ ） A ．()1,3,5B ．()4,3,2C ．()2,3,8-D ．()2,3,8-5. （多选）已知正方体1111ABCD A B C D -的棱长为1，,,P Q R 分别在111,,AB CC D A 上，并满足111(01)1D R AP CQ a a PB QC RA a===<<-，设1,,AB i AD j AA k ===，设PQR ∆的重心为G ，下列说法正确的是（ ）A ．向量,,i j i j k +-可以构成一组基底B ．当12a =时，111j+333DG i k =-C ．当13a =时，PQ 在平面1ADD ．对任意实数a ，总有0RG DG ⋅=6.已知空间三点A (1，-1，-1)，B (-1，-2，2)，C (2，1，1)，则AB 在AC 上的投影向量的模是______.7.设空间向量,,i j k 是一组单位正交基底，若空间向量a 满足对任意的,,x y a xi y j --的最小值是2，则3a k +的最小值是_________．8.已知空间中三点(),1,2A m -，()3,1,4B -，()1,,1C n -． (1)若A ，B ，C 三点共线，求m n +的值；(2)若AB ，BC 的夹角是钝角，求m n +的取值范围．【课后练习】1.若点(2,5,1)A --，(1,4,2)B ---，(3,3,)C m n +-在同一条直线上，则m n -=（ ） A ．21B ．4C ．-4D ．102.已知直线2,l l l 的方向向量分别为()()1,4,2,2,1,a b m =-=-，若12l l ⊥，则m 等于（ ） A ．0B ．1C ．2D ．33.设,x y ∈R ，向量(,1,1),(1,,1),(2,4,2)a x b y c ===-，且,a c b c ⊥∥，则||x y +=（ ） A ．1B ．2C ．3D ．44.已知(1,0,1)a =，(,1,2)b x =，且3a b ⋅=，则向量a 与b 的夹角为（ ） A ．60︒B ．120︒C ．30D ．150︒5. （多选）对于非零空间向量a ，b ，c ，现给出下列命题，其中为真命题的是（ ） A ．若0a b ⋅<，则a ，b 的夹角是钝角 B ．若()1,2,3a =，()1,1,1b =--，则a b ⊥ C ．若a b b c ⋅=⋅，则a c =D ．若()1,0,0a =，()0,2,0b =，()0,0,3c =，则a ，b ，c 可以作为空间中的一组基底 6．（多选）已知空间向量()2,1,1a =--，()3,4,5b =，则下列结论正确的是（ ） A ．()2//a b a + B ．53a b = C ．()56a a b ⊥+D ．a 与b 夹角的余弦值为7．（多选）已知空间中三点()0,1,0A ，()1,2,0B ，()1,3,1C -，则正确的有（ ） A ．AB 与AC 是共线向量 B ．AB 的单位向量是()1,1,0C ．AB 与BC 夹角的余弦值是D ．平面ABC 的一个法向量是()1,1,3-8. 平面α经过点()0,0,2A 且一个法向量()1,1,1n =--，则平面α与x 轴的交点坐标是______．9．已知()1,1,2A -，()1,0,1B -．设D 在直线AB 上，且2AD DB =，设1,,13C λλλ⎛⎫++ ⎪⎝⎭，若CD AB ⊥，则实数λ=______．10.空间中，两两互相垂直且有公共原点的三条数轴构成直角坐标系，如果坐标系中有两条坐标轴不垂直，那么这样的坐标系称为“斜坐标系”.现有一种空间斜坐标系，它任意两条数轴的夹角均为60°，我们将这种坐标系称为“斜60°坐标系”.我们类比空间直角坐标系，定义“空间斜60°坐标系”下向量的斜60°坐标：,,i j k 分别为“斜60°坐标系”下三条数轴（x 轴､y 轴､z 轴）正方向的单位向量，若向量n xi yj zk =++，则n 与有序实数组（x ，y ，z ）相对应，称向量n 的斜60°坐标为[x ，y ，z ]，记作[,,]n x y z =. (1)若[]1,2,3a =，[1,1,2]b =-，求a b +的斜60°坐标；(2)在平行六面体11ABCD ABC D -中，AB =AD =2，AA 1=3，1160BAD BAA DAA ∠=∠=∠=，如图，以{}1,,AB AD AA 为基底建立“空间斜60°坐标系”.①若1BE EB =，求向量1ED 的斜60坐标； ①若[]2,,0AM t =，且1AM AC ⊥，求AM .。

空间向量坐标运算空间向量是指具有大小和方向的直线段，在三维空间中通常用坐标表示。

空间向量的坐标运算包括向量的加法、减法、数量乘法、点乘和叉乘等。

下面将详细介绍这些运算。

1. 向量的加法和减法向量的加法和减法是指将两个向量相加或相减得到一个新的向量，其坐标运算规律如下：- 加法：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的和的坐标为(u1+v1, u2+v2, u3+v3)；- 减法：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的差的坐标为(u1-v1, u2-v2, u3-v3)。

2. 向量的数量乘法向量的数量乘法是指将一个向量乘以一个实数得到一个新的向量，其坐标运算规律如下：- 数量乘法：若向量u的坐标为(u1, u2, u3)，实数k，则向量u 乘以k的坐标为(k*u1, k*u2, k*u3)。

3. 向量的点乘向量的点乘又称为内积，是指将两个向量进行乘法运算得到一个标量（实数），其计算公式如下：- 点乘：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的点乘的结果为u1*v1 + u2*v2 + u3*v3。

4. 向量的叉乘向量的叉乘又称为外积，是指将两个向量进行乘法运算得到一个新的向量，其计算公式如下：- 叉乘：若向量u的坐标为(u1, u2, u3)，向量v的坐标为(v1, v2, v3)，则向量u和v的叉乘的坐标为((u2*v3 - u3*v2), (u3*v1 -u1*v3), (u1*v2 - u2*v1))。

通过以上的描述可以看出，向量的加法、减法、数量乘法都是按照对应位置进行运算，只要对应坐标进行相加、相减或乘以相同的实数即可。

点乘和叉乘则需要对应坐标进行特定的运算。

需要注意的是，向量的坐标运算不关心向量的起点和终点，只关心向量的大小和方向。

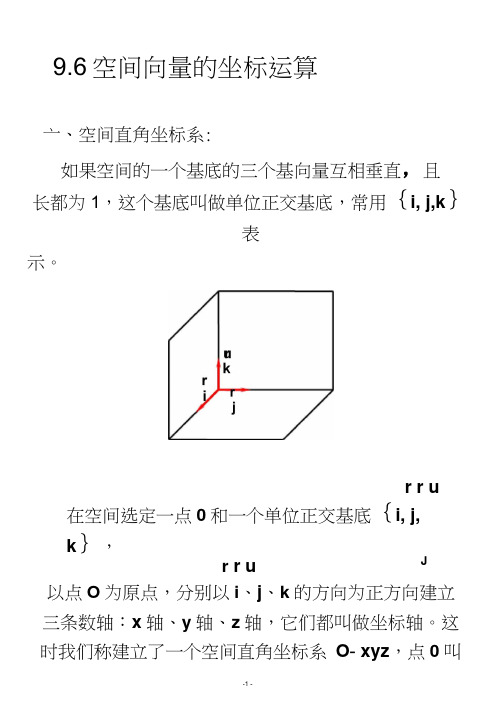
9.6空间向量的坐标运算亠、空间直角坐标系:如果空间的一个基底的三个基向量互相垂直，且长都为1，这个基底叫做单位正交基底，常用｛i, j,k｝表示。

r r u 在空间选定一点0和一个单位正交基底｛i, j,k｝，r r u J 以点O为原点，分别以i、j、k的方向为正方向建立三条数轴：x轴、y轴、z轴，它们都叫做坐标轴。

这时我们称建立了一个空间直角坐标系O- xyz，点0叫r r u做原点，向量i、j、k都叫做坐标向量。

通过每两个坐标轴的平面叫做坐标平面，分别称为xOy平面，yOz 平面，zOx平面。

u注意：①作空间直角坐标系O- xyz时，一般使? xOy 135 °（或45 °）, ? yOz 90 °。

②在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系。

说明右手直角坐标系的特点是：从Ox到Oy是逆时针方向。

③如无特别说明，以后建立的坐标系都是右手直角坐标系。

给定一个空间直角坐标系和向量a，且设i、j、k 为坐标向量，根据空间向量基本定理可知：存在唯一的有序实数组(a i,a2, a3)，使r r r ua = a i i + a2 j + a3 k有序实数组(a i,a2,a3)叫做向量\在空间直角坐标系O- xyz中的坐标，可简记作ra = (a i, a2, a3)z在空间直角坐标系O- xyz中，对空间任一点A，r对应一个向量OA，于是存在唯一的有序实数组x、y、z，使um r r uOA = xi + yj + zk有序实数组(x, y, z)叫做点A的坐标，记作A (x,y,z )，其中x 叫做点A 的横坐标，y 叫做点A 的 纵坐标,z 叫做点A 的竖坐标。

二、空间向量的直角坐标运算：r rI •设 a = (a i , a 2, a 3)? b = (bi ,6 ,b s )，则 ① a + b = (a i + b,a 2 + 6,a 3+ b 3); r r② a - b = (a i - b i ,a 2- b 2,a 3- b s );r③ I a = (l a i ,l a 2,l a 3)(l ? R );r r④ a ?b a i b i + a 2 b 2 + a 3 b s ;r r⑤ a 八 b ? a i b i a 26+ a 3b s = 0;l a i = l bi ^a 2 l b 2(l ? R ) =l b 3①AB 的中点坐标是 严产，皿产，电产); uuur uuur uuur② AB = OB - OA =(X 2- x i , y 2- y i 卫-Z i )。

空间向量运算的坐标公式首先，我们需要明确什么是空间向量。

空间向量是具有大小和方向的量，可以用箭头表示。

在空间中，我们通常使用坐标系来描述向量的位置和方向。

坐标系分为直角坐标系和斜坐标系两种。

直角坐标系由三条相互垂直的坐标轴构成，分别为X轴、Y轴和Z轴，构成一个三维空间。

而斜坐标系是以线段手段两个切平面之间的夹角小于90度的坐标系。

根据空间向量的定义，我们可以将向量表示为一个三元组(a,b,c)，其中a、b、c分别表示向量在X轴、Y轴和Z轴上的投影长度。

例如，向量A可以表示为(Ax,Ay,Az)，向量B可以表示为(Bx,By,Bz)。

根据向量的定义，我们可以得到以下关于向量的基本性质：1.向量相等：当且仅当两个向量的对应分量相等时，它们相等。

即，向量A=向量B当且仅当Ax=Bx,Ay=By,Az=Bz。

2.向量的数量乘法：向量与一个实数相乘，其结果仍然是一个向量。

公式为：k*向量A=(k*Ax，k*Ay，k*Az)。

3.向量的加法：两个向量相加的结果是一个新的向量，其坐标分别为对应坐标的和。

公式为：向量A+向量B=(Ax+Bx，Ay+By，Az+Bz)。

4.向量的减法：两个向量相减的结果是一个新的向量，其坐标分别为对应坐标的差。

公式为：向量A-向量B=(Ax-Bx，Ay-By，Az-Bz)。

5. 向量的线性组合：对于n个向量A1, A2, ... An和n个实数k1, k2, ... kn，他们的线性组合记作k1 * A1 + k2 * A2 + ... + kn * An，其中k1, k2,..., kn为各自的系数。

线性组合的结果仍然是一个向量。

以上是关于向量的基本性质和运算规则。

在实际运算中，我们可以根据这些规则进行计算，将向量的坐标代入公式，求出运算结果的坐标。

除了基本运算外，我们还可以进行向量的点积和叉积运算。

1.向量的点积也称为内积或数量积，其结果是一个实数。

两个向量A 和B的点积公式为：A·B=Ax*Bx+Ay*By+Az*Bz。

9.6 空间向量的坐标运算一、空间直角坐标系：如果空间的一个基底的三个基向量互相垂直，且长都为1，这个基底叫做单位正交基底，常用{},,i j k r r u r表示。

在空间选定一点O 和一个单位正交基底{},,i j k r r u r，以点O 为原点，分别以i r 、j r 、k u r的方向为正方向建立三条数轴：x 轴、y 轴、z 轴，它们都叫做坐标轴。

这时我们称建立了一个空间直角坐标系-O xyz ，点O 叫做原点，向量i r 、j r 、k u r都叫做坐标向量。

通过每两个坐标轴的平面叫做坐标平面，分别称为xOy 平面，yOz 平面，zOx 平面。

注意：O xyz时，一般使①作空间直角坐标系-?xOy135o（或45o），?yOz90o。

②在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系。

说明右手直角坐标系的特点是：从Ox到Oy是逆时针方向。

③如无特别说明，以后建立的坐标系都是右手直角坐标系。

给定一个空间直角坐标系和向量a r，且设i r 、j r 、k u r为坐标向量，根据空间向量基本定理可知：存在唯一的有序实数组(),,a a a 123，使=++a a i a j a k 123r r r u r有序实数组(),,a a a 123叫做向量a r在空间直角坐标系-O xyz 中的坐标，可简记作()=,,a a a a 123r在空间直角坐标系-O xyz 中，对空间任一点A ，对应一个向量OA uu u r，于是存在唯一的有序实数组x 、y 、z ，使=++OA xi y j zk u u u r r r u r有序实数组(),,x y z 叫做点A 的坐标，记作(),,A x y z ，其中x 叫做点A 的横坐标，y 叫做点A 的纵坐标，z 叫做点A 的竖坐标。

二、空间向量的直角坐标运算：Ⅰ．设()=,,a a a a 123r ，()=,,b b b b 123r，则 ①()+=+++,,a b a b a b a b 112233r r； ②()-=---,,a b a b a b a b 112233r r；③()()=?,,a a a a R l l l l l 123r； ④?++a b a b a b a b 112233r r； ⑤^?+=a b a b a b a b 1122330r r；⑥()ì=ïïï??íïïï=ïî//a b a b a b R a b l l l l 112233r r 。