七年级“图形认识初步”检测试题

七年级数学图形的初步认识测试卷考试时间：60分钟；满分：100分姓名：___________班级：___________考号：___________考卷信息：本卷试题共23题，单选10题，填空6题，解答7题，满分100分，限时60分钟，本卷题型针对性较高，覆盖面广，选题有深度，可衡量学生掌握本章内容的具体情况！一．选择题（共10小题，满分30分，每小题3分）1．（3分）如图，点A，B在直线l上，下列说法错误的是（）A．线段AAAA和线段AAAA是同一条线段B．直线AAAA和直线AAAA是同一条直线C．图中以点A为端点的射线有两条D．射线AAAA和射线AAAA是同一条射线2．（3分）如图，某单位要在河岸l上建一个水泵房引水到C处．他们的做法是：过点C 作CCCC⊥ll于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是（）A．两点确定一条直线B．两点之间，直线最短C．两点之间，线段最短D．垂线段最短3．（3分）若∠A＝30°18ʹ，∠B＝30°15ʹ30ʺ，∠C＝30.25°，则这三个角的大小关系正确的是（）A．∠C＞∠A＞∠B B．∠C＞∠B＞∠AC．∠A＞∠C＞∠B D．∠A＞∠B＞∠C4．（3分）已知平面上A，B，C三点，过每两点画一条直线，那么直线的条数有（）A．3条B．1条C．1条或3条D．0条5．（3分）图①是由五个完全相同的小正方体组成的立体图形，将图①中的一个小正方体改变位置后得到图②，则图①与图②的三视图不相同的是（）A．主视图B．俯视图C．左视图D．主视图、俯视图和左视图都不同6．（3分）如图线段AAAA=8cm，点PP在射线AAAA上从点AA开始，以每秒2cm的速度沿着射线AAAA 的方向匀速运动，则PPAA=13AAAA时，运动时间为（）A．83秒B．3秒C．83秒或163秒D．3秒或6秒7．（3分）已知∠αα，∠ββ互补，那么∠ββ与12(∠αα−∠ββ)之间的关系是（）A．和为45° B．差为45° C．互余D．差为90°8．（3分）如图，C为线段AD上一点，点B为CD的中点，且AD=9，BD=2，若点E在直线AD上，且EA=1，求BE的长为（）A．4 B．6或8 C．6 D．8 9．（3分）如图，直线AAAA与CCCC相交于点OO,∠AAOOCC=60∘，一直角三角尺EEOOEE的直角顶点与点OO重合，OOEE平分∠AAOOCC，现将三角尺EEOOEE以每秒3∘的速度绕点OO顺时针旋转，同时直线CCCC也以每秒9∘的速度绕点OO顺时针旋转，设运动时间为tt秒（0≤tt≤40），当CCCC平分∠EEOOEE时，tt的值为（）A．2.5B．30C．2.5或30D．2.5或32.5 10．（3分）如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点MM1，NN1；第二次操作：分别取线段AAMM1和AANN1的中点MM2,NN2；第三次操作：分别取线段AAMM2和AANN2的中点MM3,NN3；……连续这样操作10次，则每次的两个中点所形成的所有线段之和MM1NN1+MM2NN2+⋯+MM10NN10=()A．20−1029B．20+1029C．20−10210D．20+10210二．填空题（共6小题，满分18分，每小题3分）11．（3分）已知直线AB，CD相交于点O，OE平分∠AOD，|∠BOD−∠AAOOCC|＝30°，∠COE 的度数=____．12．（3分）如图，∠BOD＝45°，∠AOE＝90°，那么图中小于或等于90°的角有____个，它们的度数之和是_____．13．（3分）将一个长为4厘米，宽为3厘米的长方形，绕它的一边所在的直线旋转一周，得到的圆柱体的体积是___________.14．（3分）如图，若添上一个正方形，使它能折叠成一个正方体，且使相对面上的数字之和相等，则共有几种不同的添法___________．15．（3分）直线l上的三个点A、B、C，若满足BC＝12AB，则称点C是点A关于点B的“半距点”．如图1，BC＝12AB，此时点C就是点A关于点B的一个“半距点”．如图2若M、N、P三个点在同一条直线m上，且点P是点M关于点N的“半距点”，MN＝6cm．则MP＝________cm．16．（3分）把一根绳子对折成一条线段AB，在线段AB上取一点P，使AP：PB＝1：3，将绳子从点P处剪断，若剪断后的三段绳子中最长的一段为18cm，则三段绳子中最短的一段的长为_____．三．解答题（共7小题，满分52分）17．（6分）如图，已知直线l和直线外三点A，B，C，按下列要求画图：(1)画射线AAAA；(2)连接AACC；(3)在直线l上确定点E，使得AAEE+CCEE最小．18．（6分）（1）如图，若点A，O，B在同一条直线上，∠AAOOCC:∠AAOOCC=8:1，OD是∠AOC 内部的一条射线，∠CCOOCC=2∠CCOOAA，射线OE平分∠AOC．求∠DOE的度数；（2）若点A，O，B不在同一条直线上，射线OC是∠AOB（∠AOB是小于平角的角）内部的一条射线．∠AAOOCC:∠AAOOCC=8:1，∠CCOOCC=2∠CCOOAA，射线OE平分∠AOC．当∠AAOOCC=αα(0°<αα<180°)时，则∠DOE的度数为．（用含αα的代数式表示）19．（8分）综合实践问题情景：某综合实践小组进行废物再利用的环保小卫士行动．他们准备用废弃的宣传单制作装垃圾的无盖纸盒．操作探究：(1)若准备制作一个无盖的正方体纸盒，图1中的___________图形经过折叠能围成无盖正方体纸盒．(2)如图2是小明的设计图，把它折成无盖正方体纸盒后与“小”字相对的是___________(3)如图3，有一张边长为40cm的正方形废弃宣传单，小华准备将其四角各剪去一个小正方形，折成无盖长方体纸盒．①请你在图3中画出示意图，用实线表示剪切线，虚线表示折痕．②若四角各剪去了一个边长为5cm的小正方形，这个纸盒的容积．20．（8分）综合与探究已知线段AAAA=15，P，Q是线段AAAA上的两点（点P在点Q的左边），且PPPP=5．(1)如图1，若点C在线段AAAA上，且AACC=12AACC，当P为AACC的中点时，求AAPP的长．(2)若M为线段AAPP的中点，N为线段AAPP的中点．①如图2，当线段PPPP在线段AAAA上时，求线段MMNN的长；②当线段PPPP在线段AAAA的延长线上时（点P，Q都在AAAA的延长线上），猜想线段MMNN的长是否发生变化？请说明理由．21．（8分）一个几何体由大小相同的立方块搭成，从上面看到的形状如图所示，其中小正方形中的数字表示在该位置的立方块个数．（1）在所给的方框中分别画出该儿何体从正面，从左面看到的形状图；（2）若允许从该几何体中拿掉部分立方块，使剩下的几何体从正面看到的形状图和原几何体从正面看到的形状图相同，则最多可拿掉个立方块．22．（8分）已知：如图，点M是线段AB上一定点，AB＝12cm，C、D两点分别从M、B 同时出发以1cm／s、3cm／s的速度沿直线BA向左运动，运动方向如箭头所示（C在线段AM上，D在线段BM上）（1）若AM＝4cm，当点C、D运动了2s，此时AC＝_____，DM＝_____；（直接填空）（2）若点C、D运动时，总有MD＝3AC，①求线段AM的值，②若N是直线AB上一点，且AN－BN＝MN，求MMMM AAAA的值23．（8分）如图，以直线AB上一点O为端点作射线OC，使∠BOC=70°，将一块直角三角板DOE直角顶点放在点O处．(1)如图1，若直角三角板DOE的一边OD放在射线OB上，则∠COE=____________°；(2)如图2，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OC恰好平分∠BOE，求∠BOD、∠COE的度数；(3)如图3，将直角三角板DOE绕点O转动，如果OD始终在∠BOC的内部，试猜想∠BOD 和∠COE有怎样的数量关系？并说明理由．。

第四章 图形的初步认识单元测验试卷初一 班 座号 姓名 成绩（满分100分， 时间90分钟）一． 选择题(共每题4分，共32分)1.①平角是一条直线. ②线段AB 是点A 与点B 的距离.③射线AB 与射线BA 表示同一条射线. ④过一点有且只有一条直线与已知直线平行. ⑤圆柱的侧面是长方形。

以上说法正确的有( )A .0个 B.1个 C.2个 D.3个2．在下列立体图形中，不属于多面体的是（ ）A ．正方体B ．三棱柱C ．长方体D ．圆锥体 3.两个锐角的和（ ）A ．一定是锐角B 一定是直角C 一定是钝角D 可能是钝角、直角或锐角 4.平面上有三点A 、B 、C ，如果AB=8，AC=5，BC=3，则（ ） A 点C 在线段AB 上 B 点B 在线段AB 的延长线上C 点C 在直线AB 外D 点C 可能在直线AB 上，也可能在直线AB 外 5.如右图所示，B 、C 是线段AD 上任意两点，M 是AB 的中点，N 是CD 中点，若MN=a ，BC=b ，则线段AD 的长是（ ） A 2（a-b ） B 2a-b C a+b D a-b 6.如图，115︒∠=,90AOC ︒∠=,点B 、O 、D 在同一直线上， 则2∠的度数为（ ）A ． 75︒B ．15︒C ．105︒D ．165︒7.在海上，灯塔位于一艘船的北偏东40度方向，那么这艘船位于这个灯塔的（ ）A 南偏西50度方向B 南偏西40度方向C 北偏东50度方向D 北偏东40度方向8.如图,////,//AB EF DC EG BD , 则图中与1∠相等的角共有( )个A 6个B .5个C .4个 D.2个二． 填空题(3+3+3+4+8=21分)9.不在同一直线上的四点最多能确定 条直线。

10.如右图,点C 是 AOB ∠的边OA 上一点，D 、E 是OB 上两点， 则图中共有 条线段， 条射线, 个小于平角的角.11.如图,点C 是线段AB 上一点，点D 、E 分别是线段AC 、BC 的中点. 如果AB=a,AD=b,其中a>2b,那么CE=A DB MC N ABC DEFGH1ABCDE O A BC D EABCDO1212.（1） ?'2330︒= ︒ 78.36_________'____"︒︒=（2）5245'3246'_________'︒︒︒-= 18.32634'_____︒︒︒+= 13.如图,①如果12∠=∠,那么根据 ,可得 // .得14.如图，AOB ∠为已知角，请画出AOB ∠的平分线OC ，在OC 上任取一点P ，过P 点分别作两边OA 、OB 的垂线段PM 、PN ；用尺子量出PM 、PN 的长，并比较PM 、PN 的大小（请保留作图痕迹）(6分)15.在如图所示，将方格中的图形向右平移3格，再向上平移4格，画出平移后的图形.(3分))16.(1) 一个角的余角比它的补角29还多1︒，求这个角.(2)已知互余两角的差为20︒ ,求这两个角的度数.AB OAB C17.如图，AD=12DB ， E 是BC 的中点，BE=1AC=2cm ，求线段DE 的长.ABD18如图,直线//a b ,1(225)x ∠=-︒,2(175)x ∠=-︒,求1,2∠∠的度数.19．在下图中,已知直线AB 和直线CD 被直线GH 所截,交点分别为E 、F 点，AEF EFD ∠=∠.（1）写出//AB CD 的根据;（2）若ME 是AEF ∠的平分线, FN 是EFD ∠的平分线, 则EM 与FN 平行吗?若平行,试写出根据.ABC DEFGMNa b 1 2l20． 如图，已知：//AD BC ，且DC AD ⊥于D ，求证：①DC BC ⊥②12180∠+∠=︒21.如图， CD AB ⊥于D ， GF AB ⊥于F ，140,250∠=︒∠=︒，求B ∠度数.ABC D 12345A BCD EFG1234。

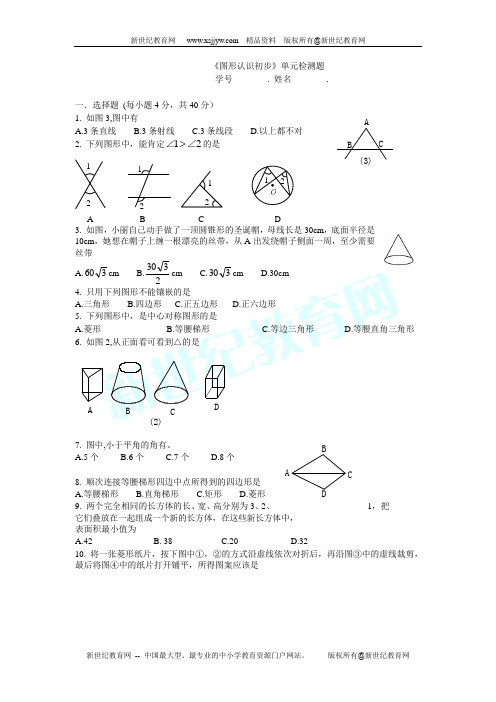
DA B C 《图形认识初步》单元检测题学号________. 姓名________.一．选择题 (每小题4分，共40分）1. 如图3,图中有 A.3条直线 B.3条射线 C.3条线段 D.以上都不对2. 下列图形中，能肯定12 ∠∠的是3. 如图，小丽自己动手做了一顶圆锥形的圣诞帽，母线长是30cm ，底面半径是10cm ，她想在帽子上缠一根漂亮的丝带，从A 出发绕帽子侧面一周，至少需要丝带A.360cmB.2330cm C.330cm D.30cm 4. 只用下列图形不能镶嵌的是A.三角形B.四边形C.正五边形D.正六边形5. 下列图形中，是中心对称图形的是A.菱形B.等腰梯形C.等边三角形D.等腰直角三角形6. 如图2,从正面看可看到△的是C (2)AD B7. 图中,小于平角的角有。

A.5个 B.6个 C.7个 D.8个8. 顺次连接等腰梯形四边中点所得到的四边形是A.等腰梯形B.直角梯形C.矩形D.菱形 9. 两个完全相同的长方体的长、宽、高分别为3、2、1，把它们叠放在一起组成一个新的长方体，在这些新长方体中，表面积最小值为A.42B. 38C.20D.3210. 将一张菱形纸片，按下图中①，②的方式沿虚线依次对折后，再沿图③中的虚线裁剪，最后将图④中的纸片打开铺平，所得图案应该是1 2 122 1A B C D C(3)A B二.简答题 （每小题3分，共24分)11. 在平面上有任意四点,过其中任意两点画直线,能画_______条直线.12. 图是一个五角星图案，中间部分的五边形ABCDE 是一个正五边形，则图中∠ABC 的度数是___________13. 如图，将一条直的等宽纸带折叠，AB 为折痕，∠CDE=320，则∠EAB=_________.14. 一幅图案.在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形，则第三个正多边形的边数是_________.15. 在直径为1000mm 的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=800mm ，则油的最大深度为__________mm 。

第四章 图形认识初步目标检测试卷（四）一、 精心选一选：（每小题3分，共30分）1、过不在一条直线直上的A 、B 、C 三点中每两个点作一条直线，共可作直线（ ）A 1条B 2条C 3条D 4条2、8点30分，时钟的时针与分针所夹的角度是（ ）A 60°B 70°C 75°D 80°3、如图，共有（ ）个小于180°的角A 5B 6C 7D 84、如图，哪一个图形能够折叠成一个无盖的盒子（ ）AB C D5、正方体的三视图为（ ）A 三个大小一样的正方形B 一个正方形和两个长方形C 三个大小不一样的正方形D 以上都不对6、一个角是钝角,那么这个角的一半是（ ）A 锐角B 直角C 钝角D 以上都有可能7、下列说法中正确的是（ ）A 延长线段AB B 延长射线OAC 在直线AB 的延长线上取一点CD 延长线段BA 到C ，使BC=AB8、若两个角的度数和为90°，则这两个角中至少有一个角不大于（ ）A 30°B 45°C 50°D 55°9、38°15′和38.15°的关系是( )A 38°15′＞38.15°B 38°15′＜38.15°C 38°15′=38.15°D 以上都有可能10、下列说法正确的是（ ）A 在角的一边的延长线上取一点AB 角的两边张的越开,角就越大C 用一个放大倍率为2倍的放大镜放大一个20°的角是40°D 角的两边伸的越长,角就越大二、 耐心填一填：（每小题3分，共30分）1、直线有 个端点，射线有 个端点，线段有 个端点2、21周角= 平角= 直角= ° 3、一个几何体的三种视图如图，它是4、立体图形可分为 体、 体和 体 3题图 主视图 左视图 俯视图5、圆柱的侧面展开图是 ，圆锥的侧面展开图是 ，棱柱的侧面展开图是6、68°12′的余角为7、如图，图中有 条线段8、点A 是线段BC 外一点，一定有AB+AC BC ，理由是9、如图，OC 是∠AOB 的平分线，则∠AOC = 10、将一个直角三角尺绕着一条直角边旋转一周得到的几何体是 三、用心做一做：（本大题共60分）1、计算下列各题：（每小题4分，共8分）（1）、22°18′×5 （2）90°-57°23′27″2、（本题8分）已知线段AB=8cm ，点C为线段AB 上任一点，M 是AC中点，N是BC 中点，求线段MN 的长？3、（本题8分）读下列语句并画出图形：（1）画直线AC ；（2）画线段AB ；（3）画射线BC ；（4）直线AC 与BD 相交于点O4、（本题12分）指出下面每组左面三个图形是右面物体分别从哪个方向观察到的图形，如图（1）（2）C D A B E 7题图 · · · · · A O C B 9题图· A · B · D·C5、（本题12分）如图所示，O 是直线AB 上一点，OC 是任意一条射线，OD 一平分∠AOB ，OE 平分∠BOC ，那么射线OD 与OE 互相垂直吗？请说明理由6、（本题12分）如图所示，一辆汽车在马路上行驶，∠AOB=40°，∠CO’D=140°,若这辆汽车向右拐,则需拐多少度的角?若这辆汽车向左拐,则需拐多少度的角?参考答案：一、1、C ；2、C ；3、C ；4、D ；5、A ；6、A ；7、A ；8、B ；9、A ；10、B二、1、0，1，2；2、1，2，90；3、三棱柱；4、柱，锥，球；5、长方形，扇形，长方形；6、21°48′；7、10；8、＞，两点之间线段最短；9、∠BOC ；10、圆锥；三、1、（1）111°30′，（2）32°36′33″；2、4cm ；3、略；4、（1）俯视图，左视图、主视图，（2）主视图、俯视图、左视图；5、互相垂直；6、140°、40°。

初一几何图形初步试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是几何图形？A. 圆B. 三角形C. 正方形D. 直线答案：D2. 一个正方形的边长为4厘米，它的周长是多少厘米？A. 8厘米B. 12厘米C. 16厘米D. 20厘米答案：C3. 一个圆的半径是5厘米，它的直径是多少厘米？A. 10厘米B. 15厘米C. 20厘米D. 25厘米答案：A4. 下列哪个图形是轴对称图形？A. 正方形B. 圆形C. 长方形D. 所有选项答案：D5. 如果一个三角形的三个内角之和为180度，它是什么类型的三角形？A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等边三角形答案：B二、填空题（每题2分，共10分）6. 平行四边形的对边________。

答案：平行且相等7. 一个圆的周长公式是________。

答案：C = 2πr8. 如果一个多边形的内角和是900度，那么它是________边形。

答案：六9. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的斜边长度是________厘米。

答案：510. 一个正六边形的内角是________度。

答案：120三、简答题（每题5分，共15分）11. 描述什么是几何图形的对称性？答案：几何图形的对称性是指图形在某个点、直线或平面上翻转或反射后，能够与原图形完全重合的性质。

12. 解释什么是相似图形？答案：相似图形是指两个图形在形状上完全相同，但大小可以不同，且它们的对应角相等，对应边成比例。

13. 什么是圆周角定理？答案：圆周角定理是指一个圆周角的度数是它所截取的弧所对圆心角的一半。

四、计算题（每题10分，共20分）14. 已知一个三角形的三个顶点坐标分别为A(1,2)，B(4,6)，C(7,4)，请计算这个三角形的面积。

答案：首先计算AB和AC的长度，然后使用海伦公式计算三角形的面积。

15. 一个圆的半径为7厘米，求这个圆的面积。

答案：使用圆的面积公式A = πr²，代入半径r=7厘米，计算得到面积。

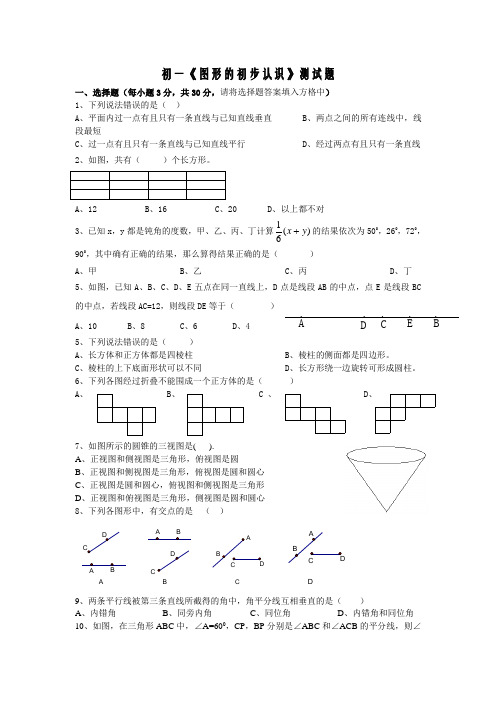
初一《图形的初步认识》测试题一、选择题（每小题3分，共30分，请将选择题答案填入方格中） 1、下列说法错误的是（ ）A 、平面内过一点有且只有一条直线与已知直线垂直B 、两点之间的所有连线中，线段最短C 、过一点有且只有一条直线与已知直线平行D 、经过两点有且只有一条直线 2、如图，共有（）个长方形。

A 、12B 、16C 、20D 、以上都不对3、已知x ，y 都是钝角的度数，甲、乙、丙、丁计算)(61y x 的结果依次为500，260，720，900，其中确有正确的结果，那么算得结果正确的是（ ） A 、甲B 、乙C 、丙D 、丁5、如图，已知A 、B 、C 、D 、E 五点在同一直线上，D 点是线段AB 的中点，点E 是线段BC 的中点，若线段AC=12，则线段DE 等于（ ） A 、10B 、8C 、6D 、45、下列说法错误的是（ ）A 、长方体和正方体都是四棱柱B 、棱柱的侧面都是四边形。

C 、棱柱的上下底面形状可以不同D 、长方形绕一边旋转可形成圆柱。

6、下列各图经过折叠不能围成一个正方体的是（ ）A、B 、C 、D 、7、如图所示的圆锥的三视图是( ).A 、正视图和侧视图是三角形，俯视图是圆B 、正视图和侧视图是三角形，俯视图是圆和圆心C 、正视图是圆和圆心，俯视图和侧视图是三角形D 、正视图和俯视图是三角形，侧视图是圆和圆心8、下列各图形中，有交点的是 （ ）ABA BCBACD9、两条平行线被第三条直线所截得的角中，角平分线互相垂直的是（ ） A 、内错角 B 、同旁内角 C 、同位角 D 、内错角和同位角 10、如图，在三角形ABC 中，∠A=600，CP ，BP 分别是∠ABC 和∠ACB 的平分线，则∠C. . . . AD E B.P=（ ） A 、900B 、1000C 、1100D 、1200二、填空题（每小题3分，共30分） 11、18.03°=__________°__________′12、平面上有四个点，过其中每两个点画直线，可以画________________________条。

七年级（上）《图形认识初步》单元试卷班姓名分数一、选择题（每小题3分，共30分）1. 平面上任意三点，经过其中任意两点画直线，共可画直线的条数为（）A.一条B.两条C.三条D.四条2. 点C在线段AB上，下列条件不能确定点C是线段的中点的是（）A.AB=BCB.AC+BC=ABC.AB=2ACD.BC= ½AB3. 如图，在射线AD上取两点B、C，则图中共有多少条射线( )A.4B.3C.2D.14.可近似看作直线的是（）A.绷紧的琴弦B.探照灯射出的光线C.孙悟空的金箍棒D. 太阳的光线5.已知点A、B、C都在直线l 上，且AB=6cm，BC=2cm则A、C两点间的距离是（）A.4厘米B.8厘米C.4厘米或8厘米D.12厘米6. 如果线段AB=10厘米，MA+MB=15厘米，那么下列说法正确的是（）A.点M在线段AB 上B.点M在直线AB上C.点M在线段AB外D.点M可能在直线AB上，也可能在直线AB外7.下列说法正确的有（）①过两点有且只有一条直线②射线是直线的一半③两点之间线段最短④若AB=BC，则点B是线段AC的中点A.1个B.2个C.3个D.4个8. 下列说法中，不正确的是（）A.任何线段都能度量它们的长度B.因为线段有长度，所以它们之间都能比较大小C.利用圆规配合刻度尺可以进行线段的度量，也可以比较它们的大小D.两条直线也可以进行度量和比较大小9. 如图，小明从家到学校有四条路可走，其中最近的路是（）A. （4）B. （3）C. （2）D. （1）10. 若AC=BC=4厘米，则AB长为（）A.8厘米B.2厘米C.12厘米D.无法确定(4)(3)(2)(1)二、填空题（每小题3分，共30分）11.如果点是直线a上的三点，那么在直线a上以为端点共有条射线.12.如果点是直线a上的n个点，那么在直线a上以为端13.右图中，共有条线段.14.用钉子把一根细木条钉在墙上，木条可以绕着钉子转动，根据的是经过一点可以画条直线；当用两个钉子把木条钉住时，木条就被固定了，根据的是.15.乘火车从A站出发，沿途经过3个车站可到达B站，那么A、B两站间共有种不同的车票.16.在直线L上取三点A,B,C ，使得AB =4厘米,BC =6厘米，如果O 是线段AC 的中点，则线段OB 的长为.17.直线AB上有一点C，直线AB外有一点D，则A、B、C、D四点能确定的直线有条.18.已知线段AB=8，平面上有一点P，若PA=5，则当PB= 时，点P在AB上..19. 延长线段AB至C，使BC=3AB，则BC= AC.20. 在纸上画出四个点（其中任意三点都不在同一直线上），经过每两个点用直尺画直线，一共可以画条直线.三、解答题（每小题8分，共40分）21.线段AB上有点C，M、N分别AC、BC是的中点.（1）若AC=2，BC=4，求MN的长度；（2）若AM=1，BC=4，求MN的长度；（3）若AB=6，求MN的长度.22.已知三条线段a,b,c在同一直线上，它们有共同的起点，a的终点是b的中点，c的中点是b的终点，且a+b+c=7cm，求a,b,c的长.23.如图所示，已知线段AB上有任意两点C、D，M、N分别为AC、DB的中点，且AB=a，CD =b，求MN 的长24.在线段AB 的延长线上取一点c ，使BC =3AB ，在AB的反向延长线上取一点D，使DA= ½AB，点E为DB的中点.若DE=6mm，求BC ,DC的长.25.(1)如图，已知点C在线段AB上，线段AC=10cm ，BC=6cm ，点M、N分别是AC、BC的中点，求线段MN的长度；(2)根据（1）中的计算过程和结果，设AC+BC=a ，其他条件不变，你能猜测出MN的长度吗？用一句简洁的话表述你发现的规律；(3)对于（1）题，如果我们这样叙述它：“已知线段AB=10cm,BC =6cm,点C在直线AB上，点M、N分别是AC、BC的中点，求MN的长度.”结果会有变化吗？如果有，求出结果.NAM C。

第四章《图形认识初步》 综合测试题（满分120 分时间90 分钟）一、选择题（每题 3 分，共 30 分）1． ①平角是一条直线；②射线是直线的一半；③射线一个扩大 2 倍的放大镜去看一个角， 这个角会扩大= 120 °50. ?AB 与射线 BA 表示同一条射线；④用2 倍；⑤两点之间，线段最短； ⑥ 120.5 °以上说法正确的有 (A.0 个B.12．以下四个图中，能用∠)个 C.2 个 D.3 个1、∠ AOB 、∠ O 三种方法表示同一个角的是（）3．以下表达正确的选项是（） A ． 180°是补角B 120°和 60°互为补角 C 120 °和 60°是补角 D 60°是 30°的补角4. 如图 1 表示一个用于防震的 L 形的包装用泡沫塑料，当从上边看这一物体时看到的图形形状是（）A ．B ．C ．D ．(图 1)5．以下图形中，哪一个是正方体的睁开图（）6．甲看乙的方向为南偏西25°，那么乙看甲的方向是 （）A ．北偏东 75° B．南偏东 75° C．北偏东 25° D ．北偏西 25°7．若∠ A 的余角是 70°，则∠ A 的补角是（）A ． 70°B ．110°C ． 20°D ． 160°8．如图，AOC和BOD都是直角，假如D CAOB150 ，那么 COD（）AA 、30B 、40C 、50D 、60BO9.经过随意三点中的两点共可画出（）A ．1 条直线B ． 2 条直线C ．1 条或 3 条直线D ． 3 条直线10. 如下图，从O点出发的五条射线，能够构成角的个数是（）．A．10个B．9个C．8个D．4个二、填空题（每题 3 分，共 30 分）11．橙子近似 ______ 体，菠萝近似 _______ 体，角柜近似 _______ 体，金字塔近似 _______体，粉笔盒近似 _______体。

数学华师大版（2024）七年级上册第3章图形的初步认识单元测试一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.下列现象中，属于中心投影的是()A.白天旗杆的影子B.阳光下广告牌的影子C.灯光下演员的影子D.中午小明跑步的影子2.对于如图所示的几何体，说法正确的是()A.几何体是三棱锥B.几何体有6条侧棱C.几何体的侧面是三角形D.几何体的底面是三角形3.如图是某几何体的三视图，则该几何体是()A. B. C. D.4.下列几何体中，从左面看到的图形是三角形的几何体共有()A.1B.2C.3D.45.如图,学校C 在蕾蕾家B 南偏东55︒的方向上,点A 表示超市所在的位置,90ABC ∠=︒,则超市A 在蕾蕾家B 的()A.北偏西25︒的方向上B.南偏西25︒的方向上C.北偏西35︒的方向上D.南偏西35︒的方向上6.如图，16cm AB =，10cm AD BC ==，则CD 等于()A.4cmB.6cmC.8cmD.10cm 7.下列平面图形中,经过折叠不能围成正方体的是()A. B. C. D.8.如图，点O 在直线AB 上，90COB EOD ∠=∠=°，那么下列说法错误的是()A.1∠与2∠相等B.AOE ∠与2∠互余C.AOD ∠与1∠互补D.AOE ∠与COD ∠互余9.已知线段12cm AB =,点C 是直线AB 上一点,4cm BC =,点M 是线段AB 的中点,点N 是线段BC 的中点,则线段MN 的长度是()A.4cmB.6cmC.4cm 或8cmD.6cm 或8cm10.如图，射线OC 平分AOB ∠，射线OD 平分BOC ∠，则下列等式中成立的有()①COD AOD BOC ∠=∠-∠；②COD AOD BOD ∠=∠-∠；③22COD AOD AOB ∠=∠-∠；④13COD AOB ∠=∠.A.①②B.①③C.②③D.②④二、填空题（每小题4分，共20分）11.在下列生活、生产现象中：可以用基本事实“两点确定一条直线”来解释的是________(填序号).①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上.12.如图，已知点O 在直线AB 上，16515∠=︒'，27830∠=︒'，则12∠+∠=_________，3∠=_________.13.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______.14.如图,已知线段16cm AB =,点M 在AB 上:1:3AM BM =,P ,Q 分别为AM 、AB 的中点,则PQ 的长为____________.15.如图，126AOB ∠=︒，射线OC 在AOB ∠外，且2BOC AOC ∠=∠，若OM 平分BOC ∠，ON 平分AOC ∠，则MON ∠=_________.三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）某几何体的三视图如图所示.（1）该几何体的名称是_______；（2）根据图中的数据，求该几何体的侧面积.（结果保留π）17.（8分）如图，是一个长方体纸盒的平面展开图，已知纸盒中相对的两个面上的数互为相反数.(1)分别写出a 、b 的值；(2)先化简，再求值：()22242325a b a b ab a b ab ⎡⎤---+⎣⎦18.（10分）如图，是由一些棱长都为1的小正方体组合成的简单几何体.（1）该几何体的表面积(含下底面)为______；（2）请画出这个几何体的三视图并用阴影表示出来；（3）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加______个小正方体.19.（10分）如图，点A ，O ，B 在同一条直线上，射线OD 和射线OE 分别平分AOC ∠和BOC ∠.(1)求DOE ∠的度数；(2)①图中BOE ∠的补角是______；②直接写出图中与COE ∠互余的角______.20.（12分）如图，点C 在线段AB 上，点M ，N 分别是AC ，BC 的中点.（1）若9cm AC =，6cm CB =，求线段MN 的长.（2）若C 为线段AB 上任一点，满足cm AC CB a +=，其他条件不变，你能猜想出MN 的长度吗？请说明理由.（3）若C 在线段AB 的延长线上，且满足cm AC BC b -=，点M ，N 分别为AC ，BC 的中点，你能猜想MN 的长度吗？请画出图形，写出你的结论，并说明理由.21.（12分）已知：AOB ∠，过点O 引两条射线OC ，OM ，且OM 平分AOC ∠.(1)如图，若120AOB ∠=︒，30BOC ∠=︒，且点C 在AOB ∠的内部.①请补全图形；②求出MOB ∠的度数；以下是求MOB ∠的度数的解题过程，请你补充完整.AOC AOB BOC ∠=∠-∠ ，120AOB ∠=︒，30BOC ∠=︒，答案以及解析1.答案：C解析：A.白天旗杆的影子为平行投影，所以A选项不合题意；B.阳光下广告牌的影子为平行投影，所以B选项不合题意；C.灯光下演员的影子为中心投影，所以C选项符合题意；D.中午小明跑步的影子为平行投影，所以D选项不合题意.故选：C.2.答案：D解析： 该几何体是三棱柱，∴底面是三角形，侧面是四边形，有3条侧棱，∴D说法正确，A、B、C说法错误，故选：D.3.答案：A解析： 该几何体的主视图与左视图都是矩形，俯视图是一个圆，∴该几何体是圆柱，故选：A.4.答案：B解析：第一个几何体从左面看到的图形是圆形；第二个几何体从左面看到的图形是三角形；第三个几何体从左面看到的图形是长方形；第四个几何体从左面看到的图形是正方形；第五个几何体从左面看到的图形是三角形；∴从左面看到的图形是三角形的几何体共有2个，故选：B.5.答案：D解析：如图所示：由题意可得：255∠=︒,90ABC ∠=︒,∴1905535∠=︒-︒=︒,∴超市A 在蕾蕾家B 的的南偏西35︒的方向上.故选：D.6.答案：A解析：因为16cm AB =，10cm AD BC ==，所以1010164(cm)CD AD BC AB =+-=+-=.7.答案：C解析：由展开图可知:A 、B 、D 能围成正方体,故不符合题意;C 、围成几何体时,有两个面重合,不能围成正方体,故符合题意:故选:C.8.答案：D解析：∵90COB EOD ∠=∠=︒，∴1290COD COD ∠+∠=∠+∠=︒，∴12∠=∠，故A 选项正确；∵190AOE ∠+∠=︒，∴290AOE ∠+∠=︒，即AOE ∠与2∠互余，故B 选项正确；∵2180AOD ∠+∠=︒，12∠=∠，∴1180AOD ∠+∠=︒，即AOD ∠与1∠互补，故C 选项正确；无法判断AOE ∠与COD ∠是否互余，例如当1230∠=∠=︒时，60COD AOE ∠∠==︒，120AOE COD ∠+∠=︒，不互余，故D 选项错误；故选：D.9.答案：C解析：当点C 在线段AB 上时,点M 是线段AB 的中点,点N 是线段BC 的中点,16cm 2AM BM AB ∴===,12cm 2CN BN BC ===,624cm MN BM BN ∴=-=-=,当点C 在线段AB 的延长线上时,点M 是线段AB 的中点,点N 是线段BC 的中点,16cm 2AM BM AB ∴===,12cm 2CN BN BC ===,628cm MN BM BN ∴=+=+=,综上所述,线段MN 的长度是4cm 或8cm ,故选C.10.答案：B解析：OC 平分AOB ∠，OD 平分BOC ∠，AOC BOC ∴∠=∠，COD BOD∠=∠COD AOD AOC ∠=∠-∠ ，AOC BOC∠=∠COD AOD BOC∴∠=∠-∠故①正确；BOD BOC∠≠∠ COD AOD BOD∴∠≠∠-∠故②错误；AOD AOC COD∠=∠+∠ ()222AOD AOC COD AOB COD∴∠=∠+∠=∠+∠222AOD AOB AOB COD AOB COD∴∠-∠=∠+∠-∠=∠22COD AOD AOB∴∠=∠-∠故③正确；12COD BOC ∠=∠ ，12BOC AOB ∠=∠111224COD AOB AOB ∴∠=⨯∠=∠故④错误；故选：B.11.答案：①④/④①解析：①用两颗钉子就可以把木条固定在墙上，可以用基本事实“两点确定一条直线”来解释；②把笔尖看成一个点，当这个点运动时便得到一条线，可以用基本事实“无数个点组成线”来解释；③把弯曲的公路改直，就能缩短路程，可以用基本事实“两点之间线段最短”来解释；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上，可以用基本事实“两点确定一条直线”来解释；综上可得：①④可以用“两点确定一条直线”来解释，故答案为：①④.12.答案：14345︒'；3615︒'解析：因为16515∠=︒'，27830∠=︒'，所以126515783014345'''∠+=+=︒∠︒︒，所以3180(12)180143453615︒''∠=︒-∠+∠=︒-=︒.13.答案：左视图解析：如图,该几何体正视图是由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,故三种视图面积最小的是左视图.故答案为左视图14.答案：6cm解析：根据已知条件得到4cm AM =.12cm BM =,根据线段中点的定义得到2cm 12AP AM ==,8cm 12AQ AB ==,从而得到答案.解析：∵16cm AB =,:1:3AM BM =,∴4cm AM =.12cm BM =,∵P ,Q 分别为AM ,AB 的中点,∴2cm 12AP AM ==,8cm 12AQ AB ==,∴6cm PQ AQ AP =-=；故答案为：6cm .15.答案：117︒解析：因为360AOB BOC AOC ∠+∠+∠=︒，所以360BOC AOC AOB ∠+∠=︒-∠.因为OM 平分BOC ∠，ON 平分AOC ∠，所以12MOC BOC ∠=∠，12CON AOC ∠=∠，所以1122MON MOC CON BOC AOC ∠=∠+∠=∠+∠()111()360180222BOC AOC AOB AOB =∠+∠=︒-∠=︒-∠11801261172=︒-⨯︒=︒，故答案为117︒.16.答案：（1）圆锥（2）()2dm 解析：（1）由三视图可知，原几何体为圆锥.故答案为：圆锥.（2）根据图中数据知，圆锥的底面半径为4，高为6，∴=，∴圆锥的侧面积为()218πdm 2⨯⨯⨯=.17.答案：(1)3a =-，5b =(2)2a b ab -+，60-解析：（1）由长方体展开图的特点可知3a =-，()55b =--=；（2）()22242325a b a b ab a b ab ⎡⎤---+⎣⎦()22242635a b a b ab a b ab =--++()2245a b a b ab =--2245a b a b ab=-+2a b ab=-+当3a =-，5b =时，原式()()23535451560=--⨯+-⨯=--=-.18.答案：（1）28（2）见解析（3）2解析：（1）()()42624211⨯+⨯+⨯⨯⨯()81281=++⨯281=⨯28=所以该几何体的表面积(含下底面)为28，（2）如图所示：（3）由分析可知，最多可以再添加2个小正方体19.答案：(1)90DOE ∠=︒(2)COD ∠和AOD∠解析：(1) 点A ，O ，B 在同一条直线上，180AOC BOC ∴∠+∠=︒，射线OD 和射线OE 分别平分AOC ∠和BOC ∠，12COD AOC ∴∠=∠，12COE BOC ∠=∠，()11190222COD COE AOC BOC AOC BOC ∴∠+∠=∠+∠=∠+∠=︒，90DOE ∴∠=︒；(2)①图中BOE ∠的补角是AOE ∠；②直接写出图中与COE ∠互余的角COD ∠和AOD ∠，故答案为：COD ∠和AOD ∠.20.答案：（1）7.5cm（2）1cm 2a ，理由见解析（3）能，1cm 2MN b =，理由见解析解析：（1）因为9cm AC =，点M 是AC 的中点，所以1 4.5cm 2CM AC ==.因为6cm BC =，点N 是BC 的中点，所以13cm 2CN BC ==，所以7.5cm MN CM CN =+=，所以线段MN 的长度为7.5cm .（2）1cm 2MN a =.理由：因为C 为线段AB 上一点，且M ，N 分别是AC ，BC 的中点，所以11()cm 22MN MC CN AC BC a =+=+=.（3）能.当点C 在线段AB 的延长线上时，如图，1cm 2MN b =.理由：因为点M 是AC 的中点，所以12CM AC =.因为点N 是BC 的中点，所以12CN BC =，所以11()cm 22MN CM CN AC BC b =-=-=.②AOC AOB BOC ∠=∠-∠ ，90AOC ∴∠=︒.AOC BOC AOB ∴∠=∠+∠12AOM AOC ∴∠=∠=AOC BOC AOB ∴∠=∠-∠1β。

七级数学第四章几何图形初步测试题（新课标）（时限： 100分钟总分： 100 分）一、选择题：将以下各题正确答案的代号填在下表中。

每题 2 分，共 24 分。

题号123456789101112答案1.如图是一个小正方体的睁开图，把睁开图折叠成小正方体后，有“建”字一面的相对面上的字是（）A.和B.谐C.社D.会2.下边左侧是用八块完整同样的小正方体搭成的几何体，从上边看该几何体获得的图是（）建设和谐社第 1题图会A B C D3.如图，四个图形是由立体图形睁开获得的，相应的立体图形按序是（）A. 正方体、圆柱、三棱柱、圆锥B. 正方体、圆锥、三棱柱、圆柱C. 正方体、圆柱、三棱锥、圆锥D. 正方体、圆柱、四棱柱、圆锥第 3题图4.如图，关于直线AB，线段 CD，射线 EF，此中能订交的是（）CBB A B DA AF C DEF E F EA B C D5.以下说法中正确的选项是（）A.画一条 3 厘米长的射线B.画一条 3 厘米长的直线C.画一条 5 厘米长的线段D.在线段、射线、直线中直线最长6.如图，将一副三角尺按不一样地点摆放，摆放方式中∠与∠互余的是（）ααβββαβαA B C D1 CD ；③ CD ＝ 2CE ；7.点 E 在线段 CD 上，下边四个等式① CE ＝ DE ；② DE ＝2④CD ＝ 1DE.此中能表示 E 是线段 CD 中点的有（）2A.1个B.2个C. 3个D.4个8. C 是线段 AB 上一点， D 是 BC 的中点，若 AB ＝ 12cm ，AC ＝ 2cm ，则 BD 的长为（）A. 3cmB. 4cmC. 5cmD. 6cm9.如图是一正方体的平面睁开图，若AB ＝4，则该正方体 A 、B 两点间的距离为（）A. 1B. 2 AC. 3D. 410.用度、分、秒表示 91.34°为（ ）第 9题图BA. 91°20/24//B. 91° 34/C. 91° 20/ 4//D. 91° 3/ 4//11.以下说法中正确的选项是（）A.若∠ AOB ＝ 2∠ AOC ，则 OC 均分∠ AOBB.延伸∠ AOB 的均分线 OCC.若射线 OC 、 OD 三等份∠ AOB ，则∠ AOC ＝∠ DOCD.若 OC 均分∠ AOB ，则∠ AOC ＝∠ BOC12.甲、乙两人各用一张正方形的纸片ABCD 折出一个 45°的角（如图） ，两人做法以下：DCD (B)CDNCP1MABAAB乙甲甲：将纸片沿对角线 AC 折叠，使 B 点落在 D 点上，则∠ 1＝ 45°；乙：将纸片沿AM 、 AN 折叠，分别使 B 、 D 落在对角线 AC 上的一点 P ，则∠ MAN ＝ 45°关于两人的做法，以下判断正确的选项是（）A.甲乙都对B.甲对乙错C.甲错乙对D.甲乙都错二、填空题：本大题共8 小题，每题3 分，共 24 分。