下载文档原格式
《运筹学》第三版（清华大学出版社）P79例1，表上作业法，运用西北角法确定初始基可行解。
西北角法是从西北角（左上角）格开始，在格内的右下角标上允许取得的最大数；然后按行（列）标下一格的数；若某行（列）的产量（销量）已满足，则把该行（列）的其他格划去；如此进行下去，直至得到一个基本可行解的方法。
西北角法的例子： P79例1从表1中可知，总的产量=总的销量，故产销是平衡的。
第一步：列出运价表和调运物资平衡表。
运用表上作业法时，首先要列出被调运物资的运价表和供需平衡表（简称平衡表），如表1，2所示。
第二步：编制初始调运方案。
首先在表2的西北角方格（即左上角方格，对应变量x11），尽可能取最大值：x11=min{3,7}=3将数值3填入该方格(见表3)。
由此可见x21,x31必须为0，即第一列其他各方格都不能取非零值，划去第一列。
在剩下的方格中，找出其西北角方格x12，x12=min{6,7-3}=4将4填入它所对应方格，第一行饱和，划去该行。
再找西北角方格x22，x22=min{6-4,4}=2将2填入x22所对应方格，于是第二列饱和，划去该列。
继续寻找西北方格为x23，x23=min{5,4-2}=2将2填入x23所对应方格，第二行饱和，划去该行。
剩下方格的西北角方格为x33，x33=min{5-2,9}=3将3填入x33所对应方格，第三列饱和，划去该列。
最后剩下x34方格，取x34 = 6。
这样我们就找到了m＋n-1＝3＋5-1＝7个基变量，它们为：x11 = 3,x12 = 4,x22 = 2,x23 = 2,x33 = 3,x34 = 6。
显然它们用折线连接后不形成闭回路。
这就是西北角法所找初始基可行解，所对应的目标值为：2×200＋1×250＋3×150＋1×150＋3×250＋3×300＋4×200＝4000我们找到的初始基可行解可通过各行方格中数值之和是否等于产量，各列方格中数值之和是否等于销量来简单验证。
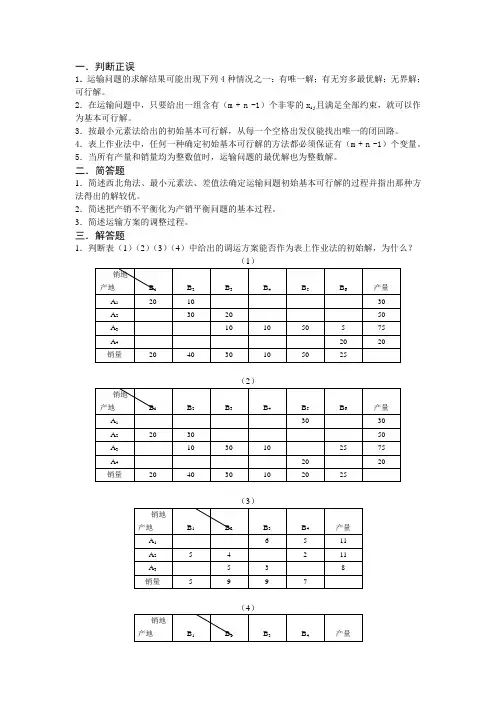
3.3试对、最小元素法、和vogel法进行比较，分析给出的解之质量不同的原因。
3.7试判断表3-30和表3-31中给出的调运方案可否作为表上作业法迭代时的基可行解？为什么？表3-313.11表3-36示出一个运输问题及它的一个解，试问：(1) 表中给出的解是否为最优解？请用位势法进行检验。
C由1变为3，所给的解是否仍为最优解？若不是，请求出最优解。
(2) 若价值系数24(3) 若所有价值系数均增加1，最优解是否改变？为什么？(4) 若所有价值系数均乘以2，最优解是否改变？为什么？4.2 利用图解法解下列目标规划问题：(1) min {}+++-+1323211),2(,d P d d P d Pst.⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=≥=-+=-+=-+++-+-+-+-3,2,10,,,40401502213322211121i d d x x d d x d d x d d x x i i (2) min {})5.1(,,),(4342312431---+++++d d P d P d P d d PSt.⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=-+=-+=-++=-+++-+-+-+-+-4,3,2,10,,,1530100402144233122211121i d d x x d d x d d x d d x x d d x x i i4.3 用单纯形法解下列目标规划问题：（1） min {})35(,,),(2343322111++--+-++d d P d P d P d d Pst.⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=≥=-+=-+=-+++-+-+-+-3,2,10,,,1400325005800213322211121i d d x x d d x d d x d d x x i i (2) min {}+--+-+144332211),35(,,d P d d P d P d PSt.⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=-+=-+=-++=-+++-+-+-+-+-4,3,2,10,,,457090802144233122211121i d d x x d d x d d x d d x x d d x x i i4.4对于目标规划问题min {})53(),35(,,3243234211++--+-++d d P d d P d P d PSt.⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=-+=-+=-+=-+++-+-++-+-+-4,3,2,10,,,10457080214413322211121i d d x x d d d d d x d d x d d x x i i（1） 用单纯形法求问题的满意解；（2） 若目标函数变为min {}+++---++4432332211),53(),35(,d P d d P d d P d P则满意解有什么变化？（3） 分别对第二和第三优先级各目标权系数作灵敏度分析。
3.3试对、最小元素法、和vogel法进行比较，分析给出的解之质量不同的原因。
3.7试判断表3-30和表3-31中给出的调运方案可否作为表上作业法迭代时的基可行解？为什么？表3-313.11表3-36示出一个运输问题及它的一个解，试问：(1) 表中给出的解是否为最优解？请用位势法进行检验。
C由1变为3，所给的解是否仍为最优解？若不是，请求出最优解。
(2) 若价值系数24(3) 若所有价值系数均增加1，最优解是否改变？为什么？(4) 若所有价值系数均乘以2，最优解是否改变？为什么？4.2 利用图解法解下列目标规划问题：(1) min {}+++-+1323211),2(,d P d d P d Pst.⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=≥=-+=-+=-+++-+-+-+-3,2,10,,,40401502213322211121i d d x x d d x d d x d d x x i i (2) min {})5.1(,,),(4342312431---+++++d d P d P d P d d PSt.⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=-+=-+=-++=-+++-+-+-+-+-4,3,2,10,,,1530100402144233122211121i d d x x d d x d d x d d x x d d x x i i4.3 用单纯形法解下列目标规划问题：（1） min {})35(,,),(2343322111++--+-++d d P d P d P d d Pst.⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=≥=-+=-+=-+++-+-+-+-3,2,10,,,1400325005800213322211121i d d x x d d x d d x d d x x i i (2) min {}+--+-+144332211),35(,,d P d d P d P d PSt.⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=-+=-+=-++=-+++-+-+-+-+-4,3,2,10,,,457090802144233122211121i d d x x d d x d d x d d x x d d x x i i4.4对于目标规划问题min {})53(),35(,,3243234211++--+-++d d P d d P d P d PSt.⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=-+=-+=-+=-+++-+-++-+-+-4,3,2,10,,,10457080214413322211121i d d x x d d d d d x d d x d d x x i i（1） 用单纯形法求问题的满意解；（2） 若目标函数变为min {}+++---++4432332211),53(),35(,d P d d P d d P d P则满意解有什么变化？（3） 分别对第二和第三优先级各目标权系数作灵敏度分析。
西北角法是一种求解线性规划问题的方法，其步骤如下：
1. 确定问题的目标函数和约束条件。
目标函数是我们希望最大化或最小化的函数，约束条件是限制我们的决策变量的取值范围的条件。
2. 找到问题的最优解。
最优解是指在满足约束条件的情况下，使目标函数达到最大值或最小值的决策变量的取值。
最优解可以通过求解线性规划问题的标准形式来找到。
3. 确定最优解的位置。
最优解通常位于问题的可行解区域的某个角落，即最优解的决策变量的取值可能是整数或有限小数。
因此，我们需要找到问题的最优解的位置，以便我们可以确定最优解的决策变量的取值。
4. 确定最优解的方向。
最优解的方向是指从问题的可行解区域的某个点出发，沿着最优解的方向移动到最优解的位置的方向。
最优解的方向可以通过计算决策变量的梯度向量来确定。
5. 确定最优解的位置。
一旦我们确定了最优解的方向，我们可以沿着最优解的方向移动到最优解的位置。
最优解的位置可以通过计算最优解所在的格子的决策变量的取值来确定。
6. 确定最优解的值。
一旦我们确定了最优解的位置，我们可以计算最优解所在的格子的决策变量的取值，从而确定最优解的值。
最优解的值是目标函数在最优解的位置上的函数值。
7. 检查最优解是否满足约束条件。
一旦我们确定了最优解的位置和值，我们需要检查最优解是否满足约束条件。
如果最优解不满足约束条件，则我们需要重新开始求解过程，直到找到一个满足约束条件的最优解为止。
![10.表上作业法初始可行解的确定-优化[12页]](https://img.taocdn.com/s1/m/07c160faf18583d0486459e4.png)
《运筹学》第三版（清华大学出版社）P79例1，表上作业法，运用西北角法确定初始基可行解。
西北角法是从西北角（左上角）格开始，在格内的右下角标上允许取得的最大数；然后按行（列）标下一格的数；若某行（列）的产量（销量）已满足，则把该行（列）的其他格划去；如此进行下去，直至得到一个基本可行解的方法。
西北角法的例子：P79例1
从表1中可知，总的产量=总的销量，故产销是平衡的。
第一步：列出运价表和调运物资平衡表。
运用表上作业法时，首先要列出被调运物资的运价表和供需平衡表（简称平衡表），如表1，2所示。
第二步：编制初始调运方案。
首先在表2的西北角方格（即左上角方格，对应变量x11），尽可能取最大值：
x
=min{3,7}=3
11
将数值3填入该方格(见表3)。
由此可见x21,x31必须为0，即第一列其他各方格都不能取非零值，划去第一列。
在剩下的方格中，找出其西北角方格x12，x
=min{6,7-3}=4
12
将4填入它所对应方格，第一行饱和，划去该行。
再找西北角方格x22，
x
=min{6-4,4}=2
22
将2填入x22所对应方格，于是第二列饱和，划去该列。
继续寻找西北方格为x23，
x
=min{5,4-2}=2
23
将2填入x23所对应方格，第二行饱和，划去该行。
剩下方格的西北角方格为x33，
x
3=min{5-2,9}=3
3
将3填入x33所对应方格，第三列饱和，划去该列。
最后剩下x34方格，取x34 = 6。
这样我们就找到了m＋n-1＝3＋5-1＝7个基变量，它们为：x11= 3,x12= 4,x22 = 2,x23 = 2,x33 = 3,x34 = 6。
显然它们用折线连接后不形成闭回路。
这就是西北角法所找初始基可行解，所对应的目标值为：
2×200＋1×250＋3×150＋1×150＋3×250＋3×300＋4×200＝4000
我们找到的初始基可行解可通过各行方格中数值之和是否等于产量，各列方格中数值之和是否等于销量来简单验证。
利用西北角法找初始基可行解简单可行，但也存在问题。
例如在表3中可见c
= 4，单价高于该行其他各方格，最简单想法是单价小的情况下多运些货物，35
这样总运费会更小些，最小元素法就改进了西北角法的缺点。
