高中数学-柱锥台和球的体积教案

1.1.7 柱锥台和球的体积【教学目标】知识与技能:理解祖暅原理，能使用祖暅原理和长方体体积公式推导出柱体、锥体、台体和球的体积公式，并可以使用体积公式求几何体的体积过程与方法:学生通过实例理解祖暅原理，借助长方体体积公式和祖暅原理推出柱的体积公式，学生通过小组探究、合作交流得到锥体的体积公式，运用化未知为已知的方法，接触到了立体几何中“割”“补”的思想方法.情感态度价值观:通过知识的发现过程，形成科学的研究价值观，收获研究成功的喜悦. 【重点】理解祖暅原理，能用祖暅原理推出柱、锥和球的体积公式【难点】用祖暅原理推出柱、锥和球的体积公式【教学过程】一. 知识回顾长方体的体积公式V abc Sh==圆柱的体积公式V Sh=圆锥的体积公式13V Sh =二. 新授课现在有1套3副扑克牌，整体摆放如图⑴，若有另1套3副扑克牌，经过变换，如图⑵，提问◇1:摆放图⑴的三幅扑克牌，你有办法求出体积吗？预设◇1:长方体，体积公式V abc=；提问◇2:摆放图⑵的三幅扑克牌，体积是多少呢？预设◇2:与摆放图⑴的三幅扑克牌的体积相同；提问◇3:对于图⑵的三幅扑克牌，你是怎么样得到体积的呢？预设◇3:两副扑克大小一样，每张牌都一样，张数一样，故体积相同.1.祖暅原理:幂势既同，则积不容异.原理说明:○1“幂”——截面面积（所有的截面）；②“势”——几何体的高；③等底面积、等高的柱体体积相同；④等底面积、等高的锥体体积相同；2.柱体体积公式V Sh=提问◇1:棱柱是如何产生的？预设◇1:看成一个多边形（包括图形围成的平面部分）上各点都沿着同一个方向移动相同的距离所形成的几何体.提问◇2:圆柱是如何产生的？预设◇2:a.矩形绕一边旋转得到的，追问:圆柱能否看成某平面图形移动相同的距离所形成；b. 圆柱可以看成一个圆（包括圆的内部）上各点都沿着同一个方向移动相同的距离所形成的几何体.提问◇3:现在有一个长方体、一个圆柱、一个棱锥，等底面积、等高，它们的体积有什么关系？请说明理由.预设◇3:体积相同.等底面积，说明用水平面截得的①截面面积相等，等高说明几何体②高相等，由祖暅原理，得“积不容异”.提问◇4:这些柱体体积怎么计算？预设◇4:柱体体积公式V Sh=.小结:通过祖暅原理和长方体体积公式，圆柱的体积公式V Sh=是完全正确的.学生活动：自由举手发言，说清楚想法和过程.设计意图:柱体体积公式的得到，只需要简单的使用祖暅原理即可，让学生在问题中不断认识到祖暅原理的使用方法.3.锥体体积公式13V Sh =提问◇1:对于学习过的锥体是你知道哪种锥体的体积公式？你是怎么得到的.预设◇1:圆锥13V Sh=，通过取等底面积，等高的圆柱和圆锥倒水试验的方法得到.提问◇2:等底面积，等高的圆锥和棱锥之间体积会怎么样呢？我们取最特殊的棱锥，正三棱锥.你有办法证明吗？预设◇2:学生自主思考，小组讨论后，表述讨论结果. 小结1.:等底面积、等高的锥体体积相同.提问◇3:等底面积、等高的柱体之间体积相同和锥体之间体积相同，对于柱体和锥体之间的体积关系我们还没有证明，你能用今天学习的知识证明：三棱锥的体积是等底面积、等高的三棱柱体积的关系吗？13V V =锥柱.学生活动：小组讨论，汇报讨论结果.预设◇3:将三棱柱切割成三个三棱锥，如图，现只需要说明三个三棱锥体积相同即可. ⑴ ''B'C'A ABC B A V V --=,等底面积，等高的锥体积相等； ⑵ ''''B'C'A B BC B A V V --=,等底面积，等高的锥体积相等； ⑶ 13V V =锥柱.小结2: 1133V V Sh ==锥柱设计意图:让学生体会割补的思想方法，能够使用祖暅原理解释数学问题.学生进一步体会祖暅原理的使用.可能出现换底的三棱锥体积问题，可以做适当的铺垫. 三. 课堂探究 4.球体体积公式343V R π=问题探究、如图，将半径为R 的半球和底面半径为R 、高为R 的圆柱放在同一水平面上，现在圆柱中挖去一个底面半径为R 、高为R 圆锥.若用任意一个平行于水平面的平面去截这两个几何体，通过计算比较两个截面面积的大小关系.你能从中发现什么数学结论？学生活动：学生自主解决问题，投影解决问题过程.预设：两个截面面积的大小相等，两个几何体的体积相等.球的体积公式343V R π=球. 小结: 343V R π=球. 设计意图:通过计算得到数学结论，让学生体会发现结论的过程. 四. 课堂练习例题、如图所示，在长方体ABCD-A'B'C'D'中，用截面截下一个棱锥C-A'DD'，求棱锥C-A'DD'的体积与剩余C'A部分的体积之比.设计意图:割补长方体得到体积关系或者计算得到关系都可以，可以让学生体会割补的思想方法和计算的功能.巩固练习1、已知长方体形的铜块长、宽、高分别为2、4、8，将它铸成一个球形的铜块（不计损耗），求铸成的球形铜块的半径；2、某工厂将一块正方体铜块铸成了三个半径为1的球，求原正方体的棱长.设计意图:巩固练习，熟悉数学公式.五. 课外探究已知台体的上下底面面积分别为S’、S，台体的高为h，你可以借助今天学到的知识和方法推出台体的体积吗？设计意图:学生自主解决问题，体会补形的思想，熟悉锥体的体积公式.六. 课后作业学案卷课后作业【板书设计】。

1.1.7柱、锥、台和球的体积一、教学目标1、理解祖暅原理的内容；2、了解柱、锥、台体的体积公式的推导；3、掌握柱、锥、台体和球的体积公式。

4、能运用公式求柱体，锥体，台体和球的体积重点：体积计算及公式的推导方法难点：祖暅原理的理解及体积公式的应用二、知识梳理对祖暅原理的理解：关键词：夹在，两个平行平面，任意平面所截，截面的面积总相等1、柱体的体积一般柱体的体积公式V =，其中S为底面面积，h为棱柱的高。

棱柱〔圆柱〕的高是指两底面之间的距离，即从一底面上任意一点向另一个底面作垂线，这点与垂足〔垂线与底面的交点〕之间的距离。

2、锥体的体积圆锥的体积公式是V=〔S为底面面积，h为高〕，它是同底等高的圆柱的体积的13。

棱锥的体积也是同底等高的棱柱体积的13，即棱锥的体积V=〔S为底面面积，h为高〕。

棱锥与圆锥的体积公式类似，都是棱锥〔圆锥〕的高是指从顶点向底面作垂线，顶点与垂足〔垂线与底面的交点〕之间的距离。

3、台体的体积由于圆台〔棱台〕是由圆锥〔棱锥〕截成的，因此可以利用两个锥体的体积差，得到园台〔棱台〕的体积公式：V=，其中S'，S分别为上、下底面面积，h为圆台〔棱台〕的高。

圆台〔棱台〕的高是指两个底面之间的距离。

4、球的体积：设球的半径为R，那么它的体积为V=球，是以R为自变量的函数。

三、[例题解析]阅读课本例1与例2完成课后练习A第1，2，3题补充例题2、直棱柱底面是菱形，面积为S，过两不相邻侧棱的截面面积分别为m，n，求直棱柱的体积2、假设干毫升水倒入底面半径为2的圆柱形器皿中，量得水面的高度为6，假设将这些水倒入轴截面是正三角形的倒圆锥形器皿中，那么水面的高度为3、过球面上三点A、B、C的截面到球心的距离等于球半径的一半、且AC＝BC＝AB＝6，求球的体积。

[限时训练]1、正方体的全面积是S,那么它的体积是( )()A()B()C()D2、假设圆柱和圆锥的底面直径,高都与球的直径相等,那么圆锥,球,圆柱的体积比是( )()A4:2:3()B1:2:3 ()C2:1:3 ()D8:32:243、台体中一个平行于底面的截面把台体分成上下两部分，假设台体的上底面面积，截面面积，下底面面积之比为1：4：9，那么截面把台体分成上下两部分的体积的比值为〔〕()A 827()B719()C513()D354、如果轴截面为正方形的圆柱的侧面积为S，那么圆柱的体积等于〔〕〔A〔B〔C〔D5、圆柱的侧面展开图是边长为2和4的矩形，那么圆柱的体积是;6、三棱锥的三条侧棱两两垂直，三个侧面的面积分别为6，4，3，那么三棱锥的体积为;7、一个钢球的直径是5，那么它的体积是；假设球半径变为原来的2倍，体积变为原来的倍;8、棱长均相等的正四棱锥的全面积为)2361cm +，那么它的体积为； 9、一个正三棱台的上，下底面边长分别为3cm 和6cm ，高是32cm ，求三棱台的〔1〕侧棱长；〔2〕斜高；〔3〕体积.10、棱台的两个底面面积分别是245cm 2和80cm 2，截得这个棱台的棱锥的高为35cm ，求这个棱台的体积[课后作业]习题1-1A 第7，8，9题。

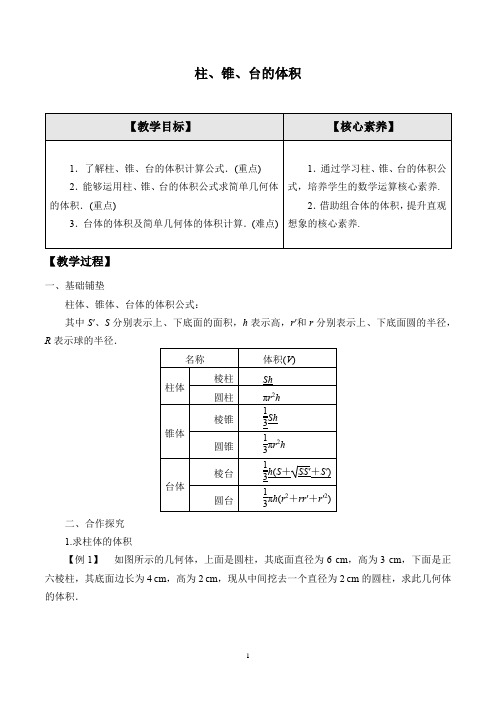
柱、锥、台的体积【教学过程】一、基础铺垫柱体、锥体、台体的体积公式：其中S′、S分别表示上、下底面的面积，h表示高，r′和r分别表示上、下底面圆的半径，R表示球的半径．二、合作探究1.求柱体的体积【例1】如图所示的几何体，上面是圆柱，其底面直径为6 cm，高为3 cm，下面是正六棱柱，其底面边长为4 cm，高为2 cm，现从中间挖去一个直径为2 cm的圆柱，求此几何体的体积．[解] V 六棱柱＝34×42×6×2＝483(cm 3)，V 圆柱＝π·32×3＝27π(cm 3)，V 挖去圆柱＝π·12×(3＋2)＝5π(cm 3)，∴此几何体的体积：V ＝V 六棱柱＋V 圆柱－V 挖去圆柱＝(483＋22π)(cm 3)．【规律方法】计算柱体体积的关键及常用技巧（1）计算柱体体积的关键：确定柱体的底面积和高.（2）常用技巧：①充分利用多面体的截面及旋转体的轴截面，构造直角三角形，从而计算出底面积和高. ②由于柱体的体积仅与它的底面积和高有关，而与柱体是几棱柱，是直棱柱还是斜棱柱没有关系，所以我们往往把求斜棱柱的体积通过作垂直于侧棱的截面转化成求直棱柱的体积.2.求锥体的体积【例2】 在如图三棱台ABC ­A 1B 1C 1中，AB ∶A 1B 1＝1∶2，求三棱锥A 1­ABC ，三棱锥B ­A 1B 1C ，三棱锥C ­A 1B 1C 1的体积之比．[思路探究] AB ∶A 1B 1＝1∶2―→S △ABC ∶S △A 1B 1C 1―→计算VA 1­ABC ―→计算VC ­A 1B 1C 1―→计算VB ­A 1B 1C[解] 设棱台的高为h ，S △ABC ＝S ，则S △A 1B 1C 1＝4S .∴VA 1­ABC ＝13S △ABC ·h ＝13Sh ，VC ­A 1B 1C 1＝13S △A 1B 1C 1·h ＝43Sh .又V 台＝13h (S ＋4S ＋2S )＝73Sh ，∴VB ­A 1B 1C ＝V 台－VA 1­ABC －VC ­A 1B 1C 1＝73Sh －Sh 3－4Sh 3＝23Sh ，∴体积比为1∶2∶4．【规律方法】三棱柱、三棱台可以分割成三个三棱锥，分割后可求锥体的体积和柱体或台体的体积关系，割补法在立体几何中是一种重要的方法．3.求台体的体积【例3】 已知正四棱台两底面边长分别为20 cm 和10 cm ，侧面积是780 cm 2．求正四棱台的体积．[思路探究] 可以尝试借助四棱台内的直角梯形．求出棱台底面积和高，从而求出体积．[解] 如图所示，正四棱台ABCD ­A 1B 1C 1D 1中，A 1B 1＝10 cm ，AB ＝20 cm.取A 1B 1的中点E 1，AB 的中点E ，则E 1E 是侧面ABB 1A 1的高．设O 1．O 分别是上、下底面的中心，则四边形EOO 1E 1是直角梯形．由S 侧＝4×12(10＋20)·E 1E ＝780，得EE 1＝13，在直角梯形EOO 1E 1中，O 1E 1＝12A 1B 1＝5，OE ＝12AB ＝10，∴O 1O ＝E 1E 2－OE －O 1E 12＝12，V 正四棱台＝13×12×(102＋202＋10×20)＝2 800 (cm 3)．故正四棱台的体积为2 800 cm 3．【规律方法】求台体的体积关键是求出上、下底面的面积和台体的高．要注意充分运用棱台内的直角梯形或圆台的轴截面寻求相关量之间的关系．三、课堂总结1．本节课的重点是掌握柱体、锥体、台体的体积的求法．2．本节课要重点掌握的规律方法（1）求空间几何体的体积的方法．（2）求与组合体有关的体积的方法．3．本节课的易错点是求与三视图有关的几何体的体积时，易把相关数据弄错．四、课堂练习1．思考辨析（1）夹在两个平行平面间的两个几何体，被平行于这两个平面的某个平面所截，如果截得的两个截面面积相等，则这两个几何体的体积相等．()（2）锥体的体积只与底面积和高度有关，与其具体形状无关．()（3）由V锥体＝13S·h，可知三棱锥的任何一个面都可以作为底面．()[答案]（1）×（2）√（3）√2．如果轴截面为正方形的圆柱的侧面积是4π，那么圆柱的体积等于() A．πB．2πC．4πD．8πB[设轴截面正方形的边长为a，由题意知S侧＝πa·a＝πa2．又∵S侧＝4π，∴a＝2．∴V圆柱＝π×2＝2π.]3．已知圆锥SO的高为4，体积为4π，则底面半径r＝________.3[由已知得4π＝13πr2×4，解得r＝ 3.]4．一个正三棱锥底面边长为6，侧棱长为15，求这个三棱锥体积．[解]如图所示，正三棱锥S­ABC．设H为正三角形ABC的中心，连接SH，则SH的长即为该正三棱锥的高．连接AH并延长交BC于E，则E为BC的中点，且AE⊥BC．∵△ABC是边长为6的正三角形，∴AE＝32×6＝3 3.∴AH＝23AE＝2 3.在△ABC 中，S △ABC ＝12BC ·AE ＝12×6×33＝9 3.在Rt △SHA 中，SA ＝15，AH ＝23， ∴SH ＝SA 2－AH 2＝15－12＝ 3.∴V S ­ABC ＝13S △ABC ·SH ＝13×93×3＝9．。

柱体、锥体、台体的体积教案二时柱体、锥体、台体的体积（一）教学目标1．知识与技能（1）了解几何体体积的含义，以及柱体、锥体与台体的体积公式（不要求记忆公式）（2）熟悉台体与柱体和锥体之间体积的转换关系（3）培养学生空间想象能力和思维能力2．过程与方法（1）让学生通过对照比较，理顺柱体、锥体、台体之间的体积关系（2）通过相关几何体的联系，寻找已知条的相互转化，解决一些特殊几何体体积的计算3．情感、态度与价值观通过柱体、锥体、台体体积公式之间的关系培养学生探索意识（二）教学重点、难点重点：柱体、锥体、台体的体积计算难点：简单组合体的体积计算（三）教学方法讲练结合教学环节教学内容师生互动设计意图新导入1．复习柱体、锥体、台体表面积求法及相互关系教师设问，学生回忆师：今天我们共同学习柱体、锥体、台体的另一个重要的量：体积复习巩固点出主题探索新知柱体、锥体、台体的体积1．柱体、锥体、台体的体积公式：V柱体= Sh (S是底面积，h为柱体高)V锥体= (S是底面积，h为锥体高)V台体= (S′，S分别为上、下底面面积，h为台体的高)2．柱体、锥体、台体的体积公式之间的关系师：我们已经学习了正方体，长方体以及圆柱的体积公式，它们的体积公式是什么？生：V = Sh (S为底面面积，h为高)师：这个公式推广到一般柱体也成立，即一般柱体体积公式：V = Sh (S为底面面积，h为高)师：锥体包括圆锥和棱锥，锥体的高是指从顶点向底面作垂线，顶点与垂足之间的距离(投影或作出) 锥体的体积公式都是V = (S为底面面积，h为高)师：现在请对照柱体、锥体体积公式你发现有什么结论生：锥体体积同底等高的柱体体积的师：台体的结构特征是什么？生：台体是用平行于锥体底面的平面去截锥体，截得两平行平面间的部分师：台体的体积大家可以怎样求？生：台体的体积应该等于两个锥体体积的差师：利用这个原理我们可以得到台体的体积公式V =其中S′、S分别为上、下底面面积，Q为台体的高(即两底面之间的距离)师：现在大家计论思考一下台体体积公式与柱体、锥体的体积公式有什么关系？生：令S′=0，得到锥体体积公式令S′=S，得到柱体体积公式柱体、锥体、台体的体积公式只要求了解，故采用讲授式效率会更高因台体的体积公式的推导需要用到后面知识，故此处不予证明，只要学生了解公式及公式的推导思路培养探索意识，加深对空间几何体的了解和掌握典例分析例 1 有一堆规格相同的铁制(铁的密度是78g/3)六角螺帽(如图)共重8g，已知底面是正六边形，边长为12，内孔直径为10，高为10，问这堆螺帽大约有多少个( 取314，可用计算器)？解：六角螺帽的体积是六棱柱体积与圆柱体积的差，即≈296 (3) = 296(3)所以螺帽的个数为8×1000÷(78×296)≈ 22(个)答：这堆螺帽大约有22个师：六角螺帽表示的几何体的结构特征是什么？你准备怎样计算它的体积？生：六角螺帽表示的几何体是一个组合体，在一个六棱柱中间挖去一个圆柱，因此它的体积等于六棱柱的体积减去圆柱的体积学生分析，教师板书过程师：求组合体的表面积和体积时，要注意组合体的结构特征，避免重叠和交叉等空间组合体的体积计算关键在于弄清它的结构特征典例分析例2 已知等边圆柱（轴截面是正方形的圆柱）的全面积为S，求其内接正四棱柱的体积【解析】如图，设等边圆柱的底面半径为r，则高h = 2r，∵S = S侧+ 2S底= 2 + ，∴∴内接正四棱柱的底面边长a=2r sin4°=∴V = S底•h == 4• ，即圆柱的内接正四棱柱的体积为教师投影例2并读题师：要解决此题首先要画出合适的轴截面图帮助我们思考，要求内接正四棱柱的体积，只需求出等边圆柱的底面圆半径r，根据已知条可以用S表示它大家想想，这个轴截面最好选择什么位置生：取内接正四棱柱的对角面师：有什么好处？生：这个截面即包括圆柱的有关量，也包括正四棱柱的有关量学生分析，教师板书过程师：本题是正四棱柱与圆柱的相接问题解决这类问题的关键是找到相接几何体之间的联系，如本例中正四棱柱的底面对角线的长与圆柱的底面直径相等，正四棱柱的高与圆柱的母线长相等，通过这些关系可以实现已知条的相互转化旋转体类组合体体积计算关键在于找好截面，找到这个截面，就能迅速搭好已知和未知的桥梁随堂练习1．下图是一个几何体的三视图(单位：)，画出它的直观图，并求出它的表面积和体积答案：232 22．正方体中，H、G、F分别是棱AB、AD、AA1的中点，现在沿三角形GFH所在平面锯掉正方体的一个角，问锯掉的这块体积是原正方体体积的几分之几？答案：学生独立完成培养学生理解能力，空间想象能力归纳总结1．柱体、锥体、台体的体积公式及关系2．简单组合体体积的计算3．等积变换学生归纳，教师补充完善巩固所学，提高自我整合知识能力后作业13 第二时习案学生独立完成固化知识提升能力备用例题例1：三棱柱AB – A1B11中，若E、F分别为AB、A的中点，平面EB11F将三棱柱分成体积为V1、V2的两部分，那么V1:V2 = 7: 【分析】不妨设V1对应的几何体AEF – A1B11是一个棱台，一个底面的面积与棱柱的底面积相等，另一个底面的面积等于棱柱底面的；V2对应的是一个不规则的几何体，显然这一部分的体积无法直接表示，可以考虑间接的办法，用三棱柱的体积减去V1表示【解析】设三棱柱的高为h，底面的面积为S，体积为V，则V = V1 + V2 = Sh∵E、F分别为AB、A的中点∴∴V1:V2 = 7:【评析】本题求不规则的几何体1B1—EBF的体积时，是通过计算棱柱AB—A1B11和棱台AEF—A1B11的体积的差求得的例2：一个底面直径为20的装有一部分水的圆柱形玻璃杯，水中放着一个底面直径为6，高为20的一个圆锥形铅锤，当铅锤从中取出后，杯里的水将下降几厘米？( =314)【解析】因为圆锥形铅锤的体积为(3)设水面下降的高底为x，则小圆柱的体积为(20÷2)2x = 100 x (3) 所以有60 =100 x，解此方程得x = 06 ()答：铅锤取出后，杯中水面下降了06。

课题：柱体、锥体、台体的表面积与体积（一）一、教学目标1、知识与技能（1）通过对柱、锥、台体的研究，掌握柱、锥、台的表面积的求法。

（2）能运用公式求解，柱体、锥体和台的全积，并且熟悉台体与柱体和锥体之间的转换关系。

（3）培养学生空间想象能力和思维能力。

2、过程与方法（1）让学生经历几何全的侧面展一过程，感知几何体的形状。

（2）让学生通对照比较，理顺柱体、锥体、台体三间的面积的关系。

3、情感与价值通过学习，使学生感受到几何体面积的求解过程，对自己空间思维能力影响。

从而增强学习的积极性。

二、教学重点、难点重点：柱体、锥体、台体的表面积计算难点：台体表面积公式的推导三、学法与教学用具1、学法：学生通过阅读教材，自主学习、思考、交流、讨论和概括，通过剖析实物几何体感受几何体的特征，从而更好地完成本节课的教学目标。

2、教学用具：实物几何体，投影仪四、教学设想一、复习准备：1. 讨论：正方体、长方体的侧面展开图？→正方体、长方体的表面积计算公式？2. 讨论：圆柱、圆锥的侧面展开图？→圆柱的侧面积公式？圆锥的侧面积公式？二、讲授新课：1. 教学表面积计算公式的推导：①讨论：如何求棱柱、棱锥、棱台等多面体的表面积？（展开成平面图形，各面面积和）②练习：求各面都是边长为10的等边三角形的正四面体S-ABC的表面积.一个三棱柱的底面是正三角形，边长为4，侧棱与底面垂直，侧棱长10,求其表面积.③讨论：如何求圆柱、圆锥、圆台的侧面积及表面积？（图→侧→表）圆柱：侧面展开图是矩形，长是圆柱底面圆周长，宽是圆柱的高（母线）， S=2，S=2，其中为圆柱底面半径，为母线长。

圆锥：侧面展开图为一个扇形，半径是圆锥的母线，弧长等于圆锥底面周长，侧面展开图扇形中心角为360rlθ=⨯，S圆锥侧=rlπ， S圆锥表=()r r lπ+，其中为r圆锥底面半径，l为母线长。

圆台：侧面展开图是扇环，内弧长等于圆台上底周长，外弧长等于圆台下底周长，侧面展开图扇环中心角为360R rlθ-=⨯，S圆台侧=()r R lπ+，S圆台表=22()r rl Rl Rπ+++.④练习：一个圆台，上、下底面半径分别为10、20，母线与底面的夹角为60°，求圆台的表面积. （变式：求切割之前的圆锥的表面积）2. 教学表面积公式的实际应用：①例1：一圆台形花盆，盘口直径20cm，盘底直径15cm，底部渗水圆孔直径1.5cm，盘壁长15cm. 为美化外表而涂油漆，若每平方米用100毫升油漆，涂200个这样的花盘要多少油漆？（黑板上画图）讨论：油漆位置？→如何求花盆外壁表面积？列式→计算→变式训练：内外涂②练习：粉碎机的上料斗是正四棱台性，它的上、下底面边长分别为80mm、440mm，高是200mm, 计算制造这样一个下料斗所需铁板的面积.（黑板上画图）3. 小结：表面积公式及推导；实际应用问题三、巩固练习：1. 已知底面为正方形，侧棱长均是边长为5的正三角形的四棱锥S-ABCD，求其表面积.2. 圆台的上下两个底面半径为10、20, 平行于底面的截面把圆台侧面分成的两部分面积之比为1：1，求截面的半径.3. ，求这个圆锥的表面积.*4. 圆锥的底面半径为2cm，高为4cm，求圆锥的内接圆柱的侧面积的最大值.*5. 面积为2的菱形，绕其一边旋转一周所得几何体的表面积是多少？四、小结：（见黑板版书）五、作业。

柱、锥、台和球的体积教学设计课题柱、锥、台和球的体积课型新授课教学目标知识与技能：掌握柱、锥、台和球的体积公式．过程与方法：通过本节学习，能运用公式求解柱、锥、台和球的体积情感态度与价值观：通过本节学习，增强学生的立体感觉与空间想象能力，增强探索问题的兴趣与好奇心学情分析本节课是必修二第一章的最后一节，学生在之前学习中已经对空间几何体的棱柱、棱锥、棱台，和圆柱、圆锥、圆台和球的结构特征及性质有所了解，并且能够运用棱柱、棱锥、棱台和球的表面积公式解决问题，这都为本课的学习打下了基础，学生对柱锥台球的体积公式有较强的学习兴趣。

重难点柱体、锥体、台体和球的体积计算教具多媒体环节教学过程师生活动设计意图旧知回顾复习长方体体积公式长方体的体积等于它的长、宽、高的积．V长方体= abc长方体的体积等于它的底面积S和高h的积V长方体= Sh学生思考回答回顾必要的基础知识导入演示教师将一摞本放在桌面上，改变这摞本的形状，引导学生观察，改变前后高度是否发生变化，每个本的面积是否发生变化，整个形状的体积是否发生变化学生观察教师演示激发学生学习兴趣．新知探究一、柱体的体积定理：柱体（棱柱、圆柱）的体积等于它的底面积S 和高h 的积．V Sh=柱体推论：底面半径为r，高为h圆柱的体积是V圆柱= πr2h例 1 一个正方体和一个圆柱等高，并且侧面积相等，求这个正方体和圆柱的体积之比二、锥体的体积如图：三棱柱AD1C1-BDC,底面积为S,高为h.问:从A点出发棱柱能分割成几个三棱锥？学生类比推理学生解答学生观察思考归纳结论提高学生的计算能力进一步巩固体积公式推出锥体体积公式提高学生类比学习能力。

课题：柱体、锥体、台体的表面积与体积（二）教学要求：了解柱、锥、台的体积计算公式；能运用柱锥台的表面积公式及体积公式进行计算和解决有关实际问题.教学重点：运用公式解决问题.教学难点：理解计算公式之间的关系.教学过程：一、复习准备：1. 提问：圆柱、圆锥、圆台的表面积计算公式？2. 练习：正六棱锥的侧棱长为6, 底面边长为4, 求其表面积.3. 提问：正方体、长方体、圆柱、圆锥的体积计算公式？二、讲授新课：1. 教学柱、锥、台的体积计算公式：① 讨论：等底、等高的棱柱、圆柱的体积关系？② 根据正方体、长方体、圆柱的体积公式，推测柱体的体积计算公式？→给出柱体体积计算公式：Sh V =柱 （S 为底面面积，h 为柱体的高）→h r Sh V 2π==圆柱③ 讨论：等底、等高的圆柱与圆锥之间的体积关系？ 等底等高的圆锥、棱锥之间的体积关系？④ 根据圆锥的体积公式公式，推测锥体的体积计算公式？→给出锥体的体积计算公式：Sh V 31=锥 S 为底面面积，h 为高） ⑤ 讨论：台体的上底面积S ’，下底面积S ，高h ，由此如何计算切割前的锥体的高？ → 如何计算台体的体积？⑥ 给出台体的体积公式：'1()3V S S h =台 （S ，'S 分别上、下底面积，h 为高）→ '2211()()33V S S h r rR R h π==++圆台 （r 、R 分别为圆台上底、下底半径）⑦ 比较与发现：柱、锥、台的体积计算公式有何关系？从锥、台、柱的形状可以看出，当台体上底缩为一点时，台成为锥；当台体上底放大为与下底相同时，台成为柱。

因此只要分别令S ’=S 和S ’=0便可以从台体的体积公式得到柱、锥的相应公式。

从而锥、柱的公式可以统一为台体的体积公式讨论：侧面积公式是否也正确？ 圆柱、圆锥、圆台的侧面积和体积公式又可如何统一？2. 教学体积公式计算的运用：① 出示例：一堆铁制六角螺帽，共重11.6kg, 底面六边形边长12mm ，内空直径10mm ，高10mm ，估算这堆螺帽多少个？（铁的密度7.8g/cm3）讨论：六角螺帽的几何结构特征？ → 如何求其体积？ → 利用哪些数量关系求个数？→列式计算→小结：体积计算公式②练习：将若干毫升水倒入底面半径为2cm的圆柱形容器中，量得水面高度为6cm；若将这些水倒入轴截面是正三角形的倒圆锥形容器中，求水面的高度.3. 小结：柱锥台的体积公式及相关关系；公式实际运用.三、巩固练习：1. 把三棱锥的高分成三等分，过这些分点且平行于三棱锥底面的平面，把三棱锥分成三部分，求这三部分自上而下的体积之比。

1.1.7 柱、锥、台和球的体积教学目标1.理解祖暅原理的内容.2.了解柱、锥、台体的体积公式的推导.3.掌握柱、锥、台和球的体积公式． 知识梳理知识点一 祖暅原理1．内容：幂势既同，则积不容异．2．含义：夹在两个平行平面间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等． 3．应用：等底面积、等高的两个柱体或锥体的体积相等． 知识点二 柱、锥、台、球的体积公式其中S ′、S 分别表示上、下底面的面积，h 表示高，r ′和r 分别表示上、下底面的半径，R 表示球的半径． 例题探究题型一 柱体、锥体、台体的体积例1 (1)圆柱的侧面展开图是长12 cm ，宽8 cm 的矩形，则这个圆柱的体积为( ) A.288πcm 3 B.192π cm 3 C.288π cm 3或192π cm 3 D ．192π cm 2【答案】C【解析】当圆柱的高为8 cm 时，V ＝π×⎝⎛⎭⎫122π2×8＝288π(cm 3)，当圆柱的高为12 cm 时，V ＝π× ⎝⎛⎭⎫82π2×12＝192π(cm 3)． (2)一空间几何体的三视图如图所示，则该几何体的体积为( )A ．2π＋2 3B ．4π＋23C ．2π＋233D ．4π＋233【答案】C【解析】该空间几何体由一圆柱和一正四棱锥组成，圆柱底面半径为1，高为2，体积为2π，四棱锥的底面边长为2，高为3，所以体积为13×(2)2×3＝233，所以该几何体的体积为2π＋233.反思感悟 (1)求简单几何体的体积．若所给的几何体为柱体、锥体或台体，则可直接利用公式求解．(2)求以三视图为背景的几何体的体积．应先根据三视图得到几何体的直观图，然后根据条件求解．跟踪训练1 (1)正方体的表面积为96，则正方体的体积为( ) A ．48 6 B ．64 C ．16 D ．96 【答案】B(2)一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.【答案】20π3【解析】根据三视图知，该几何体上部是一个底面直径为4 m ，高为2 m 的圆锥，下部是一个底面直径为2 m ，高为4 m 的圆柱． 故该几何体的体积V ＝13π×22×2＋π×12×4＝20π3(m 3)．题型二 球的体积例2 (1)设长方体的长、宽、高分别为2a ，a ，a ，其顶点都在一个球面上，则该球的体积为________． 【答案】6πa 3【解析】长方体的体对角线是其外接球的直径，由长方体的体对角线为(2a )2＋a 2＋a 2＝6a ，得球的半径为62a ，V ＝43π⎝⎛⎭⎫62a 3＝6πa 3. (2)如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器厚度，则球的体积为( )A.500π3 cm 3B.866π3 cm 3C.1 372π3cm 3D.2 048π3 cm 3【答案】A【解析】作出该球轴的截面如图所示，依题意BE ＝2，AE ＝CE ＝4，设DE ＝x ，故AD ＝2＋x ，因为AD 2＝AE 2＋DE 2，解得x ＝3，故该球的半径AD ＝5，所以V ＝43πR 3＝500π3(cm 3)．反思感悟 (1)求球的体积，关键是求球的半径R .(2)球与其他几何体组合的问题，往往需要作截面来解决，所作的截面尽可能过球心、切点、接点等．跟踪训练2 (1)一平面截一球得到直径为2 5 cm 的圆面，球心到这个平面的距离是2 cm ，则该球的体积是( ) A ．12π cm 3 B ．36π cm 3 C ．646π cm 3 D ．108π cm 3【答案】B【解析】设球心为O ，截面圆心为O 1，连接OO 1，则OO 1垂直于截面圆O 1，如图所示．在Rt △OO 1A 中，O 1A ＝ 5 cm ， OO 1＝2 cm ，∴球的半径R ＝OA ＝22＋(5)2＝3(cm)， ∴球的体积V ＝43×π×33＝36π(cm 3)．(2)设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，求该球的体积． 解 由题意知，该三棱柱为正三棱柱，且侧棱与底面边长相等，均为a . 如图，P 为三棱柱上底面的中心，O 为球心，易知AP ＝23×32a ＝33a ，OP ＝12a ，所以球的半径R 满足R 2＝OA 2＝⎝⎛⎭⎫33a 2＋⎝⎛⎭⎫12a 2＝712a 2， 所以R ＝723a ，所以V 球＝43πR 3＝72154a 3.题型三 几何体体积的求法 命题角度1 等体积法例3 如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，E 为线段B 1C 上的一点，求三棱锥A －DED 1的体积．解 1A DED V 三棱锥－ ＝1E DD A V 三棱锥－＝13×12×1×1×1＝16. 反思感悟 (1)利用转换底面以便于找到几何体的高，从而求出几何体的体积． (2)利用等体积法可求点到平面的距离．跟踪训练3 如图，在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，求点A 到平面A 1BD 的距离d .解 在三棱锥A 1－ABD 中，AA 1⊥平面ABD ，AB ＝AD ＝AA 1＝a ， A 1B ＝BD ＝A 1D ＝2a ， ∵1A ABD V －＝1A A BD V － ，∴13×12a 2·a ＝13×12×2a ×32·2a ·d ，∴d ＝33a . 命题角度2 割补法例4 如图，在多面体ABCDEF 中，已知平面ABCD 是边长为4的正方形，EF ∥AB ，EF ＝2，EF 上任意一点到平面ABCD 的距离均为3，求该多面体的体积．解 如图，连接EB ，EC .四棱锥E －ABCD 的体积 V 四棱锥E －ABCD ＝13×42×3＝16.∵AB ＝2EF ，EF ∥AB ， ∴S △EAB ＝2S △BEF ，∴V 三棱锥F －EBC ＝V 三棱锥C －EFB ＝12V 三棱锥C －ABE ＝12V 三棱锥E －ABC＝12×12V 四棱锥E －ABCD ＝4. ∴多面体的体积V ＝V 四棱锥E －ABCD ＋V 三棱锥F －EBC ＝16＋4＝20.反思感悟 当一个几何体的形状不规则时，无法直接运用体积公式求解，这时一般通过分割与补形，将原几何体分割或补形成较易计算体积的几何体，从而求出原几何体的体积． 跟踪训练4 如图，一个底面半径为2的圆柱被一平面所截，截得的几何体的最短和最长母线长分别为2和3，求该几何体的体积．解 用一个完全相同的几何体把题中几何体补成一个圆柱，如图，则圆柱的体积为π×22×5＝20π，故所求几何体的体积为10π.课堂小结1．计算柱体、锥体和台体的体积时，关键是根据条件找出相应的底面面积和高，要充分运用多面体的有关截面及旋转体的轴截面，将空间问题转化为平面问题．旋转体的轴截面是用过旋转轴的平面去截旋转体而得到的截面．例如，圆柱的轴截面是矩形，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形，球的轴截面是过球心的平面截球所得的圆面．2．在求不规则的几何体的体积时，可利用分割几何体或补全几何体的方法转化为柱、锥、台、球的体积计算问题. 达标检测1.已知高为3的棱柱ABC —A 1B 1C 1的底面是边长为1的正三角形(如图)，则三棱锥B 1—ABC 的体积为( )A.14B.12C.36D.34【答案】D【解析】V ＝13Sh ＝13×34×3＝34.2．一个球的表面积是16π，则它的体积是( ) A ．64π B.64π3 C ．32π D.32π3【答案】D【解析】设球的半径为R ，则由题意可知4πR 2＝16π，故R ＝2.所以球的半径为2，体积V ＝43πR 3＝323π. 3．现有一个底面直径为20 cm 的装有一部分水的圆柱形玻璃杯，水中放着一个底面直径为 6 cm ，高为20 cm 的圆锥形铅锤，铅锤完全浸没在水中．当铅锤从水中取出后，杯里的水将下降( ) A ．0.6 cm B ．0.15 cm C ．1.2 cm D ．0.3 cm【答案】A【解析】设杯里的水下降h cm ， 由题意知π⎝⎛⎭⎫2022h ＝13×20×π×32， 解得h ＝0.6 cm.4．圆锥的轴截面是等腰直角三角形，侧面积是162π，则圆锥的体积是( ) A.64π3 B.128π3C ．64πD ．1282π【答案】A【解析】设圆锥的母线为l ，底面半径为r . 由题意知，l ＝2r ，① S 侧＝πrl ＝162π，② 由①②可得r ＝4，l ＝42， V 圆锥＝13πr 2h ＝π3r 2l 2－r 2＝643π.5．某几何体的三视图如图所示，则该几何体的体积是________．【答案】16π－16【解析】由三视图可知该几何体是一个圆柱内部挖去一个正四棱柱，圆柱底面圆半径为2，高为4，故体积为16π；正四棱柱底面边长为2，高为4，故体积为16，故题中几何体的体积为16π－16.。

课题：柱、锥、台和球的体积
1.棱柱和圆柱的体积
2.棱锥和圆锥的体积
一、教学目标：
⒈知识目标：掌握棱柱、圆柱、棱锥、圆锥的体积的推导方法，理解祖暅原理，会应用棱柱、圆柱、棱锥、圆锥的体积公式。

⒉能力目标：通过学习祖暅原理，理解祖暅原理的内涵，体验空间与平面问题互相转化的方法，体会到复杂的体积问题怎样转化为简单的体积问题而得到解决，从而提高学生的数学思维能力。

⒊德育目标：学生通过学习祖暅原理，了解我国古代数学家在这方面作出的突出成就，受到爱国主义教育，提高学习数学的兴趣。

二、教学重点与难点：
重点是棱柱、圆柱、棱锥、圆锥的体积公式的推导方法。

难点是对祖暅原理的理解和棱柱、圆柱、棱锥、圆锥的体积公式的应用。

三、教学方法与教学手段：
教学方法：本节课的课型为“新授课”。

虽然学生初中已经学习了圆柱、圆锥的体积的公式，但用的是实验验证的方法，并没有从根本上理解圆柱、圆锥的体积公式的由来，本课采用推导的方法，以长方体的体积公式和祖暅原理为基础推导出几种几何体的体积公式，通过不同形式的探究过程，让学生积极参与到教学活动中来，并且始终处于积极的问题探究和辨析思考的学习气氛中。

教学手段：采用多媒体辅助教学，增强直观性，增大课堂容量，提高效率。

五、板书设计：。