导数复习
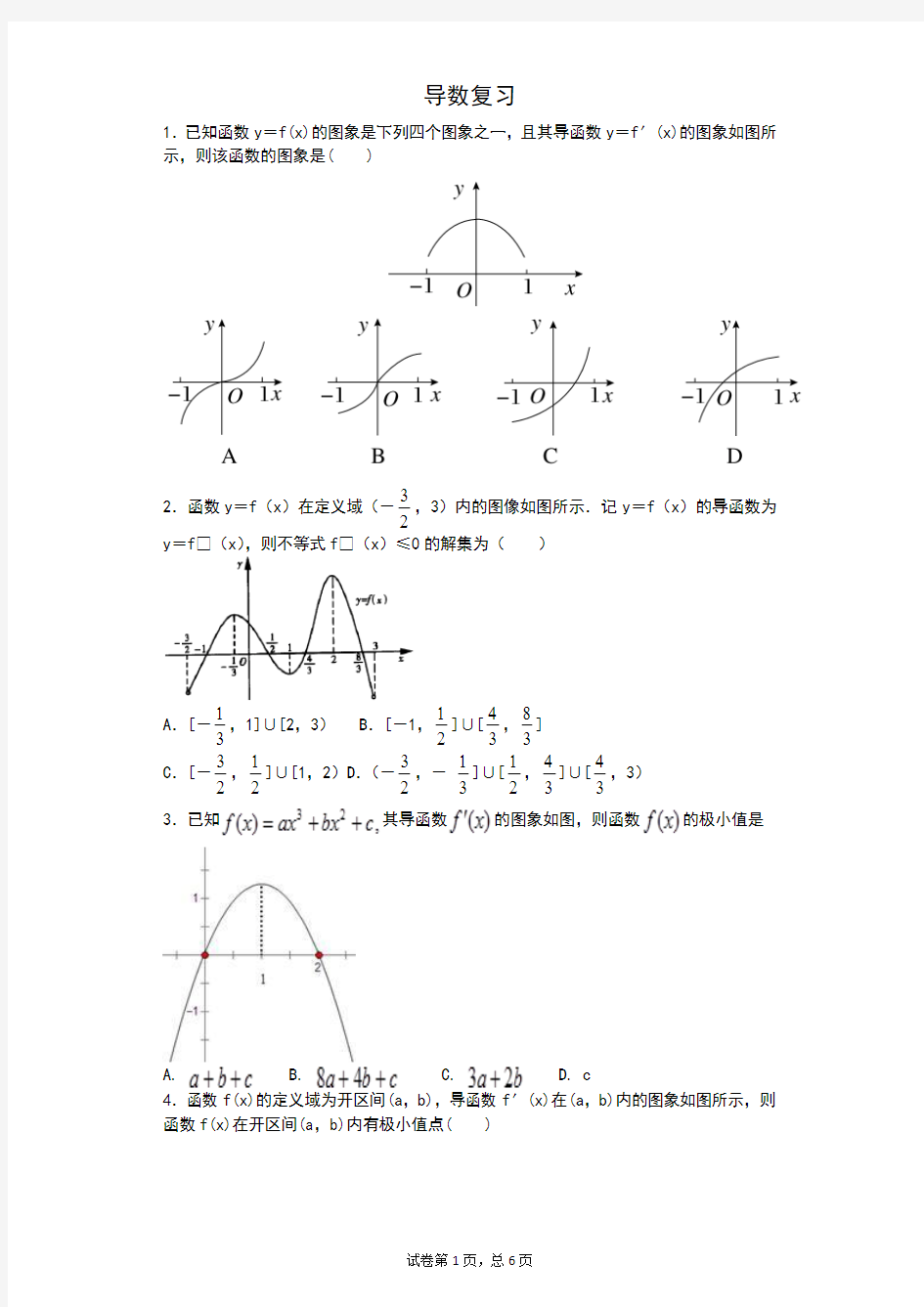
1.已知函数y =f(x)的图象是下列四个图象之一,且其导函数y =f′(x)的图象如图所示,则该函数的图象是( )
2.函数y =f (x )在定义域(-
3
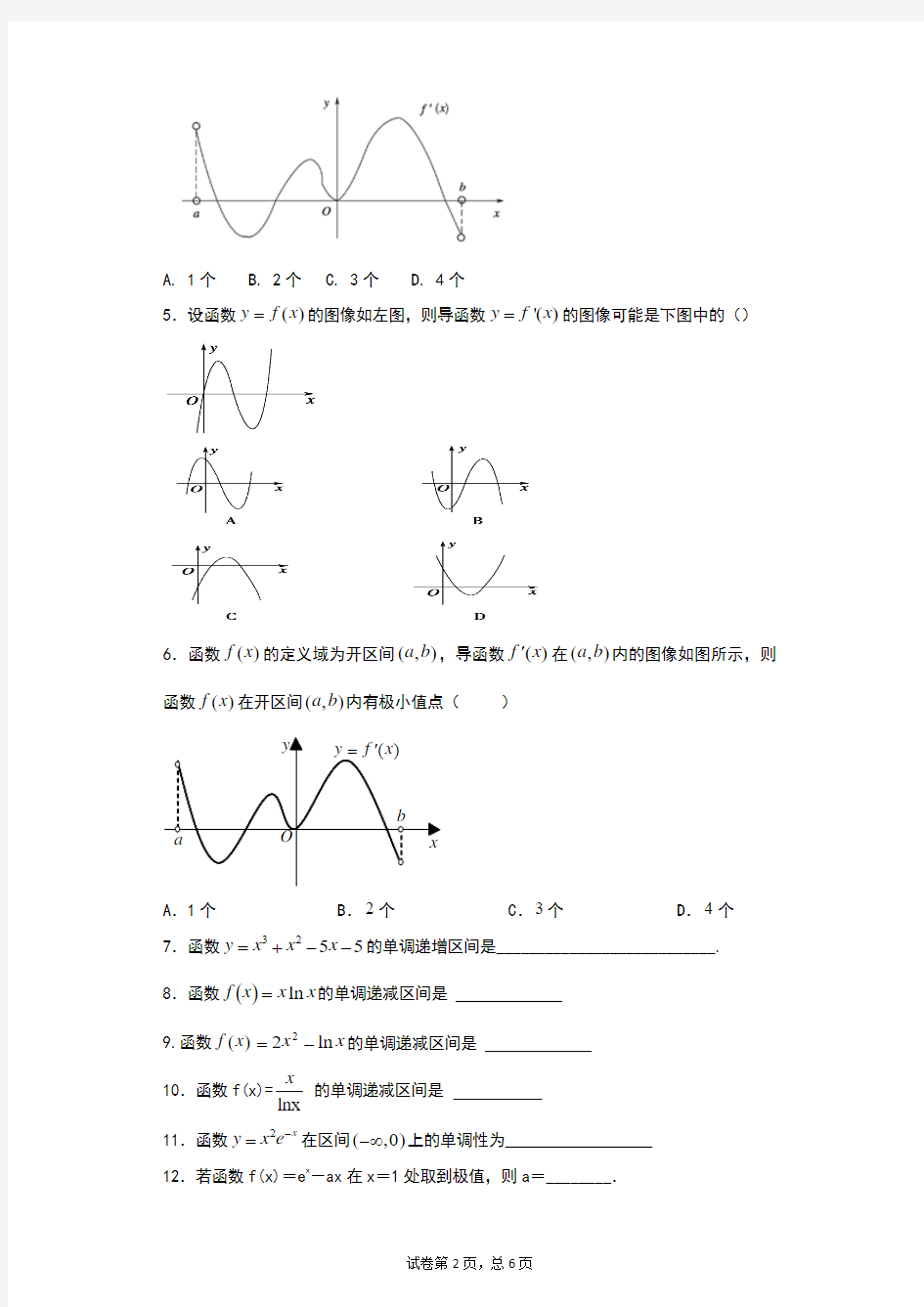
2
,3)内的图像如图所示.记y =f (x )的导函数为y =f (x ),则不等式f (x )≤0的解集为( )
A .[-13,1]∪[2,3)
B .[-1,12]∪[43,8
3] C .[-32,12]∪[1,2)D .(-32,- 13]∪[12,43]∪[43
,3)
3.已知
其导函数
的图象如图,则函数
的极小值是
A.
B. C.
D. c 4.函数f(x)的定义域为开区间(a ,b),导函数f′(x)在(a ,b)内的图象如图所示,则函数f(x)在开区间(a ,b)内有极小值点( )
A. 1个
B. 2个
C. 3个
D. 4个
5.设函数()y f x =的图像如左图,则导函数'()y f x =的图像可能是下图中的()
6.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图像如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )
A .1个
B .2个
C .3个
D .4个 7.函数32
55y x x x =+--的单调递增区间是___________________________. 8.函数()x x x f ln =的单调递减区间是
9.函数()f x x x ln 22
-=的单调递减区间是
10.函数f(x)=
lnx
x
的单调递减区间是 11.函数2x
y x e
-=在区间(,0)-∞上的单调性为
12.若函数f(x)=e x
-ax 在x =1处取到极值,则a =________.
13.函数()443
13
+-=
x x x f 在[]3,0上的极值点是______,极值是_______. 14. 已知函数x x x f ln 2)(2-=,则)(x f 的极小值是 .
15. 已知函数32()332f x x x x =--+,则此函数的极大值点是 .
16.已知函数3227y x ax bx =+++在1x =-处有极大值,在3x =处有极小值,则a =
b =
17.函数x e x f x -=)(在]1,1[-上的最小值是 . 18.函数y =x +sinx ,x ∈[0,2π]的值域为________.
19. 当]1,1[-∈x 时,函数x e
x x f 2
)(=的值域是 .
20.3()31f x x x =-+在[-2,2]上的最大值是 . 21.函数
3()34f x x x =-,[0,1]x ∈的最大值是
22.函数3
12)(x x x f -=在区间]3,3[-上的最小值是
23.函数5123223+--=x x x y 在]3,0[上的最大值与最小值的差等于____________ 24.函数f(x)=13
x 3-x 2
-3x -1的图象与x 轴的交点个数是________. 25.(1,1)2
x
y x =
--+曲线在点处的切线方程为 . 26.函数()x
f x xe =在其极值点处的切线方程为____________.
27.函数()ln f x x =的图像过(1,1)的切线方程是 .
28.已知函数()4ln f x x x =-,则曲线()y f x =在点(1,(1))f 处的切线方程为 . 29.设曲线2
x
y xe x =+在原点处切线与直线10x ay ++=垂直,则a =
30.已知直线l 过点)1,0(-,且与曲线x x y ln =相切,则直线l 的方程为 . 31.函数()ln x
f x e x =?在点()1,0处的切线方程为 .
32.曲线()4ln f x x x =-在x e =处的切线的斜率k = .ln y x x =
33.已知函数()a ax x x x f -+-=
23
3
1 (a ∈R). (1)当3-=a 时,求函数()x f 的极值;
(2)若函数()x f 的图象与x 轴有且只有一个交点,求a 的取值范围.
34.已知函数
22
()2ln (0)f x x a x a =->. (1)若()f x 在1x =处取得极值,求实数a 的值; (2)求函数()f x 的单调区间;
(3)若()f x 在[1]e ,
上没有零点,求实数a 的取值范围. 35.设函数2
1()ln 2
f x c x x bx =+
+(),,0R c c b ∈≠,且1x =为()f x 的极值点. (Ⅰ) 若1x =为()f x 的极大值点,求()f x 的单调区间(用c 表示); (Ⅱ)若()0f x =恰有两解,求实数c 的取值范围. 36.已知函数()m x x g x x x f +=+-=ln 6,8)(2. (1)求)(x f 在区间]1,[+t t 上的最大值)(t h ;
(2)若)(x f y =的图象与)(x g y =的图象有且仅有三个不同的交点,求实数m 的取值范围.
37.已知函数)0,()(23≠∈-+=a b a R x x bx ax x f 是常数,、, 取得极值时,函数和且当)(21x f x x == (1)求函数)(x f 的解析式;
(2)若曲线)(x f y =与)02(3)(≤≤---=x m x x g 有两个不同的交点,求实数m 的取值范围.
38.已知函数()a ax x x x f -+-=
23
3
1 (a ∈R). (1)当3-=a 时,求函数()x f 的极值;
(2)若函数()x f 的图象与x 轴有且只有一个交点,求a 的取值范围. 39.已知函数
.
(1)设x=0是f(x)的极值点,求m ,并讨论f(x)的单调性; (2)当m ≤2时,证明f(x)>0.
40.已知函数()e (1)x f x x =+.
(1)求曲线()y f x =在点(0,(0))f 处的切线方程;
(2)若对于任意的(,0)x ∈-∞,都有()f x k >,求k 的取值范围. 41.已知函数2()2()3x f x e x a =--+,a ∈R .
(1)若函数()y f x =的图象在0x =处的切线与x 轴平行,求a 的值; (2)若0x ≥,()0f x ≥恒成立,求a 的取值范围. 42.已知函数∈+=
a x
a
x x f (ln )(R ). (1)若曲线)(x f y =在点))1(,1(f 处的切线与直线01=--y x 平行,求a 的值; (2)在(1)条件下,求函数)(x f 的单调区间和极值; (3)当1=a ,且1≥x 时,证明:.1)(≤x f 43.已知函数32
()f x x ax bx c =+++在2
3
x =-与1x =时都取得极值 (1)求,a b 的值与函数()f x 的单调区间
(2)若对[1,2]x ∈-,不等式2
()f x c <恒成立,求c 的取值范围
44.已知函数3
()4f x ax bx =-+.当2x =时,函数()f x 取得极值43
-
. (1)求函数()f x 的解析式;
(2)若方程()f x k =有3个解,求实数k 的取值范围. 45.已知函数ln ()()x a
f x a x
+=
∈R . (1)求函数()f x 的单调区间和极值; (2)当1a =,且1x ≥时,证明:()f x ≤1. 46.已知函数2
()ln f x x x ax =--,a R ∈. (1)当1a =时,求()f x 的最小值; (2)若()f x x >,求a 的取值范围. 47.已知函数2
1()ln 2
f x ax x x =
-+(,0a R a ∈≠) (1)当2a =时,求曲线()y f x =在(1,(1))f 处的切线方程;
(2)若在区间[)1,+∞上函数()f x 的图象恒在直线y ax =下方,求a 的取值范围. 48.已知函数3
21()43
f x x ax =
-+,且2x =是函数()f x 的一个极小值点. (1)求实数a 的值;
(2)求()f x 在区间[1,3]-上的最大值和最小值.
49.设函数)0(ln )(2>-=x bx x a x f ,若函数)(x f 在1=x 处与直线2
1
-=y 相切, (1)求实数a ,b 的值;(2)求函数],1[)(e e
x f 在上的最大值.
参考答案
1.B
【解析】函数f(x)在[-1,1]上为增函数,当x ∈(-1,0)时f′(x)由小到大,则f(x)图象的增长趋势由缓到快,当x ∈(0,1)时f′(x)由大到小,则f(x)的图象增长趋势由快到缓,故选B 项. 2.A 【解析】
3.D
【解析】由导函数的图象知当
时,
,当
时,
,所
以函数
的极小值为
,选D.
4.A
【解析】由f′(x)的图象可知,函数f(x)在区间(a ,b)内,先增、再减、再增、最后再减,故函数f(x)在区间(a ,b)内只有一个极小值点,故选A. 5.D 【解析】
试题分析:由()y f x =图象知,函数先增,再减,再增,对应的导数值,应该是先大于零,再小于零,最后大于0.故选D. 考点:导数与函数的单调性. 6.A 【解析】
试题分析:设导函数)(x f '在),(b a 内的图像与x 轴的交点(自左向右)分别为1234,,,x x x x ,其中12340x x x x <<=<,则由导函数的图像可得:当1(,)x a x ∈时,()0f x '>,12(,)x x x ∈时,()0f x '<且1()0f x '=,所以1x 是函数()f x 的极大值点;当12(,)x x x ∈时,()0f x '<,
23(,)x x x ∈时,()0f x '>且2()0f x '=,所以2x 是函数()f x 的极小值点;当23(,)
x x x ∈或34(,)x x x ∈时,()0f x '>,故3x 不是函数()f x 的极值点;当34(,)x x x ∈时,()0f x '>,而当4(,)x x b ∈时,()0f x '<,且4()0f x '=,所以4x 是函数()f x 的极大值点;综上可知,函数)(x f 在开区间),(b a 内有极小值点只有1个,故选A. 考点:1.函数的图像;2.函数的导数与极值. 7.5
(,
)3
-∞-和(1,)+∞
【解析】
试题分析:因为2
325(35)(1)y x x x x '=+-=+-,由0y '>可得1x >或5
3
x <-,所以函数3
2
55y x x x =+--的单调递增区间是5
(,)3
-∞-和(1,)+∞. 考点:函数的单调性与导数.
8.
)1,0(e 【解析】解:因为1y x ln x y'1ln x(x 0)y'00x e =∴=+>∴<∴<<,故递减区间为1
(0,)e
9.)2
1
,
0( 【解析】解:因为
214x 1(2x 1)(2x 1)
f '(x)4x (x 0)
x x x 1
f '(x)02x 100x 2
-+-=-==>∴<∴-<∴<<
10.(0,1),(1,e)
【解析】函数的定义域为(0,1)?(1,+∞),令'2ln 1
(
)ln (ln )
x x x x -=<0得ln 1x <,所以0x e <<,故函数f(x)=
lnx
x
的单调递减区间是(0,1),(1,e)。 11.单调递减 【解析】略 12.e
【解析】由题意,f ′(1)=0,因为f ′(x)=e x
-a ,所以a =e. 13.2=x , 3
4- 【解析】
()()[]()3
?2314440,0,33
14
2,2242433f x x x f x x x f =
-+∴=-==?-?+=-
令导数为在得:极值
14.1
【解析】解:因为
222(x 1)(x 1)f (x)x 2ln x f '(x)2x (x 0)
x x
x (0,1)f '(x)0;x (1,)f '(x)0;+-=-∴=-
=>∴∈<∈+∞>时,则时,则
)(x f 的极小值是f(1)=1
15.21-
【解析】∵f (x )=x 3
-3x 2
-3x+2
∴f′(x )=3x 2
-6x-3
当f′(x )=0时,3x 2
-6x-3=0 ∴x 2
-2x-1=0
∴(x-1)2
=2 ∴x=1±
令f′(x )>0,得x <1-或x >1+
令f′(x )<0,得1-
<x <1+
∴函数的单调增区间为(-∞,1-),(1+
,+∞),函数的单调减区间为(1-,
1+
)
∴函数的极大值点是x=1-
故答案为:x=1-
16.3- ;9- 【解析】略 17.1 【解析】
试题分析:因为()1x
f x e '=-,()00,()00f x x f x x ''>?>
[1,0]-单调递减,在[0,1]单调递增,从而函数x e x f x -=)(在]1,1[-上的最小值是
0(0)01f e =-=.
考点:函数的最值与导数. 18.[0,2π]
【解析】由y ′=1+cosx ≥0,所以函数y =x +sinx 在[0,2π]上是单调增函数,所以值域为[0,2π]. 19.[0,e]
【解析】22
222()x x x x
xe x e x x f x e e
--'== ,()f x ∴在区间(1,0)-上是减函数,f(x)在区间(1,2)上是增函数,所以当x=0,f(x)取得最小值0.因为f(-1)=e,f(1)=1
e
,显然最大值为e,
所以f(x)的值域为[0,e]. 20.3
【解析】2
()330,1,1
f x x x x '=-=∴=-=, (1)3,(1)1,(2)1,(2)3f f f f -==--=-= .所以最大值为3.
21.1 【解析】
2
1211
()3120,,22
f x x x x '=-=∴=-=,
由于max 1
31
(0)0,()()1,()1222
f f x f f x ===
-=∴=极大. 22.9
【解析】略 23.20 【解析】略 24.3
【解析】f′(x)=x 2
-2x -3=(x +1)(x -3),函数在(-∞,-1)和(3,+∞)上是增函数,在(-1,3)上是减函数,由f(x)极小值=f(3)=-10<0,f(x)极大值=f(-1)=2
3
>0知函数f(x)的图象与x 轴的交点个数为3. 25.012=+-y x 【解析】
试题分析:由()2
+=
=x x x f y 得()21'
=-f ,所以所求切线的斜率为2,由点斜式可得)1(21+=+x y ,整理得012=+-y x .
考点:利用导数求切线方程. 26.1y e
=- 【解析】
试题分析:()()'1x
x
x
f x e xe e x =+=+,令()'0f x =得1x =-.()111f e e
--=-=- , ∴切点为11,e ?
?-- ??
?.因为切线斜率为0,所以所求得切线方程为1y e =-.
考点:导数的几何意义. 27.1y x =-
考点:利用导数求曲线的切线. 28.340x y +-=
【解析】
试题分析:函数()4ln f x x x =-,所以函数'
4
()1f x x
=-
,切线的斜率为:﹣3,切点为:(1,1)
所以切线方程为:340x y +-=,故答案为:340x y +-=. 考点:利用导数研究曲线上某点切线方程. 29.1 【解析】
试题分析:由题意得2x x y e xe x '=++,在原点处的切线的斜率00100 1.k e e =+?+=又该切线与直线x+ay+1=0垂直,直线x+ay+1=0的斜率21
k a
=-, 由121k k =-,解得1a =.
考点:本题考查利用导数研究曲线的切线,两直线垂直的充要条件
【原创理由】本题考查导数的几何意义,两条直线垂直的条件,意在考查学生的运算求解能力.
30.1-=x y 【解析】
试题分析:将()ln f x x x =求导得()ln 1f x x '=+,设切点为00(,)x y ,l 的方程为
000(ln 1)()y y x x x -=+-,因为直线l 过点)1,0(-,所以0001(ln 1)(0)y x x --=+-.又
000ln y x x =,所以0000001l n (l n 1),1,0x x x x x y --=-+∴==.所以切线方程为1-=x y .
考点:导数的应用. 31.0ex y e --= 【解析】
试题分析:对函数求导得x e x e x f x x
+='ln )(,所以e e e f k =+
='=1
1ln )1(11
,由点斜式,切线方程为)1(0-=-x e y ,整理得0ex y e --=. 考点:导数的几何意义.
32.2 【解析】
试题分析:因为x x y ln =,所以'
4
x y x
-=
,所以它在e x =处的切线的斜率21ln =+=e k .
考点:导数的应用.
33. (1)当1-=x 时, ()x f 取得极大值为()=
-1f 314
33131=++--;
当3=x 时, ()x f 取得极小值为()39927313+--?=f 6-=. (2)a 的取值范围是()+∞,0.
【解析】
试题分析:(1)遵循“求导数,求驻点,讨论驻点两侧导数值符号,确定极值”. (2) 根据 ()x f '= a x x +-22,得到△= a 44-= ()a -14 . 据此讨论:① 若a ≥1,则△≤0,
此时()x f '≥0在R 上恒成立,f (x )在R 上单调递增 . 计算f (0)0<-=a ,()023>=a f ,得到结论.
② 若a <1,则△>0,()x f '= 0有两个不相等的实数根,不妨设为1212x x x x <,,(). 有1212 2 x x x x a +==,.
给出当x 变化时,()()x f ,x f '的取值情况表. 根据f (x 1)·f(x 2)>0, 解得a >0.作出结论. 试题解析: (1)当3-=a 时,()333
123
+--=
x x x x f , ∴()x f '()()13322
+-=--=x x x x .
令()x f '=0, 得 121,3x x =-=. 2分
当1- >x f , 则()x f 在()1,-∞-上单调递增; 当31<<-x 时,()0' , 则()x f 在()3,1-上单调递减; 当3>x 时,()0' >x f , ()x f 在()+∞,3上单调递增. 4分 ∴ 当1-=x 时, ()x f 取得极大值为()=-1f 3 1433131=++--; 当3=x 时, ()x f 取得极小值为()399273 1 3+--?= f 6-=. 6分 (2) ∵ ()x f '= a x x +-22 , ∴△= a 44-= ()a -14 . ①若a ≥1,则△≤0, 7分 ∴()x f '≥0在R 上恒成立, ∴ f (x )在R 上单调递增 . ∵f (0)0<-=a ,()023>=a f , ∴当a ≥1时,函数f (x )的图象与x 轴有且只有一个交点. 9分 ② 若a <1,则△>0, ∴()x f '= 0有两个不相等的实数根,不妨设为1212x x x x <,,(). ∴1212 2 x x x x a +==,. 当x 变化时,()()x f ,x f '的取值情况如下表: 11分 ∵02121=+-a x x , ∴1212x x a +-=. ∴()a ax x x x f -+-=1213 113 1 = 1211213 1231x x ax x x -++- ()131231 x a x -+= ()[] 233 1 211-+=a x x . 同理()2x f ()[] 233 12 22-+=a x x . ∴()()()[]()[] 23239 12 2212121-+?-+=?a x a x x x x f x f ()()()() ()[ ] 2222122121292391-++-+=a x x a x x x x ()()[](){} 22122122922391-+-+-+=a x x x x a a a ()339 4 2+-=a a a . 令f (x 1)·f(x 2)>0, 解得a >0. 而当10<=<-=a f a f , 13分 故当10< 综上所述,a 的取值范围是()+∞,0. 14分 考点:应用导数研究函数的极值、单调性及函数的图象,分类讨论思想. 34.(1)1;(2)单调递增区间为()a +∞,,单调递减区间为(0)a ,;(3)0a << 【解析】 试题分析:(1)求函数极值分四步,一是求函数定义域(0)+∞, ,二是求函数导数2()() ()x a x a f x x +-'= ,三是根据导数为零将定义区间分割,讨论导数值正负()0x a ∈,, ()0f x '<;()x a ∈+∞,,()0f x '>,,四是根据导数符号变化确定极值点1a =;(2)利 用导数求函数单调性,也是四个步骤.一是求出定义域:,二是求导数,三是分析导数符号变 化情况,四是根据导数符号写出对应单调区间:减区间为(0)a ,,增区间()a +∞,; (3)() f x 在[1]e , 上没有零点,即()0f x ≠在[1]e ,上恒成立,也就是min ()0f x >或max ()0f x <,又(1)10f =>,只须在区间[1]e ,上min ()0f x >.以下有两个思路,一是求最小值,需分类讨论,当a e ≥时,m i n ()()f x f e =.当1a e <<时,m i n ()().f x f a =当01a <≤时, m i n ()(1).f x f =二是变量分离,22 2,((1,])ln x a x e x ≤∈,只需求函数2 (),((1,])ln x h x x e x =∈的最 小值. 试题解析:解:(1) 22 ()2ln (0)f x x a x a =->的定义域为(0)+∞,. 1分 22()2a f x x x '=-2222x a x -= 2()() x a x a x +-=. 2分 ()f x 在1x =处取得极值, (1)0f '∴=,解得1a =或1a =-(舍). 3分 当1a =时,()01x ∈,,()0f x '<;()1x ∈+∞,,()0 f x '>, 所以a 的值为1. 4分 (2)令()0f x '=,解得x a =或x a =-(舍). 5分 当x 在(0)+∞, 内变化时,() ()f x f x ',的变化情况如下: 由上表知()f x 的单调递增区间为()a +∞, ,单调递减区间为(0)a ,. 8分 (3)要使()f x 在[1 ]e ,上没有零点,只需在[1]e ,上min ()0f x >或max ()0f x <, 又(1) 10f =>,只须在区间[1]e , 上min ()0f x >. (ⅰ)当a e ≥时,()f x 在区间[1]e ,上单调递减, 22min ()()20f x f e e a ==->, 解得 0a << 与a e ≥矛盾. 10分 (ⅱ) 当1a e <<时,()f x 在区间[1)a , 上单调递减,在区间(]a e ,上单调递增, 2min ()()(12ln )0f x f a a a ==-> , 解得0a << 1a <<分 (ⅲ)当01a <≤时,()f x 在区间[1]e , 上单调递增,min ()(1)0f x f =>,满足题意. 综上,a 的取值范围为0a << 分 考点:利用导数求函数极值、单调区间、取值范围 35.解:2'()c x bx c f x x b x x ++=++=,又'(1)0f = 所以(1)() '()x x c f x x --= 且1c ≠,10b c ++= 。。。。。。。2分 (I )因为1x =为()f x 的极大值点,所以1c > 当01x <<时,'()0f x >;当1x c <<时,'()0f x <;当x c >时,'()0f x > 所以()f x 的递增区间为(0,1),(,)c +∞;递减区间为(1,)c .。。。。。。。4分 (II )①若0c <,则()f x 在(0,1)上递减,在(1,)+∞上递增 ()0f x =恰有两解,则(1)0f <,即102b +<,所以1 02 c -<<; ②若01c <<,则21()()ln 2f x f c c c c bc ==+ +极大,1 ()(1)2 f x f b ==+极小 因为1b c =--,则22 ()ln (1)ln 022 c c f x c c c c c c c =++--=--<极大 1 ()2 f x c =--极小,从而()0f x =只有一解; ③若1c >,则22 ()ln (1)ln 022 c c f x c c c c c c c =+ +--=--<极小,1()2f x c =--极大, 则()0f x =只有一解. 综上,使()0f x =恰有两解的c 的范围为1 02 c - <<. 。。。。。10分 【解析】本试题主要是考查了导数在研究函数中的运用。 (1)因为1x =为()f x 的极大值点,则可以得到参数b,c 的关系式,并利用导数求解()f x 的单调区间, (2)因为()f x 的递增区间为(0,1),(,)c +∞;递减区间为(1,)c ,那么对于参数c 进行讨论,进而分析函数图像与x 轴的位置关系。 36.(1)?? ? ??>+-≤≤<++-=4,843,163,76)(22t t t t t t t t h ; (2))3ln 615,7(-∈m . 【解析】(1)本小题是二次函数在特定区间上的最值问题,属于轴定区间动的类型.只需讨论对称轴的三种位置即可. (2)本小题可转化为()()()F x f x g x =-有三个不同的零点即可.然后再利用导数研究F(x)的图像特征,数形结合,求出m 的取值范围. (1)()164)(2 +--=x x f , 当41<+t 即3 76)1()(2++-=+=t t t f t h ; 当14+≤≤t t 即43≤≤t 时,16)4()(==f t h ; 当4>t 时,)(x f 在[]1,+t t 上单调递减,t t t f t h 8)()(2 +-==, 综上,?? ? ??>+-≤≤<++-=4,843,163,76)(22t t t t t t t t h (2)函数)(x f y =与)(x g y =的图象有且仅有三个不同的交点,即函数 )()()(x f x g x -=?的图象与x 的正半轴有且仅有三个不同的交点, ) 0() 3)(1(2682)(', ln 68)(2>--=+-=+--=x x x x x x x m x x x x ?? 当()1,0∈x 时,)(,0)('x x ??>是增函数; 当()3,1∈x 时,)(,0)('x x ?是增函数; 当3,1==x x 时,0)('=x ? 153ln 6)3()(,7)1()(2-+=?=?-=?=?∴m x m x 极小值极大值, 当x 充分接近0时,0)( 必须且只需,3ln 61570 153ln 6)(0 7)(-< ?<-+=?>-=?m m x m x 极小值极大值 则)3ln 615,7(-∈m . 37.(Ⅰ)3213()64f x x x x =- +-. (Ⅱ)0≤m<13 12 . 【解析】(1)由题意知x=1,x=2就是方程2 ()3210f x ax bx '=+-=的两个根,然后利用根与系数的关系可建立关于a,b 的方程,解出a,b 的值,进而确定f(x)的解析式。 (2)本小题转化为323ax bx x x m +-=--即32 20ax bx x m +++=在[-2,0]上有两个不 同的实数根,然后构造函数32 ()2g x ax bx x m =+++利用导数研究其极值,最值画出草图,数形结合不难解决。 解:(Ⅰ)()f x '=3ax 2 +2bx -1,……………………………………………………………(1分) 依题意,(1)f '=(2)f '=0,即3210, 12410. a b a b +-=??+-=? 解得a =16- ,b =34,经检验a =1 6-,b =34符合题意. ∴32 13()64 f x x x x =-+-.…………………………………………(5分) (Ⅱ)曲线y =f (x )与()g x =3x m --(20)x -≤≤有两个不同的交点, 即 32 132064 x x x m ---=在[-2,0]有两个不同的实数解. 设)x (? = 3213264x x x m ---,则213 ()222 x x x ?'=--, 由()0x ?'=,得x = 4或x = -1, ∵x ∈[-2,0],∴当x (-2,-1)时,()0x ?'>,于是φ(x )在[-2,-1]上递增; 当x (-1,0)时,()0x ?'<,于是φ(x )在[-1,0]上递减.………(9分) 依题意有3232 13(2)(2)(2)2(2)0,6413(1)(1)(1)2(1)0,64(0)0,m m m ????-=------≤?? ?=------>?? =-≤??? ………………(11分) 解得0≤m< 13 12 ……… (12分) 38.(1)当1-=x 时, ()x f 取得极大值为 ()=-1f 3 143313 1=++--; 当3=x 时, ()x f 取得极小值为()399273 13+--?=f 6-=. (2)a 的取值范围是()+∞,0. 【解析】 试题分析:(1)遵循“求导数,求驻点,讨论驻点两侧导数值符号,确定极值”. (2)根据 ()x f '= a x x +-22 ,得到△= a 44-= ()a -14 . 据此讨论:① 若a ≥1,则△≤0, 此时()x f '≥0在R 上恒成立,f (x )在R 上单调递增 . 计算f (0)0<-=a ,()023>=a f ,得到结论. ② 若a <1,则△>0,()x f '= 0有两个不相等的实数根,不妨设为1212x x x x <,,(). 有1212 2 x x x x a +==,. 给出当x 变化时,()()x f ,x f '的取值情况表. 根据f (x 1)·f(x 2)>0, 解得a >0.作出结论. 试题解析: (1)当3-=a 时,()333 123 +--= x x x x f , ∴()x f '()()13322+-=--=x x x x . 令()x f '=0, 得 121,3x x =-=. 2分 当1- , 则()x f 在()3,1-上单调递减; 当3>x 时,()0'>x f , ()x f 在()+∞,3上单调递增. 4分 ∴ 当1-=x 时, ()x f 取得极大值为()=-1f 3 1433131=++--; 当3=x 时, ()x f 取得极小值为()399273 1 3+--?= f 6-=. 6分 (2) ∵ ()x f '= a x x +-22 , ∴△= a 44-= ()a -14 . ① 若a ≥1,则△≤0, 7分 ∴()x f '≥0在R 上恒成立, ∴ f (x )在R 上单调递增 . ∵f (0)0<-=a ,()023>=a f , ∴当a ≥1时,函数f (x )的图象与x 轴有且只有一个交点. 9分 ② 若a <1,则△>0, ∴()x f '= 0有两个不相等的实数根,不妨设为1212x x x x <,,(). ∴1212 2 x x x x a +==,. 当x 变化时,()()x f ,x f ' 的取值情况如下表: 11分 ∵02121=+-a x x , ∴1212x x a +-=. ∴()a ax x x x f -+-=1213 113 1 = 1211213 1231x x ax x x -++- ()131231 x a x -+= ()[] 233 1 211-+=a x x . 同理()2x f ()[] 233 12 22-+=a x x . ∴()()()[]()[] 23239 12 2212121-+?-+=?a x a x x x x f x f ()()()() ()[ ] 2222122121292391-++-+=a x x a x x x x ()()[](){} 22122122922391-+-+-+=a x x x x a a a ()339 4 2+-=a a a . 令f (x 1)·f(x 2)>0, 解得a >0. 而当10<=<-=a f a f , 13分 故当10< 考点:应用导数研究函数的极值、单调性及函数的图象,分类讨论思想. 39.(1)m=1(讨论见解析); (2)见解析. 【解析】(1) . 由x=0是f(x)的极值点得f '(0)=0,所以m=1. 于是f(x)=e x -ln(x+1),定义域为(-1,+∞),. 函数 在(-1,+∞)上单调递增,且f '(0)=0,因此当x ∈(-1,0)时, f '(x)<0;当x ∈(0,+∞)时, f '(x)>0. 所以f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增. (2)当m ≤2,x ∈(-m ,+∞)时,ln(x+m )≤ln(x+2),故只需证明当m=2时, f(x)>0. 导数及其应用 【考纲说明】 1、了解导数概念的某些实际背景(如瞬时速度,加速度,光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念。 2、熟记八个基本导数公式;掌握两个函数和、差、积、商的求导法则,了解复合函数的求导法则,会求某些简单函数的导数。 3、理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值。 【知识梳理】 一、导数的概念 函数y=f(x),如果自变量x 在x 0处有增量x ?,那么函数y 相应地有增量y ?=f (x 0+x ?)-f (x 0),比值x y ??叫做函数y=f (x )在x 0到x 0+x ?之间的平均变化率,即x y ??=x x f x x f ?-?+)()(00。如果当0→?x 时,x y ??有极限,我们 就说函数y=f(x)在点x 0处可导,并把这个极限叫做f (x )在点x 0处的导数,记作f’(x 0)或y’|0x x =。 即f (x 0)=0lim →?x x y ??=0lim →?x x x f x x f ?-?+)()(00。 说明: (1)函数f (x )在点x 0处可导,是指0→?x 时,x y ??有极限。如果x y ??不存在极限,就说函数在点x 0处不可导, 或说无导数。 (2)x ?是自变量x 在x 0处的改变量,0≠?x 时,而y ?是函数值的改变量,可以是零。 由导数的定义可知,求函数y=f (x )在点x 0处的导数的步骤: (1)求函数的增量y ?=f (x 0+x ?)-f (x 0); (2)求平均变化率x y ??=x x f x x f ?-?+) ()(00; (3)取极限,得导数f’(x 0)=x y x ??→?0lim 。 二、导数的几何意义 函数y=f (x )在点x 0处的导数的几何意义是曲线y=f (x )在点p (x 0,f (x 0))处的切线的斜率。也就是说,曲线y=f (x )在点p (x 0,f (x 0))处的切线的斜率是f’(x 0)。相应地,切线方程为y -y 0=f/(x 0)(x -x 0)。 三、几种常见函数的导数 ①0;C '= ②() 1;n n x nx -'= ③(sin )cos x x '=; ④(cos )sin x x '=-; ⑤();x x e e '=⑥()ln x x a a a ' =; ⑦ ()1ln x x '= ; ⑧()1 l g log a a o x e x '=. 四、两个函数的和、差、积的求导法则 法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差), 即: ( .)' ''v u v u ±=± 法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个函数乘以第二个函数的导数, 即: .)('''uv v u uv += 若C 为常数,则' ''''0)(Cu Cu Cu u C Cu =+=+=.即常数与函数的积的导数等于常数乘以函数的导数: .)(''Cu Cu = 法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方: ? ?? ??v u ‘=2' 'v uv v u -(v ≠0)。 形如y=f [x (?])的函数称为复合函数。复合函数求导步骤:分解——求导——回代。法则:y '|x = y '|u ·u '|x 五、导数应用 1、单调区间: 一般地,设函数)(x f y =在某个区间可导, 导数复习 1.已知函数y =f(x)的图象是下列四个图象之一,且其导函数y =f′(x)的图象如图所示,则该函数的图象是( ) 2.函数y =f (x )在定义域(- 3 2 ,3)内的图像如图所示.记y =f (x )的导函数为y =f (x ),则不等式f (x )≤0的解集为( ) A .[-13,1]∪[2,3) B .[-1,12]∪[43,8 3] C .[-32,12]∪[1,2)D .(-32,- 13]∪[12,43]∪[43 ,3) 3.已知 其导函数 的图象如图,则函数 的极小值是 A. B. C. D. c 4.函数f(x)的定义域为开区间(a ,b),导函数f′(x)在(a ,b)内的图象如图所示,则函数f(x)在开区间(a ,b)内有极小值点( ) A. 1个 B. 2个 C. 3个 D. 4个 5.设函数()y f x =的图像如左图,则导函数'()y f x =的图像可能是下图中的() 6.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图像如图所示,则函数)(x f 在开区间),(b a 内有极小值点( ) A .1个 B .2个 C .3个 D .4个 7.函数32 55y x x x =+--的单调递增区间是___________________________. 8.函数()x x x f ln =的单调递减区间是 9.函数()f x x x ln 22 -=的单调递减区间是 10.函数f(x)= lnx x 的单调递减区间是 11.函数2x y x e -=在区间(,0)-∞上的单调性为 12.若函数f(x)=e x -ax 在x =1处取到极值,则a =________. 高中导数知识点归纳 1 一、基本概念 2 1. 导数的定义: 3 设0x 是函数)(x f y =定义域的一点,如果自变量x 在0x 处有增量x ?,则函数值y 也4 引起相应的增量)()(00x f x x f y -?+=?;比值x x f x x f x y ?-?+=??)()(00称为函数)(x f y =在点0x 5 到x x ?+0之间的平均变化率;如果极限x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000存在,则称函数6 )(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数。 7 ()f x 在点0x 处的导数记作x x f x x f x f y x x x ?-?+='='→?=) ()(lim )(00000 8 2 导数的几何意义:(求函数在某点处的切线方程) 9 函数)(x f y =在点0x 处的导数的几何意义就是曲线)(x f y =在点))(,(0x f x 处的切线的10 斜率,也就是说,曲线)(x f y =在点P ))(,(0x f x 处的切线的斜率是)(0'x f ,切线方程为11 ).)((0'0x x x f y y -=- 12 3.基本常见函数的导数: 13 ①0;C '=(C 为常数) ②()1;n n x nx -'= 14 ③(sin )cos x x '=; ④(cos )sin x x '=-; 15 ⑤();x x e e '= ⑥()ln x x a a a '=; 16 ⑦()1ln x x '=; ⑧()1l g log a a o x e x '=. 17 二、导数的运算 18 1.导数的四则运算: 19 高三专题复习——导数在解题中常用的有关结论(需要熟记): (1)曲线yf(x)在x x处的切线的斜率等于f(x0),切线方程为 0 y f(x)(xx)f(x) 000 (2)若可导函数yf(x)在xx0处取得极值,则f x。反之,不成立。 ()0 (3)对于可导函数f(x),不等式f(x)0(0)的解集决定函数f(x)的递增(减)区间。 (4)函数f(x)在区间I上递增(减)的充要条件是:xIf(x)0(0)恒成立 (5)函数f(x)在区间I上不单调等价于f(x)在区间I上有极值,则可等价转化为方程 fx在区间I上有实根且为非二重根。(若f(x)为二次函数且I=R,则有0)。 ()0 (6)f(x)在区间I上无极值等价于f(x)在区间在上是单调函数,进而得到f(x)0或 fx0在I上恒成立 () (7)若xI,f(x)0恒成立,则f x0;若xI,f(x)0恒成立,则 () min f(x)0 max (8)若x0I,使得f(x)0,则f(x)max0;若x0I,使得 0 f x0,则f(x)min0. () (9)设f(x)与g(x)的定义域的交集为D若xDf(x)g(x)恒成立则有f(x)g(x)0 min (10)若对x1I1、x I, 22 f(x)g(x)恒成立,则 12 f xgx. ()() minmax 若对x1I1,x2I2,使得f xgx,则 ()() 12 f xgx. ()() minmin 若对xI,x 2I2,使得 11 f xgx,则f(x)max g(x)max. ()() 12 (11)已知f(x)在区间I上的值域为A,,g(x)在区间 1 I上值域为B,2 若对x I, 11 x I,使得f(x1)= 22 g(x)成立,则AB。 2 (12)若三次函数f(x)有三个零点,则方程f(x)0有两个不等实根x1、x2,且极大值大 于0,极小值小于0. (13)证题中常用的不等式: x ①lnxx1(x0)②ln(x+1)x(x1)③e1x x ④e1x⑤ln1(1) xx x x12 ⑥l nx11 22 x22x (x0) 考点一:导数几何意义:角度一求切线方程 1.(2014·洛阳统考)已知函数f(x)=3x+cos2x+sin2x,a=f′3 过曲线y=x 上一点P(a,b)的切线方程为() π ,f′(x)是f(x)的导函数,则4 2014高考文科数学:导数知识点总结 (4) x x sin )(cos -='. (5) x x )(ln = ';e a x x a log )(log ='. (6) x x e e =')(; a a a x x ln )(='.(7)' ' ' ()u v u v ±=±. (8)' ' ' ()uv u v uv =+. (9)'' '2 ()(0)u u v uv v v v -= ≠. (10)2' 11x x -=?? ? ?? (11) ()x x 21' = 5.导数的应用 ①单调性:如果0)(' >x f ,则)(x f 为增函数;如果0)(' 高考复习资料 指数函数、对数函数与幂函数 知识回顾 Ⅰ、指数函数的概念及运算性质 1n 叫根指数,a 叫被开方数(平方根,立方根,n 次方根的概念)。0的任何次方根 都等于00 2、两个等式:A 、n>2时,且n N +∈时,n a = B 、n a ;n 00 a a a a a ≥?=? -∈> 正数的负分数指数幂的意义:10,,,1)m n m n a a m n N n a -+= = >∈> 0的正分数指数幂等于0,0的负分数指数幂没有意义。 4、指数概念由整数扩充到有理数后,指数的运算性质由5条合并成3条 ①(0,,)r s r s a a a a r s Q +?=>∈ ②()(0,,)r s rs a a a r s Q =>∈ ③()(0,0,)r r r ab a b a b r Q =?>>∈ Ⅱ、对数的概念及运算性质 1、概念:log ,(0,1)x a y a x y a a =?=>≠,以10为底的对数叫做常用对数:10log lg a a =;以e=2.71828为底的对数叫自然对数:log ln e a a = 2、对数的性质:对数log ,(0,1)a N a a >≠的性质:①0N >;②log 10a =;③log 1a a = 3、对数的运算法则: ①log a M N ?=____________________;②log a M N =____________________;③log n a M =____________________; ④log a =______________;⑤换底公式:log a b =______________; 换底公式推论:log n m a b =_______________; ⑥倒数公式:log log 1a b b a ?=;⑦对数恒等式:log log 10log 1a b a a a a b ===①②③④log log log a b a b c c ?= Ⅲ、指数、对数函数的概念 (1)指数函数的概念:函数x y a =叫做指数函数,其中a 是一个大于零且不等于1的常量,函数的定义域为R ; (2)对数函数的概念:函数log a y x =叫做对数函数,其中a 是一个大于零且不等于1的常量,函数的值域是R 。 Ⅳ、幂函数的概念 形如y x α=的函数称为幂函数(α为常数),重点掌握11 1,2,3,,,123 α=-时的幂函数及其图像。 Ⅴ、幂函数的性质和图像 幂函数的图像分为二大类,三种情况。A 类:当0a >时,a y x =在第一象限内为增函数,A 类分两种情况; B 类:当0a <时,a y x =在第一象限内为减函数,B 类只有一种情况。 导 数 知识要点 1. 导数(导函数的简称)的定义:即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 注:①x ?是增量,我们也称为“改变量”,因为x ?可正,可负,但不为零. ②以知函数)(x f y =定义域为A ,)('x f y =的定义域为B ,则A 与B 关系为B A ?. Ps :二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f (x )的导数y '=f '(x )仍然是x 的函数,则y '=f '(x )的导数叫做函数y=f (x )的二阶导数。 2. 函数)(x f y =在点0x 处连续与点0x 处可导的关系: ⑴函数)(x f y =在点0x 处连续是)(x f y =在点0x 处可导的必要不充分条件. ⑵如果)(x f y =点0x 处连续,那么)(x f y =在点0x 处可导,是不成立的. 3. 导数的几何意义: 就是曲线)(x f y =在点))(,(0x f x 处的切线的斜率,也就是说,曲线)(x f y =在点P ))(,(0x f x 处的切线的斜率是)(0'x f ,切线方程为).)((0'0x x x f y y -=- 4. 求导数的四则运算法则: ''')(v u v u ±=±)(...)()()(...)()(''2'1'21x f x f x f y x f x f x f y n n +++=?+++=? ''''''')()(cv cv v c cv u v vu uv =+=?+=(c 为常数) )0(2''' ≠-= ?? ? ??v v u v vu v u 注:①v u ,必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导. 例如:设x x x f 2sin 2)(+ =,x x x g 2 cos )(-=,则)(),(x g x f 在0=x 处均不可导,但它们和=+)()(x g x f x x cos sin +在0=x 处均可导. 5. 复合函数的求导法则:)()())(('''x u f x f x ??=或x u x u y y '''?= 复合函数的求导法则可推广到多个中间变量的情形. 6. 函数单调性: ⑴函数单调性的判定方法:设函数)(x f y =在某个区间可导,如果)('x f >0,则)(x f y =为增函数;如果)('x f <0,则)(x f y =为减函数. ⑵常数的判定方法; 如果函数)(x f y =在区间I 恒有)('x f =0,则)(x f y =为常数. 注:①0)( x f 是f (x )递增的充分条件,但不是必要条件,如32x y =在),(+∞-∞上并不是都有0)( x f ,有一个点例外即x =0时f (x ) = 0,同样0)( x f 是f (x )递减的充分非必要条件. ②一般地,如果f (x )在某区间有限个点处为零,在其余各点均为正(或负),那么f (x )在该区间上仍旧是单调增加(或单调减少)的. 7. 极值的判别方法:(极值是在0x 附近所有的点,都有)(x f <)(0x f ,则)(0x f 是函数)(x f 的极大值,极小值同理) 当函数)(x f 在点0x 处连续时, ①如果在0x 附近的左侧)('x f >0,右侧)('x f <0,那么)(0x f 是极大值; ②如果在0x 附近的左侧)('x f <0,右侧)('x f >0,那么)(0x f 是极小值. 数学选修2-2导数及其应用知识点必记 1.函数的平均变化率是什么? 答:平均变化率为 = ??=??x f x y x x f x x f x x x f x f ?-?+=--)()()()(111212 注1:其中x ?是自变量的改变量,可正,可负,可零。 注2:函数的平均变化率可以看作是物体运动的平均速度。 2、导函数的概念是什么? 答:函数)(x f y =在0x x =处的瞬时变化率是x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或0|'x x y =,即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 3.平均变化率和导数的几何意义是什么? 答:函数的平均变化率的几何意义是割线的斜率;函数的导数的几何意义是切线的斜率。 4导数的背景是什么? 答:(1)切线的斜率;(2)瞬时速度;(3)边际成本。 5、常见的函数导数和积分公式有哪些? 函数 导函数 不定积分 y c = 'y =0 ———————— n y x =()*n N ∈ 1'n y nx -= 1 1n n x x dx n +=+? x y a =()0,1a a >≠ 'ln x y a a = ln x x a a dx a =? x y e = 'x y e = x x e dx e =? log a y x =()0,1,0a a x >≠> 1 'ln y x a = ———————— ln y x = 1'y x = 1 ln dx x x =? sin y x = 'cos y x = cos sin xdx x =? cos y x = 'sin y x =- sin cos xdx x =-? 6、常见的导数和定积分运算公式有哪些? 高中导数知识点归纳 一、基本概念 1. 导数的定义: 设0x 是函数)(x f y =定义域的一点,如果自变量x 在0x 处有增量x ?,则函数值y 也引起相应的增量)()(00x f x x f y -?+=?;比值x x f x x f x y ?-?+=??)()(00称为函数)(x f y =在点0x 到x x ?+0之间的平均变化率;如果极限x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000存在,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数。 ()f x 在点0x 2 函数)(x f y =的切线的斜率, ②()1;n n x nx -'= ④(cos )sin x x '=-; ⑤();x x e e '= ⑥()ln x x a a a '=; ⑦()1ln x x '=; ⑧()1l g log a a o x e x '=. 二、导数的运算 1.导数的四则运算: 法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差), 即: ()()()()f x g x f x g x '''±=±???? 法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个 函数乘以第二个函数的导数,即:()()()()()() f x g x f x g x f x g x ''' ?=+ ?? ?? 常数与函数的积的导数等于常数乘以函数的导数:). ( )) ( (' 'x Cf x Cf=(C 为常数) 法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方: () () ()()()() () () 2 f x f x g x f x g x g x g x ' ??'' - =≠ ?? ?? 。 2.复合函数的导数 形如)] ( [x f y? = 三、导数的应用 1. ) (x f在此区间上为减函数。 恒有'f0 ) (= x,则)(x f为常函数。 2.函数的极点与极值:当函数)(x f在点 x处连续时, ①如果在 x附近的左侧)('x f>0,右侧)('x f<0,那么) (0x f是极大值; ②如果在 x附近的左侧)('x f<0,右侧)('x f>0,那么) (0x f是极小值. 3.函数的最值: 一般地,在区间] , [b a上连续的函数) (x f在] , [b a上必有最大值与最小值。函数) (x f在区间上的最值 ] , [b a值点处取得。 只可能在区间端点及极 求函数) (x f在区间上最值 ] , [b a的一般步骤:①求函数) (x f的导数,令导 定积分 一、知识点与方法: 1、定积分的概念 设函数()f x 在区间[,]a b 上连续,用分点011i i n a x x x x x b -=<<<<<<=……把区间[,]a b 等分成n 个小区间,在每个小区间1[,]i i x x -上取任一点(1,2,,)i i n ξ=…作和式 1 ()n n i i I f x ξ== ?∑ (其中x ?为小区间长度) ,把n →∞即0x ?→时,和式n I 的极限叫做函数()f x 在区间[,]a b 上的定积分,记作:?b a dx x f )(,即?b a dx x f )(=1 lim ()n i n i f x ξ→∞ =?∑ 。 这里,a 与b 分别叫做积分下限与积分上限,区间[,]a b 叫做积分区间,函数()f x 叫做被积函数,x 叫做积分变量,()f x dx 叫做被积式。 (1)定积分的几何意义:当函数()f x 在区间[,]a b 上恒为正时,定积分()b a f x dx ?的几何意 义是以曲线()y f x =为曲边的曲边梯形的面积。 (2)定积分的性质 ① ??=b a b a dx x f k dx x kf )()((k 为常数);② ???± = ±b a b a b a dx x g dx x f dx x g x f )()()()(; ③???+ = b a c a b c dx x f dx x f dx x f )()()((其中a c b <<)。 2、微积分基本定理 如果()y f x =是区间[,]a b 上的连续函数,并且()()F x f x '=,那么: ()()|()()b b a a f x dx F x F b F a ==-? 3、定积分的简单应用 (1) 定积分在几何中的应用:求曲边梯形的面积由三条直线 ,()x a x b a b ==<,x 轴及一条曲线()(()0)y f x f x =≥围成的 曲边梯的面积? = b a dx x f S )(。 如果图形由曲线y 1=f 1(x ),y 2=f 2(x )(不妨设f 1(x )≥f 2(x )≥0),及直线x =a ,x =b (a 导数及其应用 知识点总结 1、函数()f x 从1x 到2x 的平均变化率:()()2121 f x f x x x -- 2、导数定义:()f x 在点0x 处的导数记作x x f x x f x f y x x x ?-?+='='→?=)()(lim )(00000;. 3、函数()y f x =在点0x 处的导数的几何意义是曲线 ()y f x =在点()()00,x f x P 处的切线的斜率. 4、常见函数的导数公式: ①'C 0=; ②1')(-=n n nx x ;③x x cos )(sin '=; ④x x sin )(cos '-=; ⑤a a a x x ln )('=;⑥x x e e =')(; ⑦a x x a ln 1)(log '=;⑧x x 1)(ln '= 5、导数运算法则: ()1 ()()()()f x g x f x g x '''±=±????; ()2 ()()()()()()f x g x f x g x f x g x '''?=+????; ()3()()()()()()()()()20f x f x g x f x g x g x g x g x '??''-=≠????????. 6、在某个区间(),a b 内,若()0f x '>,则函数()y f x =在这个区间内单调递增; 若()0f x '<,则函数()y f x =在这个区间内单调递减. 7、求解函数()y f x =单调区间的步骤: (1)确定函数()y f x =的定义域; (2)求导数'' ()y f x =; (3)解不等式'()0f x >,解集在定义域内的部分为增区间; (4)解不等式'()0f x <,解集在定义域内的部分为减区间. 8、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时: ()1如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; ()2如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 9、求解函数极值的一般步骤: (1)确定函数的定义域 (2)求函数的导数f ’(x) (3)求方程f ’(x)=0的根 (4)用方程f ’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格 (5)由f ’(x)在方程f ’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况 10、求函数()y f x =在[],a b 上的最大值与最小值的步骤是: ()1求函数()y f x =在(),a b 内的极值; ()2将函数()y f x =的各极值与端点处的函数值()f a ,()f b 比较,其中最大的一个是最大值,最小的一个是最小值. 《导数及其应用》知识点总结 一、导数的概念和几何意义 1. 函数的平均变化率:函数()f x 在区间12[,]x x 上的平均变化率为: 2121 ()() f x f x x x --。 2. 导数的定义:设函数()y f x =在区间(,)a b 上有定义,0(,)x a b ∈,若x ?无限趋近于0时,比值00()()f x x f x y x x +?-?=??无限趋近于一个常数A ,则称函数()f x 在0x x =处可导,并称该常数A 为函数()f x 在0x x =处的导数,记作0()f x '。函数()f x 在0x x =处的导数的实质是在该点的瞬时变化率。 3. 求函数导数的基本步骤:(1)求函数的增量00()()y f x x f x ?=+?-;(2)求平均变化率:00()()f x x f x x +?-?;(3)取极限,当x ?无限趋近与0时,00()() f x x f x x +?-?无限趋近与一个常数A ,则 0()f x A '=. 4. 导数的几何意义: 函数()f x 在0x x =处的导数就是曲线()y f x =在点00(,())x f x 处的切线的斜率。由此,可以利用导数求曲线的切线方程,具体求法分两步: (1)求出()y f x =在x 0处的导数,即为曲线()y f x =在点00(,())x f x 处的切线的斜率; (2)在已知切点坐标和切线斜率的条件下,求得切线方程为000()()y y f x x x '-=-。 当点00(,)P x y 不在()y f x =上时,求经过点P 的()y f x =的切线方程,可设切点坐标,由切点坐标得到切线方程,再将P 点的坐标代入确定切点。特别地,如果曲线()y f x =在点00(,())x f x 处的切线平行与y 轴,这时导数不存在,根据切线定义,可得切线方程为0x x =。 5. 导数的物理意义: 质点做直线运动的位移S 是时间t 的函数()S t ,则()V S t '=表示瞬时速度,()a v t '=表示瞬时加速度。 二、导数的运算 1. 常见函数的导数: (1)()kx b k '+=(k , b 为常数); (2)0C '=(C 为常数); (3)()1x '=; (4)2()2x x '=; (5)32()3x x '=; (6)211()x x '=-; (7 )'; (8)1()ααx αx -'=(α为常数); §14. 导 数 知识要点 1. 导数(导函数的简称)的定义:设0x 是函数)(x f y =定义域的一点,如果自变量x 在0x 处有增量x ?,则函数值y 也引起相应的增量)()(00x f x x f y -?+=?;比值x x f x x f x y ?-?+= ??) ()(00称为函数)(x f y =在点0x 到x x ?+0之间的平均变化率;如果极限x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000存在,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数, 记作)(0'x f 或0|'x x y =,即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 注:①x ?是增量,我们也称为“改变量”,因为x ?可正,可负,但不为零. ②以知函数)(x f y =定义域为A ,)('x f y =的定义域为B ,则A 与B 关系为B A ?. 2. 函数)(x f y =在点0x 处连续与点0x 处可导的关系: ⑴函数)(x f y =在点0x 处连续是)(x f y =在点0x 处可导的必要不充分条件. 可以证明,如果)(x f y =在点0x 处可导,那么)(x f y =点0x 处连续. 事实上,令x x x ?+=0,则0x x →相当于0→?x . 于是)] ()()([lim )(lim )(lim 0000 00 x f x f x x f x x f x f x x x x +-+=?+=→?→?→ 导数及其应用 一.导数概念的引入 1. 导数的物理意义:瞬时速率。一般的,函数()y f x =在0x x =处的瞬时变化率是 000 ()() lim x f x x f x x ?→+?-?, 我们称它为函数()y f x =在0x x =处的导数,记作0()f x '或0|x x y =', 即0()f x '=000 ()() lim x f x x f x x ?→+?-? 2. 导数的几何意义:曲线的切线.通过图像,我们可以看出当点n P 趋近于 P 时,直线PT 与曲线相切。容易知道,割线n PP 的斜率是00 ()() n n n f x f x k x x -= -,当点n P 趋近于 P 时,函数()y f x =在0x x =处的导数就是切线PT 的斜率k ,即000 ()() lim ()n x n f x f x k f x x x ?→-'==- 3. 导函数:当x 变化时,()f x '便是x 的一个函数,我们称它为()f x 的导函数. ()y f x =的导函数有 时也记作y ',即0 ()() ()lim x f x x f x f x x ?→+?-'=? 例一: 若2012)1(/=f ,则x f x f x ?-?+→? )1()1(l i m 0 = ,x f x f x ?--?+→?) 1()1(lim 0= ,x x f f x ??+-→?4)1()1(lim 0= , x f x f x ?-?+→?)1()21(lim 0= 。 二.导数的计算 1)基本初等函数的导数公式: 2 若()f x x α =,则1 ()f x x αα-'=; 3 若()sin f x x =,则()cos f x x '= 4 若()cos f x x =,则()sin f x x '=-; 5 若()x f x a =,则()ln x f x a a '= 第十一节变化率与导数、导数的计算 [备考方向要明了] [归纳·知识整合] 1.导数的概念 (1)函数y=f(x)在x=x0处的导数: 称函数y=f(x)在x=x0处的瞬时变化率 lim Δx→0f(x0+Δx)-f(x0) Δx=lim Δx→0 Δy Δx为函数y=f(x)在x=x0处的导数,记作f′(x0)或y′|x=x0, 即 f′(x0)=lim Δx→0Δy Δx=lim Δx→0 f(x0+Δx)-f(x0) Δx. (2)导数的几何意义: 函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y=f(x)上点P(x0,y0)处的切线的斜率(瞬时速度就是位移函数s(t)对时间t的导数).相应地,切线方程为y-y0=f′(x0)(x-x0). (3)函数f(x)的导函数: 称函数f ′(x )=lim Δx → f (x +Δx )-f (x ) Δx 为f (x )的导函数. [探究] 1.f ′(x )与f ′(x 0)有何区别与联系? 提示:f ′(x )是一个函数,f ′(x 0)是常数,f ′(x 0)是函数f ′(x )在x 0处的函数值. 2.曲线y =f (x )在点P 0(x 0,y 0)处的切线与过点P 0(x 0,y 0)的切线,两种说法有区别吗? 提示:(1)曲线y =f (x )在点P (x 0,y 0)处的切线是指P 为切点,斜率为k =f ′(x 0)的切线,是唯一的一条切线. (2)曲线y =f (x )过点P (x 0,y 0)的切线,是指切线经过P 点.点P 可以是切点,也可以不是切点,而且这样的直线可能有多条. 3.过圆上一点P 的切线与圆只有公共点P ,过函数y =f (x )图象上一点P 的切线与图象也只有公共点P 吗? 提示:不一定,它们可能有2个或3个或无数多个公共点. 2.几种常见函数的导数 3.导数的运算法则 (1)[f (x )±g (x )]′=f ′(x )±g ′(x ); (2)[f (x )·g (x )]′=f ′(x )g (x )+f (x )g ′(x ); (3)f (x )g (x )′=f ′(x )g (x )-f (x )g ′(x )[g (x )]2(g (x )≠0). 4.复合函数的导数 复合函数y =f (g (x ))的导数和函数y =f (u ),u =g (x )的导数间的关系为y x ′=y u ′·u x ′,即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积. 导数知识点总结 考试内容: 导数的背影.导数的概念.多项式函数的导数.利用导数研究函数的单调性和极值.函数的最大值和最小值. 考试要求: (1)了解导数概念的某些实际背景.(2)理解导数的几何意义.(3)掌握函数,y=c(c为常数)、y=xn(n∈N+)的导数公式,会求多项式函数的导数.(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值.(5)会利用导数求某些简单实际问题的最大值和最小值. 知识要点: 1. 导数(导函数的简称)的定义:设0x 是函数)(x f y =定义域的一点,如果自变量x 在0x 处有增量x ?,则函数值y 也引起相应的增量 ) ()(00x f x x f y -?+=?;比值x x f x x f x y ?-?+= ??) ()(00称为函数)(x f y =在点0x 到 x x ?+0之间的平均变化率;如果极限x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000存在,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或0 |'x x y =,即)(0'x f = x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 注: ①x ?是增量,我们也称为“改变量”,因为x ?可正,可负,但不为零. ②以知函数)(x f y =定义域为A ,)('x f y = 的定义域为B ,则A 与B 关系为 B A ?. 2. 函数)(x f y =在点0x 处连续与点0x 处可导的关系: ⑴函数)(x f y =在点0x 处连续是)(x f y =在点0x 处可导的必要不充分条件. 可以证明,如果)(x f y =在点0x 处可导,那么)(x f y =点0x 处连续. 事实上,令x x x ?+=0,则0x x →相当于0→?x . 于是)]()()([lim )(lim )(lim 0000 00 x f x f x x f x x f x f x x x x +-+=?+=→?→?→ ). ()(0)()(lim lim ) ()(lim )]()()([ lim 000'0000000000 x f x f x f x f x x f x x f x f x x x f x x f x x x x =+?=+??-?+=+???-?+=→?→?→?→?⑵如果)(x f y =点0x 处连续,那么)(x f y =在点0x 处可导,是不成立的. 例:||)(x x f =在点00=x 处连续,但在点00=x 处不可导,因为x x x y ??=??||, 当x ?>0时,1=??x y ;当x ?<0时,1-=??x y ,故 x y x ??→?0lim 不存在. 注:①可导的奇函数函数其导函数为偶函数. ②可导的偶函数函数其导函数为奇函数. 高二数学复习讲义—导数及其应用 知识归纳 1.导数的概念 函数 y=f(x),如果自变量 x 在 x 0 处有增量 ?x ,那么函数 y 相应地有增量 ?y =f (x 0 + ?x ) -f (x 0 ),比值 ?y 叫做函数 y=f (x )在 x 0 ?x 到 x 0 + ?x 之 间 的 平 均 变 化 率 , 即 ?y = f (x 0 + ?x ) - f (x 0 ) 。如果当 ?x → 0 时, x ?x ? y 有极限,我们就说函数 y=f(x)在点 x 处 ?x 可导,并把这个极限叫做 f (x )在点 x 0 处 的导数,记作 f’(x 0 )或 y’| x =x 0 。 即 f (x )= lim ?y = lim f (x 0 + ?x ) - f (x 0 ) 。 0 ?x →0 ?x ?x →0 ?x 说明:(1)函数 f (x )在点 x 0 处可导,是指 ?x → 0 时, ??y x 有极限。如果 ??y x 不存在极 限,就说函数在点 x 0 处不可导,或说无导数。(2)?x 是自变量 x 在 x 0 处的改变量,?x ≠ 0 4.两个函数的和、差、积的求导法则法则 1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差), 即: ( u ± v )' = u ' ± v ' . 法则 2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个函 数 乘 以 第 二 个 函 数 的 导 数 , 即 : (uv )' = u ' v + uv ' . 若 C 为常数, (Cu )' = C 'u + Cu ' = 0 + Cu ' = Cu ' . 即常数与函数的积的导数等于常数乘以函数的导数: (Cu )' = Cu ' . 法则 3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的 ? u ? u ' v - uv ' 积再除以分母的平方: ? ‘ = v 2 ? v ? (v ≠ 0)。 形如 y=f [?(x ) ]的函数称为复合函数。复合 函数求导步骤:分解——求导——回代。法 时,而 ?y 是函数值的改变量,可以是零。由导数的定义可知,求函数 y=f (x )在点 x 0 处的导数的步骤:(1)求函数的增量 ?y =f (x 0 + ?x )-f (x 0 ); (2)求平均变化率 ?y = f (x + ?x ) - f (x 0 ) ; ?x ?x (3)取极限,得导数 f’(x 0 )= lim ?y 。 ?x →0 ?x 2.导数的几何意义 函数 y=f (x )在点 x 0 处的导数的几何意义是曲线 y=f (x )在点 p (x 0 ,f (x 0 ))处的切线的斜率。也就是说,曲线 y=f (x )在点 p (x 0 ,f (x 0 ))处的切线的斜率是 f’(x 0 )。 / 相应地,切线方程为 y -y 0 =f (x 0 )(x -x 0 )。 3.几种常见函数的导数: ① C ' = 0; ② (x n )' = nx n -1; ③ (sin x )' = cos x ;④ (cos x )' = -sin x ; ⑤ (e x )' = e x ; ⑥ ( a x )' = a x ln a ; ⑦ (ln x )' = 1 ; ⑧ (l o g a x )' = 1 log a e . x x导数有关知识点总结、经典例题及解析、近年高考题带答案
导数知识点
最新高中数学导数知识点归纳总结
高二数学导数知识点总结及习题练习
高考文科数学导数知识点总结
函数导数知识点
高中数学导数知识点归纳总结
高中数学人教版选修2-2导数及其应用知识点总结
重点高中数学导数知识点归纳总结
高考积分,导数知识点精华总结
导数及其应用(知识点总结)
(完整版)导数知识点总结及应用
(精心整理)高中数学导数知识点归纳总结
高中数学导数知识点归纳
高三数学一轮复习(知识点归纳与总结):变化率与导数、导数的计算
(完整word版)高三数学导数知识点归纳总结,推荐文档
导数知识点总结及例题讲解