拉氏变换分析 习题课

第四章 习题解4-1 根据拉氏变换定义，求下列函数的拉普拉斯变换。

（1）ate --1（2）()()t t 5cos 73sin 2+ （3）tet 3-（4）()t et5cos 4-（5）()[]tb e at --cos 1（6）()tett 22531-++（7）5232++t t （8）()te t 732--δ（9）()t Ω2cos （10）t t e e βα--- （11）()t et5cos 22-（12）()ϕω+t cos解：（1）)(111]1[a s s a s s e L at +=+-=-- （2）()()2579657323]5cos 73sin 2[222222+++=+++⨯=+s s s s s s t t L （3）23)3(1][+=-s et L t（4）())](21[)](21[]5cos [)54()54(45544t j t j t t j t j t te e e jL e e e j L t eL --+-----+=+= 25)4(5)541541(212++=+++-+=s j s j s j （5）()[]()]cos []cos 1[at e e L e at L t b t b tb ----=-22)(1ab s a b s ++++=（6）由于1!][+=n ns n t L ,由s 域频移特性得()]53[]531[222222t t t t e t te e L e t t L ----++=++ 3232)2(207)2(10)2(3)2(1+++=+++++=s s s s s s （7）32232526526]523[ss s s s s t t L ++=++=++ （8）()732]32[7+-=--s et L tδ（9）()()22242121]2cos 2121[]cos [Ω+⋅+=Ω+=Ωs ss t L t L （10）))((11][βααββαβα++-=+-+=---s s s s e eL t t（11）在（9）的计算结果基础上由s 域频移特性得()25)2(221)2(21]5cos [222+++⋅++=-s s s t e L t （12）()]sin sin cos cos []cos [ϕωϕωϕωt t L t L -=+222222s i n c o s s i n c o s ωϕωϕωϕωωϕ+-=+-+=s s s s s4-7 求下列函数的拉普拉斯反变换。

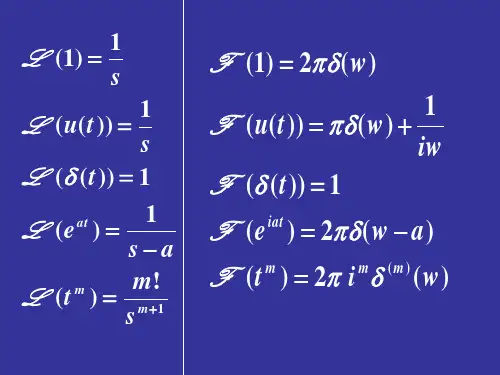
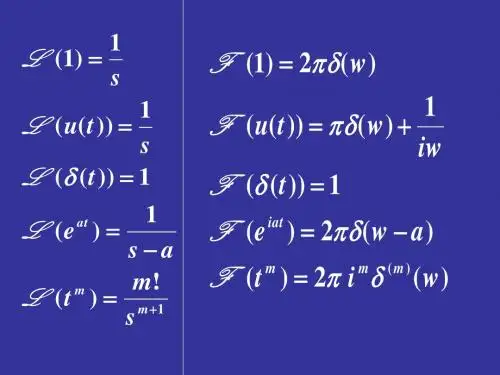
拉普拉斯变换、复频域分析习题课1. 求下列函数的拉氏变换。

（1）1at e-- （2）sin 2cos t t + （3）2t te - （4）sin(2)t e t -（5）(12)t t e -+ （11）1()t t e e αββα---- （13）(2)(1)t te u t --- （15）()ta t e f a-，设已知[()]()L f t F s = 解：（1）11[1]()at a L e s s a s s a --=-=++ （2）2221221[sin 2cos ]111s s L t t s s s ++=+=+++ （3）221[](2)t L te s -=+ （4）22[sin(2)](1)4t L e t s -=++ （5）23[(12)](1)ts L t e s -++=+ （11）11111[()]()()()t t L e e s s s s αββαβααβαβ---=+=--++++ （13）由于(2)(1)(1)(1)[(1)](1)t t t teu t e t e e u t -------=-+- （15）[()](1)ta t L e f aF as a-=+2求下列函数的拉氏变换，注意阶跃函数的跳变时间。

（1）()(2)tf t e u t -=- （2）(2)()(2)t f t e u t --=- （3）(2)()()t f t e u t --= （4）()sin(2)(1)f t t u t =-（5）()(1)[(1)(2)]f t t u t u t =----解：（1）因为(2)2()(2)t f t ee u t ---=-，所以 222(1)11[()]11s s L f t e e e s s ---+==++ （2）21[()]1s L f t e s -=+ （3）因为2()()t f t e e u t -=，所以2[()]1e Lf t s =+ （4） ()sin[2(1)2](1) {sin[2(1)]cos 2cos[2(1)]sin 2}(1)f t t u t t t u t =-+-=-+-- 2222cos 2sin 22cos 2sin 2[()]()444s s s s L f t e e s s s --+=+=+++ （5）()(1)(1)(2)(2)(2)f t t u t t u t u t =-------222221111[()][1(1)]s s s s s L f t e e e s e e s s s s-----=--=-+ 3求下列函数的拉普拉斯逆变换。

7．利用拉氏变换的性质求下列函数的拉氏变换.（1）()teet fatbt-=. （2）()ttt f2sin2=.（3）()tttt fωωωcossin-=（4）()ttt fωsh=.解（1）&()[]=t f&⎰∞=⎥⎦⎤⎢⎣⎡-satbttee&[]duee atbt-⎰∞∞--=--=⎪⎭⎫⎝⎛---=s s bsasaubuduaubulnln11|（2）&()[]=t f&[]2222)1(2sindsdtt-=&[]t2sin()3222224161242+-=⎪⎭⎫⎝⎛+=sssdsd（3）&()[]=t f&[]=-tttωωωcossin&[]ωω-tsin&[]ttωcosdsdsωωω++=22&[]⎪⎭⎫⎝⎛+++=2222cosωωωωωωsst()22232ωω+=s（4）&()[]=t f&[]dsdttsh-=ω&[]tshω()222'21121ωωωω-=⎪⎭⎫⎝⎛+---=ssss8．求下列函数的拉氏逆变换.（1）().412+=ssF（2）().14ssF=（3）()().114+=ssF（4）().31+=ssF（5）().9322++=sssF（6）()()().313-++=ssssF（7）().612-++=ssssF（8）().134522+++=ssssF解（1）()=t f&()[]211=-sF&ts2sin214221=⎥⎦⎤⎢⎣⎡+-（2）()=t f&!31141=⎥⎦⎤⎢⎣⎡-s&313161!3ts=⎥⎦⎤⎢⎣⎡+-（3）由&341611ts=⎥⎦⎤⎢⎣⎡-及位移性质&()[]()t feasF at=--1得()=t f&()[]=-sF1&()t e ts--=⎥⎦⎤⎢⎣⎡+3416111（4）()=t f&()[]=-sF1&tes3131--=⎥⎦⎤⎢⎣⎡+（5）()=t f&()[]21=-sF&+⎥⎦⎤⎢⎣⎡+-921ss&tts3sin3cos29321+=⎥⎦⎤⎢⎣⎡+-（6）()=t f&()[]=-sF1&()()⎥⎦⎤⎢⎣⎡-++-3131sss=&231133211=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+---ss&213-s11-⎥⎦⎤⎢⎣⎡-&⎥⎦⎤⎢⎣⎡+-111stt ee--=21233（7）()=t f&()[]=-sF1&=⎥⎦⎤⎢⎣⎡-++-6121sss&⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛++--3223511ss53=&52211+⎥⎦⎤⎢⎣⎡--s&tt ees321525331--+=⎥⎦⎤⎢⎣⎡+（8）()=t f&()[]=-sF1&=⎥⎦⎤⎢⎣⎡+++-1345221sss&()()⎥⎦⎤⎢⎣⎡++++-22132122ss2=&()()31322221+⎥⎦⎤⎢⎣⎡+++-ss&()⎥⎦⎤⎢⎣⎡++-221323s()ttetete ttt3sin3cos6313sin313cos2222+=+=---9．设()()t ftf21,均满足拉氏变换存在定理的条件（若它们的增长指数均为c）且&()[](),11sFtf=&()[](),22sFtf=，则乘积()()t f t f21的拉氏变换一定存在，且&()()[]()()⎰∞+∞--=ii2121i21ββπdqqsFqFtftf其中.Re,0cs+>>ββ证由于()()t ftf21,均满足拉氏变换存在定理的条件以及增长指数均为c，知乘积()()t f t f21也一定满足拉氏变换存在的定理的条件且增长指数为.2c根据拉氏存在定理的证明当c>β时，&()()[]()()⎰+∞-=2121,dtetftftftf st在0Re cs+≥β上存在且一致收敛.由于()()⎰∞+∞-=ii11i21ββπdteqFtf qt而&()()[]()()⎰+∞-=2121dtetftftftf st()()⎰⎰+∞-∞+∞-⎪⎭⎫⎝⎛=2i i 1i21dt e t f dq e q F st qt ββπ()()⎰⎰+∞--∞+∞-=0)(2i i 1i 21dtdq e t f q F q s ββπ()()dqq s F q F -=⎰∞+∞-2i i 1i 21ββπ10．求下列函数的拉氏逆变换（像原函数），并用另一种方法加以验证.（1）().122a s s F +=（2）()()().b s a s s s F --=（3）()()()2b s a s cs s F +++=（4）()()222222a sa s s F ++=（5）()().1322s a s s F +=（6）()()()b s a s s s F ++=1（7）().144a s s F -= （8）()()22112--+=s s s s s F（9）()().1122-=s s s F （10）()()()4122++=s s ss F（1）解法1 ()=t f &()[]=-s F 1&⎥⎦⎤⎢⎣⎡+⋅-2211a s a aa 1=&a ata s a sin 221=⎥⎦⎤⎢⎣⎡+- 解法2()⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡+=i ,Res i ,Res 2222a a s e a a s e t f st st a at a e a e at at sin i 2i 2i i =-=-解法3 ()=t f &=⎥⎦⎤⎢⎣⎡+-2211a s &⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+---i 1i 1i 211a s a s a i 21a =（&-⎥⎦⎤⎢⎣⎡--i 11a s &⎥⎦⎤⎢⎣⎡+-i 11a s ） ()a at e e a at at sin i 21i i =-=-（2）解法1 ()=t f &()[]=-s F 1&()()⎥⎦⎤⎢⎣⎡---b s a s s1()()()()⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡--=b b s a s se a b s a s se st st ,Res ,Res()bt at bt at be ae b a a b be b a ae --=-+-=1解法2 ()=t f&()[]=-sF1&()()⎥⎦⎤⎢⎣⎡---bsass1=&⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-----bsbasaba11ba-=1（a&bas-⎥⎦⎤⎢⎣⎡--11&⎥⎦⎤⎢⎣⎡--bs11()btat beaeba--=1（3）解法1 ()=t f&()[]s F1-()()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-++++⎥⎥⎦⎤⎢⎢⎣⎡-+++=bbsasecsabsasecs stst,Res,Res22()()bsstateascsdsdabeac-=-⎪⎭⎫⎝⎛+++--=2()()btbtat ebacatebabcebaac-----+--+--=22解法2 ()=t f&()[]=-sF1&()()⎥⎦⎤⎢⎣⎡+++-21bsascs=&()()()⎥⎦⎤⎢⎣⎡+⋅--++⋅--++⋅---2221111bsbabcbsbacaasbaac()2baac--=&()211bacaas--+⎥⎦⎤⎢⎣⎡+-&baacbs--+⎥⎦⎤⎢⎣⎡+-11&()⎥⎥⎦⎤⎢⎢⎣⎡+-211bs ()()btbtat tebabcebacaebaac-----+--+--=22（4）解法1 ()=t f&()[]=-sF1&()⎥⎥⎦⎤⎢⎢⎣⎡++-2222212asas=&⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛+++⋅-'222212123assasaaa23=&21221+⎥⎦⎤⎢⎣⎡+-asa&⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛+'221assattatacos21sin23-=解法2 ()=t f&()[]s F1-()()⎥⎥⎦⎤⎢⎢⎣⎡-+++⎥⎥⎦⎤⎢⎢⎣⎡++=i,2Resi,2Res2222222222aeasasaeasas stst()()i222i222i2i2asstasst easasdsdeasasdsd-==-++++=ta t a t a t a te e a te e a i i i i 41i 4341i 43-----= at t at a cos 21sin 23-=（5）解法1 ()=t f &()2322111a s a s =⎥⎦⎤⎢⎣⎡+-&()⎥⎦⎤⎢⎣⎡+--223111a s s s(12a =&-⎥⎦⎤⎢⎣⎡-311s &())1221⎥⎦⎤⎢⎣⎡+-as s⎰-=t t a 03221(1&)1221dt a s ⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛-=⎰t atdt a t a 032sin 12121()at a t a cos 1121432--=解法2 ()=t f &()⎥⎦⎤⎢⎣⎡+-32211s a s()()()⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+=i ,Res i ,Res 0,Res 322322322a s a s e a s a s e s a s e stst st()()3i 3i 02222i i 2i i 221a a e a a e a s e ds d ta t a s st --+⎪⎪⎭⎫ ⎝⎛+=-=()at a t a cos 1121422--=（6）解法1 ()=t f &()()⎥⎦⎤⎢⎣⎡-+-b s a s s 11=&()()⎥⎦⎤⎢⎣⎡+⋅--+⋅-+⋅-b s b a b a s b a a s ab 1111111=ab 1&()b a a s -+⎥⎦⎤⎢⎣⎡-111&()b a b a s -1-⎥⎦⎤⎢⎣⎡+-11&⎥⎦⎤⎢⎣⎡+-b s 11()()bt at e b a b e b a a ab -----+=111解法2 ()=t f &()()⎥⎦⎤⎢⎣⎡++-b s a s s 11()()()()()()⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡++=b b s a s s e a b s a s s e b s a s s e stst st ,Res ,Res 0,Res()()bt at e b a b e b a a ab -----+=111（7）解法1 ()=t f&⎥⎦⎤⎢⎣⎡--4411as=&⎥⎦⎤⎢⎣⎡+-⎪⎭⎫⎝⎛+---22331211141asaaasasa()ataeeaatat sin214133--=-()atatasinsh213-=解法2 ()=t f&⎥⎦⎤⎢⎣⎡--4411as⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-=i,Resi,Res,Res,Res44444444aaseaaseaaseaase stststst()()3i3i33i4i444aeaeaeae t ataatst-++-=--()atatasinsh213-=（8）解法1 ()=t f&()=⎥⎦⎤⎢⎣⎡--+-221112ssss&()⎥⎦⎤⎢⎣⎡-+-+--2112121sss=&+⎥⎦⎤⎢⎣⎡--s11&+⎥⎦⎤⎢⎣⎡--121s&()⎥⎦⎤⎢⎣⎡--2112stt tee221++-=解法2()=t f&()⎥⎦⎤⎢⎣⎡--+-221112ssss()()⎥⎦⎤⎢⎣⎡--++⎥⎦⎤⎢⎣⎡--+=1,112Res0,112Res2222stst essssessss12121=⎪⎪⎭⎫⎝⎛-++-=sstesssdsdtt tee221++-=（9）解法1 ()=t f&()[]=-sF1&()⎥⎦⎤⎢⎣⎡--11221ss=&()teessstt--=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛+----21111112121tsht-=解法2 ()()()()⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=1,1Res1,1Res0,1Res222222ssessesset fstststtteesedsd ttsst-=-+⎪⎪⎭⎫⎝⎛-=-=sh2212（10）解法1 ()=t f &()()⎥⎦⎤⎢⎣⎡++-41221s s s =&⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-+-4131221s s s s(31=&-⎥⎦⎤⎢⎣⎡+-121s s &()t t s s 2cos cos 31)421-=⎥⎦⎤⎢⎣⎡+-解法2 =)(t f &()()⎥⎦⎤⎢⎣⎡++-41221s s s()()()()()()()()⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡-+++⎥⎦⎤⎢⎣⎡++=i 2,41Res i 2,41Res i ,41Res i ,41Res 22222222s s se s s se s s se s s se stst st st ()()()()()i 41i 4i 2i 41i 4i 24i i 2i 4i i 2i 2i 22i 22i 2i -+-++++--++=--tt t t e e e e6666i 2i 2i i t t t t e e e e --+++= ()t t 2cos cos 31-=。

第14 章 Laplace 变换1． 求下列函数的拉氏变换 （1）1cos wtw- （2）chwt 解 （1）{}{}220sin 1cos sin ()tL wt wt wL Lwzdz w p p p w -⎧⎫===⎨⎬+⎩⎭⎰（2）{}{}22111122wt wt pL chwt L e e p w p w p w-⎧⎫=+=+=⎨⎬-+-⎩⎭ 2．求下列函数的逆拉氏变换 （1）2845p p p +++； （2）222()p p a + 其中a ＞0。

解 （1）111222821645(2)1(2)1p p L L L p p p p ---⎧⎫⎧⎫⎧⎫++=+⎨⎬⎨⎬⎨⎬++++++⎩⎭⎩⎭⎩⎭22cos 6sin tt et e t --=+（2）1222sin ()2pt at L p a a -⎧⎫=⎨⎬+⎩⎭3. 设11()sin f t wt w=，2()f t chwt =，其中w ≠0,求12()()f t f t *。

解法1 由于{}{}{}1212L f f L f L f *=⋅ {}12211()sin L f t L wt w p w⎧⎫==⎨⎬+⎩⎭ {}{}222()pL f t L chwt p w ==-所以 {}1222221pL f f p w p w*=⋅+- 2222222()2()p pw p w w p w =--+2211cos 22L chwt L wt w w ⎧⎫⎧⎫=-⎨⎬⎨⎬⎩⎭⎩⎭2211cos 22L chwt wt w w ⎧⎫=-⎨⎬⎩⎭1221(cos )2f f chwt wt w *=- 解法2 由卷积定义求1201()()sin ()tf t f t w chw t d wτττ*=-⎰()()01sin 2w t w t te e w d w ττττ---+=⎰ ()()0011sin sin 22t t w t w t e w d e w d w w ττττττ---=+⎰⎰ 22221111sin cos sin 4444wt wt wt e wt w w w w =--++-2211cos 44wtt e w w -+ 2211cos 222wt wt e e wt w w -+=-21(cos )2chwt wt w =- 4．求解'1(0)0x x x +=⎧⎨=⎩解 对方程施行Laplace 变换，并注意初始条件：x(0)=0,我们有 [][][]'1L x L x L +=[][]1pL x L x p+=[]11111(1)1(1)L x p p p p p p ==-=-++--[]11111(1)tx L L x L e p p ---⎡⎤==-=-⎢⎥--⎣⎦5. 求解2'3(0)2tx x e x -⎧-=-⎨=⎩解 对方程两边施以Laplace 变换，并注意初始条件x(0)=0,则有[][]2'3tL x L x L e -⎡⎤-=-⎣⎦[][]3(0)2pL x x L x p ---=+ []311(1)(2)21L x p p p p -==--++-11211()()21t tx t L x L e e p p ---⎡⎤==-=-⎢⎥+-⎣⎦6. 求解01"(0),'(0)tx x e x x x x ⎧+=⎨==⎩解 对方程两边施以Laplace 变换得[][]"tL x L x L e ⎡⎤+=⎣⎦[][]20111p L x px x L x p --+=- 解得 []0122221111121212111x p x p L x p p p p p =--++-++++ 所以 101222211111()21212111x p x p x t L p p p p p -⎡⎤=--++⎢⎥-++++⎣⎦01111()cos ()sin 222t e x t x t =+-+- 7. 求解01"(0),'(0)tx x e x x x x ⎧-=⎨==⎩解 对方程两边施以Laplace 变换得 [][]"t L x L x L e ⎡⎤-=⎣⎦[][]201'(0)1p L x p xx L x p ---=- []201111p L x px x p ⎡⎤-=++⎣⎦- 解得 []2111()2(1)4(1)4(1)L x t p p p =-+--+ 012211x p x p p ++-- []101111()(())244t t t x t L L x t te e e x cht x sht --==-+++8. 求解"'2"'4(0)1,'(0)2,"(0)2x x x x x x --=⎧⎨===-⎩解 对方程两边施行Laplace 变换，并注三个初始条件，则有[][][][]"'2"'4L x L x L x L -+=[][]322(0)'()"(0)2(0)'(0)p x p x px x x p L x px x ⎡⎤------+⎣⎦[]4(0)L x x p-=[][][]3224222241p L x p p p L x p pL x p--+-+++-=[]224(1)5p p L x p p-=+- 解得 []222254()(1)(1)(1)p L x t p p p p p =-+--- 23421p p p =+-- 所以 []1()()342tx t L L x t t e -==+-9. 求解21"'2(0)'(0)"(0)0t x x t e x x x ⎧+=⎪⎨⎪===⎩ 解 对方程两边施以Laplace 变换并利用初始条件有 [][]21"'2tL x L x L t e ⎡⎤+=⎢⎥⎣⎦[][]3221(0)'(0)"(0)(1)p L x p x px x L x p ---+=-解得 []331()(1)(1)L x t p p =-+- 当331231,,ii p p e p e ππ-=-==是一阶极点，p=1是三阶极点，由留数计算公式：22331111Re ()lim 2(1)(1)ptpt p p d s F p e e dp p p →=⎡⎤⎡⎤=⎢⎥⎣⎦!+-⎣⎦2133448t t tt e te e =-+31311(1)Re ()|(1)24ptptt p p e p s F p e e p -=-=--⎡⎤==-⎣⎦+3332(1)Re ()|3i i pt ptp e p e e p s F p e p ππ==-⎡⎤==⎣⎦3Re ()iptp es F p e π-=⎡⎤=⎣⎦所以221331()44824t t t t t x t t e te e e -=-+--21cos 32te10. 求解3''21'4'30(0)(0)0x y x x y y x y ++=⎧⎪++=⎨⎪==⎩解 对方程组两边施行Laplace 变换，并设[][](),(),X L x t Y L y t ==得 1(32)(43)0p X pY p pX p Y ⎧++=⎪⎨⎪++=⎩解得 221111111765(116)5(1)431133(11176)25(1)10(116)Y p p p p p X p p p p p p --⎧==+⎪++++⎪⎨+⎪==--⎪++++⎩所以 [][]61116111113()251011()55t t t tx t L X e e y t L Y e e ------⎧==--⎪⎪⎨⎪==-+⎪⎩11. 求解0sin ()sin()()ta t G t t z G z dz =--⎰，a 为常数。

第十五章 拉普拉斯变换典型习题解答与提示习 题 15-11．（1）提示：2()f t t =， ￡20[()]()ptpt f t f t edt t e dt +∞+∞--==⎰⎰，求广义积分后可得￡32[()]f t p =，(0)p >； （2）提示：4()tf t e -=，￡40[()]()pt t pt f t f t e dt e e dt +∞+∞---==⎰⎰，￡1[()](4)4f t p p =>-+； （3）因302()12404t f t t t ≤<⎧⎪=-≤<⎨⎪≥⎩，则￡242[()]()3(1)ptptpt f t f t edt edt e dt +∞---==+-⎰⎰⎰24024,(0)31,(0)pt pt p e e p p p --=⎧⎪=⎨-+≠⎪⎩4234,(0)4,(0)p pe e p pp --⎧+-≠⎪=⎨⎪=⎩； （4）因()tf t te -=， 则￡2(1)(1)0001[()]()1ptp tp t f t f t edt tedt td e p +∞+∞--+-+⎛⎫===- ⎪+⎝⎭⎰⎰⎰ (1)(1)0111p t p t te e dt p p +∞+∞-+-+=-+++⎰ (1)21(1)(1)p tep p +∞-+=->-+21(1)(1)p p =>-+。

2．（1）￡231[()](263)(0)f t p p p p=+->； （2）￡2262[()](0)41pf t p p p =->++； （3）因()1tf t te =+，则￡[()]f t =￡(1)+￡()tte1(1)[p=+-￡()]t e ' （微分性） 222111(1)(1)(1)p p p p p p p -+=+=>--； （4）因3()sin 4tf t e t =，又因￡24(sin 4)()16t F p p ==+，则由位移性知￡24[()](3)(3)(3)16f t F p p p =-=>-+； （5）方法一 因22()tf t t e-=，又￡232[]()(0)t F p p p ==>，则由位移性知 ￡32[()](2)(2)(2)f t F p p p =+=>-+； 方法二 因￡21(),(2)2tep p -=>-+，则由微分性知 ￡2312[()](1)(2)2(2)f t p p p ''⎛⎫=-=>- ⎪++⎝⎭； （6）因21()sin (1cos 2)2f t t t ==-，则￡1[()][2f t =￡(1)-￡22112(cos 2)](0)24(4)p t p p p p p ⎛⎫=-=> ⎪++⎝⎭； （7）因1()sin 2cos 2sin 42f t t t t ==， 则￡1[()]2f t =￡22142(sin 4)(0)21616t p p p =⨯=>++；（8）因()sin()sin cos cos sin f t t t t ωϕωϕωϕ=+=+， 则￡[()]cos f t ϕ=￡(sin )sin t ωϕ+￡2222cos sin (cos )p t p p ωϕϕωωω=+++22cos sin (0)p p p ωϕϕω+=>+； （9）因11()(21)222f t t t t μμμ⎡⎤⎛⎫⎛⎫=-=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 则由延滞性知￡121[()](0)p f t ep p-=>； （10）因3()sin 2tf t tet -=，又￡22(sin 2)(0)4t p p =>+， 则由位移性知￡322(sin 2)(3)(3)4t e t p p -=>-++，故再由微分性知 ￡22224(3)[()](3)(3)4[(3)4]p f t p p p '⎡⎤+=-=>-⎢⎥++++⎣⎦； （11）因4()cos 24tf t et π-⎛⎫=+ ⎪⎝⎭，又因￡cos 242t π⎡⎤⎛⎫+= ⎪⎢⎥⎝⎭⎣⎦￡222(cos 2sin 2)244p t t p p ⎫-=-⎪++⎝⎭2224p p -=+，则由位移性知￡22[()](4)2(4)4p f t p p +=⨯>-++。

拉氏变换逆变换例题拉氏变换和逆变换是信号处理中常用的工具，本文将提供几个拉氏变换和逆变换的例题，帮助读者更好地理解这些概念。

例题1：求函数f(t)=sin(2πt)的拉氏变换。

解：根据拉氏变换的定义，我们有：F(s) = ∫0∞ e^(-st) sin(2πt) dt这个积分可以通过分部积分来求解。

设u = sin(2πt)，dv = e^(-st) dt，则du/dt = 2πcos(2πt) 和 v = (-1/s) e^(-st)。

因此，F(s) = (∫0∞ u dv) = [(uv) |0∞ - ∫0∞ v du/dt dt]= [(sin(2πt) (-1/s) e^(-st)) |0∞ - ∫0∞ (-1/s) e^(-st) 2πcos(2πt) dt]= [(0 - 0) - (2π/s) ∫0∞ e^(-st) cos(2πt) dt]= (2π/s) [(1/(s^2 + 4π^2)]因此，f(t)=sin(2πt)的拉氏变换为F(s) = (2π/s) [(1/(s^2 + 4π^2)]例题2：求函数F(s) = (s + 2)/(s^2 + 4s + 5)的拉氏逆变换。

解：我们可以通过部分分式分解来求解逆变换。

设F(s) = A/(s + α) + B/(s + β)，则F(s) = A/(s + α) + B/(s + β) = (As + Aα + Bs + Bβ)/(s^2 + (α + β)s + αβ)比较系数可得：Aα + Bβ = 2，A + B = 1，Aβ + Bα = 0。

解得A = 2/(3-2i)，B = 1/(3-2i)。

因此，F(s) = (s + 2)/(s^2 + 4s + 5) = 2/(3-2i) /(s + (2-i)) + 1/(3-2i) /(s + (2+i))我们可以使用拉氏逆变换的表格或者将其转化为指数函数，最终得到f(t) = (2/5) e^(-2t) sin(t) + (1/5) e^(-2t) cos(t) 以上就是本文的拉氏变换和逆变换例题，希望能对读者在学习信号处理中有所帮助。