几种收敛函数的介绍

k均值聚类算法的收敛准则函数
常见的收敛准则函数有两种：平均误差平方和（SSE）和轮廓系数。

1.平均误差平方和（SSE）：
平均误差平方和是一种度量聚类质量的准则函数。

它衡量了每个数据
点与其所属簇的质心之间的距离之和，表示了簇内离散程度的度量。

SSE
计算公式如下：
SSE = Σ(Σdist(xi, ci))^2
其中，xi表示第i个数据点，ci表示第i个数据点所属的簇的质心，dist(x, c)表示数据点x与质心c之间的距离。

2.轮廓系数：
轮廓系数是一种度量聚类结果的准则函数，用于评估聚类的紧密性和
区分度。

它通过度量簇内样本的紧密度和不同簇之间的分离度来刻画聚类
的质量。

轮廓系数的计算公式如下：
s(i) = (b(i) - a(i))/max(a(i), b(i))
其中，a(i)表示数据点i到同簇其他点的平均距离，b(i)表示数据点
i到其他簇的平均最短距离。

s(i)的取值范围在-1到1之间，值越接近1
表示聚类效果越好。

综上所述，k均值聚类算法的收敛准则函数是SSE和轮廓系数。

根据
具体的应用场景和需求，可以选择合适的准则函数来评估聚类的质量和判
断算法的收敛性。

几个常见的收敛,发散积分
收敛或发散积分是数学中常见的一种技术，用于计算函数的积分值。

它被广泛用于计算和估算各种积分的值以及计算其他数学公式的值，包括：对数函数、指数函数、正弦函数、余弦函数、反余弦函数、反正弦函数等。

积分一般分为两类：收敛积分和发散积分。

收敛积分是指当函数的图像在某一点上发生改变时，它收敛到一个特定的点，而发散积分是指函数在某一点上发生改变时，它会发散到更高的水平。

收敛积分一般有三种形式：矩形收敛积分、梯形收敛积分和辛普森收敛积分。

矩形收敛积分是一种基本的收敛积分，它将函数的图形分成若干个矩形，每个矩形由一个左端点和一个右端点构成，积分值就是给定区域内所有矩形的面积之和。

梯形收敛积分和矩形收敛积分类似，区别只在于它将函数的图形分成若干个梯形，每个梯形由一个上端点、一个左端点和一个右端点构成，积分值就是给定区域内所有梯形面积之和。

最后，辛普森收敛积分是一种改进的收敛积分，它以一种更加精确的方式计算函数的积分值，它将函数的图形分成若干个辛普森三角形，每个三角形由一个顶点和两个底边构成，积分值就是给定区域内所有辛普森三角形的面积之和。

发散积分一般也有三种形式：拉格朗日发散积分、双曲发散积分和伽马发散积分。

拉格朗日发散积分是一种常见的发散积分，它通过划分不同的部分来进行发散积分，每个部分包含一个头部和一个尾部，每一部分的积分值就是从头部到尾部的积分值之和，最后积分值就是所有部分的积分值之和。

双曲发散积分和拉格朗日发散积分类似，也是划分不同的部分，每个部分由头部和尾部构成，不同的是，每部分的积分值不是从头部到尾部的积分值之和，而是经过特殊函数变换后的积分值之和。

概率论中的收敛-正文概率论中的极限定理和数理统计学中各种统计量的极限性质，都是按随机变量序列的各种不同的收敛性来研究的。

设{X n,n≥1}是概率空间(Ω,F,P)（见概率）上的随机变量序列，从随机变量作为可测函数看，常用的收敛概念有以下几种：以概率1收敛若,则称｛X n,n≥1｝以概率1收敛于X。

强大数律（见大数律）就是阐明事件发生的频率和样本观测值的算术平均分别以概率 1收敛于该事件的概率和总体的均值。

以概率 1收敛也常称为几乎必然（简记为α.s）收敛,它相当于测度论中的几乎处处（简记为α.e.）收敛。

依概率收敛若对任一正数ε,都有，则称{X n,n≥1}依概率收敛于X。

它表明随机变量X n与X发生较大偏差(≥ε)的概率随n无限增大而趋于零。

概率论中的伯努利大数律就是最早阐明随机试验中某事件 A发生的频率依概率收敛于其概率P(A)的。

依概率收敛相当于测度论中的依测度收敛。

r阶平均收敛对r≥1,若X n-X的r阶绝对矩(见矩)的极限,则称{X n,n≥1}r阶平均收敛于X。

特别，当r=1时，称为平均收敛；当r=2时,称为均方收敛，它在宽平稳过程（见平稳过程）理论中是一个常用的概念。

弱收敛设X n的均值都是有限的，若对任一有界随机变量Y都有,则称{X n,n≥1}弱收敛于X。

由平均收敛可以推出弱收敛。

从随机变量的分布函数（见概率分布）看，常用的有如下收敛概念。

分布弱收敛设F n、F分别表示随机变量X n、X的分布函数,若对F的每一个连续点x都有，则称X n的分布F n弱收敛于X的分布F,也称X n依分布收敛于X。

分布弱收敛还有各种等价条件，例如,对任一有界连续函数ƒ(x)，img src="image/254-6.gif" align="absmiddle">。

分布弱收敛是概率论和数理统计中经常用到的一种收敛性。

中心极限定理就是讨论随机变量序列的标准化部分和依分布收敛于正态随机变量的定理。

三大收敛定理引言在数学领域，收敛是一个重要的概念。

当一个数列或函数的值越来越接近一个确定的极限值时，我们称之为收敛。

收敛定理是指一系列定理，用于判断数列或函数是否收敛以及极限的性质。

本文将介绍三大收敛定理，分别是柯西收敛准则、夹逼定理和单调有界数列定理。

这些定理是数学分析中最重要的基本定理之一。

一、柯西收敛准则柯西收敛准则是判断数列是否收敛的一种重要方法。

柯西收敛准则的基本思想是：如果对于任意给定的正数ε，存在一个自然数N，使得当n和m大于等于N时，数列的前n个元素和前m个元素之差的绝对值小于ε，则该数列是收敛的。

表达式表示如下：对于任意给定的ε>0，存在自然数N，对于任意n,m>N，有|an - am| < ε。

二、夹逼定理夹逼定理是用来判断函数极限的一种重要方法。

夹逼定理的基本思想是：如果一个函数在某个区间上的两个函数夹住，且两个函数的极限相等，则这个函数的极限也相等。

具体的说：假设函数f(x)、g(x)和h(x)在区间[a, b]内定义，并且当x在这个区间上时，有g(x) ≤ f(x) ≤ h(x)。

如果当x趋于某个值c时，有lim(g(x)) = lim(h(x)) = L，则lim(f(x))也等于L。

三、单调有界数列定理单调有界数列定理是判断数列是否收敛的一种常用方法。

该定理分为两部分：单调有上界的数列必有极限，以及单调有下界的数列必有极限。

单调有上界的数列必有极限可以表述为：如果一个实数数列递增且有上界，那么这个数列是收敛的。

同理，单调有下界的数列必有极限可以表述为：如果一个实数数列递减且有下界，那么这个数列也是收敛的。

实例应用下面我们通过一个实例来应用上述三大收敛定理。

例：判断数列{(-1)^n/n}是否收敛。

首先，我们可以通过柯西收敛准则来判断数列是否收敛。

对于任意给定的ε>0，我们有：|an - am| = |(-1)^n/n - (-1)^m/m| ≤ 2/n ≤ ε。

可测函数列常见的几种收敛摘 要：本文介绍了可测函数列常见的几种收敛：一致收敛、几乎一致收敛、几乎处处收敛、依测度收敛等以及它们之间的关系．关键字：可测函数列；一致收敛；几乎一致收敛；几乎处处收敛；依测度收敛前言在数学分析中我们知道一致收敛是函数列很重要的性质，比如它能保证函数列的极限过程和(R)积分过程可交换次序等．可是一般而言函数列的一致收敛性是不方便证明的，而且有些函数列在其收敛域内也不一定是一致收敛的，如文中所给的例2函数()f x 在收敛域[0,1]内不一致收敛，但对于一个0δ>当0δ→时在[0,]δ内一致收敛，这不见说明了一致收敛的特殊性，也验证了我们平时常说的“矛盾的同一性和矛盾的斗争性是相联系的、相辅相成的”[1]1 可测函数列几种收敛的定义1.1 一致收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集E 上的实值函数．若对于0,ε∀>存在,K N +∈使得对于,k K x E ∀≥∀∈都有()()k f x f x ε-<则称}{()k f x 在E 上一致收敛到()f x ．记作： u k f f −−→(其中u 表示一致uniform)．1.2 点点收敛若函数列12(),(),(),,(),k f x f x f x f x 在点集D E ⊂上每一点都收敛，则称它在D 上点点收敛．例1 定义在[0,1]E =上的函数列1(),1k f x kx=+则()k f x 在E 上点点收敛到函数 1,0,()0,0 1.x f x x =⎧=⎨<≤⎩ 而且还能看出{()}k f x 在[]0,1上不一致收敛到()f x ，但对于0,{()}k f x δ∀>在[,1]δ上一致收敛到()f x ．1.3 几乎一致收敛[3]设E 是可测集，若0,,E E δδ∀>∃⊂使得(\),m E E δδ<在E δ上有u k f f −−→则称{()}k f x 在E 上几乎一致收敛与()f x ，并记作...a u k f f −−→(其中a.u ．表示几乎一致almost uniform) ．例2 定义在[]0,1E =上的函数()k k f x x =在[]0,1上收敛却不一致收敛．但是只要从[]0,1的右端点去掉任一小的一段使之成为[]()0,10,0δδδ->→则{()}k f x 在此区间上就一致收敛，像这样的收敛我们就可以称之为在[]0,1E =上几乎一致收敛与0．1.4 几乎处处收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集n E R ⊂上的广义实值函数．若存在E 中点集Z ，有()0,m Z =及对于每一个元素\x E Z ∈，有lim ()()k x f x f x →∞= 则称{()}k f x 在E 上几乎处处收敛与()f x ，并简记为,.[]k f f a e E →或..a e k f f −−→若上文的例1也可以称之为在[]0,1上几乎处处收敛与()f x ．1.5 依测度收敛例3在[0,1)上构造函数列{()}k f x 如下：对于k N +∈，存在唯一的自然数i 和j ，使得2,i k j =+其中02,i j ≤≤令1[,)22()(),1,2,,[0,1).i i k j j f x x k x χ+==∈任意给定的0[0,1),x ∈对于每一个自然数i ，有且仅有一个j ，使得01[,)22i i j j x +∈．数列0{()}f x 中有无穷多项为1，有无穷多项为0．由此可知，函数列{()}k f x 在[0,1)上点点不收敛．因此仅考虑点收敛将得不到任何信息．然而仔细观察数列0{()}k f x 虽然有无穷多个1出现，但是在“频率”意义下，0却也大量出现．这一事实可以用点集测度语言来刻画．只要k 足够大，对于01,ε<≤点集{[0,1)()0}{[0,1)()1}1[,)22k k i ix f x x f x j j ε∈-≥=∈=+= 的测度非常小．事实上 1({[0,1)()0})2k i m x f x ε∈-≥=． 这样对于任给的0,δ>总可以取到0,k 也就是取到0,i 使得当0k k >时，有({[0,1)()0})1k m x f x εδ∈-<>-其中02i δ-<．这个不等式说明，对于充分大的h ，出现0的“频率”接近1．我们将把这样一种现象称为函数列{()}k f x 在区间[0,1)上依测度收敛到零函数，并将抽象出以下定义[3]：设12(),(),(),,(),k f x f x f x f x 是可测集E 上几乎处处有限的可测函数．若对于任意给定的0,ε>有lim (())0,k x m E f f ε→∞->= 则称{()}k f x 在E 上依测度收敛到函数()f x ，记为.m k f f −−→2 可测函数列几种收敛的关系2.1 点点收敛与一致收敛的关系由上述定义我们可以知道u k f f −−→，必有{()}k f x 点点收敛于()f x ．如例1．反之则不一定成立，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则()f x 也是可测函数．2.2 几乎处处收敛与一致收敛的关系由定义可知有一致收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→．反之则不然，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则极限函数()f x 也是可测函数．应用：从数学分析我们知道一致收敛的函数列对于求极限运算和(R)积分运算、微分运算与(R)积分运算等可以交换次序．2.3 几乎处处收敛与一致收敛的关系叶果洛夫(E ΓopoB )定理[5]：设(),{}n m E f <∞是E 上一列a.e ．收敛于一个a.e ．有限的函数f 的可测函数，则对于任意的0δ>，存在子集E E δ⊂，使{}n f 在E δ上一致收敛，且(\)m E E δδ<．注 定理中“()m E <∞”不可去掉如：例4定义在(0,)E =+∞的函数列1,(0,]()(1,2,).0,(,)m x m x m x m f ∈⎧==⎨∈+∞⎩ 则m f 在(0,)+∞上处处收敛于1，但对于任何正数δ及任何可测集E δ，当时(\)m E E δδ<时，m f 在E δ上不一致收敛于1．这是因为，当时(\)m E E δδ<时，E δ不能全部含于(0,]m 中，必有(,)m E m x δ∈+∞ ，于是有()0m m x f =．sup ()1()11m m m x E f x f x δ∈-≥-=所以()m x f 在E δ上不一致收敛与1，也即定理中“()m E <∞”不可去掉[4]．由定义我们知道一致收敛必是几乎处处收敛的，反之则不成立．但它们又有密切的关系，即使上述定理告诉我们几乎处处收敛“基本上”是一致收敛的(在除去一个测度为任意小集合的子集上)．应用 由上述定理我们还可以得到“鲁津定理”：设()f x 是E 上a.e ．有限的可测函数，则对于任意的0δ>，存在闭子集E F δ⊂，使()f x 在F δ上是连续函数，且(\)m E F δδ<．也就是说：在E 上a.e ．有限的可测函数“基本上”是连续的(在除去一个测度为任意小集合的子集上)．也即我们可以用连续函数来逼近a.e ．有限的可测函数．2.4几乎处处收敛与依测度收敛的关系例5 取(0,1]E =，将E 等分，定义两个函数：(1)111,(0,]2()10,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩， (1)210,(0,]2()11,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩． 然后将(0,1]四等分、八等分等等．一般的，对于每个n ，作2n 个函数：()11,(,]22()1,2,,2.10,(,]22n n n n j n j j x x j j j x f -⎧∈⎪⎪==⎨-⎪∉⎪⎩ ．我们把(),1,2,,2{}n j x j f = ，先n 按后按j 的顺序逐个的排成一列：(1)(1)()()()12122(),(),,(),(),,(),n n n n x f x f x f x f x f (1)()()n j x f 在这个序列中是第22n j N -+=个函数．可以证明这个函数列是依测度收敛于零的．这是因为对于任何的0σ>，()0[]n j f E σ-≥或是空集(当1σ>)，或是1,22(]n n j j - (当01σ<≤)，所以 ()102([])n j n f m E σ-≥≤ (当时1σ>时，左端为0)．由于当2(1,2,,2.)2n n j j N -+== 趋于∞时n →∞，由此可见()([0])0lim n j N m E f σ→∞-≥=， 也即()()0m n j x f −−→．但是函数列(1)在上的任何一点都不收敛．事实上，对于任何点0(0,1]x ∈，无论n 多么大，总存在j ，使01(,]22n n j j x -∈，因而()0()1n j x f =，然而()10()0n j x f +=或()10()0n j x f -=，换言之，对于任何0(0,1]x ∈，在()0(){}n j x f 中必有两子列，一个恒为1，另一个恒为0．所以序列(1)在(0,1]上任何点都是发散的．这也就说明依测度收敛的函数列不一定处处收敛，也就是说依测度收敛不能包含几乎处处收敛，但仍有：黎斯(F ．Riesz) [5] 设在E 上{}n f 测度收敛于f ，则存在子列{}i n f 在E 上a.e ．收敛于f ．例6 如例4，当()1()m x n f →→∞当x E ∈．但是当01σ<<时，1[](,)m f E m σ-≥=+∞且(,)m m +∞=∞．这说明}{n f 不依测度收敛于1．这个例子又说明了几乎处处收敛也不包含依测度收敛，但是有下述关系： 勒贝格(Lebesgue) [5] 设mE <∞，{}n f 是E 上a.e ．有限的可测函数列， {}n f 在E 上a.e ．收敛于a.e ．有限的函数f ，则()()m n x f x f −−→．此定理中的“mE <∞”不可去掉，原因参看例1．定理也说明在的在的条件mE <∞下，依测度收敛弱于几乎处处收敛．有以上定理黎斯又给出了一个用几乎处处收敛来判断依测度收敛的充要条件： 设mE <∞，{}n f 是E 上的可测函数列，那么{}n f 依测度收敛于f 的充要条件是：{}n f 的任何子列{}k n f 中必可找到一个几乎处处收敛于f 的子序列．证明（必要性） 由于{}n f 依测度收敛于f ，由定义知道这时{}n f 的的任何子序列{}k n f 必也依测度收敛于f ，由黎斯定理可知{}k n f 中必存在几乎处处收敛于f 的子序列．（充分性） 如果{}n f 不依测度收敛于f ，即存在一个0σ>，使得()n f f m E σ-≥不趋于0．因此必有子序列{}k n f ，使得(())0.lim kn k m E f f a σ→∞-≥=> 这样{}k n f 就不可能再有子序列几乎处处收敛于f 了，否则由勒贝格定理知将有{}k n f 依测度收敛于f ，即(())0.lim kn k m E f f σ→∞-≥= 这与上式矛盾，所以{}n f 依测度收敛于f ．应用 依测度收敛在概率统计中有重要的意义，如例3；它也是证明中心极限定理的重要依据，由中心极限定理我们可以知道用一个正态分布来模拟一个样本容量较大的样本的概率分布， 从而简化了大样本概率分布的处理和计算[7]．结束语：上述定义中的各种收敛的极限函数都是唯一的，而且从本文还可以知道一致收敛是最强的收敛，它蕴含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛．各种收敛都有不同的意义，在各种实践中作用也各不同．参考文献：[1]马克思主义基本原理概论教材编写课题组．马克思主义基本原理概论[M]．高等教育出版社，2009,7[2] 华东师范大学数学系．数学分析(第三版)[M]．高等教育出版社，2001,6．[3] 郭懋正．实变函数与泛函分析[M]．北京大学出版社，2005,2[4] 柳藩，钱佩玲．实变函数论与泛函分析[M]．北京师范大学出版社，1987．[5] 程其襄，张奠宙，魏国强等．实变函数与泛函分析既基础[M]．高等教育出版社，2003,7．[6] 夏道行，严绍宗等复旦大学数学系主编．实变函数与应用泛函分析基础[M]．上海科学技术出版社．1987．[7] 茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．高等教育出版社，2004,7．。

可测函数列稀有的几种收敛之相礼和热创作择要：本文引见了可测函数列稀有的几种收敛：同等收敛、几乎同等收敛、几乎处处收敛、依测度收敛等以及它们之间的关系．关键字：可测函数列；同等收敛；几乎同等收敛；几乎处处收敛；依测度收敛前言在数学分析中我们晓得同等收敛是函数列很紧张的性子，比方它能包管函数列的极限过程和(R)积分过程可交换次序等．可是一样平常而言函数列的同等收敛性是不方便证明的，而且有些函数列在其收敛域内也纷歧定是同等收敛的，如文中所给的例2函数()f x 在收敛域[0,1]内纷歧致收敛，但对于一个0δ>当0δ→时在[0,]δ内同等收敛，这不见阐明了同等收敛的特殊性，也验证了我们平常常说的“矛盾的同一性和矛盾的斗争性是相联系的、相反相成的”[1]1可测函数列几种收敛的定义1.1同等收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集E 上的实值函数．若对于0,ε∀>存在,K N +∈使得对于,k K x E ∀≥∀∈都有则称}{()k f x 在E 上同等收敛到()f x ．记作：u k f f −−→(其中u 暗示同等uniform)．1.2点点收敛若函数列12(),(),(),,(),k f x f x f x f x 在点集D E ⊂上每一点都收敛，则称它在D 上点点收敛． 例1定义在[0,1]E =上的函数列1(),1k f x kx =+则()k f x 在E 上点点收敛到函数 而且还能看出{()}k f x 在[]0,1上纷歧致收敛到()f x ，但对于0,{()}k f x δ∀>在[,1]δ上同等收敛到()f x ． 1.3几乎同等收敛[3]设E 是可测集，若0,,E E δδ∀>∃⊂使得(\),m E E δδ<在E δ上有u k f f −−→则称{()}k f x 在E 上几乎同等收敛与()f x ，并记作...a u k f f −−→(其中a.u ．暗示几乎同等almost uniform)．例2定义在[]0,1E =上的函数在[]0,1上收敛却纷歧致收敛．但是只需从[]0,1的右端点往掉任一小的一段使之成为[]()0,10,0δδδ->→则{()}k f x 在此区间上就同等收敛，像这样的收敛我们就可以称之为在[]0,1E =上几乎同等收敛与0．1.4几乎处处收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集n E R ⊂上的广义实值函数．若存在E 中点集Z ，有()0,m Z =及对于每一个元素\x E Z ∈，有 则称{()}k f x 在E 上几乎处处收敛与()f x ，并简记为,.[]k f f a e E →或..a e k f f −−→ 若上文的例1也可以称之为在[]0,1上几乎处处收敛与()f x ．1.5依测度收敛例3在[0,1)上构造函数列{()}k f x 如下：对于k N +∈，存在独一的自然数i 和j ，使得2,i k j =+其中02,i j ≤≤令 恣意给定的0[0,1),x ∈对于每一个自然数i ，有且仅有一个j ，使得01[,)22i i j j x +∈．数列0{()}f x 中有无量多项为1，有无量多项为0．由此可知，函数列{()}k f x 在[0,1)上点点不收敛．因此仅考虑点收敛将得不到任何信息．但是细致观察数列0{()}k f x 虽然有无量多个1出现，但是在“频率”意义下，0却也大量出现．这一现实可以用点集测度言语来刻画．只需k 充足大，对于01,ε<≤点集的测度非常小．现实上1({[0,1)()0})2k i m x f x ε∈-≥=．这样对于任给的0,δ>总可以取到0,k 也就是取到0,i 使得当0k k >时，有其中02i δ-<．这个不等式阐明，对于充分大的h ，出现0的“频率”接近1．我们将把这样一种征象称为函数列{()}k f x 在区间[0,1)上依测度收敛到零函数，并将笼统出以下定义[3]： 设12(),(),(),,(),k f x f x f x f x 是可测集E 上几乎处处无限的可测函数．若对于恣意给定的0,ε>有则称{()}k f x 在E 上依测度收敛到函数()f x ，记为.m k f f −−→2可测函数列几种收敛的关系2.1点点收敛与同等收敛的关系由上述定义我们可以晓得u k f f −−→，必有{()}k f x 点点收敛于()f x ．如例1．反之则纷歧定成立，如例2．而且还可以得到假如{()}k f x 可测集E 上的可测函数列，则()f x 也是可测函数．2.2几乎处处收敛与同等收敛的关系由定义可知有同等收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→．反之则否则，如例2．而且还可以得到假如{()}k f x 可测集E 上的可测函数列，则极限函数()f x 也是可测函数．使用：从数学分析我们晓得同等收敛的函数列对于求极限运算和(R)积分运算、微分运算与(R)积分运算等可以交换次序．2.3几乎处处收敛与同等收敛的关系叶果洛夫(E ΓopoB)定理[5]：设(),{}n m E f <∞是E 上一列a.e ．收敛于一个a.e ．无限的函数f 的可测函数，则对于恣意的0δ>，存在子集E E δ⊂，使{}n f 在E δ上同等收敛，且(\)m E E δδ<．注定理中“()m E <∞”不成往掉如：例4定义在(0,)E =+∞的函数列则m f 在(0,)+∞上处处收敛于1，但对于任何负数δ及任何可测集E δ，当时(\)m E E δδ<时，m f 在E δ上纷歧致收敛于1．这是由于，当时(\)m E E δδ<时，E δ不克不及全部含于(0,]m 中，必有(,)m E m x δ∈+∞，于是有()0m m x f =．以是()m x f 在E δ上纷歧致收敛与1，也即定理中“()m E <∞”不成往掉[4]．由定义我们晓得同等收敛必是几乎处处收敛的，反之则不成立．但它们又有紧密的关系，即便上述定理告诉我们几乎处处收敛“基本上”是同等收敛的(在除往一个测度为恣意小集合的子集上)．使用由上述定理我们还可以得到“鲁津定理”：设()f x 是E 上a.e ．无限的可测函数，则对于恣意的0δ>，存在闭子集E F δ⊂，使()f x 在F δ上是连续函数，且(\)m E F δδ<．也就是说：在E 上a.e ．无限的可测函数“基本上”是连续的(在除往一个测度为恣意小集合的子集上)．也即我们可以用连续函数来逼近a.e ．无限的可测函数．2.4几乎处处收敛与依测度收敛的关系例5取(0,1]E =，将E 等分，定义两个函数：(1)111,(0,]2()10,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩，(1)210,(0,]2()11,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩．然后将(0,1]四等分、八等分等等．一样平常的，对于每个n ，作2n 个函数：()11,(,]22()1,2,,2.10,(,]22n n n n j n j j x x j j j x f -⎧∈⎪⎪==⎨-⎪∉⎪⎩．我们把(),1,2,,2{}n j x j f =，先n 按后按j 的顺序逐一的排成一列： ()()n j x f 在这个序列中是第22n j N -+=个函数．可以证明这个函数列是依测度收敛于零的．这是由于对于任何的0σ>，或是空集(当1σ>)，或是1,22(]n n j j -(当01σ<≤)，以是(当时1σ>时，左端为0)．由于当2(1,2,,2.)2n n j j N -+==趋于∞时n →∞，由此可见 ()([0])0lim n j N m E f σ→∞-≥=，也即()()0m n j x f −−→．但是函数列(1)在上的任何一点都不收敛．现实上，对于任何点0(0,1]x ∈，无论n 多么大，总存在j ，使01(,]22n n j j x -∈，因此()0()1n j x f =，但是()10()0n j x f +=或()10()0n j x f -=，换言之，对于任何0(0,1]x ∈，在()0(){}n j x f 中必有两子列，一个恒为1，另一个恒为0．以是序列(1)在(0,1]上任何点都是发散的．这也就阐明依测度收敛的函数列纷歧定处处收敛，也就是说依测度收敛不克不及包含几乎处处收敛，但仍有：黎斯(F ．Riesz)[5]设在E 上{}n f 测度收敛于f ，则存在子列{}in f 在E 上a.e ．收敛于f ． 例6 如例4，当()1()m x n f →→∞当x E ∈．但是当01σ<<时，且(,)m m +∞=∞．这阐明}{n f 不依测度收敛于1．这个例子又阐明了几乎处处收敛也不包含依测度收敛，但是有下述关系：勒贝格(Lebesgue)[5]设mE <∞，{}n f 是E 上 a.e ．无限的可测函数列，{}n f 在E 上a.e ．收敛于a.e ．无限的函数f ，则()()m n x f x f −−→．此定理中的“mE <∞”不成往掉，缘故原由参看例1．定理也阐明在的在的条件mE <∞下，依测度收敛弱于几乎处处收敛．有以上定理黎斯又给出了一个用几乎处处收敛来判别依测度收敛的充要条件：设mE <∞，{}n f 是E 上的可测函数列，那么{}n f 依测度收敛于f 的充要条件是：{}n f 的任何子列{}kn f 中必可找到一个几乎处处收敛于f 的子序列．证明（必要性） 由于{}n f 依测度收敛于f ，由定义晓得这时{}n f 的的任何子序列{}kn f 必也依测度收敛于f ，由黎斯定理可知{}kn f 中必存在几乎处处收敛于f 的子序列． （充分性）假如{}n f 不依测度收敛于f ，即存在一个0σ>，使得不趋于0．因此必有子序列{}kn f ，使得 这样{}kn f 就不成能再有子序列几乎处处收敛于f 了，否则由勒贝格定理知将有{}kn f 依测度收敛于f ，即这与上式矛盾，以是{}n f依测度收敛于f．使用依测度收敛在概率统计中有紧张的意义，如例3；它也是证明中心极限定理的紧张根据，由中心极限定理我们可以晓得用一个正态分布来模仿一个样本容量较大的样本的概率分布，从而简化了大样本概率分布的处理和计算[7]．结束语：上述定义中的各种收敛的极限函数都是独一的，而且从本文还可以晓得同等收敛是最强的收敛，它包含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛．各种收敛都有分歧的意义，在各种理论中作用也各分歧．参考文献：[1]马克思主义基来源根基理概论教材编写课题组．马克思主义基来源根基理概论[M]．高等教育出版社，2009,7[2]华东师范大学数学系．数学分析(第三版)[M]．高等教育出版社，2001,6．[3]郭懋正．实变函数与泛函分析[M]．北京大学出版社，2005,2[4]柳藩，钱佩玲．实变函数论与泛函分析[M]．北京师范大学出版社，1987．[5]程其襄，张奠宙，魏国强等．实变函数与泛函分析既根底[M]．高等教育出版社，2003,7．[6]夏道行，严绍宗等复旦大学数学系主编．实变函数与使用泛函分析根底[M]．上海科学技术出版社．1987．[7]茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．高等教育出版社，2004,7．。

常见收敛发散级数表常见收敛发散级数表收敛和发散是微积分中非常重要的概念，通过研究不同级数的收敛性质，我们可以更好地理解数学中的数列和级数。

本文将介绍一些常见的收敛和发散级数。

1. 调和级数：调和级数是最简单的级数之一，它的一般形式为：1 + 1/2 + 1/3 + 1/4 + ...调和级数是发散的，也就是说，它的和无穷大。

这个结论是由数学家埃德马·费马在17世纪证明的。

2. 几何级数：几何级数是一种形如a + ar + ar^2 + ar^3 + ...的级数，其中a为首项，r为公比。

当|r| < 1时，几何级数收敛，其和为a/(1-r)。

当|r| ≥ 1时，几何级数发散。

3. 幂级数：幂级数是形如∑(n=0到无穷) [an(x-c)^n]的级数，其中an是系数，c是常数。

幂级数的收敛半径R可以通过求解极限lim(n→∞) |an/an+1|来确定。

当|x-c| < R时，幂级数收敛；当|x-c| > R时，幂级数发散。

4. 斯特林级数：斯特林级数是一个近似级数，用于估算阶乘的近似值。

斯特林级数的一般形式为：n! ≈√(2πn) (n/e)^n该级数是收敛的，但是注意，它只是对阶乘的估算，并不精确。

5. Fourier级数：Fourier级数是用一组三角函数的无穷级数来表示周期函数的方法。

Fourier级数的收敛性和周期函数的光滑性相关。

对于光滑的函数，其Fourier级数收敛于函数本身。

然而，对于非光滑的函数，Fourier级数可能会发散或者收敛到函数的不同形式。

总结：本文介绍了一些常见的收敛和发散级数。

调和级数是发散的，几何级数在公比小于1时收敛，幂级数在一定条件下收敛，斯特林级数是对阶乘的近似，而Fourier级数用于表示周期函数。

级数的收敛性质是数学研究中的重要内容，对深入理解微积分等数学领域起到了关键作用。

目录1．前言 (1)2．概念 (1)2.1 几乎处处收敛 (1)2.2 几乎一致收敛 (1)2.3 依测度收敛 (2)3．三种收敛性之间的区别 (2)3.1 存在可测函数列几乎处处收敛而不依测度收敛 (2)3.2 存在可测函数列依测度收敛而不几乎处处收敛 (2)3.3 存在可测函数列几乎处处收敛而不几乎一致收敛 (4)4．三种收敛性的充要条件 (4)4.1 几乎处处收敛的充要条件 (4)4.2 几乎一致收敛的充要条件 (4)4.3 依测度收敛的充要条件 (6)5．三种收敛性之间的联系 (6)5.1 几乎一致收敛与几乎处处收敛 (6)5.2 依测度收敛与几乎处处收敛 (8)5.3 依测度收敛与几乎一致收敛 (10)5.4 三种收敛之间的关系图： (11)6．结论 (11)7．致谢 (12)8．参考文献 (13)n f 可测函数列三种收敛性的区别与联系摘 要： 对于可测集合E 上的几乎处处有限的可测函数列n f 来说有三种常见类型的收敛：几乎处处收敛，几乎一致收敛和依测度收敛。

本文首先介绍可测函数列三种收敛的概念，并讨论几乎处处收敛，几乎一致收敛和依测度收敛三者之间的关系。

这几种概念是伴随测度的建立而产生的新的收敛性，相对其他两种收敛性来说，依测度收敛的收敛条件是比较弱的，与熟知的处处收敛有很大的差异。

Egorov 定理、Riesz 定理和Lebesgue 定理等揭示了这几种收敛之间的关系。

关键词： 几乎处处收敛 几乎一致收敛 依测度收敛 中图分类号：O 17Difference and Connection between Three Types of Convergence of Measurable Function SequenceJiang Zhong (Tutor ：You Xuexiao)(Department of Mathematics, Hubei Normal University, Huangshi Hubei435002,China)Abstract : For the measurable function sequencewhich is finite almost everywhere on the measurable set E ,there are three types of common convergence: convergence almost everywhere, convergence almost uniform and convergence in measurable. This article has first described the concepts of those three types of convergence, and then discussed the relationship among convergence almost everywhere,convergence almost uniform and convergence in measurable . Those concepts are the new convergence,which are arised with the establishment of measure. Comparing with the other twotypes of convergence, the conditions of convergence inmeasurable are relatively weak, and has large differencewith the well-known convergence almost everywhere. TheEgorov theorem, Riesz theorem and Lebesgue theorem and soon reveal the relationship among these types of convergence.Keywords: Convergence almost everywhere Convergence almost uniform Convergence in measurable可测函数列三种收敛性的区别与联系蒋忠（指导教师，游雪肖）（湖北师范学院 数学与应用数学 湖北 黄石 435002）1．前言本文介绍了几乎处处收敛、几乎一致收敛与依测度收敛，它们是伴随测度的建立而产生的新的收敛性。

几种收敛函数的介绍在数学中，收敛函数是一类重要的函数，它们在其中一种极限意义下趋向于一些确定的值。

收敛函数在数学分析、数值计算和工程学科中都有广泛的应用。

下面我将为您介绍几种常见的收敛函数。

1.序列的收敛函数：序列是函数的一个特殊情况，它是一组按照一定顺序排列的数。

一个序列收敛到一些数，意味着当序列的项无限接近于该数时，序列的极限存在。

例如，序列1，1/2，1/3，1/4，...的极限是0，即这个序列收敛于0。

数学中有许多序列的收敛函数，如调和序列、等差数列和等比数列等。

2.函数列的一致收敛函数：函数列是指一组按照一定顺序排列的函数。

函数列的一致收敛就意味着当序列的项无限接近于一些函数时，函数列的极限存在且与该函数无关。

一致收敛函数在数学中有广泛的应用，例如在数值计算中用于逼近数值解。

函数列的一致收敛函数能够保持原始序列的收敛性质，其定义与序列的收敛函数类似。

3.幂级数的收敛函数：幂级数是一种特殊的级数，它是形如∑(a_n*x^n)的级数，其中a_n是系数序列，x是变量。

幂级数的收敛函数是指当幂级数的所有项无限接近于一些函数时，该函数在给定区间上收敛。

幂级数的收敛函数在数学分析和物理学中具有广泛的应用，例如在函数逼近、微积分和物理模型建立等方面。

4.泰勒级数的收敛函数：泰勒级数是一种特殊的幂级数，它是一个函数在其中一点附近展开成多项式的形式。

泰勒级数的收敛函数是指当泰勒级数的所有项无限接近于一些函数时，该函数在给定区间上收敛。

泰勒级数的收敛函数在数学分析和物理学中有广泛的应用，例如在函数逼近、微积分和物理模型建立等方面。

5.紧收敛函数：紧收敛函数是指对于一个给定的度量空间，其中任意序列都有子序列收敛于该函数。

紧收敛函数在函数空间理论、泛函分析和拓扑学等领域中具有重要的应用。

紧收敛函数是一种强收敛函数，能够保持原始序列的所有收敛性质。

总结起来，收敛函数是数学中一类重要的函数，它们在序列、函数列、幂级数和紧收敛函数等方面具有广泛的应用。

收敛函数1. 引言在数学中，收敛函数是一类非常重要的函数，它们在数学分析、实数理论以及其他领域中扮演着重要的角色。

本文将介绍什么是收敛函数，它们的定义以及一些典型的例子和性质。

同时，我们还将讨论收敛函数的应用以及它们在数学和实际问题中的意义。

2. 收敛函数的定义在数学中，给定一个函数序列{fn(x)}，如果对于任意的x0，都存在一个数列{an}，使得fn(x0)在n趋于无穷大时收敛到x0，那么我们称函数序列{fn(x)}在点x0处收敛。

换句话说，对于任意给定的误差ε，存在一个正整数N，使得当n>N时，|fn(x0) - x0| < ε。

3. 收敛函数的例子3.1 线性收敛函数线性函数是一种最简单的函数类型，它的图像是一条直线。

在数学中，我们称线性函数为收敛函数，因为它们具有收敛到零的特性。

例如，y = x是一个线性函数，它的图像是一条通过原点的直线。

当x趋向于无穷大时，y也趋向于无穷大，但是它们之间的差值在不断减小，最终收敛于零。

3.2 幂函数幂函数是一类常见的函数类型，它们具有形如y = x^n的形式。

当幂函数的幂指数大于1时，它们可以是收敛函数。

例如，y = x^2是一个典型的收敛函数，因为当x趋向于无穷大时，y也趋向于无穷大，但是它们之间的差值在不断减小，最终收敛于零。

4. 收敛函数的性质4.1 收敛函数的极限对于一个收敛函数fn(x)，它在点x0处的极限等于x0。

换句话说，lim┬(n→∞)⁡〖fn(x0) = x0〗。

4.2 收敛函数的一致收敛性如果一列函数{fn(x)}在定义域D上的每一个点处都收敛，并且收敛的极限也是一个定义在D上的函数f(x)，那么我们称函数序列{fn(x)}在D上一致收敛于f(x)。

4.3 收敛函数的连续性如果一个函数序列{fn(x)}在某个点x0处收敛，并且在该点的极限f(x0)存在，那么我们称f(x)在x0处是连续的。

5. 收敛函数的应用收敛函数在数学中具有广泛的应用。

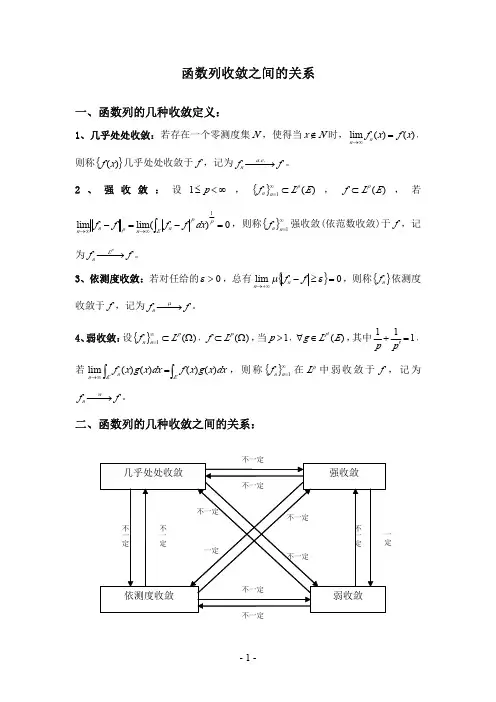
可测函数列的几种收敛的关系
1. 一致收敛：如果函数列 {fn(x)} 对于任意给定的ε > 0，都存
在一个 N，使得当 n > N 时，对于任意的 x ∈ E，都有|fn(x) − f(x)| < ε，则称函数列 {fn(x)} 在 E 上一致收敛于 f(x)，记作
fn(x) → f(x) (x ∈ E)。

一致收敛意味着收敛速度足够快，也意
味着极限函数与原函数的交换次序是可以进行的。

2. 逐点收敛：如果对于任意的 x ∈ E，函数列 {fn(x)} 都收敛
于 f(x)，即lim_n→∞ fn(x) = f(x)，则称函数列 {fn(x)} 逐点收
敛于 f(x)，也叫点态收敛。

3. 均方收敛：如果对于任意的ε > 0，有lim_n→∞ ∫[a,b] |fn(x)
− f(x)|² dx = 0，则称函数列 {fn(x)} 在 [a,b] 上均方收敛于 f(x)，记作 fn(x) ⇀ f(x) (a ≤ x ≤ b)。

均方收敛意味着收敛速度足够快，但是极限函数与原函数的交换次序一般是不可进行的。

4. 平均收敛：如果对于任意的ε > 0，有lim_n→∞ ∫[a,b] |fn(x)
− f(x)| dx = 0，则称函数列 {fn(x)} 在 [a,b] 上平均收敛于 f(x)，记作 fn(x) ⟶f(x) (a ≤ x ≤ b)。

平均收敛比逐点收敛更强，但是
收敛速度可能不够快。

高数收敛定义高数中的收敛定义是一个重要的概念，它在数学分析中有着广泛的应用。

收敛定义是指在一定条件下，数列或函数的极限存在且唯一。

在数学中，收敛的定义有多种形式，下面将介绍几种常见的收敛定义及其应用。

一、数列的收敛定义在数学中，数列是一组按照一定规律排列的数。

数列的收敛定义是指当数列的项趋向于某个确定的值时，这个数列就是收敛的。

具体地说，对于一个数列{an}，如果存在一个实数a，对于任意给定的正实数ε，总存在正整数N，使得当n>N时，满足|an-a|<ε，那么数列{an}就是收敛的，a就是数列的极限。

数列的收敛定义在实际应用中有着广泛的应用。

例如在物理学中，当我们研究某一物理过程的变化时，可以将物理量随时间变化的数值构成一个数列，通过分析这个数列是否收敛，可以得到物理过程的稳定性和趋势。

二、函数的收敛定义除了数列，函数的收敛定义也是数学分析中常用的概念。

函数的收敛定义是指当自变量趋向于某个确定的值时，函数的极限存在且唯一。

具体地说，对于一个函数f(x)，如果存在一个实数L，对于任意给定的正实数ε，总存在正实数δ，使得当0<|x-a|<δ时，满足|f(x)-L|<ε，那么函数f(x)就在x趋向于a时收敛于L，L就是函数f(x)在x趋向于a时的极限。

函数的收敛定义在微积分中有着重要的应用。

例如在求导的过程中，我们通过定义导数的极限来求出函数在某一点的导数值，这就是函数的收敛定义的应用之一。

三、级数的收敛定义在数学中，级数是指无穷多个数按照一定顺序相加的结果。

级数的收敛定义是指当级数的部分和趋向于某个确定的值时，这个级数就是收敛的。

具体地说，对于一个级数∑an，如果存在一个实数S，对于任意给定的正实数ε，总存在正整数N，使得当n>N时，满足|∑an-S|<ε，那么级数∑an就是收敛的，S就是级数的和。

级数的收敛定义在数学分析中有着广泛的应用。

例如在解析几何中，通过对级数的收敛性进行研究，可以得到曲线、曲面的性质和方程的解。

pcl库的收敛函数
PCL库的收敛函数是指在点云配准算法中，计算两个点云之间的变换矩阵时所使用的优化算法。

这种算法主要是利用了梯度下降法来优化误差函数，使得两个点云之间的误差最小化。

PCL库的收敛函数主要包括以下几种类型：
1. GradientDescent：梯度下降法是一种常用的优化算法，它利用误差函数的梯度信息来调整参数，使得误差函数的值逐渐变小，从而达到最优解。

2. NormalDistributionsTransform：NDT算法是一种基于高斯分布模型的点云配准算法，它通过计算点云的高斯分布函数来估计点云之间的变换矩阵。

3. GaussNewton：高斯牛顿法是一种非线性优化算法，它利用误差函数的二阶导数信息来求解最优解，可以更快地收敛。

4. LevenbergMarquardt：LM算法是一种广泛应用于非线性优化问题的算法，它综合了梯度下降法和高斯牛顿法的优点，既可以保证全局收敛，又具有快速的局部收敛性能。

PCL库的收敛函数在点云配准算法中发挥着重要的作用，能够提高点云配准的精度和效率，对于点云处理和机器视觉应用具有重要的意义。

- 1 -。

依概率收敛特征函数收敛依概率收敛和特征函数收敛是概率论中的两个重要概念，本文将对这两个概念进行详细介绍。

一、依概率收敛依概率收敛是指一个随机变量序列在概率意义下趋于另一个随机变量的过程。

具体来说，若随机变量序列$\{X_n\}_{n\geq1}$和随机变量$X$满足$\lim_{n\rightarrow\infty}P(|X_n-X|>\epsilon) = 0$，则称序列$\{X_n\}_{n\geq1}$依概率收敛于$X$。

其中$\epsilon$为一个正实数。

依概率收敛是指一种弱收敛，即收敛的速度比较缓慢，但是趋向于极限的概率比较大。

与之相对的是依分布收敛，即序列中的所有随机变量都具有相同的分布函数，这种收敛可以由特征函数收敛来推导。

二、特征函数收敛特征函数是概率论中常见的一个概念，一个随机变量的特征函数$\varphi_X(t)$定义为$\varphi_X(t) = E(e^{itX})$。

其中$E$表示期望，$i$为虚数单位，$t\in \mathbb{R}$。

如果随机变量序列$\{X_n\}_{n\geq1}$的特征函数$\varphi_{X_n}(t)$逐点收敛于另一个随机变量的特征函数$\varphi_X(t)$，即$\lim_{n\rightarrow\infty}\varphi_{X_n}(t)=\varphi_X(t)$，则序列$\{X_n\}_{n\geq1}$依分布收敛于$X$。

特征函数的收敛性质可以通过Fourier反演定理来推导。

具体来说，如果一个随机变量的特征函数可计算，那么它的概率密度函数可以通过$f_X(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} e^{-itx}\varphi_X(t)dt$来反演得到。

因此，特征函数收敛可以推导出依分布收敛。

三、依概率收敛和特征函数收敛的关系依概率收敛和特征函数收敛是概率论中两个不同的概念，它们之间的关系可以用以下定理来刻画。

曲线收敛的意思
曲线收敛是一个数学概念，它描述了曲线在某一点或区间内的变化趋势。

当
曲线收敛时，意味着曲线上的点逐渐靠近某个值或曲线的某个部分。

本文将介绍
曲线收敛的定义、类型和应用。

一、定义
曲线收敛是指曲线上的点随着自变量的变化而逐渐靠近某个值
或曲线的某个部分。

在数学中，曲线收敛可以用来描述函数的变化趋势，也可以用来研究曲线的性质。

二、类型
曲线收敛可以分为以下几种类型：
1. 函数收敛
函数收敛是指函数在某一点或区间内的值逐渐靠近某个值。

例如，当 x 趋近于无穷大时，函数 f(x) = 1/x 的值逐渐靠近 0，因此函
数 f(x) 在 x 趋近于无穷大时收敛于 0。

2. 数列收敛
数列收敛是指数列中的项逐渐靠近某个值。

例如，数列 1, 2, 3, 4, 5... 的和收敛于无穷大。

3. 曲线收敛
曲线收敛是指曲线上的点逐渐靠近某个值或曲线的某个部分。

例如，当 x 趋近于无穷大时，函数 y = 1/x 的图像收敛于 y 轴。

三、应用
曲线收敛在数学、物理、经济学等领域都有广泛的应用。

例如，在数学中，曲线收敛可以用来研究函数的性质和极限；在物理中，曲线收敛可以用来研究物体的运动轨迹；在经济学中，曲线收敛可以用来研究市场需求和供应的关系。

此外，曲线收敛也是机器学习和人工智能领域的重要概念。

例如，在神经网络中，曲线收敛可以用来训练模型，使模型的误差逐渐降低并最终收敛于真实值。

曲线收敛是一个重要的数学概念，它可以用来描述曲线在某一点或区间内的变化趋势。

xn收敛fxn不收敛的例子摘要：一、引言- 函数收敛和不收敛的概念- 本文的目的和结构二、函数收敛的定义- 函数级数收敛- 函数序列收敛三、函数收敛的性质- 单调有界定理- 致密性定理- 柯西收敛准则四、函数不收敛的例子- 函数f(x)=x^n在x=1处的泰勒级数- 函数f(x)=x^n在x=0处的泰勒级数五、总结- 函数收敛和不收敛的例子及其性质- 函数收敛在数学研究中的应用正文：一、引言在数学中，函数收敛是一个重要的概念，它涉及到函数的极限、连续性、可微性等性质。

本文将介绍函数收敛的定义和性质，并通过具体的例子来说明函数收敛和不收敛的情况。

二、函数收敛的定义为了更好地理解函数收敛，我们先来介绍收敛的概念。

给定一个函数f(x)，如果对于任意给定的正数ε，存在正数δ，使得当|x-a|<δ时，有|f(x)-f(a)|<ε，那么我们就说函数f(x)在点a处收敛。

根据收敛的定义，我们可以得到以下两种收敛类型：1.函数级数收敛：给定一个函数f(x)，如果它的一个级数展开式满足级数收敛，那么我们就说函数f(x)收敛。

2.函数序列收敛：给定一个函数序列{f_n(x)}，如果对于任意给定的正数ε，存在正数N，使得当n>N时，有|f_n(x)-f(x)|<ε，那么我们就说函数序列{f_n(x)}收敛。

三、函数收敛的性质函数收敛具有以下几个重要的性质：1.单调有界定理：如果函数f(x)在区间I上单调有界，那么f(x)在I上收敛。

2.致密性定理：如果函数f(x)在区间I上连续，那么f(x)在I上收敛。

3.柯西收敛准则：如果函数序列{f_n(x)}在区间I上收敛，那么对于任意给定的正数ε，存在正数N，使得当n>N时，有|f_n(x)-f(x)|<ε。

四、函数不收敛的例子我们通过两个具体的例子来说明函数不收敛的情况：1.函数f(x)=x^n在x=1处的泰勒级数：对于函数f(x)=x^n，在x=1处的泰勒级数为f(x)=n!(x-1)^n+O((x-1)^(n+1))。

函数怎么样就是收敛函数在数学分析中，函数的收敛性是一个重要的概念。

收敛函数是指当自变量趋近于某个值时，函数值也趋近于一个确定的值。

本文将从不同角度探讨函数的收敛性。

一、数列的收敛性在介绍函数的收敛性之前，我们先来看一下数列的收敛性。

数列的收敛性是函数收敛性的基础，也是我们理解和分析函数收敛性的重要工具。

对于一个数列{an}，如果存在一个实数A，使得当n趋近于无穷大时，数列的项an趋近于A，那么我们称数列{an}收敛于A。

否则，我们称数列{an}发散。

在数学分析中，有许多方法和定理来判断数列的收敛性，比如极限的定义、夹逼定理、单调有界数列定理等。

通过这些方法和定理，我们可以判断一个数列是否收敛，并求出其极限值。

二、函数的极限在函数的收敛性中，极限是一个关键概念。

函数的极限可以理解为自变量无限接近某个值时，函数值的趋势。

对于函数f(x)，当x趋近于某个值a时，如果存在一个实数L，使得当x趋近于a时，f(x)趋近于L，那么我们称函数f(x)在点a处收敛于L。

否则，我们称函数f(x)在点a处发散。

通过极限的定义，我们可以研究函数的收敛性。

对于一些简单的函数，我们可以直接根据极限的计算规则来判断其收敛性。

而对于一些复杂的函数，我们可以借助于夹逼定理、单调有界函数定理等方法来判断其收敛性。

三、函数的一致收敛性函数的一致收敛性是函数收敛性的一种重要形式。

一致收敛性是指函数在定义域上的每个点上收敛且收敛速度相同。

具体来说，对于函数序列{fn(x)}，如果对于任意给定的ε>0，存在一个自然数N，使得当n>N时，对于定义域上的任意点x，有|fn(x)-f(x)|<ε成立，那么我们称函数序列{fn(x)}在定义域上一致收敛于f(x)。

一致收敛性是函数收敛性的一种强化形式，它要求函数序列在整个定义域上都收敛，并且收敛速度一致。

一致收敛性在数学分析中有广泛的应用，比如在极限交换和级数求和等问题中都起到了重要的作用。

各种函数列收敛的总结利用余项准则证明函数列一致收敛1. 证明Sn(x)=xn,n=1,2,..., 在[0,b](0<b<1) 上一致收敛.2. 证明函数列fn(x)=(1−x)xn,n=1,2,⋯, 在[0,1] 一致收敛.利用余项准则证明函数列非一致收敛1. 证明Sn(x)=xn,n=1,2,..., 在[0,1] 上非一致收敛.2. 函数列gn(x)=(1−xn)x,n=1,2,⋯, 在[0,1] 上非一致收敛.3. 证明函数列fn(x)=xn−x2n, n=1,2,⋯, 在[0,1] 上非一致收敛.4. 设函数列fn(x)=nx(1−x)n,n=1,2,⋯, 证明: (1) 在[0,1] 上收敛; (2) 在[0,1] 上非一致收敛,但在[α,1](α>0 上非一致收敛,但在[α,1) 上一致收敛 ;(3)limn→∞∫01fn(x)dx=∫01limn→∞fn(x)dx.5. 设函数列fn(x)=n(xn−x2n),n=1,2,⋯,x∈[0,1]. (1) 求函数列fn(x) 的极限函数;(2)证明fn(x) 非一致收敛;(3)验证极限运算与积分运算不能交换顺序.含有参数函数列一致收敛1. 设fn(x)=ncx(1−x2)n,n=1,2,⋯, 讨论函数列fn(x) 在[0,1] 上的一致收敛性.2. 讨论函数列fn(x)=ncxe−nx,n=1,2,⋯,x∈[0,1] 的一致收敛性.3. 讨论函数列在指定区间上的一致收敛性:fn(x)=x(ln⁡n)αnx,n=1,2,⋯,x∈[0,+∞).4. 讨论函数列在指定区间上的一致收敛性:fn(x)=cnx1+ncnx2(c>0) ,n=1,2,⋯(1)x∈(−∞,+∞),(2)x ∈(−∞,)(,+∞)已知f(x) 连续利用闭区间连续则有界或可积必有界证明{gn(f(x)) }一致收敛1. 设f(x) 在[0,1] 上连续, f(1)=0. 证明： {f(x)xn } 在[0,1] 上一致收敛.2. 设f(x) 在[12,1] 上连续.证明：收敛的充要条件是f(1)=0.3. 设f(x) 在[0,π2] 上连续.证明： (2) {sinn⁡xf(x)} 在[0,π2] 上一致收剑的充要条件是f(π2)=0.4. 若f(x) 在[a,b] 连续, f(x)>0,gn(x)=f(x)n,n=1,2,⋯. 证明 :gn(x) 在[a,b] 上一致收敛于 1.5. 设函数f0(x) 在[a,b] 上可积,且fn(x)=∫axfn−1(t)dt, x∈[a,b],n=1,2,⋯, 证明 :{fn(x)} 在[a,b] 上一致收剑于0.6. 设u0(x) 在[a,b] 上连续,G(x,t) 在闭X 域[a,b]×[a,b] 上连续, 对∀x∈[a,b], 设un(x)=∫axG(x,y)un−1(y)dy,n,证明：{un(x)} 在[a,b] 上一致收剑于0.已知{fn(x)}递推式证明一致收敛1. 设x⩽f1(x)⩽x,fn(x)=xfn−1(x),x∈[0,1], n=1,2,⋯. 证明:(1) {fn(x)} 为单调有界数在(2)$fn(x)$在[0,1]$ 上一致收敛.与cosx 有关的函数列一致收敛求解下列各题.1. 设fn(x)=cosn⁡x,n=1,2,⋯,x∈[0,π2]. (1) 求极限函数f(x); (2) fn(x) 在[0,π2] 上是否一致收敛? (3) 是否有limn→∞∫0π2fn(x)dx=∫0π2f(x)dx.2. 设fn(x)=cos⁡x+cos2⁡x+⋯+cosn⁡x,n=1,2,⋯, 当x∈(0,π2) 时 , 求limn→∞fn(x) ,并讨论{fn(x)} 在[0,π2] 上的一致收敛性利用f(x) 连续则一致连续证明函数列一致收敛1. 设f(x) 在[0,1] 连续,令fn(t)=∫0Tf(xn)dx,t∈[0,1], n=1,2,⋯, 证明函数列 {fn(t)} 在[0,1] 上一致收敛于g(t)=tf(0)函数列为差商形式且极限函数与导数有关1. 设函数f(x) 在(a,b+1) 上有连续导数(ab), 令fn(x)=n(f(x+1n)−f(x)),x∈(a,b+1)n=1,2,⋯证明：(1) 函数列内闭一致收敛于f′(x) ,(2)2. 设f∈C1(I), I 是有界闭区间, Fn(x)=n[f(x+1n)−f(x)]. 证明:函数列 {Fn(x)} 在I 上一致收敛.如果I 是有界开区间,问 {Fn(x)} 在I 上是否一致收敛？3. 设函数f(x) 在(−∞,+∞) 上有连续导函数f′(x), 且fn(x)=en(f(x+e−n)−f(x))n=1,2,⋯.证明:函数列{fn(x)}在任一有限区间区间(a,b) 内一致收敛于f′(x) .4. 设函数f(x) 在(a,b) 上有连续导函数,定义Fn(x)=n2[f(x+1n)−f(x−1n)]x∈[a,b], n=1,2,⋯. 证明:函数列 {fn(x)}在(a,b) 处处收敛且内闭一致收敛.5. 设函数f(x) 在[0,M+1] 上连续, 记fn(x)=n(∫0x+1nf(t)dt−∫0xf(t)dt)x∈[0,M]. .证明:函数列{fn(x)} 在[0,M] 上一致收敛于f(x) .6. 设函数f(x) 在(−∞,+∞) 上连续,定义fn(x)=n2∫−1n1nf(x+t)dt,n=1,2,⋯,x∈[a,b] n=1,2⋯. 证明:函数列{fn(x)}在任何闭区间[a,b] 一致收敛于f(x) .分段函数非一致收敛的证明1. 设fn(x)=1−nx,0 证明函数列在(0,1) 上非一致收敛，但limn→∞∫01fn(x)dx=∫01limn→∞fn(x)dx.利用函数列一致收敛Cauchy 收敛准则证明复合函数列一致收敛1. 设f(x) 在[0,1] 连续, fn(t)=∫0tf(xn)dx,t∈[0,1], n=1,2,⋯, 证明函数列 {fn(t)} 在[0,1] 一致收敛于g(t)=tf(0).2. 设函数f(x,y) 在闭区域[a,A]×[b,B] 上连续,函数列{φn(x)} 在[a,A] 上一致收剑,且b⩽φn(x)⩽B. 证明:函数列Fn(x)=f(x,φn(x)),n=1,2,⋯, 在[a,A] 上一致收敛.3. 设函数f(x,y) 在闭区域[a,b]×[c,d] 上连续, 函数列{φn(x)} 在 [a, b] 上一致收剑,且a⩽φn(x)⩽b, 函数列{ψn(x)} 在[a,b] 上一致收敛,且c⩽ψn(x)⩽d. 证明 : 函数列Fn(x)=f(φn(x),ψn(x)),n=1,2,⋯, 在[a,b] 上一致收剑.4. 设函数f(x,y) 在闭X 域[x0−a,x0+a]×[y0−b,y0+b] 上连续，函数列 {φn(x)} 在[x0−a,x0+a] 上一致收剑φ(x), 且y0−b⩽φn(x)⩽y0+b. 证明：limn→∞∫x0xf(t,φn(t))dt=limn→∞∫x0xf(t,φ(t))dt.已知函数列一致收敛且每一项一致收敛证明极限函数一致连续1. 设函数列 {fn(x)} 在区间I 上一致收签于f(x) .证明:若每个fn(x) 在I 上一致连续,则f(x) 在I 上一致连续.2. 设函数项级数∑n=1∞un(x) 在I 上一致收签于s(x), 如果每个un(x) 在I 上一致连续,证明s(x) 在I 上一致连续.3. 设函数列 {fn(x)} 在区间[a,b] 上连续,在(a,b) 上一致收剑于f(x) .证明: f(x) 在[a,b] 上一致连续.4. 设un(x) 在[a,b] 上连续,∑n=1∞un(x) 在(a,b) 上一致收签于s(x). 证明: (1)∑n=1∞un(x) 在x=a,x=b 收剑;(2)∑n=1∞un(x) 在[a,b] 连续 ; (3)f(x)=∑n=1∞un(x) 在[a,b] 上一致连续.5. 设fn(x),n=1,2,⋯, 为R 上的一致连续函数,且limn→∞fn(x)=f(x), ∀x∈R1, 问 :f(x) 是否为连续函数？若答案为“是”,请给出证明;若答案为“否”,请给出反例.等度连续6. 设函数列{fn(x)}在区间[a,b] 上连续, {fn(x)} 在[a,b] 上一致收剑于f(x) .证明: {fn(x)} 在[a,b] 上等度连续 (即∀ε>0,∃δ>0, 当∀x′,x′′∈[a,b], |x′−x′′|<δ时, 对任意自然数n 有|fn(x′)−fn(x′′)|<ε利用反证法证明1. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x) ,且每个函数连续,假定每个fn(x) 在[a,b] 上不处处为负.证明f(x) 在[a,b] 上不处处为负.2. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续,若每个fn(x) 在[a,b] 上均有零点.证明f(x) 在[a,b] 上至少有一个零点.3. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续,若∫abfn(x)dx⩾0n=1,2,⋯, 证明至少存在一点x0∈[a,b] 使得f(x0)⩾0.与零点有关的问题1. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续,若f(x) 在[a,b] 上无零点,证明:(1) 当n 充分大时, fn(x) 在[a,b] 也无零点. (2) 证明: {1fn(x)} 在[a,b] 一致收敛于1f(x). {xn}与函数列复合得到新函数列证明1. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续, {xn}⊂[a,b] 且limn→∞xn=x0 . 证明: limn →∞fn(xn)=f(x0).(2) 设{Sn(x)}是函数项级数∑k=1∞uk(x) 的前n 项部分和函数列,每个Sn(x) 在[a,b] 上连续,且. ∑k=1∞uk(x) 在[a,b] 上一致收剑于S(x). 又{xn} ⊂[a,b] 且limn→∞xn=x0. 证明: limn→∞Sn(xn)=S(x0).3. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x) ,且每个函数连续,若存在xn∈[a,b] 有limn→∞fn(xn)=A.证明:存在x0∈[a,b] 使f(x0)=A.已知函数列{fn(x)}一致收敛且函数列极限是数列{an}证明数列{an}收敛1. 设连续函数列 {fn(x)} 在U(x0,δ)(δ>0) 内一致收敛,且limx→xnfn(x)=an,n∈N. 证明 {an}收敛.(南开大学 2002)利用反证法证明函数列在闭区间端点发散导致闭区间非一致收敛1. 设fn(x) 在[a,b] 上连续,且{fn(b)} 发散.证明: {fn(x)} 在[a,b] 上非一致收敛.2. 设un(x) 在[a,b] 连续,且∑n=1∞un(x) 在x=b 发散.证明∑n=1∞un(x) 在[a,b) 非一致收敛.3. 设 {Sn(x)} 在x=c 上左连续,且 {Sn(c)} 发散.证明:在任何开区间(c−δ,c)(δ>0) 内 {Sn(x)} 非一致收敛.4. 设每个un(x) 在x=c 连续,但∑n=1∞un(x) 在x=c 发散,则∀δ>0,∑n=1∞un(x) 在(c,c+δ) 上均非一致收敛.讨论∑n=1∞1(sin⁡x+cos⁡x)n 在(0,π2) 内是否一致收敛.5. 设un(x) 在(a,b] 上连续, ∑n=1∞un(x) 在(a,b) 上收敛,根据∑n=1∞un(b) 的敛散性, 讨论∑n=1∞un(x) 在(a,b) 上的一致敛散性.6. 设hn(x) 在[a,b) 连续,且fn(x)⩽hn(x)⩽gn(x),∀x ∈[a,b). 若级数∑n=1∞fn(x) 和∑n=1∞gn(x) 在(a,b) 上收敛,级数∑n=1∞hn(a) 发散,证明: (1) 级数∑n=1∞hn(x) 在(a,b) 上收敛; (2) 级数∑n=1∞hn(x) 在(a,b) 上非一致收敛.7. 设un(x) 在[a,b] 上连续,∑n=1∞un(x) 在(a,b) 上一致收敛,证明: ∑n=1∞un(a),∑n=1∞un(b) 收敛.已知函数列一致收敛且每个函数列有界证明极限函数有界和函数列一致有界1. 设函数列 {fn(x)} 在[a,b] 上一致收敛于f(x), 且.每个fn(x) 在[a,b] 有界.证明: 回极限函数f(x) 在[a,b] 有界;(2) 函数列 {fn(x)} 在[a,b] 一致有界,且limn→∞supa∈x<bfn(x)=supa<x<bf(x)2. 设函数列{fn(x)} 在区间[a,b] 上连续,且一致收敛于f(x), 若∀x∈[a,b],f(x)>0. 证明: ∃N,δ>0, 使得∀x∈[a,b],n>N 时有fn(x)>δ.3. 设函数列 {fn(x)} 在I 上一致收敛于f(x), 且存在数列{an }使得∀x∈I, 总有|fn(x)|⩽an 证明:f(x) 在I 上有界.复合函数一致收敛1. 设fn(x),n=1,2,⋯, 在[a,b] 上连续,且{fn(x)} 在[a,b] 上一致收敛于f(x) ,证明:(1) ∃M>0, 使得∀n⩾1,∀x∈[a,b] 有|fn(x)|⩽M,|f(x)|⩽M;(2) 若g(x) 在(−∞,+∞) 内连续,则g(fn(x)) 在[a,b] 上一致收敛于g(f(x)) .2. 设f(x)=∑n=0∞anxn 的收敛半径为R=+∞, 令fn(x)=∑k=0nakxk, 证明: {f(fn(x)) }在[a,b] 上一致收敛于f(f(x)) ,其中[a,b] 为任一有穷闭区间.3. 设f(u) 在区间J 上一致连续,函数列 {gn(x)} 在 I 上一致收敛于 g(x), 当x∈I 时, g(x)∈J ,且存在正整数N,使得n>N 及x∈I 时gn(x)∈J ,证明{f(gn(x))} 在I 上一致收敛于f(g(x)) .已知两个函数列分别一致收敛且极限函数有界证明函数列之积一致收敛1. 设函数列 {fn(x)} 与 {gn(x)} 在区间I 上分别一致收敛于f(x),g(x). 假定f(x) 与g(x) 都在I 上有界,证明: (1){fn(x)gn(x)} 在区间I 上一致收敛于f(x)g(x) (2) 如果 {f∗n(x)} 与 {g∗n(x)} 在区间 I 上分别收敛于f(x) 与g(x) ,能否保证必有f∗n(x)g∗n(x)} 在区间I 上一致收敛于 f(x)g(x),请说明理由. (3) 举例说明:对(1) 中的结论，“f(x) 与g(x) 在I 上有界”条件不可去.2. 设函数列 {fn(x)} 与 {gn(x)} 在(−∞,+∞) 上有界连续,且分别一致收敛于f(x) 与g(x) 证明: {fn(x)gn(x)} 在(−∞,+∞) 上一致收敛于f(x)g(x) .如果{fn(x)},{gn(x)} 在(−∞,+∞) 上不是有界函数列,举例说明上述结论不一定成立.3. 设函数列 {fn(x)} 与 {gn(x)} 在区间[a,b] 上分别一致收敛于f(x) 与g(x), 假定存在正数{Mn} 使|fn(x)|⩽Mn,|gn(x)|⩽Mn,x∈[a,b],n=1,2,3,⋯, 证明: {fn(x)gn(x)} 在区间I 上一致收敛于f(x)g(x) .4. 设函数列 {fn(x)} 与 {gn(x)} 在区间[a,b] 上分别一致收敛于f(x) 与g(x) . 证明:函数列max {fn(x),gn(x)} 在区间I 上一致收敛于max {f(x),g(x)}.与反常积分结合1. 设fn(x),n=1,2,⋯, 在[a,+∞) 上连续,且反常积分∫a+∞fn(x)dx 关于n 一致收签.又对任意M>a,{fn(x)}在[a,M] 上一致收敛于f(x),证明：(1)∫a+∞f(x)dx 收敛(2) limn→∞∫a+∞fn(x)dx=∫a+∞f(x)dx.与二重积分结合1. 设连续函数序列 {fn(x,y)} 在有界闭区域 D 上一致收剑于f(x,y), 证明: ∬Df(x,y)dxdy=limn→∞∬Dfn(x,y)dxdy。