1.实验11-1-公平的席位分配(参照惯例的席位分配方法)-实验11-2-公平的席位分配(Q值方法).doc

公平席位的分配数学(2)班学号 0907022022 高泽标摘要：讨论公平席位分配的模型已有很多。

本文首先用比例加惯例法、Q值法、D’hondt 法对问题中名额进行了分配，再对D’hondt法的合理性进行了分析，并在Q值法对绝对尾数（绝对不公平度）的处理方式基础上，提出了相对尾数模型，并讨论了其满足Young公理的1，3，4条关键词：相对尾数 Balinsky & Young不可能定理正文1 问题复述公平的席位分配问题是一个非常有趣而重要的问题，它在政治学、管理学和对策论等领域具有广泛的应用价值。

处理这个问题的最早的方法是Hamilton法，即比例加惯例法；后来出现了Q值法；1974年M.L.Balinski和H.P.Young引入了席位分配问题的公理体系研究方法，并于1982年证明了同时满足五个公理的席位分配方法是不存在的；因此，我们只能根据实际建立在一定公平准则下成立并尽量多的满足Young公理的算法。

这里，我们需要理解并运用比例加惯例法、Q值法、D’hondt法对宿舍委员会名额进行分配，继而提出更优的公平分配席位的方法。

2 模型假设2.1 合理假设2.1.1 比例加惯例法、Q值法等分配模型均为已知；2.1.2 各个宿舍相互独立互不影响，人数保持不变；2.1.3 委员分配以各宿舍人数为唯一权重。

2.2 符号约定3 模型的建立及求解3.1按比例加惯例模型分配根据比例加惯例分配模型的原理表3.2按Q 值法模型分配首先用比例分配法对名额进行初步分配，再根据表达式 C B A i ,,=对剩下的名额进行分配表2（Q 值法分配结果）：3.3 D ’hondt 模型 3.3.1 模型建立设，分别表示宿舍总人数和总分配席位数，(1,2,3i =)表示各宿舍人数，令(1,2,3,1,2,...i j ==)，则得到一个数列{}ij a ，将该数列按递减顺序重新排列，得到{}()k ij a ，其中()k ij a 表示{}()k ija 中第大的项。

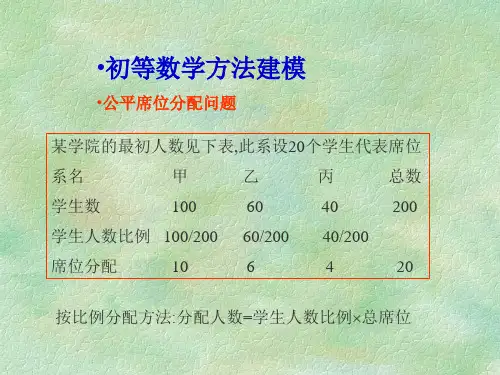
席位分配问题例题：有一个学校要召开一个代表会议，席位只有20个，三个系总共200人，分别是甲系100，乙系60,丙系40.如果你是会议的策划人，你要合理的分配会议厅的20个座位，既要保证每个系部都有人参加，最关键的就是要对个公平都公平，保证三个系部对你所安排的位置没有异议。

如何分配最为恰当？问题：（1）问20席该如何分配，如果有三名学生转系该怎样分配？（2）若增加21席又如何分配？问题的分析：一、20席分配情况：系名甲乙丙总数学生数100 60 40 200学生人数比例100/200 60/200 40/200席位分配10 6 4 20如果有三名学生转系，分配情况：系名甲乙丙总数学生数103 63 34 200学生人数比例103/200 63/200 34/200按比例分配席位10.3 6.3 3.4 20按惯例席位分配10 6 4 20二、21席位分配情况：系名甲乙丙总数学生数103 63 34 200学生人数比例103/200 63/200 34/200按比例分配席位10.815 6.615 3.57 21按惯例席位分配11 7 3 21 这个分配结果出现增加一席后，丙系比增加席位前少一席的情况，这使人觉得席位分配明显不公平。

要怎样才能公平呢？模型的建立：假设由两个单位公平分配席位的情况，设单位人数席位数单位A p1 n1单位B p2 n2要公平，应该有p1/n1 = p2/n2，但这一般不成立。

注意到等式不成立时有若p1/n1 >p2/n2 ，则说明单位A吃亏(即对单位A不公平)若p1/n1 <p2/n2 ，则说明单位B 吃亏(即对单位B不公平)因此可以考虑用算式p=|p1/n1-p2/n2|来作为衡量分配不公平程度，不过此公式有不足之处（绝对数的特点），如：某两个单位的人数和席位为n1 =n2 =10 ，p1 =120，p2=100，算得p=2另两个单位的人数和席位为n1 =n2 =10 ，p1 =1020，p2=1000, 算得p=2虽然在两种情况下都有p=2，但显然第二种情况比第一种公平。

龙源期刊网
公平的席位分配模型
作者：但琦杨廷鸿王继伟王春林
来源：《价值工程》2011年第13期
摘要：在现实生活中，人们经常会遇到席位分配的问题。

本文介绍了常用席位分配方
法，并提出了两种新方法，建立了三种分配模型，最后通过实例计算得出模型三相对比较公平。

Abstract： In real life, people often meet the distribution of seats. This paper introduces some common distribution methods of seats, and brings forward two new methods, establishes the three kinds of distribution model, and finally get the result that the third model is relatively fair through calculation.
关键词：席位分配；模型；分配方法；公平
Key words： distribution of seats; model; allocation methods; fair
中图分类号：F270·7 0 文献标识码：A 文章编号：1006-4311（2011）13-0309-02
1 问题提出
参考文献：
[1]姜启源.数学模型.北京：高等教育出版社.
[2]李晓莉.数学建模教学方法探讨.苏州科技学院学报（自然科学版），
Vol.21,No.1,Mar.2004，p56-61.
[3]n个点的最小覆盖圆的的算法./JudgeOnline/problem?id=2069.。

姜启源数学模型第三版课件公平席位分配（可编辑）2.1席位分配问题 * * 某校有200名学生，甲系100名，乙系60名，丙系40名，若学生代表会议设20个席位，问三系各有多少个席位, 按惯例分配席位方案，即按人数比例分配原则表示某单位的席位数表示某单位的人数表示总人数表示总席位数 1 问题的提出 20个席位的分配结果 20/100 ?20 4 30/100 ?20 6 50/100 ?20 10 分配方案 40/200 40 丙 60/200 60 乙 100/200 100 甲席位数所占比例人数系别现丙系有6名学生分别转到甲、乙系各3名。

17.0%?20 3.4 31.5%?20 6.351.5 %?20 10.3 分配方案 34/200 17.0% 34 丙 63/200 31.5% 63 乙103/200 51.5% 103 甲席位数所占比例人数系别 10 6 4 10 6 4 现象1 丙系虽少了6人，但席位仍为4个。

(不公平～) 为了在表决提案时可能出现10:10的平局，再设一个席位。

21个席位的分配结果 17.0%?21 3.570 31.5%?21 6.61551.5 %?21 10.815 分配方案 34/200 17.0% 34 丙 63/200 31.5% 63 乙103/200 51.5% 103 甲席位数所占比例人数系别 11 7 3 现象2 总席位增加一席，丙系反而减少一席。

(不公平～) 惯例分配方法:按比例分配完取整数的名额后，剩下的名额按惯例分给小数部分较大者。

存在不公平现象，能否给出更公平的分配席位的方案, 2 建模分析目标:建立公平的分配方案。

反映公平分配的数量指标可用每席位代表的人数来衡量。

34/4 8.5 63/6 10.5 103/1010.3 每席位代表的人数 4 6 10 席位数好 34 丙差 63 乙中 103 甲公平程度人数系别 40/4 10 60/6 10 100/10 10 每席位代表的人数 4 40 丙 6 60 乙 10 100 甲席位数人数系别 34/3 11.33 63/7 9 103/11 9.36 每席位代表的人数 3 7 11 席位数差 34 丙好 63 乙中 103 甲公平程度人数系别一般地，每席位代表的人数席位数 B A 人数单位当席位分配公平但通常不一定相等，席位分配的不公平程度用以下标准来判断。

第二章 公平的席位分配2.1 公平的席位分配 问题：三个系学生共200名（甲系100，乙系60，丙系40），代表会议共20席，按比例分配，三个系分别为10，6，4席。

现因学生转系，三系人数为103, 63, 34, 问20席如何分配。

若增加为21席，又如何分配。

比例加惯例对丙系公平吗？系别 学生 比例 20席的分配 21席的分配 人数 （%） 比例 结果 比例 结果 甲 103 51.5 10.3 10 10.815 11 乙 63 31.5 6.3 6 6.615 7 丙 34 17.0 3.4 4 3.570 3 总和 200 100.0 20.0 20 21.000 21―公平‖分配方法衡量公平分配的数量指标人数 席位A 方 p 1 n 1 当p 1/n 1= p 2/n 2 时，分配公平B 方 p 2 n 2 若 p 1/n 1> p 2/n 2 ，对A 不公平 p 1/n 1– p 2/n 2 ~ 对A 的绝对不公平度 p 1=150, n 1=10, p 1/n 1=15 p 2=100, n 2=10, p 2/n 2=10 p 1/n 1– p 2/n 2=5p 1=1050, n 1=10, p 1/n 1=105 p 2=1000, n 2=10, p 2/n 2=100 p 1/n 1– p 2/n 2=5虽二者的绝对不公平度相同,但后者对A 的不公平程度已大大降低!―公平‖分配方法: 将绝对度量改为相对度量 若 p 1/n 1> p 2/n 2 ，定义 ~ 对A 的相对不公平度类似地定义 rB(n1,n2)公平分配方案应使 rA , rB 尽量小将一次性的席位分配转化为动态的席位分配, 即设A, B 已分别有n1, n2 席，若增加1席，问应分给A, 还是B, 不妨设分配开始时 p1/n1> p2/n2 ，即对A 不公平应讨论以下几种情况: 初始 p1/n1> p2/n2 1）若 p1/(n1+1)> p2/n2 ，则这席应给 A2）若 p1/(n1+1)< p2/n2 ，应计算rB(n1+1, n2)),(///21222211n n r n p n p n p A =-3）若 p1/n1> p2/(n2+1)，应计算rA(n1, n2+1) 问：p1/n1<p2/(n2+1) 是否会出现？ 否！ 若rB(n1+1, n2) < rA(n1, n2+1), 则这席应给A 若rB(n1+1, n2) >rA(n1, n2+1), 则这席应给 B当 rB(n1+1, n2) < rA(n1, n2+1), 该席给A的定义该席给A 否则, 该席给B 定义该席给Q 值较大的一方推广到m 方分配席位，计算 该席给Q 值最大的一方：Q 值方法三系用Q 值方法重新分配 21个席位按人数比例的整数部分已将19席分配完毕 甲系：p1=103, n1=10 乙系：p2= 63, n2= 6 丙系：p3= 34, n3= 3用Q 值方法分配第20席和第21席 第20席 Q 1最大，第20席给甲系 第21席 同上 Q 3最大，第21席给丙系Q 值方法分配结果：甲系11席，乙系6席，丙系4席，公平吗？进一步的讨论Q 值方法比“比例加惯例”方法更公平吗？ 席位分配的理想化准则已知: m 方人数分别为 p 1, p 2,… , pm , 记总人数为 P = p 1+p 2+…+pm , 待分配的总席位为N 。

公平的席位分配模型班级：数（2）学号：0907022015 姓名：王秀丽摘要：本文建立数学模型的方法，通过讨论某学校的学生代表席位在不同院系之间的公平分配问题。

由于人数是一个整数，所以在通常情况下不能保证各个院系最终分得的代表席位数与其人数取相同的比例。

因此席位分配不可能在任何情况下都绝对公平，我们通过建立数学模型的方法找到尽可能使分配结果的整体不公平程度降低。

关键词：主要分数法席位分配公平度指标正文1 问题的重述有关公平分配席位的问题，由于人数是一个整数导致在一般情况下不能保证各个院系最终分得的代表席位数与其人数取相同的比例。

因此席位分配不可能在任何情况下都绝对公平，进行了各种方法的比较，经过多次试验证明主要除数法的结果要贴近实际，不公平程度较低，最后又对所用方法的科学性进行了阐明。

2 合理假设与变量说明2.1假定各系的人数已确定，且席位增加时各系的席位数不减少。

2.2在各系的席位数分配好的前提下，人数增加的系席位数不会减少。

2.3 p：总人数；i p：各方人员;i=1,2,3...nN:总席数；i N各方分配数；i=1,2,3...nA的相对不公平度：11221222//(,)/Ap n p nr n np n-=；()1122//p n p n>;B的相对不公平度：22112111//(,)/Bp n p nr n np n-=;()2211//p n p n>;3 问题的分析及模型建立初等模型（不可分割的实体分配）p：总人数；i p：各方人员; i=1，2，3……n N:总席数；i N各方分配数；i=1，2，3……nA的相对不公平度：1122 1222//(,)/Ap n p nr n np n-=()1122//p n p n>;B的相对不公平度：22112111//(,)/Bp n p nr n np n-=()2211//p n p n>;为了寻求新的，公平的席位分配方法，先讨论衡量公平的数量指标。

公平席位的分配模型1 问题提出某高校有200名学生，其中1系有100名学生，2系有60名学生，3系有40名学生，现在要成立一个20席位的委员会， 按照要求解决下述问题：问题一：问应该如何分配，使每个学生得到席位的可能性相同？ 问题二：若现在学生中存在转系的情况，1系现有103名学生，2系现有63名学生，3系现有34名学生，那么如何分配才能使其公平？ 问题三：若现在增加一个席位，即21席，那又该如何分配？ 2 合理假设与变量说明 2.1 合理假设2.1.1 模型的公平定义是相同的。

2.1.2 模型所要求的公平是绝对公平。

2.1.3 模型不考虑各系自身的要求。

2.1.4 分配到各系的名额数目均为整数。

2.2 变量说明设 P 为总人数，i P 为各方人数， （,iP P N +∈，1,2,,i n =⋅⋅⋅，n N +∈），N为总席数，i N 为各方的分配席数，（,1,2,,iNN i n+∈=⋅⋅⋅，n N +∈）且1n i i N N=∑=，1nii P P =∑=3 问题分析通常分配结果的公平与否以每个代表席位所代表的人数相等或接近来衡量。

目前沿用的惯例分配方法为按比例分配方法，即：学生代表席位分配数=学生总人数比例 总席位如果按照上述公式参与分配的一些学生代表的席位分配数出现小数，则先按席位分配数的整数分配席位，余下席位按所有参与分配学生中小数部分最大的优先分配。

得到最初学生人数及学生代表席位如下表：表1：按比例的席位分配表考虑学生转系以及增加一个席位等的情况，各系学生人数及学生代表席位变为：表2：按照比例并参照惯例的席位分配由上表（参考文献[1]）可以看出，20系应该1系10席，2系6席，3系4席这样分配，21席的分配结果由上表可知，这个结果出现增加一席后，3系比增加席位前少一席的情况，这就使人觉得席位分配明显不公平。

要怎样才能公平呢，这时需建立数学模型来解决。

4 模型建立 4.1 Q 值分配法模型设A 、B 两方的人数分别为1P ，2P ，占有的席位数分别是1N 和2N ，这两方每个席位代表的人数分别是11P N 和22P N 。

公平的席位分配模型《数学模型》实验报告实验名称:公平的席位分配成绩:___________ 实验日期 : 2009 年 5 月 4 日实验报告日期: 2009 年 5 月 18 日一、实验目的制定相对公平的席位分配方案～使席位分配尽可能的公平～此为设计型实验。

解决一些实例～比如:甲系同学103名～乙系同学63名～丙系同学34名～共200名同学～有21个席位需进行分配～求方案如何时才最为公平, 二、实验内容根据席位的相对不公平度Qi,pi^2 /ni(ni+1),i=1,2……～席位应分配给Q值较大的一方～按此方法进行分配可以求出各个系所得的席位ni。

三、实验环境MATLAB6.5四、实验步骤为了实现多方的席位分配利用了多重循环的方法～程序如下: p=input('输入各系人数:');N=input('输入总席位数:');[x,y]=size(p);n=ones(1,y);while(N>sum(n))for i=1:yQ(i)=p(i)*p(i)/(n(i)*(n(i)+1));end[i,j]=max(Q);n(j)=n(j)+1;endn五、实验结果结果为n=11,6,4。

六、实验讨论、结论寻求公平分配席位方法的关键～是建立衡量公平程度的即合理又简明的数量指标～此模型提出的指标是相对不公平度～在这个前提下得到的Q值方法应该是公平的～实验结果是成功的。

七、参考资料20个席位的分配 21个席位的分配学生人数系别学生人数的比例比例分参照惯比例分参照惯,,, 配的席位例的结果配的席位例的结果甲 103 51.5 10.3 10 10.81511 乙 63 31.5 6.3 6 6.615 7 丙 34 17.0 3.4 4 3.570 3 总和 200 100.0 20.0 20 21.000 21。