应用光学第四章复习进程
- 格式:doc
- 大小:1.23 MB
- 文档页数:21

第四章《光现象》提问试复习提纲一、光源:1.什么叫光源?自身能够发光的物体叫光源。
2光源分为那两类?①自然光源:如太阳、萤火虫;水母. 斧头鱼②人造光源:如篝火、蜡烛、油灯、电灯。
火把注:月亮本身不会发光,它不是光源。
二、光的传播1、光是怎样传播的?光在同种均匀介质中沿直线传播;光在非均匀介质中不是沿直线传播的(例如早晨,看到刚从地平线升起的太阳的位置比实际位置高)。
2、什么叫光线?常用一条带有箭头的直线表示光的径迹和方向;线是由一小束光抽象而建立的理想物理模型,建立理想物理模型是研究物理的常用方法之一。
3、光沿直线传播应用及现象有那些?①取直线:激光准直(挖隧道定向);整队集合;射击瞄准;②影子的形成:光在传播过程中,遇到不透明的物体,在物体的后面形成黑色区域即影子。
如图:在月球后1的位置可看到日全食,在2的位置看到日偏食,在3的位置看到日环食。
④小孔成像:小孔成像实验早在《墨经》中就有记载小孔成像成倒立的实像,其像的形状与孔的形状无关。
⑤限制视线:坐井观天(要求会作有水、无水时青蛙视野的光路图);一叶障目;4、光速的速度是多少?(1)在计算中,真空或空气中光速c=3×108m/s=3×105km/s;(2)真空中光速是宇宙中最快的速度;(3)光在空气中速度约为3×108m/s,光在水中速度为真空中光速的3/4,在玻璃中速度为真空中速度的2/3 。
5.什么是光年?光年是光在一年中传播的距离,光年是长度单位;1光年≈9.46×1015m ;三、光的反射1、什么叫光的反射?光从一种介质射向另一种介质表面时,一部分光被反射回原来介质的现象叫光的反射。
2、反射定律的内容有那些?反射光线与入射光线、法线在同一平面上,反射光线和入射光线分居于法线的两侧,反射角等于入射角。
光的反射过程中光路是可逆的。
(1)、什么叫法线?过光的入射点所作的与反射面垂直的直线;(2)什么叫入射角?入射光线与法线的夹角;(3)什么是反射角?法射光线与法线间的夹角。

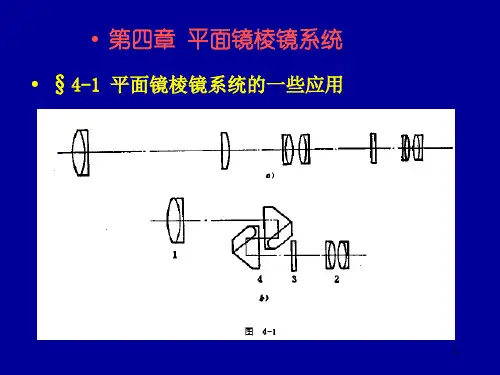


作业:习题1、 解:据题意,分别求出光孔AB 和透镜L 1经其前面的光学系统成像。
光孔前面无光学系统,其经前面光学系统成的像为其本身;透镜前面无光学系统,其经前面光学系统成的像亦为其本身。
1)由于物在无限远,光孔直径35mm 小于透镜直径40mm ,所以开口直径35mm 的光孔为孔径光阑,也是入瞳;出瞳为孔径光阑经后方光学系统所成的像:设孔径光阑AB 经L 1成像为A´B´。
由高斯公式和垂轴放大率公式得)(10010050100)50('''mm f l lf l -=+-⨯-=+=——在L 1左侧100mm )(703550100''mm y l l y =⨯--==——出瞳直径为70 mm 2)当物在透镜前300mm 处,光孔对物点的张角为 07.0503002/351≈-=tgu透镜(像L 1´)对物点的张角为 06667.03002/402≈=tgu 比较u 1、u 2可 知,透镜(像L 1´) 对物点的张角u 2小 于光孔(像)对物 点的张角(见下图)故透镜L 1为孔径光 阑、入瞳和出瞳。
可见,同一 光学系统,当物 距不同时,其孔 径光阑不同,随 着l 减少,原来 限制光束的光孔 失去限制光束的 作用,而由透镜 框内孔限制光束。
习题4 解:1)根据光通量和辐射通量的关系式有:lm e 76.01051523=⨯⨯=Φ=Φ-η2)据发光强度定义式 ΩΦ=I ,当激光束的发散角u 很小时,立体角2u w π=所以,发光强度:(cd)10512.15024.0760000)104.0(76.076.06232⨯≈=⨯⨯==Φ=-ππαw I 3)据光亮度定义式 dSw dSI L ⋅⋅Φ=⋅=θθcos cos 和 0=θ,2)2(d dS π=得光亮度:)/(101.927577536.11004.3)10(14.35024.010476.0dS L 21212236m cd w ⨯≈⨯=⨯⨯⨯⨯=⋅Φ=- 4)由 2cos rI E θ=和 0=θ得激光束在5m 远处屏幕上产生的光照度: )(10051.6510512.1cos 4262lx r I E ⨯≈⨯==θ例题:例1.两个薄凸透镜L 1和L 2的口径均为4cm ,L 1的焦距为8cm ,L 2的焦距为3cm ,L 2在L 1之后5cm ,对于平行于光轴入射的光线,求系统的孔径光阑、入射光瞳和出射光瞳。



应⽤光学第四章复习进程应⽤光学第四章本章要点1. 理想光学系统原始定义2. 理想光学系统的焦点、焦平⾯、主点、主平⾯3. 理想光学系统的节点4. 理想光学系统的物像位置关系,⽜顿公式和⾼斯公式5. 理想光学系统物⽅焦距与像⽅焦距的关系6. 理想光学系统的拉⽒不变量7. 理想光学系统的光焦度及其与焦距的关系8. 理想光学系统的垂轴放⼤率、沿轴放⼤率和⾓放⼤率及其关系9. ⼏个特殊位置的三种放⼤率10. 理想光学系统的作图法11. 理想光学系统的组合:作图法和计算法12.远距型和反远距型理想光学系统模型13. 多光组组合,正切计算法,截距计算法14. 各光组对总光焦度得贡献15. 焦距仪基本原理16. 望远镜系统的理想光学系统模型17. 视觉放⼤率概念18. 望远镜与其他光组的组合19. 薄透镜成像原理20. 厚透镜的基点和基⾯及其与光组组合的关系引⾔单个折射球⾯(或反射球⾯)单薄透镜对细⼩平⾯以细光束成完善像实际光学系统对具有⼀定⼤⼩的物(视场)以宽光束(孔径)⼀个光学系统必须由若⼲元件组成,经反复精密计算,使其成像接近完善。
开始时,⾸先将系统看成是理想的§4-1 理想光学系统及其原始定义[返回本章要点]理想光学系统——像与物是完全相似的物空间像空间点——>共轭点直线——>共轭直线直线上的点——>共轭直线上的共轭点理想光学系统理论——⾼斯光学§4-2 理想光学系统的基点和基⾯⼀、焦点F,F’与焦平⾯[返回本章要点]物⽅⽆穷远A F’: 后焦点,像⽅焦点轴上物点 F A’( 处)F:前焦点,物⽅焦点A→ F’:物⽅⽆穷远垂轴平⾯的共轭平⾯为通过 F’的垂轴平⾯(后焦平⾯,像⽅焦⾯)F’→A:像⽅⽆穷远垂轴平⾯的共轭平⾯为物⽅过 F 的垂轴平⾯(前焦平⾯,物⽅焦⾯)注意:这⾥F与F’不为共轭点,A与A’也不为共轭点⼆、主点H,H’和主平⾯[返回本章要点]延长 TE1,FS1交于Q H,H’亦为⼀对共轭点延长 SkR,EkF’交于Q’点H,H'——物(像)⽅主点,前(后)主点,QH,Q'H'——物(像)⽅主⾯,前(后)主⾯,且HQ与H'Q'共轭,β = 1,物、像⽅主⾯是⼀对β=1的物像共轭⾯光学系统总包含⼀对主点(主平⾯),⼀对焦点(焦平⾯),前者是⼀对共轭点(⾯),后者不是像⽅焦距,后焦距物⽅焦距,前焦距只要⼀对主点、⼀对焦点的相对位置⼀定,⼀个光学系统的理想模型就定了。


总复习第一章 几何光学的基本定律 返回内容提要有关光传播路径的定律是本章的主要问题。
折射定律(光学不变量)及其矢量形式反射定律(是折射定律当时的特殊情况)费马原理(极端光程定律) (实、虚)物空间、像空间概念 完善成像条件(等光程条件)及特例,由费马原理导出折射定律和反射定律第二章 球面与球面系统 返回内容提要球面系统仅对细小平面以细光束成完善像基本公式:阿贝不变量放大率及其关系:拉氏不变量反射球面的有关公式由可得。
第三章 平面与平面系统返回内容提要平面镜成镜像夹角为 α 的双平面镜的二次像特征 平行平板引起的轴向位移反射棱镜的展开,结构常数,棱镜转像系统折射棱镜的最小偏角,光楔与双光楔关键问题:坐标系判断,奇次反射成像像,偶次反射成一致像,并考虑屋脊的作用。
第四章 理想光学系统返回内容提要主点、主平面,焦点、焦平面,节点、节平面的概念高斯公式与牛顿公式:当时化为,并有三种放大率,,拉氏不变量,,厚透镜:看成两光组组合。
++组合:间隔小时为正光焦度,增大后可变成望远镜,间隔更大时为负光焦度。
--组合:总是负光焦度 +-组合:可得到长焦距短工作距离、短焦距长工作距离系统,其中负弯月形透镜可在间隔增大时变 成望远镜,间隔更大时为正光焦度。
第五章 光学系统中的光束限制 返回内容提要本部分应与典型光学系统部分相结合进行复习。
孔阑,入瞳,出瞳;视阑,入窗,出窗;孔径角、视场角及其作用 拦光,渐晕,渐晕光阑 系统可能存在二个渐晕光阑,一个拦下光线,一个拦上光线 对准平面,景像平面,远景平面,近景平面,景深 物方(像方)远心光路——物方(像方)主光线平行于光轴第六章 光能及其计算 返回内容提要本章重点在于光能有关概念、单位和像面照度计算。
辐射能通量,光通量,光谱光视效率,发光效率 发光强度,光照度,光出射度,光亮度的概念、单位及其关系 光束经反射、折射后亮度的变化,经光学系统的光能损失, 通过光学系统的光通量,像面照度总之,第七章 典型光学系统 返回内容提要本章需要熟练掌握各类典型光学系统的成像原理、放大倍率、光束限制、分辨本领以及显微镜与照明 系统、望远镜与转像系统的光瞳匹配关系,光学系统的外形尺寸计算。
应用光学第四章本章要点1. 理想光学系统原始定义2. 理想光学系统的焦点、焦平面、主点、主平面3. 理想光学系统的节点4. 理想光学系统的物像位置关系,牛顿公式和高斯公式5. 理想光学系统物方焦距与像方焦距的关系6. 理想光学系统的拉氏不变量7. 理想光学系统的光焦度及其与焦距的关系8. 理想光学系统的垂轴放大率、沿轴放大率和角放大率及其关系9. 几个特殊位置的三种放大率10. 理想光学系统的作图法11. 理想光学系统的组合:作图法和计算法12.远距型和反远距型理想光学系统模型13. 多光组组合,正切计算法,截距计算法14. 各光组对总光焦度得贡献15. 焦距仪基本原理16. 望远镜系统的理想光学系统模型17. 视觉放大率概念18. 望远镜与其他光组的组合19. 薄透镜成像原理20. 厚透镜的基点和基面及其与光组组合的关系引言单个折射球面(或反射球面)单薄透镜对细小平面以细光束成完善像实际光学系统对具有一定大小的物(视场)以宽光束(孔径)一个光学系统必须由若干元件组成,经反复精密计算,使其成像接近完善。
开始时,首先将系统看成是理想的§4-1 理想光学系统及其原始定义[返回本章要点]理想光学系统——像与物是完全相似的物空间像空间点——>共轭点直线——>共轭直线直线上的点——>共轭直线上的共轭点理想光学系统理论——高斯光学§4-2 理想光学系统的基点和基面一、焦点F,F’与焦平面[返回本章要点]物方无穷远A F’: 后焦点,像方焦点轴上物点 F A’( 处)F:前焦点,物方焦点A→ F’:物方无穷远垂轴平面的共轭平面为通过 F’的垂轴平面(后焦平面,像方焦面)F’→A:像方无穷远垂轴平面的共轭平面为物方过 F 的垂轴平面(前焦平面,物方焦面)注意:这里F与F’不为共轭点,A与A’也不为共轭点二、主点H,H’和主平面[返回本章要点]延长 TE1,FS1交于Q H,H’亦为一对共轭点延长 SkR,EkF’交于Q’点H,H'——物(像)方主点,前(后)主点,QH,Q'H'——物(像)方主面,前(后)主面,且HQ与H'Q'共轭,β = 1,物、像方主面是一对β=1的物像共轭面光学系统总包含一对主点(主平面),一对焦点(焦平面),前者是一对共轭点(面),后者不是像方焦距,后焦距物方焦距,前焦距只要一对主点、一对焦点的相对位置一定,一个光学系统的理想模型就定了。
单个折射球面、球面镜和薄透镜都相当于两个主面重合在一起的情况。
单个折射球面球面镜薄透镜H,H’,F,F’四点称为光学系统的基点四、节点和节平面——γ = 1的一对共轭点[返回本章要点]由全等得同理当光学系统的f'=-f时系统的节点与主点重合§4-3 物像位置和三种放大率、两种焦距和光焦度一、理想光学系统的物像位置关系和横向放大率β[返回本章要点]1. 以 F ,F’为原点牛顿公式2. 以 H,H’为原点由代入牛顿公式得高斯公式此时由高斯公式后面会看到单个折射球面公式具有普遍性当n'= n 时,化为与单个透镜物像公式相同,这时β与l,l'有关。
当l一定时,β与 y的大小无关二、理想光学系统两焦距的关系和拉氏公式[返回本章要点]由即并由代入之得对近轴区,有两焦距的关系结合若n'=n,则f = -f'如空气中折射系统若包含k 个反射面,则若n'=-n, 则f = f ',如反射球面理想光学系统的拉氏公式[返回本章要点]三、光束的会聚度和系统的光焦度[返回本章要点]折合物距倒数,会聚度V (-)表示发散光束折合像距V' (+)表示光束会聚折合焦距倒数,光焦度φ(-)表起发散作用(+)表示起会聚作用光焦度等于像方光束会聚度与物方光束会聚度之差它表征光学系统偏折光线的能力。
单位:屈光度——以米为单位的焦距的倒数。
眼镜的度数=屈光度数×100 [返回本章要点]四、轴向放大率、角度放大率及其与横向放大率的关系1. 轴向放大率——像与物沿轴移动量之比由xx'=ff'得xdx'+x'dx=0所以仍成立,当n’=n时立体物像不再相似2. 角放大率——像方、物方倾斜角的正切之比[返回本章要点]若 n'=n仍然成立3. 对薄透镜,几个特殊位置的β、α、γ1. 物在无穷远,像与像方焦面重合2. 物在2倍物方焦距处3. 物与物方焦面重合时4. 物与H重合[返回本章要点]正透镜成像(图中移动的黑线为物,红线为像)[返回本章要点]负透镜成像(图中移动的黑线为物,红线为像)[返回本章要点]§4-4 理想光学系统的图解求像依据①平行于光轴的光线经理想光学系统后必通过像方焦点;②过物方焦点的光线经理想光学系统后必为平行于光轴的光线;③过节点的光线方向不变;[返回本章要点]④任意方向的一束平行光经理想光学系统后必交于像方焦平面上一点;⑤过物方焦平面上一点的光线经理想光学系统后必为一束平行光。
为解决任给一条光线求其共轭光线的问题,有必要利用辅助光线1、2、3并结合依据4、5 [返回本章要点]§4-5 光学系统的组合[返回本章要点]一、两个光组的组合问题-> 已知 F1,F1',H1,H1',F2,F2',H2,H2'以及d(△),(△光学间隔)求总光组的 F,F',H,H' 解决1. 图解组合2. 找出分光组与等效总光组之间的关系3. 求出 f,f',确定H,H',F,F'的位置[返回本章要点]合成光组的像方参量以第二个光组的像方焦点、像方主点为起始点合成光组的物方参量以第一个光组的物方焦点、物方主点为起始点组合放大率:一般已知 x1, 则[返回本章要点]则一般光组在空气中,有f =-f',于是两个有一定焦距的光组组合,系统的总焦距或光焦度除与各自的光焦度有关外,还与其间隔 d 有关例:两个正光焦度薄光组组合[返回本章要点]当当当二、多光组组合[返回本章要点]所以即过渡:1. 正切计算法——初值 u1=0, h1任选[返回本章要点]2. 截距计算法[返回本章要点]由令反复利用高斯公式得各截距,最后算出f’,并有3. 各光组对总光焦度的贡献每个光组对总光焦度的贡献,除与自身的光焦度有关外,还与它在系统中的位置有关。
与前面得到的结论一致。
两个特例[返回本章要点]位于中间实像面上的光组对总光焦度无贡献此时d=0, φ=φ1+φ2二正透镜组合,越靠近总光焦度越大两个例子[返回本章要点]三、光学系统焦距的测定[返回本章要点]用左图,可得到F’,但f’=?必须用轴外平行光写成例如:135相机,底片24´36,则像高可以根据视场角求焦距注意:当节点与主点不重例如单个折射球面合时不能直接使用公式焦距测定必须提供一定角度的平行光——平行光管[返回本章要点]焦距仪(详见实验指导“焦距测量实验”)[返回本章要点]§4-6 望远镜系统[返回本章要点]望远镜系统是以平行光入射,再以平行光出射的系统系统特点焦点、主点在无穷远,焦距无穷大由得 △=0最简单的望远镜至少有两个独立光组,第一光组的像方焦点与第二光组的物方焦点重合 [返回本章要点]一、放大率β、α、γ由 得一般并有且望远镜的三种放大率均与物距无关,仅与二光组的焦距有关仍有诸放大率的关系不变二、视觉放大率 [返回本章要点]人对物体主观感觉的大小与视角有关,目视光学仪器用视觉放大率物体经目视仪器所成的像对人眼张角的一半人眼直接观察时物对人眼张角的一半对于望远镜系统物镜焦距 目镜焦距三、讨论 [返回本章要点]① 要求主观放大,故或写成②一般 f1'>0,f2'可正可负。
成倒像,观察不便,但便于测量,必要时加倒像系统成正像,用于观察,但无实像面,不能测量③当时物经望远镜成缩小像距离拉近很多对眼睛的张角变大④系统一定,则β,α,γ为定值,与物距 l 无关四、望远镜与其他光组的组合[返回本章要点]望远镜系统+望远镜系统=望远镜系统望远镜系统+有限焦距系统=有限焦距系统等效系统的像方焦点与第二系统的像方焦点重合。
焦距为将第二系统的焦距扩大到Γ倍有限焦距系统对无穷远物成像时,焦距短则像小,反之像大望远镜与眼睛组合,相当于把眼睛的焦距扩大到Γ倍[返回本章要点]§4-7 透镜一、透镜球面透镜( 主要考虑工艺过程简单 ),非球面透镜 ( 提高像质、简化结构 )双凸平凸月凸双凹平凹月凹d>tm 凸透镜 ( 双凸、平凸、月凸 ) d<tm 凹透镜 ( 双凹、平凹、月凹 )在考虑高斯总是时令 d->0 即薄透镜。
[返回本章要点]二、薄透镜[返回本章要点]结构特征薄透镜:H,H’重合,J,J’重合,f=-f'光焦度(焦距)计算正透镜,会聚透镜对平行光起会聚作用,有实的像方焦点。
负透镜,发散透镜对平行光起发散作用,有虚的像方焦点。
薄透镜的放大率薄透镜的共轭距三、厚透镜的焦距[返回本章要点]考虑厚度,由对于两个面得将其看成二薄光组组合,按当 d 0时,为厚透镜,此时代入之得到厚透镜焦距[返回本章要点]光焦度计算四、厚透镜的主面[返回本章要点]利用二光组组合求主面的的公式,可得透镜主面、焦点位置为:1. 双凸透镜[返回本章要点]当d<<|r|时,f’>0H,H’都在透镜内部,H在H’的前面当时二球心重合,主面重合于球心,f’>0此时时是正透镜,主面在内[返回本章要点]时是望远镜,f’→时是负透镜,f’<0,主面在外2. 双凹透镜不管 d 怎么变,f’<0 恒成立并也有主面也总在内部3. 平凸透镜可看成是正薄透镜+平行平板,f'=Γf1'加平板后产生轴向位移4. 平凹透镜f'< 0与 d无关可看成负薄透镜+平行平板[返回本章要点]精品文档 收集于网络,如有侵权请联系管理员删除 讨论:[返回本章要点]平凸、平凹——薄透镜 + 平板有限焦距系统 + 望远镜 双凹、弯凸——f’恒为负或正不变双凹:负+负 弯凸:但使 正+负双凸、弯凹——f’的正负与厚度有关双凸:总光焦度与 d 有关 正+正 弯凹:但使总光焦度与 d 有关 正+负厚的弯月形凹透镜可用于校正像面弯曲,它可在厚度不太大时得到正光焦度。
不同类型厚透镜都相当于二光组组合。