边界条件

边界条件的定义
边界条件是指在计算机程序、数学模型或系统设计中，定义问题的输入、输出或操作所必须满足的条件。

这些条件是问题解决的关键因素，因为如果边界条件不正确或不完整，那么计算机程序或解决方案将无
法正确工作。

边界条件通常可分为两类：输入边界条件和输出边界条件。

输入边界
条件是指在程序中需要接收的输入信息，而输出边界条件是指在程序
运行完毕后需要输出的结果。

以下是边界条件的几个基本定义:
1. 最小值和最大值- 最小值和最大值是边界条件的基本概念。

在很多
问题中，最小和最大值是非常重要的因素。

例如，在一些排序算法中，最小和最大值可能直接影响算法的效率。

2. 边界顺序- 当问题有多个边界情况的时候，它们的顺序也非常的重要。

例如，在一些搜索算法中，问题的解可能受限于某个边界情况。

如果这个边界情况与其他条件冲突，那么这个算法将无法产生有效的
解决方案。

3. 特定的值- 在一些特定的问题中，特定的值可能会与边界条件有关。

例如，在寻找图像的边缘时，边缘的像素通常被视为边界条件。

除了输入和输出边界条件，还有一些其他的边界条件需要考虑。

例如，在计算机程序中，内存和时间通常是有限的资源。

因此，程序设计者
需要考虑程序可能需要运行的时间和内存使用量。

正如你所看到的，边界条件对于任何问题的解决方案都是至关重要的。

只有当问题的输入和输出的边界清晰明确时，我们才能保证程序的正
确性和解决方案的有效性。

因此，在分析问题时，我们应该非常注意问题的边界条件，并且确保它们被正确地定义和实现。

有限元边界条件定义有限元方法是一种常用的数值分析方法，用于解决工程和科学领域中的各种物理问题。

在使用有限元方法进行计算之前，需要定义适当的边界条件。

边界条件是指在计算区域的边界上所施加的约束条件，用于模拟真实世界中的物理现象。

本文将详细介绍有限元边界条件的定义和应用。

1. 强制边界条件强制边界条件是指在计算区域的边界上施加的已知值或已知函数。

这些边界条件通常是由实验数据、分析解或其他先验知识提供的。

强制边界条件可以是以下几种类型：1.1 固定边界条件固定边界条件是指在计算区域的边界上施加的位移或变形的已知值。

例如，当我们研究一个悬臂梁的弯曲问题时，可以将梁的一端固定在原点，这样就施加了一个固定边界条件。

1.2 力边界条件力边界条件是指在计算区域的边界上施加的外力或力密度的已知值。

例如，当我们研究一个杆件的拉伸问题时，可以在杆件的一端施加一个已知的拉力，这样就施加了一个力边界条件。

1.3 热边界条件热边界条件是指在计算区域的边界上施加的温度或热流的已知值。

例如，当我们研究一个热传导问题时，可以在物体的表面上施加一个已知的温度，这样就施加了一个热边界条件。

2. 自然边界条件自然边界条件是指在计算区域的边界上施加的无约束条件。

这些边界条件通常是由物理现象本身决定的，不需要额外的输入。

自然边界条件可以是以下几种类型：2.1 自由边界条件自由边界条件是指在计算区域的边界上不施加任何约束条件。

例如，当我们研究一个流体力学问题时，可以将流体的边界设置为自由边界，这样流体可以自由地进出计算区域。

2.2 绝缘边界条件绝缘边界条件是指在计算区域的边界上施加的无热流或无质量流的条件。

例如，当我们研究一个热传导问题时，可以将物体的边界设置为绝缘边界，这样热量不能通过边界传递。

2.3 对称边界条件对称边界条件是指在计算区域的边界上施加的关于某个轴对称的条件。

例如，当我们研究一个结构的弯曲问题时，可以将结构的边界设置为对称边界，这样只需要计算一半的结构即可。

材料力学边界条件边界条件在材料力学中起到非常重要的作用，它们是物理现象或力学问题的解决方案的关键要素之一、边界条件确定了在研究区域边界上发生的物理过程和影响。

在材料力学中，常见的边界条件包括：1.位移边界条件：位移边界条件是指物体在边界上的位移情况。

常见的位移边界条件有固定边界条件、自由边界条件和摩擦边界条件等。

固定边界条件是指物体在其中一边界上的位移被限制为零，即该边界上的点不能发生位移。

自由边界条件是指物体在其中一边界上的位移没有任何限制，即该边界上的点可以自由运动。

摩擦边界条件是指物体在其中一边界上的位移受到边界面上的摩擦力所限制。

2.力边界条件：力边界条件是指物体在边界上受到的外力情况。

常见的力边界条件有固定力边界条件和自由力边界条件等。

固定力边界条件是指物体在其中一边界上受到的外力为零，即该边界上没有外力作用。

自由力边界条件是指物体在其中一边界上受到的外力没有任何限制，即该边界上的外力可以自由作用。

3.应力边界条件：应力边界条件是指物体在边界上的应力情况。

常见的应力边界条件有固定应力边界条件和自由应力边界条件等。

固定应力边界条件是指物体在其中一边界上的应力被固定为其中一个值，即该边界上的应力受到限制。

自由应力边界条件是指物体在其中一边界上的应力没有任何限制，即该边界上的应力可以自由变化。

边界条件的选择需要根据具体问题的要求和实际情况进行确定。

通常情况下，边界条件需要满足力学平衡条件、位移连续条件和应力连续条件等。

同时，边界条件的选择也需要考虑到物体的边界特性，比如是否有固定边界、自由边界或者摩擦边界等。

边界条件的正确选择对于力学问题的解决至关重要。

不恰当的边界条件会导致计算结果的不准确甚至错误。

因此，在进行模拟和计算时，需要仔细分析和确定边界条件，并考虑到实际问题的特点和要求。

总之，材料力学边界条件是研究区域边界上发生的物理过程和影响的要素，其正确选择对于解决力学问题具有重要作用。

在选择边界条件时，需要考虑到力学平衡、位移连续和应力连续等方面，以获得准确的计算结果。

数学物理方法三类边界条件
在数学物理中，常常会遇到需要考虑边界条件的问题。

根据不同的情况，可以将数学物理方法中的边界条件分为三类，第一类边界条件、第二类边界条件和第三类边界条件。

1. 第一类边界条件（Dirichlet边界条件）：
第一类边界条件是指在边界上给定了物理量的具体值。

例如，在一个热传导问题中，可以给定边界上的温度值。

在一个波动方程中，可以给定边界上的振幅值。

这类边界条件可以用数学上的等式或函数来表示。

2. 第二类边界条件（Neumann边界条件）：
第二类边界条件是指在边界上给定了物理量的导数。

例如，在一个热传导问题中，可以给定边界上的热流密度（即温度梯度）。

在一个波动方程中，可以给定边界上的振幅的导数。

这类边界条件可以用数学上的导数来表示。

3. 第三类边界条件（Robin边界条件）：
第三类边界条件是指在边界上给定了物理量的线性组合，其中既包括物理量的值，也包括物理量的导数。

例如，在一个热传导问题中，可以给定边界上的热流密度和温度的线性组合。

这类边界条件可以用数学上的线性组合来表示。

需要注意的是，以上分类只是一种常见的方式，具体问题中的边界条件可能会有其他形式。

此外，边界条件的选择和应用也取决于所研究的具体物理问题和数学模型。

在实际问题中，根据边界条件的具体形式，可以选择合适的数学方法和技巧来求解。

第二章：边界条件这一章主要介绍使用边界条件的基本知识。

边界条件能够使你能够控制物体之间平面、表面或交界面处的特性。

边界条件对理解麦克斯韦方程是非常重要的同时也是求解麦克斯韦方程的基础。

§2.1 为什么边界条件很重要用Ansoft HFSS求解的波动方程是由微分形式的麦克斯韦方程推导出来的。

在这些场矢量和它们的导数是都单值、有界而且沿空间连续分布的假设下，这些表达式才可以使用。

在边界和场源处，场是不连续的，场的导数变得没有意义。

因此，边界条件确定了跨越不连续边界处场的性质。

作为一个 Ansoft HSS 用户你必须时刻都意识到由边界条件确定场的假设。

由于边界条件对场有制约作用的假设，我们可以确定对仿真哪些边界条件是合适的。

对边界条件的不恰当使用将导致矛盾的结果。

当边界条件被正确使用时，边界条件能够成功地用于简化模型的复杂性。

事实上，Ansoft HSS 能够自动地使用边界条件来简化模型的复杂性。

对于无源RF 器件来说，Ansoft HSS 可以被认为是一个虚拟的原型世界。

与边界为无限空间的真实世界不同，虚拟原型世界被做成有限的。

为了获得这个有限空间， Ansoft HSS使用了背景或包围几何模型的外部边界条件。

模型的复杂性通常直接与求解问题所需的时间和计算机硬件资源直接联系。

在任何可以提高计算机的硬件资源性能的时候，提高计算机资源的性能对计算都是有利的。

§2.2 一般边界条件有三种类型的边界条件。

第一种边界条件的头两个是多数使用者有责任确定的边界或确保它们被正确的定义。

材料边界条件对用户是非常明确的。

1、激励源波端口（外部）集中端口（内部）2、表面近似对称面理想电或磁表面辐射表面背景或外部表面3、材料特性两种介质之间的边界具有有限电导的导体§2.3 背景如何影响结构所谓背景是指几何模型周围没有被任何物体占据的空间。

任何和背景有关联的物体表面将被自动地定义为理想的电边界（Perfect E）并且命名为外部（outer）边界条件。

边界条件
（一）概述
边界条件是刻画渗流研究区D边界上的水力特征，或者说是刻画研究区以外对研究区边界的水力作用。

如果渗流研究区包含整个地下水系统，那么边界条件表达的正是地下水系统以外在边界上的作用于地下水的关系。

对于具体问题的研究，研究范围的确定是个十分复杂和重要的问题。

（二）给定水头边界条件（第一类边界）
边界上水头动态变化已知的称为第一类边界条件。

对于二维和三维流可分别表示为：
其中：是研究区D上的第一类边界；
是上的已知水头函数。

对于稳定流问题，与t无关。

这类边界最常见的是渗流区与地表水体（如河、湖、海
等）的分界线（面），就取地表水体的水位。

其它，如定降深抽水井（放水井）的井壁，实际上可视为地下水与井水的分界面，往往取井水位为其第一类边界条件。

另外，解析发法中，常常假定含水层水平方向无限延伸，这时取无限远处的水头保持不变，这也是第一类边界条件。

当边界上水头不随时间改变时，称为定水头边界。

（三）给定流量边界条件（第二类边界）
边界单宽流量q（平面二维流问题），或渗流速度v（三维流和剖面二维流问题）已知者称为第二类边界条件。

对于平面二维和三维流（或剖面二维流）可分别表示为
其中：是研究区D上的第二类边界；
H、n分别是水头和边界的外法线方向；
是水力坡度在边界法线方向上的分量；
q、v分别是流入研究区的单宽流量和渗流速度，流入时取正值，当q=0或v=0时，称为隔水边界
（四）混合边界条件（第三类边界）
若某段边界上H和的线性组合已知，即
式中和为上述边界的已知函数，这种类型的边界条件称为第三类边界条件或混合边界条件。

边界条件定义边界条件是指在一个问题或系统中，所设定的特定条件或限制，用于测试或确定系统的行为。

边界条件在各个领域都有应用，例如软件开发、数学、物理学等等。

在软件开发中，边界条件是指在测试或运行程序时，需要考虑的各种极端情况。

下面将从不同领域的角度，讨论边界条件的定义和应用。

在数学中，边界条件是指在函数或方程中所设定的特定约束条件。

例如，在求解微分方程时，需要给定初始条件或边界条件，以确定唯一的解。

边界条件可以是函数在某一点的值，或者函数在某一区间的行为。

这些边界条件的设定，对于解的存在性和唯一性具有重要影响。

在物理学中，边界条件指的是在物理系统中所设定的限制条件。

例如，在求解波动方程时，需要考虑波函数在边界处的行为。

边界条件可以是波函数在某一点的值，或者波函数在某一区域的导数。

这些边界条件的设定，对于确定系统的行为和性质具有重要影响。

在计算机科学中，边界条件是指在程序设计或算法实现中所设定的特定限制条件。

例如，在编写排序算法时，需要考虑数组的边界条件，即数组的起始位置和结束位置。

边界条件的设定，可以避免数组越界和程序崩溃的情况发生。

边界条件的考虑也可以提高程序的效率和性能。

除了数学、物理学和计算机科学，边界条件在其他领域也有广泛的应用。

例如，在经济学中，边界条件是指经济模型中所设定的特定限制条件，用于分析和预测经济现象。

在生物学中，边界条件是指生物系统中所设定的特定约束条件，用于研究生物过程和现象。

边界条件的设定需要考虑到问题的特性和目标，以及系统的实际情况。

边界条件的选择应该合理、准确，能够准确反映问题的本质和复杂性。

同时，边界条件的设定也需要符合问题的要求和约束，以保证系统的稳定性和可靠性。

边界条件是问题或系统中所设定的特定条件或限制，用于测试或确定系统的行为。

边界条件的设定在各个领域都有重要的应用，对于解决问题和研究系统行为具有关键作用。

边界条件的设定需要考虑问题的特性和目标，以及系统的实际情况，从而保证系统的稳定性和可靠性。

自然边界条件的通俗解释一、什么是自然边界条件在自然界中，各种物理现象和过程都受到一定的限制和规律，这些限制和规律常常被称为边界条件。

自然边界条件是指自然界中存在的各种限制和规律，它们能够影响物理过程的发生和发展，同时也限制了物理系统的行为。

自然边界条件包括了空气、水、地球表面等自然元素对物理过程的影响，它们决定了物理系统的行为与演化。

二、自然边界条件对物理过程的影响2.1温度和能量传输温度是自然界中一个重要的边界条件，在很多物理过程中起着关键作用。

热量的传输受到温度差异的影响，从高温向低温的传导、传感、辐射等方式都受到温度差的驱动。

自然界中的温度差异会引发大气冷暖空气的形成，导致大气环流的发生。

2.2湿度和气候变化湿度是描述空气中水汽含量的指标，它对气候变化起着重要作用。

空气中的湿度受到水汽的蒸发和降水的影响。

湿度的变化会影响大气的稳定性，进而影响气候的转变。

在自然边界条件的限制下，湿度决定了雨水的形成和分布，影响了地球上的水循环。

2.3地形和地质结构地形和地质结构也是自然边界条件的重要组成部分。

地球表面的起伏、山脉、河流等地理特征直接影响了大气和水体的流动。

山脉作为自然边界，影响着气候的形成和降水的分布。

地质结构则决定了地下水的蓄藏和流动，对水文循环和地下水资源的分布起到重要作用。

三、自然边界条件的意义自然边界条件对各种物理过程的发生和发展起到了制约和调控的作用，它们决定了物理系统的特性和演化。

自然边界条件的研究不仅有助于对地球环境和气象气候变化的理解，还能为生态保护、资源开发等方面提供科学依据。

在气候变化的背景下，深入研究自然边界条件对物理过程的影响，有助于我们更好地预测和应对自然灾害，也能为环境保护和可持续发展提供有益的指导。

四、自然边界条件的研究方法研究自然边界条件的方法多种多样，包括实地观测、数值模拟、实验室研究等。

通过实地观测可以获取地球表面的温度、湿度、地貌等数据，以及大气和水体的运动信息。

boundary condition 条件边界条件（Boundary Conditions）是指在进行数学模型或物理模拟时，为了确定问题的解决方案而设定的特定条件。

边界条件在模拟过程中起着至关重要的作用，它们可以对问题的解决产生重大影响。

在这篇文章中，我们将讨论边界条件的定义、种类以及在不同领域中的应用。

边界条件可以分为以下几类：第一类是几何边界条件，即在模拟中给定的区域的边界上所设置的条件。

这些条件可以是给定的形状、大小、位置等。

例如，在流体力学的模拟中，我们可以设置一个固体壁面，从而确定流体在该壁面上的速度和压力分布。

第二类是物理边界条件，即在边界上给定的物理量值。

这些物理量可以是温度、浓度、吸收率等。

例如，在热传导问题中，我们可以给定热流的大小和方向，从而确定边界上的温度分布。

第三类是数值边界条件，即在数值模拟中为了保证计算的稳定性而设定的条件。

这些条件可以是数值格式所要求的数值限制，例如稳定性条件、收敛性条件等。

在计算流体力学的模拟中，我们常常需要考虑Courant-Friedrichs-Lewy（CFL）条件，以保证数值解的稳定性和收敛性。

边界条件在不同领域中扮演着重要的角色。

在物理学中，边界条件可以帮助我们理解问题的特定情况。

例如，在电磁场模拟中，我们可以设置给定位置处的电荷密度，以探索与该电荷密度相关的电场分布。

在天气模拟中，我们可以通过设置地表的气温和风速分布来预测不同地区的天气变化。

在工程学中，边界条件可以帮助我们优化设计和工艺。

例如，在建筑结构分析中，我们可以通过设置柱或梁的边界条件来确定结构的稳定性和安全性。

在流体管道系统的设计中，我们可以通过设置管道末端的边界条件来确定流体流动的特性，以便选择最合适的泵和阀门。

在计算机科学中，边界条件在算法设计和数据分析中也起着重要的作用。

例如，在图像处理中，我们可以通过在图像边界上设置边界条件来处理图像的边缘。

在机器学习中，我们可以通过定义特定的边界条件来训练和优化模型。

常微分方程的边界条件常微分方程（ODE）就像是一道数学的难题，等着我们去破解。

而边界条件就像是这道题的“约束”，没有它，方程就像没有方向的船，飘荡在数学的海洋中。

好啦，今天就带大家一起聊聊这个话题，保证不让你觉得无聊，反正这事儿跟我们的生活也有些联系嘛！1. 什么是边界条件？边界条件，简单来说，就是给方程设置一些限制条件。

就像做菜，你不能随便往锅里扔一大堆材料，要有个先后顺序，要加盐要加醋，不能忽略了。

这些条件告诉你，方程在特定点上的值或者导数应该是什么样子。

比如说，假设你在追一个目标，边界条件就像是你设定的目标，告诉你该往哪儿去，怎么才能实现。

1.1 边界条件的类型边界条件大体上可以分为两种，一种叫“初值条件”，另一种叫“边值条件”。

初值条件就像你早上起床时给自己设定的目标，比如“今天一定要早起，吃一顿营养早餐！”这个条件一旦设定，你就得努力去实现。

而边值条件则有点像你在旅途中设定的终点，“我要去海边看日出！”这时候你就得计划好路线，确保每一步都朝着那个目标走去。

1.2 为什么边界条件重要？有了边界条件，我们的常微分方程才能真正“落地”。

没有边界条件，你的方程就像一场没有结束的马拉松，跑来跑去，却不知道目的地在哪。

边界条件不仅能帮助我们找到解，还能确保解是唯一的。

这就像你在比赛时，有了明确的目标，才能不迷失方向，一路跑到终点。

2. 如何选择边界条件？选择边界条件就像挑选食材，得看具体的菜式。

你不能随便拿个土豆就往汤里扔，得根据你要做的汤类型来决定。

常微分方程的边界条件选择也一样。

我们需要根据实际问题来设定，比如物理问题中的温度、速度，甚至是市场经济中的需求量。

这些因素都能影响我们方程的结果。

2.1 物理中的应用在物理学中，边界条件尤为重要。

想象一下你在研究一个弹簧的振动，初始时弹簧的长度、质量和弹性系数都是已知的。

那么这就是你的初值条件。

再想象一下，你希望弹簧的最大伸展长度不超过某个值，这就是你的边值条件。

化学反应的边界条件定义化学反应是物质发生变化的过程，其速率受到很多因素的影响。

边界条件是指影响化学反应进行的因素和条件，进一步影响反应速率和结果。

在化学反应中，边界条件可以分为温度、浓度、压力、催化剂等方面。

首先，温度是影响化学反应速率的重要因素之一。

在一定的温度下，反应速率会随着温度的升高而增加。

这是因为温度的提高会增加分子的平均动能，使得分子碰撞的频率和能量增加，从而促进反应进行。

而当温度过高时，反应速率可能会受到热能的影响而减慢或中断。

其次，浓度也是影响化学反应的边界条件之一。

一般来说，浓度越高，分子间的碰撞频率也越高，反应速率也更快。

这是因为在高浓度下，分子更容易相遇并发生反应。

而反之，浓度过低则会减缓反应速率，甚至导致反应无法进行。

此外，压力也是影响某些反应的边界条件。

在气相反应中，当压力升高时，气体分子之间的碰撞频率增加，反应速率也会相应提高。

这是因为高压条件下，气体分子的平均自由程较短，碰撞的频率增加。

但并非所有反应都受压力影响，只有涉及气态物质的反应才会受到压力的影响。

最后，催化剂是能够改变反应速率的物质，但并不改变反应的终点物质。

催化剂通常通过提供新的反应路径来降低反应的活化能，从而促进反应进行。

催化剂可以提高反应速率，降低反应温度要求，减少副反应产生等。

因此，在进行化学反应时，选择适当的催化剂也是十分重要的。

综上所述，化学反应的边界条件包括温度、浓度、压力和催化剂等多个方面。

了解这些边界条件对于控制反应速率和结果具有重要意义。

通过合理地控制这些边界条件，可以提高反应效率，减少能量消耗，并获得更好的反应产物。

因此，在进行化学反应时，需要认真考虑这些边界条件，以达到预期的反应目的。

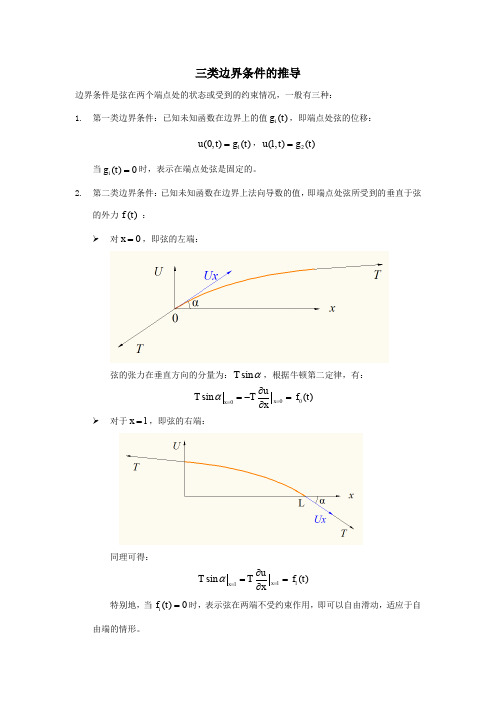
三类边界条件的推导边界条件是弦在两个端点处的状态或受到的约束情况，一般有三种：1. 第一类边界条件：已知未知函数在边界上的值()i g t ，即端点处弦的位移：1(0,)()u t g t =，2(,)()u l t g t =当()0i g t =时，表示在端点处弦是固定的。

2. 第二类边界条件：已知未知函数在边界上法向导数的值，即端点处弦所受到的垂直于弦的外力() f t ：对0x =，即弦的左端：弦的张力在垂直方向的分量为：sin T α，根据牛顿第二定律，有：000sin () x x u T Tf t x α==∂=-=∂对于x l =，即弦的右端：同理可得：sin () x l l x l u T T f t x α==∂==∂特别地，当()0i f t =时，表示弦在两端不受约束作用，即可以自由滑动，适应于自由端的情形。

3. 第三类边界条件：又称混合边界条件，它给出了未知函数和它的法线方向上的导数的线性组合在边界上的值。

对弦的一维振动问题，即已知端点处弦的位移（引起弹性支撑的力）和所受的垂直于弦线的外力。

对0x =，即弦的左端：弦对支撑外力的垂直分量为：u T x∂∂，由胡克定律知： 000(t)x x u T ku f x==∂=+∂ 设k T σ=，()()f t v t T=，可以得到，弹性支撑条件下，弦振动的边界条件为： 0()()x u u v t xσ=∂-=∂ 对于x l =，即弦的右端：弦对支撑外力的垂直分量为：u Tx ∂-∂，由胡克定律知(t)x l x l l u T ku f x ==∂-=+∂此时得到的弦振动的边界条件为： ()()x l u u v t x σ=∂+=∂对于外力()0i f t =的特殊情况，即()0v t =，边界条件在弦的两端可统一简化为：()0 (0,)x a u u a a l x σ=∂===∂。

传热问题三类边界条件
在传热学中，边界条件是解决传热问题的关键因素之一。

通常，我们将边界条件分为以下三类：
1. 第一类边界条件：直接给出边界处的温度值。

这种边界条件简单直观，适用于导热问题等。

2. 第二类边界条件：告诉你边界处的温度梯度是多少。

这与物体内部温度的变化速率有关，常用于对流换热等问题。

3. 第三类边界条件：与前两类不同，它不仅给出了温度梯度，还与温度满足一个关系式。

这类边界条件更复杂，但在实际问题中非常常见，如自然对流传热和辐射传热等。

自然对流传热是由于流体中的温度差异形成的流动导致的传热现象，物体表面的温度和热流密度通常是随时间和位置变化的。

辐射传热则是物体通过辐射方式传递热量的现象，这也与物体表面的温度和热流密度有关，而这些参数通常是随时间和位置变化的。