小学六年级数学立体图形的应用复习题

小升初重点专题：立体图形的表面积和体积（专项训练）-小学数学六年级下册苏教版一、单选题1．做一节圆柱形烟囱，至少需要多少铁皮，是求圆柱的（）。

A．侧面积B．表面积C．体积D．底面积2．一个圆锥的底面半径与高的比是1：4，它与同底等高的一个圆柱体的体积之比是（）A．1：4B．3：4C．1：3D．1：83．圆柱的底面直径扩大到原来的3倍，高不变，它的体积扩大到原来的（）倍。

A．3B．6C．9D．274．把一个棱长是20cm的正方体木块削成一个最大的圆柱，这个圆柱的体积是（）cm3 A．6280B．628C．62.8D．31405．一个棱长4米的正方体鱼池，占地（）平方米。

A．8B．16C．64D．966．将棱长为6厘米的一块正方体彩泥捏成一个底面积是48cm2的长方体，那么这个长方体彩泥的厚度是（）厘米。

A．2B．3C．4.5D．5二、判断题7．圆锥的顶点到底面上任意一点的距离都是它的高。

（）8．在不计算损耗的情况下，把一个长方体铁块熔铸成一个正方体，形状变了，所以所占空间的大小也变了。

（）9．一个棱长6厘米的正方体，体积和表面积相等。

（）10．一根长方体木料长2.8米，宽4分米，高4分米，如图所示把它锯成3段，表面积增加4×4×2=32平方分米。

（）11．一个圆柱与一个圆锥等底等高，他们的体积和是36立方米，那么圆锥的体积是9立方米。

（）三、填空题12．一个圆柱的底面半径是3分米，高是6分米，它的表面积是，体积是。

13．一个圆锥的体积是50.24立方米，底面半径是2米，它的高是米。

14．把一个体积是24立方米的圆柱削成一个最大的圆锥，削成的圆锥体积是。

15．用一根长60厘米的铁丝围成一个正方体形状的小铁筐，在外面贴上手工纸，需要平方厘米的手工纸。

16．一个正方体的棱长是6厘米，把它截成3个大小相等的长方体，表面积比原来增加平方厘米。

17．下图所示是一个长方体的平面展开图，这个长方体的长是15厘米，宽是12厘米，高是厘米。

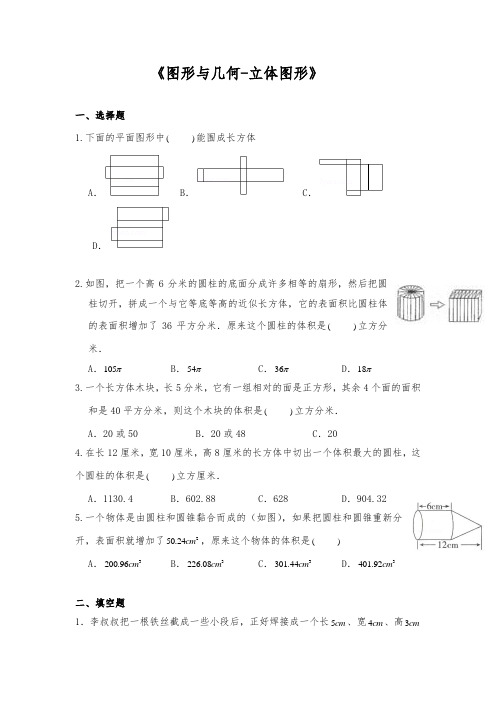
《图形与几何-立体图形》一、选择题1.下面的平面图形中()能围成长方体A．B．C．D．2.如图，把一个高6分米的圆柱的底面分成许多相等的扇形，然后把圆柱切开，拼成一个与它等底等高的近似长方体，它的表面积比圆柱体的表面积增加了36平方分米．原来这个圆柱的体积是()立方分米．A．105πB．54πC．36πD．18π3.一个长方体木块，长5分米，它有一组相对的面是正方形，其余4个面的面积和是40平方分米，则这个木块的体积是()立方分米．A．20或50 B．20或48 C．204.在长12厘米，宽10厘米，高8厘米的长方体中切出一个体积最大的圆柱，这个圆柱的体积是()立方厘米．A．1130.4 B．602.88 C．628 D．904.325.一个物体是由圆柱和圆锥黏合而成的（如图），如果把圆柱和圆锥重新分开，表面积就增加了250.24cm，原来这个物体的体积是()A．3401.92cm 200.96cm B．3301.44cm D．3226.08cm C．3二、填空题1．李叔叔把一根铁丝截成一些小段后，正好焊接成一个长5cm、宽4cm、高3cm的长方体框架，这个长方体的体积是3cm，这根铁丝原有cm．2．将36厘米长的铁丝，做成一个正方体框架，这个正方体的体积是立方厘米，表面积是平方厘米．3．用如图硬纸板做成一个无盖的长方体纸盒．这张硬纸的面积是平方厘米，这个纸盒的容积是立方厘米．4．有一张长方体铁皮（如图），剪下图中两个圆及一块长方形，正好可以做成一个圆柱体，这个圆柱体的底面半径为10厘米，那么圆柱的底面积是平方厘米，体积是立方厘米．5．一根圆柱形的木料长5米，把它锯成4段，表面积增加了12平方分米，这根木料的体积是．如果锯成4段用了9分钟，那么把它锯成6段要用分钟．6．一节长2米的通风管，它的横截面是边长4分米的正方形．做10节这样的通风管至少需要铁皮平方米．7．一个长方体木块长、宽、高分别是5cm、4cm、4cm．如果用它锯成一个最大的正方体，体积比原来减少了%．8．一个圆锥体橡皮泥，底面积是15平方厘米，高是6厘米．这个圆锥的体积是立方厘米：如果把它捏成与这个圆锥等底的圆柱，圆柱的高是厘米9．李叔叔家新买了一台空调，外观为圆柱体，底面半径30厘米，高约2米，这台空调所占空间为立方米，若需要一个防尘罩，至少需要布平方米．10．一个圆锥和一个圆柱底面积相等，圆锥高15厘米，圆柱高10厘米，圆柱体积和圆锥体积的最简整数比是．11．一根长方体木料，横截面是边长10厘米的正方形．从这根木料上截下6厘米长的一段，切削成一个最大的圆锥．圆锥的体积是2cm，约占截下这段长方体木料体积的%（百分号前面保留一位小数）．12．图中一个小球的体积是立方厘米，一个大球的体积是立方厘米．三、判断题1.长方体的面中可能有正方形，正方体的面中不可能有长方形． ( )2.把一个圆柱削成一个最大的圆锥，削去部分的体积是圆锥体积的2倍． ( )3.将圆柱的侧面展开有可能是长方形，也有可能是正方形，还有可能是平行四边形．（）4.四个棱长2厘米的正方体拼一个长方体，长方体表面积最大是96平方厘米( )四、计算题1.求下面立体图形的表面积和体积（单位)cm2.看图计算．（单位：)dm（1）如图1：①求表面积．②求体积（2）如图2：求体积．3.求如图的表面积和体积．单位()dm五、解决问题1.一个长方体的玻璃缸容器，长6dm，宽5dm，高4dm，里面的水深3.2dm，再把一个棱长为3dm的正方体铁块放入水中（完全浸没），玻璃容器里的水会溢出多少升？2.在内侧棱长为20厘米的正方体容器里装满水，将容器如图倾斜放置，流出的水正好装满一个内侧长25厘米、宽8厘米、高5厘米的长方体容器．求图中线段AB的长度．3．一个长方体，如果长增加3厘米，宽和高不变，它的体积增加96立方厘米；如果宽减少2厘米，长和高不变，它的体积减少160立方厘米；如果高增加2厘米，长和宽不变，它的体积增加80立方厘米，求原长方体的表面积．4.如图是用塑料薄膜覆盖的蔬菜大棚，长15米，横截面是一个直径2米的半圆．（1）这个大棚的种植面积是多少平方米？（2）覆盖在这个大棚上的塑料薄膜约有多少平方米？（3）大棚内的空间大约有多大？5.六一儿童节，康康把一块橡皮泥揉成圆柱形，切成三块（如图1)，表面积增加了50.24平方厘米；切成四块（如图2)，表面积增加了48平方厘米．请你算算圆柱形橡皮泥的体积是多少立方厘米．6.有一种饮料瓶的瓶身呈圆柱形（不包括瓶颈），容积是30立方厘米．现在瓶中装有一些饮料，正放时饮料的高度是20厘米，倒放时空余部分的高度为5厘米，瓶内现有饮料多少立方厘米？7.有一个高8厘米，容量为50毫升的圆形容器A，里面装满了水，现把长16厘米的圆柱B垂直放入，使B的底和A的底面接触，这时一部分水从容器中溢出，当把B从A拿走后，A中的水的高度只有6厘米，求圆柱体B的体积是多少？答案一、选择题1.D．2.B．3.A4.C．5.A．二、填空题1．60，48．2．27，54．3．432、720．4．314、6280．5．100立方分米，15．6．32．7．20．8．30，2．9．0.5652；4.0506．10．2:1．11．157；26.2．12．30，35．三、判断题1.√．2.√．3.√．4.⨯．四、计算题1.解：（1）表面积：(838333)2334⨯+⨯+⨯⨯+⨯⨯=++⨯+⨯(24249)294=⨯+57236=+11436=（平方厘米）；150体积：833333⨯⨯+⨯⨯7227=+=（立方厘米）；99答：这个组合图形的表面积是150平方厘米，体积是99立方厘米．（2）表面积：30306430306⨯⨯⨯-⨯⨯=⨯⨯-⨯900649006=⨯-540045400=-216005400=（平方厘米）；16200体积：3030304⨯⨯⨯=⨯⨯900304270004=⨯=（立方厘米）；108000答：这个组合图形的表面积是16200平方厘米、体积是108000立方厘米．2.解：（1）①表面积：23.14612 3.14(62)2⨯⨯+⨯÷⨯=+226.0856.52=（平方分米）282.6②体积：23.14(62)12⨯÷⨯=⨯⨯3.14912=（立方分米）339.12答：圆柱体的表面积是282.6平方分米，体积是339.12立方分米．（2）21⨯÷⨯+⨯3.14(42)(3 1.2)3=⨯⨯3.144 3.4=（立方分米）42.704答：体积是42.704立方分米．3.解：10106 3.1446⨯⨯+⨯⨯60075.36=+=（平方分米）675.362⨯⨯-⨯÷⨯101010 3.14(42)6=-100075.36924.64=（立方分米）答：这个图形的表面积为675.36平方分米，体积为924.64立方分米．五、解决问题1.解：33365 3.2654⨯⨯+⨯⨯-⨯⨯=+-2796120=-123120=（立方分米）3答：玻璃容器里的水会溢出3立方分米．2.解：如图：2025852(2020)-⨯⨯⨯÷⨯=-⨯÷2010002400=-÷202000400205=-=（厘米）15答：线段AB的长度是15厘米．3.解：（长⨯宽+长⨯高+宽⨯高）2⨯=÷+÷+÷⨯(9631602802)2=++⨯(328040)2=⨯1522=（平方厘米）304答：这个长方体的表面积是304平方厘米．4.解：（1）15230⨯=（平方米），答：这个大棚的种植面积是30平方米．（2）2⨯⨯÷+⨯÷，3.142152 3.14(22)=+，47.1 3.14=（平方米），50.24答：覆盖在这个大棚上的塑料薄膜约有50.24平方米．（2）2⨯÷⨯÷，3.14(22)1523.14152=⨯÷，=（立方米），23.55答：大棚的空间是23.55立方米．5.解：50.24412.56÷=（平方厘米）；假设圆柱的底面半径是r，则212.56π=，r所以212.56 3.144r=÷=，所以2r=（厘米）；圆柱的高：484(22)÷÷⨯=÷124=（厘米）3体积为：23.1423⨯⨯=⨯12.563=（立方厘米）37.68答：圆柱形橡皮泥的体积是37.68立方厘米．6.解：30[20(205)]⨯÷+，430=⨯，5=（立方厘米）；24答：瓶内现有饮料24立方厘米．7.解：圆形容器A的底面积：÷=（平方厘米）；508 6.25溢出水的体积，即放入容器A的圆柱B的体积：⨯-，6.25(86)6.252=⨯，=（毫升）；12.5圆柱体B的体积是：÷⨯，12.581612.52=⨯，=（立方厘米）；25答：圆柱体B的体积是25立方厘米．。

-小升初立体图形的综合专项试题-人教版一、解答题（题型注释）6cm ．2.如图，有两个完全相同的直角梯形重叠在一起，求阴影部分的面积．3.图是小明家住房平面图．（单位：米）（1）客厅的面积是多少平方米？（2）厨房的面积比客厅少多少平方米？（3）你还能提出什么数学问题？并尝试解决．4.如图，将半径为10厘米的四分之一圆沿着线段AB 对折．请求出阴影部分的面积．（单位：厘米）5.图形计算题（图中单位均为厘米）（1）求图1中阴影部分的面积．（2）将图2中的直角三角形分别以AB、CB两条直角边为轴旋转一周，所形成的两个圆锥的体积相差多少？6.按要求操作与解答．（1）①画一个边长为4厘米的正方形．②在正方形内画一个最大的圆．（2）假如把正方形内的圆外部分称为“阴影部分”，求阴影部分面积与圆面积的比．7.沿着图中的虚线旋转一周，可以得到一个立体图形，请回答下列问题。

（1）这个立体图形的名称：（2）求这个立体图形的体积。

8.下面的图形分别是谁看到的？9.他们看到的各是哪幅图？参数答案1.解：（6× 6−3.14×62×14）×2= 36−3.14×36×14=（36﹣28.26）×2=7.74×2=15.48（平方厘米），答：阴影部分的面积是15.48平方厘米【解析】1.首先用正方形的面积减去半径为6厘米的圆面积的14求出阴影部分面积的一半，然后再乘2即可．根据正方形的面积公式：s=a2，圆的面积公式：s=πr2，把数据代入公式解答．此题主要考查正方形的面积公式、圆的面积公式的灵活运用，关键是熟记公式．2.解：（19﹣5+19）×6÷2=（14+19）×6÷2=33×3=99（平方厘米）答：阴影部分的面积是99平方厘米．【解析】2.由题意可知：因为两个梯形的面积相等，减去中间重叠部分的面积，则可得阴影部分的面积就等于空白梯形下半部分的梯形的面积，且下半部分这个梯形的下底和高已知，上底可以求出，从而可以求其面积，也就求得了阴影部分的面积．3.（1）解：5.4×4.2=22.68（平方米），答：客厅的面积是22.68平方米（2）解：22.68﹣3.3×3.1=22.68﹣10.23=12.45（平方米），答：厨房的面积比客厅少12.45平方米（3）解：提问：卫生间的面积是多少？3.6×2.0=7.2（平方米），答：卫生间的面积是7.2平方米【解析】3.（1）根据长方形的面积公式：S=ab，可求客厅的面积；（2）根据长方形的面积公式：S=ab，可求厨房的面积，再用客厅的面积减去厨房的面积即可；（3）根据图形提供的数据，可以求出其它房间的面积，比如：卫生间的面积是多少？再利用长方形的面积公式解决即可．此题主要考查了长方形的面积公式的实际应用．关键是正确判断长方形的长和宽．4.解：×3.14×102﹣（10﹣6.2）×10÷2×2，=78.5﹣38，=40.5（平方厘米）；答：阴影部分的面积是40.5平方厘米【解析】4.由题意可知：阴影部分的面积= 14圆的面积﹣空白三角形的面积×2，利用圆和三角形的面积公式即可得解．解答此题的关键是得出：阴影部分的面积= 14圆的面积﹣空白三角形的面积×2，代入数据即可求解．5.（1）解：14×3.14×52，=0.785×25，=19.625（平方厘米）；答：阴影部分的面积是19.625平方厘米（2）解：13×3.14×32×4，=3.14×12，=37.68（立方厘米）；13×3.14×42×3，=3.14×16，=50.24（立方厘米）；50.24﹣37.68=12.56（立方厘米）；答：所形成的两个圆锥的体积相差12.56立方厘米【解析】5.（1）图1中阴影部分的面积=以5厘米为半径的14圆的面积，利用圆的面积公式即可求解；（2）由题意可知：以AB为轴旋转一周所形成的圆锥的底面半径是3厘米，高是4厘米，以CB为轴旋转一周所形成的圆锥的底面半径是4厘米，高是3厘米，利用圆柱的体积公式求出两个圆锥的体积，再据减法的意义即可求解．（1）得出阴影部分的面积等于以5厘米为半径的14圆的面积，是解答本题的关键；（2）弄清楚所形成的圆锥的底面半径和高，是解答本题的关键．6.（1）解：如图所示（2）解：圆的面积：3.14×（4÷2）2=12.56（平方厘米），阴影部分的面积=16﹣12.56，=3.44（平方厘米）；3.44：12.56=43：157答：阴影部分的面积与圆面积的比是43：157．【解析】6.（1）①先画一条4厘米的线段，再分别过这条线段的两个端点，作这条线段的4厘米垂线段连接两条垂线段的另外一个端点，所形成的图形就是边长为4厘米的正方形．②所画的最大圆的直径应该等于正方形的边长，正方形的边长已知，于是可以画出这个圆．（2）正方形的边长是4厘米，则圆的半径可以求出，进而利用圆的面积公式就可以求出这个圆的面积．阴影部分的面积=正方形的面积﹣圆的面积7.（1）圆锥（2）×3.14×32×4＝37.68（立方厘米）答：这个立体图形的体积是37. 68立方厘米。

培英小学六年级数学总复习（立体图形）班级姓名一、填空。

1、把一个圆柱削一个最大圆锥后剩下的体积是18立方米，削成的圆锥体积是（）立方米。

2、一个圆柱的侧面展开，量得展开后的长方形的长是12.56厘米，宽是3厘米，这个圆柱体的体积是( ) 立方厘米。

3、一个水杯从里面量底面直径10厘米，高15厘米，杯里的水面离杯口5厘米，这个杯子有水（）毫升。

4、用铁皮制10节同样大小的通风管，每节长是5分米，底面直径是1.2分米，至少需要（）平方分米铁皮5、一个直径8厘米圆柱形铁皮通风管，沿着高剪开得到一个正方形，通风管的长（）厘米。

6、一个圆锥的体积是24立方厘米，底面积是8平方厘米，它的高是（）厘米。

7、一根长5米的圆柱形木料，把它平均分成5段，表面积正好增加48平方分米，每段木料的体积是（）立方分米。

8、一个圆锥体容器装满水，水深12厘米，倒到和它等底的圆柱体容器中，水深（）厘米。

二、判断。

1、圆锥体积是圆柱体积的三分之一。

（）2、一个正方体的棱长6分米，那么它的体积和表面积相等。

（）3、正方体、长方体、圆柱和圆锥的体积都可以用“底面积乘高”计算。

（）三、选择。

1、正方体棱长扩大原来的3倍，表面积就扩大原来的（）。

A、 3倍B、6倍C、9倍D、27倍2、一个长方形长6厘米，宽2厘米，一长边为轴，把长方形旋转一周得到的立体图形的体积是（）立方厘米。

A、 75.36B、12.56C、226.08D、113.043、用一根48厘米长的铁丝焊接成一个长方体。

已知长方体的长、宽、高的比是1:2:3，长方体的体积是（）立方厘米。

A、 24B、48C、96D、3072四、解决问题。

1、用铁皮做一个长3米、宽0.6米、高0.4米的长方体水槽（无盖）。

大约要用多少平方米的铁皮（进一法保留整平方米数）？这个水槽最多能蓄水多少立方米？2、要粉刷一间长8米，宽6米，高4米的教室，除去门窗面积是15平方米。

粉刷的面积是多少？如果每平方米用石灰200克，一共需要石灰多少千克？3、一段圆柱体铝棒，长40厘米，底面积是31.4平方厘米。

专项九立体图形核心考点梳理考点一：长方体和正方体的认识（共3小题）1.用一根长72cm的铁丝正好可以围成一个正方体框架，这个正方体框架的棱长是( )cm。

2.如图，一个长7dm，宽4dm，高2dm的礼盒，用丝带捆扎起来，每个打结处要用1dm长的丝带，总共需要( )dm长的丝带。

3.下面的图形中，( )图沿虚线折叠后不能围成正方体。

A. B. C. D.考点二：长方体和正方体的表面积（共2小题）4.一个正方体的棱长扩大到原来的2倍，那么它的棱长总和将扩大到原来的( )倍，表面积将扩大到原来的( )倍。

5.把12个棱长都是3cm的正方体拼成一个长方体，这个长方体的表面积最大是( )cm2，最小是( )cm2。

考点三：长方体和正方体的体积（共3小题）6.一根长方体木料，长为10dm，横截面是一个面积为25dm2的正方形。

这根木料的体积是( )dm3。

7.加工一个长方体纸盒，长方体纸盒的展开图如图所示，长方体纸盒的体积( )为cm3。

8.一块长方体木料，当它的高减少2dm后，表面积减少72dm2，刚好成为一个正方体。

这个正方体的表面积是( )dm2，体积是( )dm3。

考点四：体积和体积单位、容积和容积单位、体积（容积）单位间的进率及单位换算（共2小题）9.在下面的( )里填上适当的单位。

(1)集装箱的体积大约是80( )。

(2)中国的陆地面积约是960万( )。

(3)游泳池的占地面积约为1500( )，最多可盛水4500( )。

10.在下面的括号里填上合适的数。

0.16dm3=( )mL4080dm3=( )m3400mL=( )L1.08L=( )mL考点五：求不规则物体的体积和观察物体（共3小题）11.根据下图信息，可知黑球的体积是( )立方厘米。

12.一个长方体容器的底面是正方形，容器中水的高度是1dm，如果放入3个体积一样的鸡蛋后（鸡蛋完全浸没在水中），水面高度上升了1cm且无水溢出，要求一个鸡蛋的体积，只需要再知道( )即可。

北师大版六年级数学下册方法技能分类评价10.立体图形的表面积，体积，容积的综合应用一、认真审题，填一填。

（每小题4分，共20分）1.一个棱长是4分米的正方体容器（厚度忽略不计）装满水后，倒入一个底面积是12平方分米的圆锥体容器（厚度忽略不计）里正好装满，这个圆锥体的高是（）分米。

2.一块长方形铁皮，长62.8厘米，宽31.4厘米。

如果用它围成一根圆柱形的管子，这根管子的半径是（）厘米或（）厘米。

3.如图，把一根圆柱形木料截成3段，圆柱的表面积增加了45.12平方厘米，这根木料的底面积是（）平方厘米。

4.一个圆柱的底面直径与圆锥底面直径的1相等，圆锥的高是圆柱2的3倍，圆锥的体积是12 dm3，圆柱的体积是（）dm3。

5.用3个棱长都是2厘米的正方体拼成一个长方体，拼成的这个长方体的表面积是（）平方厘米，体积是（）立方厘米。

二、仔细推敲，选一选。

（每小题5分，共20分）1.下图是由几个棱长是1 cm的正方体搭成的，将这个立体图形的表面涂上红色（底面不涂），只有三面涂上红色的正方体有多少个？有五面涂上红色的正方体有多少个？（）A. 63B. 54C. 31D. 622.下面图（）是圆柱的展开图。

3.下面的四个正方体，（）是用右边的纸折叠而成的。

A B C D4.一个直角三角形，两条直角边的长度分别是4 cm和3 cm，分别绕这两条直角边所在直线旋转一周，都可得到一个圆锥。

这两个圆锥的体积比是（）。

A.3:4B.1:1C.16:9D.9:16三、细心的你，算一算。

（共22分）1.计算下面各图形的表面积。

（单位：cm）（12分）（1）（2）2.计算下面图形的体积。

（10分）四、聪明的你，答一答。

（共38分）1.一个圆柱形蓄水池，从里面量底面直径是20米，深为5米。

（1）要在这个蓄水池的四周和底面抹上水泥，抹水泥部分的面积是多少平方米？（6分）（2）这个蓄水池最多可以蓄水多少吨？（每立方米水重1吨）（8分）2.在一个长100厘米，宽80厘米的长方体水槽中，放入一个长方体的铁块，铁块完全浸入水中时，水面上升了4厘米。

立体图形练习题六年级立体图形是数学中的一个重要概念，在小学六年级的数学学习中占有一席之地。

通过练习立体图形题目，可以帮助学生深入了解立体图形的性质和特点，从而提升其数学思维和解题能力。

本文将提供一些六年级学生常见的立体图形练习题，通过解答这些题目，帮助学生更好地掌握立体图形的知识。

1. 题目一：计算长方体的表面积和体积小明手里有一块长方体砖块，其边长分别为5厘米、8厘米和10厘米。

请帮助小明计算出这个长方体砖块的表面积和体积。

解析：长方体的表面积可通过公式2lw+2lh+2wh计算，其中l、w、h分别代表长方体的长度、宽度和高度。

带入具体数值，可以得到：表面积 = 2 × 5 × 8 + 2 × 5 × 10 + 2 × 8 × 10 = 176平方厘米长方体的体积可通过公式V = lwh计算。

带入具体数值，可以得到：体积 = 5 × 8 × 10 = 400立方厘米因此，这个长方体砖块的表面积为176平方厘米，体积为400立方厘米。

2. 题目二：判断正方体的性质小红手里有一块正方体磁铁，边长为6厘米。

请判断下列说法是否正确，并给出你的理由。

说法一：正方体的表面积等于6个正方形的面积之和。

说法二：正方体的对角线长度等于边长的平方根乘以立方根。

解析：对于说法一，正方体的表面积确实等于6个正方形的面积之和。

正方体有6个面，每个面都是正方形，所以表面积等于6个正方形的面积之和。

对于说法二，正方体的对角线长度并不等于边长的平方根乘以立方根。

正方体的对角线长度可通过勾股定理计算，即对角线长度d = √(边长的平方 + 边长的平方 + 边长的平方) = √3边长。

所以，正方体的对角线长度等于边长的平方根乘以√3，而不是立方根。

因此，说法一是正确的，而说法二是错误的。

3. 题目三：求解棱柱的面积和体积小华手里有一个棱柱，底面为一个边长为4厘米的正三角形，高度为6厘米。

小学人教版六年级下册数学第三单元《圆柱与圆锥》立体图形达标练一、圆柱和圆锥立体图形计算题1．求圆柱的表面积和体积。

2．求下面圆锥的体积。

3．求下面各圆柱的表面积。

（1）（2）4．求①号立体图形的表面积，求②号立体图形的体积。

（单位∶cm）5．求组合图形的表面积和体积。

（单位：厘米）6．计算下图的体积。

（单位：分米）7．求出这个空心水泥管的外表面积。

8．如下图，从圆柱上挖去一个圆锥，求剩下图形的体积。

（单位：厘米）9．如图所示，这个物体的体积是多少？10．求下图组合体的体积。

（单位：dm）参考答案一、圆柱和圆锥计算题1．2×3.14×2×5＝6.28×2×10＝12.56×10＝125.6（cm 2）3.14×22×2＝3.14×4×2＝12.56×2＝25.12（cm 2）125.6＋25.12＝150.72（cm 2）3.14×22×5＝3.14×4×5＝12.56×5＝62.8（cm 3）2． 13×3.14×32×6＝13×9×3.14×6＝3×3.14×6＝56.52（dm 2）3．（1）2×3.14×（20÷2）2＋2×3.14×（20÷2）×3＝6.28×102＋6.28×10×3＝6.28×100＋62.8×3＝628＋188.4＝816.4（m 2）（2）2×3.14×52＋2×3.14×5×12＝6.28×25＋6.25×5×12＝157＋31.4×12＝157＋376.8＝533.8（cm 2）4．① 3.14×(10÷2)2×2﹢3.14×5＋3.14×5×3 ＝157＋157＋47.1＝361.1②3.14×12×3×13＝3.145．（5×3＋5×4＋4×3）×2＋3.14×2×3 ＝（15＋20＋12）×2＋18.84＝47×2＋18.84＝94＋18.84＝112.84（平方厘米）5×3×4＋3.14×（2÷2）2×3＝60＋3.14×1×3＝60＋9.42＝69.42（立方厘米）6．13×3.14×32×（15－9） ＝13×3.14×9×6＝3.14×18＝56.52（立方分米）3.14×32×9＝3.14×81＝254.34（立方分米）56.52＋254.34＝310.86（立方分米）7． 7dm ＝70cm2×3.14×[（22÷2）2－（14÷2）2]＋3.14×22×70 ＝2×3.14×[112－72]＋3.14×22×70＝2×3.14×[121－49]＋3.14×22×70＝2×3.14×72＋3.14×22×70＝3.14×（2×72＋22×70）＝3.14×（144＋1540）＝3.14×1684＝5287.76（cm 2）8． 6÷2＝3（厘米）3.14×32×10－3.14×32×6×13＝3.14×9×10－3.14×9×6×13＝28.26×10－169.56×13 ＝282.6－56.52＝226.08（立方厘米）9．3.14×（22）2×3＝9.42（立方分米） 3.14×（22）2×3＝3.14×12×3＝3.14×3＝9.42（立方分米）10． 13×3.14×（2÷2）2×3×2＋3.14×（2÷2）2×（18－2×3） ＝13×3.14×1×3×2＋3.14×1×（18－6） ＝13×3.14×1×3×2＋3.14×1×12 ＝（13×3）×（3.14×2）＋3.14×12 ＝6.28＋3.14×12＝6.28＋37.68＝43.96（dm 3）。

立体图形综合（一）一、填空题（每题3分，共63分）1.一个长方体，长增加2倍，宽和高不变，体积扩大倍．2.一个底面为正方形的长方体的高增加3cm后成为一个正方体，且表面积增加了48cm2，则原长方体的体积为cm3．3.一个长方体，如果沿水平方向切开，得到两个完全相同的正方体，已知每个正方体的表面积是60平方厘米，则这个长方体的表面积是平方厘米．4.一个底面是正方形的长方体，把它的侧面展开后，正好是一个边长为20厘米的正方形，则这个长方体的体积是立方厘米．5.有一个正方体，如果高增加2厘米，就变成一个长方体，这个长方体的表面积比原来增加了96平方厘米，则原来正方体的表面积为平方厘米．6.用8个棱长1厘米的立方体拼成一个长方体，其中表面积最大的与最小的相差平方厘米．7.用一个平面去截一个长方体，把长方体分为两个多面体，则截面最多会是边形．8.一个长方体正好可以切成3个一样的正方体，切开后每个正方体的表面积是18平方厘米，那么原来这个长方体的表面积是平方厘米．9.一个长9厘米，宽6厘米，高3厘米的长方体，切成3个体积相等的长方体，表面积最大可增加平方厘米．10.一根长3.6米的长方体木料，其中有一组相对的面是正方形，其余四个面的面积之和是7.2平方米，这根木料的体积是立方米．11.长方体的棱长和是216厘米，它的长、宽、高之比为4 : 3 : 2，该长方体的体积是立方厘米．12.一个长方体的长、宽、高恰好是3个连续的自然数，并且它的体积的数值等于它的所有棱长之和的数值的2倍，那么这个长方体的表面积是．13.从三个不同方向看一个长方体，每个方向只能看到长方体的一个面，且看到的三个长方形的面积分别为4、5、20，则该长方体的体积为．14.如图，有一个边长是5的立方体，如果在它的左上方截去一个棱长分别是5、3、2的长方体，那么它的表面积减少了%．15.用一张长24厘米，宽23厘米的长方形铁皮，焊接成一个没有盖子的盒子，则焊接的盒子容积最大是立方厘米．18.如图，在棱长为3的正方体中由上到下，由左到右，由前到后，有三个底面积是1的正方形，高为3的长方体的洞，则所得物体的表面积为．19.将边长为13cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形，如图所示，剩余部分折成一个无盖的长方体盒子，该盒子的容积是cm3．20.有一个深12分米的长方体容器，其内侧底面为边长9分米的正方形，当容器底面的一边紧贴桌面倾斜如图时，容器内的水刚好不溢出，那么容器内的水有升．16. 一个棱长为5米的正方体水箱，箱内盛有水，水深4米，现把一个棱长为3米的正方体沉入水箱底部，水面的高度将是米．17. 从一个长为8厘米．宽为7厘米，高为6厘米的长方体中截下一个最大的正方体，剩下的几何体的表面积最小是平方厘米．21.如图的三个几何体，其中棱柱是（填写序号）．二、解答题（22~26题5分，27~28题6分，共37分）22.把一个长9厘米，宽7厘米，高3厘米的长方体铁块和一个棱长为5厘米的正方体铁块，熔铸成一个底面直径为10厘米的圆柱，为了防锈蚀，要在表面刷上防锈漆，求刷漆的面积是多少？（π取3.14）23.一个长方体如果长增加10厘米，则体积增加75立方厘米；如果宽增加8厘米，则体积增加80立方厘米；如果高增加6厘米，则体积增加72立方厘米，问原长方体的表面积是多少平方厘米？24.图1是边长36厘米的正方形纸板，裁掉阴影部分后将其折叠成如图2所示的长方体盒子，已知该长方体的宽是高的2倍，则它的体积是多少立方厘米？25.如图是一个五棱柱的平面展开图，图中的正方形边长都为4．按图示数据，这个五棱柱的体积为多少？26.一块长方形铁皮（如图），长25厘米，宽15厘米，从四个角分别剪去边长2厘米的小正方形，然后把四周折起来，做成没有盖子的铁盒，请你帮忙计算一下：做这样一个盒子至少需要多少铁皮？铁盒的容积是多少？27. 甲圆柱体容器是空的，乙长方体容器中水深6.28厘米，要将乙容器中的水全部倒入甲容器，这时水面离容器上沿多少厘米？（π = 3.14）28. 如图①，在底面积为100cm2、高为20cm的长方体水槽内放入一个长方体烧杯，以恒定不变的流量速度先向烧杯中注水，注满烧杯后，继续注水，直至注满水槽为止，此过程中，烧杯本身的质量、体积忽略不计，烧杯在大水槽中的位置始终不改变．水槽中水面上升的高度h（厘米）与注水时间t（秒）之间的关系如图②所示．（1）图②中点表示烧杯中刚好注满水，点表示水槽中水面恰与烧杯中水面平齐；（2）求烧杯的底面积；（3）求注水的速度及注满水槽所用的时间．难忘的一天今天，太阳照着大地，就像闪闪发光的金子一样，到处都是暖洋洋的，我的心里也是暖洋洋的。

10.立体图形一、填空。

1.张老师在实验室里把2L药水倒入如右图的两个容器中,刚好都倒满。

已知圆柱形和圆锥形容器的底面积相等,则圆柱形容器的容积是( )L,圆锥形容器的容积是( )L。

2.一根长2米,横截面直径是40厘米的圆柱体木头浮在水面上,小华发现它正好有一半露出水面。

这根木头与水接触面的面积是( )平方厘米。

3.种机器零件,圆柱部分和圆锥部分的体积比是( )。

如果圆柱部分的体积是48立方厘米,这个零件的体积是( )立方厘米。

4.如图,把一个体积为720立方厘米的圆柱形木料削成一个蛇螺,陀螺的体积为( )立方厘米。

5. 一个长6厘米,宽4厘米,高12厘米的长方体牛奶盒,装满牛奶。

笑笑在准备喝牛奶时一不小心把盒子弄歪了,洒出一些牛奶,也就是图中的空白部分。

洒出( )毫升牛奶。

6.一个圆柱形油漆桶的侧面贴着商标纸,圆柱底面直径是10cm,高25cm。

这张商标纸展开后是一个长方形,它的长是( )cm。

7. 一个高45厘米的圆锥体容器,盛满水后再倒入和它等底等高的圆柱体容器里,水面的高度是( )厘米。

8.将一张长12cm、宽6cm的长方形纸片围成一个圆柱,这个圆柱的侧面积是( )cm2。

9.一个圆柱的侧面展开后是边长为6.28厘米的正方形,这个圆柱的高是( )厘米,底面半径是( )厘米。

10.一种小桶装的纯净水大约是8L。

这样的一桶纯净水能全部倒入棱长是40厘米的正方体玻璃缸，水高（）厘米。

11．一个圆柱的底面直径是2厘米,高是3厘米,它的侧面积是( )平方厘米。

二、选择。

1. 有一个长26cm、宽18cm、高0.6cm的物体，它可能是 ( )A.冰箱B.黑板擦C.橡皮D.数学书2.把一个棱长为a厘米的正方体锯成两个相同的长方体,表面积增加( )平方厘米。

A 2aB a2 C.2a2 D.无法确定3. 把一个圆柱的底面平均分成若干个扇形,然后拼成一个近似的长方体,表表面积比原来增加了100平方厘米,圆柱的高是10厘米,那么圆柱的侧面积是( )平方厘米。