小学六年级下数学《立体图形》思维训练

1.看到实物和图形，能够直接辨析出是什么图形。
2.看到实物和图形，能够直接辨析出图形变换的方式。
形象思维
1.运用常见的几何图形的表象及其特征在其几何图形上标出各部分的名称。
2.运用平移、旋转、轴对称在方格纸上设计图案。
3.直观比较常见平面图形（或立体图形）的大小。
1.写出图形的名称并标出各部分名称。
小学数学六年级下册第三单元《总复习-解决问题的策略》思维训练知识点
层级
3C目标
类型
要点
表现
备注
基础性思维
1.认识常用的平面图形和立体图形，知道它们的特征。
2.认识图形的平移、旋转、轴对称，知道它们的特点。
3.运用平移、旋转、轴对称在方格纸上设计图案。
4.学会常见平面图形（周长和面积）和常见立体图形（表面积和体积）的相关计算。
2.能计算平面图形的组合图形的周长和面积以及立体图形的组合图形体的表面积与体积。
1.完成教材和练习册中的有关常见几何图形的计算问题。
2.会做教师提供的新情境下的有关几何图形的计算问题。
3.自己找寻有关几何图形的素材进行测算。
4.计算平面图形的组合图形的周长和面积以及立体图形的组合图形体的表面积与体积。
创新思维
1.选择合理方法或者自己想法解决较复杂的有关几何图形的计算或者应用问题。
2.能用关系图表示常见几何图形间的关系。
3.运用平移、旋转、轴对称设计富有个性的图案。
1.选择合理方法或者自己想法解决较复杂的有关常见几何图形的计算或者应用问题。。
2.迅速提出解决新情境问题的方法和策略。
3.用关系图表示常见几何图形间的关系。
4.运用平移、旋转、轴对称设计富有个性的图案。
5.准确陈述图形的变换方式及变换过程。

六年级下期第一讲 图形题例1 一个长方形(左下图)被分为9个面积不相等的小长方形。

其中A 、B 、C 、D 、E 的面积分别是A ＝160，B ＝172，C ＝215，D ＝240，E ＝300(单位：㎝2)。

原来大长方形的面积是多少平方厘米？(北京市第十一届迎春杯数学竞赛题)解：给大长方形宽上的四个点标上字母（右上图），NP MN ＝C B ＝215172＝54, PQ MN ＝D A ＝240160＝64，所以MN ∶NP ∶PQ ＝4∶5∶6。

设MN 、NP 、PQ 分别为4a 、5b 、6c ，那么原长方形的长＝a A 4＋a C 5＋a E 6＝a 1(4A ＋5C ＋6E )＝a 133。

所以原长方形的面积是a 133×(4＋5＋6)a ＝1995(㎝2)。

例2 如图，阴影部分小正六角星形的面积是16㎝2。

问：大正六角形的面积是多少平方厘米？(第五届“华杯赛”决赛题)解：小正六角星形可以分成12个相等的小正三角形，每个小正三角形的面积是16÷12＝131(㎝2)。

围绕小正六角星形的正六边形比小六角星形大了6个小等边三角形，每个小等边三角形的面积等于一个小正三角形的面积，所以正六边形的面积是16＋131×6＝24(㎝2)，而大正六角星形面积等于正六边形面积的2倍，是24×2＝48(㎝2)。

例3 如左下图，将三角形ABC 的BA 边延长1倍到D ，CB 边延长2倍到E ，AC 边延长3倍到F 。

如果三角形ABC 的面积等于1，那么三角形DEF 的面积是多少？(北京市第一届“迎春杯”数学竞赛题)D DA AC CB BE F E F解：连结CD 、AE 、BF 如右上图，那么△ACD ＝△ABC ＝1，△ADE ＝△ABE ＝2，A B CD E M N P Q A B C D E△CDF ＝△CBF ＝3，△BEF ＝6，所以，△DEF ＝1×2＋2×2＋3×2＋6＝18。

六年级思维训练教案第一章：逻辑思维训练1.1 教学目标：让学生理解逻辑思维的基本概念。

培养学生运用逻辑思维解决问题的能力。

1.2 教学内容：逻辑思维的定义与重要性。

基本逻辑思维方法：比较、分类、归纳、演绎。

1.3 教学活动：导入：通过有趣的故事引出逻辑思维的概念。

讲解：讲解逻辑思维的定义与重要性。

实践：分组讨论，让学生运用基本逻辑思维方法解决问题。

第二章：创新思维训练2.1 教学目标：让学生理解创新思维的基本概念。

培养学生运用创新思维解决问题的能力。

2.2 教学内容：创新思维的定义与重要性。

基本创新思维方法：发散思维、逆向思维、联想思维。

2.3 教学活动：导入：通过有趣的案例引出创新思维的概念。

讲解：讲解创新思维的定义与重要性。

第三章：批判性思维训练3.1 教学目标：让学生理解批判性思维的基本概念。

培养学生运用批判性思维评估与分析问题的能力。

3.2 教学内容：批判性思维的定义与重要性。

基本批判性思维方法：质疑、分析、评价、建议。

3.3 教学活动：导入：通过有趣的案例引出批判性思维的概念。

讲解：讲解批判性思维的定义与重要性。

实践：分组讨论，让学生运用基本批判性思维方法评估与分析问题。

第四章：数学思维训练4.1 教学目标：让学生理解数学思维的基本概念。

培养学生运用数学思维解决问题的能力。

4.2 教学内容：数学思维的定义与重要性。

基本数学思维方法：计算思维、几何思维、逻辑思维。

4.3 教学活动：导入：通过有趣的数学问题引出数学思维的概念。

讲解：讲解数学思维的定义与重要性。

第五章：跨学科思维训练5.1 教学目标：让学生理解跨学科思维的基本概念。

培养学生运用跨学科思维解决问题的能力。

5.2 教学内容：跨学科思维的定义与重要性。

基本跨学科思维方法：整合思维、跨界思维、创新思维。

5.3 教学活动：导入：通过有趣的跨学科案例引出跨学科思维的概念。

讲解：讲解跨学科思维的定义与重要性。

实践：分组讨论，让学生运用基本跨学科思维方法解决问题。

分析：外侧表面积为：6×10×10-4×4×4- ×22×2=536-8
内侧表面积为：16×4×3+2×(4×4- ×22)+2×2 ×2×3=192+32-8 +24 =224+16 ．
总表面积=224+16 +536-8 =760+8 =785.12(平方厘米)．
计算体积时将挖空部分的立体图形取出，如图，只要求出这个几何体的体积即可．挖出的几何体体积为：
3·如右图所示，圆锥形容器内装的水正好是它容积的 ，水面高度是容器高度的几分之几？
4·皮球掉进一个盛有水的圆柱形水桶中。皮球的直径为15厘米，水桶底面直径为60厘米。皮球有 的体积浸在水中（见右图）。问皮球掉进水中后，水桶中的水面升高了多少厘米？
分析：皮球的体积是： （立方厘米）；皮球浸在水中的部分是： （立方厘米）；水桶的底面积是： （平方厘米）；水面升高的高度是： （厘米）。
立体图形思维训练
教学目标
立体图形，主要考点集中在不规则形体的表面积与体积计算。其中有自成一类的“染色问题”，也是经常见到的“几何奥数题”。
小学阶段，我们除了学习平面图形外，还认识了一些简单的立体图形，如长方体、正方体（立方体）、直圆柱体，直圆锥体、球体等，并且知道了它们的体积、表面积的计算公式，归纳如下。
（3）如右图，在40×20的长方形铁皮的左右两侧各割下一条宽为5厘米的长方形铁皮(共二块)，分别焊到上、下的中间部分，这样做成的无盖铁皮盒的长=40-5-5-5-5=20(厘米)，宽=20(厘米)，高=5(厘米)，体积=20×20×5=2000(立方厘米)．因此，最后一种容积最大．
法2：你要想使容积最大，就要充分利用手中的铁皮，如果能将铁皮都用上那么就能得到一个最大的铁盒。如下图（1），我们从原铁皮上切割下4块5×20的长方体，如图（2），将其焊接上能做成一只深是5厘米的长方体无盖铁皮盒，那么此时的容积最大：20×20×5=2000(立方厘米)．

六年级数学思维训练教材
———————————————————————————————— 作者：
———————————————————————————————— 日期：
ﻩ
第一讲 立体图形及展开
同学们在五年级所学习的立体图形主要是长方体和正方体，从这一讲开始我们将一起研究数学竞赛中经常出现的有关长方体和正方体的问题，帮助大家提高观察能力和空间想像能力，以及掌握解答问题的技巧和方法。这一讲我们进一步研究长方体和正方体的特征及展开图
例题选讲
例1:如图,一个长方体木块,从上部和卞靠分别截去高2厘米和3厘米的长方体后,便成为一个正方体，表面积减少了1０0平方厘米，原来长方体的体积是多少立方
厘米?
【分析与解答】仔细观察右图,截去上下两个长方体后减少的表面积就是两个长方体的侧面积，也就相当于减少的是高为(2＋3)厘米的长方体的侧面积,因此高为5厘米的长方体每个侧面积是1０0÷4—25(平方厘米),那么长方体底面正方形的边长就是25÷Байду номын сангаас=5（厘米),所以原长方体的体积是：5×5×(2+5＋3)＝250（立方厘米)。
例2:一只小虫从图l所示的长方体上的A点出发，沿长方体的表面爬行,依次经过前面、上面、后面、底面,最后到达P点。请你为它设计一条最短的爬行路线。
【分析与解答】 因为小虫在长方体的表面爬行，所以我们可以将长方体的前、后、上、下西个面展开成平面图形（如图２)。又因为在平面上“两点之间的线段长度最短”,所以连接ＡP，则线段AＰ为小虫爬行的最短路线。
例题选讲
例1:图1所示的是一个正方体纸盒拆开后平摊在桌面上的形状。如果将这个展开图恢复成原来的正方体,图中的点F、点G分别与哪个点重合?
【分析与解答】为了研究方便，我们将正方体六个面分别标上序号1、２、3、4、５、6,如果将ｌ作为底面,那么4就是后面,５为右面,６为前面，2则是左面，3就是上面,(如图2)。从图中不难看出点Ｆ与点N,重合,点G与点S重合。还有一种方法就是动手制作一张展开图，折一折，结果就一目了然了,同学们不妨试试吧!

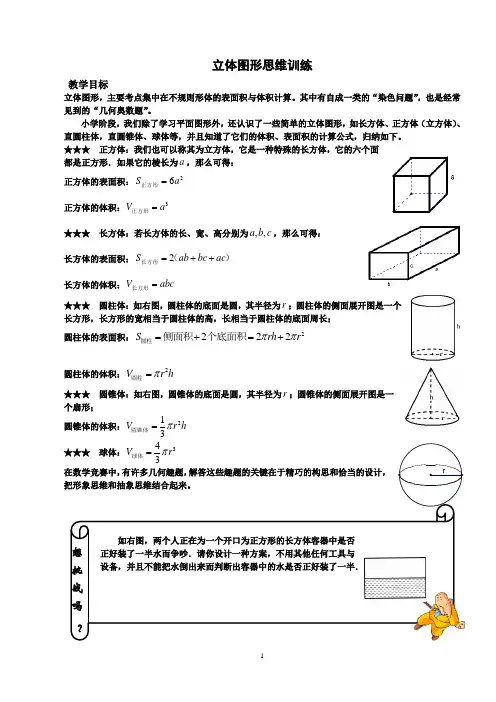
立体图形复习★知识概要一、立体图形的观察1、三视图2、小方块的数量二、棱长和：1、正方体的棱长和：棱长×122、长方体的棱长和：（长+宽+高）×4三、表面积1、正方体的表面积2、长方体的表面积3、圆柱的表面积四、体积1、长方体和正方体的体积2、圆柱和圆锥的体积五、图形的切割和拼接1、长方体，正方体，圆柱和圆锥的切割和拼接2、长方体和正方体表面染色问题六、水中浸物1、浸入水中物块的体积=上升水的体积例1、（1）如图是由五个相同的小正方体搭成的几何体，它的主视图是（）解答：B（2）由n个相同的小正方体堆成的几何体，其视图如下所示，则n的最大值是（18 ）解答：标数法，先在俯视图上把主视图和左视图信息标数演练1、（1）由一些大小相同的小正方体搭成的几何体的俯视图如右图所示，其正方形中的数字表示该位置上的小正方体的个数，那么该几何体的主视图是（B ）。

（2）小华用一些小正方体搭了一个立体图形，这个立体图形从不同方向看到的图形如下。

小华搭这个立体图形至少用了( 8 )个小正方体。

解答：标数法，先在俯视图上把主视图和左视图信息标数例2、（1）现有一根长150厘米的铁丝，用这根铁丝焊接成一个正方体框架，还剩6厘米铁丝，这个正方体框架的棱长是多少厘米？（接头处忽略不计）解答：正方体的总共棱长和：150-6=144（厘米）每条棱长：144÷12=12（厘米）（2）用两个相同的正方体木块拼成一个长方体，棱长之和减少了24厘米，这两个正方体木块原来的棱长总和是多少？解答：两个相同的正方体木块拼成一个长方体，棱长之和减少了8条棱长1条棱长：24÷8=3（厘米）棱长总和：3×12×2=72（厘米）演练2、（1）、一根铁丝，可以做成长8厘米，宽6厘米，高4厘米的长方体框架，如果用它来做一个正方体框架，做成的正方体框架棱长是多少厘米？解答：总共的棱长和：（8+6+4）×4=72（厘米）正方体每天棱长：72÷12=6（厘米）（2）一个长方体木块被截成了两个完全相同的正方体，两个正方体的棱长之和比原来长方体的棱长之和增加了16厘米，求原来长方体的长是多少厘米？解答：长方体木块被截成了两个完全相同的正方体，两个正方体的棱长之和比原来长方体的棱长之和增加了8个正方体的棱长。

（2）如果沿经过中轴线 AB 的平面切一刀，将该蛋糕分成完全相同的两部分，那表面积 之和又是多少？
【分析】 （1） 蛋糕的表面积为：
2 π1 2
1
2 π1 1
2π3 2
1
2
π23
2
10.5
π32.97
（平方分米）
（2）
新切一刀，表面积增加了
2
2
1 2
2
1
2
3 2
12
，则现在的表面积变为
44.97
【分析】 （1）每一次拼合会少两个面，拼了 3 次，表面积之和少了 32 1 6 平方厘米； （2）原正方体的表面积为 6 1 6 ，且一刀会增加两个面，增加的面积为 2，则两部分的表
面积之和为 8；根据图 2，总共切了 5 刀，表面积增加了 10，则这 18 块长方体的表面积 总和为 16。 （第四届华杯赛初赛第 3 题） 7、如图所示，有一个圆柱和一个圆锥，它们的高和底面直径标在图上，单位是厘米。请问：
超越篇
1、有一个棱长为 20 的大立方体，在它的每个角上按如图所示的方式各做一个小立方体， 于是得到 8 个小立方体。在这些立方体中，上面 4 个的棱长为 12，下面 4 个的棱长为 13。请问：所有这 8 个小立方体公共部分的体积是多少？
【分析】上面四个立方体的公共部分是一个长方体，其底面积为一个正方形，底面边长为
7、一个无盖木盒从外面量时，其长、宽、高分别为 10 厘米、8 厘米、5 厘米。已知木板厚 1 厘米，那么做一个木盒，需要这样的木板多少平方厘米？这个木盒的容积又是多少？
【分析】由于此无盖木盒的外部体积为 810 5 400 立方厘米，而木盒的容积为192 立方
厘米。则根据题意，可知需要这样的木板 400 1921208 立方厘米。

２０14年六年级数学思维训练：立体几何一、兴趣篇1.一个长方体的长、宽、高分别为3厘米、2厘米、1厘米.若它的棱长总和等于另一个正方体的棱长总和，则长方体与正方体的表面积之比是多少？长方体体积比正方体体积少多少立方厘米？２.如图,将长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长为2厘米的正方形，然后沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米?如果四角去掉边长为3厘米的正方形呢?3.用棱长是1厘米的小立方体拼成如图所示的立体图形,这个图形的表面积是多少平方厘米?4.(1)如图1，将一个棱长为6的正方体从某个角切掉一个长、宽、高分别为４、３、5的长方体，剩余部分的表面积是多少？（２）如图2，将一个棱长为５的正方体，从左上方切去一个长、宽、高分别为5、4、３的长方体，它的表面积减少了百分之几?5．（201３•北京模拟)如图是一个边长为2厘米的正方体.在正方体的上面的正中向下挖一个边长为1厘米的正方体小洞;接着在小洞的底面正中再向下挖一个边长为厘米的小洞;第三个小洞的挖法与前两个相同,边长为厘米.那么最后得到的立体图形的表面积是多少平方厘米？6．（20１2•北京模拟）(1)如图，将4块棱长为1的正方体木块排成一排,拼成一个长方体．那么拼合后这个长方体的表面积,比原来４个正方体的表面积之和少了多少?（2)一个正方体形状的木块,棱长为1，如图所示，将其切成两个长方体,这两部分的表面积总和是多少？如果在此基础上再切4刀,将其切成大大小小共1８块长方体.这1８块长方体表面积总和又是多少？7.这里有一个圆柱和一个圆锥（如图)，它们的高和底面直径都标在图上，单位是厘米.请回答:圆锥体积与圆柱体积的比是多少?８．如图,一块三层蛋糕,由三个高都为１分米,底面半径分别为1．５分米、１分米和０．５分米的圆柱体组成.请问：（1)这个蛋糕的表面积是多少平方分米？（л取3.1４）（2)如果沿经过中轴线ＡＢ的平面切一刀,将该蛋糕分成完全相同的两部分，那表面积之和又是多少?9．有大、中、小三个立方体水池,它们的内部棱长分别是6米、3米、2米，三个池子都装了半池水．现将两堆碎石分别沉没在中、小水池的水里，两个水池的水面分别升高了６厘米和４厘米．如果将这两堆碎石都沉没在大水池的水里，大水池的水面会升高多少厘米?(结果精确到小数点后两位）１0．有一个高24厘米,底面半径为10厘米的圆柱形容器，里面装了一半水,现有一根长30厘米,底面半径为2厘米的圆柱体木棒．将木棒竖直放入容器中,使棒的底面与容器的底面接触,这时水面升高了多少厘米？二、拓展篇1１．将表面积分别为54、96和１５０平方厘米的三个铁质正方体熔成一个大正方体(不计损耗),求这个大正方体的体积．１2．（201２•深圳校级模拟)一个长方体,如果长增加２厘米，则体积增加4０立方厘米;如果宽增加3厘米,则体积增加90立方厘米;如果高增加4厘米，则体积增加96立方厘米．求原长方体的表面积．1３．如图,有30个棱长为１米的正方体堆成一个四层的立体图形．请问：这个立体图形的表面积等于多少？１4.如图1,将一个棱长为10的正方体从顶点A切掉一个棱长为4的正方体,得到如图2的立体图形,这个立体图形的表面积是多少？如果再从顶点B切掉一个棱长为6的正方体,那么剩下的立体图形的表面积又是多少?15．一个正方体被切成24个大小形状一模一样的小长方体(如图)，这些小长方体的表面积之和为162平方厘米.请问:原正方体的体积是多少？16．如图是一个棱长为４厘米的正方体，分别在前、后、左、右、上、下各面的中心位置挖去一个棱长1厘米的小正方体，做成一种玩具．该玩具的表面积是多少平方厘米？如果把这些洞都打穿，表面积又变成了多少?17.一个无盖木盒从外面量时,其长、宽、高分别为1０厘米、8厘米、5厘米,已知木板厚1厘米，那么做一个木盒,需要这样的木板多少平方厘米？这个木盒的容积又是多少?1８．有一根长为20厘米,直径为6厘米的圆钢,在它的两端各钻一个４厘米深，底面直径也为6厘米的圆锥形的孔,做成一个零件（如图).这个零件的体积为多少立方厘米?（л取3.14）１9．现有一块长、宽、高分别为10厘米、8厘米、6厘米的长方体木块,把它切成体积尽可能大且底面在长方体表面上的圆柱体木块，这个圆柱体木块的体积为多少?（л取3) 20．张大爷去年用长２米宽1米的长方形苇席围成容积最大的圆柱形粮囤，今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形粮囤.今年粮囤的容积是去年粮囤容积的多少倍？２1．左边正方形的边长为4,右边正方形对角线长度为６．如果按照图中的方式旋转,那么得到的两个旋转体的体积之比是多少?22．如图一个底面长30分米，宽10分米，高12分米的长方体水池,存有四分之三池水，请问：（1）将一个高1 1分米，体积３30立方分米的圆柱放入池中，水面的高度变为多少分米? (2）如果再放人一个同样的圆柱，水面高度又变成了多少分米?(3)如果再放人一个同样的圆柱,水面高度又变成了多少分米？三、超越篇２3．有一个棱长为20的大立方体,在它的每个角上按如图的方式各做一个小立方体，于是得到８个小立方体．在这些立方体中,上面4个的棱长为12，下面4个的棱长为13．请问：所有这８个小立方体公共部分的体积是多少?24.地上有一堆小立方体,从上面看时如图1，从前面看时如图2，从左边看时如图３.这一堆立方体一共有几个?如果每个小立方体的棱长为1厘米，那么这堆立方体所堆成的立体图形表面积为多少平方厘米？25.(1)已知一个圆柱的底面直径为6厘米,高为4厘米．求它的体积和表面积;（答案用兀表示）(２)用一个半径为2５厘米,圆心角为3４５.6°的扇形围成一个圆锥，这个圆锥的体积是多少?如果圆心角是216°呢？(答案用丌表示)26．将图１、图2中的平面图形分别折叠成一个四棱锥和三棱柱,这两个立体图形的体积分别是多少?（图1正中央是一个面积为１8平方厘米的正方形，每边上分别有一个腰长为5厘米的等腰三角形;图2中的图形由三个长方形和两个直角三角形组成.）27.一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,如图圆柱体的底面直径和高都是12厘米,其内有一些水，正放时水面离容器顶１1厘米，倒放时，水面离顶部5厘米．请问:这个容器的容积是多少立方厘米?(兀取3.１４）28.有一个长方体水池，底面为边长６0厘米的正方形,里面插着一根长1米的木桩，木桩的底面是一个边长15厘米的正方形,木桩有一部分浸在水中，一部分露出水面.现在将木桩提起来2４厘米(仍有部分浸在水里），那么露出水面的木桩浸湿部分面积为多少平方厘米？29．右图是个有底无盖的容器的平面展开图，其中①是边长为18厘米的正方形,②③④⑤是同样大的等腰直角三角形，⑥⑦⑧⑨是同样大的等边三角形．那么，这个容器的容积是毫升.30.有一个三棱柱和一个正方体,三棱柱的底面是一个等边三角形,边长恰好等于正方体的面对角线长度,三棱柱的高恰好等于正方体的体对角线长度,如果正方体的棱长为6,那么三棱柱的体积为多少？ﻬ２0１4年六年级数学思维训练：立体几何参考答案与试题解析一、兴趣篇1.一个长方体的长、宽、高分别为3厘米、2厘米、1厘米.若它的棱长总和等于另一个正方体的棱长总和，则长方体与正方体的表面积之比是多少？长方体体积比正方体体积少多少立方厘米?【分析】首先根据长方体的棱长总和=（长+宽＋高）×4,求出棱长总和,用棱长总和除以１2求出正方体的棱长,再根据长方体的表面积公式:ｓ=(ab+ah＋bｈ)×2，正方体的表面积公式：s=６a2,长方体的体积公式：v=abh,正方体的体积公式:v=a3,把数据分别代入公式解答.【解答】解：（３+2+1）×4÷1２＝6×4÷12=２4÷1２＝２（厘米），（３×2＋3×1+2×1）×2:（２×2×6)＝11×２：24=22：24=1１：１2；２×2×2﹣３×2×1＝8﹣6=２(立方厘米）,答:长方体与正方体的表面积之比是1１：12,长方体体积比正方体体积少２立方厘米.2．如图,将长为13厘米，宽为９厘米的长方形硬纸板的四角去掉边长为2厘米的正方形，然后沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米？如果四角去掉边长为3厘米的正方形呢？【分析】先根据题意计算出折成的长方体的长，宽，高,即长方体的长=原长方形的长﹣２个正方形的边长，长方体的宽=原长方形的宽﹣2个正方形的边长,长方体的高=正方形的边长,再根据长方体的容积=长×宽×高,计算出容积．【解答】解：长方体的长:13﹣2﹣２＝９(厘米）长方体的宽：９﹣2﹣2=5（厘米)容积为：9×5×2=９０（立方厘米）答：这个容器的容积为９0立方厘米.如果四角去掉边长为3厘米的正方形:长方体的长：13﹣３﹣３=7(厘米）长方体的宽：9﹣3﹣3=３(厘米）容积为：7×3×3=63（立方厘米)答：这个容器的容积为63立方厘米．3.用棱长是1厘米的小立方体拼成如图所示的立体图形，这个图形的表面积是多少平方厘米?【分析】可以从上下左右前后观察各有几个正方形的面，然后用一个正方形的面的面积乘它的个数,即是这个图形的表面积，据此解答．【解答】解:上、下共:9+9=1８(个），左、右共：７+7＝１4(个），前、后共：７+7＝1４(个),表面积:1×1×（18+14+14）,＝4６（平方厘米）；答：这个图形的表面积是4６平方厘米．4．(１)如图1，将一个棱长为6的正方体从某个角切掉一个长、宽、高分别为4、3、5的长方体,剩余部分的表面积是多少？(2)如图2,将一个棱长为５的正方体，从左上方切去一个长、宽、高分别为５、4、３的长方体，它的表面积减少了百分之几?【分析】图１由图意可知，减少的面积的和新增的面的面积相等,所以剩余部分的表面积就是原来长方体的表面积．图2由图意可知，减少的是长是４,宽是3的两个长方形的面积，用减少的面积除以正方体的表面积即可.【解答】解:（１）６×6×6=2１6答:剩余部分的表面积是216.（2)２×4×3÷（5×5×6)=2４÷15０=16％答:它的表面积减少了16%.5.（20１3•北京模拟）如图是一个边长为2厘米的正方体.在正方体的上面的正中向下挖一个边长为1厘米的正方体小洞;接着在小洞的底面正中再向下挖一个边长为厘米的小洞；第三个小洞的挖法与前两个相同,边长为厘米.那么最后得到的立体图形的表面积是多少平方厘米？【分析】立体图形的好处就是可以直观视觉,虽然图形被挖去，但６个面看过去都还是面积不变的,特别是从上往下看是,3个正方体的下底面剩下的面积和等于原来的面积,这样就只增加了3个小正方体的各自的侧面;计算出原表面积再加上增加的3个小正方体的各自侧面的面积就是最后得到的立体图形的表面积.【解答】解：原正方体的表面积是:2×2×6＝24(平方厘米)，增加的面积：1×1×4+(×）×4+（×）×4，=４+×４+×4,=４+1+，=５（平方厘米),总表面积为:24＋５=29(平方厘米).答:最后得到的立体图形的表面积是29平方厘米．6．（２012•北京模拟）(1）如图,将4块棱长为1的正方体木块排成一排，拼成一个长方体.那么拼合后这个长方体的表面积，比原来4个正方体的表面积之和少了多少？（２)一个正方体形状的木块,棱长为１，如图所示，将其切成两个长方体,这两部分的表面积总和是多少？如果在此基础上再切４刀，将其切成大大小小共18块长方体．这18块长方体表面积总和又是多少?【分析】（1）观察图形可知,拼组后的长方体的表面积比原来减少了6个小正方体的面的面积，由此即可解答；（２)每切一刀，就增加2个正方体的面，所以这两部分的表面积之和就是８个正方体的面的面积之和;在此基础上再切４刀后，表面积比原来又增加了8个小正方体的面,由此即可解答．【解答】解：(1)6×１×1＝6，答：拼组后表面积减少了6.（２)切一刀，得到的两个长方体的表面积之和是：1×1×(６+2）＝8;再切4刀,则表面积之和是:１×1×（6+10)=16；答:切一刀后，表面积之和是8，再切４刀后，表面积之和是1６.７.这里有一个圆柱和一个圆锥(如图),它们的高和底面直径都标在图上,单位是厘米．请回答：圆锥体积与圆柱体积的比是多少?【分析】利用Ｖ=ｓh求得圆锥的体积,Ｖ=sh求得圆柱的体积，依此可得圆锥体积与圆柱体积的比.【解答】解：圆锥体积:圆柱体积=（×３.1４×22×4)：(3.14×４2×８）=（×2２×4)：(42×８)=１：２4；答：圆锥体积与圆柱体积的比是１：２4.8．如图，一块三层蛋糕,由三个高都为１分米，底面半径分别为１.５分米、１分米和0.5分米的圆柱体组成.请问:（1）这个蛋糕的表面积是多少平方分米？（л取3.１４)（2)如果沿经过中轴线AB的平面切一刀，将该蛋糕分成完全相同的两部分,那表面积之和又是多少？【分析】由题意可知:这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积，根据公式计算即可．如果沿经过中轴线AB的平面切一刀,将该蛋糕分成完全相同的两部分，那表面积之和圆柱的表面积加上３个长方形的面积乘以2即可．【解答】解（1）大圆柱的表面积：3.14×１.５2×2＋2×3．１4×1.5×1,=14.13+9.42，=２3.55(平方米),中圆柱侧面积:2×3.１4×1×1＝6．28（平方米）,小圆柱侧面积：2×３.1４×0．5×1=３.１4（平方米）,这个物体的表面积:23.55+6.28+3.１4＝32.97（平方米);答:这个物体的表面积是32.97平方米.(2)(1×0.5+１×1＋1×１．５)×2+32.９7=６＋3２．97＝３8．97(平方分米）答:将该蛋糕分成完全相同的两部分，那表面积之和是38.9７平方分米.9．有大、中、小三个立方体水池,它们的内部棱长分别是６米、3米、2米，三个池子都装了半池水.现将两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米.如果将这两堆碎石都沉没在大水池的水里,大水池的水面会升高多少厘米？(结果精确到小数点后两位）【分析】根据题意，因为把碎石沉没在水中，水面升高所增加的体积，就等于所沉入的碎石的体积，所以应先求出两块碎石的体积.沉入在中水池的碎石的体积，即3×3×0.０6=0.5４（米３），而沉入小水池中的碎石的体积是：2×２×0.04=0.16(米3）；然后求出两块碎石的体积和,再根据大水池的底面积，求出大水池的水面升高的高度,解决问题．【解答】解：6厘米＝０.06米4厘米=0．04米3×3×0.06＝0.５4（米3）２×2×0.04=0.1６（米３）0.５4+０.16＝0.7(米3)大水池的底面积是:6×6=36(米3)大水池的水面升高了:０.7÷３6=（米）米≈１．94(厘米)．答：大水池的水面大于会升高1.9４厘米．１0.有一个高２４厘米，底面半径为10厘米的圆柱形容器,里面装了一半水，现有一根长30厘米,底面半径为2厘米的圆柱体木棒．将木棒竖直放入容器中，使棒的底面与容器的底面接触，这时水面升高了多少厘米?【分析】放入圆柱体木棒前后的水的体积不变，根据原来水深２4÷2=12厘米,可以先求得水的体积，那么放入圆柱体木棒后，容器的底面积变小了,由此可以求得此时水的深度,进一步即可求解．【解答】解:［3.14×10２×（２4÷2）]÷(3.14×1０2﹣３．１4×2２）=(3.14×１200)÷（3．14×96)=１２0０÷９6=12.5(厘米)12.5﹣2４÷2=１2.５﹣1２=０．５（厘米)．答:这时水面升高了0.5厘米．二、拓展篇１1.将表面积分别为5４、９6和150平方厘米的三个铁质正方体熔成一个大正方体（不计损耗)，求这个大正方体的体积．【分析】因为正方体的每一个面的面积相等,所以这三个正方体的每一个面面积是9、16、25平方厘米.故三个正方体的棱长分别是３、4、5厘米．则大正方体的体积只需将三个正方体的体积相加即可．【解答】解:５4÷6＝９（平方厘米),因为3×3＝9,所以这个正方体的棱长是３厘米,9６÷6=１6(平方厘米)，因为4×4＝16，所以这个正方体的棱长是４厘米,150÷6＝２5（平方厘米)，因为5×5=2５,所以这个正方体的棱长是5厘米,33＋4３+53,=2７+64+125，=２1６（立方厘米）,答:这个大正方体的体积是２1６立方厘米．12.(2０１2•深圳校级模拟）一个长方体,如果长增加2厘米,则体积增加４0立方厘米；如果宽增加3厘米，则体积增加90立方厘米；如果高增加４厘米,则体积增加96立方厘米．求原长方体的表面积.【分析】由题意,长增加2厘米,体积增加４0立方厘米，可知宽×高×2=40立方厘米,则宽×高＝20平方厘米．同理可知长×高=30平方厘米,长×宽=24平方厘米，根据长方体的表面积=（长×宽+长×高+宽×高）×２.列式解答．【解答】解：长增加2厘米,体积增加4０立方厘米，可知宽×高×2=4０立方厘米,则宽×高=20平方厘米．同理可知长×高=９0÷3＝30平方厘米,长×宽=９６÷4＝24平方厘米,（长×宽+长×高＋宽×高)×2＝（24+30＋20）×2,=74×２，＝14８(平方厘米）；答：原长方体的表面积是１4８平方厘米．1３.如图,有3０个棱长为1米的正方体堆成一个四层的立体图形.请问：这个立体图形的表面积等于多少?【分析】这个几何体的表面积就是露出小正方体的面的面积之和，从上面看有１6个面;从下面看有1６个面;从前面看有10个面;从后面看有1０个面；从左面看有1０个面；从右面看有10个面．由此即可解决问题．【解答】解:图中几何体露出的面有：10×4+16×２=72（个）所以这个几何体的表面积是:１×１×72=72(平方米)答：这个立体图形的表面积等于7２平方米.1４．如图1,将一个棱长为10的正方体从顶点A切掉一个棱长为４的正方体,得到如图2的立体图形,这个立体图形的表面积是多少?如果再从顶点B切掉一个棱长为6的正方体，那么剩下的立体图形的表面积又是多少？【分析】将原正方体切去一个小正方体后，减少的表面积正好被新增加的表面积所补充，因此新的立体图形的表面积就等于原正方体的表面积，根据正方体的表面积公式即可求解,如果再从顶点B切掉一个棱长为6的正方体，那么剩下的立体图形的表面积是原正方体的表面积﹣边长是4的两个正方形的面积．【解答】解:１０×1０×6=6０0答:这个立体图形的表面积是60０.如果再从顶点Ｂ切掉一个棱长为6的正方体，剩下的立体图形的表面积为:10×10×６﹣4×4×２=6０0﹣3２=568答:剩下的立体图形的表面积是５68．1５.一个正方体被切成2４个大小形状一模一样的小长方体(如图),这些小长方体的表面积之和为1６2平方厘米.请问：原正方体的体积是多少？【分析】由题意，一个正方体被切成２4个大小形状一模一样的小长方体,则需要切6次,每次会增加两个答正方体的面，所以共增加12个大正方体的面，又知这些小长方体的表面积之和为162平方厘米,即原来大正方体的6＋１2=18个面的面积是1６2平方厘米,由此可求得一个面的面积，进而得到大正方体的棱长,再根据正方体的体积公式解答即可.【解答】解：一个正方体被切成24个大小形状一模一样的小长方体,则需要切６次,共增加12个大正方体的面，一个面的面积:１6２÷(１2+6)＝９（平方厘米），因为３×3=９，所以可知大正方体的棱长是3厘米,大正方体的体积：3×3×３=27(立方厘米），答:原正方体的体积是2７立方厘米.16．如图是一个棱长为４厘米的正方体，分别在前、后、左、右、上、下各面的中心位置挖去一个棱长1厘米的小正方体，做成一种玩具.该玩具的表面积是多少平方厘米?如果把这些洞都打穿,表面积又变成了多少？【分析】这个玩具的表面积是大正方体的面积,加上6个边长为1厘米的小正方体的4个侧面的面积,如果把这些洞都打穿，表面积增加4个边长4厘米的小正方体的4个侧面的面积,据此解答即可.【解答】解:玩具的表面积:4×4×6+1×１×６×4=9６+２４＝120(平方厘米）如果把这些洞都打穿,表面积:4×４×６﹣6+1.5×1×４×6=9０+３６=126（平方厘米）答：它的表面积是12０平方厘米．如果把这些洞都打穿,表面积变成了1２6平方厘米．１7.一个无盖木盒从外面量时，其长、宽、高分别为1０厘米、8厘米、5厘米，已知木板厚１厘米，那么做一个木盒,需要这样的木板多少平方厘米?这个木盒的容积又是多少?【分析】如下图:假设用长10厘米，宽8厘米，厚1厘米的木板作底面，那么4个侧面的木板的高就是（5﹣1）厘米,如果前后面用长10厘米,宽4厘米的木板,那么左右面的木板长是(8﹣1﹣１)厘米,左右面木板的宽也是4厘米．然后根据长方体表面积的计算方法，求这5个面的总面积即可．木盒里面的长是(１0﹣1﹣1)厘米，宽是（8﹣1﹣１)厘米,高是（5﹣1)厘米,再根据长方体的容积（体积）公式解答.【解答】解:如图:根据分析:4个侧面的木板的宽是:5﹣１＝4（厘米)１0×8＋10×4×2+(8﹣1﹣１)×４×2＝80+80＋6×4×2=160+48=2０8(平方厘米)(10﹣1﹣1)×(8﹣１﹣１）×(5﹣1)=8×6×4=192（立方厘米)答:做这个木盒至少需用1厘米厚的木板２０８平方厘米.这个木盒的容积是192立方厘米．１８.有一根长为２0厘米，直径为6厘米的圆钢,在它的两端各钻一个4厘米深，底面直径也为6厘米的圆锥形的孔，做成一个零件(如图).这个零件的体积为多少立方厘米？（л取３．14）【分析】根据题意可知：这个零件的体积等于圆柱的体积减去两个圆锥的体积，根据圆柱的体积公式:v＝sｈ，圆锥的体积公式:ｖ=，把数据分别代入公式解答即可．【解答】解：3．14×（6÷2)２×4×2==５65．２﹣7５.３6＝489.84（立方厘米),答：这个零件的体积为４89．84立方厘米.１9.现有一块长、宽、高分别为１0厘米、8厘米、６厘米的长方体木块，把它切成体积尽可能大且底面在长方体表面上的圆柱体木块,这个圆柱体木块的体积为多少?(л取3)【分析】削出最大的圆柱的方法有三种情况：(1）以8厘米为底面直径,6厘米为高;（2）以6厘米为底面直径,８厘米为高;（3）以6厘米为底面直径，10厘米为高,由此利用圆柱的体积公式分别计算出它们的体积即可解答.【解答】解:(1）以８厘米为底面直径,６厘米为高，３×（8÷2)２×6=３×1６×６＝2８8（立方厘米）;（2）以6厘米为底面直径,8厘米为高;3×(6÷2)2×8=３×9×8=216（立方厘米）；（3)以6厘米为底面直径，10厘米为高,３×（6÷２）2×１０＝3×9×10=２70(立方厘米）;答:这个圆柱最大的体积是288立方厘米．20.张大爷去年用长２米宽1米的长方形苇席围成容积最大的圆柱形粮囤，今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形粮囤．今年粮囤的容积是去年粮囤容积的多少倍?【分析】依据经验可得:用长方形的长作底面周长,宽作高，围成的圆柱的容积最大,据此利用圆柱的体积公式即可得解．【解答】解：π××２÷[π××1]=×2÷＝÷=4.５倍;答：今年粮囤的容积是去年粮囤容积的４．5倍．２1．左边正方形的边长为４,右边正方形对角线长度为6．如果按照图中的方式旋转，那么得到的两个旋转体的体积之比是多少？【分析】左边正方形旋转后交得到一个底面半径为，高为4的圆柱,根据圆柱的体积公式V=πr2ｈ即可求出这个圆柱的体积; 右边正方形旋后可得到两个底面半径为，高也为且底面重合的圆锥,根据圆锥的体积公式V＝πr２h即可求出这两个圆柱的体积;再根据比的意义求出两个旋转体的体积之比即可（要化成最简整数比).【解答】解：3.14×()2×4=3.1４×４×4＝50.２4,×3.1４×（）２××2＝×３.1４×9×3×2＝5６.５２，50．24:５６.52=8:9.答：两个旋转体的体积之比是８:９．２2.如图一个底面长3０分米,宽10分米，高12分米的长方体水池,存有四分之三池水，请问：（1）将一个高11分米，体积３3０立方分米的圆柱放入池中,水面的高度变为多少分米？（２）如果再放人一个同样的圆柱,水面高度又变成了多少分米?（3)如果再放人一个同样的圆柱，水面高度又变成了多少分米?【分析】（1）由题意知,原来容器中的水可以看成是长3０分米、宽10分米、高为12×＝９分米的长方体,现将一个高１1分米，体积３３0立方分米的圆柱放入池中,水面没有淹没,求出圆柱的底面积即330÷11＝30(平方分米）再用３0×９求出淹没部分圆柱的体积除以长方体的底面积即是水升高的高度,用水升高的高度加上９分米，(2、3）同(1)解答即可．【解答】解：(１）330÷11×12×＝30×9=270（立方分米)2７0÷（30×10)=270÷3０0=0.9(分米）９+0．9＝９.９(分米)答:水面的高度变为9．9分米.（2)330÷11×９．９=３0×9．9＝297(立方分米）2９7÷(30×１０）=0．99（分米）９.9+0．9９=１0.89（分米)答：水面高度又变成了10.８9分米．。

小学数学几何思维训练的方法与案例数学几何是小学数学中的重要内容，也是培养学生思维能力和创造力的重要途径之一。

本文旨在介绍一些小学数学几何思维训练的方法，并通过实际案例展示这些方法的实际应用。

一、立体图形拼凑法立体图形拼凑法是培养学生空间想象力和几何思维的一种有效方法。

通过拼凑不同的几何形状，来锻炼学生对于立体图形的认知和理解能力。

例如，老师可以给学生准备一些由不同几何形状组成的立体图形模型，让学生根据给定的条件拼凑出相应的立体图形。

这样的训练既能帮助学生理解几何形状的构成，又能刺激他们的创造力和思维灵活性。

二、图形旋转与镜像图形旋转与镜像是培养学生空间几何思维的一种有效方法。

通过让学生观察和分析图形在旋转和镜像变换中的变化，来发展他们的空间认知能力和几何思维。

例如，老师可以给学生一些平面图形，让他们猜测该图形在旋转或者镜像变换后的样子，并理由解释，从而培养学生对图形变换过程的观察力和想象力。

此外，教师还可以引导学生通过手工制作的方式进行图形的旋转和镜像变换，以加强学生的实际操作能力。

三、利用故事情境进行几何问题解决利用故事情境进行几何问题解决是培养学生几何思维的一种创新方法。

通过给学生提供一个具体的故事场景，在故事中引入几何问题，并要求学生通过分析和推理来解决问题，从而激发学生的几何思维。

例如，教师可以给学生讲述一个关于校园建设的故事，学生需要基于故事内容来解决其中的几何问题，如确定教学楼的最佳位置、路径等。

这样的训练可以帮助学生将几何问题与实际场景相结合，提升他们的问题解决能力和思维灵活性。

案例一：平行线与平行四边形的探究教师在课堂上引入一个案例：小明要修建一个公园，他希望建一个长方形的草坪。

小明找到了一块长方形的土地，他需要确定这块土地边界的样子。

请学生根据这个案例来探索平行线与平行四边形的关系。

学生可以先用铅笔和直尺在纸上画出两条平行线，然后再用直尺连结这两条平行线的端点，形成一个四边形。

立体几何1、下面四个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是______________．（填序号）2、如下图所示，棱长分别为1厘米、2厘米、3厘米的三个正方体紧贴在一起，则所得到的立体图形的表面积是平方厘米．3、下图是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形，问这个直三棱柱的体积是多少？4、有一个足够深的水槽，底面是长为16厘米、宽为12厘米的长方形，原本在水槽里盛有6厘米深的水和6厘米深的油（油在水的上方）．在水槽中放人一个长、宽、高分别为8厘米、8厘米、12厘米的铁块，那么此时油层的层高是厘米。

5、圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是立方厘米。

（结果用兀表示）6、如下图所示，从正方形ABCD 上截去长方形DEFG，其中AB=1厘米，DE=21厘米，DG=31厘米，将ABCGFE 以GC 边为轴旋转一周，所得几何体的表面积是平方厘米，体积是_____________立方厘米。

（结果用兀表示）7、若长方体的三个侧面的面积分别是6，8，12，则长方体的体积是。

8、一个圆柱和一个圆锥（如下图所示），它们的高和底面直径都标在图上，单位是厘米。

请回答：圆锥体积与圆柱体积的比是多少？9、如下图所示，一个圆柱体形状的木棒，沿着底面直径竖直切成两部分，已知这两部分的表面积之和比圆柱体的表面积大2008平方厘米，则这个圆柱体木棒的侧面积是平方厘米。

（兀取3.14）10、两个同样材料做成的球A 和B，一个实心，一个空心。

A 的直径为7、重量为22，B 的直径为10.6、重量为33.3。

问：哪个球是实心球？（球的体积公式V=34πr³）11、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成，尺寸如下图所示．问：该油罐车的容积是多少立方米？（兀=3.1416）（球的体积公式V=34πr³）12、某工厂原用长4米，宽1米的铁皮围成无底无顶的的正方体形状的围栏，现要将围栏容量增加27%，问：能否还用原来的铁皮围成？13、一个正方体的纸盒中，恰好能放人一个体积为6.28立方厘米的圆柱体，纸盒的容积有多大？（兀=3.14）．14、用若干个小正方体拼成下图所示的造型．其中有一个小孔分别由左至右、由上至下以及由前至后穿透整个造型．拼成此造型共需使用多少个小正方体？15、一个圆锥形容器甲与一个半球形容器乙，它们圆形口的直径与容器的高的尺寸如下图所示，若用甲容器取水来注满乙容器，问：至少要注水多少次？（球的体积公式：V=34πr³）16、下图是一个直圆柱形状的玻璃杯，一个长为12厘米的直棒状细吸管（不考虑吸管粗细）放在玻璃杯内，当吸管一端接触圆柱下底面时，另一端沿吸管最少可露出上底面边缘2厘米，最多能露出4厘米．则这个玻璃杯的容积为立方厘米．（取兀=3.14）17、威力集团生产的某种洗衣机的外形是长方体，装衣物部分是圆柱形的桶，直径40厘米，深36厘米，已知该洗衣机装衣物的空间占洗衣机体积的25%，长方体外形的长为52厘米，宽50厘米．问：高是多少厘米？（兀取3.14，结果保留整数）18、有两个高度一样的水瓶，瓶子的底部被钉子分别戳了一个同样大的小洞．粗瓶子的水12分钟可以漏完，细瓶子的水8分钟可以漏完．若两个瓶子同时漏水，过了一段时间后，粗瓶子中水的高度是细瓶子中的2倍．这两个瓶子同时漏了分钟．19、世界上最早的灯塔建于公元270年，塔分三层，如下图所示，每层都高27米，底座呈正四棱柱，中间呈正八棱柱，上部呈正圆锥．上部的体积是底座的体积的。

第十一讲表面积和体积（一）第一部分：趣味数学小希帕蒂娅巧算箱子体积希帕蒂娅是历史上有记载的第一位女数学家,她岀生在埃及。

希帕蒂娅小时候很聪明,有一次,父亲的朋友来拜访,送给希帕蒂娅一件礼物,装在一个用绳子捆起来的箱子里。

小希帕蒂娅高兴地解开绳子,正要去打开箱子，父亲对她说：“别急,你先拿一把尺子量量绳子的长度。

”小希帕蒂娅用尺子量了量散落在地上的3根绳子,一根长210厘米,一根长250厘米,还有一根长290厘米。

父亲说:“假设这些绳子打结的时候,都用去了10厘米,希帕蒂娅,请你算一算,这个箱子的体积是多少?”“没问题,爸爸。

”小希帕蒂娅拿出一支笔,在地上列起式子来：长+宽=(290-10)÷2=140厘米,长+高=(250-10)÷2=120厘米宽十高=(210-10)÷2=100厘米。

怎么才能求出长、宽、高呢?小希帕蒂娅歪着头想了想,低头算了起来。

她用第2个式子减去第3个式子,得到:长一宽=20厘米,再加上第1个式子,就能求出长=80厘米。

知道了长,她很快就求出了宽=60厘米,高等于40厘米。

所以箱子的体积就是：长×宽×高=80×60×40=192000立方厘米。

算完了,父亲笑着点点头,说:“现在，你打开箱子拿出礼物吧!”父亲的朋友一直在旁边看着,不禁惊叹道:好聪明的小丫头,将来一定会成为有名的数学家！第二部分：习题精讲小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。

从平面图形到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。

因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数、形”结合的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。

在解答立体图形的表面积问题时，要注意以下几点：（1）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。

（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。

六年级下册数学思想训练——比率法解几何图形题例1在△ABC中，BD︰DC=2︰3，暗影部分的面积是27平方厘米。

求△ABC 的面积。

例2在△ABC中，AD垂直于BC，CE垂直于AB，AD=8厘米，CE=7厘米，AB+BC=21厘米，△ABC的面积是多少平方厘米？基本练习1、如图，ABCD是一个梯形，E是AD的中点，线段CE把梯形分红甲、乙两部分，它们的面积之比是10︰7.求上底AB与下底CD的长度之比。

2、如图，平行四边形ABCD的周长为75厘米，以BC为底时，高是14厘米；以CD为底时，高是16厘米。

问平行四边形ABCD的面积是多少？稳固练习1、如图，一个长方形被分红8个小长方形，此中五个小长方形的面积如下图，那么此中最大的长方形面积是多少？2、如图，梯形ABCD与△DEC的面积比为6:7，BE和EC的长度分别是多少？（单位：厘米）拓展提升1、如图，BF:AB=1:6，AE:AC=1；5，CD：CB=1：4，若△ABC的面积为120平方厘米，求△DEF的面积。

2、梯形ABCD的面积为20，点E在BC上，△ADE的面积是△ABE的面积的2倍，BE的长度为2，EC的长度为5。

问：△DEC的面积是多少？比赛训练1、例题：如下图，甲圆和乙圆的面积之和是丙圆的3，甲圆内暗影部分面积占甲圆的115，乙圆内暗影部分面积占乙圆面积的，丙圆内暗影部分面积占丙2圆面积的1，那么甲。

乙两圆面积之比是多少？2、如下图，长方形AEGH与正方形BFGH的面积比为3︰2，则正方形ABCD的面积是正方形BFGH的面积的多少倍？（结果写成小数）3、如下图，已知直角三角形ABC中，BDEF是一个正方形，AD长4厘米，FC长9厘米，则直角三角形ABC的面积是多少平方厘米？（2011年全国“春蕾杯”小学生思想邀请赛）4、有三个梯形甲、乙、丙，它们的高挨次为1︰2︰3，上底之比挨次为6︰9︰4，下底之比挨次为12︰15︰10，已知梯形甲的面积是30平方厘米，那么，乙与丙两个梯形的面积之和为多少平方厘米？。

160π+40π=200π（dm³）
方法二： 拼成的大圆柱的体积：
（8÷2）²π×（10+15）=400π（dm³）
原来被截后的体积：
400π÷2=200π（dm³）
答：被截后的物体的体积是200π立方分米。
3.在一只底面半径为10cm的圆柱形玻璃容器中，水深8cm。要在容器中放入长 和宽都是8cm，高15cm的一块铁块。（1）如果把铁块横放在水中，水面上升多少 厘米？
面是朝上的敞口部分）
由题意知雨不停地下着，雨是从 敞口进入容器，如果敞口面积相同， 则降雨量相同。
容器(1)(2)(5)和例图容器一样都是直柱体,所以相同时间内降雨量相同。只要比较高度就可以了。
容器(1)和例图高度相同，需同样1小时接满；容器（2）的高度是例图高度3倍，需3小时接满；
容器（5）的高度是例图高度2倍，需2小时接满。 容器（3）可以分成3个容器（1），由于只有1个小敞口，需要一个一个小容器装满，因此需要
(1)在顶点上挖掉一个 表面积和原来相同。
(2)在棱的中间挖掉一个
32+1×1×（4-2） =34（厘米²）
答：它的表面积是32平方厘米或34平方厘米。
5. 雨哗哗地不停地下着，如在雨地里放一个如下图那样的长方体的容器（单
位：厘米），雨水将它下满要用1小时．有下列（1）～（5）不同的容器，雨水
下满各需多长时间？（注：
设圆柱的底面半径是r分米。
圆柱的体积：
r²π×2r=12.56，
得：r³=2
圆柱的高 等于棱长，也 等于底×2r=8r³
则：8r³=16
答：这个木块的体积16立方分米。
2.如图，一个圆柱形物体的底面直径是8分米，被斜截后，最低处高是10分米， 最高处高是15分米。求被截后的物体的体积。

小学数学《立体图形的认识》教案设计中的问题分析及解决方法】立体几何是小学数学的重要组成部分，不仅能够拓展学生的空间想象力，更能提高他们的分析和推理能力。

而要让学生深刻理解立体图形，实践教学是不可或缺的一环。

本文将就小学数学《立体图形的认识》教案设计中常见的问题进行分析，并提出解决方法，旨在为广大教师提供有益的参考意见。

【问题分析】1.教学进度过快教师在安排教学进度时，往往会面临时间紧迫的困境，会期望尽早来完成课程的教学，而忽略了学生充分理解知识点的时间。

如果教学进度过快，会导致学生对新知识的掌握程度大打折扣，对后续的教学产生影响。

2.学生数学思维能力弱对于立体图形的认识，除了要求学生能够观察和辨认各种形状的图形，还需要他们具备一定的数学思维能力。

但事实上，许多小学生数学思维能力较弱，缺乏对抽象概念的理解和把握，难以应对立体图形的推理和运用。

3.教学方法单一教师在教授立体图形时，往往只采用一种教学方法，如经典讲解法、示范演示法，而缺乏变化和创新，导致学生眼前一亮的机会少，枯燥单调的课程缺乏吸引力，难以全面提高学生的学习兴趣和成绩。

【问题解决方法】1.合理安排教学进度在教学立体图形时，教师应该根据每个课时内容的难易程度合理安排教学进度，多给学生一些时间来吸收新的知识点，进行巩固和反复训练。

针对不同学生的学习情况，也可以通过分节教学的方式，适当增加课程时间或费时进行提前预习与巩固复习。

2.建立完善的思维训练体系针对学生数学思维能力低下的问题，可以加强推理训练，提高学生的推理能力。

因为推理能力可以锻炼学生的逻辑思维、思考能力和创造能力，帮助他们更好的理解和掌握立体图形的认识。

此外，可以实行分层教学，将学生划分为高、中、低三个层次，对不同层次的学生开展差异化的教学，从而更好的提高学生的数学思维能力。

3.注重多种教学方法的运用除了经典的讲授法和示范演示法外，还可以采用互动讨论、实物展示、游戏体验等活动，保证立体图形的教学方式多种多样，更贴合学生的兴趣和实际情况。

几何图形的设计与构造．涉及比例与整数分解，需要添加辅助线、寻找规律或利用对称性解的较为复杂的直线形和圆的周长与面积计算问题．1．今有9盆花要在平地上摆成9行，其中每盆花都有3行通过，而且每行都通过3盆花．请你给出一种设计方案，画图时用点表示花，用直线表示行.【分析与解】如下图所示，我们给出四种不同的排法．2．已知如图12-1，一个六边形的6个内角都是120°，其连续四边的长依次是1、9、9、5厘米．求这个六边形的周长．【分析与解】如下图所示，将六边形的六条边分别延长，相交至三点，并将其标上字母，因为∠BAF=120°，而么∠IAF=180°-∠BAF=60°．又∠EFA=120°，而∠IFA=180°-∠EFA：60°，则△IAF为等边三角形．同理△BCG、△EHD、△IGH均为等边三角形．在△IAF中，有IA=IF=AF=9(厘米)，在△BGC中，有BG=GC=BC=1(厘米)，有IA+AB+BG=IG=9+9+1=19，即为大正三角形的边长，所以有IG=IH=GH=19(厘米)．则EH=IH-IF-FE=19-9-5=5(厘米)，在△EDH中，DH=EH=5(厘米)，所以CD=GH-GC-DH=19-1-5=13(厘米)．于是，原图中六边形的周长为1+9+9+5+5+13=42(厘米)．3．图12-2中共有16条线段，每两条相邻的线段都是互相垂直的．为了计算出这个图形的周长，最少要量出多少条线段的长度?【分析与解】如下图所示，我们想像某只昆虫绕图形爬行一周，回到原出发点，那么往右的路程等于往左的路程，往上的路程等于往下的路程．于是只用量出往右的路程，往下的路程，再将它们的和乘以2即为所求的周长．所以，最少的量出下列6段即可．4．将图12-3中的三角形纸片沿虚线折叠得到图12-4，其中的粗实线图形面积与原三角形面积之比为2：3．已知图12-4中3个画阴影的三角形面积之和为1，那么重叠部分的面积为多少?【分析与解】设重叠部分的面积为x，则原三角形面积为1+2x，粗实线的面棚为1+x.因此(1+2x)：(1+x)=3：2，解得x=1，即重叠部分面积为1．5．如图12-5，涂阴影部分的小正六角星形面积是16平方厘米．问：大正六角星形的面积是多少平方厘米?【分析与解】 如下图所示，在正六边形ABCDEF 中,与面积相等，12个组成小正六角星形，那么由6个及12个组成的正六边形的面积为16÷12×(12+6)=24(平方厘米)．而通过下图，我们知道，正六边形ABCDEF 可以分成6个小正三角形，并且它们面积相等，且与六个角的面积相等，所以大正六角星形的积为24÷6×12=48(平方厘米)．6．如图12-6所示，在三角形ABC 中，DC=3BD ，DE=EA ．若三角形ABC 的面积是1．则阴影部分的面积是多少?【分析与解】 △ABC 、△ADC 同高，所以底的比等于面积比，那么有33.44ADC ABC ABC DC S S S BC ∆∆∆=⨯=⨯=而E 为AD 中点，所以13.28DEC ADC S S ∆∆== 连接FD ，△DFE 、△FAE 面积相等，设,FEA S x ∆=则．FDE S ∆的面积也为x ，11.44ABD ABC S S ∆∆==12,4BDF ABD FEA FDE S S S S x ∆∆∆∆=--=-而3.8FDC FDE DEC S S S x ∆∆∆=+=+ 13:(2);()1:348BDF FDC S S x x ∆∆=-+=，解得356x =.所以，阴影部分面积为333.8567DEC FEA S S ∆∆+=+=7．如图12-7，P 是三角形ABC 内一点，DE 平行于AB ，FG 平行于BC ，HI 平行于CA ，四边形AIPD 的面积是12，四边形PGCH 的面积是15，四边形BEPF 的面积是20．那么三角形ABC 的面积是多少?【分析与解】 有平行四边形AIPD 与平行四边形PGCH 的面积比为IP 与PH 的比，即为12：15=4：5． 同理有FP:PG=20:15=4:3， DP:PE=12:20=3:5．如图12-7(a)，连接PC 、HD ，有△PHC 的面积为152△DPH 与△PHC 同底PH ，同高，所以面积相等，即152DPH S ∆=，而△DPH 与△EP H 的高相等，所以底的比即为面积的比，有::3:5DPH EPH S S DP PE ∆∆==，所以551525.3322EPH DPH S S ∆∆=⨯=⨯⨯如图12-7(b)所示，连接FH 、BP ，4108;5IFP EPH FBP IP IP S S S PH PH ∆∆∆===⨯=如图12-7(c)所示，连接FD、AP，396.42 DPG DFP APDPG PGS S SFP FP∆∆∆===⨯=有925122015872.22 ABC AIPD BEPF CGPH IFP DGP EHPS S S S S S S∆∆∆∆=+++++=+++++=8．如图12-8，长方形的面积是小于100的整数，它的内部有三个边长是整数的正方形，①号正方形的边长是长方形长的512，②号正方形的边长是长方形宽的18．那么，图中阴影部分的面积是多少?【分析与解】有①号正方形的边长为长方形长的512，则图中未标号的正方形的边长为长方形长的712.而②号正方形的边长为宽的18，所以未标号的正方形的边长为长方形宽的78.所以在长方形中有：712长=78宽，则长：宽=12：8，不妨设长的为12k，宽为8k，则①号正方形的边长为5k，又是整数，所以k为整数，有长方形的面积为962k,不大于100．所以k只能为1，即长方形的长为12，宽为8．于是，图中①号正方形的边长为5，②号正方形的边长为1，则未标号的正方形的边长为7，所以剩余的阴影部分的面积为：22212851721.⨯---=9．如图12-9，三个一样大小的正方形放在一个长方形的盒内，A和B是两个正方形重叠部分，C，D，E是空出的部分，这些部分都是长方形，它们的面积比是A：B：C：D：E=1：2：3：4：5．那么这个长方形的长与宽之比是多少?【分析与解】以下用E横表示E部分横向的长度，E坚竖表示E部分竖向的长度，其他下标意义类似．有E横：D横=5：4，A横：B横=l：2．而E横+A横=D横+B横，所以有E横：D横：A横：B横=5：4：1：2．而A横+B横+C横=E横+A横对应为5+1=6，那么C横对应为3．而A面积：B面积：C面积=1：2：3，所以A坚=B坚=C坚．有A坚+C坚竖对应为6，所以A坚=C坚对应为3．那么长方形的竖边为6+C坚对应为9，长方形横边为E横+6+D横对应为5+6+4=15．所以长方形的长与宽的比为15：9=5：3．10．如图12-10，红、黄、绿三块大小一样的正方形纸片，放在一个正方形盒内，它们之间互相叠合．已知露在外面的部分中，红色的面积是20，黄色的面积是14，绿色的面积是lO．那么，正方形盒子的底面积是多少?【分析与解】如下图所示，我们将黄色的正方形纸片向左推向纸盒的过缘，有露在外面的部分，黄色减少的面积等于绿色增加的面积，也就是说黄色、绿色部分露在外面部分的面积和不变．并且有变化后，黄色露出面积+红色部分面积，绿色露出面积+红色部分面积，都是小正方形纸片边长乘以大正方形盒子边长的积．所以，黄色露出面积+红色部分面积=绿色露出面积+红色部分面积，于是．黄色露出面积=绿色露出面积，而它们的和为14+10=24，即黄色露出面积=绿色露出面积=12．有黄：空白=红：绿，12：空白=20：12，解得空白=7.2，所以整个正方形纸盒的底面积为12+7.2+20+12=51.2．11．如图12-11，在长260厘米，宽150厘米的台球桌上，有6个球袋A，B，C，D，E，F，其中AB=EF=130厘米．现在从4处沿45°方向打出一球，碰到桌边后又沿45°方向弹出，当再碰到桌边时，仍沿45°方向弹出，如此继续下去．假如球可以一直运动，直至落入某个球袋中为止，那么它将落人哪个袋中?【分析与解】将每个点的位置用一组数来表示，前一个数是这个点到FA的距离，后一个数是点到FD的距离，于是A的位置为(0，150)，球经过的路线为：(0,150)→(150,0) →(260,110) →(220，150) →(70，0) →(0，70) →(80，150) →(230,0) →(260，30) →(140，150) →(0，10) →(10，0) →(160，150) →(260，50) →(210,0) →(60，150) →(0，90) →(90，0) →(240，150) →(260，130) →(130，0)．因此，该球最后落入E袋．12．长方形ABCD是一个弹子盘，四角有洞．弹子从A出发，路线与边成45度角，撞到边界即反弹，并一直按此规律运动，直到落人一个洞内为止．如图12-12．当AB=4，AD=3时，弹子最后落入B洞．问：若AB=1995，AD=1994时，弹子最后落入哪个洞?在落入洞之前，撞击BC边多少次?【分析与解】撞击AD边的点，每次由A向D移动2；撞击BC边的点，每次由C向B移动2．因为第一次撞击BC边的点距C点1，第一次撞击AB边的点距A点为2，1994÷2=997．所以最后落人D洞，在此之前撞击BC边997次．13．10个一样大的圆摆成如图12-13所示的形状．过图中所示两个圆心A ，B 作直线，那么直线右上方圆内图形面积总和与直线左下圆内图形面积总和的比是多少?【分析与解】直线AB 的右上方的有2个完整的圆，2个半圆，1个1个而1个1个正好组成一个完整的圆，即共有4个完整的圆．那么直线AB 的左下方有10-4=6个完整的圆，每个圆的面积相等，所以直线右上方圆内图形面积总和与直线左下圆内图形面积总和的比是4：6=2：3．14．在图12-14中，一个圆的圆心是0，半径r=9厘米，∠1=∠2=15°.那么阴影部分的面积是多少平方厘米?(π取3.14)【分析与解】有AO=OB ，所以△A OB 为等腰三角形，AO=OC ，所以△A OC 为等腰三角形.∠ABO=∠1=15°，∠AOB=180°-∠1-∠ABO=150°. ∠ACO=∠2=15°,∠AOC=180°-∠2-∠ACO=150°. 所以 ∠BOC=360°-∠AOB-∠AOC=60°，所以扇形BOC 的面积为260942.39360π⨯⨯≈(平方厘米)．15．图12-15是由正方形和半圆形组成的图形．其中P 点为半圆周的中点，Q 点为正方形一边的中点．已知正方形的边长为10，那么阴影部分的面积是多少?(π取3.14)【分析与解】 过P 做AD 平行线，交AB 于O 点，P 为半圆周的中点，所以0为AB 中点．有2ABCD DPC 101S 1010100S 12.522ππ=⨯==⨯⨯=半圆，（）. AOP OPQB 101101S 510+37.5S 105550.2222∆⎡⎤⎛⎫=⨯⨯==++⨯⨯= ⎪⎢⎥⎝⎭⎣⎦梯形（）， 阴影部分面积为ABCD AOP DPC OPQB S S S S 10012.537.55012.512.551.75.ππ∆+-=+--=+≈半圆梯形-。

第六讲 圆柱、圆锥、球体【专题知识点概述】立体图形，主要考点集中在不规则形体的表面积与体积计算。

其中有自成一类的“染色问题”，也是经常见到的“几何奥数题”。

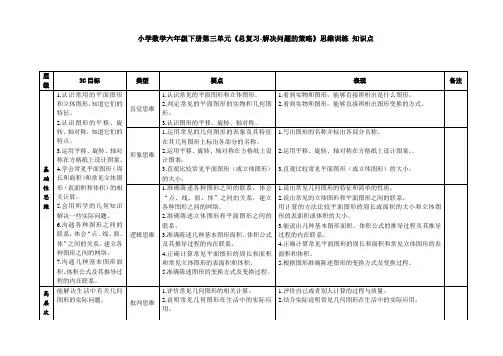
小学阶段，我们除了学习平面图形外，还认识了一些简单的立体图形，如长方体、正方体（立方体）、直圆柱体，直圆锥体、球体等，并且知道了它们的体积、表面积的计算公式，本讲重点讲解立体图形中的圆柱、圆锥和球体。

【授课批注】本讲在熟记体积和表面积公式的基础上，要鼓励学生多思考，勤动手，多画图，注重“数形结合以此来培养学生的空间想象能力。

另外，在数学竞赛中，有许多几何趣题，解答这些趣题的关键在于精巧的构思和恰当的设计，把形象思维和抽象思维结合起来。

一、圆柱、圆锥、球体圆柱体：如右图，圆柱体的底面是圆，其半径为r ；圆柱体的侧面展开图是一个长方形，长方形的宽相当于圆柱体的高，长相当于圆柱体的底面周长。

圆柱体的表面积：S 圆柱=侧面积+2个底面积=2πrh+2πr 2。

圆柱体的体积：2V r h π=圆柱圆锥体：如右图，圆锥体的底面是圆，其半径为r ；圆锥体的侧面展开图是一个扇形。

圆锥体的体积：213V r h π=圆锥体 球体：343V r π=球体 r求圆柱体的表面积．一般的方法是先求出圆柱体的侧面积，然后再加上圆柱的两个底面积。

求圆锥体的表面积需要先求出侧面积（扇形），再求出底面积（圆），两者相加即可。

【重点难点解析】1．圆柱、圆锥和球体的表面积和体积计算。

2．间接利用或逆用公式求解圆柱圆锥球体中的其它量。

3．圆柱圆锥球体等立体图形的组合图形。

【竞赛考点挖掘】1．常见较复杂的组合图形计算。

2．灵活运用公式求解体积表面积外的其余量。

【习题精讲】【例1】（难度级别※）一个底面半径的是５厘米．高是１５厘米的圆柱体，试求出它的表面积。

【分析与解】本题是较基础题型。

(１)侧面积：2x3.14x5x15=471(平方米）；(２）底面积：3.14x52=78.5（平方厘米）；(1)表面积：471+78.5x2=628(平方米）。

小学六年级数学下立体图形思维训练【知识分析】本课时是在学生学习了圆柱体和圆锥体的体积之后的拓展练习。

通过本课时的学习,学生能够根据所学的圆柱体、圆锥体的体积公式解决一些实际问题,培养学生解决问题的能力。

【例题解读】【例1】已知一个圆柱体的底面半径是4厘米,它的侧面积是60平方厘米,求它的体积是多少立方厘米？【思路简析】这道题的突破口是在“侧面积是60平方厘米”,侧面积的算法是πdh,而体积求法是πr²h,只需把60除以2,算出πrh,再乘上r（4）即可。

列式：60÷2×4＝120立方厘米【例2】一个底直径为20厘米的圆柱形木桶里装有水,水中放着一个底面直径为18厘米,高为20厘米的铁质圆锥体。

当圆锥体取出后,桶内水面降低多少厘米？【思路简析】仔细观察会发现,其实降低的水位与木桶底面积相乘就是圆锥的面积,而圆锥的面积为20×9²×3.14÷3,算出后只需除以圆柱底面积就行了。

列式：﹙20×9²×3.14÷3﹚÷﹙10²×3.14﹚=5.4厘米【例3】一个圆柱体,如果它的高增加2厘米,它的侧面积就增加50.24平方厘米。

这个圆柱体的底面半径是多少厘米？【思路简析】画一个示意图会发现增加的只是侧面积,底面积并没有增加,所以,只用50.24÷3.14÷2,算出它的底面直径,除以2就行了。

列式： 50.24÷3.14÷2÷2＝4厘米【经典题型练习】1.一个圆柱体,底面半径是5厘米,这个圆柱体的侧面积是100平方厘米。

它的体积是立方厘米？2.一个圆柱体,底面周长是6.28厘米,如果把圆柱体沿直径切成两个半圆柱体,表面积就增加20平方厘米,圆柱的体积是立方厘米？3.用直径为40毫米的圆形钢材截下一段压成直径为60毫米,高为40毫米的圆柱形零件毛坯,需要截取多少毫米圆钢？立体图形（二）【知识分析】本课时是在学生学习了立体图形之后的拓展练习。