2018届上学期北京市海淀区高三期中考试试卷+数学(文)
- 格式:doc
- 大小:653.50 KB
- 文档页数:7

北京市海淀区2023-2024学年高三上学期期中考试语文试题2023.11本试卷共8页,150分。
考试时长150分钟。
考生务必将答案答在答题纸上,在试卷上作答无效。
考试结束后,将本试卷和答题纸一并交回。
一、本大题共5小题,共18分。
阅读下面材料,完成1-5题。
材料一20世纪重要的英语诗人奥登,在评论叶芝时说过一句著名的话:“疯狂的爱尔兰驱策你进入诗歌。
”仔细思量,这里的爱尔兰,应该不但指叶芝的地域意义上的祖国,更主要指文化意义上的故乡。
奥登的话揭示了文化的强大制约力。
对于一个作家,他接受制约的方式,以及他的作品对读者的影响,都依赖于语言——准确地讲,是他使用的母语。
一种语言的最高成就,它的节奏和韵律,幽微和曲折,它的本质和秘密,也是通过最优秀的作家作品体现的。
在俄语,是普希金、托尔斯泰,英语世界不能忘记莎士比亚和哈代,而在汉语的天空,最亮的星辰是屈原和李白,是曹雪芹和鲁迅。
一位作家,他从写作中获得的幸福感,首先应该是他确信,有人分担他的思想和情感,他的喃喃自语正被千万只同一种语言的耳朵倾听。
共同的生存境遇,让他和他的读者明白什么样的话语和声音连着最深的疼痛。
而共同的文化背景,则使他们更能够听得出哪是正色厉声,哪是弦外之音,哪些静默不亚于洪钟大吕,哪些笑声其实是变形的哽咽。
他与他们之间不需要解释,相比条陈缕述,更多的是相视莫逆。
因此,一个优秀的作家,首先必定是为他的同胞而写作,以赢得他们的赞誉为目标,此外的其他动机都是可疑的“尽管今天的信息高速公路已将全球连成一个村庄,但面对不同的文化背景,有些深处的东西仍然无法转译,无法获得对等的理解它们涉及一个民族的集体意识、一种文化的深层编码,它们被封存在母语里,对一些人会敞开,对其余人却长久缄默。
我们如何使外国人懂得为什么“欲说还休,却道天凉好个秋”?(取材于彭程的相关文章)材料二从本质上说,语言文字就是特定的社团人群的生活方式,是一个特定群体内部成员之间、内部与外部之间关于如何联络、思维和识别等等的操作系统。

2018届上学期北京市海淀区高三期中考试物理试卷(附解析)一、本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,有的小题只有一个选项是正确的,有的小题有多个选项是正确的。
全部选对的得3分,选不全的得2分,有选错或不答的得0分。
把你认为正确的答案填涂在答题纸上。
1.一位同学从操场A点出发,向西走了30m,到达B点,然后又向北走了40m,达到C点。
在从A点到C点的过程中,该同学的位移大小是()A.70m B.50m C.40m D.30m2.如图所示,在光滑墙壁上用兜把足球挂在A点,足球与墙壁的接触点为B。
足球的质量为m,悬绳与墙壁的夹角为α,兜的质量不计。
则悬绳对球的拉力F的大小为()A.F = mg tanαB.F = mg sinαC.F=mg/cosαD.F=mg/tanα3.图所示,某同学站在体重计上观察超重与失重现象。
由稳定的站姿变化到稳定的蹲姿称为“下蹲”过程;由稳定的蹲姿变化到稳定的站姿称为“起立”过程。
她稳定站立时,体重计的示数为A0,关于实验现象,下列说法正确的是()A.“起立”过程,体重计的示数一直大于A0B.“下蹲”过程,体重计的示数一直小于A0C.“起立”、“下蹲”过程,都能出现体重计的示数大于A0的现象D.“起立”的过程,先出现超重现象后出现失重现象4.用图3所示装置研究摩擦力的变化规律,把木块放在水平长木板上,在弹簧测力计的指针下轻放一个小纸团,它只能被指针向左推动。
用弹簧测力计沿水平方向拉木块,使拉力由零缓慢增大。
下列说法正确的是()A.木块开始运动前,摩擦力逐渐增大B.当拉力达到某一数值时木块开始移动,此时拉力会突然变小C.该实验装置可以记录最大静摩擦力的大小D.木块开始运动前,拉力小于摩擦力5.一个弹簧振子沿x轴做简谐运动,取平衡位置O为x轴坐标原点。
从某时刻开始计时,经过二分之一的周期,振子具有沿x轴正方向的最大加速度。
图中能正确反映该弹簧振子的位移x与时间t关系的图像是()6.物体A做平抛运动,以物体被抛出的位置为原点O,以初速度v0的方向为x轴的方向、竖直向下的方向为y轴的方向,建立平面直角坐标系。

普通高等学校2018届高三招生全国统一考试模拟试题(二)数学(文)试题word含答案普通高等学校招生全国统一考试模拟试题——文科数学(二)本试卷满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题纸上。
2.回答选择题时,选出每小题答案后,用铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题纸上,写在本试卷上无效。
3.考试结束后,将本试卷和答题纸一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 $A=\{x|x-\frac{1}{2}<0\}$,$B=\{x|x-\frac{(2a+8)}{a(a+8)}<0\}$,若 $A\cap B=A$,则实数 $a$ 的取值范围是A。
$(-4,-3)$B。
$[-4,-3]$C。
$(-\infty,-3)\cup(4,+\infty)$D。
$(-3,4)$2.已知复数 $z=\frac{3+i}{2-3i}$,则 $z$ 的实部与虚部的和为A。
$-\frac{2}{5}+\frac{1}{5}i$B。
$-\frac{2}{5}-\frac{1}{5}i$C。
$\frac{2}{5}+\frac{1}{5}i$D。
$\frac{3}{5}+\frac{2}{5}i$3.某景区管理部门为征求游客对景区管理方面的意见及建议,从景区出口处随机选取 $5$ 人,其中 $3$ 人为跟团游客,$2$ 人为自驾游散客,并从中随机抽取 $2$ 人填写调查问卷,则这 $2$ 人中既有自驾游散客也有跟团游客的概率是A。
$\frac{2}{3}$B。
$\frac{1}{5}$C。
$\frac{2}{5}$D。
$\frac{3}{5}$4.已知双曲线 $E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ 的离心率为$\frac{\sqrt{10}}{3}$,斜率为 $-\frac{3}{2}$ 的直线 $l$ 经过双曲线的右顶点 $A$,与双曲线的渐近线分别交于 $M$,$N$ 两点,点 $M$ 在线段$AN$ 上,则 $\frac{AN}{AM}$ 等于A。

XXX2018年高三下学期期初考试(3月)数学(文)试题2018年全国高三文科数学统一联合考试一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合$A=\{x|x\leq1\}$,且$A\cap B=\{0,1\}$,则集合$B$可能是(。
)A.$\{x|x\geq\}$B.$\{x|x>-1\}$C.$\{-1,0,1\}$D.$\{0,1,2\}$2.已知向量$a=(1,2)$,$b=(-1,0)$,则$2a-b=$(。
)A.$17$B.$17\vec{a}$C.$5$D.$25$3.若复数$z$在复平面内对应的点的坐标是$(1,-2)$,则$z=$ (。
)A.$1-2i$B.$1+2i$C.$2-i$D.$-2-i$4.《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边同时相向打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果这两只老鼠恰好用了7天把墙打穿,则墙厚为(。
)A.$8255$尺B.$129$尺C.$2079$尺D.$65$尺5.若双曲线$C:-\frac{x^2}{x^2+y^2}=1$的离心率为3,则实数$m=$ (。
)frac{m}{m+1}$A.$1$B.$2$C.$1$或$-2$D.$1$或$2$6.已知命题$p:\exists m\in R$,使得$f(x)=x^2+mx$是偶函数;命题$q:x^2=1\Rightarrow x=1$,现给出下列命题:①$p$;②$q$的逆否命题;③$p\land q$;④$p\lor(\negq)$。
其中真命题的个数为(。
)A.$0$B.$1$C.$2$D.$3$7.如图,网格纸上小正方形的边长为$1$,粗实线画出的是某几何体的三视图,则该几何体的体积为(。
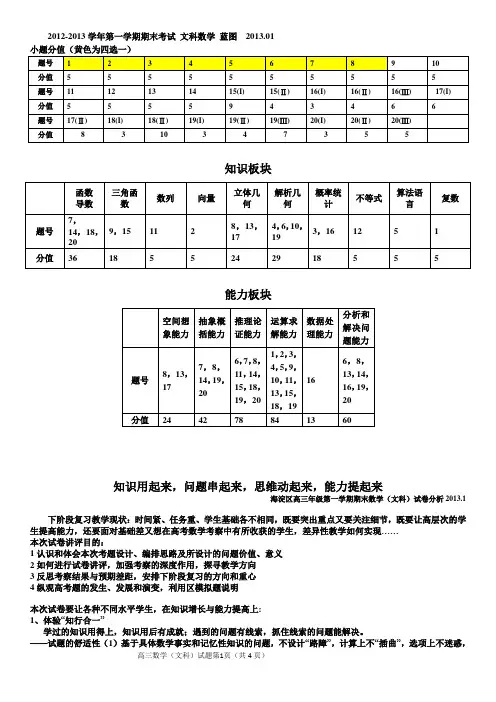
2012-2013学年第一学期期末考试文科数学蓝图2013.01知识板块能力板块知识用起来,问题串起来,思维动起来,能力提起来海淀区高三年级第一学期期末数学(文科)试卷分析2013.1下阶段复习教学现状:时间紧、任务重、学生基础各不相同,既要突出重点又要关注细节,既要让高层次的学生提高能力,还要面对基础差又想在高考数学考察中有所收获的学生,差异性教学如何实现……本次试卷讲评目的:1认识和体会本次考题设计、编排思路及所设计的问题价值、意义2如何进行试卷讲评,加强考察的深度作用,探寻教学方向3反思考察结果与预期差距,安排下阶段复习的方向和重心4纵观高考题的发生、发展和演变,利用区模拟题说明本次试卷要让各种不同水平学生,在知识增长与能力提高上:1、体验“知行合一”学过的知识用得上,知识用后有成就;遇到的问题有线索,抓住线索的问题能解决。
——试题的舒适性(1)基于具体数学事实和记忆性知识的问题,不设计“路障”,计算上不“插曲”,选项上不迷惑,不拖泥带水;(2)为考察知识板块特有的数学思维模式而设计的问题,不在问题条件上晦涩难懂,不强扯硬拽等价转化。
2、恪守“格物致知”不轻易否定学生的数学直觉,不妄断正确结果的获取过程。
只有在推究出特殊中蕴含的一般的原理和方法才能够到达理性的彼岸。
——试题的科学严谨性(1)在问题解决的道路上,合情推理的价值突出体现如(14)题(2)问;(2)考察的问题不仅需对数学结论进行合理猜想,更要有严谨论证的数学知识和能力。
3、最后“道法自然”。
顺其自然,水到渠成,思路起点与问题解决完美契合。
——试题的数学思维性(1)变量;(2)数形;(3)本次考试是高三复习阶段性检测练习,既要突出考察期中之后复习内容,也要着眼于高考,从部分知识的复习到所有数学知识的整合。
期中之后,根据区里安排的教学进度,重点复习了解析几何、立体几何和统计概率、不等式与推理证明、复数框图内容。
本次考察以上知识版块所占分值也体现了重点复习内容重点考察的目的,同时对期中以前所复习的函数导数、数列、平面向量也进行了阶段性滚动性质的考察,从所占分值和能力考察层级中可窥一斑。

海淀区2022—2023学年第一学期期中练习高三数学参考答案一、选择题二、填空题(11 (12)(0,1)(1,)+∞ (13)答案不唯一,小于1的实数均可(14)2;1−或1 (15)2;(0,2)三、解答题(16)(本小题13分)解:(Ⅰ)设等差数列{}n a 的公差为d ,因为253,25a S ==, 所以113,54525.2a d a d +=⎧⎪⎨⨯+=⎪⎩解得11,2.a d =⎧⎨=⎩所以21n a n =−. (Ⅱ)选择条件③.因为11,3b q ==, 所以13n n b −=. 因为m k a b =, 即1213k m −−= .得1312k m −+=.因为*k ∈N ,13k −为奇数,131k −+为偶数,所以*m ∈N .可得1312k m −+=.(17)(本小题14分)解:(Ⅰ)2()2sin()cos()2cos ()14444f ππππ−=−−+−−22(2(1222=⋅+− 1=−.(Ⅱ)()sin 2cos 2)4f x x x x π=+=+.所以()f x 的最小正周期为22T π==π. (Ⅲ)因为0,2x π≤≤所以52,444x πππ≤+≤当242x ππ+=,即8x π=时,()f x 取得最大值,所以()f x 在区间[0,]2π上的最大值为()8f π=;当5244x ππ+=,即2x π=时,()f x 取得最小值, 所以()f x 在区间[0,]2π上的最小值为()12f π=−.(18)(本小题14分)解:(Ⅰ)()f x 的定义域为R .2'()2f x x x =−,令'()0f x =,120,2x x ==.由表可得,()f x 的单调递增区间为(,0),(2,)−∞+∞;单调递减区间为(0,2). (Ⅱ)由函数解析式及(Ⅰ)可知44(1),(0)0,(2),(3)033f f f f −=−==−=.①当(1,2)m ∈−时,4(1,],()3x m f x ∀∈−≠−,不符合题意;②当[2,3]m ∈时,()f x 在区间[1,]m −上的取值范围是4[,0]3−,符合题意;③当3m >时,由()f x 在区间(2,)+∞上单调递增可知()(3)0f m f >=,不符合题意. 综合上述,[2,3]m ∈(19)(本小题14分) 解:(Ⅰ)在ABD △中,75BAD ∠=︒,45ABD ∠=︒,所以60ADB ∠=︒.由正弦定理:sin sin AD AB ABD ADB =∠∠,得sin 45sin 60AD AB=︒︒,所以,sin4512sin60AD AB︒=⋅==︒(km).1sin sin75sin(4530))2BAD∠=︒=︒+︒=+=,所以ABD△的面积为11sin123622ABDS AB AD BAD=⋅⋅∠=⨯⨯=+△(2km).(Ⅱ)由30BAC∠=︒,60ABC∠=︒, 得45CAD∠=︒,AC=在ACD△中由余弦定理,得2222cos363166260 CD AC AD AC AD CAD=+−⋅⋅∠=⨯+⨯−⨯=.所以,CD=(km).即点C, D之间的距离为km.(20)(本小题15分)解:(Ⅰ)当2a=时,()e2sinxf x x=−,则(0)1f=.'()e2cosxf x x=−,则'(0)1f=−.曲线()f x在(0,(0))f处的切线方程为1y x=−+.(Ⅱ)当1a=时,记()()2e sin2xg x f x x=−=−−,则'()e cosxg x x=−.当(0,x∈π)时,0e e1,cos1x x>=<,所以'()'(0)0g x g>=.所以()g x在(0,)π上单调递增.因为(0)10,()e20g gπ=−<π=−>,所以函数()2y f x=−在区间(0,π)上有且仅有一个零点.(Ⅲ)设()()cos2h x f x x=+−e sin cos2x a x x=−+−.则'()e cos sinxh x a x x=−−.设()e cos sinxs x a x x=−−.则'()e cos sinxs x x a x=−+.因为当[0,]x ∈π时,0e e 1,cos 1,sin 0x x x ≥=, 所以当0a ≥时,[0,]x ∈π时,'()0s x ≥, 所以'()h x 在区间[0,]π上单调递增()*.(1)当1a >时,'(0)10h a =−<,'()e 0h a ππ=+>, 且'()h x 在区间[0,]π上单调递增, 所以存在唯一0(0,)x ∈π,使得0'()0h x =. 当0(0,)x x ∈时,'()0h x <, 所以()h x 在区间0(0,)x 上单调递减. 可得0()(0)0h x h <=,所以与题意不符.(2)当1a =时,()e sin cos 2x h x x x =−+−. '()e cos sin x h x x x =−−由()*可知:'()h x 在区间[0,]π上单调递增, 所以当[0,]x ∈π时,'()'(0)0h x h ≥=. 所以()h x 在区间[0,]π上单调递增. 所以()(0)0h x h =区间[0,]π上恒成立. 符合题意. (3)当1a <时,()e sin cos 2e sin cos 2x x h x a x x x x =−+−>−+−.由(2)可知,此时()0h x >在区间[0,]π上恒成立. 综上所述,实数a 的取值范围是(,1]−∞. (21)(本小题15分) 解:(Ⅰ)(ⅰ)数表1不具有性质(2)p .理由:2,13,12,23,22,33,3||||||12a a a a a a −+−+−=≠.(ⅱ)存在. 3t =时,数表2具有性质()p t .(Ⅱ)不存在数表2023m A ⨯具有性质(6)p .假设存在m 使得数表2023m A ⨯具有性质(6)p ,则,11,1,21,2,1,||||||6(1,2,,1)i i i i i n i n a a a a a a i m +++−+−++−==−.即在这两行中,有6列的数不同,设其中有k 列是第i 行的数为1,第1i +行的数为0,则有6k −列是第i 行的数为0,第1i +行的数为1.所以,从第i 行到第1i +行,一共增加了62k −个1,1的个数的奇偶性不变. ……7分 所以,任意两行中,1的个数的奇偶性相同.与数表2023m A ⨯第一行有2023个1,最后一行有0个1矛盾. 所以,不存在具有性质(6)p 的数表2023m A ⨯.(Ⅲ)()f t 的最大值的为1n +.定义1m −行n 列的数表(1)m n B −⨯: 其第i 行第j 列为,,1,||1,2,,1(1,2,,)i j i j i j b a a i m j n +=−=−=,.则,{0,1}i j b ∈,且,0i j b =表示,1,,i j i j a a +两数相同,,1i j b =表示,1,,i j i j a a +两数不同. 因为数表m n A ⨯的第1行确定,所以给定数表(1)m n B −⨯后,数表m n A ⨯唯一确定. ①先证()1f t n ≤+.我们按照如下方式,构造数表n n B ⨯:对于第21s −行和第2s 行,1,2,,2n s =, 令21,2121,21,0s s s s b b −−−==,2,212,20,1s s s s b b −==,且在这两行其余的2n −列中,任选相同的1t −列都为1,其他列都为0. 于是可得到具有性质()p t 的数表(1)n n A +⨯如下:第1列第2列第3列第4列第n -1列第n 列第1行 第3行 第5行 … 第n +1行 即对于每个{2,3,,1}t n ∈−,当1m n =+时,都存在数表m n A ⨯具有性质()p t .所以()1f t n ≤+.②再证1t n =−时,()1f t n ≥+. 记,1,2,...(1,2,,)i i i i n S a a a i m =+++=.因为1t n =−是奇数,所以i S 与+1i S 的奇偶性不相同(1,2,,1i m =−).因为10m S n S ==,, 所以m 是奇数.我们考虑(1)m n B −⨯的第i 行和1i +行,因为1t n =−,所以这两行中都有1n −列为1,1列为0. 若这两行相同,则数表m n A ⨯的第i 行和第2i +行相同,2i i S S +=.若这两行不同,设其分别在第,p q 列为0()p q ≠,则数表m n A ⨯的第i 行和第2i +行只在第,p q 列上不同,其他列都相同,2||2i i S S +−≤. 因为1,0m S n S ==,其中n 是偶数. 所以1224311||||22m m m m m m n S S S S S S S S −−−−=−=−+−++−≤⨯. 所以1m n ≥+,即(1)1f n n −≥+. 结合①,(1)1f n n −=+.综上所述,()f t 的最大值的为1n +.。

海淀区高三年级第一学期期中练习数学(理科)第一部分(选择题,共40 分)一、选择题共 8 小题,每题 5 分,共 40 分。
在每题列出的四个选项中,选出切合题目要求的一项。
1.若会合,,则()A. B.C. D.【答案】 C【分析】由于会合,,因此,应选 C.2. 以下函数中,既是偶函数又在区间上单一递加的是()A. B.C. D.【答案】 A【分析】对于A, , 是偶函数,且在区间上单调递加,切合题意;对于B, 对于对于 C,是奇函数,不合题意;对于不合题意,只有合题意,应选3. 已知向量,,则既不是奇函数,又不是偶函数,不合题意;D,在区间上单一递减,A.()A. B.C. D.【答案】 D【分析】向量错误;错误;错误;,4. 已知数列知足正确,应选,则D.()A. B.C. D.【答案】 D【分析】依据条件获得:可设,,故两式做差获得:,故数列的每一项都为0,故 D 是正确的。
A , B, C,都是不正确的。
故答案为 D 。
5. 将的图象向左平移个单位,则所得图象的函数分析式为()A. B.C. D.【答案】 B【分析】将函数的图象向左平移个单位,获得函数的图象 ,所求函数的分析式为,应选 B.6. 设,则“ 是第一象限角”是“”的()A. 充足而不用要条件B. 必需而不充足条件C. 充足必需条件D. 既不充足也不用要条件【答案】 C【分析】充足性:若是第一象限角,则, ,可得,必需性:若,不是第三象限角,,,则是第一象限角,“ 是第一象限角”是“”的充足必需条件,应选 C.【方法点睛】此题经过随意角的三角函数主要考察充足条件与必需条件,属于中档题.判断充要条件应注意:第一弄清条件和结论分别是什么,而后直接依照定义、定理、性质试试.对于带有否认性的命题或比较难判断的命题,除借助会合思想化抽象为直观外,还可利用原命题和逆否命题、抗命题和否命题的等价性,转变为判断它的等价命题;对于范围问题也能够转变为包括关系来办理.7. 设(),则以下说法不正确的选项是()A.为上偶函数B.为的一个周期C.为的一个极小值点D.在区间上单一递减【答案】 D【分析】对于 A ,,为上偶函数,A正确;对于B, , 为的一个周期 ,B 正确;对于 C,), ,, 为的一个极小值点 ,C 正确,综上,切合题意的选项为D, 应选 D.8. 已知非空会合知足以下两个条件:(ⅰ ),;(ⅱ )的元素个数不是中的元素,的元素个数不是中的元素,则有序会合对的个数为()A. B. C. D.【答案】 A【分析】若会合中只有个元素,则会合中只有个元素,则,即,此时有,同理,若会合中只有个元素,则会合中只有个元素,有,若会合中只有个元素,则,即,此时有,,同理,若会合中只有个元素,则会合中只有个元素,有,若会合中只有个元素,则会合中只有个元素,则,不知足条件,因此知足条件的有序会合对的个数为,应选 A.【方法点睛】此题主要考察会合的交集、并集及会合与元素的关系、分类议论思想的应用 . 属于难题 .分类议论思想解决高中数学识题的一种重要思想方法,是中学数学四种重要的数学思想之一,特别在解决含参数问题发挥着奇异功能,大大提升认识题能力与速度.运用这类方法的重点是将题设条件研究透,这样才能迅速找准打破点. 充足利用分类议论思想方法能够使问题条理清楚,从而顺利解答,希望同学们能够娴熟掌握并应用与解题中间.第二部分(非选择题,共110 分)二、填空题共 6 小题,每题 5 分,共 30 分。

海淀区高三年级第一学期期中练习数学(理科) 2013.11本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合{1,1,2}A =-,{|10}B x x =+≥,则A B = ( ) A. {1,1,2}-B. {1,2}C. {1,2}-D.{2}2.下列函数中,值域为(0,)+∞的函数是( ) A. ()f x x =B. ()ln f x x =C. ()2x f x =D.()tan f x x =3. 在ABC ∆中,若tan 2A =-,则cos A =( )A.55 B.55-C.255D.255-4. 在平面直角坐标系xOy 中,已知点(0,0),(0,1),(1,2),(,0)O A B C m -,若//OB AC,则实数m 的值为( )A. 2-B. 12-C.12D. 25.若a ∈R ,则“2a a >”是“1a >”的(B ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件6. 已知数列{}n a 的通项公式2(313)n n a n =-,则数列的前n 项和n S 的最小值是( ) A. 3SB. 4SC. 5SD. 6S7.已知0a >,函数2πsin ,[1,0),()21,[0,),x x f x ax ax x ⎧∈-⎪=⎨⎪++∈+∞⎩若11()32f t ->-,则实数t 的取值范围为( ) A. 2[,0)3- B.[1,0)- C.[2,3) D. (0,)+∞8.已知函数sin cos ()sin cos x xf x x x+=,在下列给出结论中:①π是()f x 的一个周期; ②()f x 的图象关于直线x 4π=对称; ③()f x 在(,0)2π-上单调递减. 其中,正确结论的个数为( ) A. 0个B.1个C. 2个D. 3个二、填空题:本大题共6小题,每小题5分,共30分。

2018-2019学年北京市海淀区九年级(上)期中数学试卷一、选择题(本题共16分,每小题2分)下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.(2分)(2019•武汉模拟)抛物线y=x2+1的对称轴是()A.直线x=﹣1B.直线x=1C.直线x=0D.直线y=1 2.(2分)(2018秋•门头沟区期末)点P(2,﹣1)关于原点对称的点P′的坐标是()A.(﹣2,1)B.(﹣2,﹣1)C.(﹣1,2)D.(1,﹣2)3.(2分)(2018秋•海淀区期中)下列App图标中,既不是中心对称图形也不是轴对称图形的是()A.B.C.D.4.(2分)(2018秋•海淀区期中)用配方法解方程x2﹣2x﹣4=0,配方正确的是()A.(x﹣1)2=3B.(x﹣1)2=4C.(x﹣1)2=5D.(x+1)2=3 5.(2分)(2018秋•上杭县期末)如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为()A.2B.2C.D.26.(2分)(2018秋•克东县期末)将抛物线y=(x+1)2﹣2向上平移a个单位后得到的抛物线恰好与x轴有一个交点,则a的值为()A.﹣1B.1C.﹣2D.27.(2分)(2018秋•槐荫区期末)如图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是()A.B.C.D.8.(2分)(2018秋•海淀区期中)已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4,则y1,y2,y3,y4的最值情况是()A.y3最小,y1最大B.y3最小,y4最大C.y1最小,y4最大D.无法确定二、填空题(本题共16分,每小题2分)9.(2分)(2018秋•海淀区期中)写出一个以0和2为根的一元二次方程:.10.(2分)(2001•济南)若二次函数y=ax2+bx+c的图象如图所示,则ac0(填“>”或“=”或“<”).11.(2分)(2018秋•海淀区期中)若关于x的方程x2﹣4x+k﹣1=0有两个不相等的实数根,则k的取值范围是.12.(2分)(2018秋•海淀区期中)如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为.13.(2分)(2018秋•海淀区期中)已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是(填“锐角三角形”或“直角三角形”或“钝角三角形”).14.(2分)(2018秋•海淀区期中)在十三届全国人大一次会议记者会上,中国科技部部长表示,2017年我国新能源汽车保有量已居于世界前列.2015年和2017年我国新能源汽车保有量如图所示.设我国2015至2017年新能源汽车保有量年平均增长率为x,依题意,可列方程为.15.(2分)(2018秋•冷水江市期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c 与x轴交于(1,0),(3,0)两点,请写出一个满足y<0的x的值.16.(2分)(2018秋•海淀区期中)如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABCα中,一定成立的是(填序号).三、解答题(本题共68分,第17~22题,每小题5分;第23~26小题,每小题5分;第27~28小题,每小题5分)17.(5分)(2018秋•海淀区期中)解方程:x(x+2)=3x+6.18.(5分)(2018秋•海淀区期中)如图,将△ABC绕点B旋转得到△DBE,且A,D,C 三点在同一条直线上.求证:DB平分∠ADE.19.(5分)(2018秋•上杭县期末)下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.已知:⊙O.求作:⊙O的内接正三角形.作法:如图,①作直径AB;②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;③连接AC,AD,CD.所以△ACD就是所求的三角形.根据小董设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:在⊙O中,连接OC,OD,BC,BD,∵OC=OB=BC,∴△OBC为等边三角形()(填推理的依据).∴∠BOC=60°.∴∠AOC=180°﹣∠BOC=120°.同理∠AOD=120°,∴∠COD=∠AOC=∠AOD=120°.∴AC=CD=AD()(填推理的依据).∴△ACD是等边三角形.20.(5分)(2018秋•海淀区期中)已知﹣1是方程x2+ax﹣b=0的一个根,求a2﹣b2+2b的值.21.(5分)(2018秋•海淀区期中)生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)22.(5分)(2018秋•海淀区期中)如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b 经过点A(﹣2,0),B(﹣1,3).(1)求抛物线的解析式;(2)设抛物线的顶点为C,直接写出点C的坐标和∠BOC的度数.23.(6分)(2016秋•东丽区期末)如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).(1)求出y与x的函数关系式;(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.24.(6分)(2018秋•海淀区期中)如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.(1)求证:DE与⊙O相切;(2)若CD=BF,AE=3,求DF的长.25.(6分)(2018秋•海淀区期中)有这样一个问题:探究函数y的图象与性质.小东根据学习函数的经验,对函数y的图象与性质进行了探究.下面是小东的探究过程,请补充完成:(1)化简函数解析式,当x≥3时,y=,当x<3时y=;(2)根据(1)中的结果,请在所给坐标系中画出函数y的图象;(3)结合画出的函数图象,解决问题:若关于x的方程ax+1只有一个实数根,直接写出实数a的取值范围:.26.(6分)(2018秋•海淀区期中)在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A,B(点A在点B的左侧).(1)当a=﹣1时,求A,B两点的坐标;(2)过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.①当a=2时,求PB+PC的值;②若点B在直线l左侧,且PB+PC≥14,结合函数的图象,直接写出a的取值范围.27.(7分)(2018秋•海淀区期中)已知∠MON=α,P为射线OM上的点,OP=1.(1)如图1,α=60°,A,B均为射线ON上的点,OA=1,OB>OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.①依题意将图1补全;②判断直线AC与OM的位置关系并加以证明;(2)若α=45°,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR.根据(1)的解答经验,直接写出△POR的面积.28.(7分)(2018秋•海淀区期中)在平面直角坐标系xOy中,点A是x轴外的一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点”.(1)若点A的坐标为(0,2),点P1(2,2),P2(1,﹣4),P3(,1)中,点A 的“等距点”是;(2)若点M(1,2)和点N(1,8)是点A的两个“等距点”,求点A的坐标;(3)记函数y x(x>0)的图象为L,⊙T的半径为2,圆心坐标为T(0,t).若在L上存在点M,⊙T上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.2018-2019学年北京市海淀区九年级(上)期中数学试卷参考答案与试题解析一、选择题(本题共16分,每小题2分)下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.(2分)(2019•武汉模拟)抛物线y=x2+1的对称轴是()A.直线x=﹣1B.直线x=1C.直线x=0D.直线y=1【解答】解:∵抛物线y=x2+1,∴抛物线对称轴为直线x=0,即y轴,故选:C.2.(2分)(2018秋•门头沟区期末)点P(2,﹣1)关于原点对称的点P′的坐标是()A.(﹣2,1)B.(﹣2,﹣1)C.(﹣1,2)D.(1,﹣2)【解答】解:点P(2,﹣1)关于原点对称的点P′的坐标是(﹣2,1),故选:A.3.(2分)(2018秋•海淀区期中)下列App图标中,既不是中心对称图形也不是轴对称图形的是()A.B.C.D.【解答】解:A.此图案是轴对称图形,不符合题意;B.此图案既不是中心对称图形也不是轴对称图形,符合题意;C.此图案是轴对称图形,不符合题意;D.此图案是中心对称图形,不符合题意;故选:B.4.(2分)(2018秋•海淀区期中)用配方法解方程x2﹣2x﹣4=0,配方正确的是()A.(x﹣1)2=3B.(x﹣1)2=4C.(x﹣1)2=5D.(x+1)2=3【解答】解:∵x2﹣2x﹣4=0∴x2﹣2x=4∴x2﹣2x+1=4+1∴(x﹣1)2=5故选:C.5.(2分)(2018秋•上杭县期末)如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为()A.2B.2C.D.2【解答】解:如图:连接OP,AO∵AB是⊙O切线∴OP⊥AB,∴AP=PB AB在Rt△APO中,AP∴AB=2故选:A.6.(2分)(2018秋•克东县期末)将抛物线y=(x+1)2﹣2向上平移a个单位后得到的抛物线恰好与x轴有一个交点,则a的值为()A.﹣1B.1C.﹣2D.2【解答】解:新抛物线的解析式为:y=(x+1)2﹣2+a=x2+2x﹣1+a,∵新抛物线恰好与x轴有一个交点,∴△=4﹣4(﹣1+a)=0,解得a=2.故选:D.7.(2分)(2018秋•槐荫区期末)如图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是()A.B.C.D.【解答】解:A.此图案绕中心旋转36°或36°的整数倍能与原来的图案重合,此选项不符合题意;B.此图案绕中心旋转45°或45°的整数倍能与原来的图案重合,此选项符合题意;C.此图案绕中心旋转60°或60°的整数倍能与原来的图案重合,此选项不符合题意;D.此图案绕中心旋转72°或72°的整数倍能与原来的图案重合,此选项不符合题意;故选:B.8.(2分)(2018秋•海淀区期中)已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4,则y1,y2,y3,y4的最值情况是()A.y3最小,y1最大B.y3最小,y4最大C.y1最小,y4最大D.无法确定【解答】解:∵二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,且y3<y2<y4,∴抛物线开口向上,对称轴在0和1之间,∴P1(﹣3,y1)离对称轴的距离最大,P3(1,y3)离对称轴距离最小,∴y3最小,y1最大,故选:A.二、填空题(本题共16分,每小题2分)9.(2分)(2018秋•海淀区期中)写出一个以0和2为根的一元二次方程:x2﹣2x=0.【解答】解:∵0+2=2,0×2=0,所以以0和2为根的一元二次方程为x2﹣2x=0,故答案为:x2﹣2x=0.10.(2分)(2001•济南)若二次函数y=ax2+bx+c的图象如图所示,则ac<0(填“>”或“=”或“<”).【解答】解:∵抛物线的开口向下,∴a<0,∵与y轴的交点为在y轴的正半轴上,∴c>0,∴ac<0.故答案为<.11.(2分)(2018秋•海淀区期中)若关于x的方程x2﹣4x+k﹣1=0有两个不相等的实数根,则k的取值范围是k<5.【解答】解:根据题意得△=(﹣4)2﹣4(k﹣1)>0,解得k<5.故答案为k<5.12.(2分)(2018秋•海淀区期中)如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为110°.【解答】解:∵∠C=70°,AB∥CD,∴∠B=110°∴∠ADE=110°.故答案为:110°.13.(2分)(2018秋•海淀区期中)已知O为△ABC的外接圆圆心,若O在△ABC外,则△ABC是钝角三角形(填“锐角三角形”或“直角三角形”或“钝角三角形”).【解答】解:∵锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.又∵O为△ABC的外接圆圆心,若O在△ABC外,∴△ABC是钝角三角形,故答案为钝角三角形.14.(2分)(2018秋•海淀区期中)在十三届全国人大一次会议记者会上,中国科技部部长表示,2017年我国新能源汽车保有量已居于世界前列.2015年和2017年我国新能源汽车保有量如图所示.设我国2015至2017年新能源汽车保有量年平均增长率为x,依题意,可列方程为45.1(1+x)2=172.9.【解答】解:设我国2015至2017年新能源汽车保有量年平均增长率为x,根据题意得:45.1(1+x)2=172.9.故答案为:45.1(1+x)2=172.9.15.(2分)(2018秋•冷水江市期末)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c 与x轴交于(1,0),(3,0)两点,请写出一个满足y<0的x的值2(答案不唯一).【解答】解:∵在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于(1,0),(3,0)两点,∴当y<0的x的取值范围是:1<x<3,∴x的值可以是2.故答案是:2(答案不唯一).16.(2分)(2018秋•海淀区期中)如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABCα中,一定成立的是①③(填序号).【解答】解:如图,连接OC,设OB交CD于K.∵AB=CD,OD=OC=OB=OA,∴△AOB≌△COD(SSS),∴∠CDO=∠OBA,∵∠DKO=∠BKE,∴∠DOK=∠BEK=α,即∠BOD=α,故①正确,不妨设,∠OAB=90°﹣α,∵OA=OB,∴∠OAB=∠OBA,∴∠OBE+∠BEK=90°,∴∠BKE=90°,∴OB⊥CD,显然不可能成立,故②错误,∵CD=AB,∴,∴,∴∠ABC∠DOBα,故③正确.故答案为①③.三、解答题(本题共68分,第17~22题,每小题5分;第23~26小题,每小题5分;第27~28小题,每小题5分)17.(5分)(2018秋•海淀区期中)解方程:x(x+2)=3x+6.【解答】解:x(x+2)﹣3(x+2)=0,(x+2)(x﹣3)=0,x+2=0或x﹣3=0,所以x1=﹣2,x2=3.18.(5分)(2018秋•海淀区期中)如图,将△ABC绕点B旋转得到△DBE,且A,D,C 三点在同一条直线上.求证:DB平分∠ADE.【解答】证明:∵将△ABC绕点B旋转得到△DBE,∴△ABC≌△DBE∴BA=BD.∴∠A=∠ADB.∵∠A=∠BDE,∴∠ADB=∠BDE.∴DB平分∠ADE.19.(5分)(2018秋•上杭县期末)下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.已知:⊙O.求作:⊙O的内接正三角形.作法:如图,①作直径AB;②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;③连接AC,AD,CD.所以△ACD就是所求的三角形.根据小董设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:在⊙O中,连接OC,OD,BC,BD,∵OC=OB=BC,∴△OBC为等边三角形(三条边都相等的三角形是等边三角形)(填推理的依据).∴∠BOC=60°.∴∠AOC=180°﹣∠BOC=120°.同理∠AOD=120°,∴∠COD=∠AOC=∠AOD=120°.∴AC=CD=AD(在同圆或等圆中,相等的圆心角所对的弦相等)(填推理的依据).∴△ACD是等边三角形.【解答】(1)解:如图,△ACD为所作;(2)证明:在⊙O中,连接OC,OD,BC,BD,∵OC=OB=BC,∴△OBC为等边三角形(三条边都相等的三角形是等边三角形).∴∠BOC=60°.∴∠AOC=180°﹣∠BOC=120°.同理∠AOD=120°,∴∠COD=∠AOC=∠AOD=120°.∴AC=CD=AD(在同圆或等圆中,相等的圆心角所对的弦相等),∴△ACD是等边三角形.故答案为三条边都相等的三角形是等边三角形;在同圆或等圆中,相等的圆心角所对的弦相等.20.(5分)(2018秋•海淀区期中)已知﹣1是方程x2+ax﹣b=0的一个根,求a2﹣b2+2b的值.【解答】解:∵﹣1是方程x2+ax﹣b=0的一个根,∴1﹣a﹣b=0,∴a+b=1,∴a2﹣b2+2b=(a+b)(a﹣b)+2b=a﹣b+2b=a+b=1.21.(5分)(2018秋•海淀区期中)生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)【解答】解:如图,连接OC,AB交CD于E,由题意知:AB=0.8a+3.2a+2a=6a,所以OC=OB=3a,OE=OB﹣BE=3a﹣2a=a,由题意可知:AB⊥CD,∵AB过O,∴CD=2CE,在Rt△OCE中,由勾股定理得:CE2a,∴CD=2CE=4a,所以路面的宽度l为4a.22.(5分)(2018秋•海淀区期中)如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b 经过点A(﹣2,0),B(﹣1,3).(1)求抛物线的解析式;(2)设抛物线的顶点为C,直接写出点C的坐标和∠BOC的度数.【解答】解:(1)∵抛物线y=x2+ax+b经过点A(﹣2,0),B(﹣1,3),∴,解得,∴y=x2+6x+8.(2)∵y=x2+6x+8=(x+3)2﹣1,∴顶点C坐标为(﹣3,﹣1),∵B(﹣1,3).∴OB2=12+32=10,OC2=32+12=10,BC2=[(﹣3)﹣(﹣1)]2+(﹣1﹣3)2=20,∴OB2+OC2=BC2,则△OBC是以BC为斜边的直角三角形,∴∠BOC=90°.23.(6分)(2016秋•东丽区期末)如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).(1)求出y与x的函数关系式;(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.【解答】解:(1)∵大长方形的周长为6m,宽为xm,∴长为m,∴y=x•(0<x<2),(2)由(1)可知:y和x是二次函数关系,a<0,∴函数有最大值,当x时,y最大m2.答:窗框的长和宽分别为1.5m和1m时才能使得窗户的透光面积最大,此时的最大面积为1.5m2.24.(6分)(2018秋•海淀区期中)如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作AC的垂线交AC于点E,交AB的延长线于点F.(1)求证:DE与⊙O相切;(2)若CD=BF,AE=3,求DF的长.【解答】(1)证明:连接OD,∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BC,又∵AB=AC,∴∠1=∠2,∵OA=OD,∴∠2=∠ADO,∴∠1=∠ADO,∴OD∥AC,∵DE⊥AC,∴∠ODF=∠AED=90°,∴OD⊥ED,∵OD过0,∴DE与⊙O相切;(2)解:∵AB=AC,AD⊥BC,∴∠1=∠2,CD=BD,∵CD=BF,∴BF=BD,∴∠3=∠F,∴∠4=∠3+∠F=2∠3,∵OB=OD,∴∠ODB=∠4=2∠3,∵∠ODF=90°,∴∠3=∠F=30°,∠4=∠ODB=60°,∵∠ADB=90°,∴∠2=∠1=30°,∴∠2=∠F,∴DF=AD,∵∠1=30°,∠AED=90°,∴AD=2ED,∵AE2+DE2=AD2,AE=3,∴AD=2,∴DF=2.25.(6分)(2018秋•海淀区期中)有这样一个问题:探究函数y的图象与性质.小东根据学习函数的经验,对函数y的图象与性质进行了探究.下面是小东的探究过程,请补充完成:(1)化简函数解析式,当x≥3时,y=x,当x<3时y=3;(2)根据(1)中的结果,请在所给坐标系中画出函数y的图象;(3)结合画出的函数图象,解决问题:若关于x的方程ax+1只有一个实数根,直接写出实数a的取值范围:a<0或a≥1或a.【解答】解:(1)当x≥3时,y x;当x<3时,y3;故答案为x,3;(2)根据(1)中的结果,画出函数y的图象如下:(3)根据画出的函数图象,当a<0时,直线y=ax+1与函数y只有一个交点;当a≥1时,直线y=ax+1与函数y=3(x<3)的图象有一个交点,与函数y=x(x ≥3)无交点;当a时,直线y x+1经过点(3,3).故若关于x的方程ax+1只有一个实数根,实数a的取值范围:a<0或a≥1或a,故答案为a<0或a≥1或a.26.(6分)(2018秋•海淀区期中)在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A,B(点A在点B的左侧).(1)当a=﹣1时,求A,B两点的坐标;(2)过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.①当a=2时,求PB+PC的值;②若点B在直线l左侧,且PB+PC≥14,结合函数的图象,直接写出a的取值范围.【解答】解:(1)当a=﹣1时,有y=﹣x2﹣2x.令y=0,得:﹣x2﹣2x=0.解得x1=0,x2=﹣2.∵点A在点B的左侧,∴A(﹣2,0),B(0,0).(2)①当a=2时,有y=2x2﹣2x.令y=0,得2x2﹣2x=0.解得x1=0,x2=1.∵点A在点B的左侧,∴A(0,0),B(1,0).∴PB=2.当x=3时,y C=2×9﹣2×3=12.∴PC=12.∴PB+PC=14.②点B在直线l左侧,∵PB+PC≥14,∴3﹣x+ax2﹣2x≥14,可得:a或a≥2,由题意得A(0,0),B(,0)又A在B的左侧,所以a只可能大于0结合图象和①的结论,可得:a>0时,a≥2,27.(7分)(2018秋•海淀区期中)已知∠MON=α,P为射线OM上的点,OP=1.(1)如图1,α=60°,A,B均为射线ON上的点,OA=1,OB>OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.①依题意将图1补全;②判断直线AC与OM的位置关系并加以证明;(2)若α=45°,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR.根据(1)的解答经验,直接写出△POR的面积.【解答】解:(1)①如图所示:②结论:AC∥OM..理由:连接AP∵OA=OP=1,∠POA=60°,∴△OAP是等边三角形.∴OP=P A,∠OP A=∠OAP=60°,∵△PBC是等边三角形,∴PB=PC,∠BPC=60°,∴∠OP A+∠APB=∠BPC+∠APB,即∠OPB=∠APC,∴△OBP≌△ACP(SAS).∴∠P AC=∠O=60°,∴∠OP A=∠P AC,∴AC∥OM.(2)作PH⊥OQ于H,取PQ的中点K,连接HK,RK.∵∠PHQ=∠PRQ=90°,PK=KQ,∴HK=PK=KQ=RK,∴P,R,Q,H四点共圆,∴∠RHQ=∠RPQ=45°,∴∠RHQ=∠POQ=45°,∴RH∥OP,∴S△POR=S△POH.28.(7分)(2018秋•海淀区期中)在平面直角坐标系xOy中,点A是x轴外的一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点”.(1)若点A的坐标为(0,2),点P1(2,2),P2(1,﹣4),P3(,1)中,点A 的“等距点”是P1,P3;(2)若点M(1,2)和点N(1,8)是点A的两个“等距点”,求点A的坐标;(3)记函数y x(x>0)的图象为L,⊙T的半径为2,圆心坐标为T(0,t).若在L上存在点M,⊙T上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.【解答】解:(1)∵AP1=2﹣0=2,AP2,AP32,∴点A的“等距点”是P1,P3.故答案为:P1,P3.(2)∵点M(1,2)和点N(1,8)是点A的两个“等距点”,∴AM=AN,∴点A在线段MN的垂直平分线上.设MN与其垂直平分线交于点C,点A的坐标为(m,n),如图1所示.∵点M(1,2),点N(1,8),∴点C的坐标为(1,5),AM=AN=n=5,∴CM=3,AC4,∴m=1﹣4=﹣3或m=1+4=5,∴点A的坐标为(﹣3,5)或(5,5).(3)依照题意画出图象,如图2所示.①当⊙T1过点O时,⊙T1与L没有交点,∵⊙T1的半径为2,∴此时点T1的坐标为(0,﹣2);②当⊙T2上只有一个点M的“等距点”时,过点T2作T2M⊥图象L于点M,交⊙T2于点N,过点M作MD⊥x轴于点D,∵图象L的解析式为y x(x>0),∴∠MOT=60°,∠OT2M=30°.∵点T2的坐标为(0,t),∴OM t,DM OM t,T2M t.由“等距点”的定义可知:MN=T2M﹣T2N=DM,即t﹣2t,解得:t.综上所述:t的取值范围为﹣2<t.。

海淀区高三年级第一学期期中练习数学(文科) 2013.11本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合{1,0,1,2}A =-,{|1}B x x =≥,则A B = ( B ) A. {2}B. {1,2}C. {1,2}-D. {1,1,2}-2. 下列函数中,为奇函数的是( D )A. ()f x =B. ()ln f x x =C. ()2x f x =D. ()sin f x x =3. 已知向量(1,2),(,1)m =-=-a b ,且//a b ,则实数m 的值为( C ) A. 2- B. 12-C.12D. 24.“π6α=”是“1sin 2α=”的(A ) A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件5. 已知数列{}n a 的前n 项和为n S ,且*1110,3()n n a a a n +=-=+∈N ,则n S 取最小值时,n 的值是(B ) A. 3B. 4C. 5D. 66.若函数tan ,0,()2(1)1,0x x f x a x x π⎧-<<⎪=⎨⎪-+≥⎩在π(,)2-+∞上单调递增,则实数a 的取值范围( A )A. (0,1]B. (0,1)C. [1,)+∞D. (0,)+∞7.若函数()sin f x x kx =-存在极值,则实数k 的取值范围是( A ) A. (1,1)-B. [0,1)C. (1,)+∞D. (,1)-∞-8.已知点(1,0)B ,P 是函数e x y =图象上不同于(0,1)A 的一点.有如下结论: ①存在点P 使得ABP ∆是等腰三角形; ②存在点P 使得ABP ∆是锐角三角形;③存在点P 使得ABP ∆是直角三角形. 其中,正确的结论的个数为( B ) A. 0B.1C. 2D. 3二、填空题:本大题共6小题,每小题5分,共30分。

北京市海淀区中关村中学2018-2019学年上学期期中考试高二数学(理)试题一、选择题(本大题共8小题,每小题5分,共40分,每题只有一个正确答案,请将正确答案的序号涂在答题卡上)1.线段AB 在平面α内,则直线AB 与平面α的位置关系是( ).A .AB α⊂B .AB α⊄C .线段AB 的长短而定D .以上都不对【答案】A【解析】∵线段AB 在平面α内, ∴直线AB 上所有的点都在平面α内,∴直线AB 与平面α的位置关系是:直线AB 在平面α内, 即AB α⊂, 故选A .2.如图,1111ABCD A B C D -为正方体,下列结论错误..的是( ).DABC C 1D 1B 1A 1A .BD ∥平面11CB D B .1AC BD ⊥C .1AC ⊥平面11CB DD .异面直线AD 与1CB 角为60︒【答案】D【解析】异面直线AD 与CB 所成的角为45︒, 所以结论错误, 故选D .3.ABC △的斜二侧直观图如下图所示,则ABC △的面积为( ).A .1B .2CD .以上都不对【答案】B【解析】根据斜二测画法的原则可知:ABC △为直角三角形,底为2,高为2,所以面积是2, 故选B .4.下列说法正确的是( ).A .a b ∥,b a αα⊂⇒∥B .a b ⊥,b a αα⊂⇒⊥C .a α⊥,b a b α⊥⇒∥D .αβ⊥,a a βα⊂⇒⊥【答案】C【解析】由线面垂直的性质定理可知:a α⊥,b α⊥,则a b ∥, 故选C .5.已知三棱锥的主视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的左视图可能是( ).俯视图主视图2211A .1122 B .32 C .22D .22【答案】B【解析】根据正视图和俯视图,作出该三棱锥的几何直观图,如图所示,223O DABC则侧视图为直角三角形,且底边边长为||AD =,高为||2OC =, 故选B .6.把正方形ABCD 沿对角线AC 折起,当以A ,B ,C ,D 四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为( ).A .90︒B .60︒C .45︒D .30︒【答案】C【解析】DACO折叠后的三棱锥如图,易知当平面ACD 垂直于平面ABC 时三棱锥的体积最大, 设AC 的中点为O ,则DBO ∠即为所求, 而DOB △是等腰直角三角形, 所以45DBO ∠=︒, 故选C .7.如下图所示,已知A ,B ,C 三点不共线,P 为平面ABC 内一定点,O 为平面ABC 外任一点,则下列能表示向量OP 的为( ).A BCOPA .22OA OB OC ++ B .32OA AB AC -- C .23OA AB AC +-D .32OA AB AC +-【答案】D【解析】以AP 为对角线,以AB ,AC 所在直线为邻边做平行四边形, 则32AP AB AC =-,∴32OP AP AO AB AC OA =-=-+, 故选D .8.如下图在直三棱柱111ABC A B C -中,π2BAC ∠=,11AB AC AA ===,已知G 与E 分别为11A B 和1CC 的中点,D 与F 分别为线段AC 和AB 上的动点(不包括端点),若GD EF ⊥,则线段DF 长度的取值范围为( ).DGABC EFC 1B 1A 1A.⎫⎪⎭B.⎣⎦C.D.【答案】A【解析】建立如图所示的空间直角坐标系,则(0,0,0)A ,10,1,2E ⎛⎫ ⎪⎝⎭,1,0,12G ⎛⎫⎪⎝⎭,(,0,0)F x ,(0,,0)D y .∵GD EF ⊥,∴210x y +-=,∴DF∵01x <<,01y <<, ∴102y <<, ∴当25y =时,线段DF,当0y =时,线段DF 长度的最大值是1,(因为不包括端点,故0y =不能取,即DF 长度不能等于1), 故线段DF的长度的取值范围是:⎫⎪⎭, 故选A .二、填空题(本大题共6小题,每小题5分,共30分.请把结果填在答题纸中)9.已知αβ⊥,平面α与平面β的法向量分别为m ,n ,且(1,2,5)m =-,(3,6,)n z =-,则z =__________.【答案】3【解析】∵αβ⊥,且平面α与平面β的法向量分别为m ,n , ∴(1,2,5)(3,6,)31250m n z z ⋅=--=--+=, 解得:3z =.10.已知正四棱锥V ABCD -的底面面积为16,一条侧棱长为,则它的斜高..为__________. 【答案】6【解析】设VO 为正四棱锥V ABCD -的高,连接OB ,则VO OB ⊥,VD ABCO∵底面正方形ABCD 的面积为16, ∴4BC =,OB =又∵VB =∴6VO =, ∴正四棱锥V ABCD -的高为6.11.若一个圆锥的底面半径为1,侧面积是底面积的2倍,则该圆锥的体积为__________.【解析】设圆锥的母线长为l ,∵2ππS r ==底,【注意有文字】∴π2πS rl ==侧,【注意有文字】 ∴2l =,∴圆锥的高h∴圆锥的体积11π33V S h ==⨯底.【注意有文字】12.若一个底面是正三角形的三棱柱的主视图如下图所示,则其表面积等于__________.【答案】6+【解析】由题意知三棱柱的底面是一个边长为2的正三角形, 侧棱长是1,且侧棱与底面垂直,∴三棱柱的表面积是:12232162⨯⨯⨯⨯=+13.二面角的棱上有A 、B 两点,直线AC 、BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知4AB =,6AC =,8BD =,CD =__________.DA BC【答案】60︒【解析】E CBA D如图,过点B 作BE AC ∥,使得BE AC =, 连接CE ,DE ,则四边形ABEC 为平行四边形, ∴6BE AC ==,BE AB ⊥,CE AB ∥,CE AB =, 而BD AB ⊥,∴DBE ∠即是二面角AB αβ--的平面角, ∵BE AC ∥,AC AB ⊥,BD AB ⊥,CE AB ∥, ∴BE CE ⊥,BD CE ⊥, ∴CE ⊥平面BDE , ∴CE DE ⊥,在Rt CDE △中,4CE AB ==,CD =∴DE ==在BDE △中,2221cos 22BE BD DE DBE BE BD +-∠==⋅,∴60DBE ∠=︒,故该二面角的大小为60︒.14.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得的截面为S ,则下列命题正确的是__________(写出所有正确命题的编号).A 1①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R 满足114C R =;④当314CQ <<时,S 为五边形; ⑤当1CQ =时,S. 【答案】①②④ 【解析】①项,12CQ =时,S 为APQD , 而102CQ <<时,线段1DD 上同理,存在一点,与PQ 平行, 此时,S 为四边形,且是梯形,故命题①为真;M Q P D 1C 1A 1B 1CB AD②项,1AP D Q =,1AD PQ ∥,1APQD 是等腰梯形,故命题②为真;③项OQPD 1C 1A 1B 1C B AD当34CQ =时,如图所示,0AP DC =, ∵点P 是BC 的中点,∴CO CD AB ==, ∴1113C R C Q CO QC ==, ∴S 与11CD 的交点R 满足113C R =,故命题③为假.④项,如图所示,S 为五边形,故命题④为真;QP D 1C 1A 1B 1CB AD⑤项,如图所示,S2=, DAB C B 1A 1C 1D 1PQ故命题⑤为假.综上所述,命题正确的是:①②④.三、解答题(本大题共3小题,共30分,写出必要的解答过程) 15.已知向量(2,1,2)a =--,(1,1,4)b =-. (I )计算23a b -和23a b -. (II )求,a b . 【答案】见解析【解析】解:(I )232(2,1,2)3(1,1,4)(4,2,4)(3,3,12)(1,5,8)a b -=----=----=-.2|23|1(a b -=+=(2)cos ,||||33a b a b a b ⋅===⨯,又[],0,πa b ∈, 故π,4a b =.16.如图,四棱锥P ABCD -的底面是边长为1的正方形,侧棱PA ⊥底面ABCD ,且2PA =,E 是侧棱PA 上的动点.A BCPE(I )如果E 是PA 的中点,求证PC ∥平面BDE .(II )是否不论点E 在侧棱PA 的任何位置,都有BD CE ⊥?证明你的结论. 【答案】见解析【解析】OECBA(1)证明:连接AC 交BD 于O ,连接EO , ∵四边形ABCD 是正方形, ∴O 是AC 的中点, 又∵E 是PA 的中点, ∴PC OE ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE , ∴PC ∥平面BDE .(2)不论点E 在何位置,都有BD CE ⊥,证明如下: ∵四边形ABCD 是正方形, ∴BD AC ⊥,∵PA ⊥底面ABCD ,且BP ⊂平面ABCD , ∴BD PA ⊥, 又∵ACPA A =,∴BD ⊥平面PAC ,∵不论点E 在何位置,都有CEC 平面PAC , ∴不论点E 在何位置,都有BD CE ⊥.17.如图,在四棱锥P ABCD -中,底面ABCD 是菱形,且120ABC ∠=︒,点E 是棱PC 的中点,平面ABE 与棱PD 交于点F .D ABC EF P(1)求证:AB EF ∥.(2)若2PA PD AD ===,且平面PAD ⊥平面ABCD , 求①二面角E AF D --的锐二面角的余弦值.②在线段PC 上是否存在一点H ,使得直线BH 与平面AEF 所成角等于60︒,若存在,确定H 的位置,若不存在,说明理由. 【答案】见解析【解析】(1)证明:∵AB CD ∥,CD ⊂平面PCD ,AB ⊄平面PCD , ∴AB ∥平面PCD ,又∵AB ⊂平面ABEF ,且平面ABEF 平面PCD EF =,∴AB EF ∥,(2)①取AD 的中点O ,连接PO ,OB ,BD , ∵ABCD 是菱形,且120ABC ∠=︒,PA PD AD ==, ∴ABD △,PAD △是等边三角形, ∴PO AD ⊥,OB AD ⊥,又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,PO ⊂平面PAD ,∴PO ⊥平面ABCD ,以O 为原点,以OB ,OD ,OP 为坐标轴建立空间坐标系O xyz -,则:(0,1,0)A =-,(0,1,0)D,P,B,C,E ⎝⎭,10,2F ⎛ ⎝⎭.30,2AF ⎛= ⎝⎭,1,02EF ⎛⎫=-- ⎪ ⎪⎝⎭,设平面AEF 的法向量为(,,)n x y z =,则: 00n AF n EF ⎧⋅=⎪⎨⋅=⎪⎩,∴302102y y ⎧+=⎪⎪⎨⎪-=⎪⎩, 令1x =得:(1,3,3)n =-; ∵OB ⊥平面PAD ,∴(3,0,0)OB =为平面PAD 的一个法向量.∴cos ,||||13OB n OB n OB n ⋅===故二面角E AF D -- ②假设PC 上存在点H 便得直线BH 与平面AEF 所成角等于60︒, 则BH 与n 所成夹角为30︒,设(,2)(01)CH CP λλλ==-≤≤,则:(,22)BH BC CH λ=+=-,cos ,||||13BH n BH n BH n ⋅===, 化简得:2191260λλ--=,解得:λλ, ∴线段PC 上存在一点H ,使得直线BH 与平面AEF 所成的角等于60︒.。
北京市海淀区2022届高三年级上学期期中考试语文试题(解析版)2022.11一、本大题共8小题,共24分。
阅读下面材料,完成1-8题。
材料一“三山五园”是对北京西郊皇家园林的总称,这种说法出现于清朝中晚期。
“三山五园”包括香山静宜园、玉泉山静明园、万寿山清漪园(颐和园)、畅春园和圆明园。
静宜园位于地势较高的香山,园中建筑因山就势,参差错落,散点式镶嵌在山体之中。
“园林之胜,重在山水。
”水池作为点缀,或出现在殿前以丰富较窄的院落空间,或处于园中以增加园林趣味。
静宜园占地149公顷,1677年成为康熙的行宫,后来虽有添建,但一直保持着非常好的自然生态,深邃优雅。
静明园的个性与静宜园不同。
静明园所在的玉泉山,湖山尺度非常有限,占地仅65公顷。
玉泉山虽因泉水丰沛而得名,但水面并不大,山体狭长,呈南北走向。
在这种地形上如何建设园林呢?建筑要和湖山尺度配合好,建筑群采用散点布局,高低相映。
山顶上的香岩寺和玉峰塔规模不大,山脚下的建筑多为一层,这样就凸显出玉峰塔的高耸。
乾隆非常喜欢玉泉山的风光,亲自为静明园内十六景命名,正殿名为“廓然大公”,后殿名为“涵万象”,意蕴深远。
畅春园位于今北京大学西墙外畅春园宿舍一带,原是明代武清侯李伟修建的私家园林“清华园”,也叫“李园”,康熙时更名为畅春园。
畅春园以水景为主,水面宽阔,“江淮以北亦当第一也”,清朝改建时仍“因水成景”。
畅春园的叠山艺术也堪称一绝,原来的土山和新添建的假山,岗峰连接;加之遍植各色鲜花树木,绿树成荫,给人天人合一之感,是兼有政治和游乐功能的离宫型园林。
被称为“万园之园”的圆明园,既有金碧辉煌的宫殿,也有玲珑别透的亭台楼阁,又吸取了欧洲的建....筑形式,是世界园林的集大成者。
圆明园也是中国古典园林中平地造园的典范,园内步移景易,景观层出不穷,特色之多,首屈一指。
圆明园占地350公顷,在“三山五园”中规模最大。
有仙境、欧式园林等景....观,也有理政、居住、宗教等场所,这些层峦叠嶂的建筑都是雍正至咸丰五朝皇帝改造的结果,也大多体....现出其治国理念。
2018年海淀区高三年级第一学期期中练习数 学(理科)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合{1,1,2}A =-,{|10}B x x =+≥,则A B =( A )A. {1,1,2}-B. {1,2}C. {1,2}-D. {2}2. 下列函数中,值域为(0,)+∞的函数是( C )A. ()f x =B. ()ln f x x =C. ()2x f x =D. ()tan f x x =3. 在ABC ∆中,若tan 2A =-,则cos A =( B )B. D. 4. 在平面直角坐标系xOy 中,已知点(0,0),(0,1),(1,2),(,0)O A B C m -,若//OB AC ,则实数m 的值为( C )A. 2-B. 12-C. 12D. 25.若a ∈R ,则“2a a >”是“1a >”的( B )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件6. 已知数列{}n a 的通项公式2(313)nn a n =-,则数列的前n 项和n S 的最小值是( B ) A. 3SB. 4SC. 5SD. 6S7. 已知函数sin cos ()sin cos x xf x x x+=,在下列给出结论中:① π是()f x 的一个周期; ② ()f x 的图象关于直线x 4π=对称; ③ ()f x 在(,0)2π-上单调递减. 其中,正确结论的个数为( C ) A. 0个B.1个C. 2个D. 3个二、填空题:本大题共6小题,每小题5分,共30分。
981(21)d x x +=⎰___________.29. 已知数列{}n a 为等比数列,若13245,10a a a a +=+=,则公比q =____________.2 10. 已知23log 5,23,log 2b a c ===,则,,a b c 的大小关系为____________.a b c >>11. 函数π()2sin()(0,||)2f x x =+><ωϕωϕ的图象如图所示,则ω=______________,ϕ=__________.2π3,π612. 已知ABC ∆是正三角形, 若AC AB λ=-a 与向量AC 的夹角大于90,则实数λ的取值范围是__________.2λ>13. 定义在(0,)+∞上的函数()f x 满足:① 当[1,3)x ∈时,()1|2|f x x =--;②(3)3()f x f x =.设关于x 的函数()()F x f x a =-的零点从小到大依次为12,,,,n x x x .若1a =,则123x x x ++= ;若(1,3)a ∈,则122n x x x +++=________________.答案:14;6(31)n -三、解答题: 本大题共6小题,共80分。
海淀区2018-2019学年高三年级第一学期期中练习物理反馈试题最新试卷十年寒窗苦,踏上高考路,心态放平和,信心要十足,面对考试卷,下笔如有神,短信送祝福,愿你能高中,马到功自成,金榜定最新试卷多少汗水曾洒下,多少期待曾播种,终是在高考交卷的一刹尘埃落地,多少记忆梦中惦记,多少青春付与流水,人生,总有一次这样的成败,才算长大。
题名。
1A .如图1所示,用三段不可伸长的同种轻质细绳OA 、OB 、OC 共同悬挂一重物使其静止,其中OA 与竖直方向的夹角为30°,OB 沿水平方向,A 端、B 端固定。
若逐渐增加C 端所挂物体的质量,则最先断的绳(A )A .必定是OAB .必定是OBC .必定是OCD .OA 、OB 、OC 同时1B .如图1所示,用三段不可伸长的轻质细绳OA 、OB 、OC 共同悬挂一重物使其静止,其中OA 绳与水平之间的夹角为θ,OB 绳是水平的,A 端、B 端固定。
若分别用F A 和F B 表示OA 和OB 绳上的拉力大小,则下列判断中正确的是(B )A .F A =mg cos θB .F B =mgcot θC .F A =mgsin θD .F B =mg/sin θ1C .如图1所示,用三段不可伸长的轻质细绳OA 、OB 、OC 共同悬挂一重物使其静止,其中A 端固定,OA 绳与水平之间的夹角为θ。
最初OB 绳是水平的,现保持θ角不变,将OB 绳的B 端逐渐向上移动,在B 端到达O 点正上方的过程中,若分别用F A 和F B 表示OA 和OB 绳上的拉力大小,则下列判断中正确的是(D )A .F A 先变大后变小,FB 先变小后变大B .F A 先变小后变大,F B 先变小后变大C .F A 一直变小,F B 先变大后变小D .F A 一直变小,F B 先变小后变大2.在2016年的夏季奥运会上,我国跳水运动员获得多枚奖牌,为祖国赢得荣誉。
高台跳水比赛时,运动员起跳后在空中做出各种动作,最后沿竖直方向进入水中。
海淀区高三年级第一学期期中练习数学(理科) .11本试卷共4页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合,则集合中元素的个数为A.1 B.2 C.3 D.42.下列函数中为偶函数的是3.在△ABC中,的值为A.1 B.-1 C.12D.-124.数列的前n项和为,则的值为A.1 B.3 C.5 D.65.已知函数,下列结论错误的是A. B.函数的图象关于直线x=0对称C.的最小正周期为 D.的值域为6.“x>0 ”是“”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.如图,点O为坐标原点,点A(1,1).若函数且)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足8. 已知函数函数.若函数恰好有2个不同零点,则实数a 的取值范围是二、填空题(共6小题,每小题5分,共30分) 9.10.在△AB C 中,角A ,B ,C 的对边分别为a ,b ,c .若 c =4,则11.已知等差数列的公差,且39108a a a a +=-.若n a =0 ,则n =12.已知向量,点A (3,0) ,点B 为直线y =2x 上的一个动点.若AB a ,则点B 的坐标为 . 13.已知函数,若的图象向左平移个单位所得的图象与的图象向右平移个单位所得的图象重合,则的最小值为 14.对于数列,都有为常数)成立,则称数列具有性质. ⑴ 若数列的通项公式为,且具有性质,则t 的最大值为 ;⑵ 若数列的通项公式为,且具有性质,则实数a 的取值范围是三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程. 15.(本小题满分13分) 已知等比数列的公比,其n 前项和为(Ⅰ)求公比q 和a 5的值; (Ⅱ)求证:16.(本小题满分13分)已知函数.(Ⅰ)求的值;(Ⅱ)求函数的最小正周期和单调递增区间.17.(本小题满分13分)如图,在四边形ABCD中,AB=8,BC=3,CD=5,(Ⅰ)求BD的长;(Ⅱ)求证:18.(本小题满分13分)已知函数,曲线在点(0,1)处的切线为l(Ⅰ)若直线l的斜率为-3,求函数的单调区间;(Ⅱ)若函数是区间[-2,a]上的单调函数,求a的取值范围.19.(本小题满分14分)已知由整数组成的数列各项均不为0,其前n项和为,且(Ⅰ)求的值;(Ⅱ)求的通项公式;(Ⅲ)若=15时,Sn取得最小值,求a的值.20.(本小题满分14分)已知x为实数,用表示不超过x的最大整数,例如对于函数f(x),若存在,使得,则称函数函数.(Ⅰ)判断函数是否是函数;(只需写出结论)(Ⅱ)设函数f(x)是定义R在上的周期函数,其最小正周期为T,若f(x)不是函数,求T的最小值.(Ⅲ)若函数是函数,求a的取值范围.海淀区高三年级第一学期期中练习参考答案 数 学 (理科) .11阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
专业文档珍贵文档2018届上学期北京市海淀区高三期中考试试卷文科数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题(本题共8小题,每小题5分,共40分,只有一个选项正确,请把答案写.....在答题卷上.....) 1.若集合{}02<-=x x A ,集合{}12>=xx B ,则A B =I ( )A .RB .()2,∞-C .()2,0D .()+∞,22.命题“1sin ,0≤≥∀x x ”的否定是( ) A .0,sin 1x x ∀<> B .0,sin 1x x ∀≥> C .1sin ,0><∃x xD .1sin ,0>≥∃x x3.下列函数中,既是偶函数又在()0,+∞上单调递增的是( ) A .2)(x x f -=B .xx f -=3)(C .x x f ln )(=D .x x x f sin )(+=4.已知数列{}n a 满足12322(1,2,3,)n a a a a a n ++++==L L ,则( ) A .01<aB .01>aC .21a a ≠D .02=a5.在平面直角坐标系xOy 中,点A 的纵坐标为2,点C 在x 轴的正半轴上.在AOC △中,若cos AOC ∠=,则点A 的横坐标为( )A.B.C .3- D .36.已知向量a ,b 是两个单位向量,则“=a b ”是“2+=a b ”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件7.已知函数()()()10sin f x x ωωϕ=>+,2φπ<的部分图象如图所示,则ω,ϕ的值分别为( )A .2,3π B .2,3π-C .1,6π D .1,6π-8.若函数()2e ,02,0x x x f x ax x x ⎧≤⎪=⎨->⎪⎩的值域为1,e ⎡⎫-+∞⎪⎢⎣⎭,则实数a 的取值范围是( )A .()0,eB .()e,+∞C .(]0,eD .[)e,+∞第Ⅱ卷二、填空题(本题共6小题,每小题5分,共30分,请把答案写在答题卷上..........) 9.已知等差数列{}n a 满足12a =,246a a a +=,则公差d =_____. 10.已知向量()1,0=a ,(),m n =b ,若-b a 与a 平行,则n 的值为______. 11.已知函数()f x 是定义在R 上的周期为2的奇函数,当01x <<时,()1f x x=, 则()502f f ⎛⎫-+= ⎪⎝⎭_________.12.如图,弹簧挂着一个小球作上下运动,小球在t 秒时相对于平衡位置的高度h 厘米.由如下关系式确定:h t t =,[0)t ∈+∞,,则小球在开始振动即0t =时h 的值为_________,小球振动过程中最大的高度差为________厘米.此卷只装订不密封班级 姓名 准考证号 考场号 座位号专业文档珍贵文档13.能够说明“设x 是实数.若1x >,则311>-+x x ”是假命题的一个实数x 的值为______.14.已知非空集合B A ,满足以下两个条件: (i ){}1,2,3,4,A B A B ==∅U I ;(ii )集合A 的元素个数不是A 中的元素,集合B 的元素个数不是B 中的元素. 那么用列举法表示集合A 为_________.三、解答题(本题共6个小题,共80分.解答应写出必要的文字说明、证明过程或演...................算步骤,请把答案写在答题卷上..............) 15.(13分)已知函数()22sin cos 2cos 1f x x x x =+-.(1)求4f π⎛⎫⎪⎝⎭的值;(2)求函数()f x 的单调递增区间.16.(13分)已知等比数列{}n a 满足1238a a a =,516a =. (1)求{}n a 的通项公式及前n 项和n S ;(2)设21log n n b a +=,求数列⎭⎬⎫⎩⎨⎧+11n n b b 的前n 项和n T .专业文档珍贵文档17.(13分)如图,ABD △为正三角形,AC DB ∥,4=AC ,721cos =∠ABC .(1)求sin ACB ∠的值; (2)求AB ,CD 的长.18.(13分)已知函数()()32,3-=-=x x g x x x f . (1)求曲线)(x f y =在点(1,(1))f 处的切线方程; (2)求函数)(x f 在[]2,0上的最大值;(3)求证:存在唯一的0x ,使得()()00x g x f =.专业文档珍贵文档19.(14分)已知数列{}n a 满足121==a a ,22(1)nn n a a +=+-,∈n N*..(1)写出65,a a 的值;(2)设n n a b 2=,求{}n b 的通项公式; (3)记数列{}n a 的前n 项和为n S ,求数列{}182-n S 的前n 项和n T 的最小值.20.(14分)已知函数x x x x f ln )()(2-=. (1)求证:1是函数)(x f 的极值点;(2)设)(x g 是函数)(x f 的导函数,求证:()1g x >-.专业文档珍贵文档2018届上学期北京市海淀区高三期中考试试卷文 科 数 学 答 案第Ⅰ卷一、选择题(本题共12小题,每小题5分,共60分,只有一个选项正确,请把答案写.....在答题卷上.....) 1-4:CDCD5-8:ACBD第Ⅱ卷二、填空题(本题共4小题,每小题5分,共20分,请把答案写在答题卷上..........) 9.2 10.0 11.2-12413.214.{}3或{}1,2,4答对一个给3分.三、解答题(本题共6个小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤,请把答案写在答题卷上)15.解:(1)22sin cos 2cos 14444f ππππ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭22211=⨯-=⎝⎭; (2)()sin 2cos 224f x x x x π⎛⎫=+=+ ⎪⎝⎭.令222242k x k πππ-+π≤+≤+π,得388k x k ππππ-+≤≤+,k ∈Z ; ∴函数()f x 的单调递增区间为3,88k k ππππ⎡⎤-++⎢⎥⎣⎦,k ∈Z . 16.解:(1)设等比数列{}n a 的公比为q . ∵1238a a a =,且2132a a a =,∴328a =,得22a =,又∵35216a a q ==,∴38q =,得2q =,11a =.∴()12n n a n -*=∈N ,∴()111221112n nn n a q S q--===---; (2)∵12nn a +=,∴21log n n b a n +==,∴11111(1)1n n b b n n n n +==-++. ∴数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和11111111223111n n T n n n n ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭L . 17.解:(1)∵ABD △为正三角形,AC DB ∥,∴在ABC △中,3BAC π∠=, ∴3ACB ABC ππ⎛⎫∠=-+∠ ⎪⎝⎭.∴sin sin sin cos cos sin 333ACB ABC ABC ABC πππ⎛⎫∠=+∠=∠+∠ ⎪⎝⎭, ∵在ABC △中,cos 7ABC ∠=,()0,ABC ∠∈π,∴sin 7ABC ∠=∴1sin 72ACB ∠=+=. (2)在ABC △中,4AC =,由正弦定理得sin sin AB ACACB ABC=∠∠,∴4sin 5sin AC ACBAB ABC⋅∠===∠,专业文档珍贵文档又在正ABC △中,AB AD =,3DAB π∠=,∴在ADC △中,3DAC 2π∠=,由余弦定理得:2222cos 1625245cos 613CD AC AD AC AD DAC 2π=+-⋅∠=+-⨯⨯⋅=, ∴CD.18.解:(1)由()3f x x x =-,得()231f x x '=- ,∴()12f '=,又()10f =,∴曲线()y f x =在点()()1,1f 处的切线方程为()021y x -=-, 即220x y --=.(2)令()0f x '=,得3x =±,()f x 与()f x '在区间[]0,2的情况如下:∵()00f =,()26f =,∴函数()f x 在区间[]0,2上的最大值为6.(3)证明:设()()()333h x f x g x x x =-=-+, 则()()()233311h x x x x '=-=-+,令()0h x '=,得1x =±.()h x 与()h x '随x 的变化情况如下:则()h x 的增区间为(),1-∞-,()1,+∞,减区间为()1,1-.又()110h =>,()()110h h ->>,∴函数()h x 在()1,-+∞没有零点, 又()3150h -=-<,∴函数()h x 在(),1-∞-上有唯一零点0x . 综上,在(),-∞+∞上存在唯一的0x ,使得()()00f x g x =. 19.解:(1)31a =-,43a =,53a =-,65a =; (2)设2n n b a =,*n ∈N ,则()21222212nn n n n b b a a ++-=-=-=,∴{}n b 是以1为首项,2为公差的等差数列, ∴()11221n b n n =+-⋅=-. (3)()212121212n n n a a -+--=-=-,*n ∈N ,∴{}21n a -是以1为首项,2-为公差d 的等差数列, ∴数列{}n a 的前n 个奇数项之和为()21122n n na d n n -+=-, 由(2)可知221n a n =-, ∴数列{}n a 的前n 个偶数项之和为()2222n a a n n +=∴22n S n =,∴218218n S n -=-.∵()22218182n n S S ----=,且21816S -=-,∴数列{}218n S -是以16-为首项,2为公差的等差数列. 由2182180n S n -=-≤可得9n ≤, ∴当8n =或9n =时,数列{}218n S -的前n 项和n T 的最小值为89169722T T -⨯===-. 20.(1)证明:()()2ln f x x x x =-的定义域为()0,+∞,由()()2ln f x x x x =-得()()()()21'21ln 21ln 1f x x x x x x x x x=-+-=-+-, ∴()'10f =.当1x >时,()21ln 0x x ->,10x ->,专业文档珍贵文档∴()'0f x >,故()f x 在()1,+∞上单调递增; 当112x <<时,()21ln 0x x -<,10x -<, ∴()'0f x <,故()f x 在1,12⎛⎫⎪⎝⎭上单调递减;∴1是函数()f x 的极值点.(2)由题意可知,()()21ln 1g x x x x =-+-证明:()()21ln 12ln ln 1g x x x x x x x x =-+-=-+-,()0,x ∈+∞, 令()2ln h x x x =,()ln 1t x x x =-+-,()0,x ∈+∞,()()'2ln 1h x x =+,令()'0h x =得1ex =.()'h x ,()h x 随x 的变化情况如下:∴()min12e e h x h ⎛⎫==- ⎪⎝⎭, 即22ln e x x ≥-,当且仅当1e x =时取到等号.()1'x t x x-=,令()'0t x =得1x =,()'t x ,()t x 随x 的变化情况如下:∴()()min 10t x t ==,即1ln 0x x --≥,当且仅当1x =时取到等号. ∴()22ln ln 11ex x x x +-+->->-.即()1g x >-.。