下载文档原格式
质心位置不变定理质心位置不变定理是力学中一个重要的定理，它告诉我们在一个封闭系统中，质心的位置在没有外力作用下是恒定的。
这个定理的证明非常简单，我们可以通过几何方法来理解。
我们需要明确质心的定义。
在一个封闭系统中，如果有n个质点，分别质量为m1、m2、...、mn，它们的位置分别为(r1, r2, ..., rn)，那么这个系统的质心位置可以用以下公式表示：R = (m1r1 + m2r2 + ... + mnrn) / (m1 + m2 + ... + mn)其中，R表示质心的位置。
根据质心位置不变定理，我们可以得出结论：如果一个封闭系统受到的外力为零，那么无论这个系统中的质点如何运动，质心的位置都不会发生改变。
为了更好地理解这个定理，我们可以通过一个简单的例子来说明。
假设我们有一个由两个质点组成的封闭系统，它们的质量分别为m1和m2，位置分别为(r1, r2)。
如果没有外力作用在这个系统上，根据质心位置不变定理，我们可以得出以下结论：R = (m1r1 + m2r2) / (m1 + m2)对于这个系统来说，质心的位置只与质点的质量和位置有关，而与质点的运动状态无关。
也就是说，无论质点如何运动，质心的位置这个定理的证明非常简单，我们可以通过几何方法来理解。
假设我们有一个由n个质点组成的封闭系统，它们的质量分别为m1、m2、...、mn，位置分别为(r1, r2, ..., rn)。
我们可以将这个封闭系统看作一个整体，它的质心位置可以看作是这个整体的中心。
当没有外力作用在这个系统上时，这个整体将保持静止，质心的位置也会保持不变。
为了更好地理解这个定理，我们可以通过一个简单的例子来说明。
假设我们有一个由两个质点组成的封闭系统，它们的质量分别为m1和m2，位置分别为(r1, r2)。
如果没有外力作用在这个系统上，根据质心位置不变定理，我们可以得出以下结论：R = (m1r1 + m2r2) / (m1 + m2)对于这个系统来说，质心的位置只与质点的质量和位置有关，而与质点的运动状态无关。
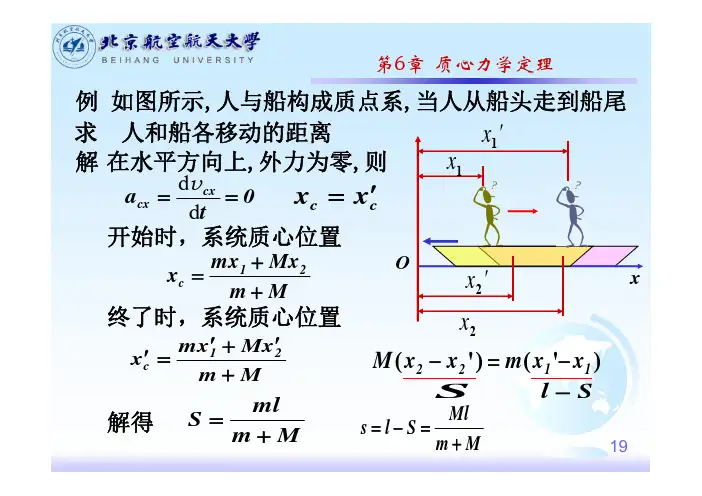
大学物理力学第六章质心运动定理（二）引言概述：大学物理力学的第六章质心运动定理（二）是质点系的动力学描述的重要内容。
本文将从引入质心的概念开始，逐步介绍质心运动定理的原理和应用。
正文：1. 质心的定义和性质：- 质心被定义为质点系中所有质点质量加权平均位置的矢量。
- 质心具有质点系中所有质点质量的总和，并且在质点系运动中保持位置不变。
- 质心的运动可以简化质点系的运动分析。
2. 质心运动定理的表述：- 质心运动定理指出，在外力作用下，质心的加速度等于质点系所受合外力与质点系总质量的比例。
- 质心的加速度可以通过所有质点受力的合力除以质点系总质量得到。
3. 质心运动定理的证明和推导：- 通过应用牛顿第二定律，可以推导出质心运动定理的表达式。
- 使用质点系质量的定义、质心的定义以及质点系中每个质点的位矢，可以推导出质心关于时间的二阶导数与质点系合外力的关系式。
4. 质心运动定理的应用：- 可以通过质心运动定理计算质心在不同外力作用下的加速度。
- 质心运动定理可以用于解决质点系的多体动力学问题。
- 质心运动定理对于研究刚体的运动也具有重要意义。
5. 质心运动定理的限制和扩展：- 质心运动定理只适用于质点系在外力作用下的运动，不适用于内力相互作用的情况。
- 在非惯性系中，质心运动定理需要进行修正。
- 质心运动定理可以扩展应用于连续体力学的问题分析。
总结：大学物理力学第六章质心运动定理（二）介绍了质心的概念和性质，阐述了质心运动定理的原理和推导过程，并探讨了质心运动定理的应用范围和限制。
掌握质心运动定理对于解决质点系的动力学问题非常重要，并且在刚体和连续体力学领域也有广泛应用。
第五章质心刚体质心运动定理ca m F v v =合外质点系的质心加速度由合外力确定，与内力无关。
牛顿定律的独特性质：如果它在某一小尺度范围内是正确的，那么在大尺度范围内也将是正确的。
特殊的质点系——刚体m1l5.1.2 质点系动力学量的分解质心参考系：随质心一起运动的平动参考系，简称质心系。
在质心系中质心静止==c c v r v v常矢量质心系中的运动图象各质点从质心四面散开，或向质心八方汇聚。
质心成为一个运动中心，运动时时刻刻是“各向同性的”。
质点系的动量质点系的动量等于质心的动量c p p v v =质点系相对质心的动量总是为零0=′=′∑ii i v m p vv 质点系中各质点m i 相对质心的运动),(i i v r ′′v v m iO Ci r ′v ir v Cr v 在任一参考系中质点系的动量、动能和角动量与质心运动的关系核反应中的资用能质点系的角动量i c i i c i v v v r r r ′+=′+=v v v v v v ,∑×=iii i v m r L v v v ∑∑∑∑′×′+×⎟⎠⎞⎜⎝⎛′+⎟⎠⎞⎜⎝⎛′×+⎟⎠⎞⎜⎝⎛×=i i i i c i i i i i i c c i i c v m r v r m v m r v m r L v v v v v v v v v ∑′×′=′×=′+=ii i i c c c c v m r L v m r L L L L vv v v v v v v v , ,质点系的角动量可分解成质心角动量与质点系相对质心的角动量之和同一参考点质心为参考点m iOCi r ′v ir v Cr v 其中5.1.3 质心参考系质心系一般是非惯性系，引入平移惯性力ci a m v −在质心系中质点系的动能定理和角动量定理质心系中质点系的动量恒为零，质点系的动量定理不必考虑。
第六章质心
质点组的运动比较复杂，采用两种眼光来处理
二、着眼于把握质点组的总体运动，再分析各个质点之间的相对运动。
即将质点组的复杂运动分解为这两种运动的叠加，这是一种新的途径，可将力学理论推向一个新的境界。
一、着眼于每个质点，平等地对待每个质点，将相互作用分为内部的外部的，分析了内部相互作用的若干特点之后，确定了质点组的动量变化定理及其守恒条件，机械能变化定理及其守恒条件，和角动量变化定理及其守恒条件，成功地解决了一批典型的力学问题，诸如：
–两体碰撞
–火箭推进速度–三种宇宙速度–有心运动
这标志着我们把牛顿力学理论推进到一个新的阶段。
是否存在这样一种运动，它反映了质点组总体运动的宏观特点？
θ
θ
2
λ
2R
m
说明
(1)质心相对于质点组的位置与坐标系无关，
质心的位置完全由质点组的质量分布决定
(2)对于密度均匀，形状对称的物体，其质心在物体的几何中心处
对于一般物体，质心不一定在物体上
例如圆环的质心在圆环的轴心上
锥体上滚
②物体若有某种对称性，质心就位于对称的位置。
它与牛顿第二定律在形式上完全相同，相应于系统的质量全部集中于系统的质心，在合外力的作用下，质心以加速度a c 运动
∑==N i i
C F a M 1
凡是由牛顿第二定律直接导出的定理，如质点动量变化定理，机械能变化定理，质点角动量变化定理，均适用于质心。
只需将质点的质量改换为质点组的总质量，力改换为合外力
系统内力不会影响质心的运动
定向爆破
质心参考系
质心参考系：随质心一起运动的平动参考系，简称质心系。
质心系以可以是惯性系，也可以是非惯性系。
在质心系中质心静止
c v i r c
r ic
r C
O
i
质心系中所有质点相对于质心的动量之和为零.若选质心为参考点,则质心的坐标始终为零。
质点组整体随质心的运动+各质点相对于质心的运动
质点组的复杂运动通常可分解为：
核反应中的资用能
高能粒子碰静止靶粒子能量利用率低，采用对撞
质心动能定理
质心系中质点组动能定理的微分形式
k
dE dW dW dW =++惯外内()()()0
i c i c i i c c i
i
dW m a dr a d m r a d Mr =-⋅=-⋅=-⋅=∑∑
惯k
k E W W dE dW dW ∆=+=+外内外内 ,质心系中质点组动能定理的微分形式和积分形式
与惯性系完全相同，机械能定理也相同。
质心系中质心位置矢量为常量
=c r d 0
=惯dW
m
m M。
