第4节 质心与质心运动定理

质心运动定理讲解
质心运动定理指的是质点系的质心以恒定的速度沿着直线运动，
且其所受合外力等于其质量与加速度的积。

这个定理结合了牛顿第二
定律和质点系的质心公式，表达了质心运动的关键性质。

牛顿第二定律指出，物体受到的合外力等于其质量乘以加速度。

对于质点系，可以将其看成一个由若干个质点组成的系统。

此时，质
点系的质心可以看作是其所有质点质量之和的加权平均值。

因此，如
果我们知道了质点系受到的合外力，就可以计算出质点系的总加速度，从而推导出质心的运动规律。

具体来说，如果质点系受到的合外力为F，质点系的质量为M，
质心的速度为v，则根据牛顿第二定律有F=Ma。

又根据质点系的质心
公式，有Mv=Σmivi，其中Σmivi表示所有质点的质量与速度之积之和。

这里我们假设质点系并不发生转动，因此质心的速度与角速度均
为常数。

将上述两个式子联立，可以得到Mv=F/a，也就是质心的加速度与外力和质点系质量之比相等。

因此，质心的运动可以看成是一个受到
恒定加速度的匀加速直线运动，其速度随时间线性增加。

总之，质心运动定理给出了描述质点系运动的一个关键性质。

通
过计算质心的加速度，我们可以推导出质心的运动规律，从而了解整
个质点系的运动情况。

质心运动定律
质心运动定律指的是质点系统的质心在受到外力的作用下运动
的规律。

根据牛顿第二定律，质心所受的合外力等于质点系统的总质量乘以质心的加速度。

因此，质心的运动可以看做是一个单独的质点在受力下的运动。

质心运动定律有以下几个特点：
1.质心的运动是质点系统中所有质点运动的平均化结果。

2.质心的运动状态与质点系统中的相对位置、互相作用力等无关。

3.质心的运动方向与受力方向相同或相反，具体取决于系统所受的合外力方向。

质心运动定律在工程、物理、天文学等领域有着广泛的应用。

例如，在火箭发射时，需要控制火箭的质心位置以保证火箭的稳定性。

在天文学中，质心运动定律常常被用于研究行星、恒星等天体的运动规律。

- 1 -。

第五章质心刚体质心运动定理ca m F v v =合外质点系的质心加速度由合外力确定，与内力无关。

牛顿定律的独特性质：如果它在某一小尺度范围内是正确的，那么在大尺度范围内也将是正确的。

特殊的质点系——刚体m1l5.1.2 质点系动力学量的分解质心参考系：随质心一起运动的平动参考系，简称质心系。

在质心系中质心静止==c c v r v v常矢量质心系中的运动图象各质点从质心四面散开，或向质心八方汇聚。

质心成为一个运动中心，运动时时刻刻是“各向同性的”。

质点系的动量质点系的动量等于质心的动量c p p v v =质点系相对质心的动量总是为零0=′=′∑ii i v m p vv 质点系中各质点m i 相对质心的运动),(i i v r ′′v v m iO Ci r ′v ir v Cr v 在任一参考系中质点系的动量、动能和角动量与质心运动的关系核反应中的资用能质点系的角动量i c i i c i v v v r r r ′+=′+=v v v v v v ,∑×=iii i v m r L v v v ∑∑∑∑′×′+×⎟⎠⎞⎜⎝⎛′+⎟⎠⎞⎜⎝⎛′×+⎟⎠⎞⎜⎝⎛×=i i i i c i i i i i i c c i i c v m r v r m v m r v m r L v v v v v v v v v ∑′×′=′×=′+=ii i i c c c c v m r L v m r L L L L vv v v v v v v v , ,质点系的角动量可分解成质心角动量与质点系相对质心的角动量之和同一参考点质心为参考点m iOCi r ′v ir v Cr v 其中5.1.3 质心参考系质心系一般是非惯性系，引入平移惯性力ci a m v −在质心系中质点系的动能定理和角动量定理质心系中质点系的动量恒为零，质点系的动量定理不必考虑。

质心运动定理讲解
质心运动定理是物理学中的一个重要定理，它描述了一个物体的质心在外力作用下的运动规律。

质心是一个物体的所有质点的平均位置，它是一个重要的物理量，可以用来描述物体的运动状态。

根据质心运动定理，一个物体的质心在外力作用下的运动规律可以用以下公式表示：
F = ma
其中，F表示物体所受的外力，m表示物体的质量，a表示物体的加速度。

这个公式表明，一个物体所受的外力越大，它的加速度就越大，质心的运动速度也就越快。

质心运动定理的应用非常广泛，它可以用来解释很多物理现象。

例如，当一个物体受到一个施加在它上面的力时，它的质心会向着力的方向运动。

这个现象可以用质心运动定理来解释，因为当一个物体受到外力时，它的质心会受到相同的力，从而产生加速度，导致质心运动。

质心运动定理还可以用来解释物体的旋转运动。

当一个物体旋转时，它的质心也会随着旋转，但是质心的运动速度和旋转速度是不同的。

这个现象可以用质心运动定理来解释，因为当一个物体旋转时，它的质心会受到向心力的作用，从而产生向心加速度，导致质心运动。

质心运动定理是物理学中一个非常重要的定理，它可以用来解释很多物理现象。

通过理解和应用质心运动定理，我们可以更好地理解物体的运动规律，从而更好地掌握物理学知识。

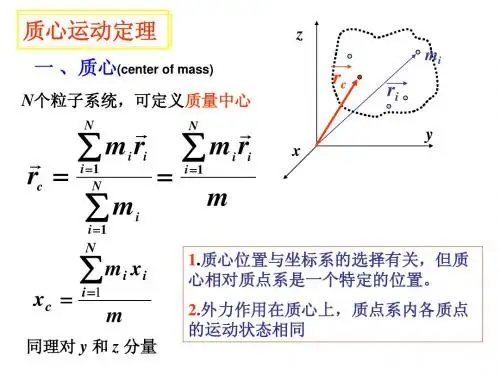
质心与质心运动定律一、质心1. 定义我们先来回顾一下牛顿第二定律:是对单个质点而言的,由于质点系内各质点的运动情况各不相同,加速度也各不相同,并不能简单的等效于 (M是体系的总质量),但对质点系而言,确实存在一个特殊点C,而使成立,这个ac是该特殊点C的加速度.这个特殊点称为质心.2. 质心的位置如果将质点系各质点参量记为mi 、ri、vi、xi、yi、zi……，质点系质心记为C则对于由两个质点构成的简单质点系，质心在它们连线上，将这两个质点的质量分别记为m1和m2，间距记为l，那么质心与两者的间距依次为：二、质心运动定律1.质心动量定理：外力对体系的冲量等于质心动量的增量。

2.质心运动定律：体系总质量与质心加速度的乘积等于外力的矢量和，或者说，在诸外力作用下，体系质心的加速度等于质量为体系总质量的质点在这些外力共同作用下的加速度。

对一个质点系而言，同样可以应用牛顿第二定律。

三、习题1.试求匀质三角形板的质心位置。

答案：三条中线的焦点：即几何中的重心2. 试求匀质三角形框架的质心位置。

答案：三边中点构成的小三角形的内心。

3. 一轻弹簧两端各系有质量分别为m和2m的物块，用系于质量为m的物块上的细线悬挂在支点O上，如图。

今将细线突然剪断，求该瞬时体系质心的加速度。

答案：g。

4. 用质心运动定理解：长为l、总质量为m的柔软绳索盘放在水平台面上。

用手将绳索的一端以恒定速率vo向上提起，求当提起高度为x时手的提力F。

5. 如图所示，用劲度系数为k的轻弹簧连接质量分别为m1、m2的木块，放在光滑的水平面上。

让第一个木块紧靠竖直墙，在第二个木块的侧面上施加水平压力，将弹簧压缩l长度。

撤去这一压力后，试求系统质心可获得的最大加速度值和最大速度值。

多说两句：体系的总动量为：质心的动能为：质点系相对质心的动能为：质点系的总动能为：（克尼希定理）☆在使用质心参照系时要特别主要克尼希定理的使用！。