质心运动定理动量定理

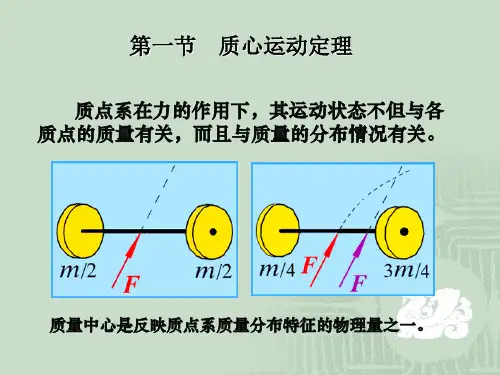
质心系动量定理
质心系动量定理，是在物理学中常常使用的一个定理，它是描述一个系统动量守恒的定理。

在物理学中，质心系是一个非常有用的概念，它可以帮助我们更好地理解物体的运动状态。

首先，让我们来了解一下什么是质心。

质心是一个物体所有质点的平均位置，它是一个重要的物理量。

在物理学中，我们经常使用质心来描述一个物体的运动状态。

接下来，我们来了解一下什么是动量。

动量是一个物体的运动状态的量度，它是一个矢量量。

在物理学中，我们使用动量来描述一个物体的运动状态。

在物理学中，质心系动量定理是指：在一个封闭系统中，系统质心的速度等于系统所有质点动量之和除以系统总质量。

这个定理可以用来证明一个系统的动量守恒。

举个例子来说，假设有两个质点A和B，它们的质量分别为m1和m2，速度分别为v1和v2。

那么这个系统的总质量为
m1+m2，总动量为m1v1+m2v2。

根据质心系动量定理，这个系统的质心速度为(m1v1+m2v2)/(m1+m2)。

当然，在实际应用中，我们可能会遇到更加复杂的系统，但是质心系动量定理的原理是一样的：系统质心的速度等于系统所有质点动量之和除以系统总质量。

总之，质心系动量定理是一个非常重要的物理定理，在物理学中有着广泛的应用。

它可以帮助我们更好地理解物体的运动状态，并且可以用来证明一个系统的动量守恒。

第十一章 质心运动定理 动量定理一、目的要求1．质点系（刚体、刚体系）是动力学的主要力学模型，解决质点系（刚体、刚体系）动力学问题的主要方法有三类：（1）达朗伯原理；（2）动力学基本定理；（3）动力学普遍方程和拉格朗日方程。

2．对质点系（刚体、刚体系）的质心、动量有清晰的理解，能熟练地计算质点系（刚体、刚体系）的动量，能熟练地应用质点系的动量定理、质心运动定理（包括相应的守恒定律）求解动力学问题。

二、基本内容1．基本概念质点系的质心、质点系（刚体、刚体系）的动量、2．主要公式（1）质点系（刚体、刚体系）质心的计算 1）矢径形式 M r m r i i c 或 Mr m r ic i c 2）直角坐标形式Mx m x i i c ，M y m y i i c ，M z m z i i c 其中 k z j y i x r i i i i 为第i 个质点到固定点O 的矢径。

k z j y i x r c c c c 为质点系的质心到固定点O 的矢径。

ic r 为第i 个刚体的质心到固定点O 的矢径。

m i 为第i 个质点的质量，i m M 为质点系（刚体、刚体系）的质量。

（2）质点系（刚体、刚体系）动量的计算1）矢径形式 c i i v M v m P2）投影形式ix i x v m p ，iy i y v m p ，iz i z v m p ，222z y x P P P P注意：动量是矢量，需要时还要计算动量的方向。

（3）动量定理（质心运动定理）n i (e)i F dt p d 1 )(1n i (e)i c F a M 式中 n i c i i v M v M p 1 ，是质点系某瞬时的动量， n i e i F 1)( 是质点系所受外力的主矢量。

c a 为质点系心的加速度。

三、重点和难点1．重点：（1）质点系（刚体、刚体系）质心、动量的计算。

（2）质点系动量定理、质心运动定理。

2．难点：质点系动量定理、质心运动定理的应用。

刚体质心运动的动量定理
一、定义和概述
刚体质心运动是指刚体绕其质心进行的运动。

刚体质心运动的研究是刚体动力学中的重要部分，其研究的主要内容包括质心的位移、速度和加速度等。

而动量定理则是质心运动的基本定理之一，用于描述质心运动的动量变化和力矩之间的关系。

二、刚体质心运动的特点
刚体质心运动具有以下特点：
1.刚体的质心始终在同一直线上运动，即质心轨迹是一条直线或一个点。

2.刚体的角动量等于零，因为刚体绕质心的运动可以分解为质心的平动和相对于质心的旋转运动，而旋转运动的角动量为零。

3.刚体的动量等于质心的动量，因为刚体中任意一点的动量都与质心的动量相同。

三、动量定理在刚体质心运动中的应用
在刚体质心运动中，动量定理可以表述为：对于刚体绕其质心的运动，其动量的变化率等于作用在刚体上的外力对质心的力矩。

这个定理可以用来描述刚体在力矩作用下的质心运动规律。

具体来说，假设刚体的质量为m，质心的位置为r(t)，则刚体的动量为p=m*r(t)。

设外力F作用于刚体上，其作用点相对于质心的位置为f(t)，则外力对质心的力矩为M=F*f(t)。

根据动量定理，有dp/dt=M，即m*dr(t)/dt=M。

这个公式可以用来求解刚体在力矩作用
下的质心运动规律。

四、结论
综上所述，动量定理是刚体质心运动的基本定理之一，它可以用来描述刚体在力矩作用下的质心运动规律。

在具体的应用中，可以通过对动量定理进行变换和化简，求解出刚体在给定外力矩作用下的质心运动轨迹、速度和加速度等物理量。

质心运动定理3、质心运动定理质心运动定理问题：内力是否影响质心的运动？(e)1d ()d n C ii mv F t==∑由(e)1d d n C ii v m F t ==∑得(e)1nC ii ma F ==∑或质点系的质量与质心加速度的乘积等于作用于质点系外力的矢量和.－－质心运动定理质心运动定理与动力学基本方程有何相似与不同之处？质心运动定理常量质心运动定理质心运动定理内力不能改变质心的运动汽车发动机的气体压力是原动力通过传动机构使主动轮转动地面摩擦力(e)1nC ii ma F ==∑ma F=质点系质心的运动可看成质点的运动，此质点集中了质点系的质量及其所受的力爆破山石通过质心运动轨迹， 确定石块堆落地点 ma F=是公理，描述质点运动状态变化规律(e)1nC ii ma F ==∑是导出定理，描述质心运动状态变化规律质心运动守恒定律(e)Cx xma F=∑(e)Cy yma F=∑(e)Cz zma F=∑2(e)Cnv m F ρ=∑(e)C t v m F t =∑d d (e)0bF=∑在直角坐标轴上的投影式为:在自然轴上的投影式为:(e)F ∑≡若 则 常矢量 C v =(e)0xF∑≡若 则 常量 =Cxv若初始静止，质心位置不变 若初始速度投影等于0， 质心在该轴坐标不变质心运动定理均质曲柄AB长为r,质量为m1,假设受力偶作用以不变的角速度ω转动,并带动滑槽连杆以及与它固连的活塞D ,如图所示.滑槽、连杆、活塞总质量为m2,质心在点C .在活塞上作用一恒力F .不计摩擦及滑块B的质量,求:作用在曲柄轴A处的最大水平约束力Fx .例1t m m m m r t x a C Cxωωcos 2d d 2121222⎪⎭⎫⎝⎛++-==tm m r F F x ωωcos 2212⎪⎭⎫⎝⎛+-=⎪⎭⎫⎝⎛++=212m ax2m m r F F ω最大水平约束力为应用质心运动定理()FF a m m x Cx -=+21()21211cos cos 2m m b r m r m x C +⋅⎥⎦⎤⎢⎣⎡++=ϕϕ分析整体，受力如图所示。

动量定理质心运动定理动量定理质心运动定理质点的动量定理可以表述为:质点动量的微分，等于作用于质点上力的元冲量。

用公式d(mv),Fdt表达为 (17-7)d(mv),Fdt (17-8)tptp2211设时刻质点系的动量为，时刻质点系的动量为，将(17-8)式积分，积分区tt21间为从到，得t2p,p,Fdt21,t 1 (17-9)t2Fdt,I,tttF211记，称为力在到时间间隔内的冲量。

式(17-9)为质点系动量定理的积分形式，它表明质点系在某时间间隔内的冲量的改变量，等于作用在质点系上的外力主矢在该时间间隔内的冲量。

(e)(i)MFFiii对于质点系而言，设为质点所受到的外力，为该质点所受到的质点系内力，根据牛顿第二定律得dv(e)(i)im,F，F(e)(i)iiima,F，Fdtiiii 即mi除了火箭运动等一些特殊情况，一般机械在运动中可以认为质量不变。

如果质点的质量不dmv()(e)(i)ii,F，Fiidt变，则有上式对质点系中任一点都成立，n个质点有n个这样的方程，把这n个方程两端相加，得ndm(v),iinn()()ei,1i,，FF,,iidt,1,1iinn(e)(i)FF,,iii,1i,1 质点系的内力总是成对地出现，内力的矢量和等于零。

上式中是质点dp(e),F(e)RFdtR系上外力的矢量和，即外力系的主矢，记作，则上式可写为(17-10)1这就是质点系动量定理的微分形式，它表明:质点系的动量对时间的导数等于作用在质点系上外力的矢量和。

(e)dp,Fdt 将式(17-10)写成微分形式 Rtptptt222111 设时刻质点系的动量为，时刻质点系的动量为，上式从到积分，得t2(e)p,p,Fdt21R,t,I1 (17-11)p,p0 当外力主矢为零时，由上式可推出质点系的动量是一常矢量，即这表明当作用在质点系上的外力的矢量和为零时，质点系的动量保持不变，这就是质点系的动量守恒定理。

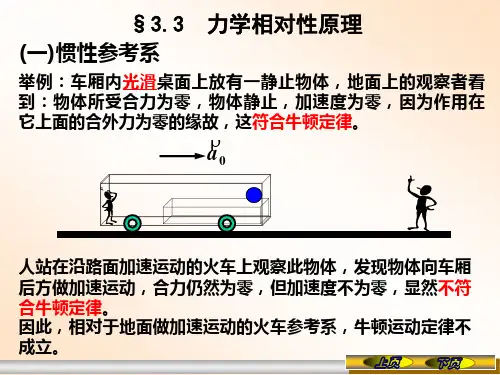
求腰长为a 等腰直角三角形均匀薄板的质心位置。

求腰长为等腰直角三角形均匀薄板的质心位置。

解：dm = 2xσdx a/ 2 y a 三角形质心坐标x 三角形质心坐标c是xc ∫ xdm = ∫ = ∫ dm ∫ 0 a/ 0 2 a = 2 3 2σxdx 2σx dx 2 O x dx x 这个结果和熟知的三角形重心位置一致。

这个结果和熟知的三角形重心位置一致。

11三、质心运动定理右边: 右边: r d 据质点系动量定理: 据质点系动量定理∑ F = (∑m v . n n i=1 i dt i i=1 i i d d d r (∑m v = ∑m ( = ∑m r. dt d t ∑m dt n 2 n n i=1 i i i=1 i 2 i=1 n i 2 n i=1 i 2 c i=1 i r ∑m r n 上式第二步分子, 上式第二步分子, 分母均乘以 dt 故质点系动量定理: 故质点系动量定理 2 上式中, 上式中, r dr 2 ∑ m, i=1 i c r 质心的加速度, 为质点系质心的加速度,用 aC 表示, r ∑F n i =1 i r = ma C ______称为质心运动定理. ______称为质心运动定理. 称为质心运动定理 12r ∑F n i =1 i r = ma C 此式表示，此式表示，质点系质心的运动与这样一个质点的运动具有相同的规律，运动具有相同的规律，该质点的质量等于质点系的总质量，质量，作用于该质点的力等于作用于质点系的外力的质心运动定律。

矢量和。

这个结论称为质心运动定律矢量和。

这个结论称为质心运动定律。

表明: 表明不管物体的质量如何 Y 分布，分布，也不管外力作用在物体的什么位置上，体的什么位置上，质心的运动就象是物体的质量全部都集中于此，集中于此，而且所有外力也 C 都集中作用其上的一个质点 O X 的运动一样。

的运动一样。

质心运动反映了质点系的整体运动趋势。

动量定理 质心运动定理质点的动量定理可以表述为：质点动量的微分，等于作用于质点上力的元冲量。

用公式表达为 Fv =)(m dt d（17-7）dt m d F v =)( （17-8）设1t 时刻质点系的动量为1p ，2t 时刻质点系的动量为2p ，将（17-8）式积分，积分区间为从1t 到2t ，得⎰=-2112t t dtF p p （17-9）记IF =⎰21t t dt ，称为力F 在1t 到2t 时间间隔内的冲量。

式（17-9）为质点系动量定理的积分形式，它表明质点系在某时间间隔内的冲量的改变量，等于作用在质点系上的外力主矢在该时间间隔内的冲量。

对于质点系而言，设)(e i F 为质点i M 所受到的外力，)(i i F 为该质点所受到的质点系内力，根据牛顿第二定律得)(i i (e)ii i m F F a += 即)()(i i e i iidt d m F F v +=除了火箭运动等一些特殊情况，一般机械在运动中可以认为质量不变。

如果质点的质量i m 不变，则有 )()()(i i e i i i dt m d F F v +=上式对质点系中任一点都成立，n 个质点有n 个这样的方程，把这n 个方程两端相加，得∑∑∑===+=ni i i ni e ini i i dtm d 1)(1)(1)(F F v质点系的内力总是成对地出现，内力的矢量和∑=ni i iF1)(等于零。

上式中∑=ni e iF1)(是质点系上外力的矢量和，即外力系的主矢，记作)(e RF ，则上式可写为)(e R dt d F p= （17-10）这就是质点系动量定理的微分形式，它表明：质点系的动量对时间的导数等于作用在质点系上外力的矢量和。

将式（17-10）写成微分形式dt d e R )(F p =设1t 时刻质点系的动量为1p ，2t 时刻质点系的动量为2p ，上式从1t 到2t 积分，得⎰=-21)(12t t e R dtF p p I =（17-11）当外力主矢为零时，由上式可推出质点系的动量是一常矢量，即0p p =这表明当作用在质点系上的外力的矢量和为零时，质点系的动量保持不变，这就是质点系的动量守恒定理。