结构化学 第九章 离子化合物 [兼容模式]
- 格式:pdf
- 大小:4.09 MB
- 文档页数:77
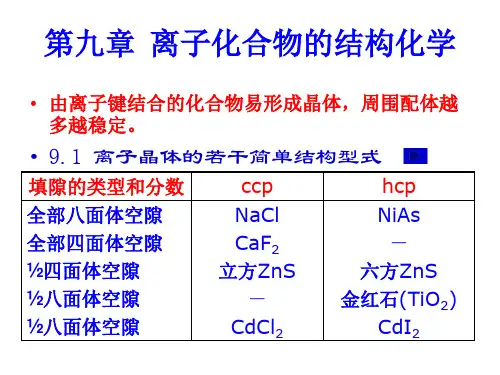








第九章离子化合物地结构化学
离子化合物的结构一般由阳离子和阴离子组成,它们通过离子键相互吸引在一起。
阳离子通常为金属离子,具有较小的离子半径和正电荷,阴离子则为非金属离子,通常具有较大的离子半径和负电荷。
离子化合物的结构可以是离子晶体、氧化物型、卤化物型等不同类型。
离子晶体是最常见的离子化合物结构类型,它的晶格是由阳离子和阴离子按照一定的比例和排列方式组成的。
阳离子和阴离子的比例决定了离子化合物的化学式,而它们的排列方式则决定了离子化合物的晶格。
离子晶体的晶格结构可以通过X射线衍射等方法进行研究。
晶格结构的解析揭示了离子化合物中离子的排列方式、配位数以及离子键的键长和键角等重要参数。
离子化合物的晶格结构分为简单离子晶体、离子对极化晶体以及各向异性晶体等不同类型。
离子化合物的晶格结构对其性质具有重要影响。
离子化合物的硬度、熔点、热稳定性等性质与晶格结构有关。
晶格结构中存在的空隙和缺陷也会对离子化合物的性质产生影响。
除了离子化合物的结构外,离子化合物的电导性和溶解度也是重要的研究内容。
离子化合物在溶液中可以电离成离子,形成电解质。
离子化合物的电导性与其离子的浓度、移动性以及溶解度有关。
离子化合物的溶解度可以通过溶解度积常数来描述。
溶解度常数与离子化合物的晶格能、溶剂的极性、温度等因素相关。
总之,离子化合物的结构化学研究揭示了离子间的相互作用和离子化合物的晶格结构。
这些研究对于理解离子化合物的性质和应用具有重要意义。

第九章离子化合物的结构化学离子化合物是由阴阳离子通过离子键连接而成的化合物。
离子化合物的结构化学主要研究其晶体结构和离子键的特性。
在离子化合物的结构中,离子的排列方式、离子大小和电荷、晶格常数等因素都对化合物的性质产生重要影响。
离子化合物的晶体结构可以通过X射线衍射等方法进行研究。
根据阴阳离子的大小和电荷,离子化合物的晶体结构可以分为离散型和连续型。
离散型的离子化合物晶体结构中,阳离子和阴离子排列在空间中形成一个三维网络,阳离子和阴离子之间通过离子键相互连接。
此外,离散型的离子化合物中阳离子和阴离子的配位数也会对晶体结构产生影响。
例如,钠氯化物(NaCl)是一种典型的离散型离子化合物,其中钠离子和氯离子的配位数均为6、连续型的离子化合物晶体结构中,阳离子和阴离子排列在空间中形成一个连续的正负电荷分布,阳离子和阴离子之间通过离子键相互连接。
常见的连续型离子化合物有铁氰化钾(K4[Fe(CN)6])和硫酸铜(CuSO4)等。
离子键是离子化合物中阴阳离子之间的强相互作用力。
离子键的强度取决于离子的电荷和离子的大小。
通常情况下,离子的电荷越大,离子键的强度越大。
而离子的大小则会影响离子键的长度。
通过离子键的形成,离子化合物的阴阳离子可以达到电中性。
离子化合物的结构化学研究对于理解离子化合物的性质具有重要意义。
例如,结构化学的研究可以揭示离子化合物的稳定性和熔点等物理性质。
此外,结构化学还可以为离子化合物的制备和应用提供指导。
以钠氯化物为例,由于其晶体结构的稳定性和离散型离子连接的特性,钠氯化物在化工领域中被广泛应用于制备其他化合物和材料,如氯化钠溶液的电解制氯等。
总之,离子化合物的结构化学研究对于深入理解离子化合物的性质和应用具有重要意义。
通过研究离子化合物的晶体结构和离子键特性,可以为离子化合物的制备和应用提供理论依据和指导,促进相关领域的发展。

离子化合物的结构化学离子键是由正离子与负离子之间的静电相互吸引力形成的一种化学键。
在离子化合物中,金属原子失去一个或多个电子,形成正离子,而非金属原子则获得这些电子,形成负离子。
这种正负电荷的吸引力使得离子之间形成稳定的晶体结构。
离子的结构可以通过离子半径、电荷数、电场效应等因素来解释。
离子半径是指离子的中心到其最外层电子轨道的距离。
正离子的离子半径通常小于其原子半径,因为它们失去了一个或多个电子。
而负离子的离子半径通常大于其原子半径,因为它们获得了一个或多个电子。
这种离子半径的差异导致了离子之间的空间排列方式。
离子的电荷数也会影响离子化合物的结构。
正离子的电荷数越大,其吸引力越大,离子之间的结合越紧密,晶体结构越稳定。
相反,负离子的电荷数越多,其排斥力越大,晶体结构越不稳定。
电场效应是指离子周围的电场对离子结构的影响。
电场中的离子会受到周围离子的电荷吸引和排斥力的影响,从而影响其排列方式。
如果离子的电荷数相同,但大小不同时,较大的离子会被周围的电子云推开,使其晶体结构呈现出空间扩展的特点。
离子化合物的晶体结构通常是由离子排列而成的。
离子可以沿着规则排列的路径组成晶格。
最常见的晶体结构是离子化合物的立方紧密堆积(rock-salt结构)和六方最密堆积(cesium chloride结构)。
在立方密堆结构中,正离子和负离子是以等距离排列的,形成一个规则的晶格。
而在六方密堆结构中,两种离子交替排列,并且每个正离子周围有六个负离子。
离子化合物的结构对其性质有重要影响。
由于离子之间的电荷吸引力,离子化合物通常具有高熔点和高沸点。
它们还具有良好的溶解性,因为水等极性溶剂能够与离子之间的电荷相互作用。
此外,离子化合物还有很高的硬度和脆性,因为其结构中离子的排列方式容易被破坏。
总之,离子化合物的结构化学研究离子之间的相互作用、离子的排列方式以及其性质。
了解离子化合物的结构对于理解其物理和化学性质以及其应用具有重要意义。