中国海洋大学全日制本科课程期末考试试卷

中国海洋大学2021年秋季学期《线性代数》课程试卷试卷 A 考试方式 闭卷 考试时间（120分钟）一. 单项选择题1.设非齐次线性方程组B AX =中,,)(r A r n m =⨯则下列结论成立的为( )A.r=m 时,方程组有解;B.r=n 时,方程组有唯一解;C.m=n 时,方程组有唯一解;D.r<n 时,方程组有无穷解. 解: A.r=m 时,系数矩阵的秩等于增广矩阵的秩.2.设A 为m ×n 矩阵,B 为n 维列向量,则下列结论成立的是( ) A. 若0=AX 仅有零解,则B AX =有唯一解; B. 若0=AX 有非零解,则B AX =有无穷解; C. 若B AX =有无穷解,则0=AX 仅有零解; D. 若B AX =有无穷解,则0=AX 有非零解. 解: D.若B AX =有无穷解,则n A r <)(,故0=AX 有非零解.3.设A 为n 阶实矩阵,TA 是A 的转置矩阵,则对于线性方程组(I): 0=AX 和(II) 0=AX A T,必有 ( )A.(II)的解是(I)的解,(I)的解也是(II)的解;B.(II)的解是(I)的解,但(I)的解不是(II)的解;C.(I)的解不是(II)的解,(II)的解也不是(II)的解;D.(I)的解是(II)的解,但(II)的解不是(I)的解. 解: A.设 ),0(0≠=ξξA 则),0(00≠=⋅=ξξT T A A A 所以,(I)的解是(II)的解; 反之,设 ),0(0≠=ηηA A T则),0(0)()()(≠==ηηηηηA A A A T T T η为一个列向量,所以必有: 0=ηA .亦即: (II)的解是(I)的解. 因此,选A.4.21,ββ是非齐次线性方程组B AX =的两个不同解,21,αα是对应导出组的基础解系.21,k k 为任意常数,则B AX =的通解为( )A.;2)(2121211ββααα-+++k k B.;2)(2121211ββααα++-+k k C.;2)(2121211ββββα-+++k k D..2)(2121211ββββα++-+k k解: B.211,ααα-线性无关,并且是导出组的解,所以211,ααα-为导出组的一个基础解系;221ββ+为B AX =的特解,故选(B).5.设321,,ααα为四元线性方程组B AX =的三个解向量,且3)(=A r ,T)4,3,2,1(1=α,T )3,2,1,0(32=+αα,c 为任意常数,则B AX =的通解为( )A.,11114321⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛c B. ,32104321⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛c C. ,54324321⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛c D. ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛65434321c解: C.T )4,3,2,1(1=α为B AX =的一个特解.其导出组的基础解系仅含一个向量,且)(2321ααα+-为导出组的一个非零解, 故B AX =的通解为)](2[3211αααα+-+c .6.齐次线性方程组AX =,0111113212=⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛x x x λλλλ若存在三阶非零方阵B 满足0=AB ,则( ) A.λ=-2,且|B |=0; B. λ=-2,且|B |≠0; C. λ=1,且|B |=0; D. λ=1,且|B |≠0. 解: C.B 的三个列向量均为0=AX 的解向量,即方程组0=AX 有非零解,故|A |=-(2)1-λ=0,从而λ=1;当λ=1时,r(A )=1,故0=AX 基础解系包含两个向量,矩阵B 的三个列向量必线性相关, 所以|B |=0.7.若TT )1,1,0(,)2,0,1(21-==ξξ均为方程组0=AX 的解,则A 为( )A.()112-, B. ⎪⎪⎭⎫⎝⎛--110102,C. ⎪⎪⎭⎫ ⎝⎛--110201 , D. ⎪⎪⎭⎫ ⎝⎛--110224解: A.解一:TT )1,1,0(,)2,0,1(21-==ξξ线性无关,故基础解系的秩≥2,从而r(A )=1,答案为(A);解二:令),(21ξξ=X ,一一验证可得(A)中矩阵满足0=AX ,故选(A).8.已知,96342321⎪⎪⎪⎭⎫ ⎝⎛=t Q P 为三阶非零阵,且,0=PQ 则( )A.P t ,6=的秩必为1;B. P t ,6=的秩必为2;C. P t ,6≠的秩必为1;D. P t ,6≠的秩必为2. 解: C.若0=PQ ,则必有)(Q r 小于或等于方程组0=PX 的基础解系所包含向量个数.从而 .3)()(≤+Q r P r 又因为P 为三阶非零阵, 所以.0)(≠P r若,6≠t 则,2)(=Q r 此时必有,113)(0=-≤<P r 即必有.1)(=P r若,6=t 则,1)(=Q r 此时必有,213)(0=-≤<P r 即必有1)(=P r 或.2)(=P r 所以应选C.9.设.),,(,),,(,),,(321332123211T T T c c c b b b a a a ===ααα则三直线0=++i i i c y b x a 其中)3,2,1(022=≠+i b a i i 交于一点的充分必要条件为( )A. 321,,ααα线性相关;B. 321,,ααα线性无关;C. );,(),,(21321αααααr r =D. 321,,ααα线性相关; 21,αα线性无关. 解: D.三直线有一交点,说明21,αα线性无关, 3α可由21,αα线性表示.故选(D);二.填空题 1.设);,,2,1,(,j i n j i a a j i ≠=≠ ,⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=----11312112232221321 (1111)n n n n n n n a a a a a a a a a a a a A ,,111,21⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛= B x x x X n 则方程组B X A T=的解为 . 解: (1,0,0,…,0)T .|A |为范得蒙行列式,故|TA |≠0,方程组有唯一解.矩阵方程对应的线性方程组为 ⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++---1 (11)132211232222111321211n n n n n n n n n x a x a x a x x a x a x a x x a x a x a x由观察可知 (1,0,0,…,0)T 为方程组的解.2.设⎪⎪⎪⎭⎫ ⎝⎛--=11334221t A ,B 为三阶非零矩阵,且0=AB ,则=t . 解: 3-=t若0=AB ,则B 的列向量为齐次线性方程组0=AX 的解.B 为三阶非零矩阵,所以齐次线性方程组0=AX 有非零解.从而有,0||=A 解得3-=t .3.若向量组321,,ααα线性无关,(1) 321332123211222αααβαααβαααβ-+=+-=++-=，，线性 ； (２)3213321232113432232αααηαααηαααη++=++=++=，，线性 ．解: (1) 相关;(2)无关对(1)中向量有⎪⎪⎪⎭⎫ ⎝⎛---=211121112),,(,),,(321321αααβββ,321,,βββ线性无关0211121112≠---,故(1)相关;类似可得(2)无关.4.向量组)2,5,4,0(),0,,0,2(),1,1,2,1(321--==-=αααt 的秩为2,则t = 解: t =3.解一:用行列式为0.0321=ααα 得t =3解二:用矩阵的初等变换得 t =3.5.n 阶矩阵A 各行元素和为0,且r(A )=n-1,则方程组0=AX 的通解为 解: k(1,1,…,1),k 为任意常数.(1,1,…,1)满足方程,方程基础解系仅含一个向量, 故通解为k(1,1,…,1),k 为任意常数. 三.计算题1.设向量组)2(,,,21≥n n ααα 线性无关,,,,,,111322211ααβααβααβααβ+=+=+=+=--s s s s s讨论s βββ,,,21 的线性关系. 解:设02211=+++s s k k k βββ ,整理得:)()()(122111=++++++-s s s s k k k k k k ααα ,由)2(,,,21≥n n ααα 线性无关得1211=+==+=+-s s s k k k k k k ,线性方程组对应的系数行列式为1)1(111000 (00110)0001110001--+==s D所以,(1)当s 为奇数时,D=2≠0,方程组仅有零解, s βββ,,,21 线性无关;(2) 当s 为偶数时,D=0,方程组有非零解, s βββ,,,21 线性相关. 2.设A 为n m ⨯矩阵,B 为m n ⨯矩阵,E 为n 阶单位阵()n m >.已知E BA =,试判断A 的列向量组是否线性相关?为什么? 解: 因为 ,)()()(n E r AB r A r ==≥ 另一方面, n A r ≤)(显然成立, 所以必有 .)(n A r = 从而A 的列向量组线性无关.3. 设向量组321,,ααα线性相关,向量组432,,ααα线性无关,问:(1) 1α能否用32,αα线性表示? (2) 4α能否用321,,ααα线性表示?解: (1) 由向量组432,,ααα线性无关可知32,αα线性无关,而321,,ααα线性相关,故必有1α可用32,αα线性表示.(2) 若4α能由321,,ααα线性表示,由(1)结果知4α应能由32,αα线性表示,这与432,,ααα线性无关矛盾. 所以4α不能由321,,ααα线性表示.4.设);,,2,1(),,,(21n r r i a a a T in i i i <== α是n 维实向量,且r ααα,,,21 线性无关.已知Tn b b b ),,,(21 =β是线性方程组 ⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++0.............................00221122221211212111n rn r r n n n n x a x a x a x a x a x a x a x a x a的非零解向量,试判断向量组βααα,,,,21r 的线性关系.解: 设有一组数k k k k r ,,,,21 使得 02211=++++βαααk k k k r r 成立.因为Tn b b b ),,,(21 =β是线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++0.............................00221122221211212111n rn r r n n n n x a x a x a x a x a x a x a x a x a 的解,且0≠β,所以有: ),,,2,1(0r i T i ==βα即:),,,2,1(0r i i T ==αβ因此,在02211=++++βαααk k k k r r 两侧同乘Tβ得02211=++++ββαβαβαβT r T r T T k k k k ,即:0=ββT k .但0≠ββT,故必有0=k .从而由02211=++++βαααk k k k r r 得 02211=+++r r k k k ααα .r ααα,,,21 线性无关,所以有: 021====r k k k .因此, 向量组βααα,,,,21r 的线性无关.四.证明题1. 设有向量组(I) 321,,ααα,(II) ,,,,4321αααα(III) ,,,,5321αααα 且r(I)=r(II)=3,r(III)=4,证明: 45321,,,ααααα-线性无关. 证明: 设,0)(454332211=-+++αααααk k k k 由r(I)=r(II)=3得4α可由321,,ααα唯一线性表示,设为3322114ααααl l l ++=,代入得,0)()()(54343324221411=+-+-+-ααααk k l k k l k k l k 因为,,,,5321αααα线性无关,所以 ,04433422411==-=-=-k k l k k l k k l k 从而04321====k k k k ,得证.2.对n 阶方阵A ,若存在正整数k 使得0=αk A ,且01≠-αk A .证明向量组ααα1,,,-k A A 线性无关.证明: 设1110=+++--αααk k A t A t t上式两侧同乘以1-k A :)(11101=+++---αααk k k A t A t t A即)1(21110=+++---αααk k k k A t A t A t由0=αk A 得 0)1(21====-+αααk k k A A A所以应有10=-αk A t而01≠-αk A ,从而必有00=t .因此有111=++--ααk k A t A t 同理上式两侧同乘以2-k A 得 01=t .类似可得12===-k t t所以向量组ααα1,,,-k A A 线性无关性得证.3.设321,,ααα为齐次线性方程组0=AX 的一个基础解系. 证明: 133221,,αααααα+++也是该方程组的一个基础解系. 证明: 因为)3,2,1(0==i A i α,所以, 0)(2121=+=+ααααA A A .即: 21αα+为方程组0=AX 的一个解.同理可得: 1332,αααα++也是方程组0=AX 的解. 以下只需证明133221,,αααααα+++的线性无关性. 设0)()()(133322211=+++++ααααααk k k ,整理得:)()()(332221131=+++++αααk k k k k k因为321,,ααα线性无关,所以必有322131=+=+=+k k k k k k解得: 0321===k k k 即: 321,,ααα线性无关.4.设t ααα,,,21 是齐次线性方程组0=AX 的一个基础解系,0≠βA . 证明t αβαβαββ+++,,,,21 线性无关.证明: 设0)()()(22110=+++++++t t k k k k αβαβαββ其中tj k j ,2,1(=)为任意实数.则)(22110=++++∑=t t tj j k k k k αααβ (*)上式两侧同乘以A 得)(22110=++++∑=t t tj j A k A k A k A k αααβ因为t ααα,,,21 是齐次线性方程组0=AX 的一个基础解系, 所以应有021====t A A A ααα . 从而)(0=∑=tj j A k β而0≠βA ,所以必有 0=∑=tj jk代入(*)得 02211=+++t t k k k ααα由t ααα,,,21 线性无关得 021====t k k k 又由0=∑=tj jk得 00=k所以必有t αβαβαββ+++,,,,21 线性无关.。

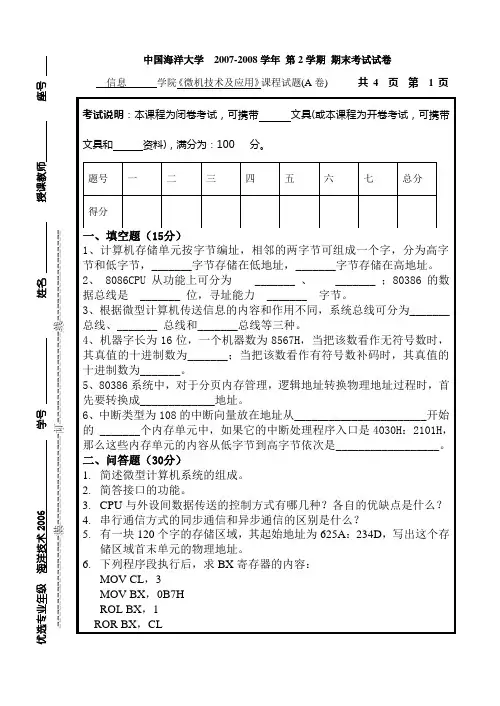
信息学院《微机技术及应用》课程试题(A卷) 共4 页第 1 页授课教师命题教师或命题负责人签字年月日院系负责人签字年月日共4 页第2 页中国海洋大学2007-2008学年第2学期期末考试试卷三、指令正误判断，对正确指令写出源操作数、目的操作数的寻址方式，对错误指令指出原因（设VAR1, VAR2为字变量, L1为标号）（20分）（1）MOV SI，120 （2）MOV AX, [BX]（3）MOV BP, AL （4）MOV CS, BX（5）MOV [BX][SI], 3 （6）ADD AX, LENGTH VAR1（7）SUB [DI], 99H （8）PUSH 200H（9）XCHG AX, ES （10）JMP L1+5四、分析下列程序，回答问题。

（共10分）1．MOV AX，50MOV CX，5LOP：SUB AX，CXLOOP LOPMOV BUF，AXHLT上述程序段执行后，[BUF]＝?2．MOV CL，3MOV BX，0B7HROL BX，1ROR BX，CL执行上述程序段后BX的内容是。

3．STRING DB ‘A VBNDGH!234%Y*’COUNT DW ？………MOV BX，OFFSET STRINGMOV CX，0LOP：MOV AL，[BX]CMP AL，‘*’JE DONEINC CXINC BXJMP LOPDONE：MOV COUNT，CXHLT上述程序段的功能是。

共4 页第4 页六、按下图叙述8086最小模式下的读周期时序。

要求：以T1、T2、T3、T4状态为叙述顺序，且在此4个状态下某引脚上信号变化的话，必须在叙述中解释该引脚的变化。

（15分）。

中国海洋大学期末考试20经济法概论试题及参考答案中国海洋大学继续教育学院命题专用纸（函授）一、单项选择题（本大题共20小题，每小题2分，共40分）1.构成法的基本组织细胞是（）A.法律规范B.法的部门C.法的体系D.法条2.参加经济法律关系，依法享有经济权利、承担经济义务的组织或者个人被称为是（）A.经济法主体B.经济法客体C.经济权利D.经济义务3.不属于全民所有制工业企业职工代表大会的职权的是（）A.对企业经营方针、年度计划、重大技术改造提出意见和建议B.解聘企业中层行政领导干部C.审议决定职工福利基金使用的方案D.对企业各级行政领导干部进行评议、监督4.公司债券的发行规模由（）A.董事会确定B.董事长确定C.股东会确定D.国务院确定5.执行政府定价或者政府指导价的，在合同约定的交付期限内政府价格调整时，按照（）A.合同签订时的价格计算B.交付时的价格计算C.双方当事人协商D.由买方决定6.债权人应当自提存之日起5年内到提存机关领取提存物，逾期不领取的，提存物扣除提存费用后归（）所有。

A.债务人 B.债权人 C.提存部门 D.国家7.由三维造型构成的商标被称为（）A.文字商标B.组合商标C.立体商标D.图形商标8.下列关于不当低价销售行为的表述中，不正确的是（）A.该行为发生在商品销售环节B.该行为牟取了暴利C.该行为采用低于商品成本价格的方式进行销售D.该行为的目的在于排挤竞争对手，维持或者争取自身的竞争优势9.消费者协会是为保护消费者权益而建立的（）A.国家机关B.行业组织C.社会团体D.司法机关10.以下属于不正当竞争的是（）A.季节性降价中，以低于成本的价格进行销售B.因清偿债务、转产、歇业而以低于成本的价格销售商品C.假冒他人的注册商标D.以低于成本的价格处理有效期限即将到期的商品或者其他积压的商品11.经营者应通过各种载体表明其经营资格和身份，这是经营者的（）A.标志经营资格义务B.出具凭证义务C.提供真实信息义务D.质量担保义务12.纳税人不依法纳税的，将受到法律的制裁，这体现的是税收的（）A.固定性B.强制性C.确定性D.无偿性13.各国金融体制一般都以（）为主导。

中国海洋大学2012-2013学年第1学期期末考试试卷及参考答案计算机网络B卷一．选择题（本大题共20个空，每空1分，共20分）错填、不填均无分1：对计算机网络按照信号频带占用方式来划分，可以分为：A．双绞线网和光纤网B．局域网和广域网C．基带网和宽带网D．环形网和总线形网答案：C2：下面不属于网络拓扑结构的是：A．环形结构B．总线结构C．层次结构D．网状结构答案：C3：下列有关网络拓扑结构的叙述中，最准确的是：A．星形结构的缺点是，当需要增加新的工作站时成本比较高B．树型结构的线路复杂，网络管理也较困难C．早期局域网中最普遍采用的拓扑结构是总线结构D．网络的拓扑结构是指网络结点间的分布形式答案：C4：190.168.2.56属于以下哪一类IP地址？( )A.A类B.B类C.C类D.D类答案：B5：为了实现长距离传输，模拟传输系统都使用放大器来使信号中的能量得到增加。

经过放大器后，信号中的噪声分量将_____________。

A．增大 B．减小C．不变 D．不一定答案：A6：以下哪种说法是错误的？A）网络层为报文穿越网络提供了路由选择功能。

B）网络层提供了不同系统的应用进程之间的通信服务。

C）传输层提供了面向连接和无连接的两种类型的服务。

D）传输层为不同系统间应用进程的通信提供了支持。

答案：B7：在OSI/RM模型中，提供路由选择功能的层次是A）物理层 B）数据链路层 C）网络层 D）传输层答案：C8：TCP/IP的网络层A）是面向连接的B）是无连接的C）使用虚电路D）能够提供可靠的传输答案：B9：计算机网络的体系结构是指_____。

A）计算机网络的分层结构和协议的集合B）计算机网络的拓扑结构C）计算机网络的协议集合D）计算机网络的分层结构答案：A10：在以太网中, 如果网卡发现某个帧的目的地址不是自己的：A）它将该帧递交给网络层, 由网络层决定如何处理B）它将丢弃该帧，并向网络层发送错误消息C）它将丢弃该帧，不向网络层提供错误消息D）它将向发送主机发送一个NACK (not acknowledged) 帧答案：C11：在路由器互联的多个局域网中，通常要求每个局域网的( )A.数据链路层协议和物理层协议必须相同B.数据链路层协议必须相同，而物理层协议可以不同C.数据链路层协议可以不同，而物理层协议必须相同D.数据链路层协议和物理层协议都可以不相同答案：D12：某路由器收到了一个IP数据报，在对其首部进行校验后发现该数据报存在错误，路由器最有可能采取的动作是( )A) 纠正该IP数据报的错误B) 将该IP数据报返给源主机C) 抛弃该IP数据报D) 通知目的主机数据报出错答案：C13：下面的IP地址中哪一个是B类地址( )A) 10.10.10.1 B) 191.168.0.1 C) 192.168.0.1 D) 202.113.0.1答案：B14：以下哪项不是UDP协议的特性（）A) 提供可靠服务B) 提供无连接服务C) 提供端到端服务D) 提供全双工服务答案：A15：高层互连是指传输层及其以上各层协议不同的网络之间的互连。

中国海洋大学学年第学期期末考试试卷
法政学院《行政法学》课程试题(A卷)
3、行政优先权；
4、一事不再罚
四、论述（30分）
1、简述比例原则的内容。

2、《行政许可法》对省级政府规章设定行政许可规定了哪些限制？
3、简述国家赔偿责任的构成要件。

五、案例分析（10分）
申请人赵××原为某市一中外合资企业合同工，1999年3月26日被聘到该公司企管部工作，工资标准2500元／月，试用期为3个月，期间工资按80％执行。

试用期满后，公司将其调入综合管理部工作。

1999年9月，公司鉴于其本人工作表现，决定予以辞退。

赵××以该公司未按2500元／月的工资标准发放和未给其办理社保为由，向市劳动局投诉，要求对公司予以查处，保护其本人合法权益。

市劳动局调查后，
对该公司进行了处罚，同时责成妥善处理赵××反映的有关情况。

申请人认为市劳动局对公司处罚过轻，向市人民政府申请行政复议。

市人民政府经审查后对该公司作出了加重处罚的变更复议决定。

该公司对此提出了两点异议：第一，行政复议申请人应为行政管理相对人，本案中赵××不是市劳动局行政处罚的对象，因而其不具有复议申请人资格；第二，根据禁止不利变更原则的要求，复议机关的复议决定不应加重处罚。

问题：请根据行政复议法的相关规定对该公司提出的两点异议加以评析。

命题教师或命题负责人签字
年月日院系负责人签字
年月日。

大学物理Ⅱ2A 答案一、选择题1、C2、D3、C4、C5、D6、A 二、填空题1、5.00×10-5T2、v BL sin θ a3、π-21或π234、π5、46、I 0/87、48、2/112)2/(eU m h e 三、计算题1、2、解：(1) 振动方程 )22cos(06.00π+π=ty )cos(06.0π+π=t (SI) 3分(2) 波动表达式 ])/(cos[06.0π+-π=u x t y 3分])21(cos[06.0π+-π=x t (SI)(3) 波长 4==uT λ m 2分 3、解：双缝干涉条纹：(1) 第k 级亮纹条件： d sin θ =k λ第k 级亮条纹位置：x k = f tg θ ≈f sin θ ≈kf λ / d相邻两亮纹的间距：∆x = x k +1－x k =(k ＋1)f λ / d －kf λ / d =f λ / d=2.4×10-3 m=2.4 mm 5分 (2) 单缝衍射第一暗纹： a sin θ1 = λ单缝衍射中央亮纹半宽度：∆x 0 = f tg θ1≈f sin θ1 ≈f λ / a ＝12 mm∆x 0 / ∆x =5 ∴ 双缝干涉第±5极主级大缺级． 3分∴在单缝衍射中央亮纹范围内，双缝干涉亮纹数目N = 9 1分分别为k = 0，±1，±2，±3，±4级亮纹1分或根据d / a = 5指出双缝干涉缺第±5级主大，同样得该结论的3分．四、问答题1、不是，解释略2、答案略3、答案略4、答：成功：从理论上解释了氢原子光谱的实验规律，并从理论上算出里德伯常量．1分玻尔首先提出了原子系统能量量子化的概念和角动量量子化的假设．1分玻尔创造性的提出了定态、跃迁等重要概念，为近代量子物理的建立奠定了基础．1分局限性：由于未能预见微观粒子的波粒二象性，虽然提出正确的量子假设，但未能完全脱离经典理论的影响，仍采用经典理论的思想和处理方法，因此不能正确说明氢原子内部的微观粒子运动．2分。