检测系统的基本特性
- 格式:doc
- 大小:279.00 KB
- 文档页数:8









第3章 测量系统的基本特性3.1概述测量的目的是通过检测传感、信号调理、信号处理、显示和记录,将被测的物理量提供给测量者。
测量系统是在整个测量过程中所用到的各种仪器和装置的组合。
为了正确描述或反映被测的物理量,实现不失真测量,获取和分析测量系统特性尤为重要。
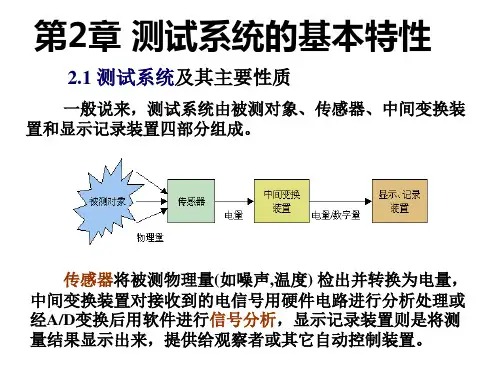
测量系统示意图见图3-1所示,其中x (t )表示测量系统的输入量, y (t )表示测量系统的输出量,h (t )表示测量系统的输入与输出的关系,即测量系统的传递特性。
三者之间一般有如下关系:1) 测量系统传递特性已知,输出可测,则由此可推断导致该输出的输入量。
工程上称为载荷识别或环境预估。
2) 测量系统传递特性和输入已知,则可推断和估计系统的输出量。
工程上称为响应预估。
3) 系统的输入和输出可测取或已知,推断系统的传递特性。
这个过程称为系统辨识或参数识别。
图3-1测量系统框图理想的测量系统应具有单值的、确定的输入输出关系,且输入输出之间呈线性关系。
然而,大多数实际测量系统都不可能在较大的工作范围内完全保持线性,而只能在一定的工作范围和误差允许范围内近似的作为线性处理。
如果测量系统的输入x (t )和输出y (t )之间的关系可用下列常系数线性微分方程来描述:(3-1)当a n ,a n-1,…,a 0和b n ,b n-1,…,b 0均为不随时间变化的常数时,则被描述的系统称)()()()()()()()(0111101111t x b dtt dx b dt t x d b dt t x d b t y a dt t dy a dt t y d a dt t y d a m m m m m m n n n n n n ++⋅⋅⋅++=++⋅⋅⋅++------为时不变系统或定常系统,且该系统满足单值性并具有确定的输入输出关系,即满足理想系统的要求。
但是严格地说,许多实际测量系统都是时变的。
因为构成系统的材料和元部件的特性并非稳定。
例如电子元件中电阻、半导体器件,弹性材料的弹性模量等都会受温度影响而随时间产生变化,它们的不稳定会导致上述微分方程中系数的时变性。
第2章 检测系统的基本特性2.1 检测系统的静态特性及指标 2.1.1检测系统的静态特性 一、静态测量和静态特性 静态测量:测量过程中被测量保持恒定不变(即dx/dt=0系统处于稳定状态)时的测量。
静态特性(标度特性):在静态测量中,检测系统的输出-输入特性。
n n x a x a x a x a a y +++++= 332210例如:理想的线性检测系统: x a y 1= 如图2-1-1(a)所示带有零位值的线性检测系统:x a a y 10+= 如图2-1-1(b)所示二、静态特性的校准(标定)条件――静态标准条件。
2.1.2检测系统的静态性能指标 一、测量范围和量程1、 测量范围:(x min ,x max )x min ――检测系统所能测量到的最小被测输入量(下限) x max ――检测系统所能测量到的最大被测输入量(上限)。
2、量程: min max x x L -= 二、灵敏度Sdxdyx y S x =∆∆=→∆)(lim 0串接系统的总灵敏度为各组成环节灵敏度的连乘积321S S S S =三、分辨力与分辨率1、分辨力:能引起输出量发生变化时输入量的最小变化量min x ∆。
2、分辨率:全量程中最大的min x ∆即min maxx ∆与满量程L 之比的百分数。
四、精度(见第三章)五、线性度e Lmax..100%L L F S e y ∆=±⨯ max L ∆――检测系统实际测得的输出-输入特性曲线(称为标定曲线)与其拟合直线之间的最大偏差..S F y ――满量程(F.S.)输出注意:线性度和直线拟合方法有关。
最常用的求解拟合直线的方法:端点法最小二乘法图2-1-3线性度a.端基线性度;b.最小二乘线性度四、迟滞e H%100..max⨯∆=S F H y H e 回程误差――检测系统的输入量由小增大(正行程),继而自大减小(反行程)的测试过程中,对应于同一输入量,输出量的差值。
ΔHmax ――输出值在正反行程的最大差值即回程误差最大值。
迟滞特性五、稳定性与漂移稳定性:在一定工作条件下,保持输入信号不变时,输出信号随时间或温度的变化而出现缓慢变化的程度。
时漂: 在输入信号不变的情况下,检测系统的输出随着时间变化的现象。
温漂: 随着环境温度变化的现象(通常包括零位温漂、灵敏度温漂)。
2.2 检测系统的动态特性及指标动态测量:测量过程中被测量随时间变化时的测量。
动态特性――检测系统动态测量时的输出-输入特性。
常用实验的方法:频率响应分析法――以正弦信号作为系统的输入;瞬态响应分析法――以阶跃信号作为系统的输入。
2.2.1 检测系统的传递函数线性系统的微分方程(数学模型表达式)x b dt dx b dtx d b dt x d b y a dt dy a dt y d a dt y d a m m m m m m n n n n n n 0111101111++++=++++------线性系统的传递函数1110111)()()(a s a s a s a b s b s b s b s X s Y s H n n n n m m m m ++++++++==---- 令ωj s =可得到检测系统的频率特性)(ωj H :)()()()(ωφωωωj j s e K j H s H ⋅===一 、零阶系统1、系统方程: x b y a 00=或0y K x =2、传递函数: 0)(K s H =3、频率特性: 0)(K j H =ω 幅频特性: 0)(K K =ω 相频特性: 0)(=ωφ零阶系统是一个与时间和频率无关的系统,输出量的幅值与输入量的幅值成确定的比例关系,通常称为比例系统或无惯性系统。
二、 一阶系统微分方程: x b y a dt dy a 001=+或x K y dtdy 0=+τ 传递函数: 0()1K H s sτ=+⋅频率特性: 0()1K H j j ωωτ=+(图2-2-1)幅频特性()K ω=相频特性 Φ(ω)=-arctan (ωτ)三、二阶系统1、微分方程:x b y a dt dy a dt y d a 001222=++或x K y dt dydty d 00222021=++⋅ωξω2、传递函数:20002220020()()2()21Y s K K H s sX s s s s ωξξωωωω===++++ 3、频率特性:0200()1()2()K H j j a ωωωξωω=-+(图2-2-2)幅频特性()K ω=相频特性 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=)()(2arctan)(00ωωωωξωφ2.2.2 检测系统的阶跃响应和时域动态性能指标 一、 检测系统的阶跃响应 阶跃输入响应)(t y :)]([)(1s H sAL t y ⋅=- 1、零阶系统的阶跃响应A K t y 0)(=)0(>t ――幅值为A K 0的阶跃信号。
2、一阶系统的阶跃响应)1()(0τt e A K t y --= )0(>t一阶系统的稳态输出为A K y t y t 0)()(=∞=∞→一阶系统在阶跃输入下的归一化(即A K t y 0/)()阶跃响应曲线(图2-2-3(a)):τt e AK t y y t y --==∞1)()()(0 一阶系统在阶跃输入下的相对动态误差为%100%100)()()()(⨯-=⨯∞∞-=-τεt e y y t y t一阶系统在0=τ时即变成零阶系统,零阶系统在阶跃输入下的相对动态误差0)(=t ε。
3、二阶系统的阶跃响应(1)当0=ξ即无阻尼时, [])cos(1)(00t A K t y ω-=特点:输出量)(t y 围绕稳态值A K 0作等幅振荡,振荡频率是系统的固有频率0ω。
(2)当10<<ξ即欠阻尼时,00()1)t d y t K A t ξωωφ-⎡⎤=-+⎢⎥⎢⎥⎣⎦特点:输出信号为衰减振荡,其振荡角频率(阻尼振荡角频率)为d ω,幅值按指数衰减。
ξ越大,即阻尼越大,衰减越快。
(3)当1>ξ即过阻尼时,⎥⎥⎦⎤⎢⎢⎣⎡---+--+-=----+-tteeA K t y 0202)1(22)1(2201211211)(ωξξωξξξξξξξξ 特点:系统没有振荡,是非周期性过渡过程。
(4)当1=ξ即临界阻尼时,阶跃响应为:000()1(1)ty t K A t eωω-⎡⎤=-+⎣⎦特点:输出量)(t y 以指数规律逼近稳态值,是欠阻尼状态到过阻尼状态的转折点。
二、 检测系统的时域动态性能指标 1 、响应时间s t在工程上通常规定系统响应的相对动误差达到且不超过某一允许值m ε,即m t εε≤)(所需最小时间称为响应时间记为s t 。
1)一阶系统的响应时间为5%1ln()3m s mt εττε==≈2)欠阻尼的二阶系统的相对动态误差为n t n n n e AK AK t y y y t y t 000)()()()()(ξωε-±=-=∞∞-=3)欠阻尼二阶系统的响应时间s t 令m n t εε=)(可得,5%001ln3mm s n t t εεξωξω===≈2 、峰值时间p t ――输出响应达到第一个正峰值所需要的时间2dd p T t ==ωπ 可见,峰值时间p t 等于振荡周期d T 的一半。
3、 超调量σ――超调量指峰值时间对应的相对动态误差值,记为σ:0010()()()()p dt p p y t y M t e e e y K Aπξωξωωσε-⨯--∞======∞A K t y y t y M p p 01)()()(-=∞-=称为第一次过冲量或最大过冲量。
4、阻尼比系数ξ:2012)ln(11ln 11⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+=A K M πσπξ5、二阶系统的固有角频率0ω:0ω==2.2.3 检测系统的正弦响应和频域动态性能指标一、线性检测系统的稳态正弦响应若系统输入正弦信号: t X t X m ωsin )(= 则稳态输出为同频率正弦信号:()sin()m y t y t ωϕ=+二者的幅值之比取决于该系统的幅频特性)(ωK 在ω处的值:)(ωK X y mm= 二者的相位差ϕ取决于该系统的相频特性)(ωφ在ω处的值)(ωφϕ=因此,改变输入正弦信号的频率ω观察稳态输出响应的幅值变化和相位滞后,就可求得系统的幅频特性和相频特性。
1、零阶系统: 0)(K K =ω,0)(=ωφ,2、一阶系统和二阶系统:在直流激励即0=ω时,才有0)0()(K K K ==ω,0)0()(==φωφ。
在正弦激励即0≠ω时,0)(),0()(K K K K ≠≠ωω,频域动态相对误差定义为:00()(0)()(0)()()1(0)K K K K K K K K ωωωεω--===-一阶系统的频域动态相对误差为:()1εω=- 二阶系统的频域动态相对误差为:()1εω=-二 、检测系统的频域动态性能指标 1、带宽频率B ω定义――幅频特性)(ωK 的值下降到频率为零时的幅频特性值0)0(K K =的21时所对应的频率,即2)(0K K B =ω1)一阶系统的带宽频率τω1=B2)二阶系统的带宽频率 0ωω=B (当21=ξ时)2、工作频带g ω定义――频域动态相对误差小于所规定的允许值δ所对应的频率范围。
即()g εωδ≤一阶系统的工作频带g ω为g ω=3、二阶系统谐振频率r ω定义――幅值特性曲线出现峰值即0)(=ωωd dk 时的频率。
只有在210≤≤ξ时,幅频特性才出现峰值,峰值(谐振)频率r ω为:2021ξωω-=r该峰值为 ()2012ξξω-=K K r2.2.4 无失真检测条件输出波形与输入波形完全相似,只是瞬时值放大了K 0倍,时间滞后了τ,即)()(0τ-=t x K t y一、非线性失真(谐波失真)给系统输入单一正弦波时,若系统为线性的, 则输出仍然是一个正弦波,而且频率也相同。
若系统存在非线性,则输出将包括多个不同频率的正弦波。
这种由于系统的非线性造成的失真,称为“非线性失真”或“谐波失真”。
通常用谐波失真系数来衡量系统产生非线性失真的程度。
+++++=2322212322A A A A A D系统的谐波失真系数越小,则输出信号的保真度越高。
谐波失真系数与输入幅度之间存在如图2-2-5所示的关系。
二、线性系统不失真条件)()(0τ-=t x K t y 即)()(0ωωωτj X e K j Y j -=故系统的频率响应H(j ω)应满足ωτωωωj e K j X j Y j H -==0)()()(1、K (ω)=|H(j ω)|=K 0即幅频特性应当是水平直线,否则产生“幅度失真”2、Φ(ω)=-ωτ即相频特性是过原点的负斜率直线,否则产生“相位失真” 实际的检测系统,很难在无限频带宽度上同时满足这两个条件,因此只能根据实 际需要优先保证在被测信号所占的频段上满足其中的一个条件(一般情况下多优先保证不产生或减小幅度失真)就可以了。