实验二：探究弹力和弹簧伸长量的关系实验报告

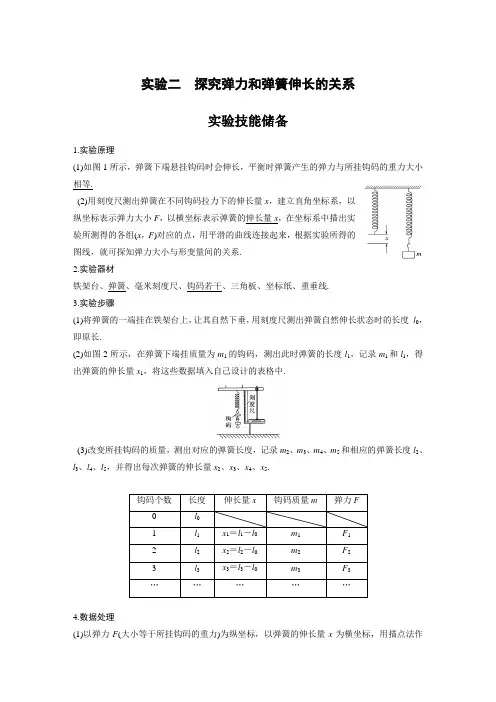
实验二探究弹力和弹簧伸长的关系实验技能储备1.实验原理(1)如图1所示，弹簧下端悬挂钩码时会伸长，平衡时弹簧产生的弹力与所挂钩码的重力大小相等.(2)用刻度尺测出弹簧在不同钩码拉力下的伸长量x，建立直角坐标系，以纵坐标表示弹力大小F，以横坐标表示弹簧的伸长量x，在坐标系中描出实验所测得的各组(x，F)对应的点，用平滑的曲线连接起来，根据实验所得的图线，就可探知弹力大小与形变量间的关系.2.实验器材铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重垂线.3.实验步骤(1)将弹簧的一端挂在铁架台上，让其自然下垂，用刻度尺测出弹簧自然伸长状态时的长度l0，即原长.(2)如图2所示，在弹簧下端挂质量为m1的钩码，测出此时弹簧的长度l1，记录m1和l1，得出弹簧的伸长量x1，将这些数据填入自己设计的表格中.(3)改变所挂钩码的质量，测出对应的弹簧长度，记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5，并得出每次弹簧的伸长量x2、x3、x4、x5.钩码个数长度伸长量x 钩码质量m 弹力F0l01l1x1＝l1－l0m1F12l2x2＝l2－l0m2F23l3x3＝l3－l0m3F3……………4.数据处理(1)以弹力F(大小等于所挂钩码的重力)为纵坐标，以弹簧的伸长量x为横坐标，用描点法作图.用平滑的曲线连接各点，得出弹力F随弹簧伸长量x变化的图线.(2)以弹簧的伸长量为自变量，写出图线所代表的函数表达式.首先尝试一次函数，如果不行则考虑二次函数.(3)得出弹力和弹簧形变量之间的定量关系，解释函数表达式中常数的物理意义.5.注意事项(1)不要超过弹性限度：实验中弹簧下端挂的钩码不要太多，以免弹簧被过度拉伸，超过弹簧的弹性限度.(2)尽量多测几组数据：要使用轻质弹簧，且要尽量多测几组数据.(3)观察所描点的走向：本实验是探究型实验，实验前并不知道其规律，所以描点以后所作的曲线是试探性的，只是在分析了点的分布和走向以后才决定用直线来连接这些点.(4)统一单位：记录数据时要注意弹力及弹簧伸长量的对应关系及单位.考点一教材原型实验例1如图3甲所示，用铁架台、弹簧和多个质量均为m的钩码，探究在弹性限度内弹簧弹力与形变量的关系.(1)为完成实验，还需要的实验器材有：_________________________________________.(2)实验中需要测量的物理量有：_____________________________________________.(3)图乙是弹簧弹力F与弹簧形变量x的F－x图线，由此可求出弹簧的劲度系数为___ N/m.图线不过原点是由于___________________________________.(4)为完成该实验，设计实验步骤如下：A.以弹簧形变量为横坐标，以弹力为纵坐标，描出各组(x，F)对应的点，并用平滑的曲线连接起来B.记下弹簧不挂钩码时其下端在刻度尺上的刻度l0C.将铁架台固定在桌子上，并将弹簧的一端系在横梁上，在弹簧附近竖直固定一把刻度尺D.依次在弹簧下端挂上1个、2个、3个、4个……钩码，并分别记下钩码静止时弹簧下端所对应的刻度，并记录在表格内，然后取下钩码E.以弹簧形变量为自变量，写出弹力与形变量的关系式，首先尝试写成一次函数，如果不行，则考虑二次函数F.解释表达式中常数的物理意义G.整理仪器请将以上步骤按操作的先后顺序排列出来：_______________.例2一个实验小组在“探究弹簧弹力与形变量的关系”的实验中：(1)甲同学在做该实验时，通过处理数据得到了图4甲所示的F－x图象，其中F为弹簧弹力，x为弹簧长度.请通过图甲，分析并计算，该弹簧的原长x0＝________ cm，弹簧的劲度系数k ＝________ N/m.该同学将该弹簧制成一把弹簧测力计，当弹簧测力计的示数如图乙所示时，该弹簧的长度x＝________ cm.(2)乙同学使用两条不同的轻质弹簧a和b，得到弹力与弹簧长度的关系图象如图丙所示.下列表述正确的是________.A.a的原长比b的长B.a的劲度系数比b的大C.a的劲度系数比b的小D.测得的弹力与弹簧的长度成正比1.利用如图5所示装置做探究弹簧弹力与形变量关系的实验，所用的钩码每个质量为30 g.实验中，先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个加挂在弹簧下端，稳定后依次测出相应的弹簧总长度，将数据填在表中.(弹力始终未超过弹性限度，取g＝10 m/s2)记录数据组12345 6钩码总质量(g)0306090120150弹簧总长(cm) 6.007.118.209.3110.4011.52(1)实验需要的器材，除铁架台、弹簧、钩码若干、坐标纸、重垂线、铅笔之外，还需要的一件器材是________.(2)根据表中所列6组数据，在图6甲坐标系中作出弹簧弹力大小F跟弹簧总长度x之间的函数关系的图线.(3)根据函数图线，求出弹簧的劲度系数为________ N/m(保留两位有效数字).(4)某同学画图象时横轴没取弹簧总长，而是取了弹簧的形变量，结果其图线仍然没有经过坐标原点，如图乙所示，图线不过坐标原点的原因是____________________________________.考点二拓展创新实验例3在“探究弹力和弹簧形变量的关系，并测定弹簧的劲度系数”的实验中，实验装置如图7所示，所用的每个钩码的重力相当于对弹簧提供了向右恒定的拉力.实验时先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在绳子的下端，每次测出相应的弹簧总长度.(1)有一个同学通过以上实验测量后把6组数据描点在坐标图8中，请作出F－L图线.(2)由此图线可得出该弹簧的原长L0＝________ cm，劲度系数k＝________ N/m.(3)图线上端出现弯曲的原因是____________________________________________.(4)该同学实验时，把弹簧水平放置与弹簧悬挂放置相比较，优点在于：___________________________________.缺点在于：__________________________________.2.橡皮筋也像弹簧一样，在弹性限度内伸长量x与弹力F成正比，即F＝kx，k的值与橡皮筋的原长L 、横截面积S 有关，理论与实验都证明k ＝Y SL ，其中Y 是由材料决定的常数，材料力学中称之为杨氏模量.(1)在国际单位中，杨氏模量Y 的单位应为________. A.N B.m C.N/mD.N/m 2(2)某同学通过实验测得该橡皮筋的一些数据，作出了外力F 与伸长量x 之间的关系图象如图9所示，由图象可求得该橡皮筋的劲度系数k ＝________ N/m.图9(3)若橡皮筋的原长为10.0 cm ，横截面积为1.0 mm 2，则该橡皮筋的杨氏模量Y 的大小是________(只填数字，单位取(1)中正确单位，结果保留两位有效数字).3.某实验小组探究弹簧的劲度系数k 与其长度(圈数)的关系.实验装置如图10所示.一均匀长弹簧竖直悬挂，7个指针P 0、P 1、P 2、P 3、P 4、P 5、P 6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处；通过旁边竖直放置的刻度尺，可以读出指针的位置，P 0指向0刻度.设弹簧下端未挂重物时，各指针的位置记为x 0；挂有质量为0.100 kg 的砝码时，各指针的位置记为x .测量结果及部分计算结果如下表所示(n 为弹簧的圈数，取重力加速度为9.80 m/s 2).已知实验所用弹簧总圈数为60，整个弹簧的自由长度为11.88 cm.P 1 P 2 P 3 P 4 P 5 P 6 x 0(cm) 2.04 4.06 6.06 8.08 10.03 12.01 x (cm) 2.64 5.26 7.81 10.30 12.93 15.41 n 10 20 30 40 50 60 k (N/m) 163 ① 56.0 43.6 33.8 28.8 1k(m/N) 0.006 1②0.017 90.022 90.029 60.034 7(1)将表中数据补充完整：①________，②________.(2)以n 为横坐标，1k 为纵坐标，在图11给出的坐标纸上画出1k－n 图象.(3)图中画出的直线可近似认为通过原点.若从实验中所用的弹簧截取圈数为n的一段弹簧，该弹簧的劲度系数k与其圈数n的关系表达式为k＝________ N/m，该弹簧的劲度系数k与其自由长度l0(单位为m)的关系表达式为k＝________ N/m.实验二探究弹力和弹簧伸长的关系目标要求 1.会通过实验探究弹力和弹簧伸长的关系.2.进一步理解胡克定律，掌握以胡克定律为原理的拓展实验的分析方法.实验技能储备1.实验原理(1)如图1所示，弹簧下端悬挂钩码时会伸长，平衡时弹簧产生的弹力与所挂钩码的重力大小相等.图1(2)用刻度尺测出弹簧在不同钩码拉力下的伸长量x，建立直角坐标系，以纵坐标表示弹力大小F，以横坐标表示弹簧的伸长量x，在坐标系中描出实验所测得的各组(x，F)对应的点，用平滑的曲线连接起来，根据实验所得的图线，就可探知弹力大小与形变量间的关系.2.实验器材铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重垂线.3.实验步骤(1)将弹簧的一端挂在铁架台上，让其自然下垂，用刻度尺测出弹簧自然伸长状态时的长度l0，即原长.(2)如图2所示，在弹簧下端挂质量为m1的钩码，测出此时弹簧的长度l1，记录m1和l1，得出弹簧的伸长量x1，将这些数据填入自己设计的表格中.图2(3)改变所挂钩码的质量，测出对应的弹簧长度，记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5，并得出每次弹簧的伸长量x2、x3、x4、x5.4.数据处理(1)以弹力F(大小等于所挂钩码的重力)为纵坐标，以弹簧的伸长量x为横坐标，用描点法作图.用平滑的曲线连接各点，得出弹力F随弹簧伸长量x变化的图线.(2)以弹簧的伸长量为自变量，写出图线所代表的函数表达式.首先尝试一次函数，如果不行则考虑二次函数.(3)得出弹力和弹簧形变量之间的定量关系，解释函数表达式中常数的物理意义.5.注意事项(1)不要超过弹性限度：实验中弹簧下端挂的钩码不要太多，以免弹簧被过度拉伸，超过弹簧的弹性限度.(2)尽量多测几组数据：要使用轻质弹簧，且要尽量多测几组数据.(3)观察所描点的走向：本实验是探究型实验，实验前并不知道其规律，所以描点以后所作的曲线是试探性的，只是在分析了点的分布和走向以后才决定用直线来连接这些点.(4)统一单位：记录数据时要注意弹力及弹簧伸长量的对应关系及单位.考点一教材原型实验例1如图3甲所示，用铁架台、弹簧和多个质量均为m的钩码，探究在弹性限度内弹簧弹力与形变量的关系.图3(1)为完成实验，还需要的实验器材有：_________________________________________.(2)实验中需要测量的物理量有：_____________________________________________.(3)图乙是弹簧弹力F与弹簧形变量x的F－x图线，由此可求出弹簧的劲度系数为___ N/m.图线不过原点是由于___________________________________.(4)为完成该实验，设计实验步骤如下：A.以弹簧形变量为横坐标，以弹力为纵坐标，描出各组(x，F)对应的点，并用平滑的曲线连接起来B.记下弹簧不挂钩码时其下端在刻度尺上的刻度l0C.将铁架台固定在桌子上，并将弹簧的一端系在横梁上，在弹簧附近竖直固定一把刻度尺D.依次在弹簧下端挂上1个、2个、3个、4个……钩码，并分别记下钩码静止时弹簧下端所对应的刻度，并记录在表格内，然后取下钩码E.以弹簧形变量为自变量，写出弹力与形变量的关系式，首先尝试写成一次函数，如果不行，则考虑二次函数F.解释表达式中常数的物理意义G.整理仪器请将以上步骤按操作的先后顺序排列出来：_______________.答案(1)刻度尺(2)弹簧原长、弹簧所受外力与弹簧对应的长度(3)200弹簧自身重力的影响(4)CBDAEFG解析(1)根据实验原理可知还需要刻度尺来测量弹簧原长和挂上钩码后的长度.(2)根据实验原理，实验中需要测量的物理量有弹簧的原长、弹簧所受外力与弹簧对应的长度.(3)取题图乙中(0.5 cm,0)和(3.5 cm,6 N)两个点，代入F＝kx解得x＝200 N/m，由于弹簧自身的重力，使得实验中弹簧不加外力时就有形变量.(4)根据实验操作的合理性可知，实验步骤的先后顺序为CBDAEFG.例2(2019·河南八市重点高中联盟第三次模拟)一个实验小组在“探究弹簧弹力与形变量的关系”的实验中：图4(1)甲同学在做该实验时，通过处理数据得到了图4甲所示的F －x 图象，其中F 为弹簧弹力，x 为弹簧长度.请通过图甲，分析并计算，该弹簧的原长x 0＝________ cm ，弹簧的劲度系数k ＝________ N/m.该同学将该弹簧制成一把弹簧测力计，当弹簧测力计的示数如图乙所示时，该弹簧的长度x ＝________ cm.(2)乙同学使用两条不同的轻质弹簧a 和b ，得到弹力与弹簧长度的关系图象如图丙所示.下列表述正确的是________. A.a 的原长比b 的长 B.a 的劲度系数比b 的大 C.a 的劲度系数比b 的小D.测得的弹力与弹簧的长度成正比 答案 (1)8 25 20 (2)B解析 (1)当弹力为零时，弹簧处于原长状态，故原长为x 0＝8 cm ，在F －x 图象中斜率表示弹簧的劲度系数，则k ＝ΔF Δx ＝60.24 N/m ＝25 N/m ，题图乙中弹簧测力计的示数F ＝3.0 N ，根据F ＝kx ，可知：x ＝F k ＝3.025 m ＝0.12 m ＝12 cm ，故此时弹簧的长度x 总＝x ＋x 0＝20 cm.(2)在题图丙中，图线与L 轴的交点横坐标表示弹簧原长，故b 的原长大于a 的原长，故A 错误；图线斜率表示劲度系数，故a 的劲度系数大于b 的劲度系数，故B 正确，C 错误；弹簧的弹力与弹簧的形变量成正比，故D 错误.1.利用如图5所示装置做探究弹簧弹力与形变量关系的实验，所用的钩码每个质量为30 g.实验中，先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个加挂在弹簧下端，稳定后依次测出相应的弹簧总长度，将数据填在表中.(弹力始终未超过弹性限度，取g ＝10 m/s 2)图5(1)实验需要的器材，除铁架台、弹簧、钩码若干、坐标纸、重垂线、铅笔之外，还需要的一件器材是________.(2)根据表中所列6组数据，在图6甲坐标系中作出弹簧弹力大小F跟弹簧总长度x之间的函数关系的图线.图6(3)根据函数图线，求出弹簧的劲度系数为________ N/m(保留两位有效数字).(4)某同学画图象时横轴没取弹簧总长，而是取了弹簧的形变量，结果其图线仍然没有经过坐标原点，如图乙所示，图线不过坐标原点的原因是____________________________________. 答案(1)刻度尺(2)见解析图(3)27(4)弹簧自身重力的影响解析(1)需要刻度尺测量弹簧的总长.(2)弹簧弹力与弹簧总长度x的关系图线如图所示.(3)图线的斜率表示弹簧的劲度系数.k＝1.66×10－2N/m≈27 N/m.(4)图线不过原点的原因是弹簧自身有重力，竖直悬挂时的长度大于水平放置时的长度.考点二拓展创新实验例3(2020·广东东莞六中模拟)在“探究弹力和弹簧形变量的关系，并测定弹簧的劲度系数”的实验中，实验装置如图7所示，所用的每个钩码的重力相当于对弹簧提供了向右恒定的拉力.实验时先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在绳子的下端，每次测出相应的弹簧总长度.图7(1)有一个同学通过以上实验测量后把6组数据描点在坐标图8中，请作出F －L 图线.图8(2)由此图线可得出该弹簧的原长L 0＝________ cm ，劲度系数k ＝________ N/m. (3)图线上端出现弯曲的原因是____________________________________________. (4)该同学实验时，把弹簧水平放置与弹簧悬挂放置相比较， 优点在于：___________________________________. 缺点在于：__________________________________.答案 (1)见解析图 (2)5 20 (3)弹簧的形变量超出其弹性限度 (4)避免弹簧自身所受重力对实验的影响 弹簧与桌面及绳子与滑轮间存在的摩擦造成实验的误差 解析 (1)描点作图，F －L 图线如图所示(2)当弹力为零时，弹簧的形变量为零，此时弹簧的长度等于弹簧的原长，可知弹簧的原长L 0＝5 cm.根据胡克定律知k ＝ΔFΔx，可知图线的斜率表示劲度系数， 则k ＝ΔF Δx ＝1.20.06N/m ＝20 N/m.(3)图线上端出现弯曲的原因是弹簧的形变量超出其弹性限度.(4)优点在于消除了弹簧悬挂时弹簧自身所受重力对实验的影响；缺点在于水平放置时弹簧与桌面及绳子与滑轮间存在的摩擦造成实验误差.2.(2020·湖北荆门市龙泉中学、宜昌一中联考)橡皮筋也像弹簧一样，在弹性限度内伸长量x 与弹力F 成正比，即F ＝kx ，k 的值与橡皮筋的原长L 、横截面积S 有关，理论与实验都证明k ＝Y SL ，其中Y 是由材料决定的常数，材料力学中称之为杨氏模量.(1)在国际单位中，杨氏模量Y 的单位应为________. A.N B.m C.N/mD.N/m 2(2)某同学通过实验测得该橡皮筋的一些数据，作出了外力F 与伸长量x 之间的关系图象如图9所示，由图象可求得该橡皮筋的劲度系数k ＝________ N/m.图9(3)若橡皮筋的原长为10.0 cm ，横截面积为1.0 mm 2，则该橡皮筋的杨氏模量Y 的大小是________(只填数字，单位取(1)中正确单位，结果保留两位有效数字). 答案 (1)D (2)500 (3)5.0×107解析 (1)根据表达式k ＝Y S L 得Y ＝kLS ，已知k 的单位是N/m ，L 的单位是m ，S 的单位是m 2，所以Y 的单位是N/m 2，D 正确，A 、B 、C 错误. (2)由题图得k ＝ΔF Δx ＝5.0 N0.01 m ＝500 N/m.(3)由k ＝Y S L 得Y ＝kLS＝5.0×107 N/m 2.3.某实验小组探究弹簧的劲度系数k 与其长度(圈数)的关系.实验装置如图10所示.一均匀长弹簧竖直悬挂，7个指针P 0、P 1、P 2、P 3、P 4、P 5、P 6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处；通过旁边竖直放置的刻度尺，可以读出指针的位置，P 0指向0刻度.设弹簧下端未挂重物时，各指针的位置记为x 0；挂有质量为0.100 kg 的砝码时，各指针的位置记为x .测量结果及部分计算结果如下表所示(n 为弹簧的圈数，取重力加速度为9.80 m/s 2).已知实验所用弹簧总圈数为60，整个弹簧的自由长度为11.88 cm.图10(1)将表中数据补充完整：①________，②________.(2)以n 为横坐标，1k 为纵坐标，在图11给出的坐标纸上画出1k－n 图象.图11(3)图中画出的直线可近似认为通过原点.若从实验中所用的弹簧截取圈数为n 的一段弹簧，该弹簧的劲度系数k 与其圈数n 的关系表达式为k ＝________ N/m ，该弹簧的劲度系数k 与其自由长度l 0(单位为m)的关系表达式为k ＝________ N/m.答案 (1)①81.7 ②0.012 2 (2)见解析图 (3)1.75×103n (1.67×103n ～1.83×103n 均可)3.47l 0(3.31l 0～3.62l 0均可) 解析 (1)①k ＝mg x 2＝0.100×9.80(5.26－4.06)×10－2N/m ≈81.7 N/m ；②1k ＝181.7m/N ≈0.012 2 m/N ； (2)描点法，画一条直线，让大部分的点都落在直线上，不在线上的点均匀分布在直线两侧，如图所示.(3)设直线的斜率为a ，则有1k ＝an ，即k ＝1a ·1n ，通过计算可得k ≈1.75×103n ；弹簧共60圈，则有n ＝60l 00.118 8，把其代入k ＝1a ·1n 中可得k ≈3.47l 0.。

实验二探究弹簧弹力和弹簧伸长的关系1.实验原理(1)如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与所挂钩码的重力大小相等。

(2)用刻度尺测出弹簧在不同钩码拉力下的伸长量x,建立直角坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x、F)对应的点,用平滑的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系。

2.实验器材铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重垂线。

3.实验步骤(1)将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出弹簧在自然伸长状态时的长度l0,即原长。

(2)如图所示,在弹簧下端挂质量为m1的钩码,测出此时弹簧的长度l1,记录m1和l1,填入自己设计的表格中。

(3)改变所挂钩码的质量,测出对应的弹簧长度,记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5,并得出每次弹簧的伸长量x1、x2、x3、x4、x5。

4.数据分析(1)列表法将得到的F、x填入设计好的表格中,可以发现弹力F与弹簧伸长量x的比值在误差允许的范围内是相等的。

(2)图象法以弹簧伸长量x为横坐标,弹力F为纵坐标,在坐标轴上描出F、x各组数据相应的点,作出的拟合曲线是一条过坐标原点的直线。

(3)函数法弹力F与弹簧伸长量x满足F=kx的关系。

5.注意事项(1)不要超过弹簧的弹性限度:实验中弹簧下端挂的钩码不要太多,以免弹簧被过分拉伸,超过弹簧的弹性限度。

(2)尽量多测几组数据:要使用轻质弹簧,且要尽量多测几组数据。

(3)观察所描点的走向:本实验是探究性实验,实验前并不知道其规律,所以描点以后所作的曲线是试探性的,只是在分析了点的分布和走向以后才决定用直线来连接这些点。

(4)统一单位:记录数据时要注意弹力及弹簧伸长量的对应关系及单位。

【典例1】如图甲所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系。

实验：探究弹簧伸长量与弹力的关系一、实验目的1．探究弹力与弹簧伸长的关系。

2．学会利用列表法、图象法、函数法处理实验数据。

3．验证胡克定律。

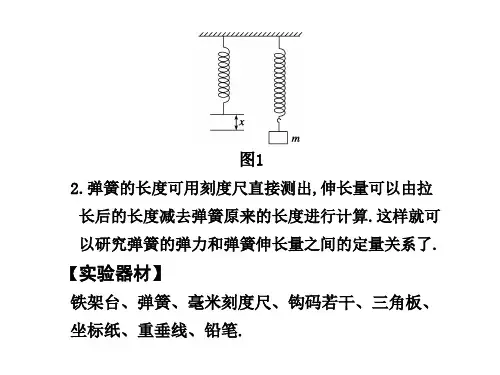
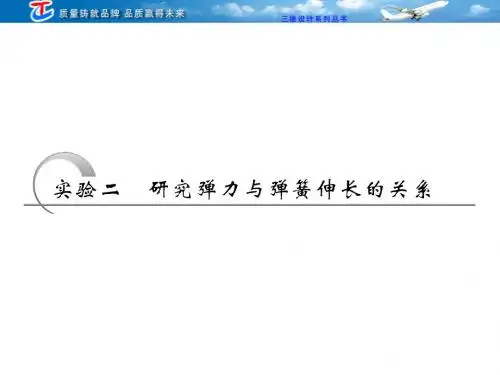
二、实验原理1．如图1所示，在弹簧下端悬挂钩码时弹簧会伸长，平衡时弹簧产生的弹力与所挂钩码的重力大小相等。

图12．弹簧的长度可用刻度尺直接测出，伸长量可以由拉长后的长度减去弹簧原来的长度进行计算。

这样就可以研究弹簧的弹力和弹簧伸长量之间的定量关系了。

3．求弹簧的劲度系数：弹簧的弹力F与其伸长量x成正比，比例系数k＝Fx，即为弹簧的劲度系数；另外，在F－x图象中，直线的斜率也等于弹簧的劲度系数。

三、实验器材铁架台、弹簧、毫米刻度尺、钩码若干、坐标纸。

四、实验步骤1．按图2安装实验装置，记下弹簧下端不挂钩码时所对应的刻度l0。

图22．在弹簧下端悬挂一个钩码，平衡时记下弹簧的总长度并记下钩码的重力。

3．增加钩码的个数，重复上述实验过程，将数据填入表格，以F表示弹力，l表示弹簧的总长度，x＝l－l0表示弹簧的伸长量。

1．以弹力F(大小等于所挂钩码的重力)为纵坐标，以弹簧的伸长量x为横坐标，用描点法作图。

连接各点，得出弹力F随弹簧伸长量x变化的图线，如图3所示。

图32．以弹簧伸长量为自变量，写出弹力和弹簧伸长量之间的函数关系，函数表达式中常数即为弹簧的劲度系数，这个常数也可据F－x图线的斜率求解，k＝ΔF Δx。

六、误差分析由于弹簧原长及伸长量的测量都不便于操作，存在较大的测量误差，另外由于弹簧自身的重力的影响，即当未放重物时，弹簧在自身重力的作用下，已经有一个伸长量，这样所作图线往往不过原点。

七、注意事项1．所挂钩码不要过重，以免弹簧被过分拉伸，超出它的弹性限度。

2．每次所挂钩码的质量差尽量大一些，从而使坐标上描的点尽可能稀一些，这样作出的图线精确。

3．测弹簧长度时，一定要在弹簧竖直悬挂且处于平衡状态时测量，刻度尺要保持竖直并靠近弹簧，以免增大误差。

4．描点画线时，所描的点不一定都落在一条直线上，但应注意一定要使各点均匀分布在直线的两侧。

实验二探究弹力和弹簧伸长的关系注意事项1．安装实验装置：要保持刻度尺竖直并靠近弹簧。

2．不要超过弹性限度：实验中弹簧下端挂的钩码不要太多，以免超过弹簧的弹性限度。

3．尽量多测几组数据：要使用轻质弹簧，且要尽量多测几组数据。

4．观察所描点的走向：不要画折线。

5．统一单位：记录数据时要注意弹力及弹簧伸长量的对应关系及单位。

误差分析1．钩码标值不准确，弹簧长度测量不准确带来误差。

2．画图时描点及连线不准确也会带来误差。

热点一实验原理与实验操作【例1】某中学的物理兴趣实验小组在“探究弹力和弹簧伸长量的关系”的实验时，分成了两组来进行探究分析。

图1（1）小组甲对两个劲度系数不同的弹簧A和弹簧B进行了探究，根据测量的实验数据以弹簧的伸长量（x）为纵坐标，以弹簧的弹力（F）为横坐标，在同一坐标系中作出了两弹簧的图象，从图象上看两弹簧的图线的后半段均向上发生了弯曲，其原因是________________________________________________________，如果选用其中的一个弹簧制作成精确度比较高的弹簧测力计，则应选（填“A”或“B”）。

（2）小组乙的同学完成了如下的操作：a．将带铁夹的铁架台放在水平桌面上，将弹簧的一端固定在铁夹上使其呈自然状态，并在竖直的弹簧附近平行弹簧固定一刻度尺b．以弹簧的伸长量（x）为纵坐标，以弹簧的弹力（F）为横坐标，根据以上测量的数据在坐标系中描点，并用一条平滑的线连接起来c．写出弹簧的弹力与弹簧形变量的关系式，并对该关系式中的常量进行解释d．从刻度尺上读出弹簧下端不悬挂钩码时，弹簧下端所对应的刻度尺上的刻度值，记为L0e．然后在弹簧的下端依次悬挂1、2、3、4…个钩码，当弹簧稳定时，依次读出弹簧下端所对应的刻度值，分别记为L1、L2、L3、L4…并将对应的数据记录在表格中，随后将钩码取下请将以上的实验步骤按照正确的顺序排列，将步骤前的字母填在横线上：。