8第八讲二维随机变量函数的分布与数学期望(22)

求 随 机 变 量 函 数 Y X 2的 数 学 期 望 .
解 : (法 一 ) 先 求 Y的 分 布 律 为
E(Y )
4
y p
k 1 k k
0 0.25 1 0.40 4 0.25 9 0.10
2.30
(法 二 )
E(Y )
E( X
2)
x p 6
k 1
2 k
k
(2) 2 0.10 (1)2 0.10 02 0.25
)]
k
1
g
(
x
k
)
pk
（2）设X是连续型随机变量，其概率密度为f (x).
若
广
义
积
分
g(x)
f
(x)dx绝
对
收
敛
，
则
E ( Y ) E [ g ( X )] g ( x ) f ( x ) d x
Note：此定理简单易用！若先求出Y的分布,很多题目要复杂的多．
例 2 设 随 机 变 量 X的 分 布 律 为
数学期望（二维）
二维随机变量的数学期望
定义1 对 二 维 随 机 变 量 （ X , Y ） , 它 的 数 学 期 望 为
E（X ,Y） E ( X ), E ( Y )
离散型 P { X xi , Y y j } pij ,
E ( X ) x i p i•
xi p ij ,
i1
i1 j1
连续型 （ X ,Y）, f ( x , y )
i, j 1, 2,
哦 E ( Y )
j 1
y j p j
该公式可y p接i 应1 用j 1
直
ij
！j

ex x 0
f (x) 0 x0
其中>0，试分别就以上两种联结方式写出L的寿 命Z的概率密度．
第14页/共16页
小结
离散型——分布律 归一性 概率计算
分布函数与分布立场律的互变
边缘分布律
多维随机变量
分布函数 归一性 概率计算
二维随机变量函数的分布
连续型——概率密度 归一性 概率计算
分布函数与概率密度的互变
一般地，设随机变量X1, X2，..., Xn独立且Xi 服从正态分布N(i ,i2),i=1,...,n, 则
n
n
n
ai Xi ~ N(
ai i ,
ai2
2 i
)
i 1
i 1
i 1
第10页/共16页
例3.卡车装运水泥,设每袋水泥的重量X(kg) 服从N(50,2.52)分布,该卡车的额定载重量为 2000kg,问最多装多少袋水泥,可使卡车超载
例1 设二维r.v.( X,Y )的概率分布为
pij X -1
1
2
Y
-1
14 16 18
0
1 4 1 8 1 12
求X Y, X Y, XY,Y X 的概率分布
第1页/共16页
解 根据( X,Y )的联合分布可得如下表格： P 1 4 1 4 1 6 1 8 1 8 1 12
( X,Y ) (-1,-1)(-1,0)(1,-1) (1,0) (2,-1) (2,0) X +Y -2 -1 0 1 1 2 X -Y 0 -1 2 1 3 2 X Y 1 0 -1 0 -2 0 Y / X 1 0 -1 0 -1/2 0
具有可加性的两个离散分布
设 X ~B (n1, p), Y ~B (n2, p), 且独立， 则 X + Y ~ B ( n1+n2, p)

P抽{X取抽两取0支一,Y都支是绿0}绿笔 笔,一3支 红2笔 3 8 3 , 0 0 2 2 28
P{X 0,Y 1} 3 2 3 8 3 , 01 1 2 14
故 F ( x2 , y2 ) F ( x2 , y1 ) F ( x1 , y1 ) F ( x1 , y2 ) 0.
4.二维随机变量的分类 二维离散型随机变量及其分布：分布律、分布函数 二维连续型随机变量及其分布：分布密度、分布函数
二、二维离散型随机变量及其分布
1. 定义若二维随机变量 ( X, Y ) 所取的可能值是有限 对或无限可列多对,则称 ( X, Y ) 为二维离散型随机 变量. 2. 二维离散型随机变量的分布律
xi x y j y
其中和式是对一切满足 xi x, y j y 的i, j求和.
三、二维连续型随机变量及其分布
1. 定义对于二维随机变量( X , Y ) 的分布函数 F ( x, y),
如果存在非负的函数 f (x, y) 使对于任意 x, y 有
yx
F ( x, y)
几何上, z f ( x, y) 表示空间的一个曲面.

f ( x, y)d x d y 1,
表示介于 f (x, y)和 xOy 平面之间的空间区域的全部 体积等于1.
P{( X ,Y ) G} f ( x, y) d x d y,
G
P{( X ,Y ) G }的值等于以G为底 , 以曲面z f ( x, y) 为顶面的柱体体积.
一、二维随机变量及其分布 1.二维随机变量的定义
设 E 是一个随机试验, 它的样本空间是 S {e},
设 X X (e) 和 Y Y (e) 是定义在 S 上的随机变量,

y1
y2
y3
...
p11
p12
p13
...
p21
p22
p23
...
p31
p32
p33
...
例1 设试验E为掷一颗骰子，观察出现的点数，定 义两个随机变量如下
X 表示骰子出现的点数.
1, 当出现奇数点时, Y 2,当出现偶数点时.
试求X与Y的联合分布律．
解 (X，Y)可能取值为(1,1)、(1,2)、(2,1)、(2,2)、(3,1)、(3,2)、 (4,1)、(4,2)、(5,1)、(5,2)、(6,1)、(6,2)．
f (x, y)
1
1 (x2y2)
e 2 2
, x, y
2 2
G {(x, y) | x 2 y 2 2} ， P{( X ,Y ) G}(P{X 2 Y 2 2})
求
．
解 P{(X ,Y )G} f (x, y)dxdy
P{x1 X x2 , y1 Y y2} F(x2 , y2 ) F(x1, y2 ) F(x2 , y1 ) F(x1, y.1 )
y y2 y1
o x1
x2 x
二、二维离散型随机变量
定义 若二维随机变量 (X，Y) 所有可能取的值是有限 对或可列无穷多对，则称 (X，Y) 为二维离散型随机变 量． 设二维离散型随机变量 (X，Y) 所有可能取值为
f (x, y)dxdy


x
y
f
(u, v)dudv．
则称(X，Y)为二维连续型随机变量，称f(x,y)为(X，Y)的概率密度或X、Y的 联合概率密度．

一、二维随机变量 在实际应用中，有些随机现象需要同时用两个或以 上的随机变量来描述. 例如，研究某地区学龄前儿童
前儿童的发育情况时，就要同时抽查儿童的身高 X、 体重Y , 这里，X和 Y是定义在同一样本空间
S{某地区的全部学龄前儿童}
上的两个随机变量. 在这种情况下，我们不但要研究 多个随机变量各自的统计规律，而且还要研究它们之 间的统计相依关系，因而需考察它们的联合取值的统
(x 2 , y2)
y1
O x1
x2 x
图 2.
二维随机变量的分布函数
P { x 1 x x 2 ,y 1 y y 2 } F ( x 2 ,y 2 ) F ( x 2 ,y 1 )
F ( x 1 ,y 2 ) F ( x 1 ,y .1 ).
二维随机变量的分布函数
P { x 1 x x 2 ,y 1 y y 2 } F ( x 2 ,y 2 ) F ( x 2 ,y 1 ) F ( x 1 ,y 2 ) F ( x 1 ,y 1 ). 若已知 (X,Y)的分布函数F(x,y),则可由F(x,y) 导出 X和 Y各自的分布函数 FX(x)和 FY(y):
F X ( x ) P { X x } P { X x , Y } F(x, )
F Y ( y ) P { Y y } P { X , Y y } F (, y)
.
二维随机变量的分布函数
P { x 1 x x 2 ,y 1 y y 2 } F ( x 2 ,y 2 ) F ( x 2 ,y 1 ) F ( x 1 ,y 2 ) F ( x 1 ,y 1 ). 若已知 (X,Y)的分布函数F(x,y),则可由F(x,y) 导出 X和 Y各自的分布函数 FX(x)和 FY(y):

, = � � 2
4


7

+∞
1 −+


, = � � 2
4


+∞
=�

+∞

−− � −

= ()− () =
从而系统的平均寿命为万小时.
(

),且相互独立





联合密度函数为(,)= ()
1 −+
2
= �4

, > ,>
,
, 其他
系统寿命为{ห้องสมุดไป่ตู้,}.平均寿命为 ({,}).
6
1 −+
2
联合密度函数为(,)=�4

, > ,>
,
, 其他
1 −+
2
(,
平均寿命为
4
+∞ +∞ )
({,})= � �



(, )
,





−∞
−∞
因积分区域关于= 对称,
且被积函数交换,不变. 故


+∞
1 −+
分
度
布
律
为
,
= , = = ,,∈ ℕ+, ⋯ ,
+∞
+∞
若���(,(
),)
,绝对收敛,
−∞ −∞

令= ,,则
+∞
+∞
,) ,
8
谢谢观看!

FX ( x) F ( x,) FY ( y) F (, y) 分别称 FX ( x)和 FY ( y) 为F ( x, y)关于 X 和Y 的
边缘分布函数. 联合分布函数的性质
完12
联合分布函数的性质
随机变量 ( X ,Y )的联合分布函数
F ( x, y) P{ X x,Y y}.
联合分布函数的性质：
(1) 0 F ( x, y) 1, 且
y
(x, y)
对任意固定的 y, F (, y) 0,
O
x
对任意固定的 x, F ( x,) 0,
F (,) 0, F (,) 1;
注：以上四个等式可从几何上进行说明.
（2）F ( x, y) 关于 x 和 y 均为单调非减函数，即
13
联合分布函数的性质
是定义在 S 上的两个随机变量，称( X ,Y )为定义在 S
上的二维随机变量或二维随机向量.
注： 一般地，称 n 个随机变量的整体 X ( X1, X2 , , Xn )为 n 维随机变量或随机向量.
完
3
二、二维随机变量的分布函数
二维随机变量 ( X ,Y )的性质不仅与 X 及 Y 有关，
而且还依赖于这两个随机变量的相互关系, 故需
F(x, y) P{X x,Y y} 就是随机点 ( X ,Y ) 落入区域
{(t, s) | t x, s y}
的概率(如图1).
由概率的加法法则，随机点( X ,Y ) 落入矩形域
{ x1 x x2 , y1 y y2 }
的概率
P{ x1 x x2 , y1 y y2 } F ( x2 , y2 ) F ( x2 , y1 )
4
二维随机变量的分布函数

i0
i0
k
ei 1 1
i0 i!
e ki 2 2
(k i)!
1 e(12 ) k!
k i1
k! i!(k
i)!1i2ki
(1 2 )k e(12 ) k!
，
1.2 连续型随机变量的函数分布
1、Z=X+Y的分布
设 X 与Y 的联合概率密度为 f (x ，y) ，则 Z X Y 的概率密度为
2π
试证明 Z X Y 服从 N(0，2) ．
1.2 连续型随机变量的函数分布
证明 利用卷积公式可得
1 x2 ( z x)2
fZ (z) fX (x) fY (z x)dx 2π e 2 e 2 dx
1
2π
1
e dx ．
2x
z 2
2
z2 2
2
2π
作变量替换，令 2x z t ，则有 2
Fmax (z) FX (z)FY (z)
N=min{X,Y}分布函数 Fmin (z) 1[1 FX (z)][1 FY (z)] ．
1.2 连续型随机变量的函数分布
例3.24 设某种型号的电子元件的寿命（以小时计）近似服从N （160,202)，随机地选取4只，求没有电子元件寿命小于180小时的概率．
求 Z 的分布律．
解
由题意可知
P{X
i}
ei 1 1
(i 0，1，2 ， ) ， P{Y
j}
ej 2 2
( j 0，1，2， ) ，
i!

j!
则 Z X Y 可能取的值为 0，1，2 ， ．因 X 与Y 相互独立，故有
k
k
P{Z k} P{X Y k} P{X i ，Y k i} P{X i}P{Y k i}

边缘概率密度函数的计算方法
边缘概率密度函数是二维连续随机变量的两个随机变量的Fra bibliotek缘分布的密度函数。
边缘分布函数的例子
例如，对于二维正态分布，边缘分布函数是标准正态分布函数。
二维随机变量及其分布函 数
本节将介绍二维随机变量的定义、表示方法，以及二维离散和连续随机变量 的分布函数和分布密度函数。
二维随机变量的定义
二维随机变量是由一对随机变量组成的随机变量，可以用一个有序对表示(X, Y)，其中X和Y是两个单独的随机变量。
二维随机变量的表示方法
二维随机变量可以用概率分布函数或概率密度函数来表示其取值范围和概率 分布。
二维离散随机变量的分布函数
二维离散随机变量的分布函数是一个二维数组，其中每个元素表示随机变量 取对应值的概率。
二维连续随机变量的分布密度函数
二维连续随机变量的分布密度函数表示随机变量的取值在某个区域内的概率密度。
边缘分布函数的定义
边缘分布函数指的是一个随机变量的分布函数，忽略另一个随机变量的影响。

分布函数，再研究离散型随机变量的分布律，进而研究二维连续
型随机变量的概率密度，最后再考虑随机变量的独立性和随机变
量函数的分布．
图3-1
多维随机变量及其分布
二维随机变量及其分布函数
1.2 联合分布函数
定义 2 设 (X ，Y) 是一个二维随机变量，对于任意的 x，y ，称
定义在整个实平面上的二元函数
边缘分布函数 FX (x) 和 FY ( y) 可以由 (X ，Y ) 的分布函数 F(x ，y) 来确定，事实上 FX (x) P{X x} P{X x ，Y } F(x ， ) ，
即
FX
(x)
F(x
，
)
lim
y
F(x
，y)
．
（3-5）
类似地，有
FY
(
y)
F(
，y)
lim
x
F(x
，y)
．
（3-6）
y)
A(B
arctan
x)
C
π 2
0，
多维随机变量及其分布
二维随机变量及其分布函数
1.3 边缘分布函数
解得
A 1 ，B π ，C π ，
π2
2
2
于是， (X ，Y) 的分布函数为
F(x
，y)
1 π2
π 2
arctan
x
π 2
arctan
y
．
因此，两个边缘分布函数分别为
FX
(x)
F(x
多维随机变量及其分布
二维随机变量及其分布函数
1.3 边缘分布函数
例 已知二维随机变量 (X ，Y) 的分布函数为 F(x ，y) A(B arctan x)(C arctan y) ( x ，y ) ，

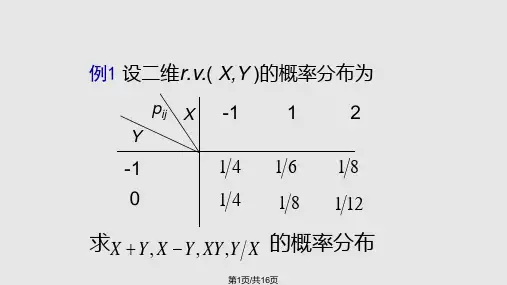
解:
1 x2 y2
f (x, y) e 2 , ( x , y )
2
FZ (z) P(Z z) P( X 2 Y 2 z)
当z<0,显然FZ(z)=0,
当z≥0,
FFFFZZZZ((((zzzz))))xx2xx222yy2yy222zz2zz22222122111eeeexx2xx22222y22y2yy2d22dddxxxxddddyyyy
( x z )2 2
e dx 22 2
2
2 e 令x z t e2 e e edt dx 2 e 2
zzz44222
e2 dx e2 4
z
2
4
(( xx
t
2
zz 22
))22
(x
z 2
)2
z2 4
1
z2
e4
2
X~ N(μ1 , σ12) Y~ N(μ2 , σ22) X与Y相互独立
二维离散型随机变量函数的分布
设(X,Y)为离散型随机变量，
P(X xi ,Y y j ) pij, i, j 1,2,...
Z=g(X,Y)为一维离散型随机变量.若对于 不同的(xi,yj),g (xi,yj)的值互不相同,则Z的 分布律为
P(Z g(xi , y j )) pij i, j 1,2,...
k
p(i)q(k i) i0
离散型 卷积公式
例3:设X,Y相互独立,且X~P(λ1), Y~P(λ2) 证明:Z=X+Y~P(λ1+λ2)
证: P( X k) 1k e1 , k0,1,2,,
k!
P(Y k) k2 e2 , k0,1,2,,
k!
P(Z k) P( X Y k) Pik0( X i,Y k i)