当前位置：文档之家 › abaqus教程ABAQUS墙体滞回曲线例题

abaqus教程ABAQUS墙体滞回曲线例题

  • 格式：pdf
  • 大小：1.29 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

Abaqus作习题讲解3

Abaqus作习题讲解3

出的对话框中定义载荷名称为 Load-Pressure，分 析步选择 Step-1，载荷类型选择 Mechanical： Pressure，单击 Continue，选择尚未确定的左侧的 三条边， 单击提示区中的 Done 按钮进入 Edit Load 对话框，输入 Magnitude:16e6,单击 Ok 完成内压 施加。 14. 在环境栏 Module 中选择 Mesh，Object 选择 Part 选项。执行 SeedEdge By Number， 在图形窗口选择底部横边和 X 坐标为 0 的竖直 边，单击提示区中的 Done 按钮，在 basic 选项 卡中选择 By Number：Number of elements，输 入种子数 5， 在 Constrains 选项卡中选择 Do not allow the number of elements to change，单击 Ok 完成设置。 同样方法设置内侧圆弧、 线段种 子数依次为 30、8、30。
15.单击工具箱中 （Mash Part） ，单击提示区 OK to mesh the part 后面的 Yes 完成网格划分。 16.在工具箱中单击 （Assign Element Type） ，在 弹出的 Element Type 对话框 中选择线性隐式四边形单元 CAX4R,单击 Ok 完成单元类 型的选择,保存模型。 17.在环境栏 Module 后 面选择 Job，进入该模块后， 单击工具箱中的 （Job
Manager） ，点击弹出的对话 框下部的 Create，在新的对 话框 Create Job 中定义作业 名称为 Pressure-vessel， 单击 Continue， 进入 Edit Job 对话 框，输入作业描述 Description： Static analysis of a pressure vessel，其他为默 认设置，单击 OK，在 Job Manager 中出现作业 Pressure-vessel，单击对话框 右部的 Write Input 可以输出 与作业同名的.inp 文件，单 击 Submit 提交作业， 进行计 算；单击 Monitor 弹出 Link Monitors 对话框， 可以对作业运行 情况进行监视。 18.执行 PlotContoursOn Both Shapes， 显示模型变形前后的 云图。 19.执行 OpinionsCommon， 在弹出的 Common Plot Opinions 对 话框，切换到 Basic 选项卡，选中 Deformation Scale Factor 栏中，默 认的时 Auto-compute， 即程序自动 选择变形放大系数，本例默认为放大 385.206 倍的结果。选择 Uniform 前面的单选按钮，在出现的 Value 后面自定义均匀放大系数为 150，单击 Apply 按钮即可；也可通过 Nonuniform 分别定义 X、Y、Z 方向的放 大系数。 20.执行 ReportField Output，在弹出的 Report Field Output 对话框输出变量 Output Variable 栏中 Position 下选择 Unique Nodal 然后在下拉列表中选择 U: Spatial displacement 下面的 U1，单击 Apply 按钮，

ABAQUS使用例题

ABAQUS使用例题
*Concrete tension stiffening
2030.1, 0
2010., 0.0000282563
1232.19, 0.00014944
849.073, 0.000257466
660.524, 0.000359008
548.371, 0.000458002
473.404, 0.000555757
同理，依样设定加载梁的尺寸，得到加载梁部件。
这样，第一步部件尺寸设定就完成了。
图4
第二步：部件使用材料的设定
加载梁使用c50混凝土，砌体使用与实验相对应的材料参数。
由于模拟是针对砌体，所以不考虑加载梁的塑性，因此加载梁只设定密度和弹性。
而砌体则以混凝土塑性损伤本构模型来模拟，要设定密度、弹性、混凝土损伤塑性。
看本例题之前，请务必先找着文献[1]中P75——P101中提供的例题完全照做一遍，以熟悉基本的操作流程。
下面是本例题的操作过程，模拟一片砌体墙片的滞回实验。
第一步：模型部件的建立
进入ABAQUS（中文版），在左方菜单中，选择“部件”，鼠标右键点击一下，选择“创建”，进入模型的部件创建菜单。模型中往往有一个或者多个部件构成。如图1，设定部件名称，其他选项如图1所示。
以上内容中混凝土材料参数的设定参见资料[2]，砌体材料参数的设定参见资料[3]。
第三步：将材料属性赋予模型
设定了材料参数后，还要对将材料参数“赋予”模型。其操作菜单如图5
图5
首先建立两个界面SECTION-1和SECTION-2如图5左边红框所示，将两种材料（C50混凝土与砌体材料）“注入”SECTION-1和SECTION-2中，然后点击右边红框中的图标，选择截面所要“赋予”的对象，即可完成材料参数赋予模型的操作。

有限元基础教程Abaqus软件例题详解2

有限元基础教程Abaqus软件例题详解2

弹出 Create Instance 对话框，在 Parts 栏中选择部件，在实体 类型（Instance Tpye）后面选择 Independent（mesh on instance） ，单击 OK 确定。 11.（定义分析步）在环境栏 Module 后选择 Step，进入 分析步模块，单击工具箱中 （Create Step） ，在弹出的对
击工具箱中
（Create Boundary Condition） ， 在
弹出的对话框中输入边界的名称 BC-fixed-left， 分 析步选择后面定义的初始分析步 Apply-PF，边缘 条件类型选择 Mechanical： Displacement/Rotation，单击 Continue， 用鼠标在 图形区域选择模型左下角点 1,单击鼠标中键，在 弹出的 Edit Boundary Condition 对话框中，选中 U1、~UR3 前面的复选框，即约束所有自由度， 单击 Ok 完成左端梁下部固定约束。 15.同样方法对右端梁下部进行边界条件的 施加。 16.单击工具箱中的 （Create Load）在
轴正向，单击提示区的 Create Datum 按钮，完成第一条边坐标系的创建。然后按照同样方法设置另外两条 边坐标系的创建。 9.执行 AssignBeam Section Orientation 命令， 在 图形窗口中单击选中部件 的组编竖直梁，单击提示区 中的 Done 按钮， 输入 n1 方 向的方向矢量（0.0,0.0， -1.0） ，回车，单击提示区中 的 Ok 按钮确认。然后同样 方法完成两外梁的方向设 定。 10.（定义装配体）在环 境栏 Module 后面选择 Assembly，进入装配模块， 单击 （Instance Part） ，
示区 OK to mesh the part 后面的 Yes 完成网格划分并保存模型。

abaqus降低滞回曲线承载力的方法

abaqus降低滞回曲线承载力的方法

一、介绍在工程领域中，结构的稳定性和强度是至关重要的。

滞回曲线是描述结构在承受载荷时的非线性行为的重要工具，而滞回曲线的承载力则是评估结构受力性能的关键指标。

在abaqus软件中，我们可以通过一些方法来降低滞回曲线的承载力，从而提高结构的安全性和可靠性。

二、方法一：增加受力区域的强度在abaqus中，我们可以通过增加结构受力区域的强度来降低滞回曲线的承载力。

具体操作是在模型中对受力区域进行加固，可以在软件中设置增加的材料参数或者受力区域的截面尺寸，从而增加受力区域的强度，减小滞回曲线的承载力。

三、方法二：减小加载速率另一种降低滞回曲线承载力的方法是减小结构的加载速率。

abaqus软件中可以通过控制载荷的施加速率来实现这一目的。

减小加载速率可以使结构在受力过程中更加平稳地变形，降低结构材料的应力水平，从而减小滞回曲线的承载力。

四、方法三：优化结构材料和截面设计除了通过增加受力区域的强度和减小加载速率来降低滞回曲线的承载力外，对结构的材料和截面设计进行优化也是一种重要的方法。

abaqus软件提供了丰富的材料和截面设计选项，可以根据具体的工程需求进行设计和优化，从而达到降低滞回曲线承载力的目的。

五、方法四：优化边界条件结构的边界条件对其受力性能有重要影响，因此优化边界条件也是降低滞回曲线承载力的关键方法之一。

abaqus软件中可以通过调整边界条件的设定来优化结构的受力状态，从而降低滞回曲线的承载力，提高结构的稳定性和安全性。

六、总结在abaqus软件中采取适当的方法，可以有效降低滞回曲线的承载力，提高结构的安全性和可靠性。

通过增加受力区域的强度、减小加载速率、优化结构材料和截面设计以及优化边界条件等方法的应用，可以使结构在受力过程中表现出更好的非线性行为，为工程实践提供更可靠的支撑和保障。

七、方法五：考虑温度影响在实际工程中，结构在受力过程中受到温度变化的影响是不可避免的，而温度的变化会对材料的性能产生影响，进而影响滞回曲线的承载力。

abaqus连接器滞回规则

abaqus连接器滞回规则

abaqus连接器滞回规则全文共四篇示例，供读者参考第一篇示例：abaqus是一种用于有限元分析的工程软件，它在连接器中可以模拟材料的滞回行为。

滞回是指材料在受力过程中产生的应力和应变之间的不对称性，这是由于材料内部微观结构的变化导致的。

连接器滞回规则是用来描述连接器在受力过程中材料的滞回行为的规则，它可以帮助工程师更准确地预测结构在强烈加载下的行为。

在abaqus中，连接器是用来连接两个结构件或者不同类型的结构件的元素，连接器可以通过滞回规则来描述连接器的滞回行为。

滞回规则可以通过定义连接器的性能来模拟结构在受力过程中的行为，进而更准确地评估结构的稳定性和强度。

abaqus连接器的滞回规则通常包括以下几种常见的模型：1. 线性弹簧模型：线性弹簧模型是一种简单的滞回规则，它假设连接器在受力过程中的应力和应变呈线性关系。

这种模型适用于连接器在受力较小的情况下，简单直观，但在受力较大时可能不准确。

2. 弹簧-阻尼模型：弹簧-阻尼模型是一种结合了弹簧和阻尼两种性质的滞回规则，它可以更准确地描述连接器在受力过程中的行为。

弹簧模型用来描述连接器的弹性特性，而阻尼模型用来描述连接器在受力过程中的能量损耗，从而更全面地描绘连接器的性能。

3. Bouc-Wen模型：Bouc-Wen模型是一种常用的非线性滞回规则，它可以更准确地模拟连接器在受力过程中的非线性行为。

Bouc-Wen模型是基于一系列非线性微分方程建立的，可以描述连接器在不同加载条件下的滞回特性。

abaqus连接器滞回规则是一种非常重要的工程分析方法，它可以帮助工程师更准确地评估结构的性能和稳定性。

通过对连接器的滞回行为进行合理的建模和模拟，可以更好地指导工程实践，提高结构设计的准确性和安全性。

ABAQUS的连接器滞回规则模型设计已经成为结构仿真建模的重要一环，希望未来能继续深入研究和发展这方面的技术，为工程领域的发展做出更大的贡献。

第二篇示例：Abaqus连接器滞回规则是在Abaqus软件中用于描述连接器件在加载和卸载过程中的非线性行为的一种规则。

abaqus经典例题集

abaqus经典例题集

abaqus经典例题集下面是一些abaqus的经典例题，以帮助大家更好地理解和掌握这款强大的有限元分析软件。

1.线性弹性问题例题1：在一个长方形平板上施加均匀分布的载荷，求解板的应力和应变。

解题步骤：-创建模型，定义几何参数和材料属性；-划分网格；-应用边界条件；-施加载荷；-求解；- 后处理，查看结果。

2.非线性问题例题2：一个简支梁在受力过程中，梁的横截面半径发生变化。

求解梁的挠度和应力。

解题步骤：-创建模型，定义几何参数、材料属性和边界条件；-划分网格；-应用材料的本构关系；-施加载荷；-求解；- 后处理，查看结果。

3.热力学问题例题3：一个平板在均匀温度差的作用下，求解热应力和温度分布。

解题步骤：-创建模型，定义几何参数、材料属性、边界条件和温度差；-划分网格；-应用热力学本构关系；-施加温度边界条件；-求解；- 后处理，查看结果。

4.耦合问题例题4：一个悬臂梁在受到弯曲应力和剪切应力的同时，还受到温度的变化。

求解梁的应力和温度分布。

解题步骤：-创建模型，定义几何参数、材料属性、边界条件、载荷和温度变化；-划分网格；-应用耦合场本构关系；-施加边界条件、载荷和温度边界条件；-求解；- 后处理，查看结果。

5.接触问题例题5：两个物体相互挤压，求解接触面上的应力和接触力。

解题步骤：-创建模型，定义几何参数、材料属性、边界条件和接触属性；-划分网格；-应用接触算法；-施加边界条件和接触力；-求解；- 后处理，查看结果。

通过以上五个经典例题的讲解，相信大家对abaqus的应用有了更深入的了解。

在实际应用中，我们应根据具体问题选择合适的分析类型，并灵活运用所学知识。

希望大家能在实践中不断提高，成为优秀的有限元分析工程师。

abaqus混凝土滞回曲线

abaqus混凝土滞回曲线

Abaqus混凝土滞回曲线1.引言混凝土结构在受到外部荷载作用时常常出现非弹性的行为，这种行为在很大程度上可以通过滞回曲线来描述。

A b aq us是一种用于有限元分析的软件工具，可以用来模拟混凝土结构的滞回曲线。

本文将介绍如何在A b aq us中创建和分析混凝土滞回曲线。

2.混凝土材料模型在A ba qu s中，混凝土的滞回曲线可以通过选择适当的材料模型来模拟。

其中较为常用的模型包括弹塑性模型、本构模型和损伤模型等。

这些模型可以根据混凝土的力学性质和行为来选择。

2.1弹塑性模型弹塑性模型是最简单且常用的混凝土材料模型之一。

它假设混凝土在受到荷载时具有弹性行为和塑性行为。

这种模型主要用来模拟混凝土的线弹性行为，无法准确描述混凝土的非线性行为。

2.2本构模型本构模型考虑了混凝土在受到荷载时的非线性行为，并能较好地描述混凝土的滞回性能。

常见的本构模型有Ma n de r、Ho gn es ta d、P o po vi cs等。

这些模型能够较为准确地模拟混凝土的滞回曲线，但需要输入较多的材料参数。

2.3损伤模型损伤模型是一种相对较为复杂的混凝土材料模型，它考虑了混凝土在受到荷载时的损伤过程。

损伤模型不仅能够模拟滞回曲线，还能够模拟混凝土的破坏过程。

常见的损伤模型有L ine a rD am ag e、N o nl in ea rD am ag e等。

3. Ab aqus中的混凝土滞回曲线分析在A ba qu s中，通过以下几个步骤可以实现混凝土滞回曲线的分析：3.1创建几何模型首先，在Ab aq us中创建混凝土结构的几何模型。

可以通过绘制几何图形或导入C AD文件来创建所需的几何形状。

3.2定义材料性质在A ba qu s中，需要定义混凝土材料的力学性质，包括弹性模量、泊松比、强度参数等。

这些参数将决定混凝土的行为。

3.3应用荷载在几何模型上定义所需的荷载，可以包括静态荷载、动态荷载等。

荷载的大小和方式将对混凝土的响应产生影响。

abaqus橡胶滞回曲线

abaqus橡胶滞回曲线

abaqus橡胶滞回曲线全文共四篇示例，供读者参考第一篇示例：Abaqus橡胶滞回曲线是指在ABAQUS软件中模拟出的橡胶材料在加载和卸载的过程中所表现出的应力-应变关系的曲线。

橡胶是一种具有高度弹性和可逆变形特性的材料，其应力-应变关系呈现出明显的滞回效应，即在加载和卸载的过程中，材料的应力-应变曲线并不完全重合，形成一个闭合的环形曲线。

橡胶材料的滞回性质是由于其分子链在加载和卸载的过程中会发生损伤和重新排列所致。

在加载过程中，橡胶的分子链会逐渐拉伸并形成应变，但在卸载过程中，这些分子链并不完全恢复到初始状态，而是会有一定程度的残留变形。

这种现象导致了橡胶在不同加载路径下呈现出不同的应力-应变关系，形成了滞回曲线。

在ABAQUS软件中，通过建立合适的橡胶材料模型和定义相应的材料参数，可以有效地模拟出橡胶材料的滞回曲线。

ABAQUS中常用的橡胶材料模型包括Mooney-Rivlin模型、Neo-Hookean模型、Yeoh模型等，这些模型可以描述不同条件下橡胶材料的应力-应变关系，从而实现了对橡胶滞回性质的准确模拟。

在进行橡胶材料的滞回曲线模拟时，需要考虑多种因素，如材料的应力-应变特性、加载路径、温度等。

通过对这些因素的综合考虑和合理调整，可以得到较为真实和精确的橡胶滞回曲线。

在实际工程中，橡胶材料的滞回性质对其在振动、减震、密封等方面的应用具有重要意义，因此准确模拟和理解橡胶滞回曲线对于优化设计和改进材料性能具有重要意义。

ABAQUS橡胶滞回曲线的模拟可以帮助工程师了解橡胶材料的应力-应变特性和滞回性质，为工程实践提供重要参考。

通过对橡胶材料的滞回曲线进行深入研究和分析，可以有效地优化设计方案，提高产品性能，推动工程技术的发展与进步。

ABAQUS软件在橡胶材料研究领域的应用将会为工程师们的工作带来更多的便利和可能性。

第二篇示例：Abaqus橡胶滞回曲线是描述橡胶材料非线性特性的重要参数之一。

abaqus后处理输出滞回曲线

abaqus后处理输出滞回曲线

abaqus后处理输出滞回曲线ABAQUS后处理是一种用于分析模拟结果的工具，可以通过输出滞回曲线来评估材料的性能和行为。

滞回曲线是描述材料在加载和卸载过程中应力和应变之间的关系的图形。

滞回曲线提供了材料的弹性和塑性变形的信息，对于结构材料的设计和评估至关重要。

该曲线所描述的行为是材料在曲线上的不同阶段所受到的应力变化情况。

滞回曲线通常是通过对模拟结果进行后处理来生成的。

在ABAQUS 中，可以通过定义输出请求输出所需的结果变量。

例如，可以选择输出节点的应力和应变，然后使用这些结果来绘制滞回曲线。

ABAQUS提供了很多用于绘制滞回曲线的工具和选项。

可以选择输出不同方向上的应力和应变，也可以选择输出整个结构或特定区域的结果。

此外，还可以使用ABAQUS/Viewer等工具来可视化结果，并使用图形编辑工具进行进一步的分析和处理。

绘制滞回曲线的过程通常包括以下步骤：1.定义输出请求：在ABAQUS的输入文件中，需要定义输出请求来指定要输出的结果变量。

这包括选择要输出的节点和单元，以及要输出的应力和应变的方向。

2.运行模拟：使用ABAQUS的求解器运行分析模拟。

在求解器运行过程中，会生成用于后处理的结果文件。

3.打开结果文件：使用ABAQUS/Viewer工具打开结果文件。

在ABAQUS/Viewer中，可以查看模拟结果和生成滞回曲线。

4.绘制滞回曲线：在ABAQUS/Viewer中，选择要绘制滞回曲线的节点和单元。

然后，使用绘图工具绘制滞回曲线。

绘制的滞回曲线通常是一个封闭的环形图形，表示材料在加载和卸载过程中的应力和应变变化。

曲线的形状和特征可以用来评估材料的弹性和塑性行为。

滞回曲线的分析和解释需要考虑材料的特性和载荷条件。

例如，在应力-应变曲线中，可以观察到材料的屈服点、塑性区域、极限强度等。

这些信息可以帮助工程师评估材料的可靠性和安全性，并做出相应的设计和优化决策。

总结起来，ABAQUS后处理可以输出滞回曲线来描述材料的弹性和塑性行为。

abaqus输入滞回曲线

abaqus输入滞回曲线

abaqus输入滞回曲线
在Abaqus中模拟滞回曲线通常涉及到定义材料的本构模型。

在滞回曲线的情境下，常用的本构模型之一是弹塑性模型，其中包含了弹性阶段和塑性阶段。

以下是一些在Abaqus中定义滞回曲线的步骤：
1.定义材料：在Abaqus中，首先需要定义材料的本构模型。

对于滞回曲线，可以选择合适的本构模型，如弹塑性模型。

可以使用Abaqus提供的现成本构模型，或者根据材料的滞回性质自定义本构模型。

2.指定滞回曲线：如果使用的是自定义本构模型，需要在材料定义中指定滞回曲线的参数。

这可能包括弹性刚度、塑性刚度、屈服强度等。

3.设置加载条件：在模拟中，需要设置加载条件，模拟材料受到的外部力或位移。

这可以通过加载步骤和加载边界条件来实现。

4.运行分析：定义完材料、本构模型和加载条件后，运行Abaqus分析。

Abaqus会根据定义的材料性质和加载条件，模拟滞回曲线的形成过程。

5.分析结果：分析完成后，可以查看Abaqus生成的结果文件，其中包含了模拟过程中的各种信息，包括应力、应变、变形等。

可以通过结果文件中的数据来获取滞回曲线的信息。

请注意，具体的步骤和操作可能会因您所使用的Abaqus版本和具体问题而有所不同。

建议查阅Abaqus的官方文档或使用手册，以获取更详细和针对您特定问题的信息。

abaqus连接器滞回规则

abaqus连接器滞回规则

abaqus连接器滞回规则
Abaqus中的连接器滞回规则是指在模拟结构或材料在加载和卸载过程中的非线性行为。

滞回是指材料或结构在加载和卸载过程中出现的能量损失和非弹性变形。

在Abaqus中，可以通过定义连接器的滞回规则来模拟材料或结构的非线性行为。

Abaqus提供了多种连接器滞回规则，包括可压缩弹簧、塑性连接器、弹塑性连接器等。

这些规则可以用来模拟材料的非线性应力-应变关系，以及结构在受力过程中的非线性变形行为。

在Abaqus中，用户可以根据具体的材料性质和结构特点选择合适的连接器滞回规则。

通过定义连接器的滞回规则，可以更准确地模拟材料和结构在复杂加载条件下的行为，从而提高分析的准确性和可靠性。

总之，Abaqus中的连接器滞回规则是用来模拟材料和结构在加载和卸载过程中的非线性行为的重要工具，通过合理选择和定义滞回规则，可以更准确地模拟材料和结构的非线性行为，从而提高分析的准确性和可靠性。

abaqus例题手册

abaqus例题手册

abaqus例题手册
ABAQUS是一款功能强大的有限元分析软件，广泛应用于各种工程领域。

其例题手册旨在帮助用户更好地理解和使用ABAQUS，通过具体的例题展示软件的使用方法和分析过程。

以下是ABAQUS例题手册中一些常见的例题：
1. 悬臂梁分析：该例题主要演示了如何使用ABAQUS对悬臂梁进行静态和动态分析，包括模型的建立、网格划分、边界条件和载荷的施加、求解过程以及结果的后处理等。

2. 薄板弯曲分析：该例题通过一个简单的薄板弯曲问题，介绍了ABAQUS 在处理弯曲问题时的基本步骤，包括模型的建立、材料属性的定义、边界条件和载荷的施加、求解过程以及结果的解释。

3. 疲劳分析：该例题通过一个简单的疲劳分析问题，介绍了如何使用ABAQUS进行疲劳寿命预测。

该例题展示了如何定义材料的疲劳属性、如何进行循环载荷的施加以及如何解释结果。

4. 冲击分析：该例题通过一个简单的冲击分析问题，介绍了如何使用ABAQUS进行冲击模拟。

该例题展示了如何定义材料的冲击属性、如何设置冲击条件以及如何解释结果。

5. 热分析：该例题通过一个简单的热分析问题，介绍了如何使用ABAQUS
进行温度场模拟。

该例题展示了如何定义材料的热属性、如何设置热边界条件和载荷以及如何解释结果。

以上是ABAQUS例题手册中一些常见的例题，通过这些例题的介绍，用户
可以更好地了解ABAQUS的功能和应用，提高软件的使用效率和分析精度。

abaqus计算回弹及方法

abaqus计算回弹及方法

Abaqus回弹计算过程回弹分析我倒是做过两个，说下简要步骤吧，同样是仅供参考啊1.首先用·explicit做成型过程的分析，加载方式选位移加载比较好，加载的幅值选smooth step（平滑变化）2.可适当的用质量放大来加快这一准静态分析的过程3.分析完成后可用standard观察工件的回弹，具体做法是：1.Model-Copy Model2.在新复制的模型中仅留下成型件，删除其他一切无关的边界条件以及上下模，包括在Explicit中定义的接触属性3.在step模块中创建predefine field request-others-initial state-last frame/last step（导入的job名称为之前做成型分析的那个job的名称）4.删除原来所有的后续分析步，并新建一个static，general的分析步5.创建一个新的作业提交分析，并观察回弹大致就是这样吧，希望对你有用！回弹分析，从explicit导入standard计算。

先copy explicit中模型进入standard模块，然后做一下改进，删除各个part、set和surface等，只留下需要回弹分析的变形体。

删除分析步，删除接触和属性。

然后在step中建立一个static分析步骤。

设置计算为非线性。

然后定义居于前面成形结果的回弹分析，在Model Tree中打开Predefined Fields，选择Initia作为分析步，Other最为类别，选择Initial State，然后在视窗中选择需要分析的回弹体，然后点击done，然后Edit Predefined Field，选择你成形分析的job名字。

然后一致ok下去，对称的边界哦条件还要施加。

你可以在amplitude中设置，比如说你分析步设置时间为6s，然后在amplitude中设置0，0；4，1（也就是在4秒时冲头应景达到了要求的位移，也就是液晶冲完，那么剩下的2秒就是停留的时间了），然后在另外设置一个分析步把冲头往回移就可以了小弟这些天正好在做冲压回弹，刚做成功，从simwe论坛上学了很多东西。

abaqus教程ABAQUS墙体滞回曲线例题

abaqus教程ABAQUS墙体滞回曲线例题

看本例题之前，请务必先找着文献[1]中P75——P101中提供的例题完全照做一遍，以熟悉基本的操作流程。

下面是本例题的操作过程，模拟一片砌体墙片的滞回实验。

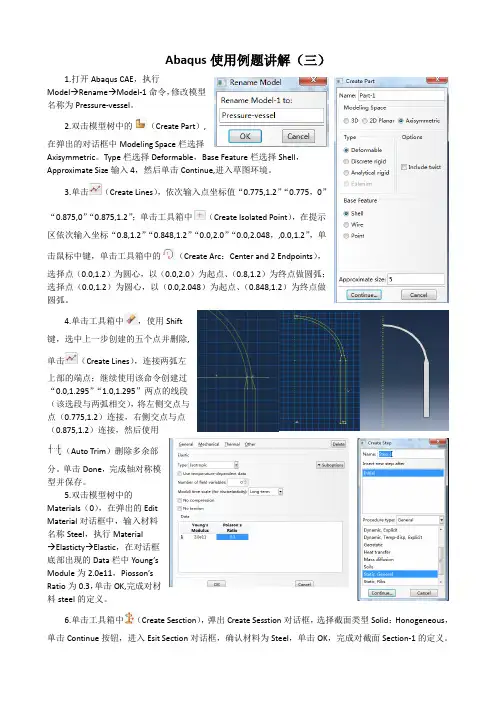
第一步：模型部件的建立进入ABAQUS（中文版），在左方菜单中，选择“部件”，鼠标右键点击一下，选择“创建”，进入模型的部件创建菜单。

模型中往往有一个或者多个部件构成。

如图1，设定部件名称，其他选项如图1所示。

图1然后中间的主操作界面出现，如图2。

此平面默认的在平行于计算机显示器的方向为XY平面，我们如图2，按照现实中墙体立面的尺寸画出墙体立面框，然后点击“完成”，弹出的菜单如图3.图2图3此处的“深度”一项就是设定墙体部件的厚度，输入0.24（墙体厚度0.24m），点击确定。

于是得到了墙体部件的基本视图如图4所示。

同理，依样设定加载梁的尺寸，得到加载梁部件。

这样，第一步部件尺寸设定就完成了。

图4第二步：部件使用材料的设定加载梁使用c50混凝土，砌体使用与实验相对应的材料参数。

由于模拟是针对砌体，所以不考虑加载梁的塑性，因此加载梁只设定密度和弹性。

而砌体则以混凝土塑性损伤本构模型来模拟，要设定密度、弹性、混凝土损伤塑性。

以上内容中混凝土材料参数的设定参见资料[2]，砌体材料参数的设定参见资料[3]。

第三步：将材料属性赋予模型设定了材料参数后，还要对将材料参数“赋予”模型。

其操作菜单如图5图5首先建立两个界面SECTION-1和SECTION-2如图5左边红框所示，将两种材料（C50混凝土与砌体材料）“注入”SECTION-1和SECTION-2中，然后点击右边红框中的图标，选择截面所要“赋予”的对象，即可完成材料参数赋予模型的操作。

第四步：安装配件在第一步谁定好了部件后，实际上部件就像积木玩具的各个零件一样还是零散分开的，这时候，就要使用装配件功能如图6所示。

图6用得较多的是红框中两个移动功能，非常简单，就是通过在空间坐标系中将部件平移到正确的位置即可。

ABAQUS例题

ABAQUS例题

对于梁的分析可以使用梁单元、壳单元或是固体单元。

Abaqus的梁单元需要设定线的方向，用选中所需要的线后，输入该线梁截面的主轴1方向单位矢量(x,y,z)，截面的主轴方向在截面Profile设定中有规定。

注意：因为ABAQUS软件没有UNDO功能，在建模过程中，应不时地将本题的CAE模型（阶段结果）保存，以免丢失已完成的工作。

简支梁，三点弯曲，工字钢构件，结构钢材质，E=210GPa，μ=0.28，ρ=7850kg/m3（在不计重力的静力学分析中可以不要）。

F=10kN，不计重力。

计算中点挠度，两端转角。

理论解：I=2.239×10-5m4，w中=2.769×10-3m，θ边=2.077×10-3。

文件与路径：顶部下拉菜单File, Save As ExpAbq00。

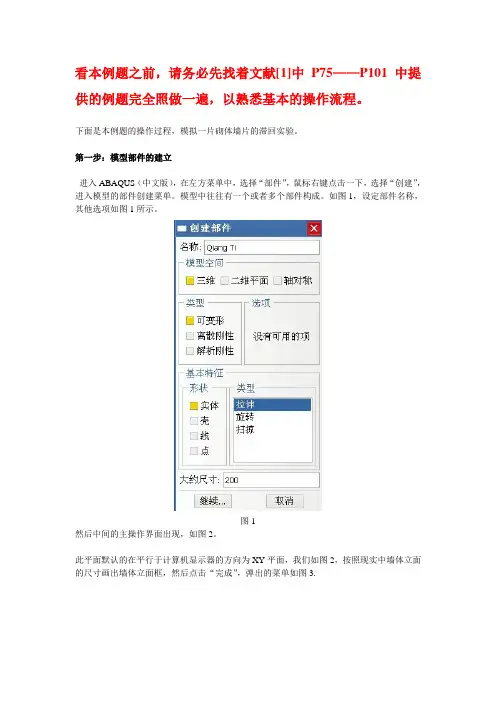
一部件1 创建部件：Module，Part，Create Part，命名为Prat-1；3D，可变形模型，线，图形大约范围10(程序默认长度单位为m)。

2 绘模型图：选用折线，从(0,0)→(2,0)→(4,0)绘出梁的轴线。

3 退出：Done。

二性质1 创建截面几何形状：Module，Property，Create Profile，命名为Profile-1，选I型截面，按图输入数据，l=0.1，h=0.2，b l=0.1，b2=0.1，t l=0.01，t2=0.01，t3=0.01，关闭。

2 定义梁方向：Module，Property，Assign Beam Orientation，选中两段线段，输入主轴1方向单位矢量(0,0,1)或(0,0,-1)，关闭。

3 定义截面力学性质：Module，Property，Create Section，命名为Section-1，梁，梁，截面几何形状选Profile-1，输入E=210e9（程序默认单位为N/m2，GPa=109 N/m2），G=82.03e9，ν=0.28，关闭。

基于ABAQUS的混凝土剪力墙滞回性能的模拟_范浩

基于ABAQUS的混凝土剪力墙滞回性能的模拟_范浩
目前，已有很多学者对 CDP 模型进行了探讨，如 张劲等［6］给出了损伤因子的计算方法，并且认为 CDP 模型能够较好地模拟剪力墙的骨架曲线，正确反映构 件的损伤状况，但无法反映剪力墙的捏拢特性。方秦 等［7］较为详细地介绍了 CDP 模型的特点，并采用三
维实体单元模拟了素混凝土材料在单轴及双轴应力 下的力学性能以及混凝土梁、板构件的抗弯性能。尧 国皇等［8］采用 CDP 模型及实体单元模拟了钢管混凝 土柱-钢筋混凝土梁节点的竖向加载性能和循环荷载 作用性能，但其数值模拟结果并没有相应的试验数据 验证。陆新征等［9］较为简要地介绍了 CDP 模型的特 征以及模型各参数的建议取值。
本文将详细讨论 CDP 本构模型各参数的设置方 法，并结合剪力墙的试验结果，对 CDP 本构模型的准 确性进行验证，为 CDP 模型更好的服务于实际工程 提供参考。 1 CDP 模型简介
采用 CDP 模型定义一个相对完整地混凝土材料 本构的格式如下［10］：
作者简介： 范浩，硕士研究生，Email： fanhao1956@ gmail． com。
混凝土材性试验结果及相关参数取值
混凝土强度 等级 C40 C60 C80
轴心抗压强度平均 弹性模量［14］
值［14］/ MPa
dcu E0 /MPa
32． 1
33218
0． 5
52． 1
37214
0． 5
73． 2
41233
0． 5
表1
α 0． 1 0． 1 0． 1
规范钢筋循环加载本构受拉软化则采用基于应变木concretetensionstiffeningtypestrain的直线形式如图所示软jlq1的数值计算结果及相应的试验曲线如图混凝土材料的密度p2700kgin3材料的阻尼设为力应变模型隐式是指全过程均采用隐式分析方dampingbeta310这两项设置在显式分析中法求解显式则指竖向荷载的求解采用隐式分析方是必不可少的由于本文分析的试件均为静力加载试法而水平位移荷载则用绝对值为01ms2以保证惯验引入阻尼的目的不是耗能而是有效减小显式分性力导致的误差可以忽略的加速度替代并采用显析过程中的数值震荡

Abaqus常见问题技巧设置案例汇总

Abaqus常见问题技巧设置案例汇总

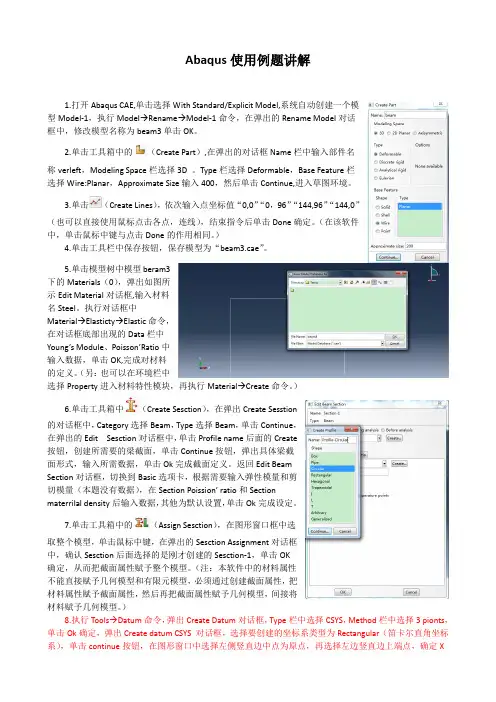
Abaqus常见问题技巧设置案例汇总Abaqus常见问题汇总如何取得节点的坐标！用a=mdb.models['你的模型'].parts['PART-1'].nodes[211].coordinates可以取得坐标，对坛子里像我一样的初学者们有借鉴作用。

扭距加载我最近在算一个题目,一个大筒体上有三个接管端面固定,大筒体两端加载扭距,但是不知道如何加载.请各位高手能赐教谢谢1. 将大筒体两端要施加扭矩的节点分别定义为两个Nset:left, right.2. 分别在大筒体两端的圆心处定义两个reference node: rp-left,rp-right.3. 用如下命令将两个节点集绕3轴旋转的自由度与参考点耦合起来,其他自由度度是否耦合根据具体问题而定:*KINEMATIC COUPLING, REF NODE=rp-leftleft, 6,6*KINEMATIC COUPLING, REF NODE=rp-rightright, 6,64. 在两个参考点上施加绕3轴旋转的弯矩.友情提醒:reference node也有自由度,注意相应的边界条件.ABAQUS多处理器进行并行计算的效果研究环境：ABAQUS6.3+8 IntelXeon 700MHz CPU+4G Ram+Win2k AdvServer SP3在命令行模式下，abaqus命令的下面三个参数进行并行计算的控制：[cpus=number-of-cpus][parallel={loop | domain | supernode | tree}][domains=number-of-domains]ABAQUS/Explicit:parallel参数可选domain,loopdomain进行拓扑域并行，loop进行循环级并行（默认）但在NT系统下，不支持loop参数cpus数要可以整除domains数，也就是一个cpu可以进行多个domain 的计算以Getting Started with ABAQUS/Explicit6.5 Example: circuit board drop testcircuit.inp分析为例(standard_memory = "256 Mb")1cpu:abaqus job=circuit intcup利用率100%，运行时间506s2cpu:abaqus job=circuit parallel=domain domains=4 cpus=2 int 每个cup利用率接近100%，运行时间402s4cpu:abaqus job=circuit parallel=domain domains=4 cpus=4 int 每个cup利用率为80%左右，运行时间297s8cpu:abaqus job=circuit parallel=domain domains=8 cpus=8 int 每个cup利用率为40%左右，运行时间364sABAQUS/Standard:parallel参数可选supernode,treesupernode(默认)对单波前进行并行处理，tree对多波前同时进行并行处理domains参数无效对于线性方程并有稀疏刚度矩阵的模型并行计算有效以ABAQUS Release Notes2.7 Parallel sparse solvert1-std.inp分析为例(standard_memory = "1000 Mb")1cpu:abaqus j=t1-std intcup利用率为70%左右，运行时间390s4cpu (supernode):abaqus j=t1-std parallel=supernode cpus=4 int所有系统cpu均被使用，每个cpu利用率运行过程中不断大幅变化，运行时间454s4cpu (tree):abaqus j=t1-std parallel=tree cpus=4 int所有系统cpu均被使用，每个cpu利用率运行过程中不断大幅变化，运行时间352s8cpu (supernode):abaqus j=t1-std parallel=supernode cpus=8 int每个cpu利用率接近100%，运行40多分钟后还无法结束8cpu (tree):abaqus j=t1-std parallel=tree cpus=8 int每个cpu利用率接近90%，运行时间545s结论：多CPU并行处理对Explicit效果显著，对Standard在很多情况下效果不明显，甚至可能使运算更慢，只使用Standard的同学基本可以不用考虑买多cpu 的机器ABAQUS和DIANA关于混凝土本构模型的讨论最近正在做一些钢筋混凝土的算例,有了些体会和感想,整好Simwe 上有朋友提起,遂写出来与大家探讨.不对之处,还望请熟悉DIANA不要见笑并多多指教,谢谢因Simwe好像最近只有注册后方能浏览故在此贴出.zftj wrote:由于钢筋的存在，通常混凝土开裂后，刚度不会马上失去，有一个软化的过程，通常国内叫拉伸强化(tension stiffening)。

Abaqus作习题讲解3

Abaqus作习题讲解3

话框，输入边界条件名称 BC-bottom，分析步选择 Step-1,边界条件类型 选择 Mechanianl：Displacement/Rotation，单击 Continue 按钮，选择 Y 坐标为 0 的边，即筒体底部的横边，单击提示区中的 Done 按钮，进入 Edit Boundary Condition 对话框，选中 U2 前面的复选框，并接受其默认 值 0，其他均为默认单击 Ok 完成对筒体底部边界条件的施加。 12.单击工具箱中 （Create Boundary Condition） ， 在弹出的 Create
Manager） ，点击弹出的对话 框下部的 Create，在新的对 话框 Create Job 中定义作业 名称为 Pressure-vessel， 单击 Continue， 进入 Edit Job 对话 框，输入作业描述 Description： Static analysis of a pressure vessel，其他为默 认设置，单击 OK，在 Job Manager 中出现作业 Pressure-vessel，单击对话框 右部的 Write Input 可以输出 与作业同名的.inp 文件，单 击 Submit 提交作业， 进行计 算；单击 Monitor 弹出 Link Monitors 对话框， 可以对作业运行 情况进行监视。 18.执行 PlotContoursOn Both Shapes， 显示模型变形前后的 云图。 19.执行 OpinionsCommon， 在弹出的 Common Plot Opinions 对 话框，切换到 Basic 选项卡，选中 Deformation Scale Factor 栏中，默 认的时 Auto-compute， 即程序自动 选择变形放大系数，本例默认为放大 385.206 倍的结果。选择 Uniform 前面的单选按钮，在出现的 Value 后面自定义均匀放大系数为 150，单击 Apply 按钮即可；也可通过 Nonuniform 分别定义 X、Y、Z 方向的放 大系数。 20.执行 ReportField Output，在弹出的 Report Field Output 对话框输出变量 Output Variable 栏中 Position 下选择 Unique Nodal 然后在下拉列表中选择 U: Spatial displacement 下面的 U1，单击 Apply 按钮，

abaqus回弹分析实例：在分析步之间传递数据

abaqus回弹分析实例：在分析步之间传递数据

Abaqus Example Problems Guide1.5.1 Springback of two-dimensional draw bendingProducts: Abaqus/Standard Abaqus/Explicit是用explicit进行成形，然后使用standard分析回弹Problem description这个例子描述了在93年成形模拟数值会议中报道的基准测试。

这个基准包括使用三种材料描述六种问题以及两种不同的夹持力。

六个问题中的一个描述如下。

原文见Taylor等人在93年的论文。

坯料初始尺寸350*35，厚度0.78.问题本质上是个平面应变问题（垂直于模型平面的尺寸是35mm）。

夹持力是2.45kN，夹具的质量是5kg。

摩擦系数0.144坯料为低碳钢，材料为弹塑性材料，弹性为各向同性，对于塑性使用Hill 异性屈服准则。

材料的性质如下：Young's modulus = 206.0 GPaPoisson's ratio = 0.3Density = 7800.Yield stress = 167.0 MPaAnisotropic yield criterion: =1.0, =1.0402, =1.24897, =1.07895, =1.0, =1.0此例是对称问题，只取一半建模。

坯料使用一行175个一阶壳单元建模。

对称的边界条件施加到对称面上。

边界条件施加到了坯料所有的节点上以模拟平面应变的条面；建模平面外的尺寸是5mm；因此，坯料的加持力经过了粗略缩放。

成形的过程由explicit中的两个分析步完成。

坯料的加持力在第一个分析步施加。

加载使用平滑分析步，以将惯性效应最小化。

第二个分析步，通过设定冲头刚体参考点的速度冲头下行70mm。

速度使用triangular smooth step amplitude 功能施加，初始速度和最终速度都是0，峰值速度在这个过程之间。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

看本例题之前，请务必先找着文献[1]中P75——P101中提供的例题完全照做一遍，以熟悉基本的操作流程。

下面是本例题的操作过程，模拟一片砌体墙片的滞回实验。

第一步：模型部件的建立进入ABAQUS（中文版），在左方菜单中，选择“部件”，鼠标右键点击一下，选择“创建”，进入模型的部件创建菜单。

模型中往往有一个或者多个部件构成。

如图1，设定部件名称，其他选项如图1所示。

图1然后中间的主操作界面出现，如图2。

此平面默认的在平行于计算机显示器的方向为XY平面，我们如图2，按照现实中墙体立面的尺寸画出墙体立面框，然后点击“完成”，弹出的菜单如图3.图2图3此处的“深度”一项就是设定墙体部件的厚度，输入0.24（墙体厚度0.24m），点击确定。

于是得到了墙体部件的基本视图如图4所示。

同理，依样设定加载梁的尺寸，得到加载梁部件。

这样，第一步部件尺寸设定就完成了。

图4第二步：部件使用材料的设定加载梁使用c50混凝土，砌体使用与实验相对应的材料参数。

由于模拟是针对砌体，所以不考虑加载梁的塑性，因此加载梁只设定密度和弹性。

而砌体则以混凝土塑性损伤本构模型来模拟，要设定密度、弹性、混凝土损伤塑性。

以上内容中混凝土材料参数的设定参见资料[2]，砌体材料参数的设定参见资料[3]。

第三步：将材料属性赋予模型设定了材料参数后，还要对将材料参数“赋予”模型。

其操作菜单如图5图5首先建立两个界面SECTION-1和SECTION-2如图5左边红框所示，将两种材料（C50混凝土与砌体材料）“注入”SECTION-1和SECTION-2中，然后点击右边红框中的图标，选择截面所要“赋予”的对象，即可完成材料参数赋予模型的操作。

第四步：安装配件在第一步谁定好了部件后，实际上部件就像积木玩具的各个零件一样还是零散分开的，这时候，就要使用装配件功能如图6所示。

图6用得较多的是红框中两个移动功能，非常简单，就是通过在空间坐标系中将部件平移到正确的位置即可。

第五步：设置分析步在模拟滞回曲线实验的拟静力计算中，因为需要循环加载时反复推拉形成的，所以在模拟的时候需要设定多个分析步。

而单纯的静力计算则只需一步就可以完成。

分析步的设定如图7所示，本次模拟一共设定了12个分析步，即表示反复推拉的模拟次数一共12次。

在设定分析步的过程中，将分析步的属性定为“静力、通用”。

除了自定义的12步以外，还有ABAQUS默认的不能删除的初始步，是调整结构受力初始状态用的。

第六步：设定约束这一步实际上是第四步的后续，第四步中我们只是把“积木玩具”完全进行了搭接，而没有进行固定。

这一步的作用就是确定“积木玩具”各个分块之间相互作用的属性与关系。

对于实验来说，加载梁是牢牢固定在气体墙之上的，因此新建一个约束，属性选择“绑定”，将加载梁与砌体牢牢固定在一起。

在设定约束的时候需要几个问题要注意，两个接触面之间最好面与面大小形状一摸一样，如本例题中，加载梁明显比砌体长出一截，加载梁底面与砌体顶面不是完全重合的，如图8所示。

这时候怎么办呢？这时候要采用拆分几何元素这项功能，如图9中红框的图标所示，最后切出的加载梁底面与砌体墙顶面刚好重合。

图7图8图9切好了以后，需要选择“绑定”约束的主面和从面，主面选择梁底面，从面选择砌体顶面。

但是选择的时候两个面试重合的，因此需要先把加载梁单独选取出来选好加载梁底面，再把砌体单独选取出来选取好砌体顶面，最后再还原。

单独选取一个部件拿出来显示的操作如图10，按照图10中1，2，3步骤来做即可选取出加载梁进行单独显示。

图10第七步：设定荷载与边界条件荷载与边界条件的初始图标如图11图11荷载，顾名思义，就是施加在构件上的荷载。

边界条件，就是构件某一部分位移状态的设定。

比如砌体底部固定于地面，此时砌体底部的边界条件就是完全固定，设定如图12。

图12实验当中，荷载有两种，一种是施加于加载梁顶面的荷载，固定为0.5MPA，一种是施加于梁侧面的荷载，为反复作用并且增大的推拉力，以求取得砌体滞回曲线。

试验中的侧向荷载一开始是按照力控制，后面根据位移控制。

但是在有限元模拟中，只需要要通过位移控制，就可以得到的滞回曲线以及相关骨架曲线，且更简便。

因此在有限元模拟中，侧向力采用位移控制即可。

因此，ABAQUS中的荷载菜单只有一项，即加载梁顶面荷载0.5MPA。

边界条件可用于位移控制，有多项，如图13所示。

鼠标右键点击“边界条件”，选择“管理器”，得到操作菜单如图13。

图13可以看到图13中，BC-1是在默认初始步就存在，并且一直传递下去的。

这是因为BC-1是砌体底面的固定边界条件，从初始就存在，并且持续到整个实验模拟的结束。

而s1到s12是每一步加载的位移控制，是一推一拉这样反复交替的荷载，只在当前步作用，因此后续步都关闭了，是“未激活”状态。

这就好比，试验中，将构件向推一毫米，不可能同时又保留了上一步所进行的拉0.5毫米的状态。

第八步：设定所需要输出的数据操作菜单如图14，一般这种拟静力的模拟只需输出“场数据”即可，历程输出是动力分析所需要的，这里不涉及到。

图14要能够总结出滞回曲线，必须能够计算出按位移控制的受力面上受到的总和力。

因此，场输出数据的选择如图15。

图15一定要把“合力与合力矩”选项，以及“位移/速度/加速度”中的子选项“平移和转动”选上。

在频率一项中，每N个增量的选项中设定为2。

这里的作用是每两个子步数只记录其中一个子步的结果，这样在运算步数较多，且每步的子步数较多的情况下可以有效减小计算结果的数据量，节省存储空间。

当然，此选项也可以设定为1，这样结果精度相对略高一些。

但是在步数和子步数较多的情况下，这么做意义不大。

第九步：进行计算鼠标右键点击“作业”，选择“新建”，自己任意命名一个任务名，如图16。

此任务就会把先前各步骤所设定好的属性“打包”，制作成一个启动项，点击运行，即可进行运算，其操作流程是鼠标右键点击“作业”——管理器——提交。

如图17。

图16图17当然，运行前也可以先进行数据检查，看看模型能否正常运行，如果意外中断则说明模型还有问题，无法正常计算，需要检查并修正。

第十步：数据整理计算完毕后，会自动跳到结果一项，你也可以再重新启动ABAQUS后，手动转至结果一项，打开想要的结果数据库，如图18。

注意图18中的四个红框，要想得到滞回曲线，必须先取的反复推拉力的作用面上受力结果。

双击“XY数据”，选择“ODB场变量输出”，再选择“唯一节点的”，最后选在“TF1”。

所谓TF1，就是total force 1，1指代X轴方向，2指代Y轴方向，3指代Z轴方向。

在图19中，我们可以明显地了解到推拉力的作用方向是X方向，因此选择TF1。

图18图19把加载梁右侧受力平面的各个受力节点全部框选住，如图20图20 这样，就可以得到该面上所有受力点的TF1数据。

然后得执行“报告”——“XY数据”图21全选其中所有数据，再选择菜单中的“设置”选项，选择出要输出的文件名称，得到最后的数据报告文件。

然后再以相同方式导出位移的数据。

最后用EXCEL整理位移与合力的数据，得到滞回曲线。

[1] 庄茁. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社, 2004[2] 附录一[3] 附录二附录一动力弹塑性分析的材料非线性参数取值一 混凝土材料:混凝土材料采用塑性损伤模型(Plastic-Damaged Model)(1).根据GB 50010-2002 混凝土强度分类 如下:C25, C30, C35, C40, C45, C50, C55, C60, C65, C70, C75, C80(1) 弹性模量:按(2)表4.1.5, 单位kN/m 2表1弹性模量C25 C30 C35 C40 C45 C502.8E7 3E73.15E7 3.25E7 3.35E7 3.25E7 C55 C60 C65 C70 C75 C803.55E7 3.6E7 3.65E7 3.7E7 3.75E7 3.8E7(2) 泊松比, 统一取 0.2 (参阅(2)的4.1.8)(3) 剪切模量: 按(2)表4.1.5中的0.4 倍采用(参阅(2)的4.1.8).(4) 密度(2): 2.5 T/m 3(5) 单轴应力-应变关系混凝土材料轴心抗压和轴心抗拉强度标准值按(2)表4.1.3采用. A: 单轴受压, 其应力-应变关系方程如下(参阅(2)C.2.1, P206): 当1≤x 时32)2()23(x αx ααy a a a −+−+=当1≥x 时 xx αx y d +−=2)1( cεεx = ∗=c f σy在 0 – 0.7f c 的应力范围为线弹性, 其弹性模量按表1. 大于0.7f c 为塑性范围, 应力-塑性应变关系如下:E σεεc c in c −= B: 单轴受拉, 其应力-应变关系方程如下(参阅(2)C.2.2, P208):当1≤x 时62.02.1x x y −=当1≥x 时 xx αx y t +−=7.1)1( tεεx = ∗=t f σy 在 0 – f t 的应力范围为线弹性, 其弹性模量按表1. 大于f t 为塑性范围, 应力-塑性应变关系如下: 0E σεεt t ck t −= 据此得到下列各等级混凝土材料在拉和压屈服后的应力(kN/m 2)-塑性应变关系:*Material, Name=C25*Concrete compression hardening应力(kN/m 2)塑性应变 11690., 016700., 0.00080869313239.8, 0.002337399841.27, 0.003863897674.36, 0.00534646248.49, 0.006802455255.01, 0.008243054527.98, 0.009674143974.73, 0.0110993540.4, 0.0125197*Concrete tension stiffening1797.8, 01780., 0.0000255151191.06, 0.000135635859.483, 0.000236563 684.527, 0.000331898 576.455, 0.000424844 502.469, 0.000516573 448.233, 0.000607596 406.519, 0.000698173 373.278, 0.000788446 131.57, 0.00355876*Material, Name=C30*Concrete compression hardening 14070., 020100., 0.000801898 14636.6, 0.00245591 10073.3, 0.00407992 7500.85, 0.00563756 5931.13, 0.00716179 4889.86, 0.00866839 4153.49, 0.0101648 3607., 0.011655 3186.09, 0.0131409*Concrete tension stiffening 2030.1, 02010., 0.0000282563 1232.19, 0.00014944 849.073, 0.000257466 660.524, 0.000359008 548.371, 0.000458002 473.404, 0.000555757 419.357, 0.000652815 378.298, 0.00074944 345.892, 0.000845777 118.271, 0.00380631*Material, Name=C35*Concrete compression hardening 16380., 023400., 0.000789431 15814.6, 0.00256253 10267.4, 0.00427092 7408.77, 0.005893955749.74, 0.00747891 4682.74, 0.00904507 3943.69, 0.0106008 3403.29, 0.0121503 2991.69, 0.0136956*Concrete tension stiffening 2222., 02200., 0.0000301427 1253.05, 0.000160189 834.315, 0.000273466 638.442, 0.000379668 524.938, 0.000483255 450.278, 0.000585609 397.041, 0.000687284 356.924, 0.000788541 325.457, 0.000889524 109.188, 0.00399589*Material, Name=C40*Concrete compression hardening 18760., 026800., 0.000764814 16909.7, 0.00265856 10469.9, 0.00444614 7378.84, 0.00613068 5650.07, 0.0077733 4562.41, 0.0093962 3819.83, 0.0110085 3282.34, 0.0126144 2876.02, 0.0142164*Concrete tension stiffening 2413.9, 02390., 0.0000309422 1263.67, 0.000170079 815.537, 0.000288349 615.229, 0.000398993 501.733, 0.000506966 428.08, 0.000613712 376.039, 0.000719794 337.082, 0.000825474 306.681, 0.00093089 101.338, 0.00417611*Material, Name=C45*Concrete compression hardening 20720., 029600., 0.00075015 17743.1, 0.00273782 10639.8, 0.00458359 7386.84, 0.00631443 5609.46, 0.00800122 4506.18, 0.00966788 3759.48, 0.0113239 3222.27, 0.0129737 2817.97, 0.0146195*Concrete tension stiffening 2535.1, 02510., 0.0000323044 1265.87, 0.000176673 802.219, 0.000297743 600.343, 0.000410999 487.385, 0.0005216 414.624, 0.000631002 363.47, 0.000739759 325.314, 0.000848128 295.619, 0.000956244 96.8983, 0.0042863*Material, Name=C50*Concrete compression hardening 22680., 032400., 0.000739885 18515.2, 0.00282136 10800.8, 0.00472398 7406.35, 0.00650139 5586.72, 0.00823314 4469.4, 0.00994455 3718.4, 0.0116453 3180.69, 0.0133399 2777.43, 0.0150306*Concrete tension stiffening 2666.4, 02640., 0.0000336591786.735, 0.000307738 584.088, 0.000423793 472.094, 0.00053722 400.477, 0.000649477 350.37, 0.00076111 313.124, 0.00087237 284.214, 0.000983389 92.4472, 0.00440455*Material, Name=C55*Concrete compression hardening 24850., 035500., 0.00072745 19297., 0.00291132 10959.8, 0.00487362 7429.12, 0.00670053 5569.63, 0.00848036 4439.05, 0.0102397 3683.89, 0.0119884 3145.52, 0.013731 2743.03, 0.0154698*Concrete tension stiffening 2767.4, 02740., 0.0000352217 1261.67, 0.00018927 774.457, 0.000315399 571.752, 0.000433514 460.697, 0.000549047 390.039, 0.000663442 340.767, 0.000777235 304.231, 0.000890669 275.923, 0.0010038789.2809, 0.00449368*Material, Name=C60*Concrete compression hardening 26950., 038500., 0.000700606 19978.3, 0.00298515 11087.9, 0.005002155552.82, 0.008696 4412.21, 0.0104977 3654.2, 0.0122888 3115.66, 0.0140739 2714.07, 0.0158551*Concrete tension stiffening 2878.5, 02850., 0.0000356383 1256.67, 0.000194702 760.756, 0.000323283 558.434, 0.000443708 448.564, 0.000561565 379.016, 0.000678302 330.681, 0.000794449 294.926, 0.000910248 267.272, 0.0010258286.0337, 0.00458981*Material, Name=C65*Concrete compression hardening 29050., 041500., 0.000671154 20635.5, 0.00305092 11227.6, 0.00511681 7477.58, 0.00702769 5554.81, 0.00888851 4402.81, 0.0107282 3640.4, 0.0125572 3100.27, 0.0143802 2698.31, 0.0161993*Concrete tension stiffening 2959.3, 02930., 0.0000362462 1252.05, 0.000198738 750.74, 0.000328992 548.949, 0.000451041 440.021, 0.000570546 371.305, 0.000688948 323.655, 0.000806774 288.463, 0.000924259 261.278, 0.0010415283.8153, 0.00465851*Material, Name=C70*Concrete compression hardening 31150., 044500., 0.000641177 21274.9, 0.00311276 11377.9, 0.00522413 7526.44, 0.0071721 5571.79, 0.00906881 4407.16, 0.0109442 3639.02, 0.0128088 3096.11, 0.0146674 2692.74, 0.0165221*Concrete tension stiffening 3019.9, 02990., 0.000036979 1248.1, 0.000201847 743.23, 0.000333282 541.959, 0.000456512 433.772, 0.000577225 365.689, 0.000696855 318.553, 0.000815919 283.779, 0.000934649 256.941, 0.0010531682.2252, 0.00470937*Material, Name=C75*Concrete compression hardening 33180., 047400., 0.000619583 21842.2, 0.00318471 11504.1, 0.00534398 7565.26, 0.00733259 5583.9, 0.00926901 4408.93, 0.0111839 3636.25, 0.0130881 3091.21, 0.0149862 2686.84, 0.0168806*Concrete tension stiffening 3080.5, 03050., 0.00003771171243.9, 0.000204919735.834, 0.000337513535.156, 0.000461909427.722, 0.000583819360.269, 0.000704663313.639, 0.000824951279.275, 0.000944913252.774, 0.0010646680.7083, 0.00475965*Material, Name=C80*Concrete compression hardening35140., 050200., 0.00060153922358.2, 0.0032568111618.5, 0.005462037601.82, 0.007490325596.63, 0.009465684412.34, 0.01141943635.46, 0.01336253088.38, 0.01529952683., 0.0172327*Concrete tension stiffening3141.1, 03110., 0.00003844371239.38, 0.000207956728.476, 0.000341687528.471, 0.000467236421.811, 0.000590329354.989, 0.000712373308.862, 0.000833873274.904, 0.000955052248.735, 0.0010760379.2484, 0.00480935(6) 损伤系数:混凝土材料进入塑性状态伴随着刚度的降低, 如下图示(1):受拉受压文献(3)Fig4. (a), (b) 给出了混凝土材料单轴拉压的滞回曲线. 该曲线已被实验和计算验证. 通过线性插值, 可以得到混凝土材料各塑性应变所对应的损伤系数如下:*Material, Name=C25*Concrete compression damage 损伤系数(d c) 塑性应变0, 00.01, 0.0008086930.207199, 0.00233739 0.410702, 0.00386389 0.540458, 0.0053464 0.69718, 0.00680245 0.78611, 0.00824305 0.84114, 0.00967414 0.877465, 0.0110990.902661, 0.0125197*Concrete tension damage损伤系数(d t) 塑性应变0, 00.01, 0.0000255150.330864, 0.000135635 0.517144, 0.000236563 0.615434, 0.000331898 0.747045, 0.000424844 0.834016, 0.000516573 0.888637, 0.000607596 0.919064, 0.000698173 0.937999, 0.000788446 0.998225, 0.00355876*Material, Name=C30*Concrete compression damage 0, 00.01, 0.0008018980.271809, 0.00245591 0.498841, 0.00407992 0.626823, 0.00563756 0.758068, 0.00716179 0.830984, 0.00866839 0.875447, 0.0101648 0.904483, 0.0116550.924462, 0.0131409*Concrete tension damage0, 00.01, 0.00002825630.577576, 0.000257466 0.671381, 0.000359008 0.78758, 0.000458002 0.862336, 0.000555757 0.908476, 0.000652815 0.933922, 0.00074944 0.949638, 0.000845777 0.998607, 0.00380631*Material, Name=C35*Concrete compression damage 0, 00.01, 0.0007894310.324164, 0.00256253 0.561223, 0.00427092 0.683386, 0.00589395 0.796302, 0.00747891 0.858328, 0.00904507 0.89589, 0.01060080.92031, 0.01215030.937062, 0.0136956*Concrete tension damage0, 00.01, 0.00003014270.430433, 0.000160189 0.620766, 0.000273466 0.709799, 0.000379668 0.814503, 0.000483255 0.880713, 0.000585609 0.921137, 0.000687284 0.943295, 0.000788541 0.956917, 0.000889524 0.998833, 0.00399589*Material, Name=C40*Concrete compression damage 0, 00.01, 0.0007648140.369042, 0.00265856 0.609331, 0.004446140.823245, 0.0077733 0.877128, 0.0093962 0.90969, 0.01100850.930844, 0.0126144 0.945352, 0.0142164*Concrete tension damage0, 00.01, 0.00003094220.471266, 0.000170079 0.658771, 0.000288349 0.742582, 0.000398993 0.836523, 0.000506966 0.895279, 0.000613712 0.930952, 0.000719794 0.95046, 0.000825474 0.962428, 0.00093089 0.998995, 0.00417611*Material, Name=C45*Concrete compression damage 0, 00.01, 0.000750150.40057, 0.00273782 0.640546, 0.00458359 0.750445, 0.00631443 0.840063, 0.00800122 0.888862, 0.00966788 0.918306, 0.0113239 0.937422, 0.0129737 0.950532, 0.0146195*Concrete tension damage0, 00.01, 0.00003230440.495671, 0.000176673 0.680391, 0.000297743 0.760819, 0.000410999 0.849034, 0.0005216 0.903712, 0.000631002 0.936711, 0.000739759 0.954691, 0.000848128 0.965692, 0.000956244*Material, Name=C50*Concrete compression damage 0, 00.01, 0.0007398850.428544, 0.00282136 0.666642, 0.00472398 0.771409, 0.00650139 0.853722, 0.00823314 0.898389, 0.00994455 0.9253, 0.01164530.942763, 0.0133399 0.954738, 0.0150306*Concrete tension damage0, 00.01, 0.00003365910.52097, 0.000183705 0.701994, 0.000307738 0.778754, 0.000423793 0.861159, 0.00053722 0.911801, 0.000649477 0.942194, 0.00076111 0.958699, 0.00087237 0.968775, 0.000983389 0.999181, 0.00440455*Material, Name=C55*Concrete compression damage 0, 00.01, 0.000727450.456423, 0.00291132 0.691273, 0.00487362 0.790729, 0.00670053 0.866219, 0.00848036 0.907065, 0.0102397 0.93165, 0.01198840.947601, 0.0137310.958541, 0.0154698*Concrete tension damage0, 00.539536, 0.00018927 0.717351, 0.000315399 0.791331, 0.000433514 0.869789, 0.000549047 0.91763, 0.000663442 0.946178, 0.000777235 0.961623, 0.000890669 0.971027, 0.00100387 0.999246, 0.00449368*Material, Name=C60*Concrete compression damage 0, 00.01, 0.0007006060.481084, 0.00298515 0.712003, 0.00500215 0.806648, 0.00687342 0.876252, 0.0086960.913899, 0.0104977 0.936577, 0.0122888 0.951309, 0.0140739 0.961426, 0.0158551*Concrete tension damage0, 00.01, 0.00003563830.559063, 0.000194702 0.733068, 0.000323283 0.804058, 0.000443708 0.877995, 0.000561565 0.922909, 0.000678302 0.949666, 0.000794449 0.964133, 0.000910248 0.972937, 0.00102582 0.999299, 0.00458981*Material, Name=C65*Concrete compression damage 0, 00.01, 0.0006711540.502758, 0.003050920.819817, 0.00702769 0.884515, 0.00888851 0.919509, 0.0107282 0.940612, 0.0125572 0.95434, 0.01438020.96378, 0.0161993*Concrete tension damage0, 00.01, 0.00003624620.572681, 0.000198738 0.743775, 0.000328992 0.812645, 0.000451041 0.883611, 0.000570546 0.926569, 0.000688948 0.952106, 0.000806774 0.965898, 0.000924259 0.974284, 0.00104152 0.999336, 0.00465851*Material, Name=C70*Concrete compression damage 0, 00.01, 0.0006411770.521912, 0.00311276 0.744318, 0.00522413 0.830867, 0.0071721 0.891435, 0.00906881 0.924204, 0.0109442 0.943987, 0.0128088 0.956872, 0.0146674 0.965746, 0.0165221*Concrete tension damage0, 00.01, 0.0000369790.582576, 0.000201847 0.751428, 0.000333282 0.818743, 0.000456512 0.887672, 0.000577225 0.929255, 0.000696855 0.953916, 0.000815919 0.967215, 0.0009346490.999364, 0.00470937*Material, Name=C75*Concrete compression damage 0, 00.01, 0.0006195830.539193, 0.00318471 0.757298, 0.00534398 0.840395, 0.00733259 0.897474, 0.00926901 0.928341, 0.0111839 0.946986, 0.0130881 0.95914, 0.01498620.967518, 0.0168806*Concrete tension damage0, 00.01, 0.00003771170.592163, 0.000204919 0.758743, 0.000337513 0.824539, 0.000461909 0.891519, 0.000583819 0.931794, 0.000704663 0.955624, 0.000824951 0.968456, 0.000944913 0.976241, 0.00106466 0.999391, 0.00475965*Material, Name=C80*Concrete compression damage 0, 00.01, 0.0006015390.554618, 0.00325681 0.768556, 0.00546203 0.848569, 0.00749032 0.902677, 0.00946568 0.931921, 0.0114194 0.94959, 0.01336250.961115, 0.0152995 0.969065, 0.0172327*Concrete tension damage0, 00.01, 0.00003844370.601485, 0.0002079560.765763, 0.0003416870.830074, 0.0004672360.895181, 0.0005903290.934206, 0.0007123730.957244, 0.0008338730.969631, 0.0009550520.977139, 0.001076030.999416, 0.00480935(7) Stiffness Recovery (1)当荷载从拉变压时, 混凝土材料的裂缝闭合, 抗压刚度恢复, 即w c=1.当荷载从压变拉时, 混凝土材料的抗拉刚度不恢复, 即w t=0.一维拉压滞回曲线示意图:(8)屈服函数(1)(3)二维屈服函数示意图:(9) 塑性流动法则(1)(3)- Drucker-Prager hyperbolic function:采用非关联的塑性势函数二. 钢材采用运动强化模型(Kinematic hardening).强屈比不小于1.2. 按(4)表2-2, P79, 可以得到下列数据(5):*MATERIAL, NAME=Q235 一组*ELASTIC (kN/m2)200e6*PLASTIC,hardening=kinematic应力(kN/m2) 塑性应变235e3, 0375e3, 0.025*DENSITY (T/m3)7.800*MATERIAL, NAME=Q235 二组*ELASTIC200e6*PLASTIC,hardening=kinematic225e3,0375e3,0.025*DENSITY7.800*MATERIAL, NAME=Q235 三组*ELASTIC200e6*PLASTIC,hardening=kinematic215e3,0375e3,0.025*DENSITY7.800*MATERIAL, NAME=Q235 四组*ELASTIC200e6*PLASTIC,hardening=kinematic205e3,0375e3,0.0257.800*MATERIAL, NAME=Q345 一组*ELASTIC200e6*PLASTIC,hardening=kinematic 345e3,0470e3,0.025*DENSITY7.800*MATERIAL, NAME=Q345 二组*ELASTIC200e6*PLASTIC,hardening=kinematic 325e3,0470e3,0.025*DENSITY7.800*MATERIAL, NAME=Q345 三组*ELASTIC200e6*PLASTIC,hardening=kinematic 295e3,0470e3,0.025*DENSITY7.800*MATERIAL, NAME=Q345 四组*ELASTIC200e6*PLASTIC,hardening=kinematic 275e3,0470e3,0.025*DENSITY7.800*MATERIAL, NAME=Q390 一组*ELASTIC*PLASTIC,hardening=kinematic 390e3,0480e3,0.025*DENSITY7.800*MATERIAL, NAME=Q390 二组*ELASTIC200e6*PLASTIC,hardening=kinematic 375e3,0480e3,0.025*DENSITY7.800*MATERIAL, NAME=Q390 三组*ELASTIC200e6*PLASTIC,hardening=kinematic 350e3,0480e3,0.025*DENSITY7.800*MATERIAL, NAME=Q390 四组*ELASTIC200e6*PLASTIC,hardening=kinematic 330e3,0480e3,0.025*DENSITY7.800*MATERIAL, NAME=Q420*ELASTIC200e6*PLASTIC,hardening=kinematic 420e3,0504e3,0.025*DENSITY7.800*MATERIAL,NAME=reo 钢筋*ELASTIC200e6*PLASTIC,hardening=kinematic345e3,0400e3,0.025*DENSITY7.800参考文献[1] ABAQUS User Manual (v6.5-1)。