线性动态电路的复频域分析演示课件

格式：ppt
大小：2.11 MB
文档页数：68

下载文档原格式

线性动态电路的复频域分析

第11页/共38页
§14 —3 拉普拉斯反变换的部分分式展开
例1：
例2：
L–1[(1–2e–s +e–2s )/s2]
=t–2(t–)(t–)+(t–2)(t–2)
第12页/共38页
部分分式展开法
F(s)s
N(s)、 D(s)s
F(s)( n>m)
p1、p2、‥‥‥ pnD(s)=0F(s)极点
第24页/共38页
3、电感
U(s)=sLI(s)–Li(0–)
u= i
U(s)=I(s)
第25页/共38页
5、含有耦合电感的电路
U1(s)=sL1I1(s)–L1i1(0–)+sMI2(s)–Mi2(0–)
自感电压
自感附加电压源
互感电压
互感附加电压源
U2(s)=sL2I2(s)–L2i2(0–)+sMI1(s)–Mi1(0–)
第13页/共38页
一、F(s)的极点为各不相等的实数根
p1p2‥‥‥pnp1、p2‥‥‥pn
L–1[F(s)]
k
(s–p1)
令s=p1
第14页/共38页
例1:
第15页/共38页
例2:
L–1[F(s)]=(t)+(t)–3e–2t+7e–3t
第16页/共38页
二、F(s)有共轭复极点
=sF(s)–f(0–)
L[f (t)]=s2F(s) – sf(0–)–f (0–)
L[fn(t)]=snF(s) – sn–1f(0–)–sn–2f (0–) ……f(n–1)(0–)
第6页/共38页
例：
uc(t)
第7页/共38页

电路的复频域分析精品PPT课件

“十一五”规划教材—电路基础
一、线性性质
若 ℒ [ f1(t)]= F1(s)，ℒ[f2(t)]= 则F2对(s任) 意常数a1及a2（实数或复数）有 ℒ[a1f1(t)+a2f2(t)] = a1ℒ[f1(t)]+a2ℒ[f2(t)] = a1F1(s)+a2F2(
即拉氏变换满足齐次性和可加性。
“十一五”规划教材—电路基础
第六章动态电路的复频域分析
6.1 拉普拉斯变换及其性质 6.2 拉普拉斯反变换 6.3 电路基本定律及电路元件的复频域形式 6.4 应用拉普拉斯变换分析动态电路 6.5 网络函数 6.6 固有频率
“十一五”规划教材—电路基础
本章要介绍的拉普拉斯变换方法是研究线性非时变动态电路的基本工具。采用拉普拉斯变换的分析方法，
1 L
t
0 uL ( )d
“十一五”规划教材—电路基础
对电感电压、电流进行拉氏变换，并由积分性质和线性性质可得
ℒ
[iL]
=
ℒ
iL[(0 )
Байду номын сангаас1 L
t
0 uL ( )d
= ℒ [iL (0 )
1]+ℒt
L 0
u[L (
)d
] ]
iL
(0 s
)
1 sL
UL
(s)
电感元件的复频域形式为：
IL
(s)
iL
解：在时域中线性非时变电容元件
iC
C
duC dt
对电容电压、电流进行拉氏变换，并根据微分性
质和线性性质可得
ℒ
[iC]
=
ℒ C[
duC dt
] = Cℒ [duC dt

电路课件电路14 线性动态电路复频域分析

14
例14-4
利用积分性质求函数f(t)＝t的象函数。解由于
f(t)t0t()d,
所以
2020/4/17
14-2 拉普拉斯变换的基本性质-5
第十四章线性动态电路的复频域分析
15
4．延迟性质
函数f(t)的象函数与其延迟函数f(t-t0)的象函数之间有如下关系若 £[f(t)]＝F(s) 则 £[f(t-t0)]＝e-st0F(s) 其中，当t＜t0时，f(t-t0)＝0。
其余为单根，F(s)可分解为
对于单根，仍采用
公式计算。
为了确定K11、K12和K13，将式(13-7)两边乘以(s-pi)3，则K11被单独分离，即
则
K11＝(s-p1)3F(s)|s＝p1
2020/4/17
14-3 拉普拉斯反变换的部分分式展开-8
第十四章线性动态电路的复频域分析
27
D(s)＝0具有重根 (2)
2020/4/17
14-2 拉普拉斯变换的基本性质-7
第十四章线性动态电路的复频域分析
17
常用函数的拉氏变换表
2020/4/17
14-2 拉普拉斯变换的基本性质-8
第十四章线性动态电路的复频域分析
18
14-3 拉普拉斯反变换的部分分式展开
用拉氏变换求线性电路时域响应，需拉氏反变换为时间函数。
第十四章线性动态电路的复频域分析
23
例14-6
求解因为
的原函数f(t)。
所以：D(s)＝0的根为 p1＝0，p2＝-2，p3＝-5 D'(s)＝3s2&同理求得：所以
2020/4/17
K2＝0.5
K3＝-0.6

复频域分析法ppt课件

1 2j
L{e2j1jt
L{eejjt t}
e
j1t 2j
}(
s121jj( s1sj1js)
1
js2
)s22
2
4
11.2 拉普拉斯变换的基本性质
2、微分性质
若
L { f (t)} F (s)
，则
L dfd(tt
)
sF
(s)
f (0 )
例题11.2: 应用微分性质求 f (t) cost 的象函数：
f (t) f1(t) f2(t) fn(t) 拉氏反变换求f(t)
8
11.3 拉普拉斯反变换
F(s)
F1(s) F2 (s)
bm s m an s n
bm1sm1 b1s b0 an1sn1 a1s a0
讨论n >m 情况
非振荡过程
(1) F2(s)=0只有单根 f (t) A1e p1t A2e p2t Ane pnt
00
0s a
0 ssaa
3、单位冲激函数
L[
(t
)]
0
(t
)e st dt
0
0
(t
)e s 0dt
1
3
11.2 拉普拉斯变换的基本性质
1、线性性质
若L[ f1(t )] F1(S ) , L[ f2(t )] F2(S )
则 L[af1(t) bf2(t)] aF1(S ) bF2(S )
F (s) L{cos t} L{ 1 d sin t} 1
dt
sL{sin t} sin t t 0
s
s2 2
3、积分性质
若 L { f (t)} F (s) ，则 L{ t f ( )d} 1 F (s)

电路分析第九章线性动态电路的复频域分析

L
(
s
)
17.5 s
]
I
L
(
s
)
5-IL(s)
- + 2 IL(s)
10/s 2
2s
5
+
10
5 s
27.5 s1
i(t) 10 (t) 5 (t) 27.5et (t) A .
1．复频域系统函数H(s)的定义：
H(s) Yf (s) L[h(t)]
F(s) 2．物理意义
—系统零状态响应象函数与激励象函数之比； —系统冲激响应的拉普拉斯变换； —激励为e st时系统零状态响应的加权函数；
H(s) H1(s) H2(s) H3(s) F(s)
H1(s)
H2(s) Yf(s)
H3(s)
3．基本运算器(加法器、数乘器、积分器) 的框图和 s域模型
数乘器
f(t)
加法器
a
y(t) = af(t)
F(s)
Y(s) = aF(s) a
f1(t) f2(t)
f (t) f1(t) f1(t) F1(s)
R sL
1 sC
有s域形式的欧姆定律
U(s) Z(s)I(s) , I(s) Y(s)U(s)
复频域分析法步骤
1. 求换路前电路的状态 uC(0-)、iL(0-)； 2.求激励f(t)的象函数F(s)；
3.画出s域电路模型
4.用s域形式的各种分析法建立方程，解出响应
变量的象函数；
5. 拉氏反变换的求出响应的时域表达式，画出响应的波形。
f(t) = e st → yf(t) = H(s)e st
3．分类
(1) 驱动(策动)点函数(响应与激励在同一端口)

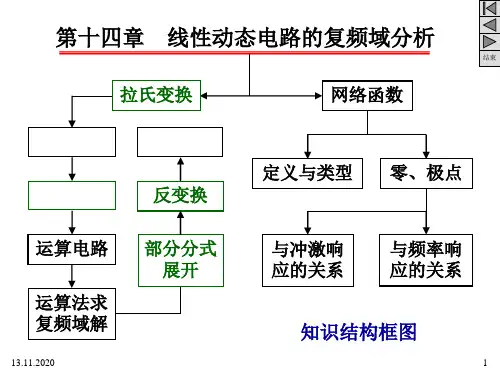
《电路》第14章线性动态电路的复频域分析PPT课件

相
量
... I1 + I2 = I
时域的正弦运算变换为复数运算。
13.11.2020
4
③拉氏变换
对应
f(t) (时域原函数)
F(s) (频域象函数)
结束
拉氏变换法的核心是把 f(t)与 F(s)联系起来，把时域问题通过数学变换化为复频域问题。
2.两个特点
①把时间域的高阶微分方程变换为复频域的代数方程；
第十四章线性动态电路的复频域分析
结束
拉氏变换
网络函数
反变换
运算电路
运算法求复频域解
13.11.2020
部分分式展开
定义与类型零、极点
与冲激响应的关系
与频率响应的关系
知识结构框图
1
重点
结束
①KL、元件VCR的运算形式，运算电路； ②运算法的求解步骤； ③网络函数的定义与类型、极点与零点的概念； ④网络函数与冲激响应、频率响应的关系。
1 2
(1+ e-t cost-e-t sint) A
13.11.2020
21
例2 稳态时闭合S。求 t≥0时的 uL(t)。
(t=0) S R1 5 R2 5
③画运算电路
结束
+
iL(t)
us1
L
- 2e–2t V 1H
++ uL us2 - - 5V
解：①求初值
iL(0-)
=
us2 R2
=1A
②求激励的象函数
ℒ [10 ] = 10/s
I(s) 2
0.3s
1.5V -+
3
+ 10
s

第14章线性动态电路的复频域分析 PPT课件

D(s) 部分分式为真分式时，需对分母多项式作因式分解，
求出D(s)=0的根。分三种情况讨论。
2020年7月1日星期三
18
情况1 D(s)=0只有单根
F(s) =
K1 s- p1
+
K2 s- p2
+
··· +
Kn s- pn
结束
p1、p2、… 、pn 为D(s)=0的n个不同单根，它们可以
实数，也可以是(共轭)复数。
(2)象函数 F(s) 一般用大写字母表示，如I(s)、U(s)，原函数f(t) 用小写字母表示，如i(t)，u(t)。
象函数F(s) 存在的条件： Re[s]=s > c。
在电气领域中所用到的都是有实际意义的(电压或电流)信号，它们的函数表达式f(t)都存在拉氏变换。所以应用时不再计较F(s)的存在条件。
2020年7月1日星期三
7
2. 典型函数的拉氏变换 P345例14-1
(1)单位阶跃函数 f(t) = e(t)
结束
F(s) =
∞
e(t) e-st dt =
0-
∞
e-st dt = -
0-
1 s
e-st
∞ 0-
ℒ
[e(t)]=
1 s
(2)单位冲激函数d(t)
∞
0+
F(s) = d(t) e-st dt = d(t) e-st dt = e-s(0)
两个特点：一是把时间域的高阶微分方程变换为复频域的代数方程；二是将电流和电压的初始值自动引入代数方程中，在变换处理过程中，初始条件成为变换的一部分。
由于解复变函数的代数方程比解时域微分方程较有规律且有效，所以拉普拉斯变换在线性电路分析中得到广泛应用。

第14章1线性动态电路的复频域分析精品PPT课件

正变换反变换
0 积分下限从0 开始，称为0 拉氏变换。
0
0
积分下限从0+ 开始，称为0+ 拉氏变换。
今后讨论的拉氏变换均为 0 拉氏变换,计及t=0时f(t)包含的冲击。
返回上页下页
简写 F f((tS))
f(t) 1F( S)
正变换反变换
注 1 F ( S ) f ( t) e s d t 0 t f ( t) e s d t tf ( t) e s d t
1est 1 s 0s
返回上页下页
(2)单位冲激函数的象函数
f(t)(t)
F (s)[ (t) ] 0
(t)e sd t t00(t
)estdt
es0 1
(3)指数函数的象函数
f(t )eat
F (s)e at e ae t sd t t
0
s
1 e( a
sa
)t
0
1 sa
证 A 1 f 1 ( t ： ) A 2 f 2 ( t) 0 A 1f1 (t) A 2f2 (t)e sd t
0 A 1f1 (t) e sd t t0 A 2f2 (t) e sd t t
A 1 F 1 (S ) A 2 F 2 (S )
返回上页下页
根据拉氏变换的线性性质，求函数与常数相乘及几个函数相加减的象函数时，可以先求各函数的象函数再进行计算。
f(t)M cte t [0, )
则 f(t)estd t M(s ec)tdt M
0
0
sC
总可以找到一个合适的s值使上式积分为有限值，即 f(t)的拉氏变换式F(s)总存在。
返回上页下页

电路原理课件11动态电路的复频域分析

1 s+a
0
(2) 单位阶跃函数
1 L[ (t )] (t )e dt e st dt e st 0 0 s (3) 冲激函数
+
st

1 s
L[ (t )] (t )e
+
0
f (t )e dt
st
0
0
f (t )e dt
st
+
0
f (t )e st dt
f(t) (t) 时，此项 0 F(s)称为象函数，用大写字母表示，如I(s)，U(s)。
f(t)称为原函数，用小写字母表示，如 i(t)，u(t)。
频域分析，而相应地称经典法为时域分析。
返回上页下页
动态电路的复频域分析 3. 典型函数的拉氏变换 (1) 指数函数
F ( s)
1 ( s a )t e sa
0
+
0
f (t )e st dt
L[e (t )] e at e st dt
at
0
2. 存在条件对于一个函数f(t)，如果存在正的有限值常数M和c，使下式成立
f (t ) Mect t [0, )
返回上页下页
动态电路的复频域分析
f (t ) Mect t [0, )
则f(t)的拉氏变换式F(s)总存在。因为

0
f (t ) e
σt
dt Me

e
例12
+
0 +
f (t t0 )ε(t t0 )e st dt
f (t t0 )e s( t t0 )e st0 dt 令t t0 τ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

F(s)称为f(t)的象函数， f(t)称为F(s)的原函数。
由F(s)到f(t)的变换称为拉普拉斯反变换，它定义为：
f(t)= ℒ -1[F(s)]= 1 2pj
c+j
F(s) est dt
c-j
式中c为正的有限常数。
11.10.2020
4
注意
(1)定义中拉氏变换的积分从 t=0- 开始，即：
②拉普拉斯反变换部分分式展开；
③应用拉普拉斯变换分析线性电路的方法和步骤；
④网络函数的的定义和极点、零点的概念。
与其它章节的联系
1 本章讲述基于拉氏变换的动态电路的分析方法，称为运算法；主要解决一般动态电路、特别是高阶动态电路的分析问题；
2 是变换域分析方法（相量法）思想的延续，把时域问题变换为复频域问题。
义域为[0， ]，求其象函数。解：
结束
ℒ [ f1(t)] = ℒ [sin(wt)] 欧拉公式 ℒ
线性性质
1 2j
ℒ
[ejwt]
-ℒ
[e-jwt
]
1 2j
(ejwt-e-jwt
)
引用
ℒ
[eat ]
=
1 s-a
=
1 2j
1
s-jw
-
1
s+jw
=
w s2+w2
ℒ [sin(wt)] = w s2+w2
由于解复变函数的代数方程比解时域微分方程较有规律且有效，所以拉普拉斯变换在线性电路分析中得到广泛应用。
11.10.20203Fra bibliotek1. 定义
一个定义在 [0, +∞] 区间的函数 f(t)，它的拉普拉斯结束变换式 F(s) 定义为：
∞
F(s)=ℒ [f(t)]= f(t)e-stdt
0-
式中s=s+jw为复数，被称为复频率；
0-
∞
e-(s-a)t dt =
0-
1 -(s-a)
e-
(s-a)t
∞ 0-
ℒ [eat]=
1 s-a
11.10.2020
6
§14-2 拉普拉斯变换的基本性质
1. 线性性质
结束
设：ℒ [ f1(t)]=F1(s)，ℒ [ f2(t)]=F2(s) A1、A2 是两个任意实常数。
则：ℒ [A1 f1(t)+A2 f2(t)] = A1F1(s)+A2F2(s)
第十四章线性动态电路的复频域分析
结束
主要内容 ①拉普拉斯变换及其与电路分析有关的性质； ②反变换的方法； ③KCL、KVL和VCR的运算形式； ④拉氏变换在线性电路中的应用； ⑤网络函数的定义与含义； ⑥极点与零点对时域响应的影响； ⑦极点与零点与频率响应的关系。
11.10.2020
1
重点
①基尔霍夫定律的运算形式、运算阻抗和运算导纳、结束运算电路（模型）；
结束
证：ℒ [ f ' (t)] =
∞ df(t) e-st dt =
∞
e-st df(t)
0- dt
∞∞
0- ∞
F(s)
= e-st f(t) - f(t) de-st = -f(0-)+ s f(t) e-st dt
0- 0-
0-
推论：ℒ [ f (n)(t)]=snF(s)-sn-1f(0-)-sn-2f '(0-)- -f (n-1)(0-) 特别，当 f(0-) = f '(0-) = =f (n-1)(0-)= 0 时则有 ℒ [ f ' (t)] = sF(s)，，ℒ [f (n)(t)] = snF(s)
结束
∞
0+
∞
F(s)=ℒ [f(t)]= f(t)e-stdt = f(t)e-stdt + f(t)e-stdt
0-
0-
0+
它计及 t=0-至 0+ ，f(t) 包含的冲激和电路动态变量
的初始值，从而为电路的计算带来方便。
(2)象函数 F(s) 一般用大写字母表示，如I(s)、U(s)，原函数f(t) 用小写字母表示，如i(t)，u(t)。
0-
∞
e-st dt = -
0-
1 s
e-st
∞ 0-
ℒ
[e(t)]=
1 s
(2)单位冲激函数d(t)
∞
0+
F(s) = d(t) e-st dt = d(t) e-st dt = e-s(0)
0-
0-
(3)指数函数 f(t) = eat (a为实数)
ℒ [d(t)]=1
F(s) =
∞
eat e-st dt =
w s2+w2
ℒ [e(t)] = 1/s，
ℒ [cos(wt)]=ℒ
1
w
dsin(wt)
dt
=
1
w
s
w s2+w2
- sin(0-)
ℒ [cos(wt)] =
s
s2+w2
ℒ [d(t)] =ℒ
de(t) dt
=
s
(
1 s
ℒ
[
f2(t)]
=
ℒ
[K(1-e-at)]
线性性质
ℒ
[K]-ℒ
[Ke-at]
引用阶跃函数和指数函数的结论
=
K s
-
K s+a
=
Ka
s(s+a)
ℒ
[K(1-e-at)]=
Ka
s(s+a)
11.10.2020
8
2. 微分性质
若 ℒ [ f(t)]=F(s)，则 ℒ [ f ' (t)] = sF(s)-f(0-)
该性质可将f (t)的微分方程化为F(s)的代数方程，是分析线性电路(系统)的得力工具。
11.10.2020
9
P347 例14-3 用微分性质求cos(wt)和d(t)的象函数。
解： dsin(wt) =w cos(wt)
de(t) = d(t)
结束
dt
dt
利用微分性质和已知结果：
ℒ [sin(wt)] =
象函数F(s) 存在的条件： Re[s]=s > c，一般都存在。
在电气领域中所用到的都是有实际意义的(电压或电流)信号，它们的函数表达式f(t)都存在拉氏变换。
11.10.2020
5
2. 典型函数的拉氏变换 P345例14-1
(1)单位阶跃函数 f(t) = e(t)
结束
F(s) =
∞
e(t) e-st dt =
证：左 = [A1 f1(t) + A2 f2(t)] e-st dt
0-
∞
∞
= A1 f1(t) e-st dt + A2 f2(t) e-st dt = 右
0-
0-
A1F1(s)
A2F2(s)
11.10.2020
7
P346 例14-2 若 f1(t)=sin(wt)， f2(t)=K(1-e-at)的定
11.10.2020
2
§14-1 拉普拉斯变换的定义
1. 引言
结束
拉普拉斯变换法是一种数学积分变换，其核心是把时间函数 f(t) 与复变函数 F(s) 联系起来，把时域问题通过数学变换化为复频域问题。
两个特点：一是把时间域的高阶微分方程变换为复频域的代数方程；二是将电流和电压的初始值自动引入代数方程中，在变换处理过程中，初始条件成为变换的一部分。

动态电路复频域分析

页数:17
线性动态电路的复频域分析演示课件

页数:68
电路邱关源版第十四章线性动态电路的复频域分析

页数:76
电子教案《简明电路基础(王美中)》电子教案、习题解答第9章动态电路的复频域分析

页数:62
电路分析-第九章线性动态电路的复频域分析

页数:26
第14章习题课线性动态电路的复频域分析

页数:33
第14章线性动态电路的复频域分析PPT课件

页数:13
第十四章--线性动态电路的复频域分析

页数:12
11动态电路的复频域分析

页数:86
第十四章动态电路的复频域分析习题答案(最新整理)

页数:8

线性动态电路的复频域分析演示课件

合集下载