平面与空间直线题型训练5.doc

空间直线、平面的平行巩固练习1．若两条直线都与一个平面平行，则这两条直线的位置关系是()A．平行B．相交C．异面D．以上均有可能解析：平行、相交、异面都有可能．故选D.答案：D2．“直线m与平面α内无数条直线平行”是“直线m∥平面α”的()A．充要条件B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件解析：由直线m∥平面α，可得直线m与平面α内无数条直线平行，反之不成立．所以“直线m与平面α内无数条直线平行”是“直线m∥平面α”的必要不充分条件．故选C.答案：C3．设l，m是两条不同的直线，α，β是两个不同的平面，且l⊂α，m⊂β，下列结论正确的是() A．若α⊥β，则l⊥βB．若l⊥m，则α⊥βC．若α∥β，则l∥βD．若l∥m，则α∥β解析：对于A，α⊥β，l⊂α，只有加上l垂直于α与β的交线，才有l⊥β，所以A错误；对于B，若l⊥m，l⊂α，m⊂β，则α与β可能平行，也可能相交但不垂直，所以B错误；对于C，若α∥β，l⊂α，由面面平行的性质可知，l∥β，所以C正确；对于D，若l∥m，l ⊂α，m⊂β，则α与β可能平行，也可能相交，所以D错误．答案：C4．下列命题正确的是()A．若两条直线和同一个平面平行，则这两条直线平行B．若两条直线和同一个平面所成的角相等，则这两条直线平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面垂直于同一个平面，则这两个平面平行解析：A中，若两条直线和同一个平面平行，则这两条直线可能平行、相交或为异面直线，故A错误；B中，若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面，故B错误；C正确；D中，若两个平面都垂直于第三个平面，则这两个平面平行或相交(例如：天花板与两个相交平面的位置关系)，D项错误．答案：C5．过三棱柱ABC-A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有()A．4条B．6条C．8条D．12条解析：如图所示，H，G，F，I是相应线段的中点，故符合条件的直线只能出现在平面HGFI中，有FI，FG，GH，HI，HF，GI共6条直线，故选B.答案：B6．已知平面α，β，γ两两垂直，直线a，b，c满足a⊂α，b⊂β，c⊂γ，则直线a，b，c的位置关系不可能是()A．两两平行B．两两垂直C．两两相交D．两两异面解析：假设a，b，c三条直线两两平行，如图所示，设α∩β＝l，因为a∥b，a⊄β，b⊂β，所以a∥β.又知a⊂α，α∩β＝l，所以a∥l，又知α⊥γ，β⊥γ，α∩β＝l，所以l⊥γ，又知a∥b，a∥l，所以a⊥γ，又知c⊂γ，所以a⊥c，所以假设不成立．故三条直线a，b，c 不可能两两平行．答案：A7．已知l，m是不同的直线，α，β是不同的平面．给出下列命题，其中正确的是()①l⊥α，m⊂β，α∥β⇒l⊥m；②l∥α，m∥β，l∥m⇒α∥β；③l⊥α，m⊂β，l∥m⇒α⊥β；④l⊥α，m⊥β，l⊥m⇒α∥ββ.A．②④B．①③C．②③④D．①②③解析：①中，因为l ⊥α，α∥β，所以l ⊥β，又m ⊂β，所以l ⊥m ，①正确．③中，因为l ⊥α，l ∥m ，所以m ⊥α，又m ⊂β，所以α⊥β，③正确．由面面平行的判定定理知②和④不正确，故选B.答案：B8．在斜三棱柱ABC-A 1B 1C 1中，点D ，D 1分别为AC ，A 1C 1上的点，若平面BC 1D ∥平面AB 1D 1，则ADDC ＝_____．解析：如图所示，连接A 1B ，与AB 1交于点O ，连接OD 1，因为平面BC 1D ∥平面AB 1D 1，平面BC 1D ∩平面A 1BC 1＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ，所以BC 1∥D 1O ，所以A 1D 1D 1C 1＝A 1O OB .同理AD 1∥DC 1，所以A 1D 1D 1C 1＝DC AD ，所以A 1O OB ＝DCAD ，又因为A 1O OB ＝1，所以DC AD ＝1，即ADDC ＝1.答案：19．如图所示，正方体ABCD-A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上．若EF ∥平面AB 1C ，则线段EF 的长度等于________．解析：在正方体ABCD-A 1B 1C 1D 1中，AB ＝2，所以AC ＝2 2.又E 为AD 中点，EF ∥平面AB 1C ，EF ⊂平面ADC ，平面ADC ∩平面AB 1C ＝AC ，所以EF ∥AC ，所以F 为DC 中点，所以EF ＝12AC ＝ 2.答案： 210．设α，β，γ是三个不同的平面，m ，n 是两条不同的直线，在命题“α∩β＝m ，n ⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.可以填入的条件有________(填序号)．解析：由面面平行的性质定理可知，①正确；当n∥β，m⊂γ时，n和m在同一平面内，且没有公共点，所以平行，③正确．答案：①或③11．在正三棱锥S-ABC中，AB＝23，SA＝25，E，F分别为AC，SB的中点．平面α过点A，α∥平面SBC，α∩平面ABC＝l，则异面直线l和EF所成角的余弦值为________．解析：因为α∥平面SBC，α∩平面ABC＝l，平面SBC∩平面ABC＝BC，所以l∥BC，取AB的中点D，连接DE，DF，则DE∥BC，所以l∥DE，所以异面直线l和EF所成角即为∠DEF(或其补角)，取BC的中点O，连接SO，AO，则SO⊥BC，AO⊥BC，又SO∩AO＝O，所以BC⊥平面SOA，又SA⊂平面SOA，所以BC⊥SA，所以DE⊥DF，在Rt△DEF中，DE＝3，DF＝5，所以EF＝22，所以cos∠DEF＝322＝64.所以异面直线l和EF所成角的余弦值为6 4.答案：6 412．如图所示，四棱锥A-BCDE中，BE∥CD，BE⊥平面ABC，CD＝32BE，点F在线段AD上．(1)若AF ＝2FD ，求证：EF ∥平面ABC ；(2)若△ABC 为等边三角形，CD ＝AC ＝3，求四棱锥A-BCDE 的体积． (1)证明：取线段AC 上靠近C 的三等分点G ，连接BG ，GF . 因为AG AC ＝AF AD ＝23，则GF ＝23CD ＝BE . 而GF ∥CD ，BE ∥CD ，故GF ∥BE . 故四边形BGFE 为平行四边形，故EF ∥BG .因为EF ⊄平面ABC ，BG ⊂平面ABC ，故EF ∥平面ABC .(2)解：因为BE ⊥平面ABC ，BE ⊂平面BCDE ， 所以平面ABC ⊥平面BCDE .所以四棱锥A-BCDE 的高即为△ABC 中BC 边上的高． 易求得BC 边上的高为32×3＝332.故四棱锥A-BCDE 的体积V ＝13×12×(2＋3)×3×332＝1534.13．如图所示，在平行四边形ABCM 中，D 为CM 的中点，以AD 为折痕将△ADM 折起，使点M 到达点P 的位置，且平面ABCD ⊥平面P AD ，E 是PB 的中点，AB ＝2BC .(1)求证：CE ∥平面P AD ；(2)若AD ＝2，AB ＝4，求三棱锥APCD 的高． (1)证明：取AP 的中点F ，连接DF ，EF ，如图所示．因为点E 是PB 的中点， 所以EF ∥AB ，且EF ＝12AB .因为四边形ABCM是平行四边形，D为CM的中点，所以AB∥CD，且CD＝12AB，所以EF∥CD，且EF＝CD，所以四边形EFDC为平行四边形，所以CE∥DF，因为CE⊄平面P AD，DF⊂平面P AD，所以CE∥平面P AD.(2)解：取AD的中点O，连接PO，CO，如图所示．在平行四边形ABCM中，D为CM的中点，AB＝2BC，AD＝2，AB＝4，所以MD＝MA＝AD＝CD＝2，所以△MAD为等边三角形，所以∠MDA＝60°，所以∠ADC＝120°，PD＝P A＝AD＝2，所以S△ACD＝12AD·CD sin∠ADC＝12×2×2×32＝3，OC＝7，因为△ADP为正三角形，所以PO⊥AD，且PO＝ 3.因为平面ABCD⊥平面P AD，平面ABCD∩平面P AD＝AD，所以PO⊥平面ABCD，所以PO⊥OC，所以PC＝PO2＋OC2＝10.在等腰三角形PCD中，易得S△PCD＝152.设三棱锥A-PCD的高为h，因为V A-PCD＝V P-ACD，所以13S△PCD·h＝13S△ACD·PO，所以h＝S△ACD·POS△PCD＝3×3152＝2155，所以三棱锥A-PCD的高为215 5.14．如图所示，在三棱柱ABC-A1B1C1中，底面△ABC是等边三角形，且AA1⊥平面ABC，D 为AB的中点．(1)求证：直线BC1∥平面A1CD；(2)若AB＝BB1＝2，E是BB1的中点，求三棱锥A1-CDE的体积．(1)证明：连接AC1，交A1C于点F，则F为AC1的中点，又D为AB的中点，所以DF∥BC1，又BC1⊄平面A1CD，DF⊂平面A1CD，所以BC1∥平面A1CD.(2)解：因为△ABC为等边三角形，D为AB中点，所以CD⊥AB，又AA1⊥平面ABC，CD⊂平面ABC，所以CD⊥AA1，因为AB∩AA1＝A，所以CD⊥平面ABB1A1，所以三棱锥的高h等于点C到平面ABB1A1的距离，即h＝CD，易求得CD＝ 3.又S△A1DE ＝2×2－12×1×2－12×1×1－12×1×2＝32，所以V A1-CDE ＝V C-A1DE＝13S△A1DE·h＝13×32×3＝32.。

空间点、直线、平面之间的位置关系测试题一、选择题（本大题共12题，每小题5分，共60分）1. 已知平面α内有无数条直线都与平面β平行，那么（ ）A ．α∥βB ．α与β相交C ．α与β重合D ．α∥β或α与β相交2. 两条直线a ，b 满足a ∥b ，b α⊂，则a 与平面α的关系是( )A.a ∥αB.a 与α相交C.a 与α不相交D.a α⊂3.对于命题：①平行于同一直线的两个平面平行；②平行于同一平面的两个平面平行；③垂直于同一直线的两直线平行；④垂直于同一平面的两直线平行.其中正确的个数有( )A. 1 个B. 2个C. 3个D. 4个4. 经过平面外两点与这个平面平行的平面 （ ）A ．只有一个B ．至少有一个C ．可能没有D ．有无数个5.过三棱柱111ABC A B C -的任意两条棱的中点作直线，其中与平面11ABB A 平行的直线共有（ ）A. 3条B. 4条C. 5条D. 6条6. a ，b 是两条异面直线，下列结论正确的是（ ）A.过不在a ，b 上的任一点P ，可作一个平面与a ，b 平行B.过不在a ，b 上的任一点P ，可作一条直线与a ，b 相交C.过不在a ，b 上的任一点P ，可作一条直线与a ，b 都平行D.过a 可以并且只可以作一平面与b 平行7.n m ,是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（ ）A ．,,m n m n αα若则‖‖‖B ．,,αγβγαβ⊥⊥若则‖C ．,,m m αβαβ若则‖‖‖D ．,,m n m n αα⊥⊥若则‖8.如图1，正四面体ABCD 的棱长均为a ，且AD ⊥平面α于A ，点B ，C ，D 均在平面α外， 且在平面α同一侧，则点B 到平面α的距离是（ ）A ．2aB ．3aC ． 22aD 3a图1 图29.如图2，已知六棱锥P ABCDEF -的底面是正六边形，,2PA ABC PA AB ⊥=平面，则下列结论正确的是Ａ.PB AD ⊥ Ｂ.平面PAB PBC ⊥平面C. 直线BC ∥平面PAE Ｄ.PD ABC ︒直线与平面所成的角为4510.点P 在正方形ABCD 所在平面外，PD ⊥平面ABCD ，PD=AD ，则PA 与BD 所成角的度 数为 （ ）A ．30°B ．45°C ．60°D ．90°11.已知二面角l αβ--的大小为50，P 为空间中任意一点，则过点P 且与平面α和平面β所成的角都是025的直线的条数为（ ）A ．2B ．3C ．4D ．5α A B CD12.在正四棱柱1111ABCD A B C D -中，顶点1B 到对角线1BD 和到平面11A BCD 的距离分别为h 和d ，则下列命题中正确的是（ ）A ．若侧棱的长小于底面的边长，则h d 的取值范围为(0,1)B ．若侧棱的长小于底面的边长，则h d 的取值范围为223(,) C ．若侧棱的长大于底面的边长，则h d的取值范围为23(,2) D ．若侧棱的长大于底面的边长，则h d 的取值范围为23(,)3+∞ 二、填空题（本大题共4小题，每小题5分，共20分）13.如图3，△ABC 和△DBC 所在两平面互相垂直，且AB=BC=BD=a,∠CBA=∠CBD=120°,则AD 与平面BCD 所成的角为 .14.在正方体ABCD —A 1B 1C 1D 1中，E 为DD 1的中点，则BD 1与过点A ，E ，C 的平面的位置关系是 .15.若一个n 面体有m 个面是直角三角形，则称这个n 面体的直度为m n，则在长方体ABCD —1111A B C D 中，四面体1A ABC -的直度为 .16.βα,表示平面，l 表示既不在α内也不在β内的直线，存在以下三个事实：①l ⊥α； ②l ∥β；③α⊥β.若以其中两个为条件，另一个为结论，构成命题，其中正确命题的个数为 个.三、解答题（本大题共6小题，共70分） 17.如图4，在正三棱柱111C B A ABC -中，点D 是棱BC 的中点．求证：(1)D C AD 1⊥；(2)1//A B 平面1ADC ．18. 如图5，已知三棱柱111ABC A B C -的侧棱与底面 垂直，90BAC ∠=，M ，N 分别是11A B ，BC的中点．（1）证明：1AB AC ⊥；（2）判断直线MN 和平面11ACC A 的位置关系，并加以证明．A B B 1 C C 1A 1 M N CB A A BC D19. 如图6，在正方体1111D C B A ABCD -中，E ，F 分别为棱AD ，AB 的中点．(1)求证：平面11C CAA ⊥平面11D CB ；(2)如果1=AB ，一个动点从点F 出发在正方体的表面上依次经过棱1BB ,11C B ,11D C ,D D 1,DA 上的点，最终又回到点F ，指出整个路线长度的最小值并说明理由.20. 如图7，四棱锥S —ABCD 的底面是边长为2a 的菱形，且 2SA SC a ==2SB SD a ==，点E 是SC 上的点，且(02).SE a λλ=<≤（1）求证：对任意的(0,2]λ∈，都有BD AE ⊥；（2）若SC ⊥平面BED ，求直线SA 与平面BED 所成角的大小.21.某厂根据市场需求开发折叠式小凳，如图8所示. 凳面为三角形的尼龙布，凳脚为三根细钢管. 考虑到钢管的受力和人的舒适度等因素，设计小凳应满足：① 凳子高度为30cm ，② 三根细钢管相交处的节点O 与凳面三角形ABC 重心的连线垂直于凳面和地面.（1）若凳面是边长为20cm 的正三角形，三只凳脚与地面所成的角均为45，确定节点O 分细钢管上下两段的比值（精确到0.01）；（2）若凳面是顶角为120的等腰三角形，腰长为24cm ，节点O分细钢管上下两段之比为2:3. 确定三根细钢管的长度（精确到0.1cm ）22.如图9所示，在边长为12的正方形AA'A 1'A 1中，点B ，C 在线段AA'上，且AB ＝3，BC ＝4，作BB 1//AA 1，分别交A 1A 1'、AA 1'于点B 1，P ，作CC 1//AA 1，分别交A 1A 1'，AA 1'于点C 1，Q ，将该正方形沿BB 1，CC 1折叠，使得A'A 1'与AA 1重合，构成如图10所示的三棱柱ABC －A 1B 1C 1．（1）在三棱柱ABC －A 1B 1C 1中，求证：AB⊥平面BCC 1B 1；（2）求平面APQ 将三棱柱ABC －A 1B 1C 1分成上、下两部分几何体的体积之比．A B C O 图9 A B C A' A 1 B 1 C 1 A 1' P Q 图A B CA 1B 1C 1P Q A D A 1 B 1 C 1 D 1E空间点、直线、平面之间的位置关系测试题一、选择题 1~6 DC BC D D 7~12 DAD C BC提示:3.对于①平行于同一直线的两个平面平行，反例为：把一支笔放在打开的课本之间；②是对的,③是错的；④是对的5.取1111,,,AC BC B C AC 中点,,,E F M N ，直线分别为,,,,,EF MN EN EM FM FN 都与平面11ABB A 平行.6.如图所示，在直线a 上任取一点P ，过P 作b ′∥b ，则a ∩b ′=P.那么a与b ′确定一个平面α.因为b ∥b ′，b ′⊂α，b ⊄α，所以b ∥α.所以过a 可以作一个平面α与b 平行.假设还可作一平面β与b 平行，则α∩β=a ，b ∥α，b ∥β，所以a ∥b.这与a 、b 异面相矛盾，即假设不成立.所以只有一个平面α.综上所述，过a 有且只有一个平面与b 平行.故选D.7. ,m n 均为直线，其中,m n 平行α，,m n 可以相交也可以异面，故A 不正确； m ⊥α，n ⊥α则同垂直于一个平面的两条直线平行；选D8．取AD 的中点M ，易证AD ⊥平面BCM ，故平面BCM //平面α，平面BCM到平面α的距离为2a ，即为B 到平面α的距离. 9.因AD 与AB 不相互垂直，排除A ；作PB AG ⊥于G ，因平面⊥PAB 平面ABCDEF ，而AG 在平面ABCDEF 上的射影在AB 上，而AB 与BC 不相互垂直，故排除B ；由EF BC //，而EF 是平面PAE 的斜线，故排除C ，故选择D.10.将图形补成一个正方体如图，则PA 与BD 所成角等于BC′与BD所成角即∠DBC′．在等边三角形DBC′中，∠DBC′=60°，即PA 与BD所成角为60°．12.设底面边长为1，侧棱长为(0)λλ>，过1B 作1111,B H BD B G A B ⊥⊥.在11Rt BB D ∆中，21112,2B D B D λ==+，由三角形面积关系得11112122B D BB h B H B D λλ⋅===+ 设在正四棱柱中，由于1,BC AB BC BB ⊥⊥， 所以BC ⊥平面11AA B B ，于是1BC B G ⊥，所以1B G ⊥平面11A BCD ，故1B G 为点1B 到平面11A BCD 的距离，在11Rt A B B ∆中，又由三角形面积关系得1111211A B BB d B G A B λ⋅===+于是2222112122h d λλλ⋅+==⋅-++， 于是当1λ>，所以222123,1132λλ+><-<+，所以23(,2)3h d ∈ 二、填空题 13. 45° 14.BD 1∥平面AEC 15.1 16.2提示：13.作AO ⊥CB 的延长线，连接OD ，则OD 即为AD 在平面BCD 上的射影，因为AO =OD =23a ,所以∠ADO =45°. 14.连接AC ，BD 相交于一点O ，连接OE ，AE ，EC .因为四边形ABCD 为正方形，所以DO ＝BO .而DE ＝D 1E ，所以EO 为△DD 1B 的中位线， 所以EO ∥D 1B ,所以BD 1∥平面AEC . 15.本题主要考查空间的垂直关系，由图形得四面体ABC A -的每个面都是直角三角形，所以144==n m . 16.由①②⇒③、①③⇒②是正确命题，由②③不能得到①. 三、解答题17.证明:（1）因为三棱柱111C B A ABC -是正三棱柱，所以⊥C C 1平面ABC ， 又⊂AD 平面ABC ，所以AD C C ⊥1.又点D 是棱BC 的中点，且ABC ∆为正三角形，所以AD BC ⊥.因为1BC C C C =，所以⊥AD 平面11B BCC ，又因为1DC ⊂平面11B BCC ，所以D C AD 1⊥．(2)连接C A 1交1AC 于点E ，再连接DE ．因为四边形11ACC A 为矩形，所以E 为C A 1的中点，又因为D 为BC 的中点，所以1//ED A B . 又1A B ⊄平面1ADC ，ED ⊂平面1ADC ，所以1//A B 平面1ADC ．18.证明：(1)因为1CC ⊥平面ABC ，又AB ⊂平面ABC ，所以1CC ⊥AB ．由条件90BAC ∠=，即AC ⊥AB ，且1ACCC C =，所以AB ⊥平面11ACC A ． 又1AC ⊂平面11ACC A ，所以1AB AC ⊥．（2）MN ∥平面11ACC A ，证明如下：设AC 的中点为D ，连接DN ，1A D ．因为D ，N 分别是AC ，BC 的中点，所以DN //=12AB ． 又1A M =1211A B ，11A B //=AB ，所以1A M //=DN ． 所以四边形1A DNM 是平行四边形．所以1A D ∥MN ．因为1A D ⊂平面11ACC A ，MN ⊄平面11ACC A ，所以MN ∥平面11ACC A ．C19.（1）证明:因为在正方体1AC 中，AA 1⊥平面A 1B 1C 1D 1，而B 1D 1⊂平面A 1B 1C 1D 1，所以 AA 1⊥B 1D 1.又因为在正方形A 1B 1C 1D 1中，A 1C 1⊥B 1D 1，所以 B 1D 1⊥平面CAA 1C 1.又因为 B 1D 1⊂平面CB 1D 1，所以平面CAA 1C 1⊥平面CB 1D 1．(2)最小值为 .如图，将正方体六个面展开成平面图形，从图中F 到F ，两点之间线段最短，而且依次经过棱BB 1，B 1C 1，C 1D 1，D 1D ，DA 上的中点，所求的最小值为 . 20解：（1）连结BD ，AC ，设BD 与AC 交于O. 由底面是菱形，得.BD AC ⊥ SB SD =，O 为BD 中点，.BD SO ∴⊥又AC SO O ⋂=，BD ∴⊥面SAC.又AE ⊂面SAC ，.BD AE ∴⊥（2）取SC 的中点F ，连结OF ，OE ，//.SA OF ∴OF ∴与平面EDB 所成的角就是SA 与平面EDB 所成的角.SC ⊥平面BED ，FE ∴⊥面BED ，E 为垂足，EOF ∴∠为所求角.在等腰CSB ∆中，2,SC BC a SB ===，得底边SB 上的高为.CH =SC BE SB CH ∴⋅=⋅，2BE ∴==.所以在1,,2Rt BES SE a ∆==中所以11.22EF a a a ∴=-=在Rt FEO ∆中，1,sin .2EFOF a EOF OF =∴∠==即直线SA 与平面BED 所成角为.6π21.解：（1）设△ABC 的重心为H ，连结OH . 由题意，得BH =设细钢管上下两段之比为λ.已知凳子高度为30. 则301OH λλ=+.因为节点O 与凳面三角形ABC 重心的连线与地面垂直，且凳面与地面平行.所以OBH ∠就是OB 与平面ABC 所成的角，亦即45OBH ∠=. 30,13BH OH λλ==+因为所以，解得0.63λ=≈.即节点O 分细钢管上下两段的比值约为0.63.（2）设120,24B AB BC ∠===所以，AC =FF设△ABC 的重心为H ，则8,BH AH ==由节点O 分细钢管上下两段之比为2:3，可知12OH =.设过点A B C ,,的细钢管分别为,,AA BB CC '''，则560.82AA CC OA ''====≈，536.12BB OB '===≈， 所以对应于A B C ,,三点的三根细钢管长度分别为60.8cm ，36.1cm 和60.8cm . 22.（1）证明:在正方形AA'A 1'A 1中，因为A'C ＝AA'－AB －BC ＝5，所以三棱柱ABC －A 1B 1C 1的底面三角形ABC 的边AC ＝5． 因为AB ＝3，BC ＝4，所以AB 2＋BC 2＝AC 2．所以AB⊥BC．因为四边形AA'A 1'A 1为正方形，BB 1//AA 1，所以AB⊥BB 1．而BC∩BB 1＝B ，BC ⊂平面BCC 1B 1，BB 1⊂平面BCC 1B 1，所以AB⊥平面BCC 1B 1．(2)解：因为AB⊥平面BCC 1B 1，所以AB 为四棱锥A －BCQP 的高．因为四边形BCQP 为直角梯形，且BP ＝AB ＝3，CQ ＝AB ＋BC ＝7，所以梯形BCQP 的面积为S BCQP ＝12(BP ＋CQ)×BC＝20．所以四棱锥A －BCQP 的体积V A －BCQP ＝13S BCQP ×AB＝20．由(1)，知BB 1⊥AB，BB 1⊥BC，且AB∩BC＝B ，AB ⊂平面ABC ，BC ⊂平面ABC ．所以BB 1⊥平面ABC ．所以三棱柱ABC －A 1B 1C 1为直棱柱．所以三棱柱ABC －A 1B 1C 1的体积为V ABC －A 1B 1C 1＝S △ABC ×BB 1＝72．故平面APQ 将三棱柱ABC －A 1B 1C 1分成上、下两部分的体积之比为72－2020＝135．。

8.5 空间直线、平面的平行练习题1．如图所示，在空间四边形ABCD中，点E，H分别是边AB，AD的中点，点F，G分别是边BC，CD上的点，且CFCB＝CGCD＝23，则下列说法正确的是()A．EF与GH平行B．EF与GH异面C．EF与GH的交点M可能在直线AC上，也可能不在直线AC上D．EF与GH的交点M一定在直线AC上2．下列说法正确的是()A．直线l平行于平面α内的无数条直线，则l∥αB．若直线a在平面α外，则a∥αC．若直线a∩b＝∅，直线b⊂α，则a∥αD．若直线a∥b，b⊂α，那么直线a平行于平面α内的无数条直线3．如果直线l，m与平面α，β，γ满足：β∩γ＝l，m∥l，m⊂α，则必有() A．l∥αB．α∥γC．m∥β且m∥γD．m∥β或m∥γ4．已知两条直线m，n，两个平面α，β，给出下面四个命题：①α∩β＝a，b⊂α⇒a∥b或a，b相交；②α∥β，m⊂α，n⊂β⇒m∥n；③m∥n，m∥α⇒n∥α；④α∩β＝a，a∥b⇒b∥β或b∥α.其中正确命题的序号是()A．①③B．②④C．①④D．②③5．已知a，b，c是空间中的三条相互不重合的直线，给出下列说法：①若a∥b，b∥c，则a∥c；②若a与b相交，b与c相交，则a与c相交；③若a⊂平面α，b⊂平面β，则a，b一定是异面直线；④若a，b与c成等角，则a∥b.其中正确的是________(填序号)．6．如图是某正方体的平面展开图(表面朝下)．关于这个正方体，有以下判断：①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE ∥平面NCF.其中判断正确的序号是________．7．下面四个命题：①分别在两个平面内的两直线平行；②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面；③如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行；④如果一个平面内的任何一条直线都平行于另一个平面，那么这两个平面平行．其中正确的命题是________．8．给出下列说法：①若平面α∥平面β，平面β∥平面γ，则平面α∥平面γ；②若平面α∥平面β，直线a与α相交，则a与β相交；③若平面α∥平面β，P∈α，PQ∥β，则PQ⊂α；④若直线a∥平面β，直线b∥平面α，且α∥β，则a∥b.其中正确说法的序号是________．9．如图，在三棱台DEF－ABC中，AC＝2DF，G，H分别为AC，BC的中点．求证：BD∥平面FGH.10．如图，在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB ∥CD，且AB＝2CD，那么在棱AB上是否存在一点F，使平面C1CF∥平面ADD1A1？若存在，求点F的位置；若不存在，请说明理由．详解：1．如图所示，在空间四边形ABCD中，点E，H分别是边AB，AD的中点，点F，G分别是边BC，CD上的点，且CFCB＝CGCD＝23，则下列说法正确的是()A．EF与GH平行B．EF与GH异面C．EF与GH的交点M可能在直线AC上，也可能不在直线AC上D．EF与GH的交点M一定在直线AC上答案D解析连接EH，FG.因为F，G分别是边BC，CD上的点，且CFCB＝CGCD＝23，所以GF∥BD，且GF＝23BD.因为点E，H分别是边AB，AD的中点，所以EH∥BD，且EH＝12BD，所以EH∥GF，且EH≠GF，所以EF与GH相交，设其交点为M，则M∈平面ABC，同理M∈平面ACD.又平面ABC∩平面ACD＝AC，所以M在直线AC上．故选D.2．下列说法正确的是()A．直线l平行于平面α内的无数条直线，则l∥αB．若直线a在平面α外，则a∥αC．若直线a∩b＝∅，直线b⊂α，则a∥αD．若直线a∥b，b⊂α，那么直线a平行于平面α内的无数条直线答案D解析由直线与平面的位置关系及直线与平面平行的判定定理，知D正确．3．如果直线l，m与平面α，β，γ满足：β∩γ＝l，m∥l，m⊂α，则必有() A．l∥αB．α∥γC．m∥β且m∥γD．m∥β或m∥γ答案D解析 ⎭⎪⎬⎪⎫β∩γ＝l ，l ⊂β，l ⊂γm ∥l ，m ⊂α⇒m ∥β或m ∥γ.若m 为α与β的交线或为α与γ的交线，则不能同时有m ∥β，m ∥γ.故选D.4．已知两条直线m ，n ，两个平面α，β，给出下面四个命题：①α∩β＝a ，b ⊂α⇒a ∥b 或a ，b 相交；②α∥β，m ⊂α，n ⊂β⇒m ∥n ；③m ∥n ，m ∥α⇒n ∥α；④α∩β＝a ，a ∥b ⇒b ∥β或b ∥α.其中正确命题的序号是( )A ．①③B ．②④C ．①④D ．②③答案 C解析 对于①，由α∩β＝a ，b ⊂α，得a ，b 共面，则a ∥b 或a ，b 相交，正确；对于②，α∥β，m ⊂α，n ⊂β可能得到m ∥n ，还有可能是直线m ，n 异面，错误；对于③，m ∥n ，m ∥α，当直线n 不在平面α内时，可以得到n ∥α，但是当直线n 在平面α内时，n 不平行于平面α，错误；对于④，由α∩β＝a ，a ∥b ，得b 至少与α，β中的一个平面平行，则b ∥β或b ∥α，正确．故选C.5．已知a ，b ，c 是空间中的三条相互不重合的直线，给出下列说法： ①若a ∥b ，b ∥c ，则a ∥c ；②若a 与b 相交，b 与c 相交，则a 与c 相交；③若a ⊂平面α，b ⊂平面β，则a ，b 一定是异面直线；④若a ，b 与c 成等角，则a ∥b .其中正确的是________(填序号)．答案 ①解析 由基本事实4知①正确；当a 与b 相交，b 与c 相交时，a 与c 可能相交、平行，也可能异面，故②不正确；当a ⊂平面α，b ⊂平面β时，a 与b 可能平行、相交或异面，故③不正确；当a ，b 与c 成等角时，a 与b 可能相交、平行，也可能异面，故④不正确．故正确说法的序号为①.6．如图是某正方体的平面展开图(表面朝下)．关于这个正方体，有以下判断：①BM ∥平面DE ；②CN ∥平面AF ；③平面BDM ∥平面AFN ；④平面BDE∥平面NCF.其中判断正确的序号是________．答案①②③④解析以面ABCD为下底面还原正方体，如图，则易判定四个判断都是正确的．7．下面四个命题：①分别在两个平面内的两直线平行；②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面；③如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行；④如果一个平面内的任何一条直线都平行于另一个平面，那么这两个平面平行．其中正确的命题是________．答案②④解析由面面平行的定义可知②④正确．8．给出下列说法：①若平面α∥平面β，平面β∥平面γ，则平面α∥平面γ；②若平面α∥平面β，直线a与α相交，则a与β相交；③若平面α∥平面β，P∈α，PQ∥β，则PQ⊂α；④若直线a∥平面β，直线b∥平面α，且α∥β，则a∥b.其中正确说法的序号是________．答案②③解析①中平面α与γ也可能重合，故①不正确．假设直线a与平面β平行或直线a⊂β，则由平面α∥平面β，知a⊂α或a∥α，这与直线a与α相交矛盾，所以a与β相交，②正确．如图，过直线PQ作平面γ，γ∩α＝a，γ∩β＝b，由α∥β，得a∥b.因为PQ∥β，PQ⊂γ，所以PQ∥b.因为过直线外一点有且只有一条直线与已知直线平行，所以直线a与直线PQ重合．因为a⊂α，所以PQ⊂α，③正确．若直线a∥平面β，直线b∥平面α，且α∥β，则a与b平行、相交和异面都有可能，④不正确．9．如图，在三棱台DEF－ABC中，AC＝2DF，G，H分别为AC，BC的中点．求证：BD∥平面FGH.证明如图，连接DG，CD，设CD∩GF＝O，连接OH.在三棱台DEF－ABC中，AC＝2DF，G为AC的中点，可得DF∥GC，DF＝GC，所以四边形DFCG为平行四边形．所以O为CD的中点．又H为BC的中点，所以OH∥BD.又OH⊂平面FGH，BD⊄平面FGH，所以BD∥平面FGH.10．如图，在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB ∥CD，且AB＝2CD，那么在棱AB上是否存在一点F，使平面C1CF∥平面ADD1A1？若存在，求点F的位置；若不存在，请说明理由．解存在这样的点F，使平面C1CF∥平面ADD1A1，此时点F为AB的中点．证明如下：∵AB∥CD，AB＝2CD，∴AF=CD且AF//CD，∴四边形AFCD是平行四边形，∴AD∥CF.又AD⊂平面ADD1A1，CF⊄平面ADD1A1，∴CF∥平面ADD1A1.又CC1∥DD1，CC1⊄平面ADD1A1，DD1⊂平面ADD1A1，∴CC1∥平面ADD1A1.又CF∥平面ADD1A1，CC1∩CF＝C，∴平面C1CF∥平面ADD1A1.。

8.5 空间直线、平面的平行(精练)【题组一 线线平行】1．(2021·全国·高一课时练习)如图，在三棱锥A -BCD 中，E ，F ，G ，H 分别是边AC ，CD ，BD ，AB 的中点，且AD =BC ，那么四边形EFGH 是( )A ．平行四边形B ．矩形C ．菱形D ．正方形【答案】C【解析】因为,H G 分别是,BA BD 的中点，所以//HG AD ，且1=2HG AD ，同理//EF AD ，且1=2EF AD ，//HE BC ，且1=2HE BC ，//GF BC ，且1=2GF BC ，又=AD BC ，可得四边形EFGH 为菱形.故选：C.2．(2021·全国·高一课时练习)如果两直线a ∥b ，且a ∥α，则b 与α的位置关系是( ) A ．相交 B ．b ∥αC ．b ⊂αD ．b ∥α或b ⊂α【答案】D【解析】由a ∥b ，且a ∥α，结合线面平行的判定定理，知b 与α平行或b ⊂α.故选：D3．(2021·全国·高一课时练习)如图，在三棱柱ABC-A 1B 1C 1中，E ，F 分别是AB ，AC 上的点，且AE ∶EB=AF ∶FC ，则EF 与B 1C 1的位置关系是_____.【答案】平行【解析】在△ABC 中，AE ∶EB=AF ∶FC ，∴EF ∥BC ，三棱柱ABC-A 1B 1C 1中，有BC ∥B 1C 1，∴EF ∥B 1C 1.故答案为：平行4．(2021·全国·高一课时练习)如图是正方体的表面展开图，E ，F ，G ，H 分别是棱的中点，则EF 与GH 在原正方体中的位置关系为______.【答案】平行【解析】由题意，将正方体的表面展开图还原构造成正方体，如图所示: 分别取AB ，AA 1的中点Q ，P ，连接EP ，FQ ，PQ ，A 1B ， 由正方体的结构特征可得EF ∥PQ ，又因为点Q ，P ，H ，G 分别是AB ，AA 1，A 1B 1，BB 1的中点，故PQ ∥A 1B ，HG ∥A 1B ， 故PQ ∥HG ，所以EF ∥GH . 故答案为：平行5．(2021·广东东莞·高一期中)如图，点P ，Q ，R ，S 分别在正方体的四条棱上，且是所在棱的中点，则直线PQ 与RS 是平行直线的图是________(填序号).【答案】①②【解析】根据正方体的结构特征，可得①②中RS 与PQ 均是平行直线，④中RS 和PQ 是相交直线，③中RS 和PQ 是是异面直线.故答案为：①②.6．(2021·全国·高一课时练习)如图，在三棱柱111ABC A B C -中，,E F 分别是,AB AC 上的点，且::AE EB AF FC =，则EF 与11B C 的位置关系是______.【答案】平行 【解析】在ABC 中，::,//AE EB AF FC EF BC =∴.又.11//BC B C ，所以11//EF B C ．故答案为：平行．7．(2021·全国·高一课时练习)如图，△ABC 和△A'B'C'的对应顶点的连线AA'，BB'，CC'交于同一点O ，且2'''3AO BO CO OA OB OC ===.(1)求证:A'B'∥AB ，A'C'∥AC ，B'C'∥BC ; (2)求'''ABC A B C S S的值.【答案】(1)证明见解析；(2)49.【解析】(1)∵AA'∩BB'=O 且2''3AO BO A O B O ==， ∴AB ∥A'B'，同理，AC ∥A'C'，BC ∥B'C'.(2)∵A'B'∥AB ，A'C'∥AC ，由图知：AB 和A'B'，AC 和A'C'方向相反，∴∠BAC=∠B'A'C'，同理，∠ABC=∠A'B'C'，∠ACB=∠A'C'B'，∴△ABC ∽△A'B'C'， ∴2'''3AB AO A B OA ==，∴2'''2439ABC A B C SS⎛⎫== ⎪⎝⎭. 8(2021·全国·高一课时练习)已知E ，F ，G ，H 为空间四边形ABCD 的边AB ，BC ，CD ，DA 上的点，若12AE AH AB AD ==，13CFCGCB CD == 证明:四边形EFGH 为梯形. 【答案】证明见解析【解析】证明：如图，在ABD中，因为12AE AHAB AD==，所以EH∥BD且EH=12BD.在BCD中，因为13CF CGCB CD==，所以FG∥BD且FG=13BD，所以EH∥FG且EH>FG，所以四边形EFGH为梯形.9．(2021·全国·高一课时练习)如图，在正方体ABCD－A1B1C1D1中，M，M1分别是棱AD和A1D1的中点．(1)求证：四边形BB1M1M为平行四边形；(2)求证：∠BMC＝∠B1M1C1．【答案】(1)证明详见解析；(2)证明详见解析．【解析】(1)在正方形ADD1A1中，M、M1分别为AD、A1D1的中点，∴MM1∥AA1，MM1=AA1．又∵AA1∥BB1，AA1=BB1，∴MM1∥BB1，且MM1＝BB1，∴四边形BB1M1M为平行四边形．(2)法一：由(1)知四边形BB1M1M为平行四边形，∴B1M1∥BM．同理可得四边形CC1M1M为平行四边形，∴C1M1∥CM．由平面几何知识可知，∠BMC和∠B1M1C1都是锐角．∴∠BMC＝∠B1M1C1．法二：由(1)知四边形BB1M1M为平行四边形，∴B1M1＝BM．同理可得四边形CC1M1M为平行四边形，∴C1M1＝CM．又∵B1C1＝BC，∴△BCM≌△B1C1M1．∴∠BMC＝∠B1M1C1．【题组二线面平行】1．(2021·全国·高一课时练习)如图，点A，B，C，M，N为正方体的顶点或所在棱的中点，则下列各图中，不满足直线//MN平面ABC的是( )A ．B ．C ．D ．【答案】D【解析】对于A ，由正方体的性质可得////MN EF AC ，可得直线//MN 平面ABC ，能满足；对于B ，作出完整的截面ADBCEF ，由正方体的性质可得MN //AD ，可得直线MN //平面ABC ，能满足；对于C ，作出完整的截面ABCD ，由正方体的性质可得MN //BD ，可得直线MN //平面ABC ，能满足；对于D，作出完整的截面，如下图ABNMHC，可得MN在平面ABC内，不能得出平行，不能满足.故选：D.2 ．(2021·福建长汀·高一期中)(多选)如图所示，P为矩形ABCD所在平面外一点，矩形对角线的交点为O，M为PB的中点，给出以下结论，其中正确的是( )A．OM∥PD B．OM∥平面PACC．OM∥平面PDA D．OM∥平面PBA【答案】AC【解析】因为矩形对角线的交点为O，所以O是BD的中点，∴为△PBD的中位线，又M为PB的中点，OM∴,//OM PD又OM⊄平面PAD,PD⊂平面PAD,所以OM∥平面PDA，故AC正确；OM与平面PAC有公共点O,与平面PBA有公共点M,故BD错误.故选：AC.3．(2021·吉林·长春市第八中学高一期中)(多选)下列四个正方体图形中，A，B为正方体的两个顶点，M、AB平面MNP的图形是( )N、P分别为其所在棱的中点，不能得出//A．B．C．D．【答案】BC【解析】对于A：连接AC，如图①所示.由MN∥AC,NP∥BC,MN∩NP=N,AC∩BC=C,可知平面MNP∥平面ACB,所以AB∥平面MNP.故不选A;对于B：连接BC交MP于D,连接DN,如图②所示由于N是AC的中点,D不是BC的中点,所以在平面ABC内AB 与DN相交,所以直线AB与平面MNP相交,故选B;对于C：连接CD,如图③所示则AB∥CD,而CD与PN相交,即CD与平面MNP相交,所以直线AB与平面MNP相交，故选C;对于D：连接CD,如图④所示.则AB∥CD∥NP,由线面平行的判定定理可知AB∥平面MNP综上所述,不能得出AB∥平面MNP的图形是B和C.故选：BC4．(2021·全国·高一课时练习)下列四个正方体图形中，,A B 为正方体的两个顶点，,,M N P 分别为其所在棱的中点，能得出//AB 平面MNP 的图形的序号是________．【答案】①④【解析】在①中：如图：因为,,M N P 分别为其所在棱的中点，所以//MN AC ，//NP BC ， 因为MN ⊄面ABC ，AC ⊂面ABC ，所以//MN 面ABC ，同理可得//PN 面ABC ， 因为MN NP N ⋂=，所以面//ABC 面MNP ，因为AB面ABC ，所以//AB 平面MNP ，故①成立；在②中，若下底面中心为O ，连接NO ，可得//NO AB ，NO ⋂面MNP N =，所以AB 与平面MNP 不平行，故②不成立；在③中：如图：平面PMN 即为平面PNBC ，因为AB ⋂面PNBC B =，所以AB 与面MNP 不平行，故③不成立；在④中：如图：//AC BD 且AC BD =，所以四边形ACDB 是平行四边形，可得//AB CD ，因为//NP CD ，所以//AB NP ，因为AB ⊄面MNP ，NP ⊂面MNP ， 所以所以//AB 平面MNP ，故④成立．故答案为：①④.5．(2021·全国·高一课时练习)已知正三棱柱ABC ﹣A 1B 1C 1的边长均为E ，F 分别是线段AC 1和BB 1的中点．(1)求证：EF //平面ABC ； (2)求三棱锥C ﹣ABE 的体积． 【答案】(1)证明见解析；(2)3.【解析】(1)证明：取AC 的中点为G ，连结GE ，GB ， 在△ACC 1中，EG 为中位线，所以EG //CC 1，112EG CC =，又因为CC 1//BB 1，CC 1＝BB 1，F 为BB 1的中点， 所以EG //BF ，EG ＝BF ，所以四边形EFBG 为平行四边形，所以EF //GB ，又EF ⊄平面ABC ，GB ⊂平面ABC ， 所以EF //平面ABC ． (2)因为E 为AC 1的中点，所以E 到底面ABC 的距离是C 1到底面ABC 的距离的一半，即三棱锥E ﹣ABC 的高h ＝12CC 1又△ABC 的面积为2S ==所以133C ABE E ABC V V --==⨯．6．(2021·全国·高一课时练习)如图，正方形ABCD 和四边形ACEF 所在平面相交．//EF AC ，AB =1EF =．求证：//AF 平面BDE ．【答案】证明见解析【解析】设AC ，BD 交于点G ，连接EG ，因为四边形ABCD 是正方形，AB =所以BC =2AC =，112AG AC ==， 又因为1EF =，所以EF AG =，又//EF AC ，所以四边形AGEF 为平行四边形．所以AF //EG ．又因为AF ⊄平面BDE ，EG ⊂平面BDE ，所以//AF 平面BDE ．7．(2021·全国·高一课时练习)如图，ABC 是正三角形，AE 和CD 都垂直于平面ABC ，且2AE AB a ==，CD a =，F 是BE 的中点，求证：//DF 平面ABC ．【答案】证明见解析【解析】证明：取AB 的中点G ，连接FG ，CG ，可得//FG AE ，12FG AE =．因为CD ⊥平面ABC ，AE ⊥平面ABC ，所以//CD AE ． 又因为12CD AE =．所以//FG CD ，FG CD =．所以四边形CDFG 是平行四边形，所以//DF CG ． 又因为CG ⊂平面ABC ，DF ⊄平面ABC ，所以//DF 平面ABC ．8．(2021·全国·高一课时练习)如图所示，已知正方形ABCD 和正方形ABEF 所在的平面相交于AB ，点M 、N 分别在AC 和BF 上，且AM FN =．求证；//MN 平面BCE ．【答案】证明见解析.【解析】如图所示，连接AN 并延长交BE 的延长线于G ，连接CG ．∵//AF BG ，∴AN FN NG NB=，又,AM FN AC FB ==，∴MC NB =， ∴FN AM NB MC=，∴AN AM NG MC =， ∴//NM CG ．∵CG ⊂平面CBE ，NM ⊄平面CBE ，∴//MN 平面BCE ．9．(2021·黑龙江齐齐哈尔·高一期末)如图，在四棱锥P ABCD -中，平面PBC ⊥平面ABCD ，90PBC ∠=︒，//AD BC ，90ABC ∠=︒，222AB AD ===，E 为PC 的中点．(1)证明：//DE 平面APB ；(2)若2BP =，求三棱锥E DBP -的体积．【答案】(1)证明见解析；(2)13. 【解析】(1)取PB 中点F ，连接FE ，FA ，∵E 是CP 的中点，∴//EF CB ，12EF CB ， ∵//AD BC ，90ABC ∠=︒，∴90DAB ∠=︒，∵1AD AB ==，∴BD 45ADB ∠=︒，则45DBC ∠=︒，又∵CD =，∴90CDB ∠=︒，可得2CB =，∴//AD CB ，12AD CB =，∴//EF AD ，EF AD =，得四边形ADEF 为平行四边形，∴//DE AF ，又DE ⊄平面ABP ，AF ⊂平面ABP ，∴//DE 平面APB ；(2)取BC 中点O ，连接DO ，∴⊥DO CB ，∵平面PBC ⊥平面ABCD ，平面PBC 平面ABCD CB =，∴DO ⊥平面PBC ，则DO 为三棱锥D EBP -的高，又∵2BC BP ==，∴BE CP ⊥，得12BE CP =∴1111111332323E DBP D EBP EBP V V DO S DO BE EP --⎛⎫⎛==⋅=⨯⨯⨯=⨯⨯= ⎪ ⎝⎭⎝△． 故三棱锥E DBP -的体积为13． 10．(2021·广西·钦州市第四中学高一月考)如图，在直三棱柱ABC ﹣A 1B 1C 1中，AB ⊥BC ，AA 1＝AC ＝2，BC ＝1，E ，F 分别是A 1C 1，BC 的中点．(1)求证：C 1F //平面ABE ；(2)求三棱锥A ﹣BCE 的体积．【答案】(1)证明见解析；【解析】(1)证明：取AB 的中点G ，连接EG ，FG ，∵E ，F ，G 分别是A 1C 1，BC ，AB 的中点，∴FG //AC ，且FG ＝12AC ，EC 1＝12A 1C 1，∵AC //A 1C 1且AC ＝A 1C 1，∴GF //EC 1且GF ＝EC 1，∴四边形FGEC 1为平行四边形，得C 1F //EG ，又∵EG ⊂平面ABE ，C 1F ⊄平面ABE ，∴C 1F //平面ABE ；(2)∵AA 1＝AC ＝2，BC ＝1，AB ⊥BC ，∴AB ．∴三棱锥A ﹣BEC 的体积V ＝V A ﹣BEC ＝V E ﹣ABC ＝113ABC S AA ⋅＝111232⨯⨯=11(2021·广西·钦州市第四中学高一月考)如图，在五面体ABCDEF 中，四边形ABCD 是直角梯形，∠BAD ＝90°，BC //AD ，AB ＝AF ＝BC ＝12AD ＝1，AF ⊥平面ABCD ，N ，G 分别为DF ，CD 的中点．(1)求证：NC //平面FAB ；(2)求三棱锥E ﹣ACG 的体积．【答案】(1)证明见解析；(2)16. 【解析】(1)取AD 的中点M ，连接NM ，CM ，在△ADF 中，∵N 是FD 的中点，M 是AD 的中点，∴//NM FA ，由于NM ⊄平面FAB ，FA ⊂平面FAB ，所以//NM 平面FAB .在梯形ABCD 中，BC //AD ，AD ＝2BC ，M 是AD 的中点，∴BC ＝AM ，BC //AM ，可得四边形ABCM 为平行四边形，则CM //AB ，由于CM ⊄平面FAB ，AB 平面FAB ，所以//CM 平面FAB .∵CM ∩NM ＝M ，∴平面NMC //平面FAB ，又NC ⊂平面NMC ，∴NC //平面FAB ；(2)∵BC //AD ，AD ⊂平面ADEF ，BC ⊄平面ADEF ，∴BC //平面ADEF ，∵BC ⊂平面BCEF ，平面BCEF ∩平面ADEF ＝EF ，∴BC //EF ，又BC ⊂平面ABCD ，EF ⊄平面ABCD ，∴EF //平面ABCD ，连接FC ，FG ，则V E ﹣ACG ＝V F ﹣ACG .∵四边形ABCD 是直角梯形，∠BAD ＝90°，BC //AD ，AB ＝AF ＝BC ＝12AD ＝1，∴CD ＝AC ACD ＝90°，CG ，又AF ⊥平面ABCD ，∴1132E ACG V CG AC AF -=⨯⨯⨯＝1111326⨯=．故三棱锥E ﹣ACG 的体积为16．12．(2021·山西·太原市第五十六中学校高一月考)如图，在正方体1111ABCD A B C D -中，E ，F ，P ，Q 分别是棱AB ，AD ，1DD ，1BB 的中点.求证：1//BC 平面EFPQ .【答案】证明见解析.【解析】在正方体1111ABCD A B C D -中，连接1AD ，因为11AB C D =且11//AB C D ，所以四边形11ABC D 是平行四边形，可得11//AD BC ，因为F ，P 分别是AD 、1DD 的中点，所以1//FP AD ，所以1//BC FP ，又FP ⊂平面EFPQ ，且1BC ⊄平面EFPQ ， 所以直线1//BC 平面EFPQ ．13．(2021·重庆第二外国语学校高一月考)如图，正三棱柱111ABC A B C -中，14AA =，ABC 的边长为6，,D E 分别为棱1,AC CC 的中点.(1)1AB //平面1BDC ；(2)求异面直线DE 与1AB 所成角的余弦值.【答案】(1)证明见解析；(2)1726【解析】(1)如图所示：连接1B C 与1BC 交于点O ，连接DO ，因为D 分别为棱AC 的中点.所以1//AB OD ，又1AB ⊄平面1BDC ，OD ⊂平面1BDC ，所以1AB //平面1BDC ；(2)由(1)知：1//AB OD ，所以EDO ∠是异面直线DE 与1AB 所成的角，连接OE ，在DEC Rt △中，DE =在1Rt BC C △中，1BC =因为三棱柱是正三棱柱，所以BD ⊥平面11A ACC ，则1BD DC ⊥，在1Rt BDC △中，112DO BC == 又3EO =，所以由余弦定理得： 222cos 2DE DO EO EDO DE DO+-∠=⋅， 22231726+-=，所以异面直线DE 与1AB 所成角的余弦值是1726. 14(2021·重庆市育才中学高一期中)如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PD ⊥平面ABCD ， 4AD PD ==，点Q 是PC 的中点.(1)求证：PA //平面BDQ ； (2)在线段AB 上是否存在点F ，使直线PF 与平面PAD 所成的角为30°？若存在，求出AF 的长，若不存在，请说明理由？【答案】(1)见解析；(2)存在，AF =【解析】(1)连结AC ，交BD 于O ，如图所示，底面ABCD 是矩形，因此O 为AC 中点，且点Q 是PC 的中点//PA QO ∴又PA ⊄平面BDQ ，QO ⊆平面BDQ PA ∴//平面BDQ (2)PD ⊥平面ABCD ，AB ⊆平面ABCD PD AB ∴⊥又AD AB ⊥，,,PD AD D PD AD =⊆平面PAD AB ∴⊥平面PAD∴直线PF 与平面PAD 所成的角即为30APF ︒∠=AF AP ∴==因此存在点F ，使直线PF 与平面PAD 所成的角为30°，此 时AF =15．(2021·江苏如皋·高一月考)如图，在多面体ABCDE 中，60ABD ∠=︒，2BD AB =，AB CD ⊥，(1)//AB DE ，且2DE AB =，点M 为EC 的中点，求证：//AM 平面BCD ；(2)若BCD △是边长为2的等边三角形，BA =N 在线段CD 上，且2DN CN =，求BN 与平面ACD 所成角的大小；【答案】(1)证明见解析；(2)30.【解析】(1)如图，取线段CD 的中点F ，连接BF ，MF在CDE △中，点M 为EC 的中点，点F 为线段CD 的中点//MF DE ∴，且12MF DE = 又//AB DE ，且2DE AB =，//AB MF ∴，AB MF =∴四边形ABFM 为平行四边形//AM BF ∴AM ⊄平面BCD ，BF ⊂平面BCD //AM ∴平面BCD(2)在ABD △中，2BD AB =，60ABD ∠=︒90BAD ∴∠=︒即AB AD ⊥ 又AB CD ⊥，AD CD D =，AD 、CD ⊂平面ACD AB ∴⊥平面ACD BNA ∴∠即为BN 与平面ACD 所成的角在BCN △中，2BC =，23CN =，由余弦定理得：BN ==又在直角三角形ABN 中，BA =BN =，AN ==cos AN BNA BN ∠== ∴BN 与平面ACD 所成角的大小为30.16(2021·山西省长治市第二中学校高一月考)如图：在四棱锥P ABCD -中，AB ∥CD ，3AB CD =，点E 是PC 上的一点，(1)若//BE 平面PAD ，求PEEC的值． (2)若平面ABE 将四棱锥分成体积相等的两部分，求PEEC的值． 【答案】(1)12；(2)2．【解析】(1)过点E 做//EF CD 交PD F 于，连接AF ，AB //CD ，CD //EF ，//BE 平面PAD ，平面PAD 平面ABEF AF =，ABEF ∴是平行四边形，13EF AB CD ==12PE EC ∴= (2)过点E 做//EF CD 交PD F 于，连接AF BF 、设PE PC,λ=则PAF PADSS=λ，2PEF PCDS S=λ13344P ABD P ABCD P BCD P ABCD CD AB,V V ,V V ----=∴==2P ABEF P ABF P BEF B APF B PEF P BAD P BCD V V V V V V V -------=+=+=+λλ231442P ABCD P ABCD P ABCD V V V ---=+=λλ，化简得：2320λλ+-=，解得：23λ=或1λ=-(舍去)，2PEEC∴=.17．(2021·河北·深州长江中学高一期中)如图，正四棱锥,4,2S ABCD SA AB -==，E 为SC 中点.(1)求证：//SA 平面BDE ； (2)求四棱锥S ABCD -的体积；【答案】(1)证明见解析；. 【解析】(1)连接AC ，交BD 于点O ，连接OE .因为四棱锥S ABCD -为正四棱锥，所以四边形ABCD 为正方形，即O 为AC 中点， 因为E 为SC 中点，所以OE 为SAC 的中位线，所以//OE SA ， 因为OE ⊂平面BDE ，SA ⊄平面BDE ，//SA 平面BDE . (2)连接SO ，如图所示：在正四棱锥S ABCD -中，SO ⊥平面ABCD ，即棱锥的高为SO ，在Rt SOB 中，SO ==211233S ABCD ABCD V SO S -=⋅=18．(2021·江苏·金陵中学高一期中)如图，在四棱锥O －ABCD 中，底面ABCD 是边长为1的菱形，∠ABC ＝4π，OA ⊥平面ABCD ，OA ＝2，M 为OA 的中点，N 为BC 的中点．(1)画出平面AMN 与平面OCD 的交线(保留作图痕迹，不需写出作法)； (2)证明：直线MN //平面OCD ； (3)求异面直线AB 与MD 所成角的大小． 【答案】(1)图形见解析；(2)证明见解析；(3)3π. 【解析】(1) 延长AN ,CD ,两直线相交于点E ，OE .为平面AMN 与平面OCD 的交线；(2)延长AN ,CD ,两直线相交于点E ,由已知12NC AD =，NC AD ，∴ N 为AE 的中点，又M 为AO 的中点，∴ MN ∥OE ， 又OE ⊂ 平面OCD ，MN ⊄平面OCD ，∴ MN ∥平面OCD ；(3)∵ AB ∥CD ，∴ 异面直线AB 与MD 所成角为CMD ∠或其补角，∵ 底面ABCD 是边长为1的菱形，∠ABC ＝4π，∴ AC =1CD =,又OA ⊥平面ABCD ，OA ＝2，M 为OA 的中点，∴ MD =MC ∴ 1cos 2CMD ∠==， ∴ =3CMD π∠，∴ 异面直线AB 与MD 所成角的大小为3π. 【题组三 面面平行】1．(2021·全国·高一课时练习)如图，E ，F ，G ，H 分别是正方体ABCD ­A 1B 1C 1D 1的棱BC ，CC 1，C 1D 1，AA 1的中点．求证：(1)EG //平面BB 1D 1D ； (2)平面BDF //平面B 1D 1H .【答案】(1)证明见解析；(2)证明见解析.【解析】(1)如图，取B 1D 1的中点O ，连接GO ，OB ，因为OG =12B 1C 1，BE =12B 1C 1，所以BE =OG ，且11////BE B C OG 所以四边形BEGO 为平行四边形，故OB //EG ， 因为OB ⊂平面BB 1D 1D ，EG ⊄平面BB 1D 1D ，所以EG //平面BB 1D 1D .(2)由于1111//,BB DD BB DD =所以四边形11BB D D 为平行四边形所以BD //B 1D 1. 连接HB ，D 1F ，1,HD BF 取P 为1DD 中点，连结,AP PF因此////,AB CD PF AB CD PF ==因此四边形ABFP 为平行四边形，故有//AP BF 又11//,AH PD AH PD =因此四边形1AHD P 为平行四边形，故有1//AP HD 故HD 1//BF .又B 1D 1∩HD 1＝D 1，BD ∩BF ＝B ，所以平面BDF //平面B 1D 1H .2．(2021·浙江·台州市路桥区东方理想学校高一月考)如图，在四棱锥P ABCD -中，四边形ABCD 为平行四边形，E ，F 分别为BC ，PC 的中点，ACBD O =．求证：(1)//OF 平面APD ； (2)平面//OEF 平面APB ．【答案】(1)证明见解析；(2)证明见解析．【解析】(1)ABCD O ⇒为AC 中点，又F 为PC 中点，∴//OF PA ，PA ⊂平面PAD ，OF ⊄平面PAD ，∴//OF 平面PAD ； (2)∵E ，F 分别为BC ，PC 的中点，∴//EF PB ，PB ⊂平面APB ，EF ⊄平面APB ∴//EF 平面APB ，同理可证：//OE 平面APB 又OEEF E =，∴平面//OEF 平面APB3．(2021·安徽·合肥艺术中学 高一期中)如图，在多面体ABCDEF 中，ABCD 是正方形，BF ⊥平面,ABCD DE ⊥平面ABCD ，,BF DE M =为棱AE 的中点.(1)证明：平面//BMD 平面EFC ；(2)若2AB BF ==，求三棱锥A CEF -的体积.【答案】(1)证明见解析；(2)43.【解析】(1)设AC 与BD 交于点N ，则N 为AC 的中点，//.MN EC ∴MN ∴⊄平面,EFC EC ⊂平面,//EFC MN ∴平面.EFCBF ⊥平面,ABCD DE ⊥平面,//ABCD BF DE ∴， ,BF DE BDEF =∴为平行四边形，//.BD EF ∴BD ⊄平面,EFC EF ⊂平面,//EFC BD ∴平面.EFC ,MN BD N ⋂=∴平面BDM //平面EFC ；(2)连接,EN FN .在正方形ABCD 中，AC BD ⊥，BF ⊥平面,.ABCD BF AC ∴⊥BF BD B ⋂=，AC ∴⊥平面BDEF ，且垂足为N ， 11142223323A CEF NEFV AC S-∴=⋅⋅=⨯⨯⨯⨯= ∴三棱锥A CEF -的体积为43. 4．(2021·广东实验中学高一期中)已知正方体1111ABCD A B C D -中，P 、Q 分别为对角线BD 、1CD 上的点，且123CQ BP QD PD ==．(1)求证//PQ 平面11A D DA ； (2)若R 是CD 上的点，当CRCD的值为多少时，能使平面//PQR 平面11B C CB ？请给出证明． 【答案】(1)证明见解析；(2)25CR CD =，证明见解析. 【解析】(1)证明：连结CP 并延长与DA 的延长线交于M 点， 因为四边形ABCD 为正方形，所以//BC AD ，故PBC PDM ∽，所以23CP BP PM PD ==， 又因为123CQ BP QD PD ==，所以123CQ CP QD PM ==，所以1//PQ MD ． 又1MD ⊂平面11A D DA ，PQ ⊄平面11A D DA ，故//PQ 平面11A D DA ； (2)当25CR CD =时，能使平面//PQR 平面11B C CB ，证明：因为25CR CD =，即有23CR RD =，故123CQ CR QD RD ==，所以1//QR DD ， 又∵11//DD CC ，∴//QR CC ，又1CC ⊂平面11B C CB ，QR ⊄平面11B C CB ， 所以//QR 平面11A D DA ， 由23CR BPRD PD==，得//PR BC ，BC ⊂平面11B C CB ，PR ⊄平面11B C CB ，所以//PR 平面11B C CB ，又PRRQ R =，所以平面//PQR 平面11B C CB ．5．(2021·浙江·嘉兴市第五高级中学高一期中)如图所示，已知点P 是平行四边形ABCD 所在平面外一点，,N K 分别为,PC PA 的中点，平面PBC 平面APD l =．(1)求证：//l BC ；(2)直线PB 上是否存在点H ，使得平面//KNH 平面ABCD ，并加以证明.【答案】(1)证明见解析；(2)当H 为PB 中点时，平面//KNH 平面ABCD ，证明见解析. 【解析】(1)因为四边形ABCD 是平行四边形，所以//BC AD ，因为AD ⊂平面PAD ，BC ⊄平面PAD ，所以//BC 平面PAD ， 又因为平面PAD 平面PBC l =，BC ⊂平面PBC ，所以//BC l ． (2)当H 为PB 中点时，平面//KNH 平面ABCD ． 证明如下：取PB 的中点H ，连接KH ，NH ，KN ， 因为,N K 分别为,PC PA 的中点，所以//NH BC ，//KH AB ，又NH ⊄平面ABCD ，BC ⊂平面ABCD ，所以//NH 平面ABCD ，同理可证//KH 平面ABCD ． 又因为KH ⊂平面KNH ，NH ⊂平面KNH ，KH NH H ⋂=， 所以平面//KNH 平面ABCD ．6．(2021·福建浦城·高一期中)如图所示，在三棱柱111ABC A B C -中，E ､F ､G ､H 分别是AB ，AC ，11A B ，11A C 的中点，求证：(1)//GH 平面1A EF ，(2)平面1//A EF 平面BCHG .【答案】(1)证明见解析；(2)证明见解析.【解析】证明：(1)因为G ，H 分别是11A B ，11A C 的中点，所以GH 是111A B C △的中位线，则11//GH B C ， 因为E ，F 分别是11A B ，11A C 的中点，所以EF 是ABC 的中位线，则//EF BC ，又因为11//B C BC ，所以//EF GH ，EF ⊂平面1A EF ，GH ⊂/平面1A EF ，所以//GH 平面1A EF ， （2）由G ，E 分别为11A B ，AB 的中点，11//A B AB ，所以1//AG EB ，1AG EB =，所以1A EBG 是平行四边形，所以1//A E GB . 1A E ⊂平面1A EF ，BG ⊂/平面1A EF ，所以//BG 平面1A EF ，又BG ⊂平面BCHG ，GH ⊂平面BCHG ，且BG GH G =，所以平面1//A EF 平面BCHG .7．(2021·江苏·无锡市堰桥高级中学高一期中)如图，在四棱柱1111ABCD A B C D -中，点M 是线段11B D 上的一个动点，E ，F 分别是BC ，CM 的中点.(1)求证：//EF 平面11BDD B ；(2)设G 为棱CD 上的一点，问：当G 在什么位置时，平面//GEF 平面11BDD B ？ 【答案】(1)证明见解析；(2)G 是DC 中点.【解析】(1)在四棱柱1111ABCD A B C D -中，连接BM ，如图，因E ，F 分别是BC ，CM 的中点，则有//EF BM ，又EF ⊄平面11BDD B ，BM ⊂平面11BDD B ， 所以//EF 平面11BDD B ；(2)G 是DC 中点，使得平面//GEF 平面11BDD B ，理由如下： 取CD 的中点G ，连接EG ，FG ，而E 是BC 的中点，于是得//EG BD ， 而EG ⊄平面11BDD B ，BD ⊂平面11BDD B ，从而得//EG 平面11BDD B ，由(1)知//EF 平面11BDD B ，EF EG E =，且,EF EG ⊂平面GEF ，因此有平面//GEF 平面11BDD B ，所以当G 是DC 的中点时，平面//GEF 平面11BDD B .8．(2021·全国·高一课时练习)如图，在正方体1111ABCD A B C D -中，S 是11B D 的中点，E ，F ，G 分别是BC ，DC ，SC 的中点，求证：(1)直线//EG 平面11BDD B ； (2)平面//EFG 平面11BDD B ．【答案】(1)证明见解析：(2)证明见解析： 【解析】(1)如图所示，连接SB ，在SBC △中，G 是SC 中点，E 是BC 中点，所以//EG SB ， 且SB ⊂平面11BDD B ，EG ⊄平面11BDD B ， 所以//EG 平面11BDD B(2)在BCD △中，E ，F 分别为BC ，DC 的中点，所以//EF BD ， 且BD ⊂平面11BDD B ，EF ⊄平面11BDD B ，所以//EF 平面11BDD B ； 由(1)得：//EG 平面11BDD B ，且因为EG EF E =，,EG EF ⊂平面EFG ，所以平面//EFG 平面11BDD B9．(2021·吉林·长春市第二十九中学高一期中)如图所示，在三棱柱111ABC A B C -中，E ，F ，G ，H 分别是AB ，AC ，1111,A B AC 的中点.(1)求证：//GH 平面ABC ； (2)求证：平面1EFA //平面BCHG . 【答案】(1)证明见解析；(2)证明见解析. 【解析】(1)在三棱柱111ABC A B C -中，因为G ，H 分别是11A B ，11A C 的中点， 所以11//GH B C ，又因为11//BC B C ，所以//GH BC .因为GH ⊄平面ABC ，BC ⊂平面ABC ，所以//GH 面ABC ； (2)因为E ，F 分别是AB ，AC 的中点，所以//EF BC . 又因为在三棱柱111ABC A B C -中，G 为11A B 的中点，所以1//AG EB ，1AG EB =，即四边形1A EBG 为平行四边形.所以1//A E BG . 因为//EF BC ，EF ⊄平面BCHG ，BC ⊂平面BCHG ，所以//EF 平面BCHG ， 因为1//A E BG ，1A E ⊄平面BCHG ，BG ⊂平面BCHG ，所以1//A E 平面BCHG ， 又因为1,EF A E ⊂平面1A EF ，且1EFA E E =，所以平面1//A EF 平面BCHG .10．(2021·江苏省镇江中学高一月考)如图，在三棱柱111ABC A B C -中，底面ABC 是正三角形，1AA ⊥平面ABC ，已知2AB =D 是11A B 的中点，E 、F 、G 分别是AC ，BC ，CD 的中点.(1)求FG 与1BB 所成角的大小； (2)求证：平面//EFG 平面11ABB A 【答案】(1)30； (2)证明见解析.【解析】(1)连接DB ，因为,G F 分别是,DC BC 的中点，所以//GF BD ， 所以异面直线FG 与1BB 所成角即为直线DB 与1BB 所成的角， 在直角1DB B中，由111,DB BB =111tan DB DBB BB ∠==, 所以130DBB ∠=.(2)由(1)知//GF BD ，BD ⊂平面11ABB A GF ⊄，平面ABB 1A 1，所以//GF 平面11ABB A ， 因为E 是AC 的中点，所以//EF AB ， 因为AB平面11ABB A ，且EF ⊄平面11ABB A ，所以//EF 平面11ABB A ，又因为EF FG F ⋂=，且,EF FG ⊂平面EFG ， 所以平面//EFG 平面11ABB A .【题组四 判断及性质定理的辨析】1．(2021·山西太原·高一期末)对于两个不同的平面α，β和三条不同的直线a ，b ，c .有以下几个命题： ①若//a b ，//b c ，则//a c ；②若//a α，//b α，则//a b ；③若//a b ，//b α，则//a α； ④若//a α，//a β，则//αβ；⑤若//a α，//αβ，则//a β. 则其中所有错误的命题是( ) A ．③④⑤ B ．②④⑤C ．②③④D ．②③④⑤【答案】D【解析】解：因为//a b ，//b c ，根据空间中直线平行的传递性，得//a c ，故①正确； 因为//a α，//b α，所以直线,a b 平行，异面，相交均有可能，故②错误； 若//a b ，//b α，则//a α或a α⊂，故③错误； 若//a α，//a β，则平面,αβ平行或相交，故④错误； 若//a α，//αβ，则//a β或a β⊂，故⑤错误. 所以错误的命题是②③④⑤. 故选：D.2 ．(2021·全国·高一课时练习)(多选)已知,a b 表示两条直线，,,αβγ表示三个不重合的平面，给出下列命题，正确的是( )A ．若,a b αγβγ==，且//a b ，则//αβB ．若,a b 相交，且都在,αβ外，//,//,//,//a b a b ααββ，则//αβC ．若//,//a b αβ，且//a b ，则//αβD ．若,//,a a b αβαβ⊂=，则//a b 【答案】BD 【解析】A ：若,a b αγβγ==，且//a b ，则,αβ可能相交、平行，错误；B ：若,a b 相交，且都在,αβ外，//,//,//,//a b a b ααββ，由面面平行的判定可得//αβ，正确；C ：若//,//a b αβ，且//a b ，则,αβ可能相交、平行，错误；D ：若,//,a a b αβαβ⊂=，由线面平行的性质定理得//a b ，正确. 故选：BD3．(2021·辽宁·大连市第一中学高一月考)已知m ，n ，p 是三条不同的直线，α，β，γ是三个不同的平面，有下列命题：①//////m nm p p n ⎧⇒⎨⎩；②若//m α，//m β，则//αβ； ③m α⊂，//n α，则//m n ；④直线//m α，直线//n α，那么//m n ； ⑤若//m α，βn//，//m n ，则//αβ；⑥若//αγ，//βγ，则//αβ． 其中正确的说法为______(填序号) 【答案】①⑥【解析】对于①，根据平行的性质有：////m n p n ⎧⎨⎩，即//m p ，故①正确；对于②，由//,//,m m αβ得//αβ或,αβ相交，故②错误； 对于③，由,//,m n αα⊂得//m n ，或,m n 异面，故③错误；对于④，由直线//m α，直线//n α，可得//m n ，m n ，异面，m n ，相交，故④错误； 对于⑤，由//,//,m n αβ//m n ，得//αβ或αβ，相交，故⑤错误； 对于⑥，若////αγβγ，，由面面平行的传递性得//αβ，故⑥正确， 故答案为：①⑥.【题组五 平行的综合运用】1．(2021·广西·玉林市育才中学高一月考).如图，正方体1111ABCD A B C D -的棱长为2， E 是棱AB 的中点， F 是侧面11AA D D 内一点，若//EF 平面11BB D D ，则EF 的长度的范围为__________.【答案】【解析】如图所示：分别取11,AD A D 的中点M ，N ，连接EM ，EN ，MN ， 因为E 为AB 的中点，所以//EM BD ，又EM ⊄平面11BB D D ，BD ⊂平面11BB D D ， 所以//EM 平面11BB D D ， 同理//MN 平面11BB D D ， 又MN EM M ⋂=，所以平面//EMN 平面11BB D D ，又F 是侧面11AA D D 内一点，且//EF 平面11BB D D ， 所以点F 的轨迹为线段MN ，故EF 的最小值为EM =最大值为EN =所以EF 的长度的范围为，故答案为：2．(2021·江苏省镇江中学高一月考)如图所示，正方体1111ABCD A B C D -棱长为3，M 、N 分别是下底面的棱11A B ，11B C 的中点，P 是上底面的棱AD 上的一点，1AP =，过P ，M 、N 的平面交上底面于PQ ，Q 在CD 上，则PQ =________.【答案】【解析】因为平面//ABCD 平面1111D C B A ， 平面ABCD ∩平面PQNM PQ =， 平面1111D C B A ∩平面PQNM MN =， 所以//MN PQ ，又因为//MN AC ， 所以//PQ AC ． 又因为1AP =，所以23PD DQ PQ AD CD AC ===，所以2233PQ AC ==⨯=故答案为： 3．(2021·安徽安庆·高一期末)在棱长为4的正方体1111ABCD A B C D -中，点P 是棱AB 的中点，过点A 作与截面1PB C 平行的截面，则所得截面的面积为____________.【答案】【解析】取CD 、A 1B 1的中点M 、N ，连结C 1M 、MA 、AN 、NC 1∵C 1N//PC ，B 1P ∥AN ，B 1P ∩CP =P ，C 1N ∩AN =N ，∴平面C 1MAN //平面PCB 1∴平面C 1MAN 就是过点A 与界面1PCB 平行的截面由图可知,平面1C MAN为菱形，且AM AN ===正方体中，1AC ==根据余弦定理，22211111cos 2?5AN NC AC ANC AN NC +-∠==-，且()10πANC ∠∈，1sin ANC ∴∠==所以截面的面积1112?sin 2S AN NC ANC =⨯∠==故答案为：4．(2021·福建南平·高一期末)如图，在棱长为2的正方体1111ABCD A B C D -中，E ，F ，G ，H 分别为11A D ，11A B ，1BB ，11B C 的中点，点P 为线段1CC 上的动点，且1(01)CPCC λλ=≤≤.(1)是否存在λ使得//HP 平面EFG ，若存在，求出λ的值并给出证明过程；若不存在，请说明理由； (2)画出平面EFG 截该正方体所得的截面，并求出此截面的面积.【答案】(1)存在，1=2λ，证明见解析；(2)画图见解析；【解析】(1)当1=2λ时，//HP 平面EFG .取11C D 中点K ，连接HK ，PK ，11B D ，则//HK 11B D ，//EF 11B D ， 如图所示：故//HK EF ，又HK ⊄平面EFG ，EF ⊂平面EFG ，//HK ∴平面EFG ，同理，//PK 平面EFG ， 又HK=PK K ，HK PK ⊂，平面HPK ，故平面//HPK 平面EFG ，HP ⊂平面HPK ，//HP ∴平面EFG ；(2)平面EFG 截正方体1111ABCD A B C D -的截面为正六边形EFGRSRT ， 如图所示：又正方体1111ABCD A B C D -的棱长为2，故正六边形EFGRSRT ，∴截面面积为：26=5．(2021·广东·珠海市第二中学高一期中)已知正方体1111ABCD A B C D -中的棱长为2，1O 是11A C 中点．(1)求证：平面11//AO D 平面1DBC ；(2)设1BB 的中点为M ，过A ､M ､1C 作一截面，交1DD 于点N ，求截面1AMC N 的面积．【答案】(1)证明见解析；(2)【解析】(1)如图，连接AC ，BD ，若AC BD O =，连接1OC ，由11//AA CC ，11AA CC =，可得四边形11AAC C 为平行四边形， ∴11//AC A C ，又11C O AO =，∴四边形11AOC O 为平行四边形，即11//AO C O ，而1AO ⊄平面1DBC ，1C O ⊂平面1DBC ， 1//AO ∴平面1DBC ，同理，11ABC D 是平行四边形，即11//AD BC ，而1AD ⊄平面1DBC ，1BC ⊂平面1DBC ， ∴1//AD 平面1DBC ，而11AO AD A ⋂=，∴平面11//AO D 平面1DBC .(2)连接AM ，1C M ，平面1AMC 与平面11AA D D 交于AN ， 由平面11//AA D D 平面11BB C C ，且平面1AMC 平面111BB C C C M =，平面1AMC 平面11AA D D AN =， 1//C M AN ∴，同理有1//AM C N ，即四边形1AMC N 为平行四边形， 在Rt ABM 与11Rt C B M 中，易知1AM C M =，即四边形1AMC N 为菱形，故N 为1DD 的中点． ∵正方体1111ABCD A B C D -的棱长为2，MN ∴1AC∴截面面积12S =⨯。

x 1 y2 z1 ． 直线与平面4x y mz 5 0 平行，则m _____ . x y2． 点 (1,0,1)到直线 的距离是______________。

3x z 03 ． 直线x 3y 5z 与平面4x 12y 20z 1 0的位置关系为 。

4． 自坐标原点指向平面： 2x 3y 6z 35 0 的单位法向量为 。

5． 平面 1 (x y 2z 2) 2 (3x 4y 2z ) 0 ，如在 z 轴上的截距为 2，则 1 : 2 ____________ 。

1．设直线 L 为 ，平面 :4x 2y z 2 0 ，则( )。

4 2 1(A ) L 平行于 (B ) L 在 上 (C ) L 垂直于 (D ) L 与 斜交 2 ． 直线与平面x y z 1的位置关系是 ( )。

(A)直线在平面内 (B)平行 (C)垂直 (D)相交但不垂直 x y z 1 0 3 ． 过点M (3， 2，1)且与直线L : 平行的直线方程是：( )。

2x y 3z 4 0(A) (B)(C) (D)4 ．过 z 轴和点(1,2，-1)的平面方程是：( )。

(A) x 2y z 6 0 (B) 2x y 0 (C) y 2z 0 (D) x z 05 ．设平面 的方程为3x 4y 5z 2 0 ，以下选项中错误的是：( )。

(A) 平面 过点(-1,0，-1)(B) 平面 的法向量为 3i 4j 5k(C) 平面 在z 轴的截距是(D) 平面 与平面 2x y 2z 2 0 垂直1．求经过点 A (3,2,1)和B (1,2,3) 且与坐标平面xOz 垂直的平面的方程。

2 ．求过点(1,2,1) 且与直线 x y z 1 0 及 x 1 y 2 z 都平行的平面方程。

x 2y z 1 0 2 1 x 2z 0 3．平面 x y z 1 0上的直线 l 通过直线 l 1 ： 与此平面的交点且与 l 1 垂y z 1 0直, 求l 的方程。

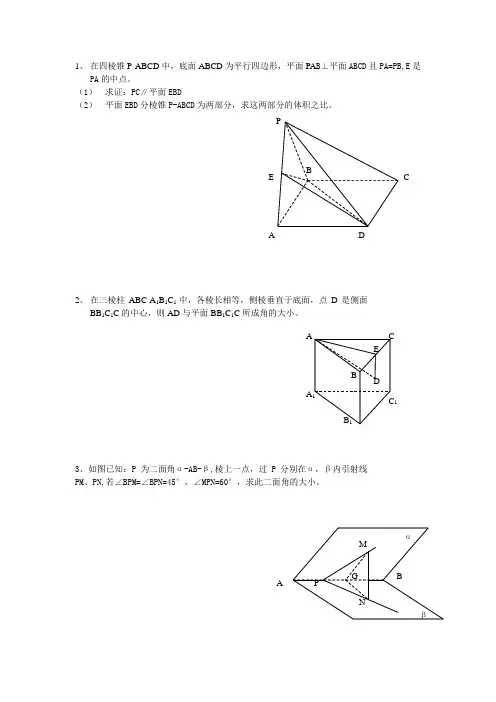
1、 在四棱锥P-ABCD 中，底面ABCD 为平行四边形，平面PA B ⊥平面ABCD 且PA=PB,E 是PA 的中点。

（1） 求证：PC ∥平面EBD（2） 平面EBD 分棱锥P-ABCD 为两部分，求这两部分的体积之比。

2、 在三棱柱ABC-A 1B 1C 1中，各棱长相等，侧棱垂直于底面，点D 是侧面BB 1C 1C 的中心，则AD 与平面BB 1C 1C 所成角的大小。

3、如图已知：P 为二面角α-AB-β,棱上一点，过P 分别在α，β内引射线PM 、PN,若∠BPM=∠BPN=45°，∠MPN=60°，求此二面角的大小。

CDA BEAA 1BB 1C 1DE A BαβPMNG CP4、 如图在四棱锥P-ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD,PA=AD=4，AB=2，以AC 中点O 为球心，AC 为直径的球面交PD 于M ，交PC 于N 。

（1） 求证：平面ABM ⊥平面PCD （2） 求直线CD 与平面ACM 所成的角 （3） 求：点N 到平面ACM 的距离5、 棱锥V-ABCD 中，ABCD 为边长为4的菱形，并且∠BAD=120°，VA=3， VA ⊥底面ABCD ，O 是AC 与BD 的交点，OE ⊥VC 于E 。

求：（1）V 到CD 的距离（2）异面直线VC 与BD 的距离 （3）点B 到平面VCD 的距离PDCBAMN OV BADCOE。

2023高考数学复习专项训练《空间中直线与平面的位置关系》一、单选题（本大题共12小题，共60分）1.（5分）设m，n为两条不同的直线，α，β为两个不同的平面，给出下列命题：①若m⊥α，m⊥β，则α//β②若m//α，m//β，则α//β③若m//α，n//α，则m//n④若m⊥α.n⊥α，则m//n上述命题中，所有真命题的序号是()A. ①④B. ②③C. ①③D. ②④2.（5分）直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，下列命题正确的是：A. l与l1，l2都不相交B. l与l1，l2都相交C. l至多与l1，l2中的一条相交D. l至少与l1，l2中的一条相交3.（5分）已知α、β是不同的平面，m、n是不同的直线，则下列命题不正确的是()A. 若m⊥α，m//n，n⊂β，则α⊥βB. 若m//α，α∩β=n，，则m//nC. 若m//n，m⊥α，则n⊥αD. 若m⊥α，m⊥β，则α//β4.（5分）已知两条直线m、n，两个平面α、β，给出下面四个命题：①m//n，m⊥α⇒n⊥α①α//β，m⊂α，n⊂β⇒m//n①m//n，m//α⇒n//α①α//β，m//n，m⊥α，⇒m⊥β其中正确命题的序号是()A. ①①B. ①①C. ①①D. ①①5.（5分）已知α，β是两个不同的平面，下列四个条件中能推出α//β的是()①存在一条直线m，m⊥α，m⊥β；②存在一个平面γ，γ⊥α，γ⊥β；③存在两条平行直线m，n，m⊂α，n⊂β，m//β，n//α；④存在两条异面直线m，n，m⊂α，n⊂β，m//β，n//α．A. ①①B. ①①C. ①①D. ①①6.（5分）棱柱的一条侧棱所在的直线与不含这条侧棱的侧面所在平面的位置关系是()A. 平行B. 相交C. 平行或相交D. 不相交7.（5分）若α，β是两个不同的平面，m，n，l是三条不同的直线，则下列命题错误的是()A. 若m⊂α，l∩α=A，且A∉m，则l与m不共面B. 若m，l是异面直线，l//α，m//α，且n⊥l，n⊥m，则n⊥αC. 若l⊂α，m⊂α，l∩m=A，l//β，m//β，则α//βD. 若l//α，m//β，α//β，则l//m8.（5分）已知平面α⊥平面β，α∩β=n，直线l⊂α，直线m⊂β，则下列说法正确的个数是()①若l⊥n，l⊥m，则l⊥β；②若l//n，则l//β；③若m⊥n，l⊥m，则m⊥α．A. 0B. 1C. 2D. 39.（5分）已知a，b为两条不同直线，α、β为两个不同平面.下列命题中正确的是()A. 若a//α，b//α，则a与b共面B. 若a⊥α，α//β，则a⊥βC. 若a⊥α，α⊥β，则a//βD. 若α//b，β//b，则α//β10.（5分）若直线l平行于平面α，则()A. α内所有直线与l平行B. 在α内不存在直线与l垂直C. α内存在唯一的直线与l平行D. α内存在无数条直线与l成60°角11.（5分）在空间中，设l是一条直线，α，β是两个不同的平面．下列结论正确的是()A. 若l//α，l//β，则α//βB. 若l⊥α，l⊥β，则α//βC. 若l//α，α//β，则l//βD. 若l//α，α⊥β，则l⊥β12.（5分）直线l⊂平面α，直线m⊄平面α，命题p：“若直线m⊥α，则m⊥l”的逆命题、否命题、逆否命题中真命题的个数为()A. 0B. 1C. 2D. 3二、填空题（本大题共5小题，共25分）13.（5分）设l，m，n是空间三条不同的直线，α，β是空间两个不重合的平面，给出下列四个命题：①若l与m异面，m//n，则l与n异面；②若l//α，α//β，则l//β；③若α⊥β，l⊥α，m⊥β，则l⊥m；④若m//α，m//n，则n//α．其中正确命题的序号有 ______ .(请将你认为正确命题的序号都填上)14.（5分）作直线a、b和平面α，则下列小组内两个事件互为对立事件的有 ______组(请填写个数).A组：“a//b”和“a⊥b”；B组：“a、b为异面直线”和“a⊥b”；C组：“a//α或a⊂α”和“a与α相交”．15.（5分）已知关于空间两条不同直线m，n，两个不同平面α，β，有下列四个命题：①若m//α且n//α，则m//n；②若m⊥β且m⊥n，则n//β；③若m⊥α且m//β，则α⊥β；④若n⊂α且m不垂直于α，则m不垂直于n.其中正确命题的序号为______．16.（5分）若α、β是两个相交平面，则在下列命题中，真命题的序号为______.(写出所有真命题的序号)①若直线m⊥α，则在平面β内，一定不存在与直线m平行的直线．②若直线m⊥α，则在平面β内，一定存在无数条直线与直线m垂直．③若直线m⊂α，则在平面β内，不一定存在与直线m垂直的直线．④若直线m⊂α，则在平面β内，一定存在与直线m垂直的直线．17.（5分）已知∠ACB=90°，P为平面ABC外一点，PC=2，点P到∠ACB两边AC，BC的距离均为√3，那么P到平面ABC的距离为________．三、解答题（本大题共6小题，共72分）18.（12分）如图，四棱锥P−ABCD中，AD//BC，AB=BC=1AD，E，F，H分别为线段AD，PC，CD的中点，AC2与BE交于O点，G是线段OF上一点．(1)求证：AP//平面BEF；(2)求证：GH//平面PAD.19.（12分）用符号语表示图中点、直线、平面的位置关系.20.（12分）如图，在正三棱柱ABC−A1B1C1中，AB=3，AA1=4，M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为√29，设这条最短路线与CC1的交点为N，求：(I)该三棱柱的侧面展开图的对角线长(II)PC和NC的长(III)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)21.（12分）如图，正方体ABCD−A1B1C1D1中，M，N分别是AB，A1D1的中点．判断直线MN与平面BB1D1D的位置关系，并说明理由．22.（12分）如图，在棱长为a的正方体ABCD−A1B1C1D1中，点E是棱D1D的中点，点F在棱B1B上，且满足B1F=2BF。

数学 空间点、直线平面之间的位置关系[基础题组练]1．已知异面直线a ，b 分别在平面α，β内，且α∩β＝c ，那么直线c 一定( ) A ．与a ，b 都相交B ．只能与a ，b 中的一条相交C ．至少与a ，b 中的一条相交D ．与a ，b 都平行2．已知空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是( ) A ．空间四边形 B ．矩形 C ．菱形D ．正方形3．已知直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 4．(2019·广州市高中综合测试(一))在四面体ABCD 中，E ，F 分别为AD ，BC 的中点，AB ＝CD ，AB ⊥CD ，则异面直线EF 与AB 所成角的大小为( )A.π6B.π4C.π3D.π25．已知棱长为a 的正方体ABCD ­A ′B ′C ′D ′中，M ，N 分别为CD ，AD 的中点，则MN 与A ′C ′的位置关系是_________．6．给出下列四个命题：①平面外的一条直线与这个平面最多有一个公共点；②若平面α内的一条直线a 与平面β内的一条直线b 相交，则α与β相交； ③若一条直线和两条平行线都相交，则这三条直线共面； ④若三条直线两两相交，则这三条直线共面． 其中真命题的序号是________．7.如图，在正方体ABCD ­A 1B 1C 1D 1中，O 为正方形ABCD 的中心，H 为直线B 1D 与平面ACD 1的交点．求证：D 1、H 、O 三点共线．8．在正方体ABCD ­A 1B 1C 1D 1中， (1)求AC 与A 1D 所成角的大小；(2)若E ，F 分别为AB ，AD 的中点，求A 1C 1与EF 所成角的大小．1．如图所示，平面α∩平面β＝l ，A ∈α，B ∈α，AB ∩l ＝D ，C ∈β，C ∉l ，则平面ABC 与平面β的交线是( )A ．直线ACB ．直线ABC ．直线CD D ．直线BC 2．在正三棱柱ABC ­A 1B 1C 1中，|AB |＝2|BB 1|，则AB 1与BC 1所成角的大小为( )A.π6B.π3C.5π12D.π23.(2019·长沙模拟)如图，在三棱柱ABC ­A ′B ′C ′中，点E ，F ，H ，K 分别为AC ′，CB ′，A ′B ′，B ′C ′的中点，G 为△ABC 的重心．从K ，H ，G ，B ′四点中取一点作为P ，使得该棱柱恰有2条棱与平面PEF 平行，则P 为________．4．如图，已知圆柱的轴截面ABB 1A 1是正方形，C 是圆柱下底面弧AB 的中点，C 1是圆柱上底面弧A 1B 1的中点，那么异面直线AC 1与BC 所成角的正切值为________．5.如图所示，A 是△BCD 所在平面外的一点，E ，F 分别是BC ，AD 的中点．(1)求证：直线EF 与BD 是异面直线；(2)若AC ⊥BD ，AC ＝BD ，求EF 与BD 所成的角．6.(综合型)如图，E ，F ，G ，H 分别是空间四边形ABCD 各边上的点，且AE ∶EB ＝AH ∶HD ＝m ，CF ∶FB ＝CG ∶GD ＝n .(1)证明：E ，F ，G ，H 四点共面；(2)m ，n 满足什么条件时，四边形EFGH 是平行四边形？ (3)在(2)的条件下，若AC ⊥BD ，试证明：EG ＝FH .【参考答案】1．已知异面直线a ，b 分别在平面α，β内，且α∩β＝c ，那么直线c 一定( ) A ．与a ，b 都相交B ．只能与a ，b 中的一条相交C ．至少与a ，b 中的一条相交D ．与a ，b 都平行解析：选C.若c 与a ，b 都不相交，则c 与a ，b 都平行，根据公理4，知a ∥b ，与a ，b 异面矛盾．2．已知空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是( ) A ．空间四边形 B ．矩形 C ．菱形 D ．正方形解析：选B.如图所示，易证四边形EFGH 为平行四边形． 因为E ，F 分别为AB ，BC 的中点， 所以EF ∥AC . 又FG ∥BD ，所以∠EFG 或其补角为AC 与BD 所成的角． 而AC 与BD 所成的角为90°，所以∠EFG ＝90°，故四边形EFGH 为矩形．3．已知直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 解析：选A.若直线a ，b 相交，设交点为P ，则P ∈a ，P ∈b .又a ⊂α，b ⊂β，所以P ∈α，P ∈β，故α，β相交．反之，若α，β相交，则a ，b 可能相交，也可能异面或平行．故“直线a 和直线b 相交”是“平面α和平面β相交”的充分不必要条件．4．(2019·广州市高中综合测试(一))在四面体ABCD 中，E ，F 分别为AD ，BC 的中点，AB ＝CD ，AB ⊥CD ，则异面直线EF 与AB 所成角的大小为( )A.π6B.π4C.π3D.π2解析：选B.取BD 的中点O ，连接OE ，OF ，因为E ，F 分别为AD ，BC 的中点，AB ＝CD ，所以EO ∥AB ，OF ∥CD ，且EO ＝OF ＝12CD ，又AB ⊥CD ，所以EO ⊥OF ，∠OEF 为异面直线EF 与AB 所成的角，由△EOF 为等腰直角三角形，可得∠OEF ＝π4，故选B.5．已知棱长为a 的正方体ABCD ­A ′B ′C ′D ′中，M ，N 分别为CD ，AD 的中点，则MN 与A ′C ′的位置关系是________________________________________________________．解析：如图，由题意可知MN ∥AC .又因为AC ∥A ′C ′， 所以MN ∥A ′C ′.答案：平行6．给出下列四个命题：①平面外的一条直线与这个平面最多有一个公共点；②若平面α内的一条直线a 与平面β内的一条直线b 相交，则α与β相交； ③若一条直线和两条平行线都相交，则这三条直线共面； ④若三条直线两两相交，则这三条直线共面． 其中真命题的序号是________．解析：①正确，因为直线在平面外即直线与平面相交或直线平行于平面，所以最多有一个公共点．②正确，a ，b 有交点，则两平面有公共点，则两平面相交．③正确，两平行直线可确定一个平面，又直线与两平行直线的两交点在这两平行直线上，所以过这两交点的直线也在平面内，即三线共面．④错误，这三条直线可以交于同一点，但不在同一平面内．答案：①②③7.如图，在正方体ABCD ­A 1B 1C 1D 1中，O 为正方形ABCD 的中心，H 为直线B 1D 与平面ACD 1的交点．求证：D 1、H 、O 三点共线．证明：如图，连接BD ，B 1D 1， 则BD ∩AC ＝O ， 因为BB 1綊DD 1，所以四边形BB 1D 1D 为平行四边形， 又H ∈B 1D ， B 1D ⊂平面BB 1D 1D ， 则H ∈平面BB 1D 1D ，因为平面ACD 1∩平面BB 1D 1D ＝OD 1， 所以H ∈OD 1.即D 1、H 、O 三点共线． 8．在正方体ABCD ­A 1B 1C 1D 1中， (1)求AC 与A 1D 所成角的大小；(2)若E ，F 分别为AB ，AD 的中点，求A 1C 1与EF 所成角的大小． 解：(1)如图，连接B 1C ，AB 1，由ABCD ­A 1B 1C 1D 1是正方体，易知A 1D ∥B 1C ，从而B 1C 与AC 所成的角就是AC 与A 1D 所成的角．因为AB 1＝AC ＝B 1C ， 所以∠B 1CA ＝60°.即A 1D 与AC 所成的角为60°.(2)连接BD ，在正方体ABCD ­A 1B 1C 1D 1中，AC ⊥BD ，AC ∥A 1C 1. 因为E ，F 分别为AB ，AD 的中点， 所以EF ∥BD ，所以EF ⊥AC . 所以EF ⊥A 1C 1.即A 1C 1与EF 所成的角为90°.[综合题组练]1．如图所示，平面α∩平面β＝l ，A ∈α，B ∈α，AB ∩l ＝D ，C ∈β，C ∉l ，则平面ABC 与平面β的交线是( )A ．直线ACB ．直线ABC ．直线CDD ．直线BC解析：选C.由题意知，D ∈l ，l ⊂β，所以D ∈β， 又因为D ∈AB ，所以D ∈平面ABC ， 所以点D 在平面ABC 与平面β的交线上． 又因为C ∈平面ABC ，C ∈β，所以点C 在平面β与平面ABC 的交线上， 所以平面ABC ∩平面β＝CD .2．在正三棱柱ABC ­A 1B 1C 1中，|AB |＝2|BB 1|，则AB 1与BC 1所成角的大小为( ) A.π6 B.π3 C.5π12D.π2解析：选D.将正三棱柱ABC ­A 1B 1C 1补为四棱柱ABCD ­A 1B 1C 1D 1，连接C 1D ，BD ，则C 1D ∥B 1A ，∠BC 1D 为所求角或其补角．设|BB 1|＝2，则|BC |＝|CD |＝2，∠BCD ＝120°，|BD |＝23，又因为|BC 1|＝|C 1D |＝6，所以∠BC 1D ＝π2.3.(2019·长沙模拟)如图，在三棱柱ABC ­A ′B ′C ′中，点E ，F ，H ，K 分别为AC ′，CB ′，A ′B ′，B ′C ′的中点，G 为△ABC 的重心．从K ，H ，G ，B ′四点中取一点作为P ，使得该棱柱恰有2条棱与平面PEF 平行，则P 为________．解析：取A ′C ′的中点M ，连接EM ，MK ，KF ，EF ，则EM 綊12CC ′綊KF ，得四边形EFKM 为平行四边形，若取点K 为P ，则AA ′∥BB ′∥CC ′∥PF ，故与平面PEF 平行的棱超过2条；因为HB ′∥MK ，MK ∥EF ，所以HB ′∥EF ，若取点H 或B ′为P ，则平面PEF 与平面EFB ′A ′为同一平面，与平面EFB ′A ′平行的棱只有AB ，不符合题意；连接BC ′，则EF ∥A ′B ′∥AB ，若取点G 为P ，则AB ，A ′B ′与平面PEF 平行．答案：G4．如图，已知圆柱的轴截面ABB 1A 1是正方形，C 是圆柱下底面弧AB 的中点，C 1是圆柱上底面弧A 1B 1的中点，那么异面直线AC 1与BC 所成角的正切值为________．解析：取圆柱下底面弧AB 的另一中点D ，连接C 1D ，AD ， 因为C 是圆柱下底面弧AB 的中点， 所以AD ∥BC ，所以直线AC 1与AD 所成角等于异面直线AC 1与BC 所成角，因为C 1是圆柱上底面弧A 1B 1的中点，所以C 1D ⊥圆柱下底面，所以C 1D ⊥AD ， 因为圆柱的轴截面ABB 1A 1是正方形， 所以C 1D ＝2AD ，所以直线AC 1与AD 所成角的正切值为2， 所以异面直线AC 1与BC 所成角的正切值为 2.答案：25.如图所示，A 是△BCD 所在平面外的一点，E ，F 分别是BC ，AD 的中点．(1)求证：直线EF 与BD 是异面直线；(2)若AC ⊥BD ，AC ＝BD ，求EF 与BD 所成的角．解：(1)证明：假设EF 与BD 不是异面直线，则EF 与BD 共面，从而DF 与BE 共面，即AD 与BC 共面，所以A ，B ，C ，D 在同一平面内，这与A 是△BCD 所在平面外的一点相矛盾．故直线EF 与BD 是异面直线．(2)取CD 的中点G ，连接EG ，FG ，则AC ∥FG ，EG ∥BD ，所以相交直线EF 与EG 所成的角，即为异面直线EF 与BD 所成的角．又因为AC ⊥BD ，则FG ⊥EG .在Rt △EGF 中，由EG ＝FG ＝12AC ，求得∠FEG ＝45°，即异面直线EF 与BD 所成的角为45°.6.(综合型)如图，E ，F ，G ，H 分别是空间四边形ABCD 各边上的点，且AE ∶EB ＝AH ∶HD ＝m ，CF ∶FB ＝CG ∶GD ＝n .(1)证明：E ，F ，G ，H 四点共面；(2)m ，n 满足什么条件时，四边形EFGH 是平行四边形？ (3)在(2)的条件下，若AC ⊥BD ，试证明：EG ＝FH . 解：(1)证明：因为AE ∶EB ＝AH ∶HD ，所以EH ∥BD . 又CF ∶FB ＝CG ∶GD ，所以FG ∥BD .所以EH ∥FG . 所以E ，F ，G ，H 四点共面．(2)当EH ∥FG ，且EH ＝FG 时，四边形EFGH 为平行四边形． 因为EH BD ＝AE AE ＋EB ＝m m ＋1，所以EH ＝m m ＋1BD .同理可得FG ＝n n ＋1BD ，由EH ＝FG ，得m ＝n .故当m ＝n 时，四边形EFGH 为平行四边形．(3)证明：当m ＝n 时，AE ∶EB ＝CF ∶FB ，所以EF ∥AC ，又EH ∥BD ，所以∠FEH 是AC 与BD 所成的角(或其补角)，因为AC ⊥BD ，所以∠FEH ＝90°，从而平行四边形EFGH 为矩形，所以EG ＝FH .。

立体几何题型与方法(理科)1．平面平面的根本性质：掌握三个公理及推论，会说明共点、共线、共面问题。

〔1〕.证明点共线的问题，一般转化为证明这些点是某两个平面的公共点〔依据：由点在线上，线在面 ，推出点在面〕， 这样可根据公理2证明这些点都在这两个平面的公共直线上。

〔2〕.证明共点问题，一般是先证明两条直线交于一点，再证明这点在第三条直线上，而这一点是两个平面的公共点，这第三条直线是这两个平面的交线。

〔3〕.证共面问题一般先根据一局部条件确定一个平面，然后再证明其余的也在这个平面，或者用同一法证明两平面重合 2. 空间直线.〔1〕. 空间直线位置关系三种：相交、平行、异面. 相交直线：共面有且仅有一个公共点；平行直线：共面没有公共点；异面直线：不同在任一平面，无公共点[注]：①两条异面直线在同一平面射影一定是相交的两条直线.〔×〕〔也可能两条直线平行，也可能是点和直线等〕②直线在平面外，指的位置关系是平行或相交③假设直线a 、b 异面，a 平行于平面α，b 与α的关系是相交、平行、在平面α. ④两条平行线在同一平面的射影图形是一条直线或两条平行线或两点.⑤在平面射影是直线的图形一定是直线.〔×〕〔射影不一定只有直线，也可以是其他图形〕⑥在同一平面的射影长相等，那么斜线长相等.〔×〕〔并非是从平面外一点．．向这个平面所引的垂线段和斜线段〕⑦b a ,是夹在两平行平面间的线段，假设b a =，那么b a ,的位置关系为相交或平行或异面.⑧异面直线判定定理：过平面外一点与平面一点的直线和平面不经过该点的直线是异面直线.〔不在任何一个平面的两条直线〕〔2〕. 平行公理：平行于同一条直线的两条直线互相平行. 等角定理：如果一个角的两边和另一个角的两边分别平行并且方向一样，那么这两个角相等〔如右图〕.〔直线与直线所成角]90,0[︒︒∈θ〕〔向量与向量所成角])180,0[ ∈θ推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角〔或直角〕相等.〔3〕. 两异面直线的距离：公垂线段的长度.空间两条直线垂直的情况：相交〔共面〕垂直和异面垂直.[注]：21,l l 是异面直线，那么过21,l l 外一点P ，过点P 且与21,l l 都平行平面有一个或没有，但与21,l l 距离相等的点在同一平面. 〔1L 或2L 在这个做出的平面不能叫1L 与2L 平行的平面〕 3. 直线与平面平行、直线与平面垂直.〔1〕. 空间直线与平面位置分三种：相交、平行、在平面.〔2〕. 直线与平面平行判定定理：如果平面外一条直线和这个平面一条直线平行，那么这条直线和这个平面平行.〔“线线平行⇒线面平行〞〕[注]：①直线a 与平面α一条直线平行，那么a ∥α. 〔×〕〔平面外一条直线〕 ②直线a 与平面α一条直线相交，那么a 与平面α相交. 〔×〕〔平面外一条直线〕③假设直线a 与平面α平行，那么α必存在无数条直线与a 平行. 〔√〕〔不是任意一条直线，可利用平行的传递性证之〕④两条平行线中一条平行于一个平面，那么另一条也平行于这个平面. 〔×〕〔可能在此平面〕 ⑤平行于同一个平面的两直线平行.〔×〕〔两直线可能相交或者异面〕 ⑥直线l 与平面α、β所成角相等，那么α∥β.〔×〕〔α、β可能相交〕〔3〕. 直线和平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.〔“线面平行⇒线线平行〞〕〔4〕. 直线与平面垂直是指直线与平面任何一条直线垂直，过一点有且只有一条直线和一个平面垂直，过一点有且只有一个平面和一条直线垂直.● 假设PA ⊥α，a ⊥AO ，得a ⊥PO 〔三垂线定理〕， ● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一：如果一条直线和一个平面的两条相交直线都垂直，那么这两条直线垂直于这个平面.〔“线线垂直⇒线面垂直〞〕直线与平面垂直的判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.性质：如果两条直线同垂直于一个平面，那么这两条直线平行.〔5〕.a.垂线段和斜线段长定理：从平面外一点．．向这个平面所引的垂线段和斜线段中，①射影相等的两条斜线段相等，射影较长的斜线段较长；②相等的斜线段的射影相等，较长的斜线段射影较长；③垂线段比任何一条斜线段短.[注]：垂线在平面的射影为一个点. [一条直线在平面的射影是一条直线.〔×〕]b.射影定理推论：如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面的射影在这个角的平分线上。

2．1空间点、直线、平面之间的位置关系一、选择题1．下列命题正确的是………………………………………………（ ） A ．三点确定一个平面 B ．经过一条直线和一个点确定一个平面 C ．四边形确定一个平面 D ．两条相交直线确定一个平面2．若直线a 不平行于平面α，且α⊄a ，则下列结论成立的是（ ） A ．α内的所有直线与a 异面 B ．α内不存在与a 平行的直线 C ．α内存在唯一的直线与a 平行 D ．α内的直线与a 都相交3．平行于同一平面的两条直线的位置关系………………………（ ） A ．平行 B ．相交 C ．异面 D ．平行、相交或异面4．正方体''''D C B A ABCD -中，AB 的中点为M ，'DD 的中点为N ，异面直线M B '与CN 所成的角是…………………………………………………（ ） A ．0 B ．45 C ．60 D ．905．平面α与平面β平行的条件可以是…………………………（ ） A ．α内有无穷多条直线都与β平行B ．直线βα//,//a a 且直线a 不在α内，也不在β内C ．直线α⊂a ，直线β⊂b 且β//a ，α//bD ．α内的任何直线都与β平行6．下列命题中，错误的是…………………………………………（ ） A ． 平行于同一条直线的两个平面平行 B ． 平行于同一个平面的两个平面平行 C ． 一个平面与两个平行平面相交，交线平行D ． 一条直线与两个平行平面中的一个相交，则必与另一个相交 7．已知两个平面垂直，下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线 ②一个平面内的已知直线必垂直于另一个平面的无数条直线 ③一个平面内的任一条直线必垂直于另一个平面④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面 其中正确的个数是…………………………………………（ ） A ．3 B ．2 C ．1 D ．08．下列命题中错误的是……………………………………（ ） A ． 如果平面βα⊥，那么平面α内所有直线都垂直于平面β B ． 如果平面βα⊥，那么平面α一定存在直线平行于平面βC ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD ．如果平面γα⊥，γβ⊥，l =⋂βα，那么γ⊥l9．直线//a 平面α，α∈P ，那么过点P 且平行于α的直线…………（ ） A ． 只有一条，不在平面α内B ．有无数条，不一定在α内C ．只有一条，且在平面α内D ．有无数条，一定在α内10．如图是正方体的平面展开图，则在这个正方体中 ①BM 与ED 平行 ②CN 与BE 异面 ③CN 与BM 成60 ④DM 与BN 垂直以上四个命题中，正确命题的序号是（ ）A ．①②③B ．②④C ．③④D ．②③④二、填空题1． 若一条直线与两个平行平面中的一个平面平行，则这条直线与另一平面的位置关系是__________________2． 正方体''''D C B A ABCD -中，AC 与'BD 所成角_______________3． 平面内一点与平面外一点连线和这个平面内直线的关系是_______________4． 已知直线b a ,和平面α,且α⊥⊥a b a ,,则b 与α的位置关系是______________ 三、解答题1． 已知长方体''''D C B A ABCD -中，32=AB ，32=AD ，2'=AA ， 求：（1）BC 与''C A 所成的角是多少？ （2）'AA 与'BC 所成的角是多少？2． 正方体''''D C B A ABCD -中，求证：平面''D AB //平面BD C '。