静电场的环路定理

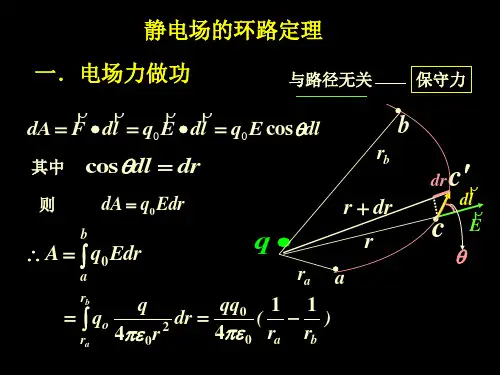
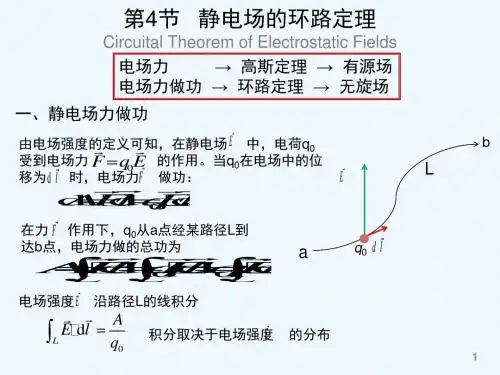
静电场的环路定理表达式
静电场的环路定理公式：D=pL/S。

在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率。

这个结论称为安培环路定理。

静电场，指的是观察者与电荷量不随时间生变化的电荷相对静止时所观察到的电场。

静电场性质
根据静电场的高斯定理
静电场的电场线起于正电荷或无穷远，终止于负电荷或无穷远，故静电场是有源场。

从安培环路定理来说它是一个无旋场。

根据环量定理，静电场中环量恒等于零，表明静电场中沿任意闭合路径移动电荷，电场力所做的功都为零，因此静电场是保守场。

根据库仑定律，两个点电荷之间的作用力跟它们的电荷量的乘积成正比，和它们距离的平方成反比，作用力的方向在它们的连线上，即F=(kq1q2)/r2；，其中q1、q2为两电荷的电荷量(不计正负性)、k为静电力常量，约为9.0e+09(N·m2)/(C2；)，r为两电荷中心点连线的距离。

注意，点电荷是不考虑其尺寸、形状和电荷分布情况的带电体。

是实际带电体的理想化模型。

当带电体的距离比它们的大小大得多时，带电体的形状和大小可以忽略不计的点电荷。

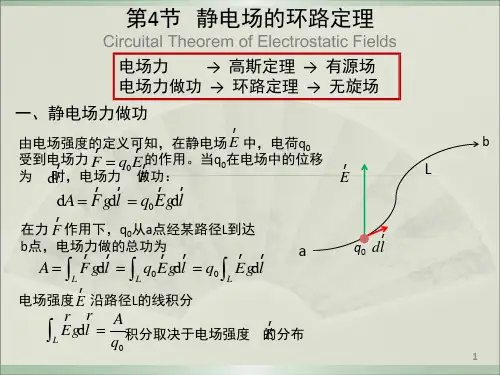
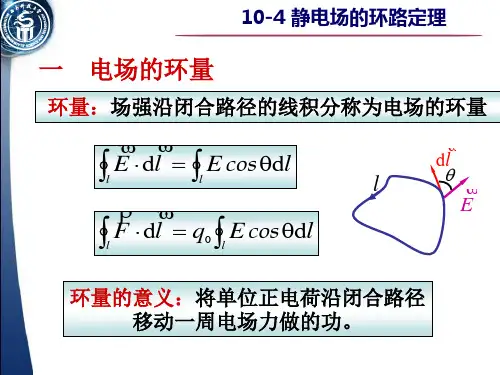
静电场的环路定理的数学表示式为
静电场的环路定理是物理学中一个重要的定理，它描述了电场的流动规律。

它
的数学表示式为：
∮E·dl=0
其中，E表示电场，dl表示电场的矢量，∮表示积分。

静电场的环路定理指出，在一个闭合的环路上，电场的矢量积分为零。

这意味着，在一个闭合的环路上，电场的矢量总和为零，也就是说，电场的流动是不变的，不会有任何变化。

静电场的环路定理可以用来解释电场的流动规律，也可以用来计算电场的大小。

它可以用来解决电场的问题，也可以用来计算电场的分布情况。

静电场的环路定理是物理学中一个重要的定理，它描述了电场的流动规律，并
且可以用来解决电场的问题。

它的数学表示式为∮E·dl=0，其中，E表示电场，
dl表示电场的矢量，∮表示积分。

它指出，在一个闭合的环路上，电场的矢量积
分为零，也就是说，电场的流动是不变的，不会有任何变化。

它可以用来解释电场的流动规律，也可以用来计算电场的大小，从而解决电场的问题。

静电场的环路定理数学表达式静电场是一个有趣的物理现象，它作用于每一个电子粒子。

静电场的研究可以追溯到古代希腊哲学家Aristotle，他认为宇宙中的物体有内在的“力量”，他将其称为“力学”。

随后雅克•笛卡尔和伽利略更进一步地探讨了这种现象，并将其称为“电力”。

然而，直到二十世纪初，电磁学家Maxwell提出了静电场的最终形式，即描述电磁场的四个基本方程，用来表示静电场的上下文，电流和电压的关系，以及电磁波在介质中的行为。

最重要的是，Maxwell提出了一项重要的理论，即电磁波可通过任意曲线而不会破坏传播，这被称为Maxwell环。

环路定理（又名Maxwell环路定理或Maxwell-Faraday方程）是一种电磁学的数学运算，它旨在确定电磁场的变化要素和电流的交互关系。

它表明：对于任意给定的点，如果其周围存在一个环形变化的电流，则电场的变化率将等于电流的变化率。

这就是说，随着电流的增加，电场也会随之增加，反之亦然。

数学上，Maxwell环路定理可以表述为：∮ E·dl = −dφ/dt这里，E表示无负载电场，dl 表示从圆环中任意一点到另一点的理想导线段，φ 表示以安培为单位的电流场。

Maxwell环路定理的形式表明，如果电流在某个特定的时间尺度内发生变化，则电磁场也会发生变化。

maxwe11环定理也表明，如果存在一个环形电路，则它会产生一个电磁场，这就是伽利略发现的现象。

有时这种电磁场也会由于算术变换而被称为电动势场。

Maxwell环路定理对研究静电场、电动势场以及电气工程具有重要意义。

它是用来解释很多电磁现象的基础，比如能量传输、电磁辐射、接地效应、电场色散等。

通过Maxwell环路定理，可以系统地推导电磁学的数学关系和定律。

Maxwell环路定理对静电场的深入理解也至关重要，其中包括球形、面形、应力线电路等多种静电场模型，它们研究无刷电机、电动车和飞机等设备。