当前位置：文档之家 › 5-4静电场的环路定理

5-4静电场的环路定理

  • 格式：ppt
  • 大小：871.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

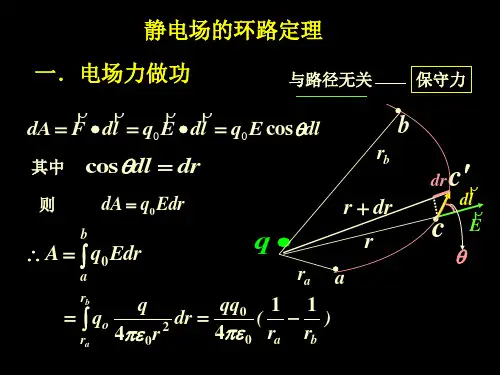
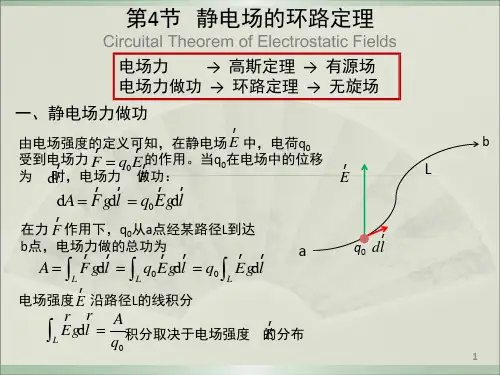
静电场的环路定理 电势

静电场的环路定理 电势

(8-22)
静电场的环路定理 电势
式中，Uab为静电场中任意两点 a、b间的电势差，也称为电压.式（ 8-22）表明，静电场中a、b两点的 电势之差等于把单位正电荷从a点沿 任意路径移到b点电场力所做的功.电 势差是绝对的.
静电场的环路定理 电势
四、 电势的计算 1. 点电荷电场的电势
设在真空中有一点电荷q，其周围的电场分布为
(8- 21)
式（8-21
a的电势在数值上等
于把单位正电荷从a点沿任意路径移到无限远电场力所做的功.在
许多实际问题中，也常选地球为电势零点.
电势是标量，在国际单位制中，电势的单位为伏特（V）.
静电场的环路定理 电势
2. 电势差
从电场力做功的角度引入电势能的概念，由式(8-19) 和式(8-20)可以看出，电势能Wa不仅与a点的电场性质有 关，还与试验电荷q0有关，因而不能用来描述电场中某场 点的性质.但是，人们发现电势能与试验电荷q0的比值与试 验电荷q0无关，仅与a点电场的性质有关.因此，用电势描 述电场的能量特征.a、b两点的电势分别用Va、Vb表示.由 式（8-18），定义
dW=F·dl=q0E·dl=q0Edlcosθ
静电场的环路定理 电势
式中，θ为E与dl的夹角.由图8-20可以看出，元位移dl在电场力 方向的投影为dlcosθ=dr，则元功可写成
静电场的环路定理 电势
既然每个点电荷的电场力对q0所做 的功都与路径无关，那么它们的代数和 也必然与路径无关.由此可以得到以下结 论：在任意带电体的电场中，电场力对 试验电荷q0所做的功只与试验电荷q0及 其始末位置有关，而与路径无关.
静电场的环路定理 电势
2. 电势叠加原理
设场源电荷是由分布在有限区域内的点电荷系q1、q2、q3、 …、qn组成，根据场强叠加原理，任一点P处的场强等于各个点电 荷在该点产生场强的矢量和，即
静电场的环路定理

静电场的环路定理

静电场的环路定理物理学第五版一、静电场力所做的功0d d A q E l=⋅l rrεqq d ˆπ4200⋅=020d d 4πqq A r εr= 点电荷的电场qq Ar ABBr Errˆl d θrd r θl l rd cos d d ˆ==⋅物理学第五版20d 4πBAr r qq r A εr=⎰)11(π400BA r r εqq -=结论: A 仅与q 0的始末位置有关，与路径无关20d d 4πqq A r εr=qq Ar ABBr Errˆl d θrd物理学第五版任意带电体的电场∑=iiE E 0d lA q E l =⋅⎰⎰∑⋅=li ilE qd 0结论：静电场力做功，与路径无关。

静电场力是保守力。

（点电荷的组合）++=+⋅+⋅=⎰⎰212010A A l d E q l d E q baba物理学第五版二、静电场的环路定理⎰⎰⋅=⋅ADCABCl E q l E qd d 000)d d (0=⋅+⋅⎰⎰CDAABCl E l E qd =⋅⎰ll E静电场是保守场结论：沿闭合路径一周，电场力作功为零.EABCD物理学第五版静电场的环流定理反映了静电场的一个重要性质。

它说明静电场是保守场（无旋场），可以引入势的概念，所以也叫势场。

根据斯托克斯公式s d E l d E ls⋅⨯∇=⋅⎰⎰)(0=⨯∇E静电场的旋度为零，静电场是无旋场物理学第五版例：用环流定理证明“静电场电力线不会闭合”。

证：用反证法证明：先假设电力线形成闭合线，则以此闭合线为路径应用环流定理El⎰⎰⎰>==⋅lEdl Edl l d E 0cos 0与 ⎰=⋅ll d E 0相矛盾说明：假设不正确，静电场的电力线不会闭合物理学第五版例：证明非无限大平行板电容器电力线不可能只分布内部。

带电平行板电容器的电场线+ + + + + + + + + + + + +- - - - - - - - - - - - -物理学第五版+ + + + + + + + + + + + +- - - - - - - - - - - - - 证：用反证法，假设外部 0=E 如图作一闭合回路 ⎰=⋅ll d E⎰⎰⎰⎰⋅+⋅+⋅+⋅DACD AB BC l d E l d E l d E l d E EL =与 ⎰=⋅l l d E 0相矛盾，A B CD说明：假设不正确。

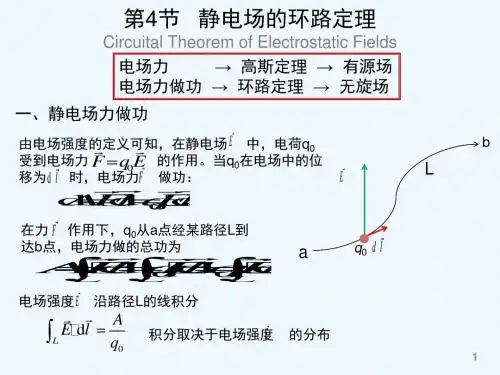
静电场的环路定理

静电场的环路定理


例3、求均匀带电球面电场中电势的分布，已知 ，q 、求均匀带电球面电场中电势的分布，已知R 微元法) 微元法 解: 方法一 叠加法 (微元法
dq = σdS = σ 2πR2 sinθdθ π 任一圆环 dS = 2 RsinθRdθ
dq 1 σ 2πR sinθdθ du = = 4πε0l 4πε0 l
B A
1 1 dr = ( − ) 2 4πε0r 4πε0 RA RB RA
q
q
2.如图已知 、-q、R 如图已知+q 如图已知 、 移至c ①求单位正电荷沿odc 移至 ，电场力所作的功 求单位正电荷沿
d q −q A = uo − uc = 0−( ) + oc 4πε0 3R 4πε0R a b c q 0 +q −q = 6 0R πε R R R
方法二
定义法
∞ P
q 4 0r2 πε
由高斯定理求出场强分布 E =
r>R r<R
r r 由定义 u = ∫ E • dl
r<R R r r ∞r r u = ∫ E • dl + ∫ E • dl
r R
0
r>R
R
dθ
O∞θຫໍສະໝຸດ lP= 0+ ∫
∞
q
4 0r πε R q = 4 0R πε
dr 2
u= ∫
r r uP = ∫ E • dl
P
∞
♠由点电荷电势公式，利用电势叠加原理计算 由点电荷电势公式，
求电偶极子电场中任一点P的电势 例1 、求电偶极子电场中任一点 的电势
Y
由叠加原理
q(r2 − r1) uP = u1 + u2 = − = 4πε0r1 4πε0r2 4πε0r1r2 q q
静电场的环路定理静电场力的功电势能

静电场的环路定理静电场力的功电势能


静电场力的功
02
电场力的定义
电场力是电荷在电场中受到的 力，其大小和方向由电场强度
和电荷的乘积决定。
电场力的大小为 F=qE，其 中 F 是电场力，q 是电荷量，
E 是电场强度。
电场力的方向与电场强度的方 向相同，即由正电荷指向负电
荷。
电场力做功的计算
电场力做功可以通过积分计算，即 W=∫F·dr，其中 W 是电场力做的功， F 是电场力，dr 是位移矢量。
在匀强电场中，电场力做功可以通过 W=qEd计算，其中 W 是电场力做 的功，q 是电荷量，E 是电场强度，d 是位移。
在非匀强电场中，需要计算电场力在路径上的积分来计算电场力做的功。
电场力做功的特点
01
电场力做功与路径无关，只与初末位置的电势差有关。
02
电场力做功是标量，没有方向。
03
电场力做功的过程是能量转化的过程，可以转化为其他形式 的能量。
电势能
03
电势能的定义
电势能是指电荷在电场中由于位置差 异而具有的能量。
电势能是电荷与电场共同具有的能量， 其大小由电场强度和电荷量共同决定。
电势能是相对的，与零电势点的选择 有关。
电势能的变化规律
1
电场力做功与路径无关，只与初末位置有关。
2
电场力做正功，电势能减少；电场力做负功，电 势能增加。
3
静电力做功与电荷的运动路径无关，只与初末位 置有关。
电势能与电场力的关系
01
电场力做功等于电势能的减少量。
02
电势能的变化量等于电场力做的功。
03 电势能与电场力做功的关系是能量守恒定律在静 电场中的具体表现。
THANKS.
静电场的环路定理、静 电场力的功、电势能
静电场的环路定理

静电场的环路定理






q
j
V V V 1 2 k q q q 1 2 n 4 r r 4 r 0 1 4 0 2 0 n
q i
电势叠加原理
V V P i r 0 i i i 4
任意带电体场中的电势
VP q
4 0r
dq
a b
即：a、b两点的电势差 = A/q0
将单位正电荷 从ab电场力作的功 与路径无关
6
例: 已知真空中两金属圆筒电极间电压为U ，半径分别为 R1、 R2 。 求：负极上静止电子到正极时的速度？ 解：由电势差的定义可得
A q ( V V )
( e)( U )
R
R
2
1
F
c
dl
q0
dr
b
r +dr
r
a
rb
+
积分
1 1 q q q q 0 0 A d r 2 a4 r 4 r 0 0 a r b
b
ra
q
——点电荷的电场力作功 只与被移动电荷距离场源电荷的距离相关 与路径无关
2
2.在点电荷系的电场中(或连续带电体的电场)

结论
b b b A q E d l q E d l q E d l 0 1 0 2 0 n a a a



电场强度的线积分与路径无关
电场力是保守力，静电场是保守力场。
3
二、环路定理
在任意电场中, 将q0从a
b L2 经L1
经L2
b电场力作功：
A q E d l 0 L
04静电场的环路定理 电势

04静电场的环路定理 电势

R
1
•II区：球壳外电势
rR
U2

r
1 E2 dl r E 2 dr r
q q dr 2 4 0 r 4 0 r
Fan
I区：球面内
r R , E1 0
1
U1
q 4 0 R
q q II区：球面外 r R , E 2 4 0 r 2 U 2 4 0 r
U 4
i i
r
（2）连续带电体：将带电体分割成无限多个电荷元， 将每个电荷元看成点电荷，根据点电荷电势公式求电 荷元的电势，迭加归结于积分。
U dU
dq 4 0 r
注意电荷元的选取！
Fan
特别注意：
点势法的使用，必须是以无穷远处为电势零点为前提 条件。
up
q 40 rp
uab
b
a
E dl
Aab Wa Wb q0 q0 q0

b
a
E dl
移动单位正电荷自 ab 过程中电场力作的功。
移动单位正电荷 自该点 “势 能零点” 过程 中电场力作的 功。
b Wa Aab • 电势定义 ua E dl a q0 q0
意义：把单位正电荷从a点沿任意路径移到b点时电 场力所作的功。 电势差和电势的单位相同，在国际单位制中，电势 的单位为：焦耳/库仑（记作J/C），也称为伏特（V） ，即1V＝1J/C。
Fan
注意几点：
1.电势是标量，只有正负之分。
2. 电势和电势能一样都是相对的量，为了让它有确 定的值，必须选择一个零点作为参考点。但电势差 的值具有绝对的意义，与零点的选择无关。 3. 电势零点的选择： •对有限带电体一般选无穷远为电势零点。 在实际问题中，也常常选地球的电势为零电势。 •对无限带电体不宜选无穷远为电势零点。此时只有电 势的相对值（即电势差）有意义。 4.电势能与电势的区别：WP 可正可负，取决于 q 和 q0 ； U只取决于场源电荷 q 。
简述静电场的环路定理

简述静电场的环路定理

简述静电场的环路定理静电场的环路定理是电磁学中的基本定理之一，它描述了静电场中电场强度的分布以及其与电荷分布之间的关系。

本文将对静电场的环路定理进行简述，重点介绍定理的含义和应用。

静电场的环路定理，又称为库仑定律或环路定理，是由法国物理学家库仑在18世纪末提出的。

定理的核心思想是在闭合路径上，电场强度沿着路径的积分等于路径内电荷的代数和与真空介电常数的乘积。

简单来说，静电场的环路定理可以用以下公式表示：∮E·dl = q/ε₀其中，∮E·dl表示电场强度沿闭合路径的环路积分，q表示路径内的总电荷，ε₀表示真空介电常数。

根据静电场的环路定理，可以推导出一些重要的结论和应用。

首先，对于闭合路径上没有电荷的情况，环路积分必然等于零。

这意味着在没有电荷存在的区域，电场强度沿着任意闭合路径的环路积分都等于零。

这个结论可以用来验证电场的无旋性，即电场强度的旋度为零。

对于闭合路径上存在电荷的情况，环路积分不等于零。

根据路径内电荷的正负情况以及电场强度的方向，可以确定环路积分的正负。

如果路径内的总电荷为正，则环路积分为正，表示电场强度沿路径的方向与路径的方向一致；如果路径内的总电荷为负，则环路积分为负，表示电场强度沿路径的方向与路径的方向相反。

静电场的环路定理可以应用于计算电场强度、电势差等物理量。

例如，在计算电场强度时，可以通过选择合适的闭合路径，利用环路定理求解电场强度的大小和方向。

在计算电势差时，可以利用环路定理将电场强度的环路积分转化为电势差的差值，从而简化计算过程。

静电场的环路定理还可以应用于电场的分布和电势的计算。

通过选择合适的闭合路径，可以根据路径内的电荷分布和已知的电场强度，求解路径上任意点的电场强度和电势。

同时，环路定理也为电场强度的计算提供了一种简便的方法，避免了直接积分计算的繁琐过程。

静电场的环路定理是电磁学中的重要定理之一，它描述了静电场中电场强度与电荷分布之间的关系。

大学物理 5.4 磁场的安培环路定理

大学物理 5.4 磁场的安培环路定理

r



l
B
例2 载流长直螺线管磁场分布
如图，均匀密绕无限长直
螺线管通有电流为I，单位
长度匝数为n）
I
解：对称性分析—— 管内垂轴

b
Ba
平面上任意一点与 B轴平行
cd b c d a
(3)磁场是有旋场 —— 电流是磁场涡旋的轴心
B dl —— 不代表磁场力的功，仅是磁场与电流的关系
L
(4)安培环路定理只适用于闭合的载流导线，对于任 意设想的一段载流导线不成立
2. 安培环路定理的应用
在静电场中，当带电体具有一定对称性时 可以利用高斯定理很方便的计算其电场分布。 在恒定磁场中，如果电流分布具有某种对称性， 也可以利用安培环路定理计算电流磁场的分布。
由 于 这 时 I 内 =0 ， 所 以 有 B=0 (在螺线环外)
l2



l1


可见，螺线环的磁场集中在
环内，环外无磁场。
对载流长直密绕螺线管，若线圈中通有电流强度为I的电
流,沿管长方向单位长度上的匝数为n，则由安培环路定理容
易求得：管内： B onI
说明
(1)积分回路绕行方向与电流方向呈右螺旋
关系
满足右螺旋关系时 Ii 0 反之 Ii 0
I
1
I
I
3
2l
I I
l
l B dl o ( I1 I2 ) l B dl o ( 2I I) oI
(2)公式中的 B 是环路上的磁感应强度，使
空间所有电流共同激发的。
L
B
LB
dr
静电场的环路定理

静电场的环路定理


§8-1 电场强度
解: (1)延长线上:
q
O
q
r
E P
E
q E 2 4 0 r l 2
q E 2 4 0 r l 2
r l
q 2rl 1 EP E E 4 0 r 4 1 l 2 4r 2


2
2018/12/12
q2
1 q1q2 F 大小： 2 4 0 r 方向： q1和q2同号 : 沿r ；q1和q2异号 : 沿 r
0 8.851012 ( N1m2C2 ) －－真空中的介电常数
2018/12/12
7
-《大学物理》University Physics
§8-1 电场强度
40 x r
2

xdq
2 3/ 2

dq 2 rdr
dE 4 0 x r
2
R 0
dr r
R
dE
x 2 rdr
2 32
x
P

E dE
4 0 x r
2
x 2 rdr
2 32

2 0
x 1 2 2 12 ( x R )
i 1
q1
q2
11
F2
P q0
F1
F
2018/12/12
-《大学物理》University Physics
§8-1 电场强度
五、电场强度的计算
1、点电荷的场强
F
F E q0
qq0 ˆ r 2 4 0 r
q0
F
q
r
E
2018/12/12
静电场的环路定理

静电场的环路定理


已知q的电场分布 E
根据定义, P点的电势为
4
q
0r
2
er
VP


P

E dl

r
q
40r
2Pdr4q04r2qe0rrP dl
q > 0时, VP为正, r V, r处V= 0 min q < 0时, VP为负, r V, r处V = 0 max
2.电场强度与电势梯度的关系
根据电势差的定义, 把单位正电荷从P1移到P2 电场力所作的功为：
dA E dn V (V dV )
r E
dn
n
P1
P2
V V dV
E dn dV
E


dV dn
grad V
E
ቤተ መጻሕፍቲ ባይዱ

dV dn
n
r E grad V
r 即:电场中某点的场强 E 等于该点电势梯度的负值
无意义
VP

P
E
dr
rP
2 0r
dr

2 0
ln
rP
r
P
P'
令某处 r = r0（有限值） V=0，则
VP

P0
P
E
dl

P
P
E dl

P0
P
E dl
r0 P0

P
P
2
0r
dr

2 0
ln
r0 r
可见：当电荷分布到无穷远时，
22
归纳 电场强度与电势的关系
积分关系：
静电场的环路定理

静电场的环路定理

静电场的环路定理
➢ 本节的研究目的
研究ห้องสมุดไป่ตู้电场的旋度特性
➢ 本节的研究内容
一、静电场环路定理的微分形式 二、静电场环路定理的积分形式
一、静电场环路定理的微分形式
E ()
0
E 0
静电场是无旋场； 静电场的电力线不可能是闭合曲线；
二、静电场环路定理的积分形式
根据斯托克斯定理
L E dL S E dS L E dL 0
分析：对闭合曲线应用环路定理
a
E dL E dL E dL 0
acbda
acb
bda
c d
E dL E dL E dL
acb
bda
adb
b
说明：两点之间的电位差与积分路径无关
二、静电场环路定理的积分形式
根据斯托克斯定理
L E dL S E dS L E dL 0
静电场的环量为零； 静电场是保守力场，位场； 静电场中电场力作功与路径无关；
本节要点
➢ 本节的研究目的 研究静电场的旋度特性；
E 0
L E dL 0
静电场的环路定理

静电场中环路定理和环流定理

静电场中环路定理和环流定理
在静电场中，环路定理是基本电磁定律之一，它描述的是沿着闭合回路的路径积分
（环路积分）与围绕路径的电场强度之积的相等关系。

具体而言，环路定理可以表示为：
∮ E·dℓ = 0
其中，E表示电场强度，dℓ表示环路上的微小位移元素，∮表示对整个环路沿着闭合
路径的积分。

这个定理的物理意义是：在一个静电场中，当你绕着一个闭合回路走一圈时，得到的
电场积分总是等于零。

这个定理对于描述物体的电荷分布和电场的特性非常重要。

同时，
环路定理也可以用于确定电场的解析表达式，来计算电势差和电荷分布的影响。

与环路定理相比，环流定理是一个更为广泛和深入的物理定律，它描述了磁场产生的
物理原理。

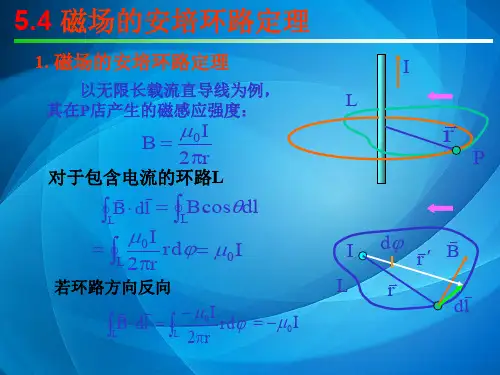
在静电场中，环流定理指的是一个围绕电流线路的环曲面上的积分，等于线路
内的电流的总和。

数学上，环流定理可以表述为：
其中，B表示磁场强度，dS表示环曲面上的微小面积元素，μ0表示真空中的磁导率，而I则表示通过线路内的电流强度。

物理上，环流定理描述了磁场沿着封闭路径的总和，或者说，从一个特定区域流出和
流入的总量。

直观上，环流定理也可以用来计算磁场的速率和强度，以及它在不同场合下
的表现形式。

总的来说，环路定理和环流定理都是物理学家和工程师们经常使用的基本定律。

通过
这两个定理，我们可以更加深入地理解力学、电学等自然现象，从而为相关的技术和应用
开发提供更为坚实的基础。

大学物理电场的环路定理及电势的计算


0
qr
3
(r R ) (r R )
4 0 r
E
令 U 0 ，沿径向积分

1 r
2

U外

P
E 外 d r q 1 r

o
4
r
qr dr
0
r
3
R
r
4 0 r
U外

q 4 0 r
E dr

R
1 r
R


a
E dl
零势点
Ecosdl
a
注意： • 选取零势点的原则：使场中电势分布有确定值 一般,场源电荷有限分布:选 U 0 场源电荷无限分布:不选 U 0 许多实际问题中选 U 地 球 0
[例一] 点电荷 q 场中的电势分布
r E
o
P
解： E
L L
静电场中任意闭合路径
静电场环路定理

E dl 0
L
路径上各点的总场强
静电场强沿任意闭合路径的线积分为零.反映了 静电场是保守力场.
凡保守力都有与其相关的势能，静电场是有势场.
三. 电势能 W
由 A保 E P W
b
A静 电 力 q 0
a
E dl (W b W a ) W a W b
dq 4 0 r
dU
4 r d r
2
4 0 r

rd r 0
R2

由叠加原理：
r
R2
R1
o P
U

dU

物理-环路定理


三、电势
1、定义
说明：
U E p
“0” E dr
q
A
（1）对有限带电体，通常 选 无限 远为电势零点
U A
E dl
A
但在工程技术中，取大地、仪器外壳等为电势零点；
（2）电场的电势分布确定后，电场力做功
W势
2、电势的计算 (1) 点电荷的电势
Q
dq
e
带电体
r
A
UdUA
? dq
4 0r
dq
U A Q 4πε0r
三、电势
例2 求一均匀带电细圆环，半径为R，带正电
荷量Q。求圆环轴线上任意点P 的电势。
dU p
z
r
O
R dl
三、电势
例3 求均匀带电薄圆盘轴线上任意点P 的电
势。设圆盘半径为R，盘上电荷面密度为 σ 。
dUp
dq 4πε0(r 2
即：静电场是无 旋场。 E 0
二、静电势能
(1) 电势能是电荷与静电场
B
所构成的系统共有的。
L1
(2) 某点电势能的大小与势
能零点的选取有关。
q
A
L2
E
但任意两点间的电势能差 与势能零点选取无关。
“0”
E pA A Fe dr
1E8pA11E年pB泊 松W把eA势B 能
(3) 库用 电仑于 学力静 的F电 解与e 学 析电， 理势发论能E展。p的了关静系：
q+
A
积分至无穷远
E
r
U(r) q
4πε0r
三、电势
(2) 点电荷系的电势
U A
推广：
i
qi 4 π ε0ri

环路定理


解：
a
r P
x
U=
q 4 0 x2 +a2 πε
x
dU qx E = Ex = − = 2 2 32 dx 4 0(x +a ) πε
U(x, y, z) =C
• 常用一组等势面描述静电场，并规定相邻两等势面之间的 常用一组等势面描述静电场， 电势差相等。 电势差相等。
点电荷的电场线与等势面
+
电偶极子的电场线与等势面
+ +
+ +
+
+
+
+场线的关系: 等势面与电场线的关系: （a） 等势面与电场线处处正交； 等势面与电场线处处正交； 电场线指向电势降低的方向； （b） 电场线指向电势降低的方向； （c） 等势面和电场线密集处场强量值大，稀疏处场强量值小。 等势面和电场线密集处场强量值大，稀疏处场强量值小。
q
r
a
r+dr r dl θ r q0 E
结论：在点电荷电场中， 结论：在点电荷电场中，电场力所作的功只与试验电荷始末 位置有关，而与试验电荷运动路径无关。 位置有关，而与试验电荷运动路径无关。
（2）在任意电荷系的电场中： 在任意电荷系的电场中：
r v E = ∑Ei
r r v r v r A= q0 ∫ E⋅ dl = q0 ∫ ∑E ⋅ dl = ∑ 0 ∫ E ⋅ dl = ∑A q i i i
例2、 均匀带电圆板，半径为 R ，电荷面密度为 σ 。求轴线上 均匀带电圆板， 电势。 任一点 P 的电势。 解： dU =
dq 4 0 x +r πε
2 2
dr r
R P
dq =σ2π rdr

静电场的保守性和环路定理


QU P −UQ =
v v = E ⋅ ∆n = En∆n = −∆U
∆U ∂U ∴ E n = − lim | |= − ∆n → 0 ∆ n ∂n
U + ∆U
∫
Q
P
v v Edl
v E
P
U
v ∆n
Q
v n
电场强度沿等势面法线方向做负功。 电场强度沿等势面法线方向做负功。
∆U ∂U ∴ E n = − lim | |= − ∆n → 0 ∆ n ∂n
Q dA MN
v v = E ⋅ d l = Edl cos θ = 0
∴θ = π / 2
M
电力线的方向指向电势降落的方向。 电力线的方向指向电势降落的方向。
因沿电力线方向移动正电荷场力做正功，电势能减少。 因沿电力线方向移动正电荷场力做正功，
规定两个相邻等势面的电势差相等， 规定两个相邻等势面的电势差相等，所以等势面较密 两个相邻等势面的电势差相等
等势面的性质： 等势面的性质： 除电场强度为零处外，电力线与等势面正交。 除电场强度为零处外，电力线与等势面正交。 N v 证明：因为将单位正电荷从等势面上M点移到 点移到N点 证明：因为将单位正电荷从等势面上 点移到 点， dl v 电场力做功为零， 电场力做功为零，而路径不为零 dl ≠ 0 E
例三、 例三、求无限长均匀带电直线的电场中的电势分布
λ E 已知场强为： 方向垂直于带电直线。 已知场强为： = 方向垂直于带电直线。 2πε 0 r 电荷线密度
若仍然选取无穷远为电势零点， 若仍然选取无穷远为电势零点，则由积分可知各点电势将为 无限大而失去意义。此时， 无限大而失去意义。此时，我们可以选取某一距带电直导线 点为电势零点， 点的电势： 为 r0的 p0 点为电势零点，则距带电直线为 r 的 点的电势：

环路定理


电子伏特

电子伏特：能量单位

带有电量+e或-e的粒子飞跃一个电势差为1V的 区间，电场力对它作的功(从而粒子本身获得 这么多能量（动能）——1eV
19 19
1eV 1.6010 C 1V 1.6010
1keV 103 eV 千 1GeV 109 eV 吉
2005.2.
J
直角坐标系表示
E总是沿着指向电势减少的方向——E与Δn相反 在数学场论中把
U :
A:
A :
例题
2005.2.
称作梯度
称作散度
称作旋度
北京大学物理学院王稼军编写
静电场的基本方程的微分形式

数学场论公式
A dS AdV
S V
面积分 体积分
A dl ( A) dS
P
电势能的 改变量
q0在 P点 的电势能
q0在 Q点 的电势能
电势增量

可以与重力做功类比
电场力做正功，电势能将减少 电场力做负功，电势能将增加

2005.2.
北京大学物理学院王稼军编写
电势的定义
0 电 场 付 出 能 量 ， 能 量少 减 APQ WPQ (电 势 能 的 减 少 与 场 源 和 0均 有 关 ， q 电 场 吸 收 能 量 ， 能 量加 增 0
静电场的环路定理

静电场力做功与路径无关 等价 于静电场力沿任意闭合回路做功 恒等于零 E dl 0

在任意电场中取一闭合回路，将试探电荷沿路径 L从 p——Q——P，电场力所做的功为
Q P L
Q
A q0 E d l q0 E d l q0 E d l
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
q 4πε0R2
E
∝r
R
−2
场强分布曲线
O
r
−1
U
电势分布曲线
q 4πε0R
∝r
上页 下页 返回 退出
O
R
r
三、由电势叠加原理求电势 例3 电荷以相同的面密度 分布在半径为 r =10cm 和 1 r2 = 20cm的两个同心球面上。设无限远处电势为零，球心 的两个同心球面上。设无限远处电势为零， 处的电势为 U0 = 300V 。 （1）求电荷面密度 ） ； （2）求两球间的电势差。 ）求两球间的电势差。
等势面与电场线的关系
r r dA = q0 E ⋅ dl = q0 E ⋅ dl ⋅ cosθ = 0
正负点电荷周围电势分布特点。 正负点电荷周围电势分布特点。
上页 下页 返回 退出
点电荷系的电势 电势叠加原理：点电荷系的电场中， 电势叠加原理：点电荷系的电场中，某点的电势 等于每个电荷单独在该点激发的电势的代数和。 等于每个电荷单独在该点激发的电势的代数和。
1 qi U =∑ πε0 ri i 4
dl
dU =
dq 4πε 0 r
1
+ + R+ o + + + + + +
r x p x
qdl = 4πε 0 2πRr
上页 下页 返回 退出
=
qdl 8π 2ε 0 R R 2 + x 2
整个圆环在p 点的电势为U = ∫ dU Nhomakorabea=∫
2πR 2
qd qdl 8π ε 0 R R + x
2 2
0
=
q 4πε 0 R + x
( - L 2)
v v A = q0 ∫L E ⋅ dl = 0
上页 下页 返回 退出
L1
静电场的环路定理 在静电场中， 在静电场中，场强沿任意闭合路径的线积 称为场强的环流）恒为零。 分（称为场强的环流）恒为零。
v v ∫ E⋅ dl = 0
L
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 综合静电场高斯定律和环路定理，可知静电场是有 综合静电场高斯定律和环路定理，可知静电场是有 源的保守力场，又由于电场线是不闭合的， 源的保守力场，又由于电场线是不闭合的，既形不 成旋涡的，所以静电场是无旋场 静电场是无旋场。 成旋涡的，所以静电场是无旋场。
"0"
上页 下页 返回 退出
电势 某点电势能WA与q0之比只取决于电场，定义为该 某点电势能 之比只取决于电场， 点的电势 单位：伏特（ ） 电势. 点的电势.单位：伏特（V）
v WA "0" v = ∫A E ⋅ dl UA = q0
由上式可以看出,静电场中某点的电势在数值上等于 由上式可以看出 静电场中某点的电势在数值上等于 单位正电荷放在该点处时的电势能,也等于 也等于单位正电 单位正电荷放在该点处时的电势能 也等于单位正电 荷从该点经任意路径到电势零点处(无穷远处 无穷远处)时电场 荷从该点经任意路径到电势零点处 无穷远处 时电场 力所做的功。 力所做的功。 练习题：在点电荷 的电场中 选取以q为中心 的电场中， 为中心、 为半 练习题：在点电荷q的电场中，选取以 为中心、R为半 径的球面上一点P作为电势零点 则与点电荷q相距为 作为电势零点， 相距为r 径的球面上一点 作为电势零点，则与点电荷 相距为 的P*点的电势为 点的电势为 。
上页 下页 返回 退出
由上式可知， 为负值； 由上式可知，在r>1 m处,VP为负值；在r<1 m 处 为正值。这个例题的结果再次表明， 处,VP为正值。这个例题的结果再次表明，在静电 场中只有两点的电势差有绝对的意义， 场中只有两点的电势差有绝对的意义，而各点的电 势值却只有相对的意义。 势值却只有相对的意义。
上页 下页 返回 退出
电势差 电场中两点电势之差(电压) 电场中两点电势之差(电压)
上式表明，静电场中两点 的电势差， 上式表明，静电场中两点A、B的电势差，等于单 的电势差 位正电荷在电场中从A经任意路径到达 经任意路径到达B点时电场 位正电荷在电场中从 经任意路径到达 点时电场 力所做的功。 力所做的功。
B
v v AAB = q0 ∫A E ⋅ dl = −∆W =WA −WB
电势能零点的选取是任意的。 电势能零点的选取是任意的。对有限带电体一般 以无限远或地球为零点。 以无限远或地球为零点。 为静电势能的零点， 0”表示 表示， 选B为静电势能的零点，用“0”表示，则
v v WA = q0 ∫A E ⋅ dl
2 2
上页 下页 返回 退出
二、从电荷分布求场强，再从场强分布求电势。 从电荷分布求场强，再从场强分布求电势。 计算均匀带电球面的电场中的电势分布。 例2 计算均匀带电球面的电场中的电势分布。球面半 径为R，总带电量为q。 解： + + + + + + + + q + （2）由高斯定律可知电场分布为； 由高斯定律可知电场分布为； + r E = 0 (r < R) + + r 1 q r + E= ⋅ 2 er (r > R) （1）取无穷远处为电势零点； 取无穷远处为电势零点；
∞
1
UP = ∫
=∫
∞
∞
P
r r E ⋅ dr
U
r
q 4πε 0 R
R
1 Uµ r
q q ⋅ 2 dr = 4πε 0 r 4πε o r
1
r
上页 下页 返回 退出
结论：均匀带电球面，球内的电势等于球表面的电势， 结论：均匀带电球面，球内的电势等于球表面的电势， 球外的电势等效于将电荷集中于球心的点电荷的电势。 球外的电势等效于将电荷集中于球心的点电荷的电势。
v v v v E =E1+E2 +L+ En
上页 下页 返回 退出
电场力对试验电荷q0做功为
v v Aab = q0 ∫ E ⋅ dl a v v v b v b v b v = q0 ∫ E1 ⋅ dl + q0 ∫ E2 ⋅ dl +L+ q0 ∫ En ⋅ dl
b
a a a
= A1 + A2 +L+ An
上页 下页 返回 退出
三、 电势(electric potential) 电势(electric
电势能 由环路定理知，静电场是保守场。 由环路定理知，静电场是保守场。 电势能。 保守场必有相应的势能，对静电场则为电势能 保守场必有相应的势能，对静电场则为电势能。 静电力的功，等于静电势能的减少。 静电力的功，等于静电势能的减少。
WA WB B v v UAB = UA −UB = − = ∫A E ⋅ dl q0 q0
AAB = q0 (U A − U B )
上式是计算电场力作功和计算 电势能变化常用公式。 电势能变化常用公式。 沿着电场线方向，电势降低。 沿着电场线方向，电势降低。 A B
上页 下页 返回 退出
四、电势的计算
qi q0 1 1 =∑ − 总功也与路径无关。 总功也与路径无关。 πε0 ria rib i=1 4
n
静电场中移动时 结论：试验电荷在任意给定的静电场中移动时， 结论：试验电荷在任意给定的静电场中移动时， 电场力对q0做的功仅与试验电荷的电量及路径的起 点和终点位置有关，而与具体路径无关。 点和终点位置有关，而与具体路径无关。 静电场是保守场，静电场力是保守力。 静电场是保守场，静电场力是保守力。
上页 下页 返回 退出
二、 静电场的环路定理
试验电荷q0在静电场中沿任意闭合路径 试验电荷 L运动一周时，电场力对 0做的功 =？ 运动一周时，电场力对q 做的功A=
安培
上页 下页 返回 退出
在闭合路径L上任取两点 在闭合路径 上任取两点P1、P2，将L分成 上任取两点 分成 L1、L2两段， 两段，
R
o + + +
4πε 0 r
（3）确定电势分布； 确定电势分布；
上页 下页 返回 退出
(1) + + + + + + + + q + + + + +
UP = ∫
∞
P
r r R r r ∞r r E ⋅ dr = ∫ E ⋅ dr + ∫ E ⋅ dr
r R
当r≤R时 时
R
o + + +
q q =∫ ⋅ 2 dr = R 4πε 4πε o R 0 r (2)当 (2)当r>R时
上页 下页 返回 退出
为了能求得P点的电势， 为了能求得 点的电势，可先应用电势差和场强 点的电势 的关系式，求出在轴上P点 和点的电势差。 的关系式，求出在轴上 点P1和点的电势差。无限 长均匀带电直线在x轴上的场强为 长均匀带电直线在 轴上的场强为
λ E= 2πε0r
于是， 点沿x轴积分可算得 点与参考点P 于是 ， 过 P点沿 轴积分可算得 点与参考点 1 点沿 轴积分可算得P点与参考点 的电势差
σ
σ
r 1 r2
上页 下页 返回 退出
例4
计算无限长均匀带电直线电场的电势分布。 计算无限长均匀带电直线电场的电势分布。
令无限长直线如图放置， 其上电荷线密度为λ 解 ： 令无限长直线如图放置 ， 其上电荷线密度为 。 计算在x轴上距直线为的任一点 处的电势。 轴上距直线为的任一点P 计算在 轴上距直线为的任一点P处的电势。 因为无限长带电直线的电荷分布 y 延伸到无限远的， 延伸到无限远的，所以在这种情 况下不能用连续分布电荷的电势 公式来计算电势V， 公式来计算电势 ，否则必得出无 x r P 限大的结果，显然是没有意义的。 限大的结果，显然是没有意义的。 O r1 P1 同样也不能直接用公式来计算电 势，不然也将得出电场任一点的 电势值为无限大的结果。 电势值为无限大的结果。