化工热力学作业2

化工热力学课后习题答案化工热力学课后习题答案解析与实践化工热力学是化学工程专业中的重要课程，它涉及到热力学原理在化工过程中的应用。

课后习题是学生巩固知识、提高能力的重要途径。

本文将针对化工热力学课后习题答案进行解析，并结合实际工程案例进行讨论。

第一题：某化工过程中，液体从100°C冷却至30°C，求其冷却前后的焓变化。

解析：根据热力学知识，焓变化可以通过温度变化和相变潜热来计算。

在这个过程中，液体从100°C冷却至30°C，因此焓变化可以表示为：ΔH = mcΔT + mL其中，m为液体的质量，c为液体的比热容，ΔT为温度变化，L为相变潜热。

实际案例：在化工生产中，液体冷却过程常常会伴随着热量的释放。

比如在冷却塔中，热水经过冷却塔顶部的喷淋装置，通过与空气的接触，将热量传递给空气，使水的温度降低。

这个过程中，热水的焓发生了变化，而释放的热量则被转化为冷却塔底部的冷却水。

第二题：某反应器中，气体从1MPa膨胀至0.1MPa，求其膨胀过程中的焓变化。

解析：气体的膨胀过程可以看作是绝热膨胀，根据绝热过程的热力学关系，焓变化可以表示为：ΔH = C_pΔT其中，C_p为气体的定压比热容，ΔT为温度变化。

实际案例：在化工生产中，气体的膨胀过程常常会伴随着功的输出。

比如在天然气输送管道中，高压天然气经过减压阀膨胀至低压，释放出的能量可以用来驱动压缩机或者发电机，实现能量的转换和利用。

通过以上两个习题的解析和实际案例的讨论，我们可以看到化工热力学的知识在实际工程中的重要性。

掌握热力学原理和应用是化学工程师必备的基本能力，通过课后习题的答案解析和实践案例的讨论，可以帮助学生更好地理解和应用这些知识，提高工程实践能力，为将来的工程实践打下坚实的基础。

化工热力学作业2-3 试根据R-K 方程2-10（)(2/1b V V T a b V RT P +--=）导出常数a 、b 与临界常数的关系式2-16、2-17（Cc P T R a 5.2242748.0= C C P RT b 08664.0=）。

2-4 某反应器容积为1.213m 3，内有45.40kg 乙醇蒸汽，温度为227℃。

试用下列三种方法求出反应器的压力。

已知实验值为2.75 Mpa 。

（a ）用理想气体方程 （b ）用R-K 方程 （c ）用三参数普遍化关联法。

2-7 试用下列三种方法计算250℃、2000KPa 水蒸气的Z 与V 。

（a ）用维里截断式2-8（21VC V R RT PV Z ++≈=），已知第二和第三维里系数的实验值为B= -0.1525 m 3·kmol -1 和C=-0.5800×10-2 m 6·kmol -2；（b ）用维里截断式2-7（RTBP RT PV Z +≈=1），其中B 用皮策普遍化关联法求出；（c ）用水蒸气表计算。

2-9 在50℃、60.97Mpa 时由0.401（摩尔分数）的氮和0.599的乙烯组成混合气体，试用下列四种方法求算混合气体的摩尔体积。

已知实验数据求出的Z 实=1.40。

（a ）理想气体方程（b ）阿玛格定律和普遍化压缩因子图；（c ）虚拟临界常数法（Kay 规则）；（d ）混合物的第二维里系数法。

2-12 选择合适的普遍化关联法计算1Kmol 丁二烯-1,3从2.53MPa 、127℃压缩到12.67 MPa 、227℃时的△H 、△S 和△V 。

已知丁二烯-1,3的T C =425.0K ，P C =4.326MPa ，V C =0.221 m 3·kmol -1，ω=0.181，理想气体等压热容C *p =22.738+222.796×10-3T －73.879×10-6T 2（kj · kmol -1K -1），或G *P /R=2.735+26.7977×10-3－8.8861×10-6T 2(T ：K)。

模拟题一一．单项选择题（每题1分，共20分）T 温度下的纯物质，当压力低于该温度下的饱和蒸汽压时，则气体的状态为（ ）饱和蒸汽 超临界流体 过热蒸汽 T 温度下的过冷纯液体的压力P （ ） >()T P s <()T P s =()T P sT 温度下的过热纯蒸汽的压力P （ ）>()T P s <()T P s =()T P s 纯物质的第二virial 系数B （ ）A 仅是T 的函数B 是T 和P 的函数C 是T 和V 的函数D 是任何两强度性质的函数 能表达流体在临界点的P-V 等温线的正确趋势的virial 方程，必须至少用到（ ）第三virial 系数 第二virial 系数 无穷项 只需要理想气体方程 液化石油气的主要成分是（ ）丙烷、丁烷和少量的戊烷 甲烷、乙烷 正己烷 立方型状态方程计算V 时如果出现三个根，则最大的根表示（ ）饱和液摩尔体积 饱和汽摩尔体积 无物理意义 偏心因子的定义式（ ）0.7lg()1s r Tr P ω==--0.8lg()1s r Tr P ω==--1.0lg()s r Tr P ω==-设Z 为x ，y 的连续函数，，根据欧拉连锁式，有（ ）A.1x y zZ Z x x y y ⎛⎫⎛⎫∂∂∂⎛⎫=-⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭B. 1y xZ Z x y x y Z ⎛⎫∂∂∂⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭C. 1y xZ Z x y x y Z ⎛⎫∂∂∂⎛⎫⎛⎫= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭D. 1y Z x Z y y x x Z ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 关于偏离函数MR ，理想性质M*，下列公式正确的是（ ）A. *RMM M =+ B. *2RMM M =-C. *R M M M =-D. *RM M M =+下面的说法中不正确的是 ( )（A ）纯物质无偏摩尔量 。

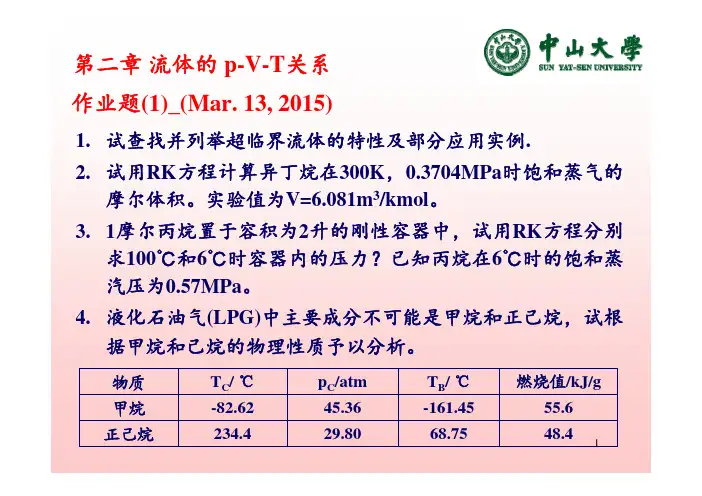
11.试查找并列举超临界流体的特性及部分应用实例.2.试用RK 方程计算异丁烷在300K ，0.3704MPa 时饱和蒸气的摩尔体积。

实验值为V=6.081m 3/kmol 。

3.1摩尔丙烷置于容积为2升的刚性容器中，试用RK 方程分别求100℃和6℃时容器内的压力？已知丙烷在6℃时的饱和蒸汽压为0.57MPa 。

4.液化石油气(LPG)中主要成分不可能是甲烷和正己烷，试根据甲烷和己烷的物理性质予以分析。

作业题(1)_(Mar. 13, 2015)第二章流体的p-V-T 关系48.455.6燃烧值/kJ/g 68.75-161.45T B / ℃29.8045.36p C /atm 234.4-82.62T C / ℃正己烷甲烷物质1.纯物质的三相点随所处压力的不同而改变，对否？为什么？2.vdW、RK方程在临界温度附近也能较准确预测饱和蒸汽压, 对吗？3.在计算pVT关系方面RK方程较SRK方程更合适，是否正确？4.一状态方程能计算汽液相平衡，一定能很好地计算pVT关系?5.在临界温度附近，vdW方程也能较准确地预测烃类流体的饱和蒸汽压，但对体积性质的预测精度仍很差，这一说法对吗？为什么？6.纯物质饱和液体的摩尔体积随温度升高而增大，饱和蒸汽的摩尔体积随温度升高而减小，对否？为什么？7.某温度T下的过热纯蒸汽的压力p小于该温度下的饱和蒸汽压, 对否？8.温度一定, 压力趋于零时, 任何气体的pV乘积也趋于零, 对否?为什么?9.纯物质临界点的数学特征为和。

10.参考教材图2-3中蒸发线上的自由度为1，所以处在蒸发线上的1mol物质，只要温度给定，其压力和体积就确定了。

这一说法对吗？如果不对，将如何改正？2。

第一章绪论1.你能说出“热质说”与“热动说”两种观点的根本区别吗？2.热力学第一定律创建的充分条件是什么？3.解释可逆过程与不可逆过程。

4.何为强度性质，何为容量性质？5.经典热力学与分子热力学的根本区别是什么？第二章流体的P-V-T关系1.用下列方法计算200o C及10atm下异丙醇气的压缩因子与体积（1）取至第三维里项内的维里方程，实验测定的维里系数B=-388cm3/molC=-26000cm3/mol2（2）用普遍化第二维里系数法计算（3）用R-K方程，由T c，P c直接计算常数a、b已知异丙醇的物理常数为：T c=508.2K P c=50.0atmV c=220.4cm3/molW=0.7002.比较分别用普遍化方法与理想气体定律计算136atm，920K下的水蒸气比容的结果，并与水蒸气表对照。

3.为了生产液氧，需将氧气由大气压力及22o C加压冷却至100atm，183K，如原有体积3L氧气，求被压缩后气体的体积。

4.1mol氨在673K时占有体积70ml，试用普遍化压缩因子及R-K方程计算其压力，并与理想气体的计算结果相比较。

第三章 纯物质的热力学性质1. 推导以下方程：1）V T T P V S )()(∂∂=∂∂2）P TP T V U V T -∂∂=∂∂)()(3）dV V PV T P T dT T P V C dH T V V V ])()([])([∂∂+∂∂+∂∂+=4）dV VTC dP P T C V dH P P V V )(])([∂∂+∂∂+=5）dV T pdT T C dS V V )(∂∂+=6）dp TVdT T C dS P P )(∂∂-=2. 使用合适的普遍化关联式计算1kmol 的1, 3-丁二烯当其从2.53MPa 及127o C 压缩至12.67MPa 及277o C 时的H ∆、S ∆、V ∆。

已知丁1, 3-丁二烯在理想气体状态时的定压摩尔热容为：K kmol kJ T T C p ⋅⨯-+=--/10879.73796.222738.22263'3. 运用R-K 方程求算125o C 、10MPa 下丙烯的剩余焓与剩余熵（假设该状态下的丙烯服从R-K 状态方程）。

第二章1. 用R-K 方程求294.3K 和1.013⨯103kPa 下甲烷的摩尔体积。

已知实验值为63(1.01310,294.3)2370.27/V Pa K cm m ol ⨯= （叠代求解）解：查附表知甲烷的特性参数为c c T K p M Pa w ===（1）应用R-K 方程计算甲烷的摩尔体积。

R-K 方程为0.5()RT a p V bTV V b =--+将上两边乘以 (V －b )／P()b V V PT)b V (a P RTb V /+--=-21将上式写成迭代格式()()b V V PTb V a b P RT V k k /k k +--+=+21122.522.560.523(8.314)(190.6)0.427480.4274832224.610ca cR T a kP m Kkm olp -⨯==⨯=⋅⋅⋅⨯6138.314190.60.086860.086640.029854.610c cRT b m km olp -⨯==⨯=⋅⨯()()11/232220.029858.314294.30.0298510131013294.30.02985k k k k V V V V +-⨯=+-⨯⨯+()()10.18540.029852.44530.02985k k k k V V V V +-=-+取3108.314294.32.41541013R T V m km olP-⨯===⋅()()3110.1854 2.41540.029852.4453 2.37042.4154 2.41540.02985V m km ol--=-=⋅+()()3120.1854 2.37040.029852.4453 2.36902.3704 2.37040.02985V m km ol--=-=⋅+()()3130.1854 2.36900.029852.4453 2.36902.3690 2.36900.02985V m km ol--=-=⋅+312.3690V m kmol -=⋅在T=294.3K 和p=1.013310kPa ⨯时摩尔体积的计算值与实验值的相对百分偏差为 2370.272369100%0.0542370.27-⨯=2. 工程设计中需要乙烷在3446kPa 和93.33℃下的体积数据，已查到的文献值为0.025273/m kg ，试应用下列方法进行核算： （1） 两参数压缩因子法； （2） 三参数压缩因子法；（求摩尔体积）解：查附录2的表2-1得到乙烷的特性常数为： 305.4, 4.884,0.098,30.070c c T K p M Pa M ω====（1） 两参数压缩因子法由T=273.15+93.33=366.48（K ），p=3446kPa 和c T ，c p 的数值可确定对比参数如下：366.48 1.20,305.4r cT T T ===663.446100.714.88410r cp p p ⨯===⨯由r T =1.20，r p =0.71查图得 Z=0.86因为pV=ZRT,则3330.868.314366.480.00076/0.02527/344610ZRTV m mol m kgp ⨯⨯====⨯由上可知，乙烷体积的计算值与文献值相符。

【精品】化工热力学第二章习题解答化工热力学第二章习题解答1.一个理想气体在恒定温度下，其压强与体积的关系如下所示：P = A / V^2其中P是压强，V是体积，A是常数。

求该气体的热力学过程方程。

解答：根据热力学第一定律，对于恒温过程，有dU = dq + dw = dq - PdV，其中U是内能，q是热量，w是对外界做的功。

由于该气体是理想气体，可以假设其内能只与温度有关，即dU = Cdt，其中C 是常数，t是温度。

将上式代入热力学第一定律中，得到Cdt = dq - PdV。

根据理想气体状态方程PV = nRT，其中n为物质的量，R为气体常数，T为温度。

将P = A / V^2代入上式，得到Cdt = dq - (A / V^2)dV。

对上式两边同时积分，得到∫Cdt = ∫dq - ∫(A / V^2)dV。

即Ct = q - A / V + B，其中B为常数。

综上所述，该气体的热力学过程方程为Ct = q - A / V + B。

2.一个气体在等体过程中，其压强与温度的关系如下所示：P = A * T^2其中P是压强，T是温度，A是常数。

求该气体的热力学过程方程。

解答：根据热力学第一定律，对于等体过程，有dU = dq + dw = dq - PdV，其中U是内能，q是热量，w是对外界做的功。

由于该气体是理想气体，可以假设其内能只与温度有关，即dU = Cdt，其中C 是常数，t是温度。

将上式代入热力学第一定律中，得到Cdt = dq - PdV。

根据理想气体状态方程PV = nRT，其中n为物质的量，R为气体常数，T为温度。

将P = A * T^2代入上式，得到Cdt = dq - (A * T^2)dV。

对上式两边同时积分，得到∫Cdt = ∫dq - ∫(A * T^2)dV。

即Ct = q - (A / 3)T^3 + B，其中B为常数。

综上所述，该气体的热力学过程方程为Ct = q - (A / 3)T^3 + B。

中国石油大学（北京）
石大远程
化工热力学-第二阶段在线作业
参考答案
试读一页
化工热力学-第二阶段在线作业
1. 流体（T1、P1）经节流膨胀后，流体的温度
A、不变
B、下降
C、增加
D、前三者都可能
正确答案：D
2. 对于内能是体系的状态的单值函数概念的错误理解是
A、体系处于一定的状态,具有一定的内能
B、对应于某一状态,内能只能有一数值,不能有两个以上的数值
C、状态发生变化,内能也一定跟着变化
D、对应于一个内能值,可以有多个状态
正确答案：C
3. 对于一均匀的物质，其H和U的关系为
A、H
B、H> U
C、H=U
D、不能确定。

化工热力学标准化作业一一、是否题正确划√号,错误划×号,并写清正确与错误的原因1、纯物质由蒸汽变成液体,必须经过冷凝的相变化过程;2、当压力大于临界压力时,纯物质就以液态存在;3、由于分子间相互作用力的存在,实际气体的摩尔体积一定小于同温同压下的理想气体的摩尔体积,所以,理想气体的压缩因子Z=1,实际气体的压缩因子Z＜1;4、纯物质的三相点随着所处的压力或温度不同而改变;5、在同一温度下,纯物质的饱和液体与饱和蒸汽的吉氏函数相等;6、纯物质的平衡气化过程,摩尔体积、焓、热力学能、吉氏函数的变化值均大于零,7、气体混合物的virial系数,如B、C…,是温度的函数;8、virial方程和RK方程既可以应用于汽相,又可以用于液相;9、在virial方程中,virial系数反映了分子间的相互作用;10、Pitzer普遍化方法即为普遍化的压缩因子方法;二、填空题1、T温度下的过热纯蒸气的压力p _____p s T;2、表达纯物质的汽液平衡的准则有_____吉氏函数、__________Claperyon 方程;它们能/不能推广到其它类型的相相平衡;3、Lydersen、Pitzer的三参数对应态原理的三个参数分别为___________、__________;4、对于纯物质,一定温度下的泡点压力与露点压力是______的相同／不同；一定温度下的泡点与露点,在p-T图上是______的重叠／分开,而在p-Ｖ图上是______的重叠／分开；泡点的轨迹称为___________,露点的轨迹称为___________,饱和汽、液相线与三相线所包围的区域称为___________；纯物质汽液平衡时,压力称为______,温度称为______;5、正丁烷的偏心因子ω=,临界压力p c=时,则在T r=时的蒸汽压为___________MPa;6、状态方程通常分为三类,分别是__________,__________,__________;7、在状态方程的分类中,RK方程属于__________,virial方程属于__________;8、RK方程是在vdW方程的基础上建立起来的,vdW方程的形式是p=RT/V－b －a/V2,RK方程的形式为____________________;三、计算题1、将1mol甲烷压缩贮于容积为,温度为的钢瓶内,问此甲烷产生的压力有多大分别用1理想气体状态方程；2RK方程计算;已知甲烷的临界参数为T c=,p c=;RK方程中a=,b= RT c/p c;解：2、质量为500g的氨贮于体积为30000cm3的钢弹内,钢弹浸于温度为65℃的恒瘟水浴中,试分别用下述方法计算氨的压力;1理想气体状态方程；2RK方程；3Pitzer普遍化方法;已知氨的临界常数为T c=,p c=,V c=mol,ω=;RK方程中a=,b= RT c/p c;Virial方程中B0=－；B1=－;解：3、试分别用下列三种方法求出400℃、下甲烷气体的摩尔体积;1 用理想气体方程；2 用RK 方程；3 用Virial 方程截断式1-38,其中的第II Virial 系数用Pitzer 的普遍化关联式1-42、1-43计算;解：4、将压力为．温度为477K 条件下测量的32.83m 的3NH 压缩到30.142m ,若温度为,则其压力为若干分别用下述方法计算：1 Van der Waals 方程；2 Redlich-Kwong 方程；3 Peng-Robinson 方程；4 普通化关系式; 解：5、试用下列方法计算 K 、的异丙醇蒸气V 与Z 值;已知异丙醇的Virial 系数实验值31B 388cm mol -=-⋅、62C 26000cm mol -=-⋅;1 理想气体状态方程；2 BP Z 1R T =+；3 2B CZ 1V V =++解：6、在50℃、 MPa 时由摩尔分率的氮气和摩尔分率的乙烯组成混合气体,试用下列4种方法计算混合气体的摩尔体积;已知实验数据求出的40.1.exp =Z ;1 理想气体方程；2 Amagat 定律和普遍化压缩因子图；3 虚拟临界常数法Kay 规则；4 截至第II 项的Virial 方程;解：7、试估算氨 在293K 下蒸发前后体积的变化量;已知：氨在293 K 下的蒸气压为58.5710Pa ⨯;解：8、估算150℃时乙硫醇的液体摩尔体积;已知实验值为3195.0cm mol -⋅;乙硫醇的物性为C P 5.49MPa =、C T 499K =、0.190ϖ=,31C V 207.0cm mol -=⋅;20℃时乙硫醇的饱和液体密度为30.839g cm -⋅;解：9、已知正常流体的饱和燕气压可以用经验方程：S B lg P A T=+表示,其中p 的单位为MPa,T 的单位是K,试推导出该流体偏心因子表达式;化工热力学标准化作业二一、是否题正确划√号,错误划×号,并写清正确与错误的原因1、热力学基本关系式d H =T d S +V d p 只适用于可逆过程;2、当压力趋于零时,MT,p -M ig T,p ≡0M 是摩尔容量性质;3、纯物质逸度的完整定义是,在等温条件下,d G =RT dln f ;4、当p →0时,f /p →∞;5、吉氏函数与逸度系数的关系是GT,p －G ig T,p =1=RT ln φ;6、对于一均相系统,V p T S T T S T )()(∂∂-∂∂等于Ｒ;二、填空题1、一气体符合pV-b =RT 的状态方程从V 1等温可逆膨胀到V 2,则系统的ΔS 为_____;2、理想气体状态的逸度系数等于_____;3、以吉布斯函数表示的汽液平衡准则是__________;4、以逸度表示的纯物质的汽液平衡准则是__________;5、以逸度系数表示的纯物质的汽液平衡准则是__________;三、计算题1、压力是3MPa 的饱和蒸汽置于1000cm 3的容器中,需要导出多少热量方可使一半的蒸汽冷凝可忽视液体水的体积已知水的性质表;解：2、 1 分别用PR 方程和三参效对应状态原理计算,312K 的丙烷饱和蒸气的逸度；2 分别用PR 方程和三参数对应态原理计算312K 、7MPa 丙烷的逸度；3 从饱和气相的逸度计算312K 、7MPa 丙烷的逸度;设在1～7MPa 的压力范围内液体丙烷的比容为312.06cm g -⋅,且为常数;解：3、试用普遍化方法计算丙烷气体从378K 、的初态变化到463K 、的终态时过程的H ∆和S ∆值;已知丙烷在理想气体状态下的摩尔恒压热容为： P C 22.990.1775T =+,式中T 用K 表示,11P C J mol K --⋅⋅用表示;解：4、试用Virial 方程截断式1-39推导出描述某气体的R H RT 、R S R 与f ln P的表达式;解：5、选择合适的普遍化关联方法计算1 kmol 丁二烯-1,3从,127℃压缩到、227℃时的H ∆、S ∆和V ∆;已知：丁二烯-1,3的C P 4.326MPa =、C T 425.0K =、31C V 0.221m kmol -=⋅,181.0=ϖ,理想气体的等压热容36211P C 22.738222.79610T 73.87910T (kJ kmol K )----=+⨯-⨯⋅⋅ 解： 化工热力学标准化作业三一、是否题正确划√号,错误划×号,并写清正确与错误的原因1、偏摩尔体积的定义可表示为i x p T ii n p T i i x V n nV V ≠≠∂∂=∂∂=}{,,}{,,)()(; 2、对于理想溶液,所有的混合过程性质变化均为零;3、对于理想溶液所有的超额性质均为零;答：4、系统混合过程的性质变化与该系统相应的超额性质是相同的;5、理想气体有f =p ,而理想溶液有i i ϕϕ=ˆ;6、温度和压力相同的两种理想气体混合后,则温度和压力不变,总体积为原来两气体体积之和,总内能为原两气体热力学能之和,总熵为原来两气体熵之和;7、因为G E 或活度系数模型是温度和组成的函数,故理论上i γ与压力无关;8、纯流体的汽液平衡准则为l v f f =;9、混合物系统达到汽液平衡时,总是有l vf f ˆˆ=,l v f f =,l i v i f f =; 10、理想溶液一定符合Lewis-Randall 规则和Henry 规则;4-10、理想溶液一定符合Lewis-Randall 规则和Henry 规则;11、符合Lewis-Randall 规则的溶液称为理想稀溶液;12、符合Henry 规则的溶液称为理想溶液;二、填空题1、已知某二元系统的212121211221A x A x A A x x RT G E +=则对称归一化的活度系数1ln γ是____________;2、由混合物的逸度的表达式iig i if RT G G ˆln +=知,ig i G 的状态为系统温度、p =_____的纯组分i 的理想气体状态;3、常温、常压下二元液相系统的溶剂组分的活度系数为32221ln x x βαγ+=α,β是常数,则溶质组分的活度系数表达式是=2ln γ_________________;4、偏摩尔性质的定义式为___________,其含义为_____________________________;5、若溶液性质M 为ln f ,则其偏摩尔性质i M 为______,二者间的关系式)(∑=i i M x M 为_______________________;6、若溶液性质M 为ln Φ,则其偏摩尔性质i M 为______,二者间的关系式)(∑=i i M x M 为_______________________;7、若溶液性质M 为G E /RT ,则其偏摩尔性质i M 为______,二者间的关系式)(∑=i i M x M 为_______________________;8、超额性质的定义是___________________________________;9、当M =V,U,H,C v ,C p 时,△M ig =_____;10、当M =S 时,△M ig =_________________;11、当M =A,G 时,△M ig =_________________;12、在温度、压力一定时,二元混合物的偏摩尔性质可以用摩尔性质来表达,分别是1M =_________________；2M =_________________;三、计算题1、,若干NaClB 溶解于1kg 水A 中形成的溶液的总体积的关系为V t =++2+cm 3;求n B =时,水和NaCl 的偏摩尔体积B A V V ,;解：2、常压下的三元气体混合物的32312115.03.02.0ln y y y y y y+-=ϕ,求等摩尔混合物的321ˆ,ˆ,ˆf f f ;解：3、三元混合物的各组分的摩尔分数分别为,和,在和348K 下的各组分的逸度系数分别是,和,求混合物的逸度;解：4、采用合适的方法和合理的假设计算下列甲醇1－水2系统的组分逸度a p =10325Pa,T =℃,y 1=的汽相；b p =10325Pa,T =℃,x 1=的液相;已知Antoine 方程ln p s =A －B/C+T ,甲醇的常数为A=,B=,C=－；水的常数为A=,B=,C=－;液相符合Wilson 方程,其模型参数是Λ12=,Λ21=;解：5、采用合适的方法和合理的假设计算p =,T =时下列甲醇1－水2系统的组分逸度a y 1=的气体混合物；b x 1=的液体混合物;已知Antoine 方程ln p s =A －B/C+T ,甲醇的常数为A=,B=,C=－；水的常数为A=,B=,C=－;液相符合Wilson 方程,其模型参数是Λ12=,Λ21=;解：6、已知环己烷1-苯2系统在40℃时的超额吉氏函数是G E /RT =和p 1s =,p 2s =,求γ1,γ2,lf 1ˆ,l f 2ˆ; 解：7、在T 、P 为常数时,曾有人推荐用下面一对方程来表示二元系偏摩尔体积数据：式中：a 、b 只是温度和压力的函数,试问从热力学角度考虑,上述方程是否合理解：8、在,时,乙醇1-水2所形成的溶液,其体积可以用下式表示：将乙醇和水的偏摩尔体积 表示为浓度 x 2的函数,纯乙醇,纯水的摩尔体积和无限稀释下两者的体积;解：9、某二元溶液的过量Gibbs 函数模型为G E /RT=Ax 1x 2,其中A 仅为温度的函数,试求1基于Lewis －Randall 规则的活度系数模型； 2溶液的组分逸度模型；3 ln f L 模型;21,VV解：化工热力学标准化作业四一、是否题正确划√号,错误划×号,并写清正确与错误的原因1、一个由N 个组分组成的汽液两相系统,在一定的温度、压力下达到平衡,则该两相平衡系统的基本的强度性质变量为N 个;2、在一定压力下,组成相同的混合物的露点温度和泡点温度不可能相同;3、能满足热力学一致性的汽液平衡数据就是高质量的数据;4、Gibbs-Duhem 方程是混合物中各组分的偏摩尔性质的约束关系,不仅能检验偏摩尔性质的模型,而且,在相平衡数据的检验和推算中也有很重要的作用;5、混合物的相变过程与纯物质的情形有所不同,如在等压条件下,混合物的相变过程一般是变温过程,而纯物质是等温过程;6、在二组分汽液两相平衡系统中,若真实系统偏离理想系统的程序较大,以致于在泡点线上产生极值点,称为沸腾点;二、填空题1、二元气体混合物的摩尔分数y 1=,在一定的温度和压力下,组分1的逸度系数等于,组分2的逸度系数等于,则此时混合物的逸度系数为______;2、关系式l i v i f f ˆˆ=适用的条件是______________________________;3、关系式i i s i i x p py γ=适用的条件是___________________________________;4、关系式i i s i vi i x p py γϕ=ˆ适用的条件是___________________________________; 5、汽液平衡数据的一致性检验的方法一般有两种,即_______________和_______________;化工热力学标准化作业五一、填空题1、在敞开系统中,根据能量守恒原理,进入系统的能量=离开系统的能量+__________;2、系统与环境交换的总功包括轴功和_____;流动功;3、轴功是指_____________________________________________；流动功是指________________________________________;4、熵增原理的内容是__________________________________________________;5、稳定流动状态指的是__________________________________________________;二、计算题1、某厂有一输送92℃热水的管道,由于保温不良,致使用时水温下降至67℃,试求水温降低过程的热损失与损耗功;设环境温度为25℃,已知水的定压热容为kg·K;解：2、某厂有一输送90℃热水的管道,由于保温不良,致使用时水温下降至70℃,试求水温降低过程的热损失与损耗功;设环境温度为25℃,已知水的定压热容为kg·K;解：3、某理想气体分子量为28在1089K 、下通过一透平机膨胀到,透平机的排气以亚音速排出;进气的质量流量为135.4kg h -⋅,输出功率为,透平机的热损失为16700kJ h -⋅;透平机进、出口连接管的内径为,气体的热容为111.005kJ kg h --⋅⋅设与压力无关;试求透平机排气的温度及速度;4、求海水淡化最小功;原料为含NaCl %的海水,产品为纯水,温度都是室温25℃,已知实验测得25℃海水和纯水饱和蒸气压分别和,海水的渗透压为;。