流体力学 曲面总压力

流体力学压力计算公式好的，以下是为您生成的关于“流体力学压力计算公式”的文章：咱们在生活中啊，经常能碰到跟流体有关的事儿。

比如说，水龙头里哗哗流的水，或者是吹气时嘴里吐出的那股风。

这里面可都藏着流体力学的小秘密，特别是压力的计算。

咱先来说说啥是流体。

简单说，流体就是能流动的东西，像水、空气这些。

那压力呢？就好比有个大力士在后面推流体，让它产生力量。

流体力学里的压力计算公式，就像是一把神奇的钥匙，能帮咱们解开很多谜题。

其中一个常用的公式是P = ρgh 。

这里的 P 就是压力啦，ρ 表示流体的密度，g 是重力加速度，h 是深度。

比如说，咱们去游泳的时候，在游泳池里越往下走，就会感觉水的压力越大。

为啥呢？你看啊，假设水的密度不变，重力加速度也不变，那你下潜的深度越深，h 就越大，根据这个公式，压力 P 自然也就跟着变大啦。

我记得有一次，我带着一群小朋友去水族馆玩。

在一个巨大的水族箱前，小朋友们都好奇地盯着里面游来游去的鱼。

有个特别机灵的小家伙就问我：“叔叔，为啥这些鱼在下面游好像不费劲呢？”我就趁机跟他们讲起了流体力学的压力。

我指着水族箱说：“你们看，水越深，压力就越大。

这些鱼能在下面轻松游，是因为它们的身体结构适应了这种压力变化。

”然后我给他们简单解释了这个压力计算公式。

小朋友们似懂非懂地点点头，但眼睛里充满了好奇和探索的光芒。

再比如说，咱们家里用的高压锅。

为啥食物在高压锅里能煮得更快更烂乎？就是因为里面的压力大呀！通过增加锅内气体的压力，提高了水的沸点，这样就能在更高的温度下烹饪食物，节省时间还能让食物更美味。

还有飞机飞行的时候，机翼上方和下方的气流速度不一样，产生了压力差，这才有了升力，让飞机能飞起来。

总之，流体力学的压力计算公式在咱们生活中到处都能派上用场。

它不仅仅是书本上的一堆符号和数字，更是能解释好多神奇现象的好帮手。

不管是小小的水龙头，还是大大的飞机，都离不开这个神奇的公式。

咱们多去观察，多去思考，就能发现更多流体力学带来的奇妙之处。

第一章流体的定义：流体是一种受任何微小的剪切力作用时，都会产生连续变形的物质。

能够流动的物体称为流体，包括气体和液体。

流体的三个基本特征：1、易流性：流动性是流体的主要特征。

组成流体的各个微团之间的内聚力很小，任何微小的剪切力都会使它产生变形，(发生连续的剪切变形)——流动。

2、形状不定性：流体没有固定的形状，取决于盛装它的容器的形状，只能被限定为其所在容器的形状。

（液体有一定体积，且有自由表面。

气体无固定体积，无自由表面，更易于压缩）3、绵续性：流体能承受压力，但不能承受拉力，对切应力的抵抗较弱，只有在流体微团发生相对运动时，才显示其剪切力。

因此，流体没有静摩擦力。

三个基本特性：1.流体惯性涉及物理量：密度、比容（单位质量流体的体积）、容重、相对密度（与4摄氏度的蒸馏水比较）2.流体的压缩性与膨胀性压缩性：流体体积随压力变化的特性成为流体的压缩性。

用压缩系数衡量K，表征温度不变情况下，单位压强变化所引起的流体的体积相对变化率。

其倒数为弹性模量E，表征压缩单位体积的流体所需要做的功。

膨胀性：流体的体积随温度变化的特性成为膨胀性。

体胀系数α来衡量，它表征压强不变的情况下，单位温度变化所引起的流体体积的相对变化率。

３.流体的粘性流体阻止自身发生剪切变形的一种特性，由流体分子的结构及分子间的相互作用力所引起的，流体的固有属性。

恩氏粘度计测量粘度的一般方法和经验公式，见课本的24页牛顿内摩擦定律：当相邻两层流体发生相对运动时，各层流体之间因粘性而产生剪切力，且大小为：（省略）实验证明，剪切力的大小与速度梯度（流体运动速度垂直方向上单位长度速度的变化率）以及流体自身的粘度（粘性大小衡量指标）有关。

温度升高时，液体的粘性降低，气体的粘性增加。

（原理，查课本24~25页）三个力学模型1.连续介质模型：便于对宏观机械运动的分析，可以认为流体是由无穷多个连续分布的流体微团组成的连续介质。

这种流体微团虽小，但却包含着为数甚多的分子，并具有一定的体积和质量，一般将这种微团称为质点。

《流体力学与流体机械》(上)主要公式及方程式1．流体的体积压缩系数计算式：pp V V d d 1d d 1p ρρβ=-= 流体的体积弹性系数计算式：ρρd d d d pV p VE =-= 流体的体积膨胀系数计算式：TT V V d d 1d d 1T ρρβ-==2．等压条件下气体密度与温度的关系式：tβρρ+=10t ， 其中2731=β。

3．牛顿内摩擦定律公式：yuAT d d μ±= 或 y u A T d d μτ±==恩氏粘度与运动粘度的转换式：410)0631.00731.0(-⨯-=EE ν 4．欧拉平衡微分方程式： ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂-=∂∂-=∂∂-010101z p f y p f x pf z y x ρρρ 和 ⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂-=∂∂-=∂∂-010101z pf r p f r p f z r ρθρρθ欧拉平衡微分方程的全微分式： )d d d (d z f y f x f p z y x ++=ρ )d d d (d z f r f r f p z r ++=θρθ 5．等压面微分方程式： 0d d d =++z f y f x f z y x0d d d =++z f r f r f z r θθ 6．流体静力学基本方程式：C z p=+γ或2211z p z p +=+γγ或 2211z g p z g p ρρ+=+相对于大气时： C z g p a m =-+)(ρρ 或 2211)()(z g p z g p a m a m ρρρρ-+=-+ 7．水静力学基本方程式：h p p γ+=0，其中0p 为自由液面上的压力。

8．水平等加速运动液体静压力分布式：)(0gz ax p p +-=ρ；等压面方程式：C z g ax =+；自由液面方程式：0=+z g ax 。

注意：p 0为自由液面上的压力。

9．等角速度旋转液体静压力分布式：)2(220z gr p p -+=ωγ；等压面方程式：C z g r =-222ω；自由液面方程式：0222=-z g r ω。

流体力学重点概念总结(可直接打印版)第一章绪论表面力，也称面积力，是指直接施加在隔离体表面上的接触力，其大小与作用面积成比例。

剪力、拉力和压力都属于表面力。

质量力是指作用于隔离体内每个流体质点上的力，其大小与质量成正比。

重力和惯性力都属于质量力。

流体的平衡或机械运动取决于流体本身的物理性质（内因）和作用在流体上的力（外因）。

XXX通过著名的平板实验，说明了流体的粘滞性，并提出了牛顿内摩擦定律。

根据该定律，剪切应力τ只与流体的性质有关，与接触面上的压力无关。

动力粘度μ是反映流体粘滞性大小的系数，单位为N•s/m2.运动粘度ν等于动力粘度μ除以流体密度ρ。

第二章流体静力学流体静压强具有以下特性：首先，流体静压强是一种压应力，其方向总是沿着作用面的内法线方向，即垂直于作用面，并指向作用面。

其次，在静止的流体中，任何点上的流体静压强大小与其作用面的方位无关，即同一点上各方向的静压强大小均相等。

流体静力学基本方程为P=Po+pgh，其中Po为参考压力，p为流体密度，g为重力加速度，h为液体高度。

等压面是压强相等的空间点构成的面。

绝对压强以无气体分子存在的完全真空为基准起算，而相对压强以当地大气压为基准起算。

真空度是绝对压强不足当地大气压的差值，即相对压强的负值。

测压管水头是单位重量液体具有的总势能。

在平面上，净水总压力是潜没于液体中的任意形状平面的总静水压力P，其大小等于受压面面积A与其形心点的静压强pc之积。

需要注意的是，只要平面面积与形心深度不变，面积上的总压力就与平面倾角θ无关，压心的位置与受压面倾角θ无直接关系，是通过XXX表现的，而压心总是在形心之下。

对于作用在曲面壁上的总压力，水平分力Px等于作用于该曲面的在铅直投影面上的投影（矩形平面）上的静水总压力，方向水平指向受力面，作用线通过面积Az的压强分布图体积的形心。

垂直分力Pz等于该曲面上的压力体所包含的液体重，其作用线通过压力体的重心，方向铅垂指向受力面。

流体复习整理资料第一章 流体及其物理性质1.流体的特征——流动性:在任意微小的剪切力作用下能产生连续剪切变形的物体称为流体。

也可以说能够流动的物质即为流体。

流体在静止时不能承受剪切力，不能抵抗剪切变形。

流体只有在运动状态下，当流体质点之间有相对运动时，才能抵抗剪切变形。

只要有剪切力的作用，流体就不会静止下来，将会发生连续变形而流动。

运动流体抵抗剪切变形的能力（产生剪切应力的大小）体现在变形的速率上，而不是变形的大小（与弹性体的不同之处）。

2.流体的重度：单位体积的流体所的受的重力，用γ表示。

g 一般计算中取9.8m /s 23.密度：=1000kg/，=1.2kg/，=13.6，常压常温下，空气的密度大约是水的1/8003. 当流体的压缩性对所研究的流动影响不大，可忽略不计时，这种流体称为不可压缩流体，反之称为可压缩流体。

通常液体和低速流动的气体（Ｕ<70m ／s ）可作为不可压缩流体处理。

4.压缩系数：弹性模数：21d /d pp E N m ρβρ==膨胀系数：）（K /1d d 1d /d TVV T V V t ==β5.流体的粘性：运动流体内存在内摩擦力的特性（有抵抗剪切变形的能力），这就是粘滞性。

流体的粘性就是阻止发生剪切变形的一种特性，而内摩擦力则是粘性的动力表现。

温度升高时，液体的粘性降低，气体粘性增加。

6.牛顿内摩擦定律： 单位面积上的摩擦力为：3/g N m γρ=p V V p V V p d d 1d /d -=-=β21d 1d /d d p V m NV p pρβρ=-=h U μτ=内摩擦力为： 此式即为牛顿内摩擦定律公式。

其中：μ为动力粘度，表征流体抵抗变形的能力，它和密度的比值称为流体的运动粘度ν τ值既能反映大小，又可表示方向，必须规定：公式中的τ是靠近坐标原点一侧(即t -t 线以下)的流体所受的内摩擦应力，其大小为μ du/dy ，方向由du/dy 的符号决定，为正时τ与u 同向，为负时τ与u 反向，显然，对下图所示的流动，τ＞0， 即t —t 线以下的流体Ⅰ受上部流体Ⅱ拖动，而Ⅱ受Ⅰ的阻滞。

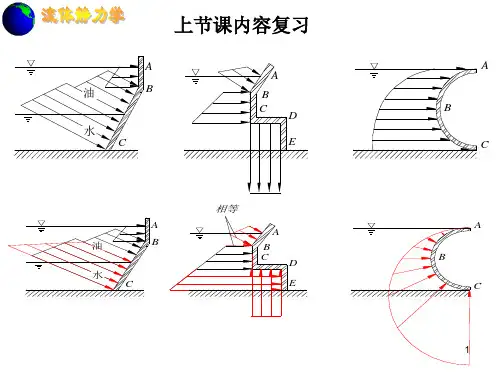
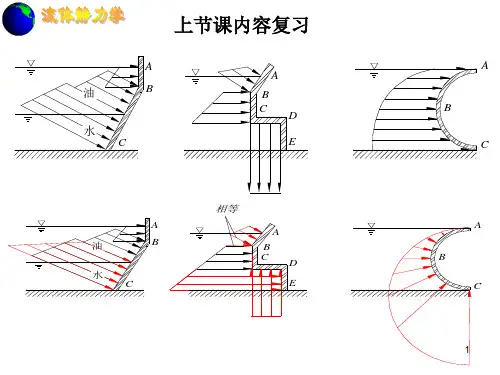
四、静止液体作用在曲面上的总压力在工程中常常会碰到曲面受压问题，如弧形间门，圆柱形油箱等。

作用在曲面随意点的液体静压强都沿其作用面的内法线方向垂直于作用面，但曲面各处的内法线方向不同，彼此互不平行，也不一定交于一点。

因此，求曲面上的总压力时，普通将其分为水平方向和铅直方向的分力分离举行计算。

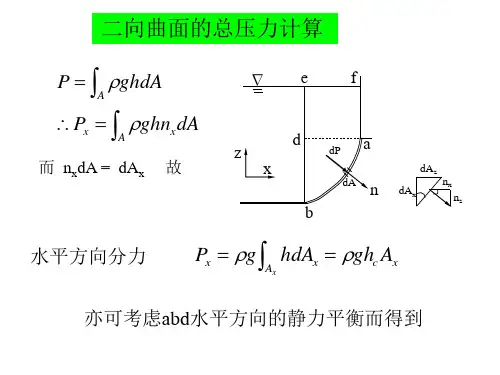
现研究二向曲面（如柱面、圆弧曲面） AB 上的液体总压力。

图 6-2-13AB 为垂直于纸面的柱体，长度l，受压曲面 AB ，其左侧承受液体的压力。

设在曲面土，深度 h 处取一极小面积dA ，作用在 dA 上的压力 dP= pdA = ρghdA ，该力垂直于面积 dA ，并与水平面成夹角a，此力可分解成水平分力 dPx = dPcosa = ρgh dAcosa和垂直分力 dPz= dP sina =ρgh dAsina .因为dAcosa 和dAsina 分离等于极小面积 dA 在铅直面和水平面上的投影．令 dAx = dAcosa， dAz=dAsina，所以 dPx =ρgh dAx及 dPz= ρgh dAz，经积分可得：式（ 6-2-9 ）右边的积分等于曲面 AB 在铅直平面上投影面积 Ax对液面的水平轴 oy 的静矩. 设h c 为 Ax的形心在液面下的吞没深度，则因此可见，作用于曲面上的液体总压力P的水平分力Px等于该曲面的铅直投影面上的总压力。

因此，可以引用求平面总压力的主意求解曲面上液体总压力的水平分力。

式（6-2-10）右边的 hdAz , 是以 dAz为底面积，水深h为高的柱体体积。

zAhdA z即受压曲面 AB 与其在自由面上的投影面积CD这两个面之间的柱体体积 ABCD ，称为压力体，以 V 表示。

所以这就是说，作用于曲面上液体总压力P的铅直分力Pz等于其压力体内的液体分量。

可见准确绘制压力体是求解铅直分力的关键.压力体是由三种面封闭所成的体积：即 1 ）曲面本身； 2 ）液体的自由表面（相对压强为零）或自由表面的延伸面； 3 ）自曲面两端向自由表面作铅垂面。

水水银题1图1、如图所示，用多管水银测压计测水箱表面的压强。

图中高程的单位为m .试求水箱表面的相对压强。

( 水银的密度3/13600m kg =ρ）2、如图所示，密度3920/kg m ρ=的油在管中流动。

用水银压差计测量长度3l m =的管流的压差，其读数为90h mm ∆=。

已知管径25d mm =,测得的油的流量434.510/Q m s -=⨯,试求油的运动粘性系数。

3、图示一密闭容器,上层为空气,中层为ρ=800kg/m 3的石油，下层为ρ=1200kg/m 3的甘油.试求：当测压管中甘油表面高程为9.14m 时压力表G 的读数。

题型一:曲面上静水总压力的计算问题(注：千万注意方向，绘出压力体）1、AB 曲面为一圆柱形的四分之一,半径R=0。

2m ，宽度(垂直纸面）B=0.8m ，水深H=1.2m,液体密度3/850m kg =ρ，AB 曲面左侧受到液体压力。

求作用在AB 曲面上的水平分力和铅直分力。

(10分） 解：（1)水平分力：RB RH g A h P z c x ⋅-==)2(ργ…….(3分） N 1.14668.02.0)22.02.1(8.9850=⨯⨯-⨯⨯=，方向向右（2分）。

（2）铅直分力：绘如图所示的压力体,则B R R R H g V P z ⎥⎥⎦⎤⎢⎢⎣⎡+-==4)(2πργ………。

（3分） 1.15428.042.014.32.0)2.02.1(8.98502=⨯⎥⎥⎦⎤⎢⎢⎣⎡⨯+⨯-⨯⨯=,方向向下（2分）。

2．有一圆滚门，长度l=10m ，直径D=4。

2m ，上游水深H1=4。

2m ，下游水深H2=2。

1m,求作用于圆滚门上的水平和铅直分压力。

ldQhG BA空 气 石 油甘 油7.623.661.529.14m11解题思路:（1)水平分力：l H H p p p x )(21222121-=-=γ 方向水平向右。

（2）作压力体，如图，则l D Al V p z 4432πγγγ⨯=== 方向垂直向上。