曲面壁静水总压力案例二.
- 格式:ppt
- 大小:693.00 KB
- 文档页数:8






第五节 作用于曲面壁上的静水总压力一、 静水总压力的两个分力水工建筑物中常碰到受压面为曲面的情况,如弧形闸门、拱坝坝面、闸墩及边墩等。
其水力计算归为曲面壁静水总压力的求解。
因曲面上各点静水压强的方向也是垂直指向作用面,各点压力互不平行,则求平面壁静水总压力的方法这里不再适用。
但是我们可以将曲面壁上的静水总压力分解为水平方向的力P x 和铅直方向的力P z ,分别求解,然后再根据求合力的法则,求出静水总压力P 。
公式推导如下。
现以弧形闸门AB 为例,讨论曲面壁静水总压力计算问题。
见图2-24。
为了确定P x 、P z ,先取宽度为b (即闸门宽度)、截面为ABC 的水体为脱离体。
z图 2-23(a)(b)(c)注意:从A点向下做一铅直平面AC ,从B点做一水平面BC ,两平面的相交于C,由曲面AB 与AC 、BC 平面包围的水体即为ABC 脱离水体,如图2-23(b )所示,研究该水体的平衡。
在图2-23中P '── 闸门AB 对水体的反作用力,与P 等值反向; x P '、z P '── P '的水平分力和铅直分力;AC P 、BC P ──作用在AC 、BC 面的静水总压力;G ── 脱离体水重。
1. 静水总压力的水平分力分析脱离水体的受力情况,如图2-23(b )所示。
列水平方向的静力平衡方程得:x P '=AC P根据作用力与反作用力大小相等,方向相反的原理,闸门受到的水平分力为x x P P '==AC P (2-33)因AC 为铅直面,而且相当于曲面AB 在铅直投影面上的投影,则由上式可知:作用于曲面壁上静水总压力的水平分力P x 等于作用于该曲面在铅直投影面上的静水总压力。
因此,求水平方向的静水总压力可归结为:将曲面投影到铅直投影平面上,再计算出铅直投影面上所受到的静水总压力即为P 的水平分力P x 。
2. 静水总压力的铅直分力P z根据静力平衡条件,列出铅直方向的静力平衡方程式得:G P P BC z -='由于BC 水平面是以BC 和b 为边的矩形平面,其面积可用A BC 表示,,所处水深为h 2,其面上各点的压强都等于2h γ,则MCBN BC BC V A h P γγ==2式中V MBCN —— 以MCBN 为底面积、b 为宽度的棱柱体体积。
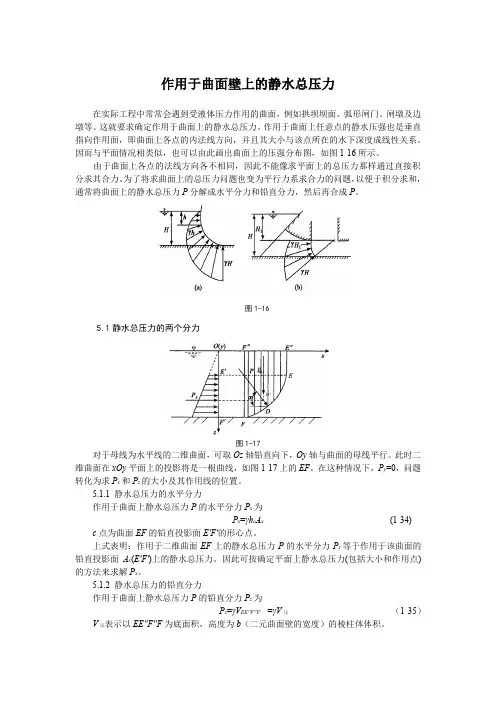
作用于曲面壁上的静水总压力在实际工程中常常会遇到受液体压力作用的曲面,例如拱坝坝面、弧形闸门、闸墩及边墩等。
这就要求确定作用于曲面上的静水总压力。
作用于曲面上任意点的静水压强也是垂直指向作用面,即曲面上各点的内法线方向,并且其大小与该点所在的水下深度成线性关系。
因而与平面情况相类似,也可以由此画出曲面上的压强分布图,如图1-16所示。
由于曲面上各点的法线方向各不相同,因此不能像求平面上的总压力那样通过直接积分求其合力。
为了将求曲面上的总压力问题也变为平行力系求合力的问题,以便于积分求和,通常将曲面上的静水总压力P分解成水平分力和铅直分力,然后再合成P。
图1-165.1静水总压力的两个分力图1-17对于母线为水平线的二维曲面,可取Oz轴铅直向下,Oy轴与曲面的母线平行。
此时二维曲面在xOy平面上的投影将是一根曲线,如图1-17上的EF。
在这种情况下,P y=0,问题转化为求P x和P z的大小及其作用线的位置。
5.1.1 静水总压力的水平分力作用于曲面上静水总压力P的水平分力P x为P x=γh c A x(1-34) c点为曲面EF的铅直投影面E′F′的形心点。
上式表明:作用于二维曲面EF上的静水总压力P的水平分力P x等于作用于该曲面的铅直投影面A x(E′F′)上的静水总压力。
因此可按确定平面上静水总压力(包括大小和作用点)的方法来求解P x。
5.1.2 静水总压力的铅直分力作用于曲面上静水总压力P的铅直分力P z为P z=γV EE′′F′′F=γV压(1-35)V压表示以EE′′F′′F为底面积,高度为b(二元曲面壁的宽度)的棱柱体体积。
上式表明:作用于二维曲面EF 上的静水总压力P 的铅直分力P z 等于压力体内水的重量。
在实际计算中,只要求得V 压,就可求得P z ,关键在于掌握压力体的构成。
5.1.3 压力体的组成压力体应由下列界面所围成:(1)受压曲面本身;(2)受压曲面在自由液面(或自由液面的延展面)上的投影面,如图1-17(或图1-18)所示;(3)从曲面的边界向自由液面(或自由液面的延展面)所作的铅直面。




项目二平面壁上静水总压力一、选择题1、压力中心是A、淹没面积的中心B、压力体的中心C、总压力的作用点D、受压面的形心答案:( C )答案分析:静水总压力的作用点就是“压力中心”,这是“压力中心”的定义。
2、压力中心位置A、受压面的形心以上B、受压面的形心以下C、受压面的形心处或受压面的形心以下D、不能确定答案:( C )答案分析:对于静止均质液体,当受压面平行液面并放置于液面以下时,受压面各点均匀受压,压力中心的位置与受压面形心重合;当受压面与液面不平行时,受压面各点非均匀受压,置于液面以下越深位置受压越大,故作为静水总压力的作用点的“压力中心”低于受压面形心的位置。
3、平面壁上静水总压力的方向A、倾斜指向受压面B、平行于受压面C、垂直指向受压面D、背离受压面答案:( C )答案分析:因为各点的水压力都垂直指向受压面,当受压面为平面时,作为各点静水压力之和的静水总压力也垂直指向受压面(这是静水压强特性是力学中平行力系求合力的原理在本课程中的应用)。
4、图解法计算静水总压力适用于受压面为A、矩形平面壁B、圆形平面壁C、任意形状平面壁D、梯形平面壁答案:( A )答案分析:图解法是应用静水压强分布图来求解静水总压力的大小和压力中心位置的方法,只有当受压面为矩形平面时,才能绘制静水压强分布图。
静水压强分布图反映矩形平面受压面沿水深方向的受压情况。
5、解析法计算静水总压力适用于受压面为A、矩形平面壁B、圆形平面壁C、梯形平面壁D、以上都对答案:( D )答案分析:解析法是利用受压平面的面积与受压平面形心点的压强乘积求解静水总压力,利用受压平面的面积、面积矩、惯性矩、受压平面形心点坐标值求解压力中心位置的方法。
该方法适用于任意形状的受压平面。
二、判断题1、曲面上静水总压力的水平分力等于曲面的铅垂投影面上所受的静水总压力。
答案:(√)答案分析:从曲面上静水总压力计算公式推导可知,曲面上静水总压力的水平分力等于曲面的铅垂投影面上所受的静水总压力,曲面上静水总压力的铅直分力等于曲面对应压力体的水重(假设注满水)。
求静水总压力例题油和水摘要:1.静水总压力的定义与计算方法2.例题:油和水的静水总压力3.静水总压力的实际应用正文:一、静水总压力的定义与计算方法静水总压力是指静止液体作用在与其接触的某个平面或曲面上的总压力。
静水压力的计算方法可以分为以下两种:1.平面上静水总压力的计算:平面上静水总压力的大小,应等于分布在平面上各点静水压强作用的总压力的总和。
作用在单位宽度的静水总压力,应等于静水压强分布图的面积。
因此整个矩形平面的静水总压力,则等于平面宽度乘以压强分布图的面积。
2.任意平面上静水总压力的计算:等于平面形心点到各顶点的静水压强乘以对应面积的矢量和。
二、例题:油和水的静水总压力假设一个容器中有油和水,油的密度为ρ1,水深为h1;水的密度为ρ2,水深为h2。
求油和水对容器底部的静水总压力。
解:根据静水总压力的计算方法,我们需要先求出油和水在容器底部的压强分布图,然后计算出静水总压力。
1.求油和水的压强分布图:根据液体压强公式pgh(其中p 为压强,g为重力加速度,h 为液体深度),可以求出油和水在容器底部的压强分布图。
2.计算静水总压力:根据静水总压力的计算方法,可以得到油和水对容器底部的静水总压力。
三、静水总压力的实际应用静水总压力在许多实际问题中有广泛的应用,如:1.消防系统:高位消防水箱的设置高度应保证最不利点消火栓静水压力。
当高位消防水箱不能满足上述静压要求时,应设增压设施。
2.容器设计:容器的设计需要考虑静水总压力对容器底部的影响,以确保容器的稳定性和安全性。
3.管道设计:在管道设计中,需要考虑静水总压力对管道的影响,以确保管道的稳定性和安全性。