第5章 SPSS均值比较T检验和方差分析
- 格式:ppt
- 大小:316.50 KB
- 文档页数:51






均值比较检验和方差分析详解演示文稿一、均值比较检验1.两个样本的均值比较:用于比较两个样本的均值是否存在显著差异。
常用的假设检验方法有t检验和z检验。
2.多个样本的均值比较:用于比较两个以上样本的均值是否存在显著差异。
常用的假设检验方法有方差分析。
针对不同的研究问题和样本特征,我们可以选择不同的假设检验方法进行均值比较。
二、方差分析方差分析是一种统计学中常用的分析方法,用于检验两个以上样本均值之间是否存在显著差异。
方差分析基于方差的分解原理,将总体方差分解为组内变异和组间变异,并通过统计检验来确定组间变异是否显著。
方差分析包括单因素方差分析和多因素方差分析两种形式。
1.单因素方差分析:适用于只有一个自变量(因素)的情况,用于比较不同水平的因素是否对观测变量有显著影响。
单因素方差分析有一元方差分析和重复测量方差分析两种形式。
2.多因素方差分析:适用于有两个或两个以上自变量(因素)的情况,用于比较多个自变量的主效应及其交互效应对观测变量的影响。
常用的多因素方差分析方法有二元方差分析和三元方差分析。
方差分析的基本思想是通过比较组间方差和组内方差的大小关系来判断样本均值之间是否有显著差异。
在进行方差分析前,需要先对数据的正态性、方差齐性进行检验,以确定方差分析是否适用。
三、均值比较检验和方差分析的步骤进行均值比较检验和方差分析的步骤如下:1.确定研究问题和样本特征:明确需要比较的样本均值或不同因素对样本均值的影响。
2.数据收集和整理:收集相应的样本数据,并进行数据清洗和整理。
3.正态性检验:对样本数据进行正态性检验,以确定是否满足方差分析的正态性假设。
4.方差齐性检验:对样本数据进行方差齐性检验,以确定是否满足方差分析的方差齐性假设。
5.假设检验:根据样本特征和研究问题,选择适当的假设检验方法进行分析。
对于均值比较检验,常用的方法有t检验和z检验;对于方差分析,常用的方法有一元方差分析和多元方差分析。
6.结果解释和报告:根据显著性检验结果,给出结论并解释研究结果。



第5章SPSS均值比较T检验和方差分析第5章主要介绍了SPSS软件中进行均值比较的方法,包括t检验和方差分析。
本文将详细介绍SPSS中进行均值比较的步骤,以及如何解读结果。
5.1t检验t检验是一种用于比较两个样本均值差异的统计方法。
在SPSS中,进行t检验的步骤如下:1.打开SPSS软件,并导入需要进行t检验的数据集。
2.选择“分析”菜单,在下拉菜单中选择“比较均值”选项,再选择“独立样本t检验”选项。
3.在弹出的对话框中,将需要比较的变量移动到“因子”框中,将“分组变量”移动到“因子”框中,并选择需要进行的假设检验类型。
4.点击“确定”按钮,等待计算结果。
5.在输出窗口中,可以查看计算结果,包括均值、标准差、样本量、t值和p值等。
通常,我们关注的是p值,如果p值小于0.05,则认为差异显著。
例如,我们想比较男性和女性的体重是否有显著差异。
我们将体重作为因变量,性别作为自变量,进行t检验。
在计算结果中,如果p值小于0.05,则可以认为男女性别对体重有显著影响。
5.2方差分析方差分析是一种用于比较三个或更多个样本均值是否存在差异的统计方法。
在SPSS中,进行方差分析的步骤如下:1.打开SPSS软件,并导入需要进行方差分析的数据集。
2.选择“分析”菜单,在下拉菜单中选择“比较均值”选项,再选择“单因素方差分析”选项。
3.在弹出的对话框中,将需要比较的变量移动到“因子”框中,将“分组变量”移动到“因子”框中,并选择需要进行的假设检验类型。
4.点击“确定”按钮,等待计算结果。
5.在输出窗口中,可以查看计算结果,包括均值、标准差、样本量、F值和p值等。
通常,我们关注的是p值,如果p值小于0.05,则认为差异显著。
例如,我们想比较不同药物对治疗效果的影响。
我们将药物作为因变量,治疗效果作为自变量,进行方差分析。
在计算结果中,如果p值小于0.05,则可以认为不同药物对治疗效果有显著影响。
通过以上步骤,我们可以在SPSS中进行均值比较、t检验和方差分析。
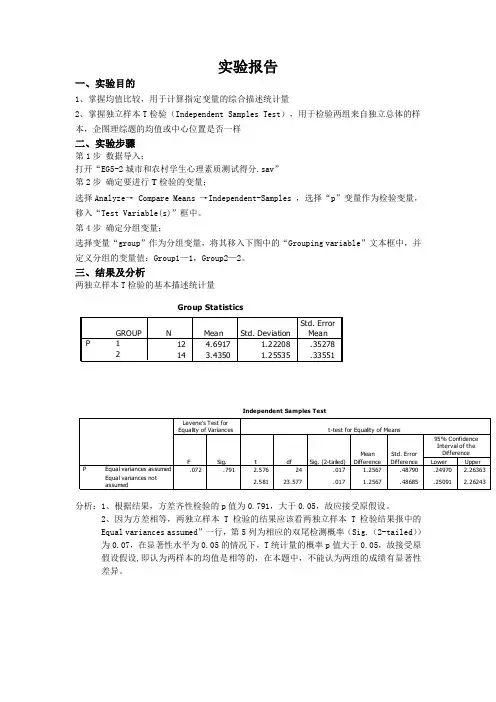
实验报告一、实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量2、掌握独立样本T检验(Independent Samples Test),用于检验两组来自独立总体的样本,企图理综题的均值或中心位置是否一样二、实验步骤第1步数据导入;打开“EG5-2城市和农村学生心理素质测试得分.sav”第2步确定要进行T检验的变量;选择Analyze→ Compare Means →Independent-Samples ,选择“p”变量作为检验变量,移入“Test Variable(s)”框中。
第4步确定分组变量;选择变量“group”作为分组变量,将其移入下图中的“Grouping variable”文本框中,并定义分组的变量值:Group1—1,Group2—2。
三、结果及分析两独立样本T检验的基本描述统计量分析:1、根据结果,方差齐性检验的p值为0.791,大于0.05,故应接受原假设。
2、因为方差相等,两独立样本T检验的结果应该看两独立样本T检验结果报中的Equal variances assumed”一行,第5列为相应的双尾检测概率(Sig.(2-tailed))为0.07,在显著性水平为0.05的情况下,T统计量的概率p值大于0.05,故接受原假设假设,即认为两样本的均值是相等的,在本题中,不能认为两组的成绩有显著性差异。
实验报告一、实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量2、掌握配对样本T检验(Paired Samples Test),用于检验两个相关的样本是否来自具有相同均值的总体。
二、实验步骤第1步数据组织;打开“EG5-1学生培训前后心理测试得分.sav”第2步确定配对分析的变量选择Analyze→ Compare Means →Paired-Samples T Test,将变量“before”和“after”添加到“Paired Variables”框中,作为一对分析的配对变量三、结果及分析分析:表“paired samples test”显示,学生培训前后的平均成绩相差 -0.158,平均成绩差值的标准差为1.5048,差值标准差的标准误为0.4344.在置信水平为95%时平均值差值的置信区间为-1.114~0.798。

spss 均数标准差 t检验SPSS均数、标准差和t检验。
在统计学中,均数、标准差和t检验是非常重要的概念和方法。
它们可以帮助研究者对数据进行分析和推断,从而得出结论和决策。
本文将从理论和实践两个方面来介绍SPSS软件在均数、标准差和t检验方面的应用。
首先,我们来看看均数和标准差。
均数是一组数据的平均值,它可以反映出这组数据的集中趋势。
而标准差则是衡量数据的离散程度,标准差越大,数据的离散程度越大。
在SPSS软件中,我们可以通过简单的操作得出数据的均数和标准差,并且可以通过图表的方式直观地展示出来。
这对于研究者来说非常方便,可以快速了解数据的特征和规律。
接下来,我们谈谈t检验。
t检验是用来比较两组数据均数是否存在显著差异的统计方法。
在SPSS软件中,进行t检验也是非常简单的,只需要输入数据和设定一些参数,就可以得出检验结果。
通过t检验,我们可以判断两组数据的均数是否存在显著差异,这对于研究者来说是非常重要的,可以帮助他们进行科学的分析和研究。
在实际的研究中,我们可以通过一个案例来说明SPSS在均数、标准差和t检验方面的应用。
假设我们想要研究两种不同的教学方法对学生成绩的影响,我们可以使用SPSS软件来进行数据的录入和分析。
首先,我们可以得出每种教学方法下学生成绩的均数和标准差,然后通过t检验来比较两种教学方法的成绩是否存在显著差异。
通过SPSS软件,我们可以快速得出结论,并且可以通过图表的方式直观地展示出来,这对于研究者来说是非常方便和有效的。
总之,SPSS软件在均数、标准差和t检验方面的应用是非常广泛和重要的。
它可以帮助研究者进行数据的分析和推断,从而得出科学的结论和决策。
通过SPSS软件,我们可以快速、准确地得出数据的特征和规律,这对于研究者来说是非常有益的。
希望本文对大家有所帮助,谢谢!以上就是本文的全部内容,希望对您有所帮助。