晶体学符号与倒格子
- 格式:pptx
- 大小:23.35 MB
- 文档页数:123

二维正格子和倒格子的转换在晶体学中,二维晶格的正格子和倒格子形成对偶关系,可以通过傅里叶变换互相转换。
具体转换方法如下:1. 正格子的矢量和倒格子的矢量都用向量符号表示,正格子用$\vec{R}$表示,倒格子用$\vec{G}$表示。
2. 正格子中一个点的位置用$\vec{r}$表示,倒格子中一个点的位置用$\vec{g}$表示。
3. 正格子和倒格子的矢量形成内积为$2\pi n$,其中$n$是整数。
即$\vec{R}\cdot\vec{G}=2\pi n$。
4. 正格子的基矢量是$\vec{a}_1$和$\vec{a}_2$,倒格子的基矢量是$\vec{b}_1$和$\vec{b}_2$。
它们的关系式是:$$\vec{a}_i\cdot\vec{b}_j=2\pi\delta_{ij}$$其中$\delta_{ij}$是克罗内克δ符号,当$i=j$时取值为1,否则取值为0。
5. 正格子和倒格子中,每个点的位置矢量可以用它在对应基矢量上的坐标表示。
即$\vec{r}=x_1\vec{a}_1+x_2\vec{a}_2$,$\vec{g}=y_1\vec{b}_1+y_2\vec{b}_2$。
6. 正格子的基矢量的长度分别为$a_1$和$a_2$,倒格子的基矢量的长度分别为$b_1$和$b_2$。
它们的关系式是:$$\vec{b}_i=\frac{2\pi}{\vec{a}_1\times\vec{a}_2}\vec{a}_j\times(-1)^{i+j}\qquad(i\neq j)$$通过以上规则,可以将一个二维正格子的坐标转换为对应的倒格子坐标。
反之,如果已知二维倒格子的坐标,也可以通过类似的方法转换为正格子坐标。



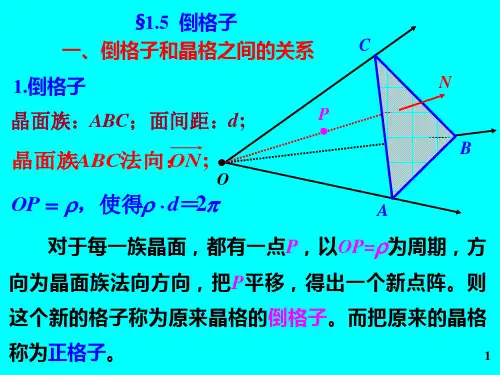
1.5.2倒格子的性质倒格子具有以下基本性质:(1)以倒格子基矢b 1,b 2,b 3为棱边构成的平行六面体称为倒格子原胞,其体积为v *。
()31232*()c v v π=⋅⨯=b b b …………………(1-5-3)(2)倒格矢112233h h h h =++G b b b 和正格子空间中面指数为(h 1h 2h 3)的晶面族正交,即G h 沿晶面族的法线方向。
我们知道,晶面族中最靠近原点的晶面ABC在123,,a a a 上的截距分别为312123,,a a a h h h ,如图1-18所示,易写出矢量CA 和CB :31133223h h h h =-=-=-=-a a CA OA OC a a CB OB OC ………………………………………………………(1-5-4) 矢量CA 和CB 都在ABC 面上,因此,只要证明00h h ⋅=⎧⎨⋅=⎩G CA G CB ,则就能说明112233h h h h =++G b b b 与面指数为(h 1h 2h 3)的晶面族正交。
实际上,利用关系式(1-5-2),2,0,i j i j i jπ=⎧⋅=⎨≠⎩a b (其中i 和j 均为1,2,3)…………………………………(1-5-2)有31112233133211223323()()0,()()0.h h h h h h h h h h h h ⋅=++⋅-=⋅=++⋅-=a a G CA b b b a a G CB b b b …………………………………………(1-5-5)(3)晶面族(h 1h 2h 3)的面间距d h 与倒格矢G h 的模成反比,关系为2h h d π=G 。
图1-18中ABC 面就是晶面族(h 1h 2h 3)中距原点最近的晶面,所以这族晶面的面间距d h 就等于原点到面ABC 的距离,而之族晶面的法线方向即为G h 的方向,其面间距为1112233111112233()2h h h hh h h d h h h h h π⋅++=⋅==++G a b b b a G b b b G 。





中文名称:倒格子英文名称:Reciprocal lattice术语来源:固体物理学倒格子,亦称倒易格子(点阵),它在固体物理学中,特别是在晶格动力学理论、晶体电子论以及晶体衍射方面有着较为广泛的应用。
1定义假定晶格点阵基矢a1、a2、a3(1、2、3表示 a 的下标,粗体字表示a1 是矢量,以下类同)定义一个空间点阵,我们称之为正点阵或正格子,若定义b1 = 2 π ( a2× a3) /νb2 = 2 π ( a3× a1) /νb3 = 2 π ( a1× a2) /ν其中 v = a1· ( a2× a3 ) 为正点阵原胞的体积,新的点阵的基矢b1、b2、b3是不共面的,因而由b1、b2、b3也可以构成一个新的点阵,我们称之为倒格子,而b1、b2、b3 称为倒格子基矢。
2性质1. 倒格子的一个矢量是和晶格原胞中一组晶面相对应的,它的方向是该晶面的法线方向,而它的大小则为该晶面族面间距倒数的2π倍。
2. 由倒格子的定义,不难得到下面的关系a i ·b j = 2 πδij3. 设倒格子与正点阵(格子)中的位置矢量分别为G = αb1+ βb2 + γb3R = ηa1 + θa2 + λa3 (α,η,β,θ,γ,λ皆为整数)不难证明G·R = 2π ( αη + βθ +γλ ) = 2π n,其中n为整数。
4. 设倒格子原胞体积为ψ,正格子原胞体积为 v ,根据倒格子基矢的定义,并利用矢量乘法运算知识,则可得到ψ v = ( 2 π )^3.5. 正格子晶面族(αβγ)与倒格子矢量G = αb1+ βb2 + γb3 正交(具体的内容及证明过程,请参考文献[1])3倒格子引入的意义这里简单的说一点,如上面的性质1,倒格子中的一个基矢对应于正格子中的一族晶面,也就是说,晶格中的一族晶面可以转化为倒格子中的一个点,这在处理晶格的问题上有很大的意义。

证明正格矢和倒格矢的关系正格矢和倒格矢是固体物理中用于描述晶体结构的两个重要的概念。
正格矢表示晶体中原子位置的空间周期性排列,而倒格矢则表示正格矢所描述的周期性结构在动量空间中的周期性。
晶体是由周期性重复单元组成的,这些单元以一定的间隔沿着晶体的各个方向排列。
这个规则的周期性排列可以用正格矢来描述。
正格矢是指晶体中原子位置的空间周期性排列,通常用一个小数定义。
在一个立方晶体中,可以将正格矢表示为n1a1 + n2a2 + n3a3,其中n1、n2、n3是整数,a1、a2、a3是三条无关联的基矢。
倒格矢是对正格矢所描述的周期性结构在动量空间中的周期性的表示。
在倒空间中,倒格矢的数目与晶体的维数相同。
通常用G来表示倒格矢。
在一个立方晶体中,倒格矢可以表示为n'1b1 + n'2b2 + n'3b3,其中n'1、n'2、n'3是整数,b1、b2、b3是三条无关联的倒空间基矢。
在晶体中,存在一个映射关系将正格矢和倒格矢联系起来。
这个关系可以通过傅里叶变换来描述。
傅里叶变换是一种数学变换,它将一个函数从时间域转换到频域或者将一个函数从空间域转换到动量域。
晶体结构中的周期性排列可以通过傅里叶变换将其转化为动量空间中的周期性。
具体来说,在周期性结构中,可以将位置空间中的函数f(r)表示为傅里叶级数的形式:f(r) = ∑g(G) * e^(iGr)其中G为倒格矢,g(G)称为结构因子,表示晶体中每个位置的复振幅。
e^(iGr)为平面波的形式,G·r为内积。
通过上述的傅里叶变换关系,可以看出正格矢和倒格矢之间存在一个简单的关系,即正格矢和倒格矢的内积为2π。
因此,可以得到如下关系:G·R = 2π(N-M)其中R为正格矢,G为倒格矢,N和M为整数。
这个关系说明了正格矢和倒格矢之间的联系。
总结起来,正格矢和倒格矢是固体物理中用于描述晶体结构的两个重要概念。