数学：沪科版九年级下 26.7 圆和圆的位置关系(课件)

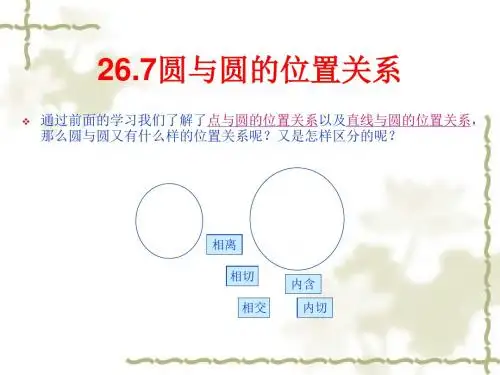
圆与圆的位置关系1．圆心距的定义两圆圆心之间的距离叫做圆心距．如图，O1O2的长度就是圆心距；我们把通过两圆圆心的直线叫做连心线，直线O1O2就是两圆的连心线．(1)我们通常用O1O2表示圆心距，实际上圆心距应该是它的长度而不是线段本身；(2)注意圆心距和连心线是不同的，圆心距是线段的长度，连心线是直线；(3)由此可知，任意两个圆的组合图形都是轴对称图形，它们的对称轴就是两圆的连心线．【例1】如图，已知O1与O2的直径都是2 cm，线段AB＝3 cm.求O1和O2的圆心距．分析：根据圆心距的定义，圆心距是连接两圆圆心的线段的长度，所以O1和O2的圆心距等于两圆半径的和再加上线段AB的长．解：∵O1与O2的直径都是2 cm，∴O1A＝O2B＝1 cm.∵O1O2＝O1A＋O2B＋AB＝1＋1＋3＝5(cm)，∴O1和O2的圆心距是5 cm.2．圆与圆的位置关系两个圆的位置关系有且只有7种情况：设两圆的半径分别是r1和r2，圆心距是d，则：(1)当圆心距d＞r1＋r2时，两个圆没有公共点，并且每个圆上的点都在另一个圆的外部，称这两个圆外离．．，如图1.(2)当d＝r1＋r2时，两个圆有唯一的公共点，并且除了这个公共点外，每个圆上的点都在另一个圆的外部，称这两个圆外切．．．．．，如图2，这个公共点叫做切点．(3)当r2－r1＜d＜r1＋r2(设r1≤r2)时，两个圆恰好有两个不同的公共点，称这两个圆相交．．，如图3.(4)当d＝r2－r1(设r1＜r2)时，两个圆有唯一的公共点，并且除了这个公共点外，一个圆上的点都在另一个圆的内部，称这两个圆内切．．．．．，如图4，这个公共点叫做切点．(5)当0＜d＜r2－r1(设r1＜r2)时，两个圆没有公共点，并且一个圆上的点都在另一个圆的内部，称这两个圆内含．．．，如图5.．．但不同心(6)当d＝0且r1≠r2时，两个圆没有公共点，并且一个圆上的点都在另一个圆的内部，两个圆的圆心重合，称这两个圆内含．．．，如图6.．．，简称它们为同心圆．．且同心(7)当d＝0且r1＝r2时，两个圆重合．．．．要判定两圆的位置关系，有两种具体的途径：(1)根据两圆公共点的个数判断①当两圆没有公共点时，两圆的位置关系是外离或内含；②当两圆有且只有一个公共点时，两圆的位置关系是内切或外切；③当两圆有两个公共点时，两圆的位置关系是相交．(2)根据两圆的半径与圆心距的关系判断．【例2－1】已知O1和O2的半径分别为3 cm和2 cm且O1O2＝1 cm，则O1与O2的位置关系为__________．解析：已知O1和O2的半径分别为3 cm和2 cm且O1O2＝1 cm，所以3－2＝1，即r1－r2＝d，因此O1和O2的位置关系为内切．答案：内切【例2－2】两圆圆心都在y轴上，且两圆相交于A，B两点，点A的坐标为(2,1)，则点B的坐标为( )．A．(－2,1) B．(－2，－1)C．(2，－1) D．(0,1)解析：∵圆心都在y轴上的两圆所构成的图形是轴对称图形，且对称轴是y轴，∴它们的交点A，B关于y轴对称．∵点A的坐标为(2,1)，且关于y轴对称的点的纵坐标不变，横坐标互为相反数，∴B点坐标为(－2,1)．答案：A【例2－3】已知A，B相切，圆心距为10 cm，其中A的半径为4 cm，则B的半径为______．解析：两圆相切，有可能两圆外切，也有可能两圆内切，所以B的半径就有两种情况．设B的半径为R.(1)如果两圆外切，那么d＝10＝4＋R，R＝6 cm；(2)如果两圆内切，那么d ＝|R－4|＝10，R＝－6(舍去)或R＝14.答案：6 cm或14 cm【例2－4】如图，O的半径为5 cm，点P是O外一点，OP＝8 cm.求：(1)以P为圆心作P与O外切，小圆P的半径是多少？(2)以P为圆心作P与O内切，大圆P的半径是多少？分析：由小圆P与O外切，可知小圆P与O的半径的和是OP的长，即8 cm，又知O的半径为5 cm，从而求出小圆P的半径；同理，大圆P与O内切，可知大圆P 与O的半径的差是OP的长，即8 cm.也能求出大圆P的半径．解：(1)设P与O外切于点A，则PA＝PO－OA，∴PA＝3 cm.(2)设P与O内切于点B，则PB＝PO＋OB，∴PB＝13 cm.【例2－5】已知：如图，△ABC 中，∠C ＝90°，AC ＝12，BC ＝8，以AC 为直径作O ，以B 为圆心，4为半径作B ．求证：O 与B 相外切． 分析：要证明两圆外切就要分别求两圆的半径和圆心距．本题中圆O 的半径很容易求出，就是线段AC 的一半，即6；圆B 的半径是4，是已知的；根据勾股定理可以求出线段OB 的长．根据d ＝R ＋r ，可以判定两圆外切．证明：连接BO .∵AC 为O 的直径，AC ＝12，∴O 的半径OC ＝12AC ＝6.∵∠C ＝90°且BC ＝8，∴BO ＝OC 2＋BC 2＝62＋82＝10.∵O 的半径R 1＝6，B 的半径R 2＝4， ∴BO ＝R 1＋R 2.∴O 与B 相外切．【例2－6】O 1和O 2交于A ，B 两点，且O 1经过点O 2.若∠AO 1B ＝90°，那么∠AO 2B 的度数是__________．错解：135°(如图1)错因分析：错解只考虑到r 2＜r 1，且O 1，O 2在公共弦AB 两侧时的情形，未考虑到r 2＞r 1，且O 1，O 2在公共弦同侧时的情形(如图2)．如果能联想：“一条弦所对的圆心角为90°，则这弦所对的圆周角为多少度”的问题，并运用分类讨论的思想画出两圆心在公共弦的同侧、两侧两种情况，且r 2＜r 1，或r 2＞r 1，则可避免错误．正解：135°或45°3．如何判定圆与圆的位置关系圆与圆的位置关系是本章中的重点知识，是近几年各地中考试题中的热点问题，也是学好圆这一章的关键，那么圆与圆的位置关系如何判定呢？一方面，可以根据两圆公共点的个数来判定． 圆与圆的位置关系共五种，是由两圆的公共点来定义的．两圆没有公共点——外离或内含；两圆有唯一公共点——外切或内切；两圆有两个公共点——相交．另一方面，可以根据两圆圆心距与半径的数量关系来判定．判定两圆的位置关系，除定义外，既可根据两圆半径与圆心距的关系来判定，又可根据两圆内、外公切线的总条数来判定．若设两圆的半径分别为R，r(R＞r)，圆心距为d，则有：(1)d＞R＋r⇔两圆外离；(2)d＝R＋r⇔两圆外切；(3)d＝R－r⇔两圆内切；(4)R－r＜d＜R＋r⇔两圆相交；(5)d＜R－r⇔两圆内含．【例3－1】若A和B相切，它们的半径分别为8 cm和2 cm，则圆心距AB为( )．A．10 cm B．6 cmC．10 cm或6 cm D．以上答案均不对解析：因为A和B相切，它们的半径分别为8 cm和2 cm，所以，当两圆相外切时，圆心距＝8＋2＝10 cm；当两圆相内切时，圆心距＝8－2＝6 cm.答案：C【例3－2】如图，用半径R＝3 cm，r＝2 cm的钢球测量口小内大的内孔的直径D．测得钢球顶点与孔口平面的距离分别为a＝4 cm，b＝2 cm，则内孔直径D的大小为( )．A．9 cm B．8 cm C．7 cm D．6 cm解析：因为a＋R＝b＋r＋O2H，a＝4，b＝2，R＝3，r＝2，所以O2H＝3.又根据两圆外切，可得O1O2＝R＋r＝3＋2＝5，根据勾股定理可得，O1H2＝O1O22－O2H2，所以O1H＝4.所以D＝R＋O1H＋r＝3＋4＋2＝9(cm)．故选A．答案：A4．利用两圆外切和内切的位置关系解题两圆外切和内切是圆与圆的几种位置关系中，具有“分界线”作用的两种特殊的位置关系，通常把这两种位置关系统称为两圆相切．解答问题时注意结合移动和变化的思想来思考，特别注意不能遗漏掉其中任何一个答案．而且在证明两圆外切或内切时通常要添加辅助线，例如作两圆的连心线或圆心距等．【例4－1】已知O1与O2的半径分别为4和5，则O1与O2内切时，O1O2等于__________．解析：当两圆内切时，d＝R－r，所以当O1与O2内切时，O1O2等于1.答案：1【例4－2】已知O1与O2的半径分别为3和5，O1O2的长是x2－10x＋16＝0的根，则O1与O2的位置关系是( )．A．外离B．外切C．内切 D．外切或内切解析：解方程x2－10x＋16＝0，得x1＝2，x2＝8.当O1O2＝2时，因为R－r＝5－3＝2，所以O1与O2内切，当O1O2＝8时，因为R＋r＝5＋3＝8，所以O1与O2外切．答案：D5．利用两圆相交的位置关系计算定理：两圆相交时，连心线垂直平分两圆的公共弦．定理：两圆相切时，连心线通过切点．当两个圆相交时，由于连心线垂直平分公共弦，可以根据线段的垂直关系求特殊线段的长和角的度数．如果两个圆是等圆，则两圆的两个公共点与两个圆的圆心都组成一个等腰三角形，据此可以求出更多的线段和角．解题时特别需要注意的是：画两圆相交时，往往只画圆心在公共弦两侧的情况，从而漏掉了圆心在公共弦同侧的情况，导致解题不全．在已知两圆半径和公共弦长，求两圆的圆心距时，应分别计算圆心在公共弦同侧和圆心在公共弦两侧时的圆心距的长．【例5】两个同样大小的肥皂泡黏在一起，其剖面如图所示(点O，O′是圆心)，分隔两个肥皂泡的肥皂膜PQ成一条直线，TP，NP分别为两圆的切线，求∠TPN的大小．分析：因为两个圆大小相同，所以半径OP＝O′P＝OO′.又TP，NP分别为两圆的切线，所以PT⊥OP，PN⊥O′P，即∠OPT＝∠O′PN＝90°，所以∠TPN等于360°分别减去∠OPT，∠O′PN，∠OPO′即可．解：∵OP＝OO′＝PO′，∴△PO′O是一个等边三角形．∴∠OPO′＝60°.又∵TP与NP分别为两圆的切线，∴∠TPO＝∠NPO′＝90°.∴∠TPN＝360°－2×90°－60°＝120°.。