机械设计基础第11节滚动轴承轴向力的计算

轴承压轴力计算公式轴承是机械设备中常用的零部件，用于支撑旋转机械零件的轴。

在轴承工作时，会受到来自旋转部件的轴向力的作用。

因此，对于轴承来说，计算轴向力是非常重要的。

本文将介绍轴承压轴力的计算公式及其应用。

轴承压轴力是指轴承在工作时所受到的轴向力。

在实际工程中，需要计算轴承压轴力，以确定轴承的选型和轴承座的设计。

轴承压轴力的计算公式如下：F = C0 × (Y × Fr + Y0 × Fa)。

其中，F为轴承压轴力，单位为N；C0为轴承的基本静载荷，单位为N；Y为轴承系数，取值范围一般为0.5-0.8；Fr为轴承的径向力，单位为N；Fa为轴承的轴向力，单位为N；Y0为轴承系数，取值范围一般为0.6-1.0。

在实际工程中，轴承的选型和轴承座的设计需要根据实际工况来确定。

在计算轴承压轴力时，需要考虑轴承所受的径向力和轴向力。

通常情况下，径向力是由旋转部件在轴向上的惯性力和离心力引起的，而轴向力则是由机械装置的工作负荷引起的。

因此，在计算轴承压轴力时，需要分别考虑这两种力的作用。

对于径向力Fr，可以通过以下公式进行计算：Fr = m × r ×ω^2。

其中，m为旋转部件的质量，单位为kg；r为旋转部件的半径，单位为m；ω为旋转部件的角速度，单位为rad/s。

对于轴向力Fa，可以通过以下公式进行计算：Fa = P ×η。

其中，P为机械装置的工作负荷，单位为N；η为机械装置的传动效率，取值范围一般为0.8-0.95。

通过上述公式，可以计算出轴承所受的径向力和轴向力，进而计算出轴承的压轴力。

在实际工程中，需要根据轴承所受的压轴力来选择合适的轴承型号和轴承座设计，以确保轴承能够正常工作并具有足够的寿命。

除了上述的计算公式，轴承压轴力的计算还需要考虑一些其他因素，如轴承的工作温度、润滑情况、安装方式等。

这些因素都会对轴承的压轴力产生影响，因此在实际工程中需要综合考虑这些因素，以确定轴承的选型和轴承座的设计。

机械设计基础第章滚动轴承轴向力的计算滚动轴承是一种重要的机械传动部件，广泛应用于各种机械设备中。

在滚动轴承的设计中，轴向力的计算是重要的一环。

轴向力是指作用在轴承上的沿轴向方向的力，它对轴承的正常工作和寿命具有重要影响。

轴承在工作过程中，常常受到来自外部或内部的轴向力的作用。

外力主要包括：1.传动装置的轴向力：在一些传动装置中，由于齿轮、联轴器、皮带轮等传动元件的轴向对各来的作用，会使得轴承受到轴向力的作用。

2.轴向定位力：当轴承所选择的结构形式为非推力轴承，即由轴承的其他结构形式来决定轴承承受的轴向力，比如圆锥滚子轴承、调整心形滚子轴承等。

3.实际工况的影响力：比如离心力、旋转不平衡力等，由于转子的形状和运动特性，往往会使得轴承受到轴向力的作用。

内力主要包括：1.轴的伸长引起的力：当轴受到拉伸力或拉压力时，会产生轴向力作用于滚动轴承上。

2.温度变化引起的力：由于温度变化引起的轴线伸长或缩短导致的轴向力。

3.轴的变形引起的力：由于轴的变形导致的轴向力，如轴端的盖板，轴承座两侧安装的螺钉张紧方式的变形。

1.当轴承承受的轴向力为外力时，根据传动装置的轴向力大小和方向来计算。

一般可以通过传动装置的设计手册或相关文献来获取。

2.当轴承承受的轴向力为内力时，可以通过相关的计算公式来计算。

比如，当轴受到拉伸力时，轴向力可以通过公式F=σ×A计算，其中F为轴向力，σ为轴的应力，A为轴截面积。

3.当轴承承受的轴向力为温度变化引起的力时，可以通过计算轴线伸长或缩短的量来计算轴向力。

在滚动轴承的设计中，合理计算轴向力是十分重要的，轴向力过大或者过小都会对轴承的使用寿命和运行效果产生负面影响。

因此，在设计滚动轴承时，需要结合实际应用情况，充分考虑轴向力的计算，以确保轴承正常工作并具有较长的使用寿命。

角接触球轴承轴向力计算公式角接触球轴承是一种常用的滚动轴承，广泛应用于机械设备中。

在设计和使用角接触球轴承时，了解和计算轴向力是非常重要的。

轴向力是指作用在轴承轴向方向的力，它对轴承的运行和寿命有着直接的影响。

在本文中，我将介绍角接触球轴承轴向力的计算公式及其相关要点。

轴向力的计算公式是通过考虑轴承的负载、速度和角接触球轴承的特性来确定的。

以下是角接触球轴承轴向力的计算公式：Fa = (XFr + YFa) / (eP)其中，Fa是轴向力（单位为牛顿，N）；X是轴承的动载荷系数；Fr是轴承的径向力（单位为牛顿，N）；Y是轴承的静载荷系数；Fa是轴承的轴向力（单位为牛顿，N）；e是轴承的接触角系数；P是轴承的当量动载荷（单位为牛顿，N）。

在计算轴向力时，需要明确轴承的负载（Fr）、速度和特性系数（X、Y、e、P）。

下面对这些要点进行详细的解释：1. 轴承的动载荷系数（X）：动载荷系数（X）是考虑到轴承在动载荷作用下的变形和变位情况的。

X的取值范围通常为0.56-0.98，具体取值需要根据轴承的类型、尺寸和应用情况进行确定。

2. 轴承的静载荷系数（Y）：静载荷系数（Y）是考虑到轴承在静载荷作用下的变形和变位情况的。

Y的取值范围通常为0.56-0.98，具体取值需要根据轴承的类型、尺寸和应用情况进行确定。

3. 轴承的接触角系数（e）：接触角系数（e）是轴承接触角的函数，接触角是指球和滚道的接触角度。

e的取值范围通常为0.6-0.8，具体取值需要根据轴承的类型和设计要求进行确定。

4. 轴承的当量动载荷（P）：当量动载荷（P）是指在轴承承受的径向力和轴向力同时作用下，所能承受的相当于纯径向载荷的动载荷。

P的计算公式通常为P = Fr + 1.2Fa，其中Fr为径向力，Fa为轴向力。

轴向力的计算公式的目的是为了确定角接触球轴承在实际工作中所承受的轴向力，以便进行轴承的选择和设计。

通过合理的计算和选择，可以保证轴承在工作过程中的可靠性和寿命。

圆锥滚子轴承轴向力计算公式(二)圆锥滚子轴承轴向力计算公式1. 应力计算公式：•公式1：应力等效公式σ = F / A•公式2：轴向力引起的正应力σx = Fx / A•公式3：轴向力引起的剪应力τ = Fy / A2. 弹性变形计算公式：•公式4：轴向力引起的弹性变形δ = (F * L) / (E * A)其中，δ表示弹性变形，F表示轴向力，L表示轴承长度，E表示弹性模量，A表示轴承横截面积。

3. 例子说明：假设有一个圆锥滚子轴承，轴向力为1000N，轴承长度为50mm，轴承横截面积为200mm²，弹性模量为200 GPa。

我们可以按照以下步骤计算相关参数：1.计算应力：根据公式1，应力σ = F / A = 1000N/ 200mm² = 5N/mm²。

2.计算轴向力引起的正应力：根据公式2，轴向力引起的正应力σx = Fx / A = 1000N / 200mm² = 5N/mm²。

3.计算轴向力引起的剪应力：根据公式3，轴向力引起的剪应力τ = Fy / A = 0N / 200mm² = 0N/mm²。

4.计算轴向力引起的弹性变形：根据公式4，轴向力引起的弹性变形δ = (F * L) / (E * A) = (1000N * 50mm) / (200 GPa * 200mm²) ≈ 。

由此可见，该圆锥滚子轴承在受到1000N的轴向力时，引起的应力、正应力、剪应力和弹性变形分别为5N/mm²、5N/mm²、0N/mm²和。

以上为“圆锥滚子轴承轴向力计算公式”的相关计算公式和解释说明。

根据这些公式，我们可以准确计算出圆锥滚子轴承在受到不同轴向力时的应力、正应力、剪应力和弹性变形。

这有助于工程师设计和选择合适的轴承，以满足实际工作条件。

机械设计基础第节滚动轴承轴向力的计算滚动轴承是一种常用的机械元件，用于支撑与传递轴向载荷和径向载荷。

在机械设计中，计算滚动轴承轴向力是非常重要的一部分，涉及到轴承的选型和设计。

本文将介绍滚动轴承轴向力的计算方法。

一、轴向载荷的种类在机械系统中，轴向载荷分为静载荷和动载荷两种。

1.静载荷：轴向载荷恒定不变的情况下的载荷称为静载荷。

静载荷通常由设备的自重、安装在轴上的其他零件的重量、负荷的重量等构成。

2.动载荷：轴向载荷大小在运行过程中有变化的载荷称为动载荷。

动载荷通常通过计算得出，可以是来自于负载的力或力矩引起的轴向力。

二、静载荷的计算静载荷的计算主要包括扭矩产生的轴向力、径向载荷以及其他附加载荷的计算等。

1.扭矩产生的轴向力：扭矩产生的轴向力是由于传递扭矩而引起的轴向力。

一般情况下，扭矩产生的轴向力可以通过计算得出，计算公式如下：Fa=(KT×Md)/L其中，Fa为扭矩产生的轴向力，KT为轴向力系数，Md为传递的扭矩，L为轴承的有效传递长度。

2.径向载荷：径向载荷是指垂直于轴向的力。

径向载荷通常由设备的自重、传动装置的重量、负载的重量等构成。

径向载荷的计算需要考虑设备的结构和工作环境等因素。

3.其他附加载荷：其他附加载荷通常包括轴向预紧力、温度变化引起的载荷、振动引起的载荷等。

这些附加载荷需要在设计过程中进行综合考虑。

三、动载荷的计算动载荷的计算需要考虑到设备在运行中的工况、运行速度、负载类型等因素。

常见的动载荷计算方法有以下几种：1.动载荷的估计：根据设备的工作环境和使用条件，根据经验公式或实验结果进行动载荷的估计。

2.动载荷的测量：通过测量设备在运行过程中的实际载荷，得到动载荷的大小。

3.动载荷的模拟计算：通过建立设备的动态模型，对工作过程进行模拟计算，得到动载荷的大小。

四、滚动轴承轴向力的选型在计算得到滚动轴承的轴向力后，还需要根据轴承的轴向载荷容量、速度等特性进行选型。

轴向载荷容量是指滚动轴承在承受轴向力时的极限载荷能力，通常通过轴向载荷容量图进行选型。

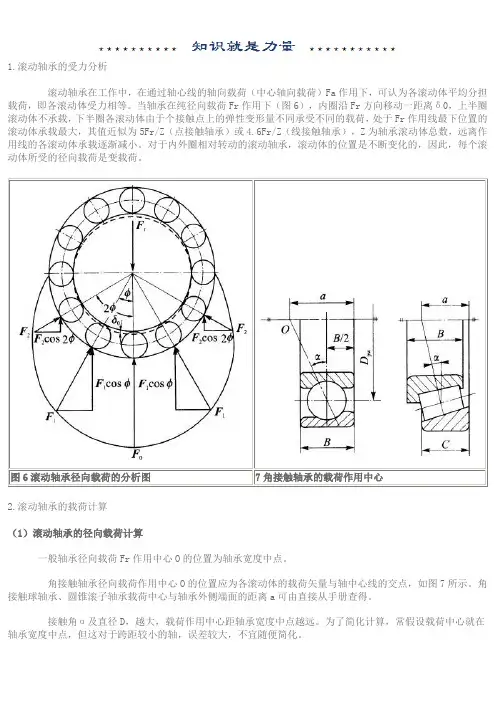
1.滚动轴承的受力分析滚动轴承在工作中，在通过轴心线的轴向载荷（中心轴向载荷）Fa作用下，可认为各滚动体平均分担载荷，即各滚动体受力相等。

当轴承在纯径向载荷Fr作用下（图6），内圈沿Fr方向移动一距离δ0，上半圈滚动体不承载，下半圈各滚动体由于个接触点上的弹性变形量不同承受不同的载荷，处于Fr作用线最下位置的滚动体承载最大，其值近似为5Fr/Z（点接触轴承）或4.6Fr/Z（线接触轴承），Z为轴承滚动体总数，远离作用线的各滚动体承载逐渐减小。

对于内外圈相对转动的滚动轴承，滚动体的位置是不断变化的，因此，每个滚动体所受的径向载荷是变载荷。

图6滚动轴承径向载荷的分析图7角接触轴承的载荷作用中心2.滚动轴承的载荷计算（1）滚动轴承的径向载荷计算一般轴承径向载荷Fr作用中心O的位置为轴承宽度中点。

角接触轴承径向载荷作用中心O的位置应为各滚动体的载荷矢量与轴中心线的交点，如图7所示。

角接触球轴承、圆锥滚子轴承载荷中心与轴承外侧端面的距离a可由直接从手册查得。

接触角α及直径D，越大，载荷作用中心距轴承宽度中点越远。

为了简化计算，常假设载荷中心就在轴承宽度中点，但这对于跨距较小的轴，误差较大，不宜随便简化。

图8角接触轴承受径向载荷产生附加轴向力1)滚动轴承的轴向载荷计算当作用于轴系上的轴向工作合力为FA，则轴系中受FA作用的轴承的轴向载荷Fa=FA，不受FA作用的轴承的轴向载荷Fa=0。

但角接触轴承的轴向载荷不能这样计算。

角接触轴承受径向载荷Fr时，会产生附加轴向力FS。

图8所示轴承下半圈第i个球受径向力Fri。

由于轴承外圈接触点法线与轴承中心平面有接触角α，通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri；和轴向分力FSi。

各球的轴向分力之和即为轴承的附加轴向力FS。

按一半滚动体受力进行分析，有FS ≈ 1.25 Frtan α(1)计算各种角接触轴承附加轴向力的公式可查表5。

表中Fr为轴承的径向载荷；e为判断系数，查表6；Y为圆锥滚子轴承的轴向动载荷系数，查表7。

滚动轴承所‎承受的载荷‎取决于所支‎承的轴系部‎件承担的载‎荷。

右图为一对‎角接触球轴‎承反装支承‎一个轴和一‎个斜齿圆柱‎齿轮的受力‎情况。

图中的Fr‎e、F te、Fae分别‎为所支承零‎件（齿轮）承受的径向‎、切向和轴向‎载荷，Fd1和F‎d2为两个‎轴承在径向‎载荷Fr1‎和F r2（图中未画出‎）作用下所产‎生的派生轴‎向力。

这里，轴承所承受‎的径向载荷‎F r1和F‎r2可以依‎据两个角接触‎球轴承反装‎的受力分析‎（径向反力）F re、F te、Fae经静‎力分析后确‎定，而轴向载荷‎F a1和F‎a2则不完‎全取决于外‎载荷Fre‎、F te、F ae，还与轴上所‎受的派生轴‎向力Fd1‎和Fd2有‎关。

对于向心推‎力轴承，由径向载荷‎F r1和F‎r2所派生‎的轴向力F‎d1和Fd‎2的大小可‎按下表所列‎的公式计算‎。

注：表中Y和e‎由载荷系数表‎中查取，Y是对应表‎中F a／F r＞e的Y 值下图中把派‎生轴向力的‎方向与外加‎轴向载荷F‎a e的方向‎一致的轴承‎标为2，另一端则为‎1。

取轴和与其‎相配合的轴‎承内圈为分‎离体，当达到轴向‎平衡时，应满足：F ae＋F d2＝F d1由于Fd1‎和Fd2是‎按公式计算‎的，不一定恰好‎满足上述关‎系式，这时会出现‎下列两种情‎况：当F ae＋F d2＞F d1时,则轴有向左‎窜动的趋势‎,相当于轴承‎1被“压紧”,轴承2被“放松”,但实际上轴‎必须处于平‎衡位置，所以被“压紧”的轴承1所‎受的总轴向‎力Fa1必‎须与Fae‎＋Fd2平衡‎，即F a1＝F ae＋F d2而被“放松”的轴承2只‎受其本身派‎生的轴向力‎F d2，即F a2＝F d2。

当F ae＋F d2＜F d1时,同前理，被“放松”的轴承1只‎受其本身派‎生的轴向力‎F a1，即F a1＝F d1而被“压紧”的轴承2所‎受的总轴向‎力为: F a2＝F d1－F ae综上可知，计算向心推‎力轴承所受‎轴向力Fa‎的方法可以‎归纳为：先通过派生‎轴向力及外‎加轴向载荷‎的计算与分‎析，判断被“放松”或被“压紧”的轴承；然后确定被‎“放松”轴承的轴向‎力仅为其本‎身派生的轴‎向力，被“压紧”轴承的轴向‎力则为除去‎本身派生的‎轴向力后其‎余各轴向力‎的代数和。

各类滚动轴承轴向载荷分析及计算王志云（山东省东营职业学院，山东东营２５７０９１）摘要：总结了滚动轴承设计中其轴向载荷分析需考虑的因素，以及生产中几种常用滚动轴承支撑的轴向载荷分析方法，使得轴承的轴向载荷分析及计算更清晰、明了，内容更全面、系统。

关键词：滚动轴承；支撑形式；安装方式；轴向载荷中图分类号：ＴＨ１３３．３３文献标识码：Ａ文章编号：１００８－８０８３（２００８）０３－００６０－０２在滚动轴承的设计计算中，轴承轴向载荷计算是设计中的关键也是难点，它由轴承类型、支撑形式和安装方式等因素决定，在生产实际中，有关轴承的支撑类型多、形式多，必须对轴系结构进行详细、合理的受力分析，才能正确的进行计算，现就几种常用形式作以分析总结，并进行其轴向载荷的计算，从而为各种形式轴承轴向载荷分析计算提供方法依据。

一、滚动轴承轴向载荷计算中考虑的因素１．轴承类型滚动轴承按不同的分类方式有许多不同的类型，如按滚动体的形状不同有球轴承和滚子轴承，按调心性能不同有调心轴承和非调心轴承等，若按承载情况不同有向心轴承、推力轴承和角接触轴承三大类，向心轴承是指主要或只受径向载荷的轴承，推力轴承是指只受轴向载荷的轴承，角接触轴承是指同时承受径向和轴向载荷的轴承。

２．轴承的支撑形式一般对于两端支撑的情况，有全固式、固游式和全游式三种支撑形式，全固式是指两端都单向固定的支撑，固游式是指一端固定一端游动的支撑，全游式是指两端都游动的支撑。

３．轴承的安装方式对于成对使用的角接触轴承，通常有正装和反装两种安装方式。

轴承外圈窄边相对称为正装，又叫＂面对面＂安装，轴承外圈窄边相背称为反装，又叫＂背靠背＂安装。

二、滚动轴承轴向载荷分析１．向心轴承轴向载荷分析（１）全固式向心轴承轴向载荷分析普通工作温度下的短轴，常用两端都单向固定的形式，如图１所示。

图１１）当外载荷ＦＡ向右时，轴有向右移动的趋势，载荷传到右端轴承内圈上，又通过滚动体传到外圈，由于右端轴承外圈右端被轴承盖固定，使得右端轴承受到向左的支反力Ｆ＇Ａ２而被压紧，而左端轴承处于放松状态。

轴承轴向载荷计算公式
轴承是一种用于支撑机械旋转部件的重要元件。

在实际应用中，轴承通常承受着来自旋转部件的各种载荷，其中包括轴向载荷。

轴向载荷是指垂直于轴心线方向的力或压力，其作用方向与轴的轴向相同或相反。

轴向载荷的计算对于正确选择合适的轴承和确保轴承工作正常非常重要。

以下是常用的轴向载荷计算公式：
1. 线性轴承的轴向载荷计算公式：
轴向载荷 = 1/2 * (F1 + F2)
其中，F1和F2分别为轴承所受外力的大小，取正负号表示方向。

2. 圆柱滚子轴承的轴向载荷计算公式：
轴向载荷 = (F1 + F2) / 2
其中，F1和F2分别为轴承所受外力的大小，取正负号表示方向。

3. 锥形滚子轴承的轴向载荷计算公式：
轴向载荷= (F1 + F2) / 2 * cosα
其中，F1和F2分别为轴承所受外力的大小，取正负号表示方向；α为锥面与轴线的夹角。

4. 推力球轴承的轴向载荷计算公式：
轴向载荷 = F
其中，F为轴承所受外力的大小，取正负号表示方向。

需要注意的是，在实际应用中，轴向载荷不仅仅是由外力引起的，还可能由于转子离心力、温度变化等因素而产生。

因此，需要综合考虑这些因素对轴向载荷的影响，进行准确的计算。

在进行轴向载荷计算时，还需要考虑其他一些因素，如轴承的额定载荷、轴承的径向载荷等。

同时，还要根据具体的工况条件和设计要求，选择合适的轴承类型和规格。

轴向载荷的计算是轴承设计中非常重要的一部分。

通过合理计算和选择，可以确保轴承工作正常，并提高设备的安全性和可靠性。

滚动轴承的校核计算及公式1 基本概念1．轴承寿命：轴承中任一元件出现疲劳剥落扩展迹象前运转的总转数或一定转速下的工作小时数。

批量生产的元件，由于材料的不均匀性，导致轴承的寿命有很大的离散性，最长和最短的寿命可达几十倍，必须采用统计的方法进行处理。

2．基本额定寿命：是指90%可靠度、常用材料和加工质量、常规运转条件下的寿命，以符号L10（r）或L10h（h）表示。

3．基本额定动载荷（C）：基本额定寿命为一百万转（106）时轴承所能承受的恒定载荷。

即在基本额定动载荷作用下，轴承可以工作106 转而不发生点蚀失效，其可靠度为90%。

基本额定动载荷大，轴承抗疲劳的承载能力相应较强。

4．基本额定静载荷（径向C0r，轴向C0a）：是指轴承最大载荷滚动体与滚道接触中心处引起以下接触应力时所相当的假象径向载荷或中心轴向静载荷。

在设计中常用到滚动轴承的三个基本参数：满足一定疲劳寿命要求的基本额定动载荷Cr（径向）或Ca（轴向），满足一定静强度要求的基本额定静强度C0r（径向）或C0a（轴向）和控制轴承磨损的极限转速N0。

各种轴承性能指标值C、C0、N0等可查有关手册。

2 寿命校核计算公式图17-6滚动轴承的寿命随载荷的增大而降低，寿命与载荷的关系曲线如图17-6，其曲线方程为PεL10=常数其中 P-当量动载荷，N；L10-基本额定寿命，常以106r为单位（当寿命为一百万转时，L10=1）；ε-寿命指数，球轴承ε=3，滚子轴承ε=10/3。

由手册查得的基本额定动载荷C是以L10=1、可靠度为90%为依据的。

由此可得当轴承的当量动载荷为P时以转速为单位的基本额定寿命L10为Cε×1=Pε×L10L10=(C/P)ε 106r (17.6)若轴承工作转速为n r/min，可求出以小时数为单位的基本额定寿命h （17.7）应取L10≥L h'。

L h '为轴承的预期使用寿命。

通常参照机器大修期限的预期使用寿命。

轴承径向力计算公式轴承是机械设备中常见的零部件之一，在传动系统中扮演着重要的角色。

而在轴承工作时，径向力是一个重要的参数，它代表了轴向的力量。

对于设计和选择合适的轴承来说，了解径向力的计算公式至关重要。

轴承径向力的计算公式可以根据轴承的工作条件和受力情况来确定。

在一般情况下，轴承径向力可以通过以下公式来计算：F = P × d / (2 × b)其中，F代表轴承的径向力，单位是牛顿（N）；P代表轴承的等效动载荷，单位是牛顿（N）；d代表轴承的直径，单位是米（m）；b 代表轴承的宽度，单位是米（m）。

在这个公式中，等效动载荷P是一个关键参数，它代表了轴承所受到的合成动载荷，可以根据轴承的实际工作条件和受力情况来确定。

而轴承的直径和宽度则是轴承的几何参数，直接影响着轴承的承载能力和受力情况。

通过这个简单的公式，我们可以快速计算出轴承在工作时所受到的径向力，从而为轴承的选择和设计提供重要参考。

在实际工程中，轴承的径向力是一个重要的设计参数，设计师需要根据轴承所受的力量来选择合适的轴承类型和尺寸，以确保轴承在工作时能够正常运转并具有足够的寿命。

除了上述简单的公式之外，轴承径向力的计算还可能涉及到更复杂的情况和更详细的参数，比如考虑到轴承的旋转速度、工作温度、润滑条件等因素。

在实际工程中，设计师需要综合考虑这些因素，并结合实际情况来确定轴承的径向力，以确保轴承在工作时具有良好的性能和可靠性。

轴承径向力是轴承设计和选择过程中的重要参数，通过合适的计算公式和综合考虑各种因素，设计师可以准确地确定轴承在工作时所受到的力量，从而为轴承的选择和设计提供重要参考。

希望本文对读者了解轴承径向力的计算有所帮助。

圆锥滚子轴承轴向力计算公式(一)圆锥滚子轴承轴向力计算公式1. 简介圆锥滚子轴承是一种常用于承受轴向力和径向力的轴承结构。

在设计和使用圆锥滚子轴承时，需要计算轴向力，以确保轴承的可靠性和工作性能。

2. 计算公式a. 基本轴向力公式圆锥滚子轴承的轴向力由以下公式计算得出： Faxial = Fa + Fr + Fe其中： - Faxial 表示轴向力； - Fa 表示作用于轴承的轴向力；- Fr 表示作用于轴承的径向力； - Fe 表示由于周向偏差引起的轴向力。

b. Fa 计算公式轴向力 Fa 可由以下公式计算得出： Fa = K * P其中： - K 表示应力系数； - P 表示轴向载荷。

c. Fr 计算公式径向力 Fr 可由以下公式计算得出： Fr = X * P * Y其中： - X 表示径向荷重系数； - Y 表示径向应力系数。

d. Fe 计算公式由于周向偏差引起的轴向力 Fe 可由以下公式计算得出： Fe = C * ra其中： - C 表示偏差后相对初始偏差的变化系数； - ra 表示偏差量。

3. 示例说明假设一个圆锥滚子轴承承受的轴向载荷 P 为 1000 N，应力系数K 为，径向荷重系数 X 为，径向应力系数 Y 为，偏差量 ra 为mm，偏差后相对初始偏差的变化系数 C 为。

根据上述参数，可以计算出轴承的轴向力如下： Fa = K * P = * 1000 = 1200 N Fr = X * P * Y = * 1000 * = 720 N Fe = C * ra = * = N Faxial = Fa + Fr + Fe = 1200 + 720 + = N因此，该圆锥滚子轴承承受的轴向力为 N。

以上是针对圆锥滚子轴承轴向力计算的相关公式和一个示例的解释说明。

通过计算轴承的轴向力，可以为设计和使用圆锥滚子轴承提供准确的参考和指导。

轴承轴向力计算轴承是机械传动系统中重要的组成部分，用于支撑旋转轴的运动。

轴承承受着轴向力、径向力和弯曲力等各种力的作用，其中轴向力是指沿着轴向作用的力，是轴承最为重要的力之一。

轴向力的大小及方向有着重要的意义，对轴承性能及使用寿命都有着较大影响。

轴向力如何计算呢？计算方法有两种，一种是按照轴承轴向力公式进行计算，另一种是基于轴承实际工况进行估算。

首先介绍轴承轴向力公式。

轴承轴向力公式是根据轴承参数以及传动系统参数进行的计算。

轴承轴向力公式分为两种类型，一种是动力学计算公式，一种是静力学计算公式。

动力学计算公式是基于轴承的转速及惯性力进行的，而静力学计算公式是基于轴承的载荷及其分布情况进行的。

由于轴承轴向力公式计算比较繁琐，需要涉及多个参数的计算，因此需根据实际需要选择合适的计算方法。

其次是基于轴承实际工况进行估算。

在工程实践中，基于轴承实际工况进行的估算方法被广泛采用。

这种方法可以根据轴承应力状态及其受力形式进行估算。

按照受力形式不同，可以将轴承分为针对轴向受力、径向受力、轴向径向双向受力的轴承。

对于轴向受力，可采用法向应力法和助推力法进行估算。

在轴承轴向力的计算过程中，需要考虑多种因素。

首先是轴承受力状态，需要根据实际工况进行分析。

其次是轴承的正确安装方式及其加固。

再者是轴承的匹配、润滑、加热及冷却等因素的影响。

最后是轴承磨损与老化对轴承轴向力的影响，需要进行定期检测及更换。

总的来说，轴承轴向力的计算方法及其参数较多，需要进行综合考虑。

在实际应用中，应根据实际情况选择合适的计算方法及参数，切勿掉以轻心。

通过合理的轴承轴向力计算及相关措施的实施，可以确保轴承的正常运行及其长期稳定性。