滚动轴承计算-xn(1)

滚动轴承寿命计算公式滚动轴承寿命计算是判断滚动轴承寿命的重要方法，它是基于滚动轴承的结构及使用条件进行分析，通过考虑滚动接触应力、脂润滑条件等因素，计算出滚动轴承的寿命。

滚动轴承寿命计算公式是基于ISO标准的经验公式，其中最常使用的是基本额定寿命公式。

滚动轴承的基本额定寿命(L10)是指在相同条件下，有10%的轴承在寿命前失效。

滚动轴承寿命分为疲劳寿命和表面疲劳寿命，其中疲劳寿命是指由于滚动和滑动过程中产生的疲劳损伤导致的寿命。

表面疲劳寿命是指由外在原因（如进入外来颗粒等）引起的表面大片剥落，导致轴承失效的寿命。

滚动轴承的基本额定寿命(L10)的计算公式如下：L10 = (C/P)^3 × (1000000/60)其中，C为基本动载荷，P为等效动载荷。

基本动载荷(C)是滚动轴承能够承受的最大载荷。

它由制造商提供，根据ISO标准进行计算。

等效动载荷(P)是指滚动轴承在使用过程中的实际载荷，它考虑了滚动轴承的载荷分布及轴承的轴向受力情况。

在实际应用中，滚动轴承的使用条件可能会发生变化，例如工作温度、转速、润滑条件等。

考虑到这些因素对寿命的影响，可以使用修正系数进行修正。

其中，温度修正系数(a1)、转速修正系数(a2)和脂润滑修正系数(a3)是常见的修正系数。

它们表示滚动轴承在不同工况下寿命与基本额定寿命之间的比值。

修正后的寿命(L)可以根据以下公式计算：L = L10 × a1 × a2 × a3同时，还有其他一些公式可以用于计算滚动轴承的寿命，例如基本动载荷的计算公式和等效载荷的计算公式。

这些公式可以根据具体的应用要求和实际情况进行选择和计算。

综上所述，滚动轴承寿命计算公式是根据滚动轴承的结构和使用条件进行分析的重要方法。

通过计算基本额定寿命和修正系数，可以得到滚动轴承的寿命。

计算公式的准确性和合理性对于滚动轴承的设计和选用非常重要，可以提高轴承的使用寿命和可靠性。

轴承寿命计算公式
右图为在大量实验研究基础上得出
的代号为6207的轴承的载荷－寿命曲
线。

该曲线表示此类轴承的载荷P与基
本额定寿命L10 之间的关系。

曲线上相
应与寿命L10为一百万转的载荷
（25.5kN），即为6207轴承的基本额定
动载荷C。

其它型号的轴承，也有与上
述曲线的函数规律完全一样的载荷－寿
命曲线。

把此曲线用公式表示为：
或 （小
时）
式中：L10为以转数计的滚动轴承基本额定寿命
L h为以小时计的滚动轴承基本额定寿命
C 为滚动轴承的基本额定动载荷（单位：N）
P 为滚动轴承的当量额定动载荷（单位：N）
n 为滚动轴承的工作转速（单位：r/min)
ε为计算指数，对于球轴承，ε＝3；对于滚子轴承，ε＝10/3。

对于在较高温度下（如高于125℃）工作的滚动轴承，上述公式中的C值
须乘以温度系数f t（见下表）,即： C t=f t C
轴承工作温度／℃≤120125150175200225250300350
温度系数f t 1.000.950.900.850.800.750.700.600.50
返　回/jp2003/jxsj/ch13/html/l10.htm[2011-11-27 15:59:27]。

一、滚动轴承承载能力的一般说明滚动轴承的承载能力与轴承类型和尺寸有关。

相同外形尺寸下，滚子轴承的承载能力约为球轴承的1.5～3倍。

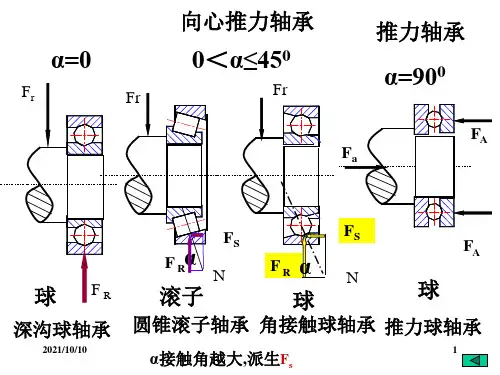
向心类轴承主要用于承受径向载荷，推力类轴承主要用于承受轴向载荷。

角接触轴承同时承受径向载荷和轴向载荷的联合作用，其轴向承载能力的大小随接触角α的增大而增大。

二、滚动轴承的寿命计算轴承的寿命与载荷间的关系可表示为下列公式：或式中：──基本额定寿命（106转）；──基本额定寿命（小时h）；C──基本额定动载荷，由轴承类型、尺寸查表获得；P──当量动载荷（N），根据所受径向力、轴向力合成计算；──温度系数，由表1查得；n──轴承工作转速（r/min）；──寿命指数（球轴承，滚子轴承）。

三、温度系数f t当滚动轴承工作温度高于120℃时，需引入温度系数（表1）表1 温度系数四、当量动载荷当滚动轴承同时承受径向载荷和轴向载荷时，当量载荷的基本计算公式为式中：P——当量动载荷，N；——径向载荷，N；——轴向载荷，N；X——径向动载荷系数；Y——轴向动载荷系数；——负荷系数五、载荷系数f p当轴承承受有冲击载荷时，当量动载荷计算时，引入载荷系数（表2）表2 冲击载荷系数f p六、动载荷系数X、Y表3 深沟球轴承的系数X、Y表4 角接触球轴承的系数X、Y表5 其它向心轴承的系数X、Y表6 推力轴承的系数X、Y七、成对轴承所受轴向力计算公式：角接触球轴承：圆锥滚子轴承：式中e为判断系数，可由表4查出；Y应取表5中的数值。

●正排列：若则若则●反排列：若则若则八、成对轴承当量动载荷根据基本公式：式中：P——当量动载荷，N；——径向载荷，N；——轴向载荷，N；X——径向动载荷系数；Y——轴向动载荷系数；——负荷系数。

九、修正额定寿命计算对于要求不同的可靠度、特殊的轴承性能以及运转条件不属于正常情况下的轴承寿命计算时，可采用修正额定寿命计算公式：式中：──特殊的轴承性能、运转条件以及不同可靠度要求下的修正额定寿命（106转）；a1──可靠度的寿命修正系数；a2──特殊的轴承性能寿命修正系数；a3──运转条件的寿命修正系数。

滚动轴承允许转速及最小载荷计算公式滚动轴承是一种常见的机械元件，广泛应用于各种机械设备中。

在设计和选择滚动轴承时，需要考虑其允许转速和最小载荷。

本文将介绍滚动轴承允许转速和最小载荷的计算公式以及相关的考虑因素。

1.允许转速的计算公式滚动轴承的允许转速是指轴承在运转过程中可以达到的最大转速。

滚动轴承的转速限制主要取决于以下几个因素：-轴承的尺寸和结构：轴承的尺寸和结构特征会影响其能够承受的转速范围。

-轴承材料的选择：轴承材料的性能和耐磨性也会影响其转速限制。

-润滑方式：轴承的润滑方式（如油润滑或脂润滑）也会对转速限制产生影响。

根据ISO281:2024《滚动轴承-动态负载评价》标准，计算滚动轴承允许转速的公式如下：\[n_a=N\cdot（\frac{60}{2π}）\]其中，\(n_a\)为滚动轴承允许转速（rpm），\(N\)为基本额定寿命（小时）。

基本额定寿命（\(N\)）是指在一定负荷和转速条件下，滚动轴承可以工作的寿命。

其计算公式如下：\[N=a_1\cdot a_2\cdot a_3\cdot a_4\cdota_5\cdot(\frac{L_h}{C})^p\]其中，\(a_1\)、\(a_2\)、\(a_3\)、\(a_4\)、\(a_5\)为调整因素，\(L_h\)为滚动轴承在额定负荷下的寿命（小时），\(C\)为基本额定动态负荷（N），\(p\)为负荷指数。

2.最小载荷的计算公式滚动轴承的最小载荷是指轴承在运行中必须承受的最小负荷。

如果负荷过小，滚动轴承可能发生滚道不均匀磨损、鸣响或振动等问题。

因此，在设计和选择滚动轴承时，需要保证轴承运行时负荷不低于最小载荷。

滚动轴承的最小载荷可以通过以下公式进行计算：\[F_a≥Kr\cdot Pr\]其中，\(F_a\)为实际的载荷（N），\(Kr\)为最小载荷系数（一般取值为0.02-0.05），\(Pr\)为基本额定动态负荷（N）。

需要注意的是，在实际工程中，滚动轴承的最小载荷还需要根据具体的工作条件进行调整，例如加大调整系数以提高轴承的可靠性。

滚动轴承寿命计算公式滚动轴承是一种常见的机械元件，用于支撑和定位机器中旋转部件。

由于滚动轴承在机械运动中承受很大的力和磨损，因此其寿命是一个重要的参数。

滚动轴承的寿命计算公式是根据轴承的工作条件来确定的。

下面将详细介绍滚动轴承寿命计算的相关参考内容。

滚动轴承的寿命可以用基本额定寿命和调整因素来计算。

基本额定寿命是指在给定的负载条件下，轴承经过100万转（或行走一定的距离）后的寿命。

调整因素是考虑到轴承在实际工作条件下可能受到的额外影响。

滚动轴承的基本额定寿命可以由以下的一般计算公式得出：L10h = (C/P)^p其中，L10h是基本额定寿命，单位是小时；C 是基本动载荷额定值，单位是N；P 是相对磨损参数，通常取为3；p 是磨损指数，取决于轴承类型和使用条件。

磨损指数p的取值范围通常为3-10，具体数值需要根据具体的轴承类型和使用条件进行确定。

不同类型的轴承有不同的磨损指数。

滚动轴承的调整因素主要包括以下几个方面：1.负载系数（fT）：通过考虑工作条件下的轴承负载大小和方向，计算负载系数。

一般情况下，负载系数在1以下。

2.可靠性调整因素（a1、a2、a3）：根据滚动轴承的可靠性要求，计算可靠性调整因素。

这些因素通常是根据统计数据和经验值得出的。

3.寿命调整因素（aISO、aSKF）：在计算基本额定寿命的基础上，根据轴承的使用条件和特殊要求进行修正。

4. 温度调整因素（aT）：考虑轴承运行温度的影响，计算温度调整因素。

以上的调整因素可以通过一定的计算公式得出，具体的计算方法可以参考相关滚动轴承的手册、标准或经验数据。

除了上述计算寿命的方法外，还可以通过实际运行数据进行判断和预测轴承寿命。

例如，通过监测轴承的振动、温度等参数，结合历史数据和经验，可以进行寿命预测和故障诊断。

总结起来，滚动轴承寿命的计算公式包括基本额定寿命的公式和各种调整因素的计算。

这些公式和因素的取值需要根据具体的轴承类型和使用条件来确定。

直线滚动轴承负载计算公式在工程设计和机械制造中，直线滚动轴承是一种常用的机械元件，用于支撑和传递载荷，使得机械设备能够平稳运行。

在设计直线滚动轴承时，需要对其负载进行计算，以确保轴承能够承受所需的载荷，从而保证机械设备的正常运行。

本文将介绍直线滚动轴承负载计算的基本原理和公式。

直线滚动轴承的负载主要包括径向载荷和轴向载荷两种。

径向载荷是指垂直于轴承轴线的力，而轴向载荷则是指沿着轴承轴线的力。

在实际工程中，轴承通常同时承受这两种载荷，因此需要对其进行综合计算。

首先我们来看一下直线滚动轴承的径向载荷计算公式。

对于径向载荷，其计算公式如下：Fr = X0 F0 + X Fa。

其中，Fr表示径向载荷，X0和X为径向载荷系数，F0和Fa分别为轴承所受的基本动载荷和轴向载荷。

在这个公式中，径向载荷系数X0和X是根据轴承的类型和使用条件进行确定的。

一般来说，X0和X的取值范围为0.1-1.0。

基本动载荷F0是指在轴承标准试验条件下，轴承在无外部载荷作用下的额定载荷。

而轴向载荷Fa则是指轴承在实际工作条件下所受的轴向载荷。

接下来我们来看一下直线滚动轴承的轴向载荷计算公式。

对于轴向载荷，其计算公式如下：Fa = Y Fr。

其中，Fa表示轴向载荷，Y为轴向载荷系数，Fr为径向载荷。

轴向载荷系数Y的取值范围通常为0.1-0.3。

在实际工程中，轴向载荷系数Y的取值需要根据轴承的类型和使用条件来确定。

一般来说，Y的取值越大，轴承所能承受的轴向载荷就越大。

在实际工程中，直线滚动轴承的负载计算需要根据具体的使用条件和要求进行综合分析。

除了上述的基本负载计算公式外，还需要考虑到轴承的寿命、疲劳强度、刚度等因素，以确保轴承能够稳定可靠地工作。

总之，直线滚动轴承的负载计算是工程设计和机械制造中的重要内容，对于确保机械设备的正常运行具有重要意义。

通过合理的负载计算，可以有效地提高轴承的使用寿命和可靠性，从而减少设备的维护成本和停机时间，提高生产效率。

滚动轴承试验计算公式引言。

滚动轴承是一种常见的机械元件，用于支撑旋转轴承的负载和减少摩擦。

在工程实践中，对滚动轴承进行试验是非常重要的，可以帮助工程师了解其性能和寿命。

在进行滚动轴承试验时，计算公式是非常关键的工具，可以帮助工程师准确地预测轴承的性能和寿命。

本文将介绍滚动轴承试验计算公式的相关内容，希望能够对读者有所帮助。

滚动轴承的基本原理。

滚动轴承是一种通过滚动元件（如滚珠、滚柱、滚子等）来减少摩擦和支撑负载的机械元件。

它通常由内圈、外圈、滚动元件和保持架等部分组成。

在使用过程中，滚动轴承可以有效地减少摩擦，提高旋转部件的运转效率，并且具有较高的承载能力和寿命。

滚动轴承试验的重要性。

滚动轴承试验是评估轴承性能和寿命的重要手段。

通过试验可以了解轴承在不同工况下的性能表现，包括承载能力、摩擦系数、寿命等。

这些数据对于工程设计和轴承选型非常重要，可以帮助工程师选择合适的轴承并预测其使用寿命。

滚动轴承试验计算公式。

在进行滚动轴承试验时，有一些常用的计算公式可以帮助工程师预测轴承的性能和寿命。

下面将介绍一些常用的滚动轴承试验计算公式。

1. 动载荷计算公式。

滚动轴承在使用过程中承受着动态载荷和静态载荷。

动态载荷是指轴承在旋转时所受的载荷，通常由动载荷系数和等效动载荷计算得出。

其计算公式如下：P = XFr + YFa。

其中，P为等效动载荷，X和Y为动载荷系数，Fr为径向载荷，Fa为轴向载荷。

2. 等效动载荷系数计算公式。

等效动载荷系数X和Y是与轴承类型和工况相关的参数，可以根据轴承的基本动载荷额定值和实际载荷计算得出。

其计算公式如下：X = （0.56 + 0.28P）/（0.56 + P）。

Y = （0.34 + 0.22P）/（0.34 + P）。

其中，P为载荷系数，可以根据实际载荷计算得出。

3. 寿命计算公式。

滚动轴承的寿命是指在特定工况下，轴承达到一定疲劳寿命的时间。

寿命计算公式可以帮助工程师预测轴承的使用寿命，其常用的计算公式为：L10 = （C/P）3。

滚轮轴承的载荷参数及其计算方法下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!滚轮轴承的载荷参数及其计算方法导言滚轮轴承是工业生产中常见的重要零部件，其承载着机器设备的载荷。

轴承滚道设计计算公式轴承是机械设备中常用的零部件，用于支撑和转动机械装置。

轴承滚道的设计是轴承性能的关键因素之一，它直接影响着轴承的寿命、承载能力和运转稳定性。

在轴承滚道设计中，计算公式是非常重要的工具，它可以帮助工程师准确地计算出所需的参数，从而确保轴承的性能符合要求。

轴承滚道设计中的计算公式涉及到多个方面，包括滚道尺寸、载荷分布、接触应力等。

下面我们将介绍一些常用的轴承滚道设计计算公式，并对其进行详细解释。

1. 轴承滚道尺寸计算公式。

轴承滚道的尺寸是影响轴承性能的重要因素之一。

一般来说，滚道的尺寸越大，轴承的承载能力就越大。

轴承滚道尺寸的计算公式可以根据轴承的类型和使用条件来确定，其中最常用的计算公式是根据滚道直径和滚道角度来计算的。

滚道直径的计算公式为：D = d + 2 (C0 / (π tan(α)))。

其中，D为滚道直径，d为滚珠直径，C0为静载荷，α为滚道角度。

滚道角度的计算公式为：tan(α) = (C0 / (π D)) (d/2)。

通过这两个公式的计算，可以确定轴承滚道的尺寸，从而满足轴承的承载能力要求。

2. 轴承载荷分布计算公式。

轴承的承载能力是其设计的关键指标之一。

在轴承滚道设计中，需要根据实际工作条件和载荷类型来确定轴承的载荷分布，以确保轴承在工作过程中能够承受来自各个方向的载荷。

轴承的载荷分布可以通过以下公式来计算：P = (F1 + F2 + ... + Fn) / cos(β)。

其中，P为轴承的总载荷，F1、F2、...、Fn为各个方向上的载荷，β为载荷的夹角。

通过这个公式的计算，可以确定轴承的总载荷，从而确定轴承的尺寸和材料。

3. 轴承接触应力计算公式。

轴承的接触应力是轴承设计中需要重点考虑的因素之一。

接触应力过大会导致轴承的磨损和损坏，因此需要通过计算来确定轴承的接触应力，以确保轴承在工作过程中能够正常运转。

轴承的接触应力可以通过以下公式来计算：σ = F / (π d B)。

滚动轴承的寿命计算一、基本额定寿命和基本额定动载荷1、基本额定寿命L10轴承寿命：单个滚动轴承中任一元件出现疲劳点蚀前运转的总转数或在一定转速下的工作小时数称轴承寿命。

由于材料、加工精度、热处理与装配质量不可能相同,同一批轴承在同样的工作条件下，各个轴承的寿命有很大的离散性，所以，用数理统计的办法来处理。

基本额定寿命L10——同一批轴承在相同工作条件下工作，其中90%的轴承在产生疲劳点蚀前所能运转的总转数（以106为单位）或一定转速下的工作时数。

（失效概率10%）。

2、基本额定动载荷C轴承的基本额定寿命L10=1（106转）时，轴承所能承受的载荷称基本额定动载荷C。

在基本额定动载荷作用下，轴承可以转106转而不发生点蚀失效的可靠度为90%。

基本额定动载荷C（1）向心轴承的C是纯径向载荷；（2）推力轴承的C是纯轴向载荷；（3）角接触球轴承和圆锥滚子轴承的C是指引起套圈间产生相对径向位移时载荷的径向分量。

二、滚动轴承的当量动载荷P定义：将实际载荷转换为作用效果相当并与确定基本额定动载荷的载荷条件相一致的假想载荷，该假想载荷称为当量动载荷P，在当量动载荷P作用下的轴承寿命与实际联合载荷作用下的轴承寿命相同。

1．对只能承受径向载荷R的轴承（N、滚针轴承）P=F r2．对只能承受轴向载荷A的轴承（推力球（5）和推力滚子（8））P= F a3．同时受径向载荷R和轴向载荷A的轴承P=X F r+Y F aX——径向载荷系数，Y——轴向载荷系数，X、Y——见下表。

径向动载荷系数X和轴向动载荷系数表12－3考虑冲击、振动等动载荷的影响，使轴承寿命降低，引入载荷系数fp—见下表。

载荷系数fp表12－4三、滚动轴承的寿命计算公式图12－9 载荷与寿命的关系曲线载荷与寿命的关系曲线方程为：=常数(12-3)3 球轴承ε——寿命指数10/3——滚子轴承根据定义：P=C，轴承所能承受的载荷为基本额定功载荷时，∴∴（106r） (12-2)按小时计的轴承寿命：（h）（12-3）考虑当工作t>120℃时，因金属组织硬度和润滑条件等的变化，轴承的基本额定动载荷C有所下降，∴引入温度系数f t——下表——对C修正表 12－5（106r）(12-4)（h）(12-5)当P、n已知，预期寿命为L h′，则要求选取的轴承的额定动载荷C为N ——选轴承型号和尺寸！（12-6）不同的机械上要求的轴承寿命推荐使用期见下表。

滚动轴承计算在机械设计中，对于滚动轴承，主要是正确选择其类型、尺寸（型号）和合理进行轴与轴承的组合设计。

在选定滚动轴承的类型、尺寸（型号），应综合考虑轴承的固定，轴承的组合定位，间隙的调整，轴承座圈与其他零件的配合，轴承的装拆和润滑、密封等问题，正确设计轴承部件的组合结构，以保证轴系的正常工作。

而在设计轴时已初选轴承为滚子轴承，现只需计算校核。

一、安装蜗轮的轴的轴承计算在设计轴时初选圆锥滚子轴承30312,e=0.35,Y=17, 径向力：FrA=J-I+F ；=3247NFrB 二廊蒋工3408N派生力：外载轴向力:Fa=468.93N皂=0.29<e,所以X A =0.4,YA=17,XB=1FrBYB=O由于为一般载荷，则fp=12,故当量载荷为：PA=f p (XA p rA÷YAFaA)=4463.5N PB=fp(XBFrB+YBFaB)=4089.6N而C r =170kN,故轴承寿命1p=^—[C]=1°6f 17OOOθY θ=775602χ104h>292000h p60n 3∣k PJ60×4014463.5J因此选用该轴承没问题。

二、蜗杆轴轴承的校核设计轴时，两端均初选轴承30307,e=0.31,Y=19FdB=—=1002N QD 2γFFdA =寸=955N轴向力：FaA=FdB+Fa2=1424NFaB=FdB=1002N当量载荷：由于区=0.43>eF 川径向力：FrA 二际F=3327N派生力：⅛-=875.53N 2Y轴向力：FaA=FdB+Fa 广7110.5N 当量载荷：由于E 型二区=0.37>e,FrB FM由于为一般载荷，则fp=12,故当量载荷为： P A =f p (XF rA +YF aA )=17808.9N而C r =75.2kN,故轴承寿命IO 6(75200Y oz3 Q--------- B 上=1405.6X1()3h>292000h60x1440^17808.9；因此选用该轴承也没问题。

滚动轴承的寿命计算1 基本额定寿命和基本额定动载荷轴承中任一元件出现疲劳点蚀前的总转数或一定转速下工作的小时数称为轴承寿命。

大量实验证明，在一批轴承中结构尺寸、材料及热处理、加工方法、使用条件完全相同的轴承寿命是相当离散的（图1是一组20套轴承寿命实验的结果），最长寿命是最短寿命的数十倍。

对一具体轴承很难确切预知其寿命，但对一批轴承用数理统计方法可以求出其寿命概率分布规律。

轴承的寿命不能以一批中最长或最短的寿命做基准，标准中规定对于一般使用的机器，以90%的轴承不发生破坏的寿命作为基准。

（1）基本额定寿命 一批相同的轴承中90%的轴承在疲劳点蚀前能够达到或超过的总转数r L （610转为单位）或在一定转速下工作的小时数()h h L 。

图1 轴承寿命试验结果可靠度要求超过90%，或改变轴承材料性能和运转条件时，可以对基本额定寿命进行修正。

（2）基本额定动载荷 滚动轴承标准中规定，基本额定寿命为一百万转时，轴承所能承受的载荷称为基本额定动载荷，用字母C 表示，即在基本额定动载荷作用下，轴承可以工作一百万转而不发生点蚀失效的概率为90%。

基本额定动载荷是衡量轴承抵抗点蚀能力的一个表征值，其值越大，轴承抗疲劳点蚀能力越强。

基本额定动载荷又有径向基本额定动载荷（r C ）和轴向基本额定动载荷（a C ）之分。

径向基本动载荷对向心轴承（角接触轴承除外）是指径向载荷，对角接触轴承指轴承套圈间产生相对径向位移的载荷的径向分量。

对推力轴承指中心轴向载荷。

轴承的基本额定动载荷的大小与轴承的类型、结构、尺寸大小及材料等有关，可以从手册或轴承产品样本中直接查出数值。

2 当量动载荷轴承的基本额定动载荷C （r C 和a C ）是在一定条件下确定的。

对同时承受径向载荷和轴向载荷作用的轴承进行寿命计算时，需要把实际载荷折算为与基本额定动载荷条件相一致的一种假想载荷，此假想载荷称为当量动载荷，用字母P 表示。

当量动载荷P 的计算方法如下：同时承受径向载荷r F 和轴向载荷a F 的轴承()P r a P f XF YF =+（1）受纯径向载荷r F 的轴承（如N 、NA 类轴承）P r P f F =（2）受纯轴向载荷a F 的轴承（如5类、8类轴承）P a P f F =（3）式中：X ——径向动载荷系数，查表1； Y ——轴向动载荷系数，查表1； P f 冲击载荷系数，见表2。