第三章 机构的运动分析--相对运动矢量方程图解法
- 格式:ppt
- 大小:2.27 MB
- 文档页数:75

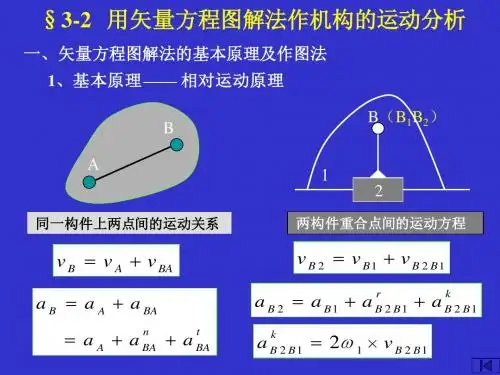



《机械原理》第三章平面机构运动分析——矢量方程图解法对机构运动分析(1)矢量方程图解法(相对运动图解法)依据的原理理论力学中的运动合成原理同一构件两点间的运动关系两构件重合点间的运动关系ω1A D C1432B C B CB v v v =+2121C C C C v v v =+矢量方程图解法(相对运动图解法)依据的原理理论力学中的运动合成原理同一构件两点间的运动关系两构件重合点间的运动关系1、根据运动合成原理列出矢量方程2、根据矢量方程图解条件作图求解基本作法二、同一构件两点间的运动分析运动合成原理:连杆上任一点(如C 点)的运动,可以看作是随同该构件上另一点B 的平动(牵连运动)和绕该点的转动(相对运动)的合成。
已知图示曲柄滑块机构原动件AB 的运动规律和各构件尺寸。
求:①图示位置连杆BC 的角速度和其上各点速度。
②连杆BC 的角加速度和其上C 点加速度。
理论力学大小:方向:?ω1l AB ?∥xx ⊥AB ⊥BC cp★求V C①由运动合成原理列矢量方程式CB B C v v v +=v B ω2②确定速度图解比例尺μv ( (m/s)/mm)/B v pb v μ=b2CB CB l ω=v (逆时针方向)2CB CBl ω=v C v v pc μ=CB v v bc μ=③作图求解未知量:大小:方向:c p★求V Ev B ω2bE v v peμ=?√ ??⊥AB ⊥EBE B EB v v v =+C EC v v =+∥xx ⊥EC √ ?e 速度多边形极点m/sc pv B ω2be 速度多边形极点①由极点p 向外放射的矢量代表相应点的绝对速度,极点p 的速度为零;②连接极点以外其他任意两点的矢量代表构件上相应两点间的相对速度,其指向与速度的下角标相反;③因为△BCE 与△bce 对应边相互垂直且角标字母顺序一致,故相似,所以图形bce 称之为图形BCE 的速度影像。
CB B C v v v +=C v v pc μ=速度影像。




《机械原理》第三章平面机构运动分析——矢量方程图解法对机构运动分析(3)ω1已知图示机构尺寸和原动件1的运动。
求构件3上C点的运动。
ADC1432B运动合成原理:1、2构件形成移动副,2构件上任意一点(如B点)的运动,可以看作是随同1构件上重合点的运动(牵连运动)和2构件相对1构件的相对运动的合成。
理论力学大小:方向:?√ ?? ⊥AB ∥ABω1已知图示机构尺寸和原动件1的运动。
求构件3上C点的运动。
ADC1432B1212BBBBvvv+=选择B为重合点不可解大小:方向:?√ ?⊥CD ⊥AC ∥ABω1已知图示机构尺寸和原动件1的运动。
求构件3上C点的运动。
ADC1432BC1、C2、C31212CCCCvvv+=pc1c2选择C为重合点32CCvv=大小:方向:?√ ?⊥CD ⊥AC ∥ABω1已知图示机构尺寸和原动件1的运动。
求构件3上C点的运动。
AD1432BC1、C2、C31212CCCCvvv+=pc1c232CCvv=22C vv pcμ=33/C CDv lω=顺时针方向ω3ω1已知图示机构尺寸和原动件1的运动。
求构件3上C点的运动。
ADC1432BC1、C2、C3大小:方向:√ ?C→D ⊥CD2333n tC C C Ca a a a==+233nC CDa lω=33tC CDa lα=ω1已知图示机构尺寸和原动件1的运动。
求构件3上C 点的运动。
AD1432BC 1、C 2、C 3大小:方向:?√ ⊥AB ∥AB212121krC C C C C C a a aa=++?√1212C C v ω?211212k C C C C av ω=科氏加速度方向是将Vc 2c1沿牵连构件角速度ω1转过90o 的方向。
ω1已知图示机构尺寸和原动件1的运动。
求构件3上C 点的运动。
AD1432BC1、C2、C3pc1c2大小:方向:√ ?√ √ ?C→D ⊥CD √ ⊥AB∥ABrCCkCCCtDCnDC1212133C2aaaaaa++=+='p1'c'k3n2'c3(')cω1已知图示机构尺寸和原动件1的运动。

第三章平面机构的运动分析十字滑块联轴器运动简图第三章平面监管机构的运动分析§3-1 研究机构运动分析最终目标的目的和方法1、运动分析:已知各构件尺寸和原动件的运动规律→从动件各点或构件的(角)位移、(角)速度、(角)加速度。
2、目的:来判断运动参数是否满足设计要求?为后继设计提供原始参数3.方法:图解法:形象直观、概念清晰。
精度不高?(速度瞬心法,相对运动图解法)解析法:高的精度。
工作量大?实验法:§3-2 速度瞬心法及其在机构速度建模上的应用1、速度瞬心:两构件作平面相对运动时,在任意瞬间总能找到这样的点:两构件的相对运动可以认为是绕该点后的转动。
深入概括速度瞬心:1)两构件上相对速度为零的重合点,即同速点; 2)瞬时具有瞬时性(时刻不同,位置不同);3)平行线两构件的速度瞬心位于无穷远,表明两构件的表明角速度相同或仅作相对移动;4)相对速度瞬心:两构件都是运动的;绝对速度瞬心:两构件之一是相对运动的(绝对速度为零的点后;并非接触点的变化速度快);2、咨询机构中瞬心的数目年K:K=n(n-1)n ——构件数(包括机架) 23、瞬心位置的确定1)直接观察法(定义法,由于直接形成运动副的呈现出两构件);2N=P23设:Vk13、1K3)曲柄滑块机构N=4⨯(4-1)=624)直动平底从动件轮轴机构5)图示机构,已知M点的速度,用速度瞬心法求出所有的瞬心,并求出VC,VD,i12。
解:直接观察:P12、P23、P34;P14=(n_-n). × VM ; P13= P12P23. × P14P34P24= P12P14 × C·P24P34 ; ω1= VM/ P14M ; VB= P14B·ω1 ω2=VB/ P12P24 ; VC= P24C·ω2ω1/ω2=( VM/ P14M)/( VB/ P12P24); VD= P24D·ω2速度瞬心法小结:1)速度瞬心法仅用于求解速度问题,不能用于求解加速度环境问题。