最新10组合变形汇总
- 格式:doc
- 大小:456.50 KB
- 文档页数:13


材料力学10组合变形组合变形是指当结构受到外力作用时,由于各个零件的不同材料及尺寸性质的差异,导致各个零件产生不同的变形现象,从而使整个结构发生整体的变形。
组合变形是结构力学的重要内容,对于工程结构的设计、安全性评估和结构稳定性分析都至关重要。
本文将介绍组合变形的概念、分析方法和影响因素。
组合变形的概念:组合变形是指由于结构中不同零件的尺寸和材料性质的不一致,而导致结构在受力时产生的整体变形。
组合变形分为两类:一是刚体体变形,即结构在受力作用下整体平移、旋转或缩放;二是构件本身变形,即结构中各零件由于尺寸和材料的不一致而产生的内部变形。
组合变形的分析方法:组合变形的分析方法主要有两种:力法和位移法。
力法是指根据梁的变形方程和杨氏模量的定义,通过计算各零件在各个截面上的张力或弯矩,从而得到整体的变形情况。
位移法是指根据构件的位移和应变关系,通过求解位移方程组,从而得到整体的变形情况。
力法和位移法都是基于弹性理论,适用于较小变形和线性弹性材料的情况。
组合变形的影响因素:组合变形的大小与结构的几何形状、零件尺寸和材料性质有关。
影响组合变形的因素主要有以下几个方面:1.结构的几何形状:结构的几何形状对组合变形有重要影响。
例如,在长梁的弯曲变形中,梁的长度和曲率半径都会影响变形的大小。
2.零件的尺寸:零件的尺寸对组合变形有重要影响。
例如,在梁的弯曲变形中,梁的截面积和转动惯量会影响变形的大小。
3.零件的材料性质:零件的材料性质对组合变形有重要影响。
例如,在梁的弯曲变形中,梁的弹性模量和截面剪切模量会影响变形的大小。
4.外力的作用方式:外力的作用方式对组合变形有重要影响。
例如,在梁的弯曲变形中,集中力和均布力对变形的影响是不同的。
除了以上几个因素外,结构的边界条件和连接方式也会影响组合变形的大小。
此外,在实际工程中,结构中可能存在的缝隙、温度变化、材料老化等因素也会对组合变形产生影响。
对于设计工程结构来说,合理控制组合变形是非常重要的。






第八章 组合变形判断 拉弯组合1、“斜弯曲时中性轴一定过截面的形心而且中性轴上的正应力为零。
”2、“当载荷不在梁的主惯性平面内,梁一定产生斜弯曲”3、“拉弯组合变形时,中性轴一定不过截面的形心”4、“杆件发生斜弯曲时,杆件变形的总挠度方向一定与中性轴相垂直。
”5、“只要杆件横截面上的轴力为零,则该横截面上的正应力各处为零”6、“承受偏心拉伸的杆件,其中性轴仍然通过截面的形心”7、“拉弯组合变形和偏心拉伸组合变形的中性轴位置都与载荷的大小无关。
”选择 拉弯组合1、应用叠加原理的前提条件是: 。
A :线弹性构件; B :小变形杆件;C :线弹性、小变形杆件;D :线弹性、小变形、直杆; 2、矩形截面偏心受压杆件发生 变形。
A :轴向压缩、平面弯曲B :轴向压缩、平面弯曲、扭转 C:轴向压缩、斜弯曲 D :轴向压缩、斜弯曲、扭转3、平板上边切h/5,在下边对应切去h/5,平板的强度。
A :降低一半;B :降低不到一半;C :不变;D :提高了;4、AB 杆的A 处靠在光滑的墙上,B 端铰支,在自重作用下发生变形, AB 杆发生 变形。
A :平面弯曲B :斜弯;C :拉弯组合;D :压弯组合;5、简支梁受力如图:梁上 。
A :AC 段发生弯曲变形、CB 段发生拉弯组合变形 B :AC 段发生压弯组合变形、CB 段发生弯曲变形C :两段只发生弯曲变形D :AC 段发生压弯组合、CB 段发生拉弯组合变形6、图示中铸铁制成的压力机立柱的截面中,最合理的是 。
7、矩形截面悬臂梁在自由端受到力P 的作用,如图。
OP 为载荷的作用线,已知I Z <I Y 。
则该梁横截面的 。
A :中性轴位于1、3象限,挠度方向可能为Of 1 B :中性轴位于1、3象限,挠度方向可能为Of 2C :中性轴位于2、4象限,挠度方向可能为Of 1D :中性轴位于2、4象限,挠度方向可能为Of 28、矩形截面拉弯组合变形时,对于横截面的中性轴有以下的结论。
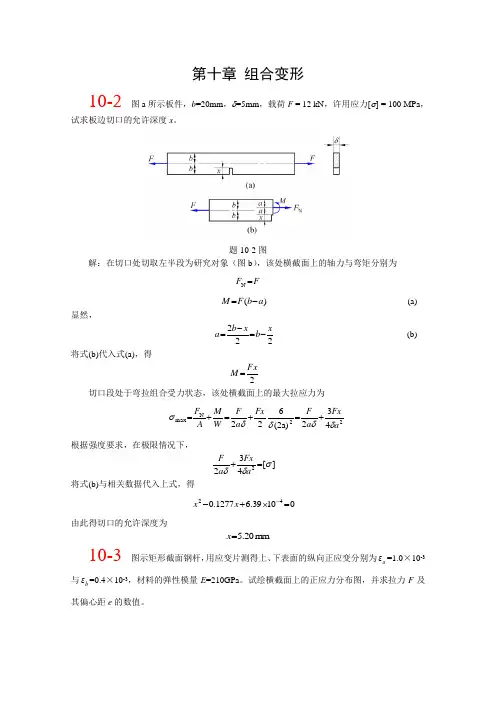
第十章 组合变形10-2 图a 所示板件,b =20mm ,δ=5mm ,载荷F = 12 kN ,许用应力[σ] = 100 MPa ,试求板边切口的允许深度x 。
题10-2图解:在切口处切取左半段为研究对象(图b ),该处横截面上的轴力与弯矩分别为F F =N)(a b F M -= (a)显然,222xb x b a -=-=(b)将式(b)代入式(a),得2FxM =切口段处于弯拉组合受力状态,该处横截面上的最大拉应力为22N max 432(2a)6 22a Fxa F Fx a F W M A F δδδδσ+=+=+=根据强度要求,在极限情况下,][4322σδδ=+a Fx a F 将式(b)与相关数据代入上式,得01039.61277.042=⨯+--x x由此得切口的允许深度为m m 20.5=x10-3 图示矩形截面钢杆,用应变片测得上、下表面的纵向正应变分别为aε=1.0×10-3与b ε=0.4×10-3,材料的弹性模量E =210GPa 。
试绘横截面上的正应力分布图,并求拉力F 及其偏心距e 的数值。
题10-3图解:1.求a σ和b σ截面的上、下边缘处均处于单向受力状态,故有MPa84Pa 104.010210 MPa 210Pa 100.1102103939=⨯⨯⨯===⨯⨯⨯==--b b a a E εσE εσ偏心拉伸问题,正应力沿截面高度线性变化,据此即可绘出横截面上的正应力分布图,如图10-3所示。
图10-32.求F 和e将F 平移至杆轴线,得 Fe M F F ==,N于是有 a za E εW Fe A F σ=+=E εW Fe AF σzb =-=代入相关数据后,上述方程分别成为 26250240=+Fe F 10500240=-Fe F 经联立求解,于是得mm 786.1m 10786.1kN 38.18N 183753=⨯=≈=-e F ,10-6 图示直径为d 的圆截面铸铁杆,承受偏心距为e 的载荷F 作用。
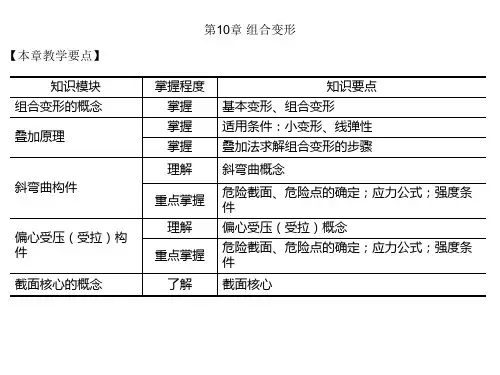
第10章组合变形§10-1 组合变形的概念1.组合变形的概念组合变形:构件往往会发生两种或两种以上的基本变形的这类变形。
在前面各章分别讨论了杆件在拉(压)、剪切、扭转和弯曲基本变形时的应力和强度计算。
工程实际中,杆件在荷载作用下所发生的变形,经常是两种或两种以上基本变形的组合,这种变形称为组合变形。
例如图10.1(a)所示屋架檩条的变形,是由y/z两个方向的平面弯曲变形组成的斜弯曲;如图10.1(b)所示厂房柱,在偏心力F作用下,会发生压缩和弯曲的组合变形;如图10.1(c)所示的卷扬机轴在力F作用下,则发生弯曲和扭转的组合变行。
2.组合变形的分析方法及计算原理处理组合变形问题的方法:1.将构件的组合变形分解为基本变形;2.计算构件在每一种基本变形情况下的应力;3.将同一点的应力叠加起来,便可得到构件在组合变形情况下的应力。
叠加原理是解决组合变形计算的基本原理叠加原理应用条件:即在材料服从胡克定律,构件产生小变形,所求力学量定荷载的一次函数的情况下,计算组合变形时可以将几种变形分别单独计算,然后再叠加,即得组合变形杆件的内力、应力和变形。
计算原理:(1)圣维南原理以静力等效力系代替构件原有的荷载,为此,要求构件为细长杆,且所求应力的截面远离外力作用点;(2)叠加原理 按各基本变形计算后进行叠加,为此,要求构件处于线弹性范围内,且变形很小,可按构件的原始形状的尺寸进行计算。
在小变形和线弹性条件下,杆件上各种力的作用彼此独立,互不影响,即杆上同时有几种力作用时,一种力对杆的作用效果(变形或应力),不影响另一种力对杆的作用效果(或影响很小可以忽略)。
因此组合变形下杆件内的应力,可视为几种基本变形下杆件内应力的叠加。
本章中组合变形下杆件的应力计算,将以各基本变形的应力及叠加法为基础。
叠加法的主要步骤:a 、将组合变形按照各基本变形的条件,分解为几种基本变形,简称分解。
b 、利用基本变形的应力计算公式,分别计算各点处的正应力和切应力。
组合变形1. 偏心压缩杆,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心的距离d 之间的关系有四种答案:(A) e d =; (B) e d >; (C) e 越小,d 越大; (D) e 越大,d 越大。
答:C2. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为max1σ、max 2σ和max 3σ,现有下列四种答案:(A)max1max 2max 3σσσ==; (B)max1max 2max 3σσσ>=; (C)max 2max1max 3σσσ>=; (D)max1max3σσσ<=max2。
答:C3.重合)。
立柱受沿图示a-a(A)斜弯曲与轴向压缩的组合; (B)平面弯曲与轴向压缩的组合; (C)斜弯曲; (D)平面弯曲。
答:B4. (A) A 点; (B) B 点; (C) C 点; (D) D 点。
答:C5. 图示矩形截面拉杆,中间开有深度为/2h 的缺口,与不开口的拉杆相比,开口处最大正应力将是不开口杆的 倍: (A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。
答:C6. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为max1σ、max 2σ和max 3σ,现有下列四种答案:(A)max1max 2max3σσσ<<; (B)max1max 2max3σσσ<=; (C)max1max3max 2σσσ<<; (D)max1max 3max 2σσσ=<。
答:C7. 正方形等截面立柱,受纵向压力F移至B 时,柱内最大压应力的比值max maxA B σσ(A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。
答:C8. 图示矩形截面偏心受压杆,其变形有下列四种答案:(A)轴向压缩和平面弯曲的组合; (B)轴向压缩、平面弯曲和扭转的组合; (C)缩和斜弯曲的组合;(D)轴向压缩、斜弯曲和扭转的组合。
10 组合变形1、斜弯曲,弯扭,拉(压)弯,偏心拉伸(压缩)等组合变形的概念;2、危险截面和危险点的确定, 中性轴的确定;如双向偏心拉伸, 中性轴方程为1 2 z o 2 y o 0i y i z3、危险点的应力计算,强度计算,变形计算、。
4、截面核心。
解题范例10.1 、定性分析图10.1 示结构中各构件将发生哪些基本变形?图10.1[解](a)AD杆时压缩、弯曲组合变形,BC杆是压缩、弯曲组合变形;AC杆不发生变形。
(b)AB杆是压弯组合变形,BC杆是弯曲变形。
(c)AB是压缩弯曲组合变形,BC是压弯组合变形。
(d)CD是弯曲变形,BD发生压缩变形,AB发生弯伸变形,BC发生拉弯组合变形。
10.2 分析图10.2 中各杆的受力和变形情况。
[ 解] (a) 力可分解成水平和竖直方向的分力(b) 所受外力偶矩作用, 产生弯曲变形。
(c) 该杆受竖向集中荷载, 产生弯曲变形.(d) 该杆受水平集中荷载(e) AB段:受弯,弯曲变形,(f) AB段:受弯,弯曲变形,(g) AB 段:斜弯曲,BC段:弯纽扭合。
, 为压弯变形。
, 偏心受压, 产生压缩和弯曲变形。
BC段: 弯曲。
10.3 分析图10.3 示构件中(AB 、BC和CD) 各段将发生哪些变形?Wz=185cm 3),其长度为 l =2.6m 。
试求当荷载 F=25kN 作用在 AB 的中点处时, 杆内的最大正应力。
设工字钢的自重可略去不计。
图 10.4[ 解] 取 AB 为研究对象,对 A 点取矩可得 F NBCY 12.5kN分别作出 AB 的轴力图和弯矩图图 10.3[ 解 ] AB 段发生弯曲变形,BC 段发生弯曲、扭转变形; CD 段发生拉伸、双向弯曲变形。
10.4 一悬臂滑车架如图10.4 所示,杆 AB 为 18 号工字钢(截面面积 30.6cm 2,25 2Fl4l/2lkNkN.mFNABFNBCXB2轴力作用时截面正应力均匀分布,F N(压) A弯矩作用时截面正应力三角形分布, M (下拉上压) Wz可知 D 截面处上边缘压应力最大 , 叠加可得最大正应力 94.9MPa (压10.5 如图 10.5 所示 , 截面为 16a 号槽钢的简支梁 , 跨长 L=4.2m, 受集度为 q 的均布荷载作用 ,q=2KN/m 。
10组合变形图10.4 斜弯曲分析参考图10 组合变形10.1 组合变形的概念和实例分析组合变形问题时,通常是先把作用在杆件上的载荷向杆件的轴线简化,即把构件上的外力转化成几组静力等效的载荷,其中每一组载荷对应着一种基本变形。
工程中,常见的组合变形主要有斜弯曲、拉伸(压缩)与弯曲的组合、弯曲与扭转的组合。
下面讨论这三种组合变形的强度计算问题。
10.2 斜弯曲10.2.1 斜弯曲时横截面上的应力外力简化 ϕϕsin ,cos z y P P P P == 内力:ϕϕcos )(cos )(y z M x l P x l P M =-=-=ϕϕsin )(sin )(z y M x l P x l P M =-=-=式中)(x l P M -=是集中力P 在横截面m-n 上所引起的弯矩,在计算中可取绝对值。
应力: 任意截面m-n 上任意点C (y ,z )处的应力可采用叠加法计算。
在xy 平面内的平面弯曲(由于z M 的作用)产生的正应力为y I M I y M zz z cos ϕσ=='由于在xz 平面内的平面弯曲(由于yM 的作用)产生的正应力为图10.1起重机构ACB 梁受力分析 图10.2传动轴受力分析z I M I z M yyy sin ϕ==σ''C 点处的正应力,即 y y z z I z M I y M +=''+'=σσσ⎪⎪⎭⎫⎝⎛+=z I y I M y zsin cos ϕϕ(10.1)10.2.2 斜弯曲时的强度计算强度条件为max 11z y cos sin M y z I I ϕϕσ⎛⎫=+≤⎪ ⎪⎝⎭[]σ (10.2) 对于有棱角的矩形截面,根据图10.4所示的应力分布,公式(10.2)还可写成 ≤+=z zmaxy y maxmax W M W M σ[]σ (10.3)若材料的抗拉强度和抗压强度不同,则应分别对1D 点和2D 点都进行强度计算。
0sin cos 0y0z =⎪⎪⎭⎫ ⎝⎛+=z I y I M ϕϕσ因为0≠M ,所以有 0sin cos 0y 0z =+z I y I ϕϕ (10.4)此即斜弯曲时的中性轴方程。
设中性轴与z 轴的夹角为α,根据公式(10.4)有ϕαtg tan yz 00I Iz y -== (10.5)由式(10.5)可得出以下两点结论:(1) 对于zy I I ≠的截面,则ϕα≠。
这表明此种梁在发生斜弯曲时,其中性轴与外力P 所在的纵向平面不垂直(图10.5b )。
(2) 对于圆形、正方形及其他正多边形截面,由于zy I I =,故可由式(10.5)得:ϕα-=,这说明中性轴总是与载荷所在的纵向面垂直,即此类截面的梁不会产生斜弯曲。
10.2.3 斜弯曲的变形计算33y y z z cos 33P l P l f EI EI ϕ==--33zz y y cos 33Pl P l f EI EI ϕ==--2z 2y f f f +=(10.6)设总挠度f 与y 轴的夹角为β(图10.6b ),则有 ϕβtg tan yz y z I If f == (10.7)关于挠度、中性轴及外力P 的位置之间的关系,现作进一步讨论:图10.6斜弯图(1) 由式(10.7)知,若梁的横截面zy I I ≠,则ϕβ≠,这说明梁在变形后的挠曲线与外力P 所在的纵向面不共面,因此,称为斜截面。
(2) 对于zy I I =的横截面(如圆形、正方形),则ϕβ=,即挠曲线与外力在同一纵向平面内。
这种情况仍是平面弯曲。
实际上,对于zy I I =的横截面,过截面形心的任何一个轴都是形心主惯性轴。
因此,外力作用将总能满足平面弯曲的条件。
(3) 由式(10.5)及式(10.7)知:中性轴与z 轴的夹角α等于挠度与y 轴的夹角β。
即和平面弯曲一样,斜弯曲时,中性轴仍垂直于挠度f 所在的平面。
【例题10.1】例10.1图所示结构的梁为16号工字钢,材料为Q 235--A 钢,〔σ〕=160MPa ,E =200GPa ,载荷P 与y 轴的夹角︒=20ϕ,P =7kN 梁的跨度l =4m 。
试校核梁的强度及计算梁中点的挠度。
解:①外力分析 将P 沿y 轴和z 轴分解,得kN 39.220sin 7sin kN 58.620cos 7cos z y =︒===︒==ϕϕP P P Py P 和zP 将分别使梁在xy 和xz 平面内产生平面弯曲。
②内力计算 任一横截面上,由y P和z P 作用产生的弯矩分别为z M 和y M ,其内力图见图(b )和(c )。
显然,在梁中点C 处,z M 和y M同时取得最大值,故为危险截面。
kN39.24439.24kN58.64458.64z y max y zmax =⨯===⨯==l P M l P M③强度计算 在作用下,截面C 的下边缘拉应力最大,上边缘压应力最大。
在y M作用下,前侧边缘产生最大拉应力,后侧边缘产生最大压应力。
应力叠加后,两边缘的交点1D 和2D 点分别产生最大拉应力和最大压应力(图d )。
查型钢表,对于16号工字钢,,cm 141,cm 1.93,cm 11303z 4y 4z ===W I I 3y cm 2.21=W 。
由公式(10.3)6363y ymax z zmax max 102.211039.2101411058.6--⨯⨯+⨯⨯=+=W M W M σ<=⨯=159.4MPa Pa 104.1596[]σ故满足强度条件。
例10.1图 工字钢结构梁若载荷不偏离y 轴(0=ϕ),C 截面弯矩最大 mkN 74474max ⋅=⨯==Pl M 故最大正应力为MPa 6.49Pa 106.4910141107663z max max =⨯=⨯⨯==-W M σ④ 挠度计算 在y P和z P 作用下, C 截面形心沿y 方向和z 方向的挠度分别为mm 1.17m 101.17101.93102004841039.248mm 88.3m 1088.3101130102004841058.64838933y 3z z 38933z 3y y =⨯=⨯⨯⨯⨯⨯⨯===⨯=⨯⨯⨯⨯⨯⨯==----EI l P f EI l P f所以,总挠度为2z 2y f f f +==mm 5.171.1788.322=+挠度f 与y 轴的夹角β(图d )为 4.488.31.17tan y z ===f f β10.3 拉伸(压缩)与弯曲的组合变形10.3.1 拉(压)与弯曲组合时的强度计算图10.7(a )所示为一等直杆,两端铰支,载荷2P 为作用在梁跨度中点C 截面上的横向力,而1P 为作用于杆两端的轴向拉力。
我们以此为例,说明杆在拉(压)与弯曲组合时的强度计算问题。
①外力分析 ②内力分析③应力分析 在C 截面上,与轴力N 对应的正应力σ'在横截面上均匀分布(图10.7c )其值为: A N ='σ 而与m ax M 对应的弯曲正应力σ''在横截面上沿截面高度线性分布(图10.7d ),其值为z M y I σ⋅''=图10.7 拉(压)与弯曲组合变形分析例10.2图 悬臂式吊车架 最大弯曲正应力在C 截面的上、下边缘,其值为 max 2W4z z M P l W W σ==④强度计算 强度条件可表示为≤+=z maxmax W M A N σ[]σ (10.8) 【例题10.2】例10.2图所示为一悬臂式吊车架,在横梁AB 的中点D 作用一集中载荷P =25kN ,已知材料的许用应力[]σ=100Mpa ,若横梁AB 为工字型梁,试选工字钢型号。
解:①横梁AB 受力分析 取横梁AB 为研究对象,如图(b )所示,由静力平衡条件解得 kN 5.12,kN 6.21,kN 25A A ===V H T将T 沿梁的轴线及梁轴线垂直的方向分解,分别为1T 和2T ,则有kN5.12212530sin kN 6.21232530cos 21=⨯=︒==⨯=︒=T T T T可见,在1T 和A H 作用下,梁承受轴向压缩;在P 、2T 和A V 作用下,梁发生弯曲变形。
因此,横梁AB 承受的是压缩与弯曲的的组合。
③内力分析 横梁AB 的轴力图及弯矩图如图(c )和(d )所示。
显然,危险截面是D 截面。
其轴力和弯矩值分别为kN 6.211-=-=T NkN25.166.2254141max =⨯⨯==Pl M④截面设计 对于工字形梁,抗拉强度与抗压强度相同。
在D 截面的上边缘。
叠加后的正应力绝对值(压应力)达到最大值,故为危险点,所以强度条件为≤+=z maxmax W M A N σ[]σ 上式中,有两个未知量,即横截面积A 和抗弯截面模量W 。
所以,仅由上式无法确定工字钢型号。
工程中一般采用试算法。
即先不考虑轴力N 的影响,只根据弯曲强度条件初选工字钢型号,然后再根据拉(压)弯组合的强度条件进行强度校核。
由弯曲正应力强度条件≤=W Mmax max σ[]σ []3633max16.2510162.510m 162.5cm 100M W σ-⨯≥==⨯=查型钢表,选取18号工字钢,23cm6.30,cm185==AW。
⑤强度校核将以上数据及已求得的N和m axM值代入拉(压)与弯曲组合的强度条件6343zmaxmax101851025.16106.30106.21--⨯⨯-⨯⨯-=+=WMANσ=94.9MPa〈[]σ故选取18号工字钢满足强度条件。
试算中,若初选出的工字钢型号,拉(压)弯组合的危险应力大于许用应力[]σ,则应重新选取工字钢。
10.3.2 偏心压缩(拉伸)现通过例题说明此类问题的强度计算。
【例题10.3】小型压力机的铸铁框架如例10.3图(a)所示。
已知材料的许用拉应力[]tσ=30MPa,许用压应力[]60c=σMPa,载荷P=42kN,立柱的截面尺寸如图(b)所示。
试校核立柱的强度。
例10.3图压力机铸铁框架解:①截面几何性质计算3241510m,7.5cm,5312.5cmyA z I-=⨯==②外力分析kN42=P23e10)5.735(1042-⨯+⨯⨯=M mN1085.173⋅⨯=③内力分析kN42==PN mkN85.17ey⋅==MM④强度计算MPa8.2Pa108.210151042633=⨯=⨯⨯=='-ANσ与弯矩yM对应的正应力沿z轴线性分布,并由公式yyIzM=''σ计算。
最大弯曲拉应力和压应力分别是32y06tmax8y17.85107.51025.210Pa25.2MPa5312.510M zIσ--⨯⨯⨯''===⨯=⨯32y 16cmax 8y 17.8510(207.5)1042.010Pa 42MPa 5312.510M z I σ--⨯⨯-⨯''===⨯=⨯从图(d )看出,叠加以上两种应力后,在截面的内侧边缘上发生最大拉应力,且<=+=''+'=MPa 282.258.2tmaxtmax σσσ[]σ 在截面的外侧边缘上,发生最大压应力,且<=-=σ'-σ''=σMPa 2.398.242tmax []σ故立柱满足强度条件。