大学物理第5章角动量守恒定律刚体的转动
- 格式:doc
- 大小:217.50 KB
- 文档页数:6



刚体动力学刚体的转动与角动量守恒定律刚体动力学——刚体的转动与角动量守恒定律刚体动力学是研究刚体运动的物理学分支,主要研究刚体的平动和转动。
在刚体的运动过程中,角动量的守恒定律是关键的一条定律,它在很多物理问题的求解中起着重要的作用。
一、刚体转动的基本概念刚体是指具有一定形状和大小的物体,在运动过程中保持其形状和大小不变的情况下,绕一个固定轴线进行旋转。
在刚体转动的过程中,存在着固定轴线上的角位移、角速度、角加速度等概念。
角位移表示刚体在转动过程中的角度变化,通常用符号θ表示;角速度表示单位时间内刚体转动的角度变化率,通常用符号ω表示;角加速度表示单位时间内角速度的变化率,通常用符号α表示。
二、刚体的转动与力矩刚体在转动过程中需受到外力的作用,这些外力可以将刚体带动产生转动现象。
力矩是刚体转动的重要力学量,它描述了力对于刚体转动的影响程度。
力矩的大小等于力乘以作用点到转轴的距离,用数学式表示为:τ = F × r其中τ表示力矩,F表示力的大小,r表示作用点到转轴的距离。
三、刚体的转动惯量与角动量刚体的转动惯量与角动量是刚体转动过程中的另外两个重要概念。
转动惯量描述了刚体对于转动的惯性程度,它的大小取决于刚体的质量分布和几何形状。
角动量描述了刚体在转动过程中的旋转性质,它等于刚体质量的转动惯量乘以角速度,用数学式表示为:L = I × ω其中L表示角动量,I表示转动惯量,ω表示角速度。
四、角动量守恒定律角动量守恒定律是刚体动力学中的一个基本定律,它表明在没有外力矩作用的情况下,刚体转动过程中的角动量保持不变。
如果一个刚体在初态时角动量为L1,在末态时角动量为L2,且没有外力矩作用,则有L1 = L2。
这一定律体现了一个自然规律,对于理解刚体的转动过程和求解相关物理问题具有重要意义。
五、应用案例角动量守恒定律可以应用于各种实际物理问题的求解中,例如刚体的转动稳定性、陀螺的运动等。


转动力学刚体的转动平衡与角动量守恒转动力学是力学研究的一个重要分支,它主要研究刚体的旋转运动。
刚体的旋转运动受到力矩和角加速度的作用,其中转动平衡和角动量守恒是转动力学的基本原理。
一、转动平衡刚体的转动平衡是指刚体处于稳定的旋转状态,不受到外力的扰动,既不会产生角加速度,也不会改变角速度。
要实现转动平衡,必须满足以下条件:1. 力矩平衡条件力矩平衡条件是指刚体上作用的力矩的代数和为零。
对于一个刚体绕固定轴的旋转运动,力矩平衡条件可以表示为:∑M = ∑(r × F) = 0其中,∑表示对刚体上所有力矩求和,r表示作用力的杠杆臂,F表示作用力。
根据力矩平衡条件,可以求解出刚体的转动平衡状态。
2. 重心位置与支撑点位置的关系对于一个转动平衡的刚体,重心必须位于支撑点上方以保持稳定。
当重心位于支撑点下方时,刚体会不稳定,并发生滚动现象。
3. 稳定、不稳定和中立平衡刚体的转动平衡可以分为稳定、不稳定和中立平衡三种情况。
当刚体偏离平衡位置时,稳定平衡会使刚体回复原位置,而不稳定平衡会使刚体继续偏离平衡位置。
中立平衡则是指刚体在偏离平衡位置后,不会有任何变化。
二、角动量守恒角动量守恒是指一个刚体在没有外力矩作用下,角动量的大小和方向保持不变。
对于一个旋转的刚体,角动量可以表示为:L = Iω其中,L表示角动量,I表示转动惯量,ω表示角速度。
根据角动量守恒定律,在没有外部力矩作用下,刚体的角动量将保持不变。
三、应用举例下面通过一个实际例子来说明转动平衡和角动量守恒的应用。
假设有一个均匀的圆盘,圆盘质量为M,半径为R。
将圆盘以转轴垂直于盘面且通过重心的方式固定,使其处于转动平衡状态。
此时,圆盘的转动平衡可以通过力矩平衡条件来解释。
由于圆盘的重心位于转轴上,且没有施加外力矩,所以∑M=0,根据这个条件可以得到圆盘上各点产生的力矩之和为零。
进一步分析可以发现,圆盘上受重力的作用产生的力矩沿转轴方向相互抵消,所以圆盘能够保持转动平衡。

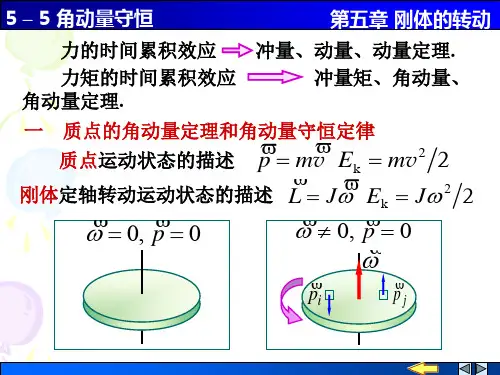
第5章 角动量守恒定律 刚体的转动5-1 质点的动量守恒与角动量守恒的条件各是什么,质点动量与角动量能否同时守恒?試说明之。
答:质点的动量守恒的条件是:当0F =时,p mv ==恒矢量。
质点的角动量守恒的条件是:当0M =时,即000,F r θπ⎧=⎪⎪=⎨⎪=⎪⎩时,L =恒矢量。
可见,当0F =时,质点动量与角动量能同时守恒。
5-2 质点在有心力场中的运动具有什么性质?答:质点在有心力场中运动时,0,0F M ≠=,则角动量守恒,即:当0M =时,L =恒矢量。
又因为有心力是保守力,则机械能守恒,即:当0ex in nc A A +=时,K P E E E =+=恒量。
5-3 人造地球卫星是沿着一个椭圆轨道运行的,地心O 是这一轨道的一个焦点。
卫星经过近地点和远地点时的速率一样吗?卫星在近地点和远地点时的速率与地心到卫星的距离有什么关系?答:卫星经过近地点和远地点时的速率不一样,由角动量守恒定律得:a ab b r mv r mv = a b b av r v r ∴= 可见,速率与距离成反比。
5-4 作匀速圆周运动的质点,对于圆周上某一定点,它的角动量是否守恒?对于通过圆心而与圆面垂直的轴上的任意一点,它的角动量是否守恒?对于哪一个定点,它的角动量守恒?答:作匀速圆周运动的质点,对于圆周上某一定点,它的角动量不守恒;对于通过圆心而与圆面垂直的轴上的任意一点,它的角动量不守恒;对于圆心定点,它的角动量守恒。
5-5 以初速度0v 将质量为m 的小球斜上抛,抛射角为θ,小球运动过程中,相对于抛射点的角动量如何变化?小球运动到轨道最高点时,相对于抛射点的角动量为多少?答:取抛射点为坐标原点,取平面直角坐标系Oxy ,y 轴正方向向上,则质点的运动方程和速度表达式为:020cos 1sin 2x v ty v t gt θθ=⎫⎪⎬=-⎪⎭ , 00cos sin x y v v v v gt θθ=⎫⎬=-⎭ 对于抛射点的角动量:()()x y y x L r mv xi y j mv i mv j xmv k ymv k =⨯=+⨯+=- 将,,,x y x y v v 代入得:201cos 2L mgv t k θ=- 当小球到达最高点时,时刻为:0sin v t gθ=,代入上式得: 小球相对于抛射点的角动量为:320sin cos 2mv L k gθθ=-。




大学物理第5章-角动量守恒定律-刚体的转动
第5章 角动量守恒定律 刚体的转动
5-1 质点的动量守恒与角动量守恒的条件各是什么,质点动量与角动量能否同时守恒?試说明之。
答:质点的动量守恒的条件是:
当0F =时,p mv ==恒矢量。
质点的角动量守恒的条件是:
当0M =时,即000,F r θπ⎧=⎪⎪=⎨⎪=⎪⎩
时,L =恒矢量。
可见,当0F =时,质点动量与角动量能同时守恒。
5-2 质点在有心力场中的运动具有什么性质?
答:质点在有心力场中运动时,0,0F M ≠=,则角动量守恒,即:
当0M =时,L =恒矢量。
又因为有心力是保守力,则机械能守恒,即:
当0ex in nc
A A +=时,K P E E E =+=恒量。
5-3 人造地球卫星是沿着一个椭圆轨道运行的,地心O 是这一轨道的一个焦点。
卫星经过近地点和远地点时的速率一样吗?卫星在近地点和远地点时的速率与地心到卫星的距离有什么关系?
答:卫星经过近地点和远地点时的速率不一样,由角动量守恒定律得:
a a
b b r mv r mv = a b b a
v r v r ∴= 可见,速率与距离成反比。
5-4 作匀速圆周运动的质点,对于圆周上某一定点,它的角动量是否守恒?对于通过圆心而与圆面垂直的轴上的任意一点,它的角动量是否守恒?对于哪一个定点,它的角动量守恒?
答:作匀速圆周运动的质点,对于圆周上某一定点,它的角动量不守恒;对于通过圆心而与圆面垂直的轴上的任意一点,它的角动量不守恒;对于圆心定
点,它的角动量守恒。
5-5 以初速度0v 将质量为m 的小球斜上抛,抛射角为θ,小球运动过程中,相对于抛射点的角动量如何变化?小球运动到轨道最高点时,相对于抛射点的角动量为多少?
答:取抛射点为坐标原点,取平面直角坐标系Oxy ,y 轴正方向向上,则质点的运动方程和速度表达式为:
020cos 1sin 2x v t y v t gt θθ=⎫⎪⎬=-⎪⎭
, 00cos sin x y v v v v gt θθ=⎫⎬=-⎭ 对于抛射点的角动量:
()()
x y y x L r mv xi y j mv i mv j xmv k ymv k =⨯=+⨯+=- 将,,,x y x y v v 代入得:
201cos 2L mgv t k θ=- 当小球到达最高点时,时刻为:0sin v t g
θ=,代入上式得: 小球相对于抛射点的角动量为:320sin cos 2mv L k g
θθ=-。
5-6 为什么说刚体平动的讨论可归结为对质点运动的研究?
答:由于刚体平动时,各点的运动状态相同,则可取刚体上任意一点运动代表刚体的运动,所以刚体的平动可用质点运动来描述。
5-7如果刚体所受的合外力为零,其合外力矩是否也一定为零?如果刚体所受合外力矩为零,其合外力是否一定为零?
答:如果0i i F =∑,但力不共轴,则力矩不为零0i i M ≠∑。
如果0i i M =∑,但力方向相同,则力不为零0i i
F ≠∑。
5-8 在某一瞬时,如果刚体受到的合外力矩不为零,其角加速度可以为零吗?其角速度可以为零吗?
答:由刚体的转动定理:M J β=
当0,0M J ≠≠时,则0M J
β=≠ 可见,力矩与角加速度有关,力矩与角速度无关,所以角速度可以为零。
5-9 两个同样大小的轮子,质量也相同。
一个轮子的质量主要集中在轮緣,另一个轮子的质量主要集中在轮轴附近。
问:
(1)如果它们的角速度相同,哪一个飞轮的动能较大?
(2)如果它们的角加速度相等,作用在哪一个飞轮上的力矩较大?
(3)如果它们的角动量相等,哪一个飞轮转得快?
答:质量主要集中在轮緣的轮子的转动惯量用J A 表示,质量主要集中在轮
轴附近的轮子的转动惯量用J B 表示。
由∑=i
i i r m J 2
Δ可知,J A >J B 。
βJ M =
A 轮相当于圆环,转动惯量 2A J mR =
B 轮相当于圆盘, 转动惯量 212
B J mR = (1)当ω一定时,转动动能 2221122
KA A E J mR ωω== 2221124
KB B E J mR ωω== 所以 kB kA E E >
(2)当β一定时,转动定理 2A A M J mR ββ== 212
B B M J mR ββ== 所以 B A M M >
(3)当L 一定时,角动量 2A A A L J mR ωω==
212
B B B L J mR ωω== 2A A L L J mR ω== , 22B B L L J mR
ω== 所以 B A ωω<
5-10 将一个生鸡蛋和一个熟鸡蛋放在桌子上使其转动,如何判断哪一个是
生的?哪一个是熟的?为什么?
答:转动时,生、熟鸡蛋所受阻力矩相同。
根据角动量定理
00t
Mdt J J ωω=-⎰
停止时,0ω=,则 0J t M
ω∆= 因为熟鸡蛋内部凝固,而生鸡蛋内部不固定,转动惯量随转动而增大,即J J >生熟,
所以t t ∆>∆生熟
生鸡蛋转动时间较长,熟鸡蛋转动时间较短。
5-11 一半径为r 的均质小球,沿两个高度相同,倾角不同的斜面无滑动地滚下,在这两种情况下,小球到达斜面下端的速率是否相同?
答:因为小球只作滚动,没有滑动,故摩擦力不作功,机械能守恒。
221122c c mgh mv J ω=
+ 其中:小球的转动惯量225
c J mr =,质心的速度c v r ω=,代入上式得:
c v ∴= 可见,只要小球从同一高度滚下,与斜面的夹角无关,则小球到达斜面下端时的速率是相同的。
5-12 一个人将两臂伸平,两手各拿一只重量相等的哑铃坐在角速度为ω的转台上(ω为人与转台共同角速度),突然,他将哑铃丢下,但两臂不动,问角动量是否守恒?它们的角速度是否改变?
答:因为0i i
M =∑,所以角动量守恒。
设人和转台的转动惯量为J ,哑铃的质量为m ,手臂的长为l ,开始时角速度为ω,丢掉哑铃时角速度为ω',由角动量守恒得:
()2
2J ml J ωω'+= 221ml J ωωω⎛⎫'∴=+> ⎪⎝⎭
可见,丢掉哑铃后,角速度变大。
5-13 你骑自行车前进时,车轮的角动量指向什么方向?当你的身体向左侧倾
斜时,对车轮加了什么方向的力矩?试根据进动原理说明这时你的自行车为什么要向左转弯。
答:当车轮前进时,角动量L方向与角速度ω方向一致,即:L Jω
=。
当你的身体向左侧倾斜时,对车轮施加了一个进动方向的力矩,即:
c d L
M r mg
dt
=⨯=
力矩改变了角动量的方向,所以自行车就向左转弯。