经纬网距离计算

利用经纬网计算距离经纬度是地理位置的坐标系，是用来描述地球表面上一个点的位置的，利用经纬度可以计算出两点之间的距离。

在计算两点之间的距离时，可以使用球面三角学的原理，也可以使用近似算法。

一、球面三角学方法球面三角学方法是求解地球表面上两点的最短距离的准确方法，也是最为常用和精确的方法。

这种方法基于地球是一个近似的球体，并使用了三角函数来计算距离。

具体步骤如下：1.将两点的经度和纬度坐标转换为弧度表示。

地球的圆周被分成360度，每个度再分成60分，每一分再分成60秒。

因此，将经度和纬度从度、分、秒转换为弧度的公式如下：弧度=（度+分/60+秒/3600）*π/1802.计算两点之间的经度差和纬度差，并转换为弧度表示。

3.使用Haversine公式计算两点之间的弧长，然后将弧度转换为所在圆的半径所对应的真实距离。

Haversine公式如下：haversine(α) = sin²(Δφ/2) + cos φ1 * cos φ2 *sin²(Δλ/2)其中，φ1和φ2为两点的纬度，Δφ为纬度差，Δλ为经度差。

4.将弧长除以地球的半径，得到最短距离。

这种球面三角学方法能够计算出两点之间的最短距离，但是计算复杂度较高。

二、近似算法近似算法是一种用于快速计算两点之间距离的方法，它并不考虑地球的形状，而是将地球视为平面进行计算。

这种方法通过计算两点之间矢量的长度来估计距离。

具体步骤如下：1.将两点的经度和纬度坐标转换为弧度表示。

2.计算两点经度之间的差值和纬度之间的差值。

3.将经度差值和纬度差值分别乘以地球的平均半径（约为6371 km），得到两个方向的分量。

4.利用勾股定理计算矢量的长度。

这种近似算法能够快速计算出两点之间的距离，但是由于没有考虑地球的形状，所以精度相对较低。

无论使用球面三角学方法还是近似算法，都可以利用经纬度计算两点之间的距离。

在实际应用中，根据需要选择合适的方法。

如果需要高精度的计算结果，可以使用球面三角学方法；如果只需要快速估计距离，可以使用近似算法。

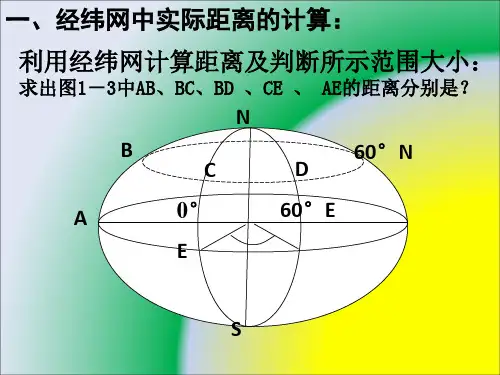
2020届高三地理复习讲解：经纬网图中距离的计算技巧一、知识讲解1.根据纬度差定经线长度：纬度1°的实际经线弧长处处相等，约是111 km,如下图中AB。

若两地在同一条经线上，只要知道两地的纬度差，就可以计算出两地之间的距离。

2.根据经度差定纬线长度:经度1°的纬线弧长由低纬向高纬递减，约是111X cosw km(9表示该纬线的纬度数值)，如图中AC。

3.图中BC的距离可根据勾股定理估算出。

注意也可以根据距离计算经纬度差，从而确定经纬度位置。

4．经纬网图中“最短距离”的确定球面最短距离是一段劣弧，沿劣弧的行进方向即为最短航线，该弧线的确定可分两个步骤进行：(1)确定“大圆”：“大圆”即球面两点所在的过球心的平面与球面的交线，如(2)确定“劣弧”：大圆上两点间的最短距离具体应该是哪一段弧线，是由“劣弧”来决定，所谓“劣弧”即两点间的弧度＜180°,如图A中的PAQ、图B中的P R Q、图C中的P^BQ均为劣弧。

5．寻找“最短航线”(1)若两地经度差等于180°，则过这两点的大圆便是经线圈。

最短航线经过两极点，方向分三种情况：图D 图E①同在北半球，先向北，过极点后再向南，如A到E。

②同在南半球，先向南，过极点后再向北，如B到D。

③两地位于不同半球，则看劣弧过哪个极点再做讨论，如A到C。

(2)在同一纬线上但不在同一经线圈上的两点：最短航线的劣弧线向较高纬度凸。

方向分两种情况：①同在北纬：如图E中从Q到P沿最短航线的航向是先向东北再向东南。

②同在南纬：如图E中从P'到Q‘沿最短航线的航向是先向西南再向西北。

二、高考经典试题1．甘德国际机场(下图)曾是世界上最繁忙的航空枢纽之一，当时几乎所有横跨北大西洋的航班都要经停该机场补充燃料。

如今，横跨北大西洋的航班不再需要经停此地。

据此完成下题。

一架从甘德机场起飞的飞机以650千米/小时的速度飞行，1小时后该飞机的纬度位置可能为( )A．66.5°N B．60°NC．53°N D．40°N解析本题考查经纬网图上距离的计算。

2020届高考地理复习讲解经纬网图中距离的计算技巧知识梳理与真题体验一、知识讲解1.根据纬度差定经线长度：纬度1°的实际经线弧长处处相等，约是111 km，如下图中AB。

若两地在同一条经线上，只要知道两地的纬度差，就可以计算出两地之间的距离。

2.根据经度差定纬线长度：经度1°的纬线弧长由低纬向高纬递减，约是111×cosφ km(φ表示该纬线的纬度数值)，如图中AC。

3.图中BC的距离可根据勾股定理估算出。

注意也可以根据距离计算经纬度差，从而确定经纬度位置。

4．经纬网图中“最短距离”的确定球面最短距离是一段劣弧，沿劣弧的行进方向即为最短航线，该弧线的确定可分两个步骤进行：(1)确定“大圆”：“大圆”即球面两点所在的过球心的平面与球面的交线，如图所示：在地球仪上，三种情况下“大圆”是确定的：一是赤道(图A)，二是经线圈(图B)，三是晨昏圈(图C)。

(2)确定“劣弧”：大圆上两点间的最短距离具体应该是哪一段弧线，是由“劣弧”来决定，所谓“劣弧”即两点间的弧度<180°，如图A 中的PAQ ︵、图B 中的PNQ ︵、图C 中的PBQ ︵均为劣弧。

5．寻找“最短航线”(1)若两地经度差等于180°，则过这两点的大圆便是经线圈。

最短航线经过两极点，方向分三种情况：①同在北半球，先向北，过极点后再向南，如A 到E 。

②同在南半球，先向南，过极点后再向北，如B 到D 。

③两地位于不同半球，则看劣弧过哪个极点再做讨论，如A 到C 。

(2)在同一纬线上但不在同一经线圈上的两点：最短航线的劣弧线向较高纬度凸。

方向分两种情况：①同在北纬：如图E 中从Q 到P 沿最短航线的航向是先向东北再向东南。

②同在南纬：如图E 中从P′到Q′沿最短航线的航向是先向西南再向西北。

二、高考经典试题1．甘德国际机场(下图)曾是世界上最繁忙的航空枢纽之一，当时几乎所有横跨北大西洋的航班都要经停该机场补充燃料。

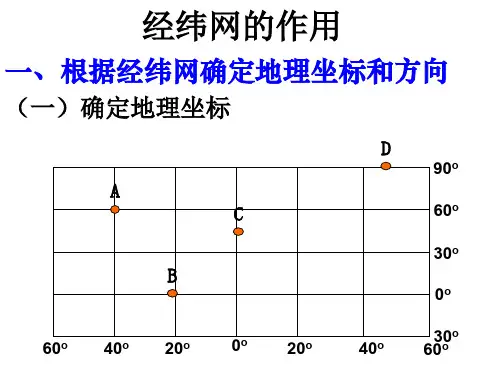
经纬度距离计算同一经线上，纬度每一度的间距是111km同一纬线上，每一经度的间距是用111乘以纬度数的余弦值算两地的实地距离时，可以用勾股定理+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ +++++++在地球仪上，与赤道相平行的圆就是纬线纬度每差1度，距离相差110千米在地球仪上，连接南北两极点的半圆就是经线经度每差1度的实地距离是：110千米*cosa其中cosa 的 a==该点所在纬度+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ +++++++经度和纬度都是一种角度。

经度是个两面角，是两个经线平面的夹角。

因所有经线都是一样长，为了度量经度选取一个起点面，经1884年国际会议协商，决定以通过英国伦敦近郊、泰晤士河南岸的格林尼治皇家天文台（旧址）的一台主要子午仪十字丝的那条经线为起始经线，称为本初子午线。

本初子午线平面是起点面，终点面是本地经线平面。

某一点的经度，就是该点所在的经线平面与本初子午线平面间的夹角。

在赤道上度量，自本初子午线平面作为起点面，分别往东往西度量，往东量值称为东经度，往西量值称为西经度。

由此可见，一地的经度是该地对于本初子午线的方向和角距离。

本初子午线是0°经度，东经度的最大值为180°，西经度的最大值为180°，东、西经180°经线是同一根经线，因此不分东经或西经，而统称180°经线。

（横纬竖经）在地球仪上与赤道平行的都是纬度与赤道垂直的都是经度纬度是个线面角。

起点面是赤道平面，线是本地的地面法线。

所谓法线，即垂直于参考扁球体表面的线。

某地的纬度就是该地的法线与赤道平面之间的夹角。

纬度在本地经线上度量，由赤道向南、北度量，向北量值称为北纬度，向南量值称为南纬度。