当前位置：文档之家 › 地球知识——经纬网(计算距离比较面积大小)

地球知识——经纬网(计算距离比较面积大小)

  • 格式：ppt
  • 大小：108.50 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

地球知识-经纬网

地球知识-经纬网

用途
1、划分地球——赤道把 地球分成南、北半球。
60°
90°
30°
0°
北极星的高度=当 地的地理纬度
30° 60° 90°
地球—经纬网—纬线和纬度
用途
1、划分地球——赤道把 地球分成南、北半球。 高、中、低纬度划分
60°
90°
66 ° 34ˊ
30° 23 ° 26ˊ
0°
低纬度 0°——30° 23 ° 26ˊ 中纬度30°——60° 30° 高纬度60°——90°
（ 07海南）2、图中甲地位于新加坡（1°16′N， 103°50′E）的（ C ）
A. 东北方
C. 西北方
B. 东南方
D. 西南方
（08模拟）读下面两个岛国示意图，回答 3．图中甲国首都A城市位于乙国首都B城市的 A．西北方向 B．东北方向 B C．西南方向 D．东南方向
东西看自转（北逆南顺），南北看极点。
（3）据经纬度找对趾点
对趾点：通过地心的直线与球面的两交点。
1、北京（40°N，116 °E）的对趾点的经纬度： （40°S，64 °W） .
（4）、计算实际距离
①赤道上一个经度的水平距离约111千米。
其它纬度：111×cos （指纬度）
②任一经线上一个纬度的水平距离约111千米。
（5））两地间最近航线方向的判断 两地间过大圆的距离最短
极 半 径——6356千米 赤道半径——6378千米
平均6371千米
球面上大圆周长：2π×6371千米≈ 40000千米 360
。
111千米/1
。
地球—经纬网—经线
用途
1.判方向
2.划分地球—— 20°W和160°E的 经线圈把地球分为 东、西半球。

地球和经纬网

地球和经纬网

b、任意两条经线的位置（赤道上的劣弧）
若同是东经度，度数大的靠东，度数小的靠西
若同是西经度，度数大的靠西，度数小的靠东 若两条经线，一个是东经度，一个是西经度，则把 两条经线度数相加。
两条经线度数和小于180度，则东经度在东，西经度在西。 两条经线度数和大于180度，则西经度在东，东经度在西。 两条经线度数和等于180度，则两条经线在同一个经线圈上。
C 、利用“井”字形来判断方位 先画井字形，后确定纬线的位置、经线的位置，标 出所求两点，然后确定方位。 （例求甲在乙的哪个方向，在井字图形中从乙向甲 走，朝向哪个方向走，甲在乙的哪个方向）
例题备课本
（4）球面上两点间最短距离的确定。
0°
南回归线
30°S
66.5°S
南极圈 S
60°S
高、中、低纬的划分
高纬度N地区 中纬度地区
60°N 30°N
低纬度地区
0°
低纬度地区
中纬度地区
高纬度地区
S
30°S 60°S
特殊纬线
0°：最长的纬线，南北半球的分界线。
30°： 低中纬度分界线。
60°： 高中纬度分界线；长度为赤道的一半。
90°： 南北极点。
赤道略鼓、两极略 扁的不规则球体。
二、地球的形状和大小的度量方法
1、基本概念：地轴、两极、赤道；
2、经度、纬度的划分和纬线、 经线的特点； 3、纬线和经线重要意义。
1、基本概念：
地轴、两极、赤道
2.纬线和经线：
纬线
经线
定 顺着东西方向环绕地球
义 仪一周的圆圈 纬线除极点外，每条纬
形 线自成圆圈，但只有赤 状 道能够平分地球
划分东、西半球的经线： 200W，1600E 1600E

经纬网的应用(例题详解)

经纬网的应用(例题详解)

赤道
下图中①点以西是东半球，以东是西半球，① 点与②③两点间的最短距离约是3330km，图中③ 点的经度是
A.160°E B.130°E C.180°E D.170°W
B
[例题]一架飞机从甲地（40°N，116°E）出
发，以1110千米/小时的速度向北方向绕经线
圈飞行，若不考虑地球自转的影响，8小时后
B.乙>甲>丙 C
C.丙>乙>甲 D.丙>甲>乙
B （2）图中a、b、c、d中不能观测到北极星 A.a B.b C.c D.d
判读面积
下图中画斜线的四块假想地，面积最大的是
75°
30° 60° A
60° 66°34′
60°
D
45°
30° 0°
B
23°26′
30° C
15°
D 60° 45° 30° 0°
到达乙地，则乙地为( B )
A．40°N，64°W
B．60°N，64°W
C．40°N，64°E
D．60°N，116°E
40°N 甲
60°N 乙
➢利用经纬网比较面积大小
在经纬网地图上，根据经纬线 组成的网格可大致判断区域面积的 大小。
在经纬线都是直线的经纬网图 上，经纬度间隔相同的网格，其纬 度越高，表示的实际范围就越小；
34° 甲
36°
乙 29°
48°
甲地（34°N，36°E）与乙地（29°N，
48°E）之间的直线距离大约为（ C ）
A、330千米
B、550千米
C、1300千米
D、1550千米
4.两地之间的最短航线问题
地球上两点间的最短航线方向问题

地球知识——经纬网(计算距离比较面积大小)

地球知识——经纬网(计算距离比较面积大小)

地球知识——经纬网(计算距离比较面积大小)
经纬网是一种地球表面的坐标系统，用于测量地球表面的位置。

经度是以本初子午线（通常是格林威治子午线）为基准，沿着赤道方向划分的360度线。

纬度是以赤道线为基准，从赤道向两极方向划分的。

通过经纬网，可以计算地球上两个点之间的距离。

这种计算常用的是大圆距离公式。

根据经度和纬度的差异，使用三角函数来计算出两点之间的弧度，然后通过地球半径来计算出两点之间的距离。

另外，经纬网也可以用来比较地球表面的大小。

可以通过计算经线和纬线之间的距离来测量面积大小。

将地球表面划分成小块，并计算每个小块的面积，然后将这些面积相加，即可得到整个地球表面的面积。

需要注意的是，由于地球是一个近似椭球体，不是一个完美的球体，所以使用经纬网计算的距离和面积可能会有一定的误差。

同时，在计算面积时还需要考虑到地球的曲率，以保证计算结果的准确性。

地球基础知识—经纬网汇总

地球基础知识—经纬网汇总

110°
130°
丙
乙
70°
丁
甲
乙在甲的 东南 方向。
60°
丙在甲的
正东 方向。
50°
丁在甲的 东北 方向。
一.判断题
• 1.在地球仪上，任意两条经线间的距离都相等 错 • 2.在地球仪上，任意两条纬线间的距离都相等 对
二、选择题
• 1.两人从南极同时出发，分别沿东经40度和 西经20度向北行进，下列情况正确的是（D） A他们将不会相遇 B他们可能会在赤道相遇 C他们之间距离始终保持不变 D在赤道上他们之间相距最远
●
C 10°S 170°W
AD
三、读图题
（一）读地球侧视图填空：
1.写出下列各点的地理坐标：
A (_0_°__,__3_0_°__E
)
B(30_°__N_,__9_0_°__E
)C
60°●
C_(_6_0_°__N_,__9_0°W )
2判断B、D所在的南北半球： 3300°°
B北__半__球__D_南__半__球__
②.大圆的相关知识 数学球大圆：球面上任意两点与球心所确定的平面 与球面相交所得的圆地理学上的大圆有：
所有经线圈 、赤道 、晨昏线 （观察地球仪写 出地理学上的大圆）
•判断图1－4中 各点之间是否 为最短距离： AB： CD： EF： •图中甲乙两点 间的最短距离 ？
具体分析：
北 南
南
北
B A
00°°
90°
0°
●B ●A
3.判断A、C所在的东、西半球 3300°°D●
●F
A_东__半__球 C__西__半__球_
4.判断各点之间的方向： A在B的_西__南__ A在C的_东__南___

高中地理课件-1.3.0地球知识——经纬网

高中地理课件-1.3.0地球知识——经纬网
南
C
试一试 A到B和C到D的方向是否一致？
西 东
同一纬线上 自转方向
南半球
D
B
A
C
3、确定球面距离
（1）同一经线上，跨纬度1°的 实际距离约是 111km （2）赤道上，跨经度1°的实际 距离是 111km
（3）任一纬线上，跨经度1°的 实际距离约是 111km×cosφ
（φ为该地纬度）
不 相 等
1、地球的形状
两极稍地扁轴，与赤地球道表略面鼓相交的的旋两转点椭球体
2、地球的大小
半径 周长
赤道半径: 6378km 极半径: 6357km 平均半径: 6371km
约4万km
表面积 5.1亿km²
北极
6357千米 极半径
表面积 5.1道
3、地球仪
（1）地轴
地球的自转轴叫地轴
A．回到M点
B．在M点正东方
C．在M点正西方 D．在M点东南方
（2）若某人从地球上某地出发，依次向正 东、正南、正西和正北方向分别前进200千 米，则其最终位置如何 ？
回到原地；回到原地以东；回到原地以西。
66.5°S （南极圈）
南低你北热中能半量高表球带纬述分分分界下界界线南线线和：：北南南0半北°北、球纬回3的分0归°界范、线线6围、0都°极吗、是圈？9赤0°道
北寒带
90°N
高纬度
北温带
中纬度
热带
低纬度 低纬度
南温带 南寒带
中纬度 高纬度
90°S
60°N 30°N 0° 30°S
60°S
3经纬网应用
相等
试一试 计算两点间的实际距离
80°
40°
M
O
60°

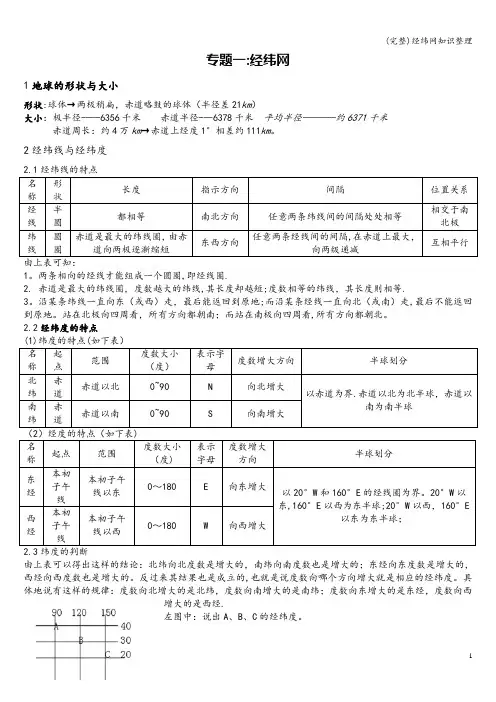
(完整)经纬网知识整理

(完整)经纬网知识整理

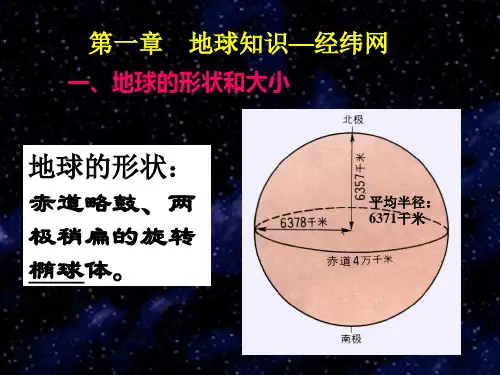
专题一:经纬网1地球的形状与大小形状:球体→两极稍扁，赤道略鼓的球体（半径差21km）大小：极半径-—-6356千米赤道半径---6378千米平均半径———-约6371千米赤道周长：约4万km→赤道上经度1°相差约111km。

2经纬线与经纬度2.1经纬线的特点名称形状长度指示方向间隔位置关系经线半圆都相等南北方向任意两条纬线间的间隔处处相等相交于南北极纬线圆圈赤道是最大的纬线圈，由赤道向两极逐渐缩短东西方向任意两条经线间的间隔,在赤道上最大，向两级递减互相平行由上表可知：1。

两条相向的经线才能组成一个圆圈,即经线圈.2. 赤道是最大的纬线圈，度数越大的纬线,其长度却越短;度数相等的纬线，其长度则相等.3。

沿某条纬线一直向东（或西）走，最后能返回到原地;而沿某条经线一直向北（或南）走,最后不能返回到原地。

站在北极向四周看，所有方向都朝南；而站在南极向四周看,所有方向都朝北。

2.2经纬度的特点(1)纬度的特点(如下表）名称起点范围度数大小（度）表示字母度数增大方向半球划分北纬赤道赤道以北0~90N向北增大以赤道为界.赤道以北为北半球，赤道以南为南半球南纬赤道赤道以南0~90S向南增大（2）经度的特点（如下表)名称起点范围度数大小（度)表示字母度数增大方向半球划分东经本初子午线本初子午线以东0～180E向东增大以20°W和160°E的经线圈为界。

20°W以东,160°E以西为东半球;20°W以西，160°E以东为东半球；西经本初子午线本初子午线以西0～180W向西增大2.3纬度的判断由上表可以得出这样的结论：北纬向北度数是增大的，南纬向南度数也是增大的；东经向东度数是增大的，西经向西度数也是增大的。

反过来其结果也是成立的,也就是说度数向哪个方向增大就是相应的经纬度。

具体地说有这样的规律：度数向北增大的是北纬，度数向南增大的是南纬；度数向东增大的是东经，度数向西增大的是西经.左图中：说出A、B、C的经纬度。

地球知识

地球知识
由于地球自西向东自转，地球上的人们看到 地球以外的天体是做东升西落的视运动现象。
2、地方时
（1）古代时间的确定：
以太阳在天空中的位置来确定时间 （2）由于地球是自西向东转，所以
东边的时间就比西边的时间早。 （3）地球自转一周转动了360°，用时是 24小时，所以：经度相差1°时间就相差4 分钟，东早西晚，越东越早，越西越晚。
球体。
遵义市2014届会考模拟题（一）
一、单项选择题
读左图完成2—3题
2、图中位于北半球、东半球的点有（ A：A点和B点 B：C点和D点
A
）
C：A点和C点
D：B点和D点
3、关于图中四点的地理坐标的描述，不正 确 的是（ B ） A.0°、30°N C.0°、20°E B.60°N、120°W D.0°、60°E
（4）地方时：因经度不同所以时间 不同。
同一经线上的地方时相同，不同经线上的地方时不同。
（5）时区和区时
经度每隔15°就划分一个时区，全球一共有 24个时区。每个时区正中间那条经线叫这个 时区的中央经线，中央经线上的地方时就是 这个时区的区时。
相差一个时区就相差一个小时，东早西晚， 越东越早，越西越晚。
自西向东穿越此线，时间不变，日期加一天，反之则减一天， 这是地球上今天和明天的分界线。
地 球 的 公 转
1、公转的方向：自西向东 北极上空看呈逆时针，南极上空看呈顺时针。 2、公转的周期：一年
四季的形成
四季更替的周期：一年
春分：3月21日前后，太阳直射 赤道，全球昼夜等长。 夏至：6月22日前后，太阳直射 北回归线，北半球昼长达最长， 北极圈内出现极昼，南半球夜长 达最长，南极圈内出现极夜。 秋分：9月23日前后，太阳直射 赤道，全球昼夜等长。 冬至：12月22日前后，太阳直射 南回归线，南半球昼长达最长， 南极圈内出现极昼，北半球夜长 达最长，北极圈内出现极夜。

地球知识——经纬网定距离

地球知识——经纬网定距离

1．黄河站至北极点的距离约为（ C ）
A、600千米
B、900千米
C、1200千米
D、1500千米
编辑版
4
一架飞机从甲地（40°N，116°E）出发，
以1110千米/小时的速度向北方向绕经线圈飞行，
若不考虑地球自转的影响，8小时后到达乙地，
则乙地为(
)B
A．40°N，64°W C．40°N，64°E
B、甲大于乙 D、无法确定
编辑版
11
A
B
蓝色圆弧AB
红色圆弧AB
黑色圆弧AB
编辑版
12
6、两地间最短航线的方向
原理:球面上任意两点间距离,是过这两点 的 大圆的劣弧长 。 ⑴若两地经度之差为180度 过两地的大圆是经线圈，过两极点为最短航程。
编辑版
13
N A
O B
S
编辑版
14
N A
O
B
S
编辑版
B．60°N，64°W D．60°N，116°E
甲40°N
60°N 乙
编辑版
5
（2）计算某段纬线的长度： 赤道上，跨经度1°的弧长约是111 km； 任 一 纬 线 （ 纬 度 为 θ ） 上 ， 跨 经 度 1° 的 弧 长 约 是 (111×cosθ)km。（思考：为什么是这样？）
r
P
θ
θR
编辑版
编辑版
21
N A
B
O
S
编辑版
22
⑵若两地经度之差不等于180度 北半球向东走：先向 东北 ，再向 东南 走。
60°N 40°N
A
B
60°E 编辑版 90°E
120°E 23

地球知识经纬网

地球知识经纬网

6、 在地球仪上，顺着 方向，围绕地球仪一周的圆圈，叫做纬线。
7、 根据纬度的不同，人们把纬度分成低纬度、 纬度、__ 纬度；低纬度是指0至 _______ 的地区。
8、 中纬度与高纬度的分界线是
，500N属于 纬度地区。
9、 在地球仪上，同南北极距离相等的大圆圈，叫
是 半球与
半球的分界线。
20° 20°
B 西经30°，南纬30°
30°
指出下列图中A、B两地所在的经度和纬度
100 150 200 250 300 400
_________________
·A
350
300
·B
250
200
350
300
250
200
A：北纬350，东经150
B：北纬250，东经250
有一天，某人来到经度0°、纬度0°的位置，很兴奋的说：“我太厉害了，我向西走一步就来到 了西半球，向东走一步，就来到了东半球，向南走一步，就来到了南半球，向北走一步，就来到了 北半球。” 你觉得他的判断对吗？
，它的周长大约为
万千米,它
五、据经纬度及经纬网判断方向
据两地经纬度判断方向 方格状或圆弧形经纬网图上辨方向 以南北极为中心的经纬网图上辨方向
五、据经纬度及经纬网判断方向 1、方向的规定 地球上的方向通常上指地平面上的方向
B A
北 西北
东北
西
西南 南
东 东南
五、据经纬度及经纬网判断方向 ➢经纬网图中方向的确定
认识经纬网
由于投影角度的不同，经纬网的图形有很多种。常 见的如下图所示：
赤道投影：即经纬网的投影中心在赤道上，全球的纬线数都能看到，经 线只能看到全球的一半

地球与地球仪基础知识 (1)全文

地球与地球仪基础知识 (1)全文

2、经线和经度
N
经线：在地
球仪上，连
接南北两极
W 并同纬线垂
0 60o 45o 30o 15o o 15o
30o 45o 60o
E
直相交的线
叫做经线。
本 初
也叫子午线。
子 午
线
S
N
读图总
结经线
的特点
W
0 60o 45o 30o 15o o 15o
E 30o 45o 60o
本 初 子 午 线
S
经线的特点
AB 等于 CD
北极
A B
CD
N
B C
60°N D
0°
60°E
A
E
赤道
利用经纬网计算距离
S
求出图中AB、BC、BD 、CE 、 AE的距离分别是？
2、经纬线长度计算
一个纬度的经线长是111km 一个经度的纬线长是
[2010高考题]2009年7月28日，我国第一个北极 科学考察站：黄河站(78°55′N，11°56′E) 建成。据此回答：
800E
C
A B
100N 50N
方法总结：
①确定南北方向 同在北纬度，纬度值大者在北； 同在南纬度，纬度值大者在南。 在南北半球的两点，北半球在北，南半球在南； ②确定东西方向 同在东经度，经度值大者在东； 同在西经度，经度值大者在西。 若分别在东西经，如下图所示：
讨论不同形状经纬网方向判断的一般方法？
60°N 40°N
A
B
60°E 90°E 120°E
二、地 图
某中学平面图
比例尺
0 20（米）
北
指向标
教学楼 传达室
办公楼 校门

第一章地球知识—经纬网

第一章地球知识—经纬网

二、地球仪 4、经纬网的应用 （1）确定地理坐标： （2）确定方向 ②即不在同一条纬线上，又不在同一条经线上 两点的方位 a南北方向的判定 两个比较点同在北纬，数值大的在北，数值小 的在南 两个比较点同在南纬，数值大的在南，数值小 的在北 南北方向是绝对的，北极是地球的最北端，向 四周均为正南方，南极则相反。
二、地球仪——形状为正球体的地球模型(示意如 图)。 1、地轴、两极与赤道：如图中P 为 地轴 ， N点 为 北极 点，S点为 南极 点。 地轴——地球自转轴。 （始终指向北极星附近） 两极——地轴的两端与 地球表面相交的两点。 赤道——地球表面垂直 于地轴的最大圆。
二、地球仪 2、经线和纬线
活动一：指出地轴、 南极、北极和赤道。
为什么说地球是一个近似圆的椭圆？
一、地球的形状和大小：
1、形状： 两极 稍扁、 赤道 略鼓的不规则 椭球体。
证据？
证明地球是球体的方法
海船 远去时， 先是看不 见船身， 最后才看 不见船的 桅杆。
一、地球的形状和大小：
2、大小
（1）、地球的平均 6371 半径____千米。 （2）地球的赤道周长约 4万 ______千米。 （3）地球表面积是 5.1亿 ______平方千米
4、经纬网的应用 （2）确定方向 ②即不在同一条纬线上，又不在同一条经线上 两点的方位 b东西方向的判定 东西方向是相对的，判断东西方向首先要选择 劣弧段，再按地球自转方向来确定东西方向。 b1.同在东经度，则经度大的在东，经度小的在 西（大东小西）； b2.同在西经度，则经度大的在西，经度小的在 东（大西小东）； b3.一个在东经，一个在西经，则要判断是否是 劣弧
2、读图，回答下列问题： （1）写出图中A、B、C三地的地理 位置：

地球知识——经纬网

地球知识——经纬网

②确定东西方向 同在东经度，经度值大者在东；同在 西经度，经度值大者在西。若分别在东西 经，如下图所示：
(2)弧线式经纬网图(以极点经纬网图为例) ①如图中A、B两点位于同一纬线上， 根据自转方向判断B在A的东方。 ②B、C位于同一经线上，根据极点 位置判断C位于B的南方。 ③C、A既不在同一经线上，也不在 同一纬线上，根据以上原理分别判 断东西南北方向，可确定C在A的 东南方 。
从赤道向两极逐渐 ⑥ 变短 ，赤道 最长
所有纬线都相互平 行
相互 关系
所有经线都相交于⑦
南、北两极点
间隔 作用
任意相邻两条经线间 任意相邻两条纬线 的间隔在⑧ 赤道 上 间的间隔⑨ 处处相等 最大 ⑩指示 南北 方向（无 ⑪指示 东西 方向 限）
(2)经度和纬度
经度 纬度
由⑬ 赤道 (0° 本初子午线 由⑫ (0°经线) 划分 纬线)向南、向北各划分 方法 向东、向西各划分180° 90° 东经的度数愈向东 分布 ⑭ 愈大 ，西经的度数愈向 规律 东⑮ 愈小 北纬的度数愈向⑯ 北 愈大；南纬的度数愈向 南愈大
3．定“距离”
•
•
(1)根据纬度差定经线长度：纬度1° 的实际经线弧长处处相等，大约是111 km， 如图中AB。若两地在同一条经线上，只要 知道两地的纬度差，就可以计算出两地之 间的距离。 • (2)根据经度差定纬线长度：经度1° 的纬线弧长由低纬向高纬递减，大约是 111×cosφ km(φ表示该纬线的纬度数 值)，如图中AC。
⑰ 20°W～0°～160°E 半球 为东半球，160°E～180°～ 划分 20°W为西半球
以⑱ 赤道 为界，以 北为北半球，以南为南 半球
(3)经纬网的意义：定位置、定方向、定距离、定范围。

地理基础知识(1)：地球的经纬网

地理基础知识(1)：地球的经纬网

一、地球的形状及大小、地球仪
6357km 地心
1、地球的形状和大小：
形状：两极略扁，赤道略鼓， 南北半球不对称 大小：平均半径6371km,赤 道周长4万km，赤道半径最 大 地球仪：在地球仪上，人们用 不同的颜色、符号和文字来表示 陆地、海洋、山脉、河湖、国家 和城市等地理事物的位置、形状 及名称等。这样可以方便我们了 解地球的面貌，了解地球表面各 种地理事物的分布。
下图示意某日昼夜分布状况，阴影部分表示黑夜。读图回答1～2题。 1．图中N、B间的距离约为( B ) A．5000千米 B．10000千米 C．15000千米 D．20000千米 2．从C地出发，经过E、 D、F地，沿最短航线最后回到C 地，下列走向中正确的是( C ) A.先向正东走，再向正西走 B.先向东北走，再向西南走 C.先向东北走，再向东南走 D.一直向东北
甲 E 乙 B F
A
图中甲乙两点间的最短距离？
C
D
甲 乙
③具有地理意义的几个大圆：
A、地球上所有的大圆都相互平分 经线圈 B、所有经线的中点都一定在赤 道上、端点一定在极点上 晨昏圈
C、晨线和昏线的中点一定在 赤道上，晨线中点的地方时是 6点、昏线中点的地方时是18 点
赤道
D、除春、秋分日外，晨线和昏线端点的地方时是0点或者12点；
2、掌握南北纬度的判断方法： 自北向南（图纸上一般从上到下），纬度数增大者为南纬，变小者 属北纬。即：北纬向北大，南纬向南大
3、高、中、低纬度的划分：0°—30°—60°—90°
4、五带的划分：
4、南北半球的划分:
三、经线及经度 1、经线：
经线有什么特点？（定义、形状、长度、
方向、距离）
定义：地球仪上，连接南北两极 和纬线垂直相交的线 形状：经线都是半圆且相交于南 北两极 长度：所有经线的长度都相等 方向：经线指示南北方向 距离：任意两条经线间的间隔赤 道上最大，向两极递减

地球知识-经纬网

地球知识-经纬网

⑵若两地经度之差不等于180度
北半球向东走：先向 东北，再向 东 ，最后向 东南 北半球向西走：先向 西北 ，再向 西 ，最后向 西南 南半球向东走：先向 东南 ，再向 东 ，最后向东北 南半球向西走：先向 西南 ，再向 西 ，最后向 西北 19、16
几条重要的经纬线
北极圈
地（60°N，90°E）到B地（60°N，140°E），若不考虑 地形因素，最近的走法是（ D） A．一直向东走 B．一直向西走
C．先向东南，再向东，最后向东北走
D．先向东北，再向东，最后向东南走
两地间的最短距离是通过这两点的大圆的劣弧
（1）若两地间的经度数和等于180，且不
在赤道上，则经过两点的大圆是经线圈。 这两点的最短航程必须经过极点。
一、地球概况
1、大小： 平均半径6371km 6378 赤道周长4万km 。 表面积5.1亿平方千米; 体积10800亿立方千米。
2、形状：两极稍扁， 赤道略鼓的旋转椭球体
3、地轴：地轴──地球自转的中心轴； 4、两极：地轴和地球表面的相交的两点。
6356.8
5、经线
定义
在地球仪上，连接 南、北两极的线。
1、圆柱（圆锥）投影经纬网图
该类图中的经线和纬线直交（或斜交）成网格，如图判读时应注 意以下规律。 (1)经线和纬线：图中横线（或弧线）代表纬线，竖线代表经线。 (2)判断南北纬和东西经：纬度数向北增大的为北纬，向南增大的 为南纬；经度数向东增大的为东经，向西增大的为西经。 （3）度数的判定：在同一幅经纬网图中，相邻两条经（纬）线之 间的度数间隔一般都是相等的。如图甲中纬度间隔为20°，经度间 隔 为20°。由此我们可以确定各点的地理位置：如图甲，A点为东 经20°、北纬20°；B点为西经20°、南纬30°。

利用经纬网计算距离

利用经纬网计算距离

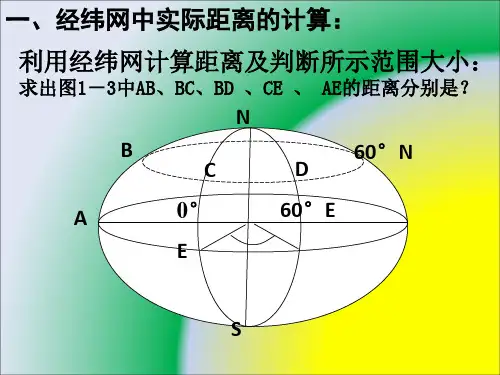
利用经纬网计算距离经纬网（也被称为地理网格或地理坐标网格）是一种用来确定地球表面上任意位置的工具。

它通过将地球分成经度和纬度的网格，并给每个点分配唯一的坐标来实现。

经纬网主要由经线和纬线组成。

经线是地球的虚拟线条，按照从南极到北极的顺序从0度到360度编号。

0度经线通过英国伦敦市的皇家天文台，因此也被称为伦敦子午线。

纬线则是地球的虚拟圈，按照纬度的大小从赤道到两极分为90度，北纬为正，南纬为负。

1.确定两个位置的经纬度坐标。

这些坐标可以通过地球仪、在线地图或GPS设备等方式获取。

2.使用球面三角学原理计算两个位置的大圆角度差。

大圆角度差是两个位置所在的经线和纬线之间的最短角度差，以角度表示。

3.将大圆角度差转换为弧度，并使用球面三角学公式计算两个位置之间的弧长。

球面三角学公式可以根据大圆角度差和半径（地球的平均半径约为6371千米）计算弧长。

4.将弧长转换为适当的单位，如千米、海里或英里，以获得位置之间的距离。

需要注意的是，这种方法计算的距离是两个位置之间的直线距离，而不是实际的行驶距离或路径长度。

实际行驶距离可能会受到地形、道路和其他因素的影响。

使用经纬网计算距离的例子如下：假设我们要计算纽约市和伦敦市之间的距离。

纽约市的经纬度是40.7128°北纬、74.0060°西经。

伦敦市的经纬度是51.5074°北纬、0.1278°西经。

首先，我们计算两个位置的大圆角度差。

纽约市和伦敦市的经度之差是74.0060°-(-0.1278°)=74.1338°。

由于伦敦市在纽约市的东面，所以大圆角度差为360°-74.1338°=285.8662°。

总的来说，利用经纬网计算距离可以帮助我们确定地球上任意两个位置之间的直线距离。

这种方法基于球面三角学原理和大圆航线理论，通过计算经纬度之间的角度差和使用球面三角学公式计算弧长来实现。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B．60°N，64°W D．60°N，116°E
甲40°N
60°N 乙
.
• 0公里，最后他位于（ A ）
A．出发点
B．出发点以西
C．出发点以北 D．出发点以东
• 某人从赤道以北30公里处出发，依次向正西、
正南、正东、正北各走100公里，最后他位于（ D ）
A．出发点
B．出发点以西
C．出发点以北 D．出发点以东
.
示意图对比 赤道
.
5.利用经纬网比较面积大小
跨经度和纬度相同的地图，纬度越高，所表示的 范围越小。（思考：为什么是这样？）
.
• 比较甲、乙、丙三个阴影区域面积的大小
乙>丙>甲.
读经纬网图，比较两图中阴影部分 面积大小正确的是：
20° 25°
（思考：为什么是这样？）
Ｎ
１°
Ｂ Ａ
Ｓ
.
（2）计算某段纬线的长度： 赤道上，跨经度1°的弧长约是111 km； 任 一 纬 线 （ 纬 度 为 θ ） 上 ， 跨 经 度 1° 的 弧 长 约 是 (111×cosθ)km。（思考：为什么是这样？）
r
P
θ
θR
.
特殊纬线距离的计算
30°纬度上任意两点上的距离约为96km×相隔经度数 60°纬度上任意两点上的距离约为111 * 1/2 km×相隔 经度数
1.1.1地球知识——经纬网
经纬网基础： 1.地球的形状和大小 2.纬线和纬度 3.经线和经度
经纬网意义： 1.确定地理坐标 2.据经纬度及经纬网判断方向 3.利用经纬网定“最短航线” 4.利用经纬网计算距离 5.利用经纬网比较面积大小
.
4.利用经纬网计算距离
（1）计算某段经线的长度： 任何一条经线上，纬度间隔1°的弧长约是111 km。
48°
甲、乙两地之间的直线距离大约为（ C ）
A、330千米
B、550千米
C、1300千米
D、1550千米
.
一架飞机从甲地（40°N，116°E）出发，
以1110千米/小时的速度向北方向绕经线圈飞行，
若不考虑地球自转的影响，8小时后到达乙地，
则乙地为( )B
A．40°N，64°W C．40°N，64°E
A、甲等于乙 B、甲大于乙 C、甲小于乙 D、无法确定
.
上图中，AM间的实际距离约为 3330 km。
MN间的实际距离约为 .
2220
km。
2004年7月28日，我国第一个北极科学考察站： 黄河站(78°55′N，11°56′E)建成。
黄河站至北极点的距离约为（ C ）
A、600千米
B、900千米
C、1200千米
D、1500千米
.
34° 甲
36°
乙 29°