江苏省苏州市2014-2015学年高一上学期期末数学试卷

XXX2014-2015学年上学期高一年级期末考试语文试卷后有答案XXX2014-2015学年上学期高一年级期末考试语文试卷本试卷满分150分，考试时间150分钟第Ⅰ卷50分一、本大题共6小题，每小题2分，共12分。

1.下列加点字注音全部正确的一项是（）A.洞穴（xuâ）吊唁（yàn）自诩（xǔ）一丘之貉（háo）B.熟稔（rěn）盘桓（huán）参与（yù）中流砥柱（dǐ）C.羞赧（nǎn）妊娠（chãn）桎梏（gù）踽踽独行（yǔ）D.瓜蔓（wàn）发酵（xiào）旖旎（yí）雨声淅沥（xī）2.下列词语中没有错别字的一项是（）A.富庶贿赂B.作践惺忪C.募集噩耗D.戏谑扭扣3.下列短语归类正确的一项是（）A.并列：B.偏正：C.动宾：D.主谓：4.下列句子中加点的成语利用恰当的一项为哪一项（）A.南美人对足球的热爱令人由衷佩服，世界杯开赛前，有的阿根廷穷人球迷，甚至一路走一路唱，计日XXX，用自己的乐观和脚步走到了巴西。

．．．．B.在就业压力进一步加大的情况下，专家提示身无长物的大学生，肯定要尽早挖掘自．．．．身优势，不断加强个人综合素质，以提高职场竞争力。

C.晚年的XXX三姐妹一个留在美国，一个留在台湾，一个留在大陆，她们虽然长时间不能见面，但一衣带水的牵挂，使得彼此的思念从未停止。

．．．．D.宽容的处世态度虽然一直被提倡，但令人遗憾的是，我们的社会中，睚眦必报的新魑魅魍魉接踵而来缠绵悱恻匆匆那年智取威虎山一步之遥打老虎行动起来唤醒没落千年的南城霸王别姬入不敷前途透社报导惮精竭虑拾人牙慧革故顶新愤发图强不径而走折冲樽俎引亢高歌蜚声文坛1XXX总是太多，犯而不校的美谈总是太少。

．．．．5.下列有关文学常识的表述，错误的一项是（）A.《左传》是我国第一部叙事详细的纪传体著作，既是汗青文献，又是散文著作。

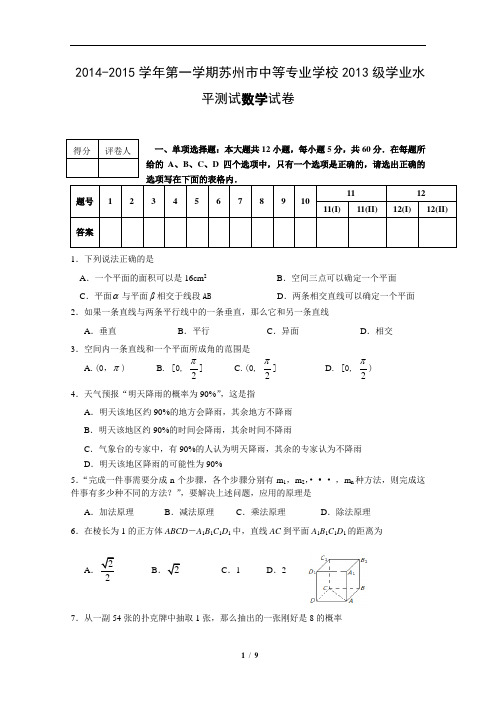
2014-2015学年第一学期苏州市中等专业学校2013级学业水平测试数学试卷一、单项选择题：本大题共12小题，每小题5分，共60分．在每题所给的A 、B 、C 、D 四个选项中，只有一个选项是正确的，请选出正确的1．下列说法正确的是A ．一个平面的面积可以是16cm 2B ．空间三点可以确定一个平面C ．平面α与平面β相交于线段ABD ．两条相交直线可以确定一个平面2．如果一条直线与两条平行线中的一条垂直，那么它和另一条直线 A ．垂直 B ．平行 C ．异面 D ．相交 3．空间内一条直线和一个平面所成角的范围是A .(0，π)B . [0,2π] C .(0, 2π] D . [0, 2π) 4．天气预报“明天降雨的概率为90%”，这是指A ．明天该地区约90%的地方会降雨，其余地方不降雨B ．明天该地区约90%的时间会降雨，其余时间不降雨C ．气象台的专家中，有90%的人认为明天降雨，其余的专家认为不降雨D ．明天该地区降雨的可能性为90%5．“完成一件事需要分成n 个步骤，各个步骤分别有m 1，m 2，• • • ，m n 种方法，则完成这件事有多少种不同的方法？”，要解决上述问题，应用的原理是 A ．加法原理 B ．减法原理 C ．乘法原理 D ．除法原理6．在棱长为1的正方体ABCD －A 1B 1C 1D 1中，直线AC 到平面A 1B 1C 1D 1的距离为 A B C ．1 D ．27．从一副54张的扑克牌中抽取1张，那么抽出的一张刚好是8的概率②① ③ ④⑤⑥⑦B 3C 1A 7 I 0 D 3G 2 E 3F 2J 0 H 1A ．154B ．19C ．227D ．18．把半径是3，4，5的三个铁球熔铸成一个大球，则大球的体积是A ．298πB .288πC .144πD .72π 9. 用数字1,2,3,4,5可以组成多少个没有重复数字的三位数A ．60B ．125C ．50D ．2510. 某中专校2014级新生共有500人，其中计算机专业125人，物流专业200人，财会专业125人，美术专业50人．现采取分层抽样的方法抽取一个容量为40的样本参加劳动周，那么计算机、物流、财会、美术专业抽取的人数分别为 A ．16，10，10,，4 B ．10，16，10，4 C ．4，16，10 ，10 D ．10，10，16，4 11．[选做题]本题包括I 、II 两小题，请选定其中一题作答．I ．十进制数（6）10 转化成二进制数为 A ．(100)2 B ．(101)2 C ．(111)2 D ．(110)2 II ．数组a =(1,2)b =(-2,6),则a b ⋅等于A ．4B ．6C ．8D ．1012．[选做题]本题包括I 、II 两小题，请选定其中一题作答． I ．根据如图的算法流程图，当输入x 的值为3A ．5 B ．6 C ．7 D ．8II ．A ．7B ．9C ．10D ．13二、填空题：本大题共5小题，每小题5分，共25分．请把答案填写在相应位置上．13．若两个平面同时垂直于第三个平面，则这两个平面的位置关系是 . 14．已知一个样本为8，12，14，18，则样本的中位数是 ． 15．()()()31=85A A PB A B =⋃已知、B 是互斥事件，且P ，，则P 的值是 . 16．[选做题]本题包括I 、II 两小题，请选定其中一题作答．第12 I 题D 1C 1B 1A 1ABCDI ． 程序框图的判断框有 个出口.II ．工作流程图中，长度最长的路径叫做 . 17． [选做题]本题包括I 、II 两小题，请选定其中一题作答．I ．101100∙++∙+= .II ．已知数组a =(1，0，1)，b =(1-，1，2)，则a +b = . 三、解答题：本大题共6小题，共65分．请把答案写在相应的位置上．解答时应写出文字说明、证明过程或演算步骤．18. （本小题满分8分）如图，ABCD-A 1B 1C 1D 1为正方体． （1） 与直线AB 异面的直线有哪些？ （2） 求A 1B 与直线CD 所成角的大小．19．（本小题满分12分）如图，在四棱锥S-ABCD 中，底面ABCD 是边长为a 的正方形，SA=a 且SA ⊥底面ABCD(1) 证明AB ⊥侧面SAD ；(2) 求四棱锥S-ABCD 的体积．BCD 第19题S20．（本小题满分10分）已知下面一组数据：24 21 23 25 2628 24 29 30 2926 25 24 27 2822 24 26 27 28填写频率分布表20.5 22.5 22.5 24.5 24.526.5 26.528.5 28.530.521.（本小题满分12分）甲、乙两名篮球运动员，甲投篮的命中率是0.6，乙投篮的命中率是0.7，两人是否投中相互之间没有影响．求：（1）甲投两次，只有一次命中的概率；（2）两人各投篮一次，只有一人命中的概率．22.（本小题满分8分）。

2014-2015学年度上学期期末考试高一化学试卷（含答案）可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl 35.5K 39 Ca 40 Zn 65 Fe 56 Cu 64注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分100分。

考试时间100分钟；2．第Ⅰ卷第Ⅱ卷答案用钢笔或签字笔写在答卷正确位置上；第I卷选择题一、选择题（本题包括20小题，每小题2分，共40分。

每小题只有一个选项符合题意。

）1．“化学，让生活更美好”，下列叙述不能直接体现这一主旨的是：A．风力发电，让能源更清洁B．合成光纤，让通讯更快捷C．合成药物，让人类更健康D．环保涂料，让环境更宜居2．下列化学用语正确的是：A．Cl－的结构示意图：B．光导纤维主要成分的化学式：SiIC．质子数为53，中子数为78的碘原子：13153D．H216O、D216O、H218O、D218O互为同位素34．下列操作中，不会发生明显颜色变化的是A．FeSO4溶液中滴入NaOH溶液B．硫酸铁溶液中滴加硫氰化钾溶液C．碳酸氢钠溶液中滴加稀盐酸D．氯化铁溶液中加入还原性铁粉5. 现有三种常见治疗胃病药品的标签：①②③药品中所含的物质均能中和胃里过量的盐酸，下列关于三种药片中和胃酸的能力比较，正确的是（）A．③＞②＞①B．①＞②＞③C．①＝②＝③D．②＞③＞①6．关于NaHCO3与Na2CO3说法正确的是：① NaHCO3固体可以做干粉灭火剂，金属钠起火可以用它来灭火② NaHCO 3粉末中混有Na 2CO 3，可配置成溶液通入过量的CO 2，再低温结晶得到提纯 ③ Ca(HCO 3)2溶解度都比其正盐的溶解度大，因此NaHCO 3的溶解度也比Na 2CO 3大 ④Na 2CO 3固体中混有NaHCO 3，高温灼烧即可⑤区别NaHCO 3与Na 2CO 3溶液，Ca(OH)2溶液和CaCl 2溶液均可用 A ．①③ B ． ③⑤ C ．②④ D ． ②⑤ 7．下列关于Na 及其化合物的叙述正确的是：A ．将钠投入FeSO 4溶液中，可以得到单质铁B ．足量Cl 2、S 分别和二份等质量的Na 反应，前者得到电子多C ．Na 2O 与Na 2O 2中阴阳离子的个数比均为1:2D ．在2Na 2O 2+2H 2O=4NaOH+O 2反应中，每生成1molO 2，消耗2mol 氧化剂 8. 下列常见金属单质的工业冶炼方法正确的是：A ．冶炼钠：电解氯化钠水溶液，同时得到副产品Cl 2、H 2B ．冶炼镁：电解熔融MgCl 2.6H 2O ，同时得到副产品Cl 2，H 2OC ．冶炼铝：电解熔融冰晶石（Na 3AlF 6），同时得到副产品Al 2O 3D ．冶炼铁：高炉中生成CO ，CO 在高温下还原铁矿石，同时得到副产品CaSiO 3 9.设N A 代表阿伏伽德罗常数，下列说法正确的是 A ．1mol MgCl 2中含有的离子数为2N AB ．标准状况下，11.2L H 2O 中含有的原子数为1.5N AC ．标准状况下，22.4L 氦气与22.4L 氯气所含原子数均为2N AD ．常温下，2.7g 铝与足量的盐酸反应，失去的电子数为0.3 N A 10. 下列物质中，既能跟稀硫酸反应，又能跟NaOH 溶液反应的是①Al 2O 3；②Mg(OH)2；③Al(OH)3；④(NH 4)2CO 3；⑤NaHCO 3；⑥AlCl 3 A ．①③⑤⑥ B ．只有①③ C ．只有②③ D ．①③④⑤ 11．等质量的两根镁条，第一根在足量氧气中加热燃烧，第二根在足量CO 2气体中加热燃烧，则下列说法正确的是：①两根镁条失去电子一样多 ②第一镁根条失去电子多 ③第二根镁失去电子多 ④两根镁的产物质量一样大 ⑤第一根镁的产物质量大 ⑥第二根镁的产物质量大A ．①④B ． ①⑥C ．③⑥D ．②⑤12. Fe 和Fe 2O 3 、Fe 3O 4的混合物，加入200mL 5mol·L -1的盐酸，恰好完全溶解，再向其中加入KSCN 溶液，未见血红色，则所得溶液中Fe 2+的物质的量浓度为(假设反应后溶液体积仍为200mL) A 、2.5mol·L -1 B 、lmol·L -1 C 、2mol·L -1 D 、5mol·L -1 13．下列选用的相关仪器符合实验要求的是A ．存放液溴B ．量取9.50 mL 水C ．称量8.55g 氯化钠固体D ．配制240 mL0.1mol/L的NaCl溶液14．下列除去杂质（括号内的物质为杂质）的方法中错误．．的是A．FeSO4 (CuSO4)：加足量铁粉后，过滤B．CO (CO2)：用NaOH溶液洗气后干燥C．MnO2 (KCl)：加水溶解后，过滤、洗涤、烘干D．CO2 (HCl)：用NaOH溶液洗气后干燥15．下列化学反应所对应的离子方程式正确的是：A．氧化铝和过量的氢氧化钠溶液反应：2OH－+Al2O3=2AlO2－+H2B．AlCl3溶液中加过量的氨水：Al3+ + 3NH3·H2O = Al(OH)3↓ + 3NH4+C．明矾溶液中加入过量的Ba(OH)2：Al3+ + SO42— + Ba2+ + 4OH—＝BaSO4↓＋AlO2—＋H2OD．向NaAlO2溶液中通入过量CO2：2AlO2－＋CO2＋3H2O＝2Al(OH)3↓＋CO32－16．已知KMnO4与浓HCl在常温下反应就能产生Cl2。

2014—2015学年度高一数学竞赛试题(含答案)2014-2015学年度高一数学竞赛试题一．选择题：本大题共5小题，每小题6分，共30分。

在每个小题给出的四个选项中，只有一个正确的答案。

1.已知集合$M=\{x|x+3<0\}$，$N=\{x|x\leq -3\}$，则集合$M\cap N$=（）A。

$\{x|x0\}$ D。

$\{x|x\leq -3\}$2.已知$\alpha+\beta=\frac{\pi}{4}$，则$(1-\tan\alpha)(1-\tan\beta)$等于（）A。

2 B。

$-\frac{2}{3}$ C。

1 D。

$-\frac{1}{3}$3.设奇函数$f(x)$在$(0,+\infty)$上为增函数，且$f(1)=0$，则不等式$f(x)-f(-x)<0$的解集为（）A。

$(-\infty,-1)\cup (0,1)$ B。

$(-1,0)\cup (1,+\infty)$ C。

$(-\infty,-1)\cup (1,+\infty)$ D。

$(0,1)$4.函数$f(x)=\ln|x-1|-x+3$的零点个数为（）A。

3 B。

2 C。

1 D。

05.已知函数$f(x)=\begin{cases}1/x。

& x\geq 4 \\ 2.&x<4\end{cases}$，则$f(\log_2 5)$=（）A。

$-\frac{11}{23}$ B。

$\frac{1}{23}$ C。

$\frac{11}{23}$ D。

$\frac{19}{23}$二．填空题：本大题共5小题，每小题6分，共30分。

将正确的答案写在题中横线上。

6.已知$0\leq x\leq \frac{\pi}{2}$，则函数$f(x)=4\sqrt{2}\sin x\cos x+\cos^2 x$的值域是\line(5,0){80}。

7.已知：$a,b,c$都不等于0，且$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$，则$\max\{m,n\}=$\line(5,0){80}，$\min\{m,n\}=$\line(5,0){80}。

XXX2014-2015学年下学期高一年级期中数学试卷。

后有答案XXX2014-2015学年下学期高一年级期中数学试卷试卷分为两卷，卷(I)100分，卷(II)50分，共计150分。

考试时间：120分钟。

卷(I)一、选择题：（本大题共10小题，每小题5分，共50分）1.若实数a，b满足a>b，则下列不等式一定成立的是（）A。

a^2<b^2B。

1/a<1/bC。

a^2>b^2D。

a^3>b^32.等差数列{an}中，若a2=1，a4=5，则{an}的前5项和S5=（）A。

7B。

15C。

20D。

253.不等式（1/x-1）>1的解集为（）A。

{x>1}B。

{x<1}C。

{x>2}D。

{x<2}4.△ABC中，三边a，b，c的对角为A，B，C，若B=45°，b=23，c=32，则C=（）A。

60°或120°B。

30°或150°C。

60°D。

30°5.已知数列{an}的前n项和为Sn，且Sn=2an-1（n∈N*），则a5=（）A。

32B。

31C。

16D。

156.等差数列{an}中，an=6-2n，等比数列{bn}中，b5=a5，b7=a7，则b6=（）A。

42B。

-42C。

±42D。

无法确定7.△ABC中，若∠ABC=π/2，AB=2，BC=3，则sin∠BAC=（）A。

4/5B。

3/10C。

5/10D。

1/108.计算机是将信息转换成二进制进行处理的，所谓二进制即“逢二进一”，如（1101）2表示二进制的数，将它转换成十进制数的形式是1×23+1×22+0×21+1×2=13，那么将二进制数（11.1）2转换成十进制数是（）{共9位}A。

512B。

511C。

256D。

2559.不等式①x2+3>3x；②a2+b2≥2(a-b-1)；③ba+≥2，其中恒成立的是（）A。

2014-2015学年上学期高一期中测试数学试题（含答案） 第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合要求的）1．下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（ ）A ．3y x =B ． 1y x =+C ．21y x =-+D ． 2x y -=2．在同一坐标系中，表示函数log a y x =与y x a =+的图象正确的是（ ）A B C D3．若1log 12a<，则a 的取值范围是( ) A ．1(0,)(1,)2+∞ B ．1(,1)2 C ．(1,)+∞ D ．1(,1)(1,)2+∞4．已知函数f(x)为定义在R 上的奇函数，当x≥0时， ()22xf x x m =++ (m 为常数)，则(1)f -的值为( )A ．－3B ．－1C ．1D ．35．设全集U =R ，{}|0P x f x x ==∈R （），，{}|0Q x g x x ==∈R （），，{}|0S x x x ϕ==∈R （），，则方程22f x x x ϕ=（）+g （）（）的解集为（ ）A ． P Q SB ．P QC ．P Q S （）D ． P Q S u （C ）5．设9.0log 5.0=a ，9.0log 1.1=b ，9.01.1=c ，则c b a , ,的大小关系为（ ）A ．c b a <<B ．c a b <<C ．a c b <<D ．b c a <<6．设}3 2, ,21 ,31 ,1{-∈α，若函数αx y =是定义域为R 的奇函数，则α的值为（ ）A ．3 ,31B ．3 ,31 ,1- C ．3 ,1- D ．31,1- 7．已知函数)(x f 是奇函数，当0>x 时，)1 ,0( )(≠>=a a a x f x，且3)4(log 5.0-=f ，则a的值为（ ）A ．3B ．3C ．9D ．238．已知函数⎪⎩⎪⎨⎧>-≤=-)1( )23(log )1( 2)(2x x x x f x ，若4)(=a f ，则实数=a （ ） A ．2-或6 B ．2-或310 C ．2-或2 D ．2或3109．方程21231=⎪⎭⎫ ⎝⎛--x x 的解所在的区间为（ ）A ．) 1 ,0 (B ．) 2 ,1 (C ．) 3 ,2 (D ．) 4 ,3 (10．已知函数bx ax y +=2和xb a y =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能 是（ ）11．已知函数)3(log 221a ax x y +-=在区间) ,2[∞+上是减函数，则a 的取值范围是（ ）A ．)4 ,(-∞B ．]4 ,4[-C ．]4 ,4(-D ．]4 ,(-∞12．若在直角坐标平面内B A ,两点满足条件：①点B A ,都在函数)(x f y =的图象上；②点B A ,关于原点对称，则称B A ,为函数)(x f y =的一个“黄金点对”．那么函数=)(x f ⎪⎩⎪⎨⎧>≤-+)0( 1)0( 222x x x x x 的“黄金点对”的个数是（ ）A ．0个B ．1个C ．2个D ．3个 第Ⅱ卷（非选择题，共90分）二、填空题：本题共4小题，共20分.13．已知集合}06|{2=--=x x x M ，}01|{=+=ax x N ，且M N ⊆，则由a 的取值组成的集合是 ．14．若x x f =)(log 5，则=-)9log 2(log 255f ．15．已知定义在R 上的偶函数)(x f 满足0)1(=-f ，并且)(x f 在)0 ,(-∞上为增函数．若0)( <a f a ，则实数a 的取值范围是 ．16．已知函数()x f 的定义域是}0|{≠∈=x R x D ，对任意D x x ∈21 ,都有：=⋅)(21x x f)()(21x f x f +，且当1>x 时，()0>x f ．给出结论：①()x f 是偶函数；②()x f 在()∞+ ,0上是减函数．则正确结论的序号是 ．三、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤。

2014—2015学年第一学期初三年级期末质量抽测数学试卷2014．12学校姓名考试编号考生须知1．本试卷共6页，共五道大题，25个小题，满分120分．考试时间120分钟．2．在试卷和答题卡上认真填写学校名称、姓名和考试编号．3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．4．考试结束，请将答题卡交回．一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个．．是符合题意的．1．已知⊙O 1和⊙O 2的半径分别为3和5，如果O 1O 2= 8，那么⊙O 1和⊙O 2的位置关系是A ．外切B.相交C.内切D.内含2．在不透明的布袋中装有2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球．．的概率是A ．15B.13C.25D.233．如图，⊙O 的直径AB=4，点C 在⊙O 上，如果∠ABC =30°，那么AC 的长是A ．1B ．2C ．3D ．24. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，使它与图中阴影部分组成的新图形构成中心对称图形，该小正方形的序号是A ．①B ．②C ．③D ．④5．如图，在△ABC 中，点D E 、分别在AB AC 、边上，DE ∥BC ，若:3:4AD AB，6AE，则AC 等于A. 3B. 4C . 6D. 86．当二次函数249y xx 取最小值时，x 的值为A ．2B ．1C ．2D ．9来源学|科|网ABC30°④③②①ABCODC BAO7．课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成30°角时，测得旗杆AB 在地面上的影长BC 为24米，那么旗杆AB 的高度约是A ．12米B ．83米C ．24米D ．243米[来源:]8．已知：如图，在半径为4的⊙O 中，AB 为直径，以弦AC （非直径）为对称轴将AC折叠后与AB 相交于点D ，如果3ADDB ，那么AC 的长为A ．214B ．27C ．42D ．6二、填空题（共4道小题，每小题4分，共16分）9．如果3cos 2A，那么锐角A 的度数为.10．如果一个圆锥的母线长为4，底面半径为1，那么这个圆锥的侧面积为．11．在1×2的正方形网格格点上放三枚棋子，按图所示的位置已放置了两枚棋子，如果第三枚棋子随机放在其它格点上，那么以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为.12．在平面直角坐标系xoy 中，直线2x 和抛物线2yax 在第一象限交于点A,过A 作ABx 轴于点B .如果a 取1，2，3，,，n 时对应的△AOB 的面积为123S S S ，，，，n S ，那么1S _____；123nS S S S _____．三、解答题（共6道小题，第13题4分，第14 -18题各5分，共29分）13.如图1，正方形ABCD 是一个 6 × 6网格的示意图，其中每个小正方形的边长为1，位于AD 中点处的点P 按图2的程序移动．（1）请在图中画出点P 经过的路径；（2）求点P 经过的路径总长．绕点A 顺时针旋转90°绕点B 顺时针旋转90°绕点C 顺时针旋转90°输入点P输出点ADPxOy[来源:.Com]14.计算：3tan302cos452sin 60．15.现有三个自愿献血者，两人血型为O 型，一人血型为A 型.若在三人中随意挑选一人献血，两年以后又从此三人中随意挑选一人献血，试求两次所献血的血型均为O 型的概率(要求：用列表或画树状图的方法解答)．[来源:]16. 如图，从热气球C 处测得地面A 、B 两处的俯角分别为30°、45°，如果此时热气球C处的高度CD 为100米，点A 、D 、B 在同一直线上，求AB 两处的距离.17. 已知抛物线与x 轴相交于两点A(1，0)，B(-3，0)，与y 轴相交于点C (0，3)．(1)求此抛物线的函数表达式；(2)如果点3,2Dm 是抛物线上的一点，求△ABD 的面积．18.如图，在△ABC 中，∠AB C =2∠C ，BD 平分∠ABC ，且2AD ，22BD ，求AB 的值.BCDADCBA四、解答题（共4道小题，每小题5分，共20分）19.如图，在平面直角坐标系xoy 中，⊙A 与y 轴相切于点3(0,)2B ，与x 轴相交于M 、N 两点.如果点M 的坐标为1(,0)2，求点N 的坐标.20.（1）已知二次函数223y xx ，请你化成2()y x h k的形式，并在直角坐标系中画出223y xx 的图象；（2）如果11()A x y ，，22()B x y ，是（1）中图象上的两点，且121x x ，请直接写出1y 、2y 的大小关系；（3）利用（1）中的图象表示出方程2210xx 的根来，要求保留画图痕迹，说明结果．21.已知：如图，在△ABC 中，AB =AC ，以AC 为直径的⊙O 与BC 交于点D ，DE ⊥AB ，垂足为E ，ED 的延长线与AC 的延长线交于点F .（1）求证：DE 是⊙O 的切线；（2）若⊙O 的半径为4，BE =2，求∠F 的度数.yxO AB MNyOxEOA22.阅读下面的材料：小明遇到一个问题：如图（1），在□ABCD 中，点E 是边BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G. 如果3AF EF，求CD CG的值.他的做法是：过点E 作EH ∥AB 交BG 于点H ，则可以得到△BAF ∽△HEF .请你回答：（1）AB 和EH 的数量关系为，CG 和EH 的数量关系为，CD CG的值为.（2）如图（2），在原题的其他条件不变的情况下，如果(0)AF a a EF，那么CD CG的值为（用含a 的代数式表示）.（3）请你参考小明的方法继续探究：如图（3），在四边形ABCD 中，DC ∥AB ，点E是BC 延长线上一点，AE 和BD 相交于点 F. 如果(00)AB BC m n mnCDBE，，，那么AF EF的值为（用含m ，n 的代数式表示）.H(1)ABCDE FG G FE DCBA(2)(3)AB CDEF五、解答题（共3道小题，第23题7分，第24、25题各8分，共23分）23.由于2013年第30号强台风“海燕”的侵袭，致使多个城市受到影响. 如图所示，A 市位于台风中心M 北偏东15°的方向上，距离612千米，B 市位于台风中心M 正东方向603千米处. 台风中心以每小时30千米的速度沿MF 向北偏东60°的方向移动（假设台风在移动的过程中的风速保持不变），距离台风中心60千米的圆形区域内均会受到此次强烈台风的影响.（1）A 市、B 市是否会受到此次台风的影响？说明理由.（2）如果受到此次台风影响,该城市受到台风影响的持续时间为多少小时?备用图24．已知二次函数y = x 2–kx + k – 1（k ＞2）.（1）求证：抛物线y = x 2–kx + k- 1（k ＞2）与x 轴必有两个交点；（2）抛物线与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ,若tan 3OAC，求抛物线的表达式；（3）以（2）中的抛物线上一点P （m,n ）为圆心，1为半径作圆，直接写出：当m 取何值时，x 轴与P 相离、相切、相交.25.已知：四边形ABCD 中，AD ∥BC ，AD=AB=CD ，∠BAD =120°，点E 是射线CD 上的一个动点（与C 、D 不重合），将△ADE 绕点A 顺时针旋转120°后，得到△ABE'，连接EE'.（1）如图1，∠AEE'= °；（2）如图2，如果将直线AE 绕点A 顺时针旋转30°后交直线BC 于点F ，过点E 作EM∥AD 交直线AF 于点M ，写出线段DE 、BF 、ME 之间的数量关系；（3）如图3，在（2）的条件下，如果CE =2，AE=27，求ME 的长.xyO–１–２1234–１–２1234E'MFEDC BAE'EDCBA图1图2E'MFEDC BA图32014—2015学年第一学期初三年级期末质量抽测数学试卷参考答案及评分标准2014．12一、选择题（共8个小题，每小题4分，共32分）题号 1 2 3 4 5 6 7 8 答案 ACDBDABA二、填空题（共4个小题，每小题4分，共16分）题号9 10 1112答案304344 ,2n(n+1)（各2分）三、解答题（共6道小题，第13题4分，第14 -18题各5分，共29分）13．解：（1）如图所示：PAB CD,,,,,,,,,,,,,,,,,,,,2分（2）由题意得,点P 经过的路径总长为：270318091802n r ．,,,,,,,,,,,4分14．解：原式=323322322,,,,,,,,,,,,,,,,,,,,,,3分=113,,,,,,,,,,,,,,,,,,,,,,4分=23．,,,,,,,,,,,,,,,,,,,,,,,,,,,,5分15．解：列表如下：O 1O 2 A O 1(O 1，O 1)(O 1，O 2)(O 1，A)O 2(O 2，O 1) (O 2，O 2) (O 2，A) A(A ，O 1)(A ，O 2) (A ，A),,,,,,,,,,,,,,,,,,,,,,,4分所以，两次所献血型均为O 型的概率为49.,,,,,,,,,,,,,,,,,,,,,,5分16．解：依题意，可知：30,45,,100,CABCBACD AB D CD 于点,,,,,,,,,,,,,,,1分,CD AB 90.CDACDB ,,,,,,,,,,,,,,,,,,,,,,,,,2分Rt 100BDC BDCD 在中，，,,,,,,,,,,,,,,,,,,,,,,3分Rt tan CDADC AAD在中，．∴31003AD CD ．,,,,,,,,,,,,,,,,,,,,,,,,,4分1003100ABADBD.,,,,,,,,,,,,,,,,,,,,,,,5分∴AB 两处的距离为(1003100)米.17．解：(1)∵抛物线与y 轴相交于点C (0，3),∴设抛物线的解析式为23y axbx .,,,,,,,,,,,,,,,,,1分∵抛物线与x 轴相交于两点(1,0),(3,0)A B ，∴30,9330.a b a b ,,,,,,,,,,,,,,,,,,,,,,,,,,,2分解得：1,2.a b∴抛物线的函数表达式为：232yxx .,,,,,,,,,,,,,,,,3分（2）∵点3(,)2D m 是抛物线上一点，∴2(23339)224m . ,,,,,,,,,,,,,,,,,,,,,,4分∴119942242ABDDSAB y . ,,,,,,,,,,,,,,,,,,5分18．解：∵BD 平分∠ABC ，∴∠ABC =2∠1=2∠2.∵∠ABC =2∠C ，∴∠C =∠1=∠2.,,,,,,,,,,,1分∴22CD BD . ,,,,,,,,,,,,2分∴32AC.又∵∠A=∠A,∴△ABD ∽△ACB .,,,,,,,,,,,,,,,,,,,,,,,,,,,3分∴AD AB ABAC.,,,,,,,,,,,,,,,,,,,,,,,,,,,4分∴22326AB AD AC .∴6AB（舍负）.,,,,,,,,,,,,,,,,,,,,,,,,,,5分四、解答题（共４道小题，每小题5分，共20分）19．解：连接AB 、AM ，过点A 作AC ⊥MN 于点C ．∵⊙A 与y 轴相切于点B(0，32)，∴AB ⊥y 轴.又∵AC ⊥MN ，x 轴⊥y 轴，∴四边形BOCA 为矩形．∴AC =OB=32，OC =BA ．∵AC ⊥MN ，∴∠ACM=90°，MC=CN ．,,,,,,,,,,,,,,,,,,,,2分∵M(12，0)，∴OM =12．在Rt △AMC 中，设AM=r.O A B MNCyx21DCBA。

高一上学期数学期末考试《必修4》试题姓名： 分数：一、选择题（每小题4分,共40分）1、与463-︒终边相同的角可以表示为(k Z)∈ （ ）A 、k 360463⋅︒+︒B 、k 360103⋅︒+︒C 、k 360257⋅︒+︒D 、k 360257⋅︒-︒2、如图，在正六边形ABCDEF 中，点O 为其中心，则下列判断错误的是（ ）A 、AB OC = B 、AB ∥DE C 、AD BE = D 、AD FC =3、α是第四象限角，12cos 13α=，sin α=（ ）A 、513B 、513-C 、512D 、512-4、2255log sin log cos 1212π+π的值是（ ） A 、4 B 、1 C 、4- D 、1-5、设()sin()cos()f x a x b x =π+α+π+β+4，其中a b 、、、αβ均为非零的常数，若(1988)3f =， 则(2008)f 的值为（ ）A 、1B 、3C 、5D 、不确定6、若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ）A 、1B 2C 3D 、27、为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像（ ）A 、向左平移5π12个长度单位 B 、向右平移5π12个长度单位 C 、向左平移5π6个长度单位 D 、向右平移5π6个长度单位8、函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示，则函数表达式为（ ） A 、)48sin(4π-π-=x y B 、)48sin(4π-π=x yC 、)48sin(4π+π=x yD 、)48sin(4π+π-=x yE DBAO9、设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ，则()f x =（ ）A 、在区间2736ππ⎡⎤⎢⎥⎣⎦，上是增函数B 、在区间2π⎡⎤-π-⎢⎥⎣⎦，上是减函数 C 、在区间84ππ⎡⎤⎢⎥⎣⎦，上是增函数 D 、在区间536ππ⎡⎤⎢⎥⎣⎦，上是减函数10、设D 、E 、F 分别是△ABC 的三边BC 、CA 、AB 上的点，且2,DC BD =2,CE EA =2,AF FB =则AD BE CF ++与BC ( )A 、互相垂直B 、同向平行C 、反向平行D ．既不平行也不垂直二、填空题（每小题4分，共16分）11、23sin 702cos 10-=-12、已知函数()2sin 5f x x π⎛⎫=ω- ⎪⎝⎭的图象与直线1y =-的交点中最近的两个交点的距离为3π，则函数()f x 的最小正周期为 。

一、填空题：（本大题共14题，每小题5分，共70分，请将答案填入答题纸填空题的相应答题线上)1。

直线30x y -+=的倾斜角为__________ 【答案】4π【解析】试题分析：由直线方程可知斜率1tan 14k παα=∴=∴=考点：直线倾斜角与斜率2。

若直线1ax y +=与(1)23a x y -+=直线平行，则实数a 的值是_______ 【答案】1- 【解析】试题分析：两直线平行则系数满足211a a a =-∴=- 考点：两直线平行的判定3。

在长方体1111ABCD A BC D -的棱所在直线中，与直线AB 异面的条数为________ 【答案】4 【解析】试题分析：与直线AB 异面的直线有111111,,,A D B C DD CC 共4条考点：异面直线4。

在等比数列{}na 中，45a=，则17a a =_________【答案】25 【解析】试题分析:由等比数列性质可知217425a aa ==考点：等比数列性质5.不等式2111x x ->+的解集为________【答案】(,1)(2,)-∞-+∞【解析】试题分析：原不等式2111x x ->+化为()()2021021x x x x x ->∴-+>∴>+或1x <-，因此不等式的解集为(,1)(2,)-∞-+∞考点：分式不等式解法6。

0,0,1x y x y ≥≥+≤，则x y -的最大值为__________ 【答案】1考点:线性规划问题7.正方体的表面积为24，则该正方体的内切球的体积为____________ 【答案】43π【解析】试题分析：正方形边长设为x 26242x x ∴=∴=,内切球的直径为2，所以体积为34433V Rππ== 考点:正方体与球的基本知识 8。

若圆22(2)()1x y a ++-=与圆22()(5)16x a y -+-=相交，则实数a 的取值范围是_______ 【答案】12a <<【解析】试题分析：两圆相交，则圆心距满足()()221212325512r r d r r a a a -<<+∴<++-<∴<<考点：两圆的位置关系9。

高一数学（苏教版）必修一午间小练：集合的基本关系（2）1．设集合A ＝{x|x ＝5－4a ＋a 2，a ∈R}，B ＝{y|y ＝4b 2＋4b ＋2，b ∈R}，则A 、B 的关系是________．2．已知集合A ＝{m ＋2，2m 2＋m}，若3∈A，则m ＝________．3．已知定义在R 上的函数()f x ，那么集合{(,)|(),}{(,)|1}x y y f x x R x y x =∈⋂=的子集有____ 个．4．已知集合A ＝}12,52,2{2a a a +-，且－3∈A ，则a =_____ ___.5．设P 是一个数集，且至少含有两个数，若对任意a 、b ∈P ，都有a+b 、a-b 、ab 、ab ∈P （除数b ≠0）则称P 是一个数域，例如有理数集Q 是数域，有下列命题： ①数域必含有0，1两个数； ②整数集是数域；③若有理数集Q ⊆M,则数集M 必为数域; ④数域必为无限集.其中正确的命题的序号是 .（把你认为正确的命题的序号都填上）6．如果{x|x 2－3x ＋2=0}⊇{x|ax －2=0}，那么所有a 值构成的集合是 .7．已知A ＝{a ＋2，(a ＋1)2，a 2＋3a ＋3}且1∈A，求实数a 的值．8．集合A ＝{x|－2≤x≤5}，集合B ＝{x|m ＋1≤x≤2m －1}．(1)若B ⊆A ，求实数m 的取值范围；(2)当x ∈R 时，没有元素x 使x ∈A 与x ∈B 同时成立，求实数m 的取值范围．9．集合A ＝,,1b a a ⎧⎫⎨⎬⎩⎭，集合B ＝{a 2，a ＋b ，0}，若A ＝B ，求a 2 013＋b 2 014的值． 10．已知集合A ＝{x|(x －2)[x －(3a ＋1)]＜0}，B ＝201x a xx a ⎧⎫⎨⎬⎩⎭－＜－（＋）. (1) 当a ＝2时，求A∩B；(2) 求使B 真包含于A 的实数a 的取值范围．参考答案1．A ＝B【解析】化简得A ＝{x|x≥1}，B ＝{y|y≥1}，所以A ＝B.2．－32【解析】因为3∈A，所以m ＋2＝3或2m 2＋m ＝3.当m ＋2＝3，即m ＝1时，2m 2＋m ＝3，此时集合A 中有重复元素3，所以m ＝1不合题意，舍去；当2m 2＋m ＝3时，解得m ＝－32或m ＝1(舍去)，此时当m ＝－32时，m ＋2＝12≠3满足题意．所以m ＝－32. 3．2【解析】解：因为已知定义在R 上的函数()f x ，那么集合{(,)|(),}{(x y y f x x R x y x =∈⋂=的元素个数必然为一个，因此它的子集有2 4．－32【解析】解：因为集合A ＝}12,52,2{2a a a +-，且－3∈A ，所以有2a 23,2a 5a=-3-=-+或解得符合题意的a=－325．①④【解析】解：当a=b 时，a-b=0、a b =1∈P ，故可知①正确．当a=1，b=2，1 2 ∉Z 不满足条件，故可知②不正确．对③当M 中多一个元素i 则会出现1+i ∉M 所以它也不是一个数域；故可知③不正确． 根据数据的性质易得数域有无限多个元素，必为无限集，故可知④正确．故答案为：①④．6．{0，1，2}【解析】解：当a=0时，空集是任何集合的子集，当2/a=1,a=2,或2/a=2,a=1,也成立，故所有的集合为{0，1，2}7．a ＝0【解析】由题意知：a ＋2＝1或(a ＋1)2＝1或a 2＋3a ＋3＝1，∴ a ＝－1或－2或0，根据元素的互异性排除－1，－2，∴ a ＝0即为所求．8．（1）m≤3（2）m ＜2或m ＞4【解析】(1)当m ＋1＞2m －1即m ＜2时，B ＝φ满足B ⊆A ；当m ＋1≤2m－1即m≥2时，要使B ⊆A 成立，则12215m m ≥⎧⎨≤⎩＋－，－，解得2≤m≤3. 综上所述，当m≤3时有B ⊆A.(2)因为x ∈R ，且A ＝{x|－2≤x≤5}，B ＝{x|m ＋1≤x≤2m－1}，又没有元素x 使x ∈A 与x∈B同时成立，则①若B＝φ，即m＋1＞2m－1，得m＜2时满足条件；②若B≠φ，则要满足条件12115m mm≤⎧⎨⎩＋－，＋＞，解得m＞4.或121212m mm≤⎧⎨⎩＋－，－＜－，无解．综上所述，实数m的取值范围为m＜2或m＞4 9．－1【解析】由于a≠0，由ba＝0，得b＝0，则A＝{a，0，1}，B＝{a2，a，0}．由A＝B，可得a2＝1.又a2≠a，则a≠1，则a＝－1.所以a2 013＋b2 014＝－1.10．（1）{x|2＜x＜5}（2）11,2⎡⎤--⎢⎥⎣⎦∪[2，3]【解析】(1) A∩B＝{x|2＜x＜5}．(2) B＝{x|a＜x＜a2＋1}．①若a＝13时，A＝Æ，不存在a使BÍA；②若a＞13时，2≤a≤3；③若a＜13时，－1≤a≤－12.故a的取值范围是11,2⎡⎤--⎢⎥⎣⎦∪[2，3]．。