当前位置：文档之家 › 实验力学盖秉政第5章应变仪

实验力学盖秉政第5章应变仪

  • 格式：ppt
  • 大小：2.67 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

(完整版)漆安慎杜禅英力学习题及答案05章

(完整版)漆安慎杜禅英力学习题及答案05章

第五章 一、基本知识小结⒈力矩力对点的力矩F r o力对轴的力矩F r k zˆ ⒉角动量质点对点的角动量 p r L o质点对轴的角动量p r k L zˆ ⒊角动量定理适用于惯性系、质点、质点系⑴质点或质点系对某点的角动量对时间的变化率等于作用于质点或质点系的外力对该点的力矩之和dtL d 0外⑵质点或质点系对某轴的角动量对时间的变化率等于作用于质点或质点系的外力对该轴的力矩之和dtdL zz ⒋角动量守恒定律适用于惯性系、质点、质点系⑴若作用于质点或质点系的外力对某点的力矩之和始终为零，则质点或质点系对该点的角动量保持不变⑵若作用于质点或质点系的外力对某轴的力矩之和始终为零，则质点或质点系对该轴的角动量保持不变⒌对质心参考系可直接应用角动量定理及其守恒定律，而不必考虑惯性力矩。

二、思考题解答5.1下面的叙述是否正确,试作分析,并把错误的叙述改正过来: （1）、一定质量的质点在运动中某时刻的加速度一经确定，则质点所受的合力就可以确定了，同时作用于质点的力矩也就确定了。

（2）、质点作圆周运动必定受到力矩的作用；质点作直线运动必定不受力矩的作用。

（3）、力与z 轴平行，所以力矩为零；力与z 轴垂直，所以力矩不为零。

（4）、小球与放置在光滑水平面上的轻杆一端连结，轻杆另一端固定在铅直轴上。

垂直于杆用力推小球，小球受到该力力矩作用，由静止而绕铅直轴转动，产生了角动量。

所以，力矩是产生角动量的原因，而且力矩的方向与角动量方向相同。

（5）、作匀速圆周运动的质点，其质量m ，速率v 及圆周半径r 都是常量。

虽然其速度方向时时在改变，但却总与半径垂直，所以，其角动量守恒。

答：（1）不正确. 因为计算力矩, 必须明确对哪个参考点. 否则没有意义. 作用于质点的合力可以由加速度确定. 但没有明确参考点时, 谈力矩是没有意义的. （2）不正确. 质点作圆周运动时, 有两种情况: 一种是匀速圆周运动, 它所受合力通过圆心; 另一种是变速圆周运动, 它所受的合力一般不通过圆心. 若对圆心求力矩, 则前者为零, 后者不为零.质点作直线运动, 作用于质点的合力必沿直线. 若对直线上一点求力矩, 必为零; 对线外一点求力矩则不为零。

用DRA-101C动态应变仪测量梁的冲击应变

用DRA-101C动态应变仪测量梁的冲击应变

用DRA-101C动态应变仪测量梁的冲击应变吕巍徐先彬北京工业大学000412班指导教师：王亲猛摘要：本文设计了一种新的实验，对梁构件在受冲击力时的变化情况进行了分析。

实验中利用数字动态应变仪测量了梁构件的动应变，在对梁构件受力情况进行分析的基础上得到了实验过程中梁构件能量损失与其他参数的关系。

关键词：动态应变仪、实验测量、电阻应变片、能量损失一、引言在材料力学中，测量构件的受力情况常用的方法之一是电测法。

这是一种狭义方法，专门用来指用电阻应变片的测量。

在被测构件上贴上电阻应变片，当构件受力后，电阻应变片的阻值发生变化，产生变形，测出应变，再通过计算，即可求得被测构件的应力。

根据构件受力情况，可分为静态测量和动态测量两种。

静态测量应用非常普遍，技术也十分成熟。

而动态应变测量特别是数字化测量目前仍是一个难点。

本实验着重对动应变的测量及能量损失的关系进行初步研究。

二、实验方案2.1 实验设备日本东京测器的10通道动态应变仪DRA-101C带有自动数据采集系统，每通道有一个16位A/D数据采集器，外置桥盒，并配有GP-IB接口卡，可直接将测量数据传送到计算机。

频率响应为10kHz。

同时具有数据存储、数字及波形监视，以及波形的时域和频域之间的转换及相关分析。

原始数据还可以转换为Excel格式。

2.2 加载方案根据仪器的这些特点，我们设计了实验加载方案。

主要研究梁在受到冲击时的受力情况，见图2。

冲击是一种瞬时应变，在冲击过程中，梁受到振动，信号中含有各种频谱成分。

梁的材料为铝型材，而冲击杆为刚性体。

图中1、2、3图1 DRA-101C多通道动态应变仪为贴片位置。

同时在撞击杆上端和中端损失一定能量。

三、理论计算假设由冲击杆的动能转移到被击打试件的系数为2α，则其动能部分为2232α⋅=mv T (1)而试件的势能可以表达为st st d d d d Q K K Q K P W d∆=∆=∆×=221))((2121(2) 其中d P 为动载荷，d ∆为动载荷下的位移，d K 为动载系数，Q 为静载荷，mg Q =，st ∆为静载荷下的位移。

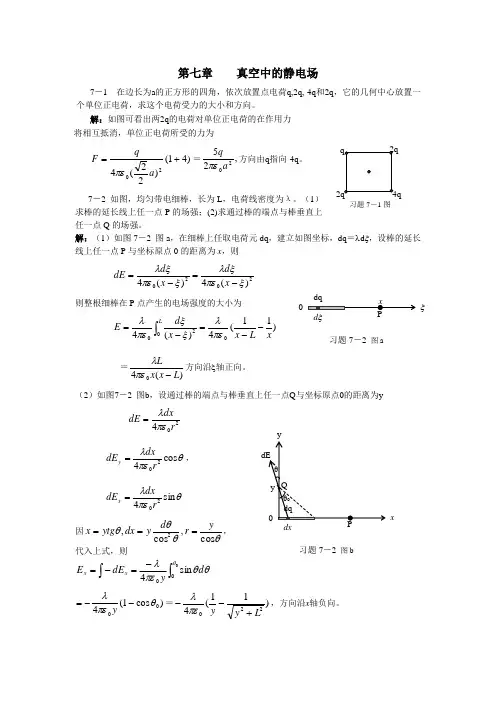
许瑞珍、贾谊明 大学物理课后答案(机械工业出版社)

许瑞珍、贾谊明 大学物理课后答案(机械工业出版社)

第七章 真空中的静电场7－1 在边长为a 的正方形的四角，依次放置点电荷q,2q,-4q 和2q ，它的几何中心放置一个单位正电荷，求这个电荷受力的大小和方向。

解：如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消，单位正电荷所受的力为)41()22(420+=a q F πε＝,2520aqπε方向由q 指向-4q 。

7－2 如图，均匀带电细棒，长为L ，电荷线密度为λ。

（1）求棒的延长线上任一点P 的场强；(2)求通过棒的端点与棒垂直上任一点Q 的场强。

解：（1）如图7－2 图a ，在细棒上任取电荷元dq ，建立如图坐标，dq ＝λd ξ，设棒的延长线上任一点P 与坐标原点0的距离为x ，则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(4002xL x x d E L--=-=⎰πελξξπελ ＝)(40L x x L-πελ方向沿ξ轴正向。

（2）如图7－2 图b ，设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y204r dxdE πελ=θπελcos 420rdxdE y =， θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===， 代入上式，则)cos 1(400θπελ--=y＝)11(4220Ly y +--πελ，方向沿x 轴负向。

习题7－1图dq ξd ξ习题7－2 图axθθπελθd y dE E x x ⎰⎰-=-=00sin 4xdx习题7－2 图byθθπελθd y dE E y y ⎰⎰==00cos 400sin 4θπελy =＝2204Ly y L +πελ 7－3 一细棒弯成半径为R 的半圆形，均匀分布有电荷q ，求半圆中心O 处的场强。

解：如图，在半环上任取d l =Rd θ的线元，其上所带的电荷为dq=λRd θ。

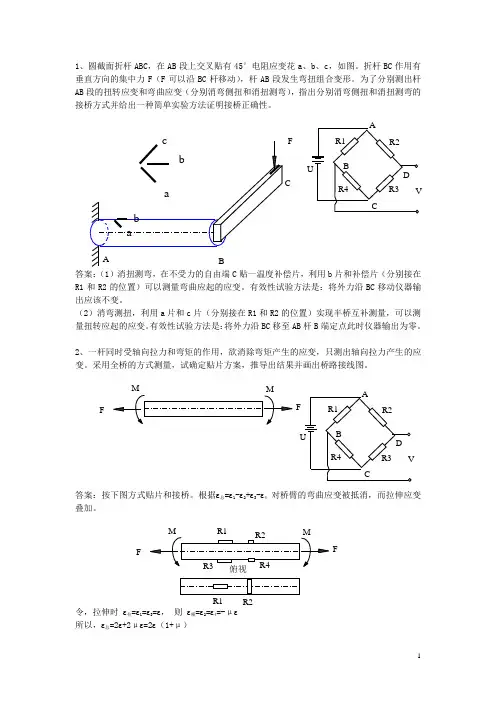
力学竞赛实验部分辅导资料.概要

力学竞赛实验部分辅导资料.概要

1、圆截面折杆ABC ，在AB 段上交叉贴有45°电阻应变花a 、b 、c ，如图。

折杆BC 作用有垂直方向的集中力F （F 可以沿BC 杆移动），杆AB 段发生弯扭组合变形。

为了分别测出杆AB 段的扭转应变和弯曲应变（分别消弯侧扭和消扭测弯），指出分别消弯侧扭和消扭测弯的接桥方式并给出一种简单实验方法证明接桥正确性。

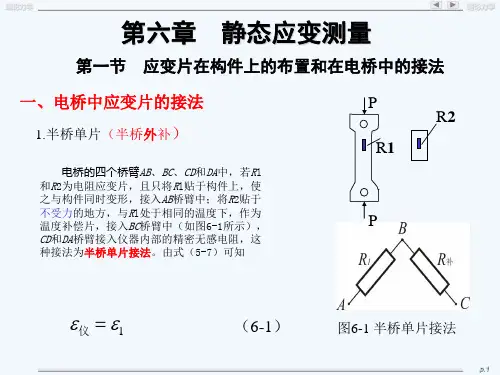
答案：（1）消扭测弯，在不受力的自由端C 贴一温度补偿片，利用b 片和补偿片（分别接在R1和R2的位置）可以测量弯曲应起的应变。

有效性试验方法是：将外力沿BC 移动仪器输出应该不变。

（2）消弯测扭，利用a 片和c 片（分别接在R1和R2的位置）实现半桥互补测量，可以测量扭转应起的应变。

有效性试验方法是：将外力沿BC 移至AB 杆B 端定点此时仪器输出为零。

2、一杆同时受轴向拉力和弯矩的作用，欲消除弯矩产生的应变，只测出轴向拉力产生的应变。

采用全桥的方式测量，试确定贴片方案，推导出结果并画出桥路接线图。

答案：按下图方式贴片和接桥。

根据ε总=ε1-ε2+ε3-ε4 对桥臂的弯曲应变被抵消，而拉伸应变叠加。

令，拉伸时 ε拉=ε1=ε3=ε， 则 ε横=ε2=ε4=-με 所以，ε总=2ε+2με=2ε（1+μ）CFFF F R2 R13、图示为一种电子称的结构图，重物G 放在称盘上的任意位置，若采用在梁AB 上贴应变片的方法测量G 的重量。

贴片基本准则是什么，试确定合理的贴片方式，贴片数量和接桥方式。

答案：因为这样做使测量值与被测物的位置无关。

采用4片应变片组成全桥，沿与水平轴45度的方向贴在中性层上。

如图所示，在梁的正向侧表面贴R1、R2两片，在梁的背向侧表面贴R3、R4两片，其中R2和R4投影重合，R1和R3投影重合。

4、图示梁受集中力的作用，侧表面贴有三片应变片测量线应变，请问哪一片的测量值与理论值有可能最接近，为什么？答案：片3的测量值于理论之可能最接近，因为，此片的位置在圣维南区的边缘，应变受圣维南区影响最小。

实验力学盖秉政第4章应变片

实验力学盖秉政第4章应变片

1 H
1 0.285 0.05
0
p.10
理论力学
第三节 应变片的类型及特点
理论力学
应变片品种繁多，分类方法各异，表4-1中列出几种常见的分类方法以及各种类型应变片的主要特点。
表4-1 各种应变片
分类方法
类型
主要特点
敏感材料
金属电阻应变片 半导体应变片
灵敏系数较低（2左右） 灵敏系数高、频响高。温度稳定性差
敏感栅电阻变化率可表示为:
R R
K仪 仪
K LL
K BB
K (1 LL
K BB
K
)
LL
即有
R K (1 H )
R
LL
式中，H KB / KL , B / L
令
K* K (1 H) , L
则有
R K *
R
L
（4-3）
p.7
理论力学
三、横向效应的影响
理论力学
制造厂在进行标定时给出的灵敏系数，是式（4-3）的 一个约定的特例，即为
/ ( )/
BL
0x
x
0
为厂家在进行标定时标定梁的泊松比。在这种情况下 0
K * K K (1 H)
L
0
（4-4）
如使用的条件和标定时的情况不同，则灵敏系数将不是
K K (1 H)
L
0
而是
K * KL (1 H )
标定时 使用时
p.8
理论力学
三、横向效应的影响
理论力学
敏系数之比，用H代表。
H=横向灵敏系数/纵向灵敏系数=KB/KL
由于应变片的加工工艺和粘贴安装等因素的影响，应
变片的横向效应系数H的实测值与理论值有所不同，H值一

实验力学-应变仪

实验力学-应变仪

所有的C用连 接片连在一起
1
静态多点应变测量的接桥方法（公用补偿片的1/4桥接法）
2
实验力学-应变电测技术
§5 测试实例
1、悬臂梁指定截面最大弯曲应变εmax 的测量
实验力学-应变电测技术
矩形截面梁自由端受集中力P。用不同的布片、组桥方式 测定A截面的最大弯曲应变εmax及桥臂系数B。根据应变的测量 值可进一步确定截面的最大应力σmax ，截面弯矩MA 。 被测点的实际应变值若为ε单，则桥臂系数B= ε仪 /ε
ΔUDB =[ε1－(－ε2)＋ε3 －(－ε4)] = 4ε1 = 4εmax
ε仪 = 4εmax；εmax=ε仪 / 4
实验力学-应变电测技术
2、偏心拉杆的应变测量、和内力的分离
实验力学-应变电测技术
一矩形截面杆件受一偏心拉力P，偏心距为e 。设拉力 引起的应变为εP ；偏心引起的最大弯曲应变为εmax 。 用不同的布片、组桥方式分离和测定杆件的轴向应变εP
电阻片，其它三个桥臂的电阻片都不参与机械变形。这
时，电桥的输出电压为：
E R1 EK U 1 4 R1 4
实验力学-应变电测技术
2、半桥测量
电桥中相邻两个桥臂（常用AB、BC桥臂）参与机械 变形的电阻片，其它两个桥臂是不参与机械变形的固定
电阻。这时电桥的输出电压为 ：
U DB
E R1 R2 EK ( ) ( 1 2 ) 4 R1 R 4
A
B
C
实验力学-应变电测技术
（3）静态多点应变测量 当测点较多，希望加一次载荷能同时读下所有测点 应变时，可利用1/4桥接法，事先把所有测点接到应变仪 的AB桥臂上，共用一枚补偿片接于公共补偿桥臂上，利 用测点转换按键同时读出各个测点的应变。

实验力学盖秉政第6章静应变测量

实验力学盖秉政第6章静应变测量

（i） 图6-20 测拉扭组合变形构件的应变 （j） （k） （l）
p.21
理论力学
(1) 测量扭转产生的应变
理论力学
按照图6-20所示的贴片方法，对于弯扭组合变形 构件，若要单独得到扭转产生的应变，可采用全桥接 法（全桥自补） 。将Rl、R2 、R3和R4作为工作片， 分别接在AB、BC、CD和DA四个桥臂上，如图6-21所示。 由式（6-3）和式（i）～（l）有
理论力学
1 拉 弯 2 拉 弯
（c） （d）
3
拉
弯
（e）
4
拉
弯
（f）
图6-13a 四个应变片测拉弯组 合变形的应变
图6-13b 构件上表面示意图
p.13
理论力学
4．拉弯组合变形时应变片在构件上的布置 （1）测量弯曲产生的应变
理论力学
① 按图6-12所示的贴片方法，可采用半桥 双片（半桥自补）接法测量，将Rl、R2作为工作 片，分别接在AB和BC桥臂上（如图6-14a所示）， CD和DA桥臂接入仪器内部的精密无感电阻。由式
1 仪
p.5
理论力学
（2）半桥双片接法 （半桥自补）
理论力学
图6-6a半桥双片接法测单向拉伸的应变
图6-6b 半桥双片接法
如图6-6a所示，在构件表面沿轴向和垂直轴向各布置一个应变片Rl、R2，分别接 在AB和BC桥臂上（如图6-6b所示），CD和DA桥臂接入仪器内部的精密无感电阻。
2
1
按这种半桥单片接法，由式（6-2）有
图6-17 测拉扭组合变形构件的应变
仪 1 2 （扭 拉）（扭 拉） 2扭
扭
1 2
仪
图6-18 半桥双片接法
p.19

实验力学盖秉政第7章动应变测量

实验力学盖秉政第7章动应变测量

一、周期性动态应变
一般，一个复杂周期性应变可用富里叶级数表示如下
(t) 0 n cos(2nf1t n ) n 1
(n 1,2,3,)
一般测量得到的复杂周期性
应变的谐波分量可能是很丰 富的，但随着谐波次数的增 高其幅值总是愈来愈小，故 在实际分折中常把高次谐波 略去，只计最低的几次。
p.9
示，称为随机性应变的均值ε a。即
lim a
T
1 T
T
(t)dt
0
动态分量可方差s2来描述，即
lim s2
1 T T
T 0
[
(t
)
a
]2
dt
方差的正平方根称称为标准差，它表示随机性应变在均值附近摆动幅 度的大小。将上式展开可得
2 a2 s2
即随机数据的均方值等于均值 (静态分量)的平方与方差(动态分量)之 和，所以说均方值是随机数据强度(强弱程度)方面的基本描述。
R(
)
lim
T
1 T
T
0
(t)
(t
)dt
自相关函数是时间位移τ的函数，在τ＝0时有最大值，且等了均方值，即
2 R(0)
当τ→∞时，自相关函数的正平方根等于ε(t)的均值，即
2 a
R()
p.19
理论力学
四、功率谱密度函数
理论力学
随机数据的一般强度可用它的均方值来描述，这个均方值是对全部谐波成 分而言的。当我们对在f到f +Δf 频率范围内的谐波成分的强度感兴趣时，就 要计算随机数据在这一频率范围内的均方值。这可用具有精确截断特性的 带通滤波器对样本记录进行滤波，将f到f +Δf 频率范围之外的谐波全部滤掉 ，然后计算滤波器输出量的平方的平均值。当记录时间T→∞，这一平方的 平均值就趋近于该频率范围内的均方值，即

振弦应变计

振弦应变计
1.3. 手册使用方法 本手册分为若干章节。每个章节都包含一类具体内容。当你需要查找某类具体内容时，可参照下表： TRITECH制造的应变计和附件类型：见第2章 ‘制造范围和附件’。 振弦应变计原理：见第3.1节 ‘工作原理’。 基本工具和附件：见第4章 ‘安装需要的工具和附件”。 在混凝土结构中安装应变计：见第5章 ‘安装方法’。 用热敏电阻测量温度：见第6章 ‘热敏电阻 – 温度电阻关系’。
需要测量应变的应用领域中使用。正号表示拉伸应变，负号
表示压缩应变
应变计三脚架 位置 TES-DS-12 5 准该可平以确面在安上一装个在平混面凝上土按大0坝°中、，45可°以、将90一°个、应1变35计°按将9四0°个安应装变在计
无应力应变容器 TES-DS-14
由于混凝土会表现出自身体积增长和热膨胀等，因此必须通 过使用应变计测量应力来加以纠正应力测量结果。为了测定 这些影响，要在现有应变计附近按水平方向在一个中空双层 变壁计容得器到(40的0读m数m减φ去x 6这00个m值m，高就)中得加到装真一实个应应力变计。从其他应
应用 1.1. 线TR，IT可EC以H远振距弦离应传变输计信是号电。子可应用变于计土，壤其、频混率凝输土出块不或受钢外结部构噪中音正影、响负，应能变够的耐测受量土中工，应包用括中：常见的湿接
• 测量大体积混凝土应变 • 测量混凝土和岩石结构中的应变 • 测定并监测混凝土&砌体大坝中的应力分布 • 研究地下洞穴和隧道支撑肋条(支护)中的应力分布 • 长期分析压力竖井、密闭混凝土和岩石覆盖层中的应力分布 • 测量和监测钢结构中的应变和结果应力
应变计支架
TES-DS-15
将应变计焊接在要测量表面应力的钢结构上
不锈钢法兰
TES-DS-16
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

仪 （1 t）（ 2 t） 1 2
（5-8）
（3）全桥互联补偿法（全桥自补） ：将四个工作应变片连接成全桥相 互补偿的方法。由式（5-3）可得
仪 （1 t）（2 t）（3 t）（4 t） 1 2 3 4 （5-9）
p.7
理论力学
理论力学
第二节 电阻应变仪的构造
一、静态电阻应变仪的工作原理
以静态应变变化为测量对象的称为静态电阻应变仪。 目前使用的静态电阻应变仪有两种类型：直流放大式（如Y －18型静态电阻应变仪）和载波放大式（如YJ－5型静态应 变仪）。
（1）测量电桥
动态电阻应变
仪的测量电桥
为交流电桥，其原理Fra bibliotek能和静态应变仪相
同。测量电桥A、
B、C、D 四个 结点及R3、R4
两个桥臂电阻
装在一个电桥
盒上，用一定
长度的屏蔽电
缆线与应变仪 相连。
图5-5 动态应变仪方框图
p.13
理论力学
理论力学
（2）动态应变仪测量的动态应变是随时间变化的，通过记录仪器得到
4．应变仪的灵敏系数 应变仪是按一定的电阻应变片的灵敏系数设计的，静态应变仪设
有调节灵敏系数的装置，而动态应变仪没有此装置，它是按固定灵敏
系数设计的，一般都是按灵敏系数K＝2.0设计的，当使用的应变片灵 敏系数K不等于2.0时，应对测量结果进行修正。
p.16
理论力学
理论力学
5．应变片电阻值（ ） 电阻应变仪使用指定阻值的电阻应变片，如120 ，当使用其它阻
化转换成电压信号变化，以供放大器进行放大。测量电桥中还包括预调 平衡电路，测量电桥的桥压由直流电源供给。
（2）直流放大器 由于测量电桥输出的电压信号很微弱，仅为微伏至毫伏数量级，所以
必须通过放大器加以放大。放大器的放大倍数一般为5×104～10×104左 右。测量时，要求采用性能稳定的低漂移直流放大器。
7．零飘 零飘是衡量仪器静态稳定性的指标，这里的静态是指放大器无信号输
入的状态。开启仪器，观察其稳定性，仪器平衡指示器可能随时间有缓慢 偏移，即仪器有少量输出的现象，这种现象称为零飘。
8．动飘 动飘是衡量仪器动态稳定性的指标，所谓动态是指放大器有信号输入
时的状态。给仪器输入一个恒定的标准应变，可观察其输出的稳定性。仪 器相对于标准应变输出的微小变化称为动飘，静态应变仪没有这项指标。
K仪仪 l △UBD
l
KE
4
(
1
2
3
4)
仪 1 2 3 4
(5-3)
上式称为测量电桥桥路联接的基本关系式
从上式可见，应变测量电桥具有邻臂相减，对臂相加的特性。
1.若四个桥臂均由电阻应变片接成，称这种接法为全桥接法；
2.若Rl和R2为电阻应变片，R3和R4为仪器内部的精密无感电阻，这种接法
p.11
理论力学
理论力学
（5）指示器 通过相敏检波器的信号输入指示器，指示器指针偏转大小和方向即
反映被测应变大小和符号。对于双桥零读数法的电阻应变仪，测量时总 是调整读数桥的可调电阻刻度盘，使指示电表指针恒指零，从读数桥的 刻度盘上就可直接读出应变值
（6）振荡器 振荡器能为电桥提供一定频率的正弦交流电作为供桥电源，即载波电
1．直流放大式静态应变仪 直流放大式静态应变仪的基本组成部分有：测量电桥、直流放大
器，A／D转换器、数字显示器、直流电源。其方框图如图5-3所示。
测量电桥
直流放大器
A／D转换器
数字显示器
直流电源
图5-3 直流放大式静态应变仪的基本组成
p.8
理论力学
一、静态电阻应变仪的工作原理
理论力学
（1）测量电桥 测量电桥是电阻应变仪的重要组成部分，它将应变片微小的电阻变
的是随时间变化的应变波形图，为了便于在应变波形图上确定所测应变值的
大小，一般会在动态应变仪内设置应变标定装置，由此装置给出代表一定标
准应变的信号，即将其作为读波形图的比例尺。应变标定电路有多种，在
Y6D－3A及YD－15动态应变仪中采用的是专用应变标定电桥，如图5-6所示。
标定电桥是由 一系列精密线绕电 阻组成，改变标定 电桥的桥臂电阻值， 即产生相应数值的 正（或负）的标准 应变，通过转换开 关K，在应变测量 前或测量后，将标 定的信号接入放大 器给出一个标准应 变信号，以进行应 变标定。
R4
(b)
其中，U DB
R1
R1
(R1 R2 ) R1 (R1 R2 )2
R1 E
。
p.3
理论力学
一、直流电桥
理论力学
同理，U DB
R2
R2
、
U DB R3
R3
和
U DB R4
R4
均采用类似的计算，
通常选取 R1 R2 R3 R4 R ，故化简得
U DB
E 4
( R1 R1
R2 R2
（6）相敏检波器、振荡器、稳压电源等装置的功能与静态应变仪基本 相同。
p.15
理论力学
理论力学
第三节 电阻应变仪的主要技术指标
电阻应变仪的主要技术指标包括
l．测量线数 测量线数是指仪器具有通道的个数，即可同时测量应变的个数。
2．测量范围
测量范围是指可测量应变量的范围，以微应变（ με ）为单位。
3．工作频率范围 工作频率范围是指仪器能测量应变频率的范围。
（3）A／D转换器 它能将放大后的电压模拟信号转换为数字信号，以便直接驱动数字显示
器。
（4）数字显示器 一般采用液晶显示器，它可将测量的应变值以数字显示出来。
（5）直流电源 直流电源可供给测量电桥、直流放大器和A／D转换器直流电压，一般
采用电池供电。
p.9
理论力学
理论力学
2．载波放大式静态应变仪
载波放大式静态应变仪与直流放大式静态应变仪的主要区别在于它的测量电桥
理论力学
（1）测量电桥
它的功能与直流放大式电阻应变仪相同，电桥输入端的桥压为振荡器 提供的正弦式载波电压。测量电桥包括电阻、电容平衡电路。
（2）读数电桥 要求精度较高的仪器（例如YJ－5型静态应变仪）都设有读数电桥，
它的四个桥臂由高精度的可调电阻器构成，且与测量电桥用同一载波振荡 器供电。读数电桥与测量电桥在输出端是串联的。 当测量电桥因感 受应变而输出一个等幅电压时，指示器指针偏移，调整读数桥桥臂电阻值， 使之输出一个与测量电桥输出电压等幅、相位相反的电压，这两个电压的
p.17
理论力学
理论力学
第四节 新型智能电阻应变仪的介绍
一、概述
YE2538 A静态应变仪采用智能化管理及串行通讯技术（RS-232C）将 计算机测试手段引入教学型测试领域，同时也适应小型工程测试的需要。
特点：
1．智能化管理； 2．电子开关切换，可靠性高； 3．通道、桥路指示灯指示试； 4．双通道显示； 5．自动平衡； 6．可采用全桥、半桥、1／4桥（公用补偿片）进行测量，连接方便； 7．两路独立补偿点； 8．所有设置参数掉电保存； 9．基于WINDOWS 操作平台的应用软件。
理论力学
I1,2 E /(R1 R2 )
I3,4 E /( R3 R4 )
U AB R1E /(R1 R2 )
U AD R4E /(R4 R3 )
而
U AB U A U B , U AD U A U D
故
U DB
UD
UB
U AB
U AD
[R1
/( R1
R2 )
R4
/( R4
R1R3 R2 R4
R3C1
R4
C2
由于 R3 R4 ， 于是
（5-5）
R1 C1
R2 C2
（5-6） 图5-2 交流电桥
可见，要使交流电桥平衡，需同时满足电阻平衡和电容 平衡两个条件。
p.6
理论力学
三、温度效应的补偿
理论力学
任何导电材料都有电阻温度效应，即其电阻会随环境温度改变而变 化，应变片丝栅材料也不例外。这种由温度改变引起的电阻变化与由变 形引起的电阻变化叠加，将引起测量误差。
为半桥接法。在半桥接法中，设电阻应变片受力变形后电阻改变量为
△Rl、△R2，而R3和R4电阻不变，则有
仪 1 2
(5-4)
p.5
理论力学
二、交流电桥
理论力学
如图5-2所示，图中C1、 C2为电 阻应变片本身及连接导线的分布 电容。对于半桥接法，R3和R4为 应变仪内部精密无感电阻，可看 作是纯阻性的，由电桥平衡条件
（4）低通滤波器 低通滤波器的作用是将由相敏检波器输出信号中的高频载波成分滤
掉，使放大后的信号与原应变形状相同。
（5）输出电路 动态应变仪将信号输出给记录仪器，各类记录仪器的输入阻抗不
同，如光线示波仪为低阻抗，而磁带记录仪为高阻抗，因此，要求电 阻应变仪有两种输出电路以满足不同记录仪器的要求。Y6D－3A只有一 种低阻的输出电路，而YD－5有两种输出电路，扩大了应变仪的使用范 围。
值的电阻应变片时，应对测量结果进行修正。
6．灵敏度 (mA/με或mV/με) 灵敏度是指应变仪输出端接有额定负载时，输出电流（或电压）与被
测应变的关系。当应变在一定范围内，输出电流与被测应变保持线性关系 时，输出电流（或电压）与应变的比值称为应变仪的灵敏度。例如Y6D－ 3A动态应变仪的灵敏度为0.1 mA／（额定负载为16Ω）。
R3 )]E
R1R3 R2 R4 (R1 R2 )(R4 R3 )
E
（a）
当 UDB 0 时，R1R3 R2 R4 ，电桥平衡。若各电阻分别有增量 R1 、R2 、R3 和 R4 时，输出端有不平衡桥压 UDB 输出。
U DB