
一、锐角三角函数真题与模拟题分类汇编(难题易错题)
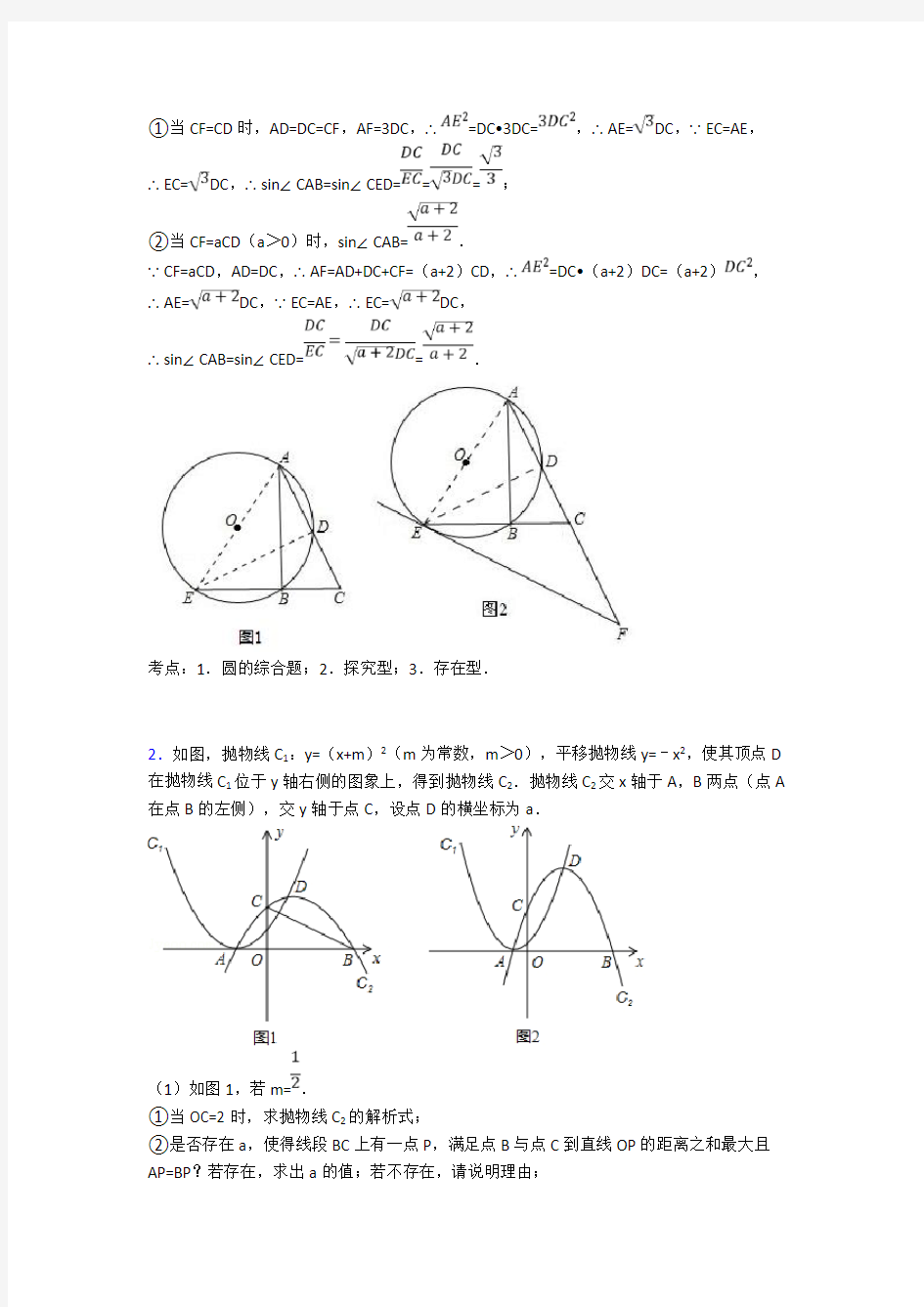
1.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O 于点E.
(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;
(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.
①若CF=CD时,求sin∠CAB的值;
②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)
【答案】(1)AE=CE;(2)①;②.
【解析】
试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于
AD=DC,根据垂直平分线的性质可得AE=CE;
(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得
∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD?AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得
sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.
试题解析:(1)AE=CE.理由:
连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,
∴AE=CE;
(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,
∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD?AF.
①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC?3DC=,∴AE=DC,∵EC=AE,
∴EC=DC,∴sin∠CAB=sin∠CED===;
②当CF=aCD(a>0)时,sin∠CAB=.
∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC?(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,
∴sin∠CAB=sin∠CED==.
考点:1.圆的综合题;2.探究型;3.存在型.
2.如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D 在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A 在点B的左侧),交y轴于点C,设点D的横坐标为a.
(1)如图1,若m=.
①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=2﹣m(0<m<)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
【答案】(1) ①y=﹣x2+x+2.②.(2)P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).
【解析】
试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C (0,2)在C2上,求出抛物线C2的解析式;
②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;
(2)解题要点有3个:
i)判定△ABD为等边三角形;
ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;
iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.
试题解析:(1)当m=时,抛物线C1:y=(x+)2.
∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+)2(I).
①∵OC=2,∴C(0,2).
∵点C在抛物线C2上,
∴﹣(0﹣a)2+(a+)2=2,
解得:a=,代入(I)式,
得抛物线C2的解析式为:y=﹣x2+x+2.
②在(I)式中,
令y=0,即:﹣(x﹣a)2+(a+)2=0,解得x=2a+或x=﹣,∴B(2a+,0);
令x=0,得:y=a+,∴C(0,a+).
设直线BC的解析式为y=kx+b,则有:
,解得,
∴直线BC的解析式为:y=﹣x+(a+).
假设存在满足条件的a值.
∵AP=BP,
∴点P在AB的垂直平分线上,即点P在C2的对称轴上;
∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,
∴OP⊥BC.
如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,
则OP⊥BC,OE=a.
∵点P在直线BC上,
∴P(a,a+),PE=a+.
∵tan∠EOP=tan∠BCO=,
∴,
解得:a=.
∴存在a=,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP"
(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+m)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.
令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).
∵OB=2﹣m,
∴2a+m=2﹣m,
∴a=﹣m.
∴D(﹣m,3).
AB=OB+OA=2﹣m+m=2.
如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=,OE=OB﹣BE=﹣m.
∵tan∠ABD=,
∴∠ABD=60°.
又∵AD=BD,∴△ABD为等边三角形.
作∠ABD的平分线,交DE于点P1,则P1E=BE?tan30°=×=1,
∴P1(﹣m,1);
在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.
在Rt△BEP2中,P2E=BE?tan60°=?=3,
∴P2(﹣m,﹣3);
易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2,且P3P4∥x轴.
∴P3(﹣﹣m,3)、P4(3﹣m,3).
综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,
其坐标为:P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).
【考点】二次函数综合题.
3.如图,矩形OABC中,A(6,0)、C(0,3、D(0,3),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60o.
(1)点B的坐标是,∠CAO= o,当点Q与点A重合时,点P的坐标
为;
(2)设点P的横坐标为x,△OPQ与矩形OABC重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
【答案】(1)(6,23). 30.(3,33)(2)
()
()
()
()
2
43
x430x3
3
31333
x x3x5
S{
23
x1235x9
3
543
x9
+≤≤
-+-<≤
=
-+<≤
>
【解析】
解:(1)(6,23). 30.(3,33).
(2)当0≤x≤3时,
如图1,
OI=x,IQ=PI?tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA,
可得
EF PE DC31
==
OQ PO DO3
33
==,∴EF=
1
3
(3+x),
此时重叠部分是梯形,其面积为:
EFQO
14343
S S EF OQ OC 3x x 432
33
==+?=+=+梯形()()
当3<x≤5时,如图2,
()HAQ EFQO EFQO 221
S S S S AH AQ
2
43331333 x 43x 3=x x 32232
?=-=-??=+---+
-梯形梯形。
当5<x≤9时,如图3,
12S BE OA OC 312x 23
23 =x 123=+?=--+()()
。
当x >9时,如图4,
111833
S OA AH 6=
22x x
=
?=??. 综上所述,S 与x 的函数关系式为:
()
()
()
()
2
43
x430x 3
3
31333
x x 3x5
232
S{
23
x1235x9
3
543
x9
x
+≤≤
-+-<≤
=
-+<≤
>
.
(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标:
∵四边形OABC是矩形,∴AB=OC,OA=BC,
∵A(6,0)、C(0,23),∴点B的坐标为:(6,23).
②由正切函数,即可求得∠CAO的度数:
∵OC233
tan CAO==
OA63
∠=,∴∠CAO=30°.
③由三角函数的性质,即可求得点P的坐标;如图:当点Q与点A重合时,过点P作PE⊥OA于E,
∵∠PQO=60°,D(0,33),∴PE=33.
∴
PE
AE3
tan60
==.
∴OE=OA﹣AE=6﹣3=3,∴点P的坐标为(3,33).
(2)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案.
4.如图,已知点从出发,以1个单位长度/秒的速度沿轴向正方向运动,以
为顶点作菱形,使点在第一象限内,且;以为圆心,为半径作圆.设点运动了秒,求:
(1)点的坐标(用含的代数式表示);
(2)当点在运动过程中,所有使与菱形的边所在直线相切的的
值.
【答案】解:(1)过作轴于,
,,
,,
点的坐标为.
(2)①当与相切时(如图1),切点为,此时,
,,
.
②当与,即与轴相切时(如图2),则切点为,,
过作于,则,
,.
③当与所在直线相切时(如图3),设切点为,交于,
则,,
.
过作轴于,则,
,
化简,得,
解得,
,
.
所求的值是,和.
【解析】
(1)过作轴于,利用三角函数求得OD、DC的长,从而求得点的坐标
⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=oc/op,表示出OC,
等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
5.如图,已知正方形在直角坐标系中,点分别在轴、轴的正半轴上,点在坐标原点.等腰直角三角板的直角顶点在原点,分别在上,且
将三角板绕点逆时针旋转至的位置,连结
(1)求证:
(2)若三角板绕点逆时针旋转一周,是否存在某一位置,使得若存在,请求出此时点的坐标;若不存在,请说明理由.
【答案】(1)证明见解析(2)存在,或
【解析】
(1)证明:∵四边形为正方形,∴
∵三角板是等腰直角三角形,∴
又三角板绕点逆时针旋转至的位置时,∴···························· 3分
(2)存在.································· 4分
∵
∴过点与平行的直线有且只有一条,并与垂直,
又当三角板绕点逆时针旋转一周时,则点在以为圆心,以为半径的圆上,························ 5分
∴过点与垂直的直线必是圆的切线,又点是圆外一点,过点与圆相切的直线有且只有2条,不妨设为和
此时,点分别在点和点,满足
·························· 7分
当切点在第二象限时,点在第一象限,
在直角三角形中,
∴∴
∴点的横坐标为:
点的纵坐标为:
∴点的坐标为··························· 9分
当切点在第一象限时,点在第四象限,
同理可求:点的坐标为
综上所述,三角板绕点逆时针旋转一周,存在两个位置,使得此时点的坐标为或································ 11分
(1)根据旋转的性质找到相等的线段,根据SAS定理证明;
(2)由于△OEF是等腰Rt△,若OE∥CF,那么CF必与OF垂直;在旋转过程中,E、F的轨迹是以O为圆心,OE(或OF)长为半径的圆,若CF⊥OF,那么CF必为⊙O的切线,且切点为F;可过C作⊙O的切线,那么这两个切点都符合F点的要求,因此对应的E点也有两个;在Rt△OFC中,OF=2,OC=OA=4,可证得∠FCO=30°,即∠EOC=30°,已知了OE 的长,通过解直角三角形,不难得到E点的坐标,由此得解.
6.2018年12月10日,郑州市城乡规划局网站挂出《郑州都市区主城区停车场专项规划》,将停车纳入城市综合交通体系,计划到2030年,在主城区新建停车泊位33.04万个,2019年初,某小区拟修建地下停车库,如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度为1:3,DE =3米,点C在DE上,CD=0.5米,CD是限高标志屏的高度(标志牌上写有:限高米),如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据2≈1.41,3≈1.73)
【答案】该停车库限高约为2.2米.
【解析】
【分析】
据题意得出
3
tan
3
B ,即可得出tan A,在Rt△ADE中,根据勾股定理可求得DE,即可
得出∠1的正切值,再在Rt△CEF中,设EF=x,即可求出x,从而得出CF3的长.【详解】
解:由题意得,
3 tan
3
B
∵MN∥AD,
∴∠A=∠B,
∴tan A=3,
∵DE⊥AD,
∴在Rt△ADE中,tan A=DE
AD
,
∵DE=3,
又∵DC=0.5,
∴CE=2.5,
∵CF⊥AB,
∴∠FCE+∠CEF=90°,
∵DE⊥AD,
∴∠A+∠CEF=90°,
∴∠A=∠FCE,
∴tan∠FCE=3
3
.
在Rt△CEF中,设EF=x,CF=3x(x>0),CE=2.5,
代入得(5
2
)2=x2+3x2,
解得x=1.25,
∴CF=3x≈2.2,
∴该停车库限高约为2.2米.
【点睛】
本题考查了解直角三角形的应用,坡面坡角问题和勾股定理,解题的关键是坡度等于坡角的正切值.
7.如图①,抛物线y=ax2+bx+c经过点A(﹣2,0)、B(4,0)、C(0,3)三点.
(1)试求抛物线的解析式;
(2)点P 是y 轴上的一个动点,连接PA ,试求5PA+4PC 的最小值;
(3)如图②,若直线l 经过点T (﹣4,0),Q 为直线l 上的动点,当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时,试求直线l 的解析式. 【答案】(1)233
384
y x x =-++;(2)5PA+4PC 的最小值为18;(3)直线l 的解析式为3
34
y x =
+或3
34
y x =--.
【解析】 【分析】
(1)设出交点式,代入C 点计算即可 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ,易证△CDP ∽△COB ,得到比例式PC PD BC OB =,得到PD=4
5
PC ,所以5PA+4PC =5(PA+
4
5
PC )=5(PA+PD ),当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小,利用等面积法求出AE=
18
5
,即最小值为18 (3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆, 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90°,即∠AQB =90°时,只有一个满足条件的点Q ,∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个;此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ,利用cos ∠QFT 求出QG ,分出情况Q 在x 轴上方和x 轴下方时,分别代入直接l 得到解析式即可 【详解】
解:(1)∵抛物线与x 轴交点为A (﹣2,0)、B (4,0) ∴y =a (x+2)(x ﹣4) 把点C (0,3)代入得:﹣8a =3 ∴a =﹣
38
∴抛物线解析式为y =﹣
38(x+2)(x ﹣4)=﹣38x 2+34
x+3 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ∴∠CDP =∠COB =90° ∵∠DCP =∠OCB ∴△CDP ∽△COB ∴
PC PD
BC OB
= ∵B (4,0),C (0,3)
∴OB =4,OC =3,BC ∴PD =
45
PC
∴5PA+4PC =5(PA+
4
5
PC )=5(PA+PD ) ∴当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小 ∵A (﹣2,0),OC ⊥AB ,AE ⊥BC ∴S △ABC =12AB?OC =1
2
BC?AE ∴AE =
6318
55
AB OC BC ?== ∴5AE =18
∴5PA+4PC 的最小值为18.
(3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,
∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90° ∴∠AQB =90°时,只有一个满足条件的点Q
∵当Q 在⊙F 上运动时(不与A 、B 重合),∠AQB =90° ∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个 此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ∴∠FQT =90°
∵F 为A (﹣2,0)、B (4,0)的中点 ∴F (1,0),FQ =FA =3 ∵T (﹣4,0) ∴TF =5,cos ∠QFT =
3
5
FQ TF = ∵Rt △FGQ 中,cos ∠QFT =3
5
FG FQ = ∴FG =
35FQ =95
∴x Q =1﹣9
455=-,
QG 125== ①若点Q 在x 轴上方,则Q (412
55
-,) 设直线l 解析式为:y =kx+b
∴404125
5k b k b -+=???-+=?? 解得:343k b ?=?
?
?=? ∴直线l :3
34
y x =
+ ②若点Q 在x 轴下方,则Q (41255
--,
)
∴直线l :3
34
y x =-
- 综上所述,直线l 的解析式为3
34
y x =
+或3
34
y x =--
【点睛】
本题是二次函数与圆的综合题,同时涉及到三角函数、勾股定理等知识点,综合度比较高,需要很强的综合能力,第三问能够找到满足条件的Q 点是关键,同时不要忘记需要分情况讨论
8.如图,正方形OABC 的顶点O 与原点重合,点A ,C 分别在x 轴与y 轴的正半轴上,点
A 的坐标为(4,0),点D 在边A
B 上,且tan ∠AOD =
1
2
,点E 是射线OB 上一动点,EF ⊥x 轴于点F ,交射线OD 于点G ,过点G 作GH ∥x 轴交AE 于点H . (1)求B ,D 两点的坐标;
(2)当点E 在线段OB 上运动时,求∠HDA 的大小;
(3)以点G 为圆心,GH 的长为半径画⊙G .是否存在点E 使⊙G 与正方形OABC 的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E 的坐标.
【答案】(1)B (4,4),D (4,2);(2)45°;(3)存在,符合条件的点为(8﹣
2,8﹣2)或(2,2)或42164216++??或16421642,77?-- ??
,理由见解析 【解析】 【分析】
(1)由正方形性质知AB=OA=4,∠OAB=90°,据此得B (4,4),再由tan ∠AOD= 1
2
得AD=
1
2
OA=2,据此可得点D 坐标; (2)由1tan 2GF GOF OF ∠==知GF=1
2
OF ,再由∠AOB=∠ABO=45°知OF=EF ,即GF=
1
2
EF ,根据GH ∥x 轴知H 为AE 的中点,结合D 为AB 的中点知DH 是△ABE 的中位线,即HD ∥BE ,据此可得答案;
(3)分⊙G 与对角线OB 和对角线AC 相切两种情况,设PG=x ,结合题意建立关于x 的方程求解可得. 【详解】
解:(1)∵A (4,0), ∴OA =4,
∵四边形OABC 为正方形, ∴AB =OA =4,∠OAB =90°, ∴B (4,4),
在Rt △OAD 中,∠OAD =90°, ∵tan ∠AOD =12
, ∴AD =
12OA =1
2
×4=2, ∴D (4,2);
(2)如图1,在Rt△OFG中,∠OFG=90°
∴tan∠GOF=GF
OF =
1
2
,即GF=
1
2
OF,
∵四边形OABC为正方形,
∴∠AOB=∠ABO=45°,
∴OF=EF,
∴GF=1
2
EF,
∴G为EF的中点,
∵GH∥x轴交AE于H,
∴H为AE的中点,
∵B(4,4),D(4,2),
∴D为AB的中点,
∴DH是△ABE的中位线,
∴HD∥BE,
∴∠HDA=∠ABO=45°.
(3)①若⊙G与对角线OB相切,
如图2,当点E在线段OB上时,
过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG2x,OF=EF=2x,
∵OA=4,
∴AF=4﹣2,
∵G为EF的中点,H为AE的中点,∴GH为△AFE的中位线,
∴GH=1
2AF=
1
2
×(4﹣22x)=2﹣2x,
则x=2﹣2x,
解得:x=22﹣2,
∴E(8﹣42,8﹣42),
如图3,当点E在线段OB的延长线上时,
x=2x﹣2,
解得:x=2+2,
∴E(8+42,8+42);
②若⊙G与对角线AC相切,
如图4,当点E在线段BM上时,对角线AC,OB相交于点M,
过点G作GP⊥OB于点P,设PG=x,可得PE=x,
EG=FG2,
OF=EF=2x,
∵OA=4,
∴AF=4﹣2,
∵G为EF的中点,H为AE的中点,
∴GH为△AFE的中位线,
∴GH =
12AF =1
2
×(4﹣22x )=2﹣2x , 过点G 作GQ ⊥AC 于点Q ,则GQ =PM =3x ﹣22, ∴3x ﹣22=2﹣2x , ∴422
7
x +=
, ∴42164216,77E ??++ ? ???
; 如图5,当点E 在线段OM 上时,
GQ =PM =22﹣3x ,则22﹣3x =2﹣2x , 解得422
7
x -=
, ∴16421642,77E ??
-- ? ???
; 如图6,当点E 在线段OB 的延长线上时,
3x ﹣22x ﹣2, 解得:422
7
x =
(舍去); 综上所述,符合条件的点为(8﹣2,8﹣2)或(2,2)或
三角形 一、选择题 1.若一个直角三角形的两边长为12和5,则第三边为() A. 13 B.13或 C. 13或5 D. 15 2.三角形的角平分线、中线和高() A. 都是射线 B. 都是直线 C. 都是线段 D. 都在三角形内 3.小明用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中框架△ABC的质量为840克,CF的质量为106克,则整个金属框架的质量为() A. 734克 B. 946克 C. 1052克 D. 1574克 4.到△ABC的三条边距离相等的点是△ABC的是() A. 三条中线的交点, B. 三条角平分线的交点 C. 三条高线的交点 D. 三条边的垂直平分线的交点 5.如图,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做使用的数学道理是() A. 两点之间线段最短 B. 三角形的稳定性 C. 两点确定一条直线 D. 长方形的四个角都是直角 6.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )
A. 100° B. 80° C. 70° D. 50° 7.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( ) A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 无法确定 8.已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( ) A. AB=DE,AC=DF- B. AC=EF,BC=DF - C. AB=DE,BC=EF- D. ∠C=∠F,AC=DF 9.若等腰三角形的顶角为80°,则它的一个底角度数为() A. 20° B. 50° C. 80° D. 100° 10.如图,点M是边长为4cm的正方形的边AB的中点,点P是正方形边上的动点,从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动,则当点P逆时针旋转一周时,随着运动时间的增加,△DMP面积达到5cm2的时刻的个数是() A. 5 B. 4 C. 3 D. 2 二、填空题 11.在△ABC中,已知∠A=30°,∠B=70°,则∠C的度数是________。 12.将一副三角板如图叠放,则图中∠α的度数为________. 13.如图,点P为△ABC三条角平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD____________PF.
锐角三角函数 1.把Rt △ABC 各边的长度都扩大3倍得Rt △A ′B ′C ′,那么锐角A ,A ′的余弦值的关系为( ) A .cosA=cosA ′ B .cosA=3cosA ′ C .3cosA=cosA ′ D .不能确定 2.如图1,已知P 是射线OB 上的任意一点,PM ⊥OA 于M ,且PM :OM=3:4,则cos α的值等于( ) A .34 B .43 C .45 D .35 图1 图2 图3 图4 图5 3.在△ABC 中,∠C=90°,∠A ,∠B ,∠C 的对边分别是a ,b ,c ,则下列各项中正确的是( ) A .a=c ·sin B B .a=c ·cosB C .a=c ·tanB D .以上均不正确 4.在Rt △ABC 中,∠C=90°,cosA=23 ,则tanB 等于( ) A .35 B C .25 D 5.在Rt △ABC 中,∠C=90°,AC=5,AB=13,则sinA=______,cosA=______,?tanA=_______. 6.如图2,在△ABC 中,∠C=90°,BC :AC=1:2,则sinA=_______,cosA=______,tanB=______. 7.如图3,在Rt △ABC 中,∠C=90°,b=20,,则∠B 的度数为_______. 8.如图4,在△CDE 中,∠E=90°,DE=6,CD=10,求∠D 的三个三角函数值. 9.已知:α是锐角,tan α=724 ,则sin α=_____,cos α=_______. 10.在Rt △ABC 中,两边的长分别为3和4,求最小角的正弦值为 10.如图5,角α的顶点在直角坐标系的原点,一边在x 轴上,?另一边经过点P (2,,求角α的三个三角函数值. 12.如图,在△ABC 中,∠ABC=90°,BD ⊥AC 于D ,∠CBD=α,AB=3,?BC=4,?求sin α,cos α, tan α的值.
一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.已知:如图,在四边形 ABCD 中, AB ∥CD , ∠ACB =90°, AB=10cm , BC=8cm , OD 垂直平分 A C .点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s ;同时,点 Q 从点 D 出发,沿 DC 方向匀速运动,速度为 1cm/s ;当一个点停止运动,另一个点也停止运动.过点 P 作 PE ⊥AB ,交 BC 于点 E ,过点 Q 作 QF ∥AC ,分别交 AD , OD 于点 F , G .连接 OP ,EG .设运动时间为 t ( s )(0<t <5) ,解答下列问题: (1)当 t 为何值时,点 E 在 BAC 的平分线上? (2)设四边形 PEGO 的面积为 S(cm 2) ,求 S 与 t 的函数关系式; (3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由; (4)连接 OE , OQ ,在运动过程中,是否存在某一时刻 t ,使 OE ⊥OQ ?若存在,求出t 的值;若不存在,请说明理由. 【答案】(1)4s t =;(2)PEGO S 四边形2 31568 8 t t =-+ + ,(05)t <<;(3)5 2t =时, PEGO S 四边形取得最大值;(4)16 5 t = 时,OE OQ ⊥. 【解析】 【分析】 (1)当点E 在∠BAC 的平分线上时,因为EP ⊥AB ,EC ⊥AC ,可得PE=EC ,由此构建方程即可解决问题. (2)根据S 四边形OPEG =S △OEG +S △OPE =S △OEG +(S △OPC +S △PCE -S △OEC )构建函数关系式即可. (3)利用二次函数的性质解决问题即可. (4)证明∠EOC=∠QOG ,可得tan ∠EOC=tan ∠QOG ,推出EC GQ OC OG =,由此构建方程即可解决问题. 【详解】 (1)在Rt △ABC 中,∵∠ACB=90°,AB=10cm ,BC=8cm , ∴22108-=6(cm ), ∵OD 垂直平分线段AC , ∴OC=OA=3(cm ),∠DOC=90°, ∵CD ∥AB ,
《等腰三角形》经典题型拓展与提高专训 1. 如图,在△ABC中,∠BAC=120°,AD⊥BC于点D,且AB+BD=DC,求∠C的度数. 2. 如图,在△ABC中,∠BAC=2∠B,CD平分∠ACB交AB于D,求证:AC+AD=BC. 3.如图,在三角形ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF,求证:(1)DE=DF.(2)DE⊥DF 4. 如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC的中点,连接EF,ED,FD.
(1)求证:ED=EF. (2)若∠BAD=60°,AC平分∠BAD,AC=6,求DF的长. 5.如图,在等腰三角形ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=70°,若点P 是等腰三角形ABC的腰上的一点,则当△DEP是以∠EDP为顶角的等腰三角形时,求∠EDP的度数. 6. 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD, DM⊥BC,垂足为M,求证:M是BE的中点. 7. 如图,AB∥CD,∠1=∠2,AD=AB+CD, 求证:(1)BE=CE;(2)AE⊥DE;(3)AE平分∠BAD.
7. 8.如图,△ABC中,AC=2AB,AD平分∠BAC交BC于D,E是AD上一点,且EA=EC,求证:EB⊥AB. 9.如图1,已知Rt△ABC,∠ABC=90°,以AC,AB为边分别向形外作等边三角形ACD,ABF,连接CF,BD. (1)求证:CF=BD; (2)如图2,若∠BAC=30°,点H为AC的中点,连接FH,BH,DH,请直接写出与△ABC全等的所有三角形.
锐角三角函数 三只钟的故事 一只小钟被主人放在了两只旧钟当中,两只旧钟滴答、滴答的走着。 一只旧钟对小钟说:“来吧,你也该工作了。可是我有点担心,你走完三千两百万次以后,恐怕会吃不消的。” “天哪!三千两百万次。”小钟吃惊不已,“要我做这么大的事?办不到,办不到!”另一支旧钟说:“别 听他胡说八道,不用害怕,你只要每秒滴答摆一下就行了。” “天下哪有这么简单的事情?”小钟将信将疑,“如果这样,我就试试吧。”小钟很轻松地每秒滴答摆一 下,不知不觉中,一年过去了,它摆了三千两百万次。 成功就是这样,把简单的事做到极致,就能成功。 例1.在Rt△ABC中,∠C=90°,若sinA=,则cosB的值是() A.B.C.D. 例2.如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D.已知cos∠ACD=,BC=4,则AC的长为() A.1 B.C.3 D.
例3.cos 60°的值等于( ) A . B . C . D . 例4.如图,在半径为1的⊙O 中,∠AOB =45°,则sinC 的值为( ) A . B . C . D . 练习一 锐角三角函数 1.已知sinA= 2 1 (∠A 为锐角),则∠A=_________,cosA_______,tanA=__________. 2.在Rt △ABC 中,∠C 为直角,1a =,2b =,则cosA=________,tanA=_________. 3.在Rt △ABC 中,∠C 为直角,AB=5,BC=3,则sinA=________, tanA=_________. 4.在Rt △ABC 中,∠C 为直角,∠A=30o,4b =,则a =__________,c =__________. 5.在Rt △ABC 中,∠C 为直角,若sinA= 5 3 ,则cosB=_________. 6.已知cosA= 2 3 ,且∠B=90o-∠A ,则sinB=__________. 7.若∠A 是锐角,且cosA=sinA ,则∠A 的度数是( ) A 、30o B 、45o C 、60o D 、不能确定 8.如图,电线杆AB 的中点C 处有一标志物,在地面D 点处测得标志物的仰角为45°,若点D 到电线杆底部点B 的距离为 a ,则电线杆AB 的长可表示为 A .a B .2a C .3 2a D .52 a D C B A
初中数学锐角三角函数的真题汇编含答案 一、选择题 1.将一副直角三角板如图放置,点C在FD的延长上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=122,则CD的长为() A.43B.12﹣43C.12﹣63D.63 【答案】B 【解析】 【分析】 过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=60°,进而可得出答案. 【详解】 解:过点B作BM⊥FD于点M, 在△ACB中,∠ACB=90°,∠A=45°,AC=122, ∴BC=AC=122. ∵AB∥CF, ∴BM=BC×sin45°= 2 12212 ?= CM=BM=12, 在△EFD中,∠F=90°,∠E=30°, ∴∠EDF=60°, ∴MD=BM÷tan60°=43, ∴CD=CM﹣MD=12﹣43. 故选B. 【点睛】 本题考查了解直角三角形,难度较大,解答此类题目的关键根据题意建立直角三角形利用所学的三角函数的关系进行解答. 2.在课外实践中,小明为了测量江中信号塔A离河边的距离AB,采取了如下措施:如
图在江边D 处,测得信号塔A 的俯角为40?,若55DE =米,DE CE ⊥,36CE =米, CE 平行于AB ,BC 的坡度为1:0.75i =,坡长140BC =米,则AB 的长为( )(精确到0.1米,参考数据:sin 400.64?≈,cos400.77?≈,tan 400.84?≈) A .78.6米 B .78.7米 C .78.8米 D .78.9米 【答案】C 【解析】 【分析】 如下图,先在Rt △CBF 中求得BF 、CF 的长,再利用Rt △ADG 求AG 的长,进而得到AB 的长度 【详解】 如下图,过点C 作AB 的垂线,交AB 延长线于点F ,延长DE 交AB 延长线于点G ∵BC 的坡度为1:0.75 ∴设CF 为xm ,则BF 为0.75xm ∵BC=140m ∴在Rt △BCF 中,()2 220.75140x x +=,解得:x=112 ∴CF=112m ,BF=84m ∵DE ⊥CE ,CE ∥AB ,∴DG ⊥AB ,∴△ADG 是直角三角形 ∵DE=55m ,CE=FG=36m ∴DG=167m ,BG=120m 设AB=ym ∵∠DAB=40° ∴tan40°= 167 0.84120 DG AG y ==+ 解得:y=78.8 故选:C 【点睛】 本题是三角函数的考查,注意题干中的坡度指的是斜边与水平面夹角的正弦值.
2016年中考数学相似三角形专题复习(一) 一、填空题 1.下面图形中,相似的一组是___________. (1) (2) (1) (2) (3) (4) 2.若x ∶(x+1)=6∶9,则x= . 3.已知线段a 、b 、c 、d 成比例,且a=6,b=9, c=12,则d= 4.在比例尺为1:10000的地图上,量得两 点之间的直线距离是2cm ,则这两地的实际 距离是________米 5.如图,两个五边形是相似形,则=a ,=c ,α= ,β= . 6. 已知△ABC ∽△DEF,AB=21cm,DE=28cm,则△ABC 和△DEF 的相似比为 . 7.△ABC 的三边长分别为 2、10、3,△ C B A ''的两边长分别为1和5,若△ABC ∽△C B A '', 则△C B A ''的第三条边长为 . 8.如图,△ABC ∽△CDB ,且AC =4,BC =3, 则BD =_________. 9.若一等腰三角形的底角平分线与底边围成的三角形与原图形相似,?则等腰三角形顶角为________度. 10.△ABC 的三边之比为3:5:6,与其相似的△DEF 的最长边是24cm,那么它的最短边长是 ,周长是 . 二、选择题 11.已知4x -5y=0,则(x+y)∶(x -y)的值为( ) A. 1∶9 B. -9 C. 9:1 D. -1∶9 12.已知,线段AB 上有三点C 、D 、E ,AB=8,AD=7,CD=4,AE=1,则比值不为1/2的线段比为( ) A.AE :EC B.EC :CD C.CD :AB D.CE :CB ╮ 23a c β 1550 950 1150 12 5 7αb ╭╮ ╯650 1150 第5题图 B C D 第8题图
2018中考数学专题练习《锐角三角函数》 (时间:100分钟 满分:120分) 一、选择题(本大题共10小题,每小题3分,共30分) 1.下列各数是有理数的是( ) A. B. 4π C. sin 45? D. 1 cos60? 2一个公共房门前的台阶高出地面1.2米,台阶拆除并改造成供轮椅行走的斜坡,数据如图1所示,则下列关系或说法正确的是( ) A.斜坡AB 的坡度是10o B.斜坡AB 的坡度是tan10? C. 1.2tan10AC =?米 D. 1.2 cos10AB = ? 米 3.在ABC ?中,A ∠,B ∠都是锐角,且1 sin 2 A = ,cos 2B =,则ABC ?三个角 的大小关系是( ) A. C A B ∠>∠>∠ B. B C A ∠>∠>∠ C. A B C ∠>∠>∠ D. C B A ∠>∠>∠ 4.如图2,在R t A B C ?中,90A ∠=?,AD BC ⊥于点D ,:3:2BD CD =,则t a n B 的值是( ) A. 32 B. 2 3 C. D. 5.如图3,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线,交AB 的延长 线于点E ,30A ∠=?,则s sin E 的值为( ) A. 1 2 B. 2 C. D.
6.数学社团的同学们对某塔的高度进行了测量,如图4,他们在A 处仰望塔顶,测得仰角为30o,再往楼的方向前进60 m 至B 处,测得仰角为60o,若学生的身高忽略不计, 1.7≈,结果精确到1m ,则该楼的高度CD 为( ) A.47 m B.51 m C.53 m D.54 m 7.如图5,点O 是摩天轮的圆心,长为110米的AB 是其垂直地面的直径,小莹在地面C 点处利用测角仪测得摩天轮的最高点A 的仰角为33o,测得圆心O 的仰角为21o,则小莹所在C 点到直径AB 所在直线的距离约为(参考数据:tan330.65?≈,tan 210.38?≈)( ) 图 5 A.169米 B.204米 C.240米 D.407米 8.如图6,在ABC ?中,已知90ABC ∠=?,点D 沿BC 自B 向C 运动(点D 与点B , C 不重合),作BE AD ⊥于E ,CF AD ⊥交AD 的延长线于F ,则BE CF +的值( ) A.不变 B.增大 C.减小 D.先变大,再变小 9.如图7,轮船从B 处以每小时50海里的速度沿南偏东30o方向匀速航行,在B 处观测灯塔A 位于南偏东75o的方向上,轮船航行半小时到达C 处,在C 处观测灯塔A 位于北偏东60o的方向上,则C 处与灯塔A 的距离是( ) A. B.
解直角三角形 学习目标、重点、难点 【学习目标】 1.理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形. 2.会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决. 【重点难点】 1.直角三角形的解法. 2.三角函数在解直角三角形中的灵活运用. 3.实际问题转化成数学模型. 知识概览图 解直角三角形的定义:在直角三角形中,由已知元素求未知元 素的过程 三边关系:a 2+b 2=c 2(勾股定理) 两锐角关系:两锐角互余 边角关系:三角函数 30°角所对的直角边等于斜边的一 半 两边一角:由勾 股定理求另一边,再求角 一边一角:由三 角函数求另两边,再求角 新课导引 【生活链接】如右图所示,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°,现有一个长6 m 的梯子. (1)使用这个梯子最高可以安全攀上多高的墙?(结果保留小数点后一位) (2)当梯子底端距离墙面2.4 m 时,梯子与地面所成的角a 等于多少?这时人 解直角三角形 直角三角形的有关性质 解直角三角形的基本类型及方法
是否能够安全使用这个梯子?(结果保留整数) 【问题探究】对于问题(1),当梯子与地面所成的角α为75°时,梯子顶端与地面的距离是使用这个梯子所能安全攀到的最大高度,即在Rt△ABC中,已知∠A=75°,斜边AB=6,求∠A的对边BC的长.由sin A=BC AB ,得BC=AB2sin A=6sin75°.由计算器求得sin 75°≈0.97,∴BC≈630.97≈5.8(m).那么对于问题(2),该如何求解呢? 教材精华 知识点1 解直角三角形的概念 如图28-30所示,在Rt△ABC中,∠C=90°,∠A=50°,c =5,如何求∠B,a,b呢? 由∠A+∠B=90°,∠A=50°,得∠B=90°-∠A=40°. 由sin A=a c ,得a=c2sin A=52sin 50°≈530.7660=3.83. 由cos A=b c ,得b=c2cos A=52cos 50°≈530.6428=3.214.上述问题中,除直角外,已知一条边和一个锐角,求另外两条边和一个锐角,于是有: 一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出其余未知元素的过程,叫做解直角三角形. 拓展直角三角形中一共有六个元素,即三条边和三个角,除直角外,另外的五个元素中,只要已知一条边和一个角或两条边,就可以求出其余的所有未知元素. 知识点2 解直角三角形的理论依据 在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边. (1)三边之间的关系:a2+b2=c2(勾股定理). (2)两锐角之间的关系:∠A+∠B=90°. (3)边角之间的关系:sin A=a c ,cos A=b c ,tan A=a b ,sin B=b c ,cos B=a c ,tan B=b a . (4)直角三角形中的有关定理.
一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s). (1)若△BDE是以BE为底的等腰三角形,求t的值; (2)若△BDE为直角三角形,求t的值; (3)当S△BCE≤9 2 时,所有满足条件的t的取值范围(所有数据请保留准确值,参考 数据:tan15°=23 【答案】(1)33 2 ;(23秒或3秒;(3)6﹣3 【解析】 【分析】 (1)如图1,先由勾股定理求得AB的长,根据点A、E关于直线CD的对称,得CD垂直平分AE,根据线段垂直平分线的性质得:AD=DE,所以AD=DE=BD,由3,可得t 的值; (2)分两种情况: ①当∠DEB=90°时,如图2,连接AE,根据3t的值; ②当∠EDB=90°时,如图3,根据△AGC≌△EGD,得AC=DE,由AC∥ED,得四边形CAED 是平行四边形,所以AD=CE=3,即t=3; (3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE 面积的变化取决于以CE作底边时,对应高的大小变化, ①当△BCE在BC的下方时, ②当△BCE在BC的上方时, 分别计算当高为3时对应的t的值即可得结论. 【详解】 解:(1)如图1,连接AE, 由题意得:AD=t, ∵∠CAB=90°,∠CBA=30°, ∴BC=2AC=6, ∴22 63 3 ∵点A、E关于直线CD的对称,
∴CD垂直平分AE, ∴AD=DE, ∵△BDE是以BE为底的等腰三角形, ∴DE=BD, ∴AD=BD, ∴; (2)△BDE为直角三角形时,分两种情况: ①当∠DEB=90°时,如图2,连接AE, ∵CD垂直平分AE, ∴AD=DE=t, ∵∠B=30°, ∴BD=2DE=2t, ∴ ∴ ②当∠EDB=90°时,如图3, 连接CE, ∵CD垂直平分AE, ∴CE=CA=3, ∵∠CAD=∠EDB=90°, ∴AC∥ED, ∴∠CAG=∠GED, ∵AG=EG,∠CGA=∠EGD, ∴△AGC≌△EGD, ∴AC=DE, ∵AC∥ED, ∴四边形CAED是平行四边形, ∴AD=CE=3,即t=3; 综上所述,△BDE为直角三角形时,t3秒; (3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE 面积的变化取决于以CE作底边时,对应高的大小变化, ①当△BCE在BC的下方时,过B作BH⊥CE,交CE的延长线于H,如图4,当AC=BH=3时, 此时S△BCE=1 2 AE?BH= 1 2 ×3×3= 9 2 , 易得△ACG≌△HBG,∴CG=BG, ∴∠ABC=∠BCG=30°,
、选择题 A. 13 C. 13 或 5 2. 三角形的角平分线、中线和高( 克,CF 的质量为106克,则整个金属框架的质量为( 4. 到厶ABC 的三条边距离相等的点是厶 ABC 的是( 5. 如图,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做使用的数学道理是 6. 如图,△ ABC 内有一点 D,且 DA=DB=DC 若/ DAB=20,/ DAC=30,则/ BDC 的大小是( 三角形 1.若一个直角三角形的两边长为 12和 5,则第三边为 D. 15 A. 都是射线 B. 都是直线 C.都是线段 D. 都在三角形内 3. 小明用同种材料制成的金属框架如图所示,已知/ B=Z E , AB=DE BF=EC 其中框架厶ABC 的质量为840 A. 734 克 B. 946 克 C. 1052 克 D. 1574 克 A. 三条中线的交点, B. 三条角平分线的交点 C.三条高线的交点 D.三条边的垂直平分线的交点 A.两点之间线段最短 角都是直角 B.三角形的稳定性 C.两点确定一条直线 D.长方形的四个 B.13 或
A. 100° B. 80° C. 70° D. 50° 7. 若一个三角形的一个外角小于与它相邻的内角,则这个三角形是() A.直角三角形 B.锐角三角形 C. 钝角三角形 D.无法确定 8. 已知在△DEF中,/ A=Z D=9C°,则下列条件中不能判定△DEF全等的是() A. AB=DE AC=DF- B. AC=EF BC=DF - C. AB=DE BC=EF- D. / C=Z F , AC=DF 9. 若等腰三角形的顶角为80°,则它的一个底角度数为() A. 20° B. 50° C. 80° D. 100° 10. 如图,点M是边长为4cm的正方形的边AB的中点,点P是正方形边上的动点,从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动,则当点P逆时针旋转一周时,随着运动时间的增加,△ DMP 面积达到5cm2的时刻的个数是() D C A 冠B A. 5 B. 4 C. 3 D. 2 二、填空题 11. 在厶ABC中,已知/ A=30°,/ B=70°,则/ C的度数是______________ 12. 将一副三角板如图叠放,则图中/ a的度数为________ ?
初三数学锐角三角函数通用版 【本讲主要内容】 锐角三角函数 包括:正弦、余弦、正切。 【知识掌握】 【知识点精析】 1. 在Rt △ABC 中,∠C =90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA 。 即 c a A A sin == 斜边的对边∠;把∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即c b A A cos =∠=斜边的邻边;把∠A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即 b a A A A t an =∠∠=的邻边的对边。 2. 锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数。 3. 特殊角的三角函数值: 30° 45° 60° sin α 1 2 22 32 cos α 32 22 12 tan α 33 1 3 4. 记忆方法: 【解题方法指导】 例1. (2000年成都市)如图,在△ABC 中,∠C =90°,∠ABC =60°,D 是AC 的中点,那么tan ∠DBC 的值是________。 锐 角 α 三 角 函 数
分析:在Rt △ABC 中,由∠ABC =60°,可知3BC AC 60tan == ,即AC =3BC ,又CD = 1 2 AC ,tan ∠DBC 可求。 解:在△ABC 中, ∵∠C =90°,∠ABC =60°, ∴tan ∠ABC =tan60°=3BC AC =, ∴AC =3BC 。 又D 是AC 中点, ∴DC = 12AC =32 BC 。 ∴2 3 BC BC 23 BC DC DBC tan = ==∠。 评析:在解题中紧紧扣住tan α的定义。 例2. (2001年四川)在Rt △ABC 中 ,CD 是斜边AB 上的高,已知3 2 ACD sin = ∠,那么=AB BC ______。 分析:由Rt △ABC 中CD ⊥AB 于D ,可得∠ACD =∠B ,由sin ∠ACD = 2 3 ,那么sinB =23,设AC =2,AB =3,则BC =32522-=,则AB BC 可求。 解:∵∠ACB =90°,CD ⊥AB 于D , ∴∠ACD =∠B 。 又sin ∠ACD =sinB = 23 , 可设AC =2,AB =3, ∴BC =32522-=。
锐角三角函数 一.知识框架 二.知识概念 1.Rt △ABC 中 (1∠A 的对边与斜边的比值是∠A 的正弦,记作sinA = ∠A 的对边 斜边 (2∠A 的邻边与斜边的比值是∠A 的余弦,记作cosA = ∠A 的邻边斜边 (3∠A 的对边与邻边的比值是∠A 的正切,记作tanA = ∠A 的对边
∠A 的邻边 (4∠A 的邻边与对边的比值是∠A 的余切,记作cota = ∠A 的邻边∠A 的对边 2.特殊值的三角函数: 锐角三角函数(1 基础扫描 1. 求出下图中sinD ,sinE 的值. 2.把Rt △ABC 各边的长度都扩大2倍得Rt △A ′B ′ C ′,那么锐角A 、A ′的正弦值的关系为( . A . sinA =sinA ′ B . sinA =2sinA ′ C . 2sinA =sinA ′ D . 不能确定 3.在Rt △ABC 中,∠C=90°,若AB =5,AC =4,则sinB 的值是( A . 35
B . 45 C . 34 D . 4 3 4. 如图,△ABC 中,AB=25,BC=7,CA=24.求sinA 的值. 25 24 7C B A 5. 计算:sin30°·sin 60°+sin45°. 能力拓展 6. 如图,B 是线段AC 的中点,过点C 的直线l 与AC 成60°的角,在直线上取一点P ,连接AP 、PB ,使sin ∠APB=1 2,则满足条件的点P 的个数是( A 1个 B 2个 C 3个
D 不存在 7. 如图,△ABC 中,∠A 是锐角,求证:1 sin 2 ABC S AB AC A ?= ?? 8.等腰△ABC 中,AB=AC=5,BC=6,求sinA 、sinB . l C B A (第7题图 85 F E D 创新学习 9. 如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( A. B C.
中考数学专题复习 三角形 20XX 年10月22日伊智教育 例1、角平分线的性质 如图,将直角边AC=6cm,BC=8cm 的直角△ABC 纸片折叠,使点B 与点A 重合,折痕为DE, 则CD 等于( ) (A) 425 (B) 322 (C) 4 7 (D) 35 例2、直角三角形斜边上的中线等于斜边的一半; 如图所示,BD 、CE 是三角形ABC 的两条高,M 、N 分别是BC 、DE 的中点。求证:MN ⊥DE C 堂上练习 1、如图,四边形ABCD 中,∠DAB=∠DCB=90o ,点M 、N 分别是BD 、AC 的中点。MN 、AC 的位置关系如何?证明你的猜想。 2、已知梯形ABCD 中,∠B+∠C =90o ,EF 是两底中点的连线,试说明AB -AD =2EF A(B) C D E
F C B 3、过矩形ABCD 对角线AC 的中点O 作EF ⊥AC 分别交AB 、DC 于E 、F ,点G 为AE 的中点,若∠AOG =30o 求证:3OG=DC A 4、如图所示;过矩形ABCD 的顶点A 作一直线,交BC 的延长线于点E ,F 是AE 的中点,连接FC 、FD 。 求证:∠FDA=∠ FCB A 例3、三角形(梯形)中位线 (a)如图,△ABC 的三边长分别为AB =14,BC =16,AC =26,P 为∠A 的平分线AD 上一点,且BP ⊥AD ,M 为BC 的中点,求PM 的长。(PM =6)
(b)如图,梯形ABCD 中,AD ∥BC ,M 是腰AB 的中点,且AD +BC =DC 。求证:MD ⊥MC 。 堂上练习 1、三角形各边长为5、9、12,则连结各边中点所构成的三角形的周长是 。 2、若梯形中位线被它的两条对角线分成三等分,则梯形的两底之比为 。 3、等腰梯形的两条对角线互相垂直,中位线长为8cm ,则它的高为( ) A 、4 cm B 、24cm C 、8cm D 、28cm 4、如图,已知△ABC 的周长为1,连结△ABC 三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,第2004个三角形的周长为( ) A 、 20031 B 、20041 C 、200321 D 、20042 1
中考数学真题汇编:锐角三角函数 (WORD版本真题试卷+名师解析答案,建议下载保存) 一、选择题 1.的值等于() A. B. C. 1 D. 【答案】B 2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是() A. B. C. D. 【答案】B 3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( ) A.3 B. C. D. 【答案】D
4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,) A. 12.6米 B. 13.1米 C. 14.7米 D. 16.3米 【答案】B 5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)() A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里 【答案】B 6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为() A. B. C. D. 【答案】B
7. 如图,已知在中,,,,则的值是() A. B. C. D. 【答案】A 8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)() A. B. C. D. h?cosα 【答案】B 二、填空题 9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行 ________小时即可到达(结果保留根号) 【答案】 10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
E C B F A D 1) 若一凸多边形的内角和等于它的外角和,则它的边数是___________. 2) 等腰三角形的底角为75°,顶角是 °,顶角的余弦值是 。 3) 如图,EF 是△ABC 的中位线,若BC =2 cm ,则EF______cm 。 4) 对角线长分别为6cm 和8cm 的菱形的边长为_____________cm . 5) 已知梯形的上底长为3cm ,中位线长为5cm ,那么下底长为______________cm . 6) 已知∠α与∠β互余,且∠α=15°,则∠β的补角为 度. 7) 如图,梯形ABCD 中,AD ∥BC ,∠D=Rt ∠,BC=CD=12,∠ABE=45°,点E 在DC 上,AE ,BC 的延长线相交于点F ,若AE=10,则S △ADE +S △CEF 的值是 . 8) △ABC 中,∠A =∠B +∠C ,则∠A =____. 9) 在Rt ⊿ABC 中,?=∠90C ,如果AB = 6,21 sin =A ,那么BC = ________. 10) 在Rt ΔABC 中,∠C=900 ,AB=3,BC=1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是 ; 11) 圆锥可以看成是直角三角形以它的一条直角边所在的直线为轴,其余各边旋转一周而成的面所围成的几何体,那么圆台可以看成是 所在的直线为轴,其余各边旋转一周而成的面所围成的几何体;如果将一个半圆以它的直径所在的直线为轴旋转一周,所得的几何体应是 . 12) 当图中的∠1和∠2满足 时,能使OA ⊥OB.(只需填上一个 条件即可) 13) 已知等腰三角形的一边等于3,一边等于6,则它的周长________ 14) 圆锥的底面圆的直径是6cm ,高为4cm ,那么这个圆锥侧面展开图的面积为 cm 2。(按四舍五入法,结果保留两个有效数字,π取 3.14) 15) 如图,在坡度1:2的山坡一种树。要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是 米; 16) 如图2,某宾馆在重新装修后,准备在大厅的楼梯上铺上某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要 _元。 17) 如图,把大小为4×4的正方形方格图形分割成两个全等图形,例如图1,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形图形分割成两个全等图形。 18) 在四边形ABCD 中,若分别给出四个条件:①AB ∥CD ,②AD =BC ,③∠A =∠C ,④AB =CD .现以其中的两个为一组,能判定四边形ABCD 为平行四边形的条件是________(只填序 号,填上一组即可,不必考虑所有可能情况). 19) 不能判定四边形ABCD 为平行四边形的题设是( ) 1. AB=CD AD=BC B 、AB=CD AB ∥CD C 、AB=CD AD ∥BC D 、AB ∥CD AD ∥BC 20) 如图,平行四边形ABCD 中,AE 平分∠DAB ,∠B=100°,则∠DAE 等于( )(A )100°(B )80°(C )60°(D )40° 21) 边长为a 的正六边形的边心距为( ) 2 1A B O E B A C D
中考数学真题汇编:锐角三角函数 一、选择题 1.的值等于() A. B. C. 1 D. 【答案】B 2.如图,过点,,,点是轴下方上的一点,连接,, 则的度数是() A. B. C. D. 【答案】B 3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的 直径是( ) A.3 B.
C. D. 【答案】D 4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度 ,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为 () (参考数据:,,) A. 12.6米 B. 13.1 米 C. 14.7 米 D. 16.3米 【答案】B 5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后 两位)(参考数据:)() A. 4.64海里 B. 5.49海 里 C. 6.12海 里 D. 6.21海里 【答案】B
6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为() A. B. C. D. 【答案】B 7. 如图,已知在中,,,,则的值是() A. B. C. D. 【答案】A 8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()
A. B. C. D. h?cosα 【答案】B 二、填空题 9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航 行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在 北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航 行________小时即可到达 (结果保留根号) 【答案】 10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。 【答案】 11.如图,把三角形纸片折叠,使点、点都与点重合,折痕分别为,,得到 ,若厘米,则的边的长为________厘米. 【答案】 12.如图,在菱形中,,分别在边上,将四边形沿翻折, 使的对应线段经过顶点,当时,的值为________.
《锐角三角函数》 一、选择题 1. 4 sin tan 5 ααα= 若为锐角,且,则为 ( ) 933425543 A B C D . . . . 2.在Rt △ABC 中,∠C = 90°,下列式子不一定成立的是( ) A .sinA = sin B B .cosA=sinB C .sinA=cosB D .∠A+∠B=90° 3.直角三角形的两边长分别是6,8,则第三边的长为( ) A .10 B .22 C .10或27 D .无法确定 4.在Rt △ABC 中,∠C=90°,当已知∠A 和a 时,求c ,应选择的关系式是( ) A .c = sin a A B .c =cos a A C .c = a ·tanA D .c = tan a A | 5、 45cos 45sin +的值等于( ) A. 2 B. 2 1 3+ C. 3 D. 1 6.在Rt △ABC 中,∠C=90°,tan A=3,AC 等于10,则S △ABC 等于( ) A. 3 B. 300 C. 50 3 D. 150 7.当锐角α>30°时,则cos α的值是( ) A .大于 12 B .小于12 C .大于3 D .小于3 8.小明沿着坡角为30°的坡面向下走了2米,那么他下降( ) A .1米 B .3米 C .23 D . 23 3 9.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=( ) (A )4 (B )5 (C )23 (D )83 3 \ 10.已知Rt △ABC 中,∠C=90°,tanA=4 3 ,BC=8,则AC 等于( ) A .6 B .32 3 C .10 D .12 二、填空题 11.计算2sin30°+2cos60°+3tan45°=_______. 12.若sin28°=cos α,则α=________. 13.已知△ABC 中,∠C=90°,AB=13,AC=5,则tanA=______.