
·125·
第11章 动量矩定理
一、是非题(正确的在括号内打“√”、错误的打“×”)
1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。 (×)
2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。(√)
3. 质点系动量矩的变化与外力有关,与内力无关。 (√)
4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。 (√)
5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。 (×)
6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。 (×)
7. 质点系对某点的动量矩定理e 1d ()d n
O
O i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。
(√)
8. 如图11.23所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+
221
3
ml mr =+,式中m 为AB 杆的质量。 (×) 9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1
d
()d n
P P i i t ==∑L M F 的形式,而
不需附加任何条件。
(×)
10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。 (×)
图11.23
二、填空题
1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。
2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。
3. 质点系的质量与质心速度的乘积称为质点系的动量。
4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的内力无关。
5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零,质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数
·126·
和等于零。
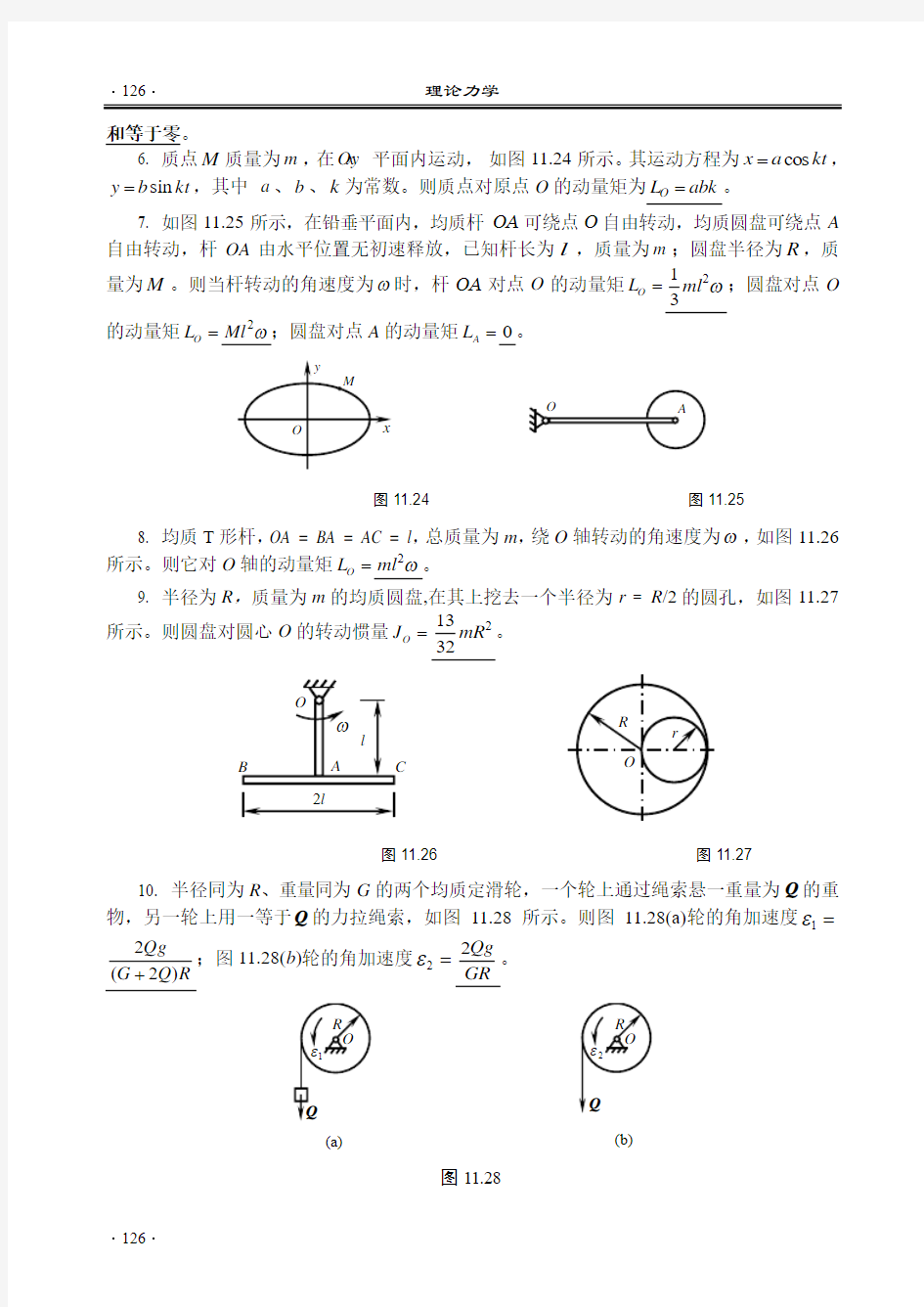
6. 质点M 质量为m ,在O x y 平面内运动,
如图11.24所示。其运动方程为kt a x cos =,kt b y sin =,其中 a 、b 、k 为常数。则质点对原点O 的动量矩为abk L O =。
7. 如图11.25所示,在铅垂平面内,均质杆OA 可绕点O 自由转动,均质圆盘可绕点A 自由转动,杆OA 由水平位置无初速释放,已知杆长为l ,质量为m ;圆盘半径为R ,质
量为M 。则当杆转动的角速度为ω时,杆OA 对点O 的动量矩O L =ω231
ml ;圆盘对点O
的动量矩O L =ω2Ml ;圆盘对点A 的动量矩A L =0。
图11.24 图11.25
8. 均质T 形杆,OA = BA = AC = l ,总质量为m ,绕O 轴转动的角速度为ω,如图11.26所示。则它对O 轴的动量矩O L =ω2ml 。
9. 半径为R ,质量为m 的均质圆盘,在其上挖去一个半径为r = R /2的圆孔,如图11.27
所示。则圆盘对圆心O 的转动惯量O J =232
13
mR 。
图11.26 图11.27
10. 半径同为R 、重量同为G 的两个均质定滑轮,一个轮上通过绳索悬一重量为Q 的重物,另一轮上用一等于Q 的力拉绳索,如图11.28所示。则图11.28(a)轮的角加速度1ε= R Q G Qg )2(2+;图11.28(b )
轮的角加速度2ε=GR
Qg
2。
(b) (a)
图11.28
·127·
三、选择题
1. 均质杆AB ,质量为m ,两端用张紧的绳子系住,绕轴O 转动,如图11.29所示。则杆AB 对O 轴的动量矩为 A 。
(A)
ω265ml (B) ω21213ml (C) ω234ml (D) ω212
1ml 2. 均质圆环绕z 轴转动,在环中的A 点处放一小球,如图11.30所示。在微扰动下,小
球离开A 点运动。不计摩擦力,则此系统运动过程中 B 。
(A) ω不变,系统对z 轴的动量矩守恒
(B) ω改变,系统对z 轴的动量矩守恒 (C) ω
不变,系统对z 轴的动量矩不守恒 (D) ω改变,系统对z 轴的动量矩不守恒
3. 跨过滑轮的轮绳,一端系一重物,另一端有一与重物重量相等的猴子,从静止开始以速度v 向上爬,如图11.31所示。若不计绳子和滑轮的质量及摩擦,则重物的速度 B 。
(A) 等于v ,方向向下 (B) 等于v ,方向向上 (C) 不等于v (D) 重物不动
图11.29 图11.30
4. 在图11.32中,摆杆OA 重量为G ,对O 轴转动惯量为J ,弹簧的刚性系数为k ,杆在铅垂位置时弹簧无变形。则杆微摆动微分方程为 D (设θθ=sin )。
(A) θθθGb ka J --=2 (B) θθθ
Gb ka J +=2 (C) θθθ
Gb ka J --=-2 (D) θθθGb ka J -=-2
图11.31 图11.32
5. 在图11.33中,一半径为R 。质量为m 的圆轮,在下列情况下沿水平面作纯滚动:(1)
·128·
轮上作用一顺时针的力偶矩为M 的力偶;(2) 轮心作用一大小等于/M R 的水平向右的力F 。若不计滚动摩擦,二种情况下 C 。
(A) 轮心加速度相等,滑动摩擦力大小相等 (B) 轮心加速度不相等,滑动摩擦力大小相等 (C) 轮心加速度相等,滑动摩擦力大小不相等 (D) 轮心加速度不相等,滑动摩擦力大小不相等
6. 如图11.34所示组合体由均质细长杆和均质圆盘组成,均质细长杆质量为M 1,长为L ,均质圆盘质量为M 2,半径为R ,则刚体对O 轴的转动惯量为 A 。
(A) 2222210)(21
3L R M R M L M J +++=
(B) 2222210)(21
12L R M R M L M J +++=
(C) 222221021
3L M R M L M J ++=
(D) 22222102
1
3R M R M L M J ++=
图11.33 图11.34
四、 计算题
11-1各均质物体的质量均为m ,物体的尺寸及绕固定轴转动角速度方向如图11.35所示。试求各物体对通过点O 并与图面垂直的轴的动量矩。
(a)
(c)
(b)
图11.35
解:(a )杆OA 对通过点O 并与图面垂直的轴的动量矩为
·129·
ωω22
1
mR J L O O =
= (b )圆盘对通过点O 并与图面垂直的轴的动量矩为
ωω22
1
mR J L O O ==
(c )圆盘对通过点O 并与图面垂直的轴的动量矩为
ωωω2222
3
)21(mR mR mR J L O O =+==
11-2 如图11.36所示,鼓轮的质量11800kg m =,半径025m r .=,对转轴O 的转动惯量2853kg m O J .=?。现在鼓轮上作用力偶矩0743kN m M .=?来提升质量22700kg m =的物体
A 。试求物体A 上升的加速度,绳索的拉力以及轴承O 的反力。绳索的质量和轴承的摩擦都忽略不计。
解:(1)选整体为研究对象,受力分析如图所示。应用质点系动量矩定理,有 gr m M r m J O 2022)(-=+ε
解得鼓轮转动的角加速度为
)/(21.325.027003.8525
.08.92700743022
2220s rad r m J gr m M O =?+??-=+-=ε 物体A 上升的加速度为
)/(8.02s m r a A ==ε
(2)要求绳索的拉力,可选物体 A 为研究对象,受力分析如图所示。应用质点运动微
分方程,有
g m F a m T 22-=
解得绳索的拉力为
)(62.288.027008.9270022kN a m g m F T =?+?=+=
(3)要求轴承O 的反力,可选鼓轮为研究对象,受力分析如图所示。应用质心运动定理,有
0=Ox F ,0'
1=--T Oy F g m F 解得 0=Ox
F ,)(26.46'1kN F g m F T Oy =+=
A
F g
A
g 2m
T F
A a
F g 1
'T
(b)
(c)
图11.36 图11.37
·130·
11-3 半径为R ,质量为m 的均质圆盘与长为l 、质量为M 的均质杆铰接,如图11.37所示。杆以角速度ω绕轴O 转动,圆盘以相对角速度r ω绕点A 转动,(1)r ωω=;(2)r ωω=-,试求系统对转轴O 的动量矩。
解:系统对转轴O 的动量矩是由杆对转轴O 的动量矩和圆盘对转轴O 的动量矩两部分组成。杆对转轴O 的动量矩为
ω23
1
Ml L O -=杆
(1)当r ωω=时,圆盘转动的绝对角速度为
a 2r ωωωω=+= 圆盘对转轴O 的动量矩为
ωωω2222
1
ml mR l mv mR L A a O --=?--=圆盘
故系统对转轴O 的动量矩为
ωωω2223
1
ml mR Ml L L L O O O ---=+=圆盘杆
(2)当r ωω=-时,圆盘转动的绝对角速度为 a 0r ωωω=+= 圆盘对转轴O 的动量矩为
ωω222
1
ml l mv mR L A a O -=?--=圆盘
故系统对转轴O 的动量矩为
ωω223
1
ml Ml L L L O O O --=+=圆盘杆
11-4 两小球C 、D 质量均为m ,用长为l 2的均质杆连接,杆的质量为M ,杆的中点固定在轴AB 上,CD 与轴AB 的夹角为θ,如图11.38所示。轴以角速度ω转动,试求系统对转轴AB 的动量矩。
解:杆CD 对转轴AB 的动量矩可表示为
θωωθ222sin 3
1
)sin (2Ml x l Mdx L l l O =?=?
-杆
球C 、D 对转轴AB 的动量矩可表示为
θω22sin ml L L D O C O ==球球
系统对转轴AB 的动量矩为
θωθω2222sin 2sin 3
1
ml Ml L L L L D O C O O O +=++=球球杆
11-5 小球M 系于线MOA 的一端,此线穿过一铅垂管道,如图11.39所示。小球M 绕轴沿半径MC R =的水平运动,转速为120r min n /=。今将线OA 慢慢拉下,则小球M 在半
径2
R
M'C '=的水平圆上运动,试求该瞬时小球的转速。
解:选小球为研究对象,小球受有重力和绳子拉力作用,受力分析如图所示。由于重力和绳子拉力对轴x 的矩均等于零,即0)(=∑
F x M ,可知小球对x 轴的动量矩保持守恒。即
·131·
有
2
'R mv mvR = 而R v ω=,2
''R
v ?
=ω,代入上式,有 4
'2
2
R R ωω=
故ωω4'=,即小球M 在半径2
R
M'C '=的水平圆上运动瞬时小球的转速为
min)/(4804'r n n ==
图11.38 图11.39
11-6 一直角曲架ADB 能绕其铅垂边AD 旋转,如图11.40所示。在水平边上有一质量为m 的物体C ,开始时系统以角速度0ω绕轴AD 转动,物体C 距D 点为a ,设曲架对AD 轴的转动惯量为z J ,求曲架转动的角速度ω与距离DC r =之间的关系。
解:选整体为研究对象,受力分析如图所示。从受力图可以看出,系统所受的全部外力对z 轴的矩等于零。系统对z 轴的动量矩也保持不变,即
ωω)()(202mr J ma J z z +=+
解得曲架转动的角速度ω与距离DC r =之间的关系为
02
2
ωωmr J ma J z z ++=
11-7 电动机制动用的闸轮重为W (可视为均质圆环),以角速度0ω绕轴转动,如图11.41所示。已知闸块与闸轮间的滑动摩擦系数为f ,闸轮的半径为r ,它对O 轴的转动惯量为2O J mr =,制动时间为0t ,设轴承中的摩擦不计。求闸块给闸轮的正压力N F 。
解:选闸轮为研究对象,受力分析如图(b )所示。我们可以应用动量矩定理来计算闸块给闸轮的正压力N F 。先计算制动后闸轮的角加速度,由运动学可知
000=+=t εωω
可知制动后闸轮的角加速度为
·132·
t t ωωε-
=-
=
式中负号表明真实的角加速度的转向与图中假设的转向相反,即闸轮作减速转动。然后应用动量矩定理,有
O d J F r ε=-
而d N F fF =,代入上式,可解得闸块给闸轮的正压力N F 为
N 0
Wr F fgt ω=
Az (a)
(b)
图11.40 图11.41
11-8 如图11.42所示两轮的半径为1R 、2R 。质量分别为1m 、2m 。两轮用胶带连接,各绕两平行的固定轴转动,若在第一轮上作用主动力矩M ,若在第二轮上作用阻力矩'M 。视圆轮为均质圆盘,胶带与轮间无滑动,胶带质量不计,试求第一轮的角加速度。
解:分别取两轮为研究对象,受力分析及运动分析如图(b)所示。对两轮分别应用动量矩定理,有
轮1: 11211)(R F F M J T T -+=ε
轮2: 2'2'122)('R F F M J T T -+-=ε
由于胶带与轮间无滑动,故有
2211εεR R =
联立求解以上三式,并将21112
1R m J =
,2
22221R m J =,1'1T T F F =,2'2T T F F =代入,可得
图11.42
)a (
)b ( T y F x 2ε x
2T
·133·
轮1的角加速度为
2
2121121)()
'
(2R R m m R M MR +-=
ε
11-9 如图11.43所示绞车,提升一重量为P 的重物,在其主动轴上作用一不变的力矩
M 。已知主动轴和从动轴的转动惯量分别为1J 、2J ,传动比21z
i z =,吊索缠绕在从动轮上,
从动轮半径为R ,轴承的摩擦力不计。试求重物的加速度。
N
F
1 'x
ε
图11.43
解:分别选主动轴、从动轮和重物组成的系统为研究对象,受力分析和运动分析如图所
示。对两轮分别应用动量矩定理,有
主动轮: 111R F M J s -=ε
主动轮: PR R F R g
P J s -=+
'22
2)(ε 由运动学知
211εεR R =
其中:s s F F =',21
112z R i z R εε===,联立求解以上三式,有
)(2212
2J i J g
PR PR Mi ++-=ε
重物的加速度为
)()(2212
2J i J g PR R PR Mi R a ++-=
=ε
11-10 如图11.44所示均质杆AB 长为l ,重为1P ,B 端固结一重为2P 的小球(球的半径不计),杆的D 与铅垂悬挂的弹簧相连以使杆保持水平位置。已知弹簧的刚度系数为k ,给小球以微小的初位移o δ,然后自由释放,试求杆AB 的运动规律。
解:选均质杆AB 和小球组成的系统为研究对象,受力分析如图所示。由刚体定轴转动微分方程,有
3
cos cos 2)31(
212221l F l P l P l g P l g P -+=+???
·134·
而)sin 3
('?l
k k F +?=?=,这里?为弹性在水平位置时的伸长量。由题意知道:杆AB 处于水平位置时系统处于平衡状态,由平衡条件可知
02
321=--?
?l P l P l k 很容易求出
l P l P l k 212
3+=??
由于?较小,可令??≈sin ,1cos ≈?,故刚体定轴转动的微分方程可写为 03
321=++??k g P P 上微分方程的通解可写为
t P P gk
B t P P gk A )3(3sin )3(3cos 2
121+++=?
由初始条件l
t 000δ??=
==,00
==t ? ,有 l
A 0δ=,0=B
杆AB 的运动规律为
t P P gk
l
)3(3cos
2
10
+=
δ?
11-11 运送矿石的卷扬机鼓轮半径为R ,重为W ,在铅直平面内绕水平轴O 转动,如图
11.45所示。已知对O 轴的转动惯量为O J ,车与矿石的总重量为W 1,作用于鼓轮上的力矩为M ,轨道的倾角为α。不计绳重及各处摩擦。求小车上升的加速度及绳子的拉力。
T
图11.44 图11.45
解:分别选整体和小车为研究对象,受力分析和运动分析如图所示。对整体应用动量矩
定理,有
R W M R g
W
J O αεsin )(121-=+
解得卷扬机鼓轮转动的角加速度为 g R W g J R
R W M O 2
11sin +-=
αε
·135·
小车上升的加速度为
gR R W g J R
R W M R a O 211sin +-==αε
由小车的运动微分方程,有
a g
W W F T 1
1sin =-α 解得绳子的拉力为
a g
W W F T 1
1sin +
=α 11-12 质量分别为21m m 、的两重物,分别挂在两条绳子上,绳又分别缠绕在半径为2
1r r 、并装在同一轴的两鼓轮上,如图11.46所示。已知两鼓轮对O 轴的转动惯量为O J ,系统在重力作用下发生运动,求鼓轮的角加速度。
解:选整体为研究对象,受力分析如图所示。应用动量矩定理,有
1
122222211)(g r m g r m r m r m J O -=++ε 解得鼓轮的角加速度为
g r m r m J r m r m O 2
2
22111
122++-=ε
11-13 重物A 质量为m 1,系在绳子上,绳子跨过不计质量的固定滑轮D ,并绕在鼓轮B 上,如图11.47所示。由于重物下降带动了轮C ,使它沿水平轨道滚动而不滑动。设鼓轮半径为
r ,轮C 的半径为R ,两者固连在一起,总质量为m 2,对于其水平轴O 的回转半径为ρ。求重物A 下降的加速度以及轮
C 与地面接触点处的静摩擦力。
A
N ω
A
'
a
图11.47
解:分别选轮子和重物A 为研究对象,受力分析和运动分析如图所示。轮子作平面运动,应用刚体平面运动微分方程,有
O s T a m F F 2=-
ερ22m R F r F s T =+
2m
Ox ε
a
g 2m
图11.46
·136·
重物A 的运动微分方程为
A T a m F g m 1'1=-
其中:εR a O =,ε)(r R a A +=,T T F F ='。联立求解,可得重物A 下降的加速度为 g R m r R m r R m a A )
()()(222212
1ρ++++=
轮C 与地面接触点处的静摩擦力为
)
()()(22221212ρρ+++-=R m r R m g
m m Rr F s
11-14 均质圆柱体A 的质量为m ,在外圆上绕以细绳,绳的一端B 固定不动,如图11.48所示。当BC 铅垂时圆柱下降,其初速度为零。求当圆柱体的轴心降落了高度h 时轴心的速度和绳子的张力。
解:选均质圆柱体A 为研究对象,受力分析和运动分析如图所示。圆柱体A 作平面运动,应用刚体平面运动微分方程,有
ma F mg T =-
R F m R T =ε22
1
由运动学关系,有
a R =ε 联立求解,可得g a 3
2=,m g F T 3
1=。 圆柱体的轴心降落了高度h 时轴心的速度为 gh ah v 33
2
2=
= 11-15 均质实心圆柱体A 和薄铁环B 的质量均为m ,半径均为r ,两者用杆AB 铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为θ,如图11.49所示。如不计杆的质量,求杆AB 的加速度和杆的内力。
sA NB
sB
图11.48 图11.49
解:分别以实心圆柱体A 和薄铁环B 为研究对象,受力分析和运动分析如图所示。由于圆柱体A 和薄铁环B 半径相等,故杆AB 作平面运动。可知圆柱体A 中心加速度A a 和薄铁环B 中心加速度B a 大小和方向相同,即B A a a =。它们转动的角加速度也相等,即B A εε=。分别列圆柱体A 和薄铁环B 的动力学方程,有
·137·
圆柱体A : B T sB ma F F mg =--θsin r F mr sB B =ε2
圆柱体B : A T sA ma F F mg =+-'sin θ
r F mr sA A =ε22
1
其中:由运动学关系,可知A A r a ε=,B B r a ε=,'T T F F =,联立求解,可得AB 的加速度和杆的内力分别为
θsin 74
g a a a B A ===
θsin 7
1
'mg F F T T -==
负号表示杆受压力作用。
11-16 在图11.50中,均质圆柱重量为Q ,半径为R ,放在倾角为60°的斜面上,一绳
绕在圆柱体上,其一端固定在A 点,此绳与A 点相连部分与斜面平行。若圆柱体与斜面间
滑动摩擦系数为1
3
f =。试求质心C 沿斜面落下的加速度。
F
F
图11.50
解:选均质圆柱为研究对象,受力分析和运动分析如图所示。均质圆柱作平面运动,应
用平面运动微分方程,有
C d T ma F F Q =--αsin
0cos =+-N F Q α
R F R F R g
Q d T -=ε2
21
其中:N d fF F =,εR a C =。联立求解可得质心C 沿斜面落下的加速度为 g a C 355.0=
11-17 如图11.51所示板的质量为1m ,受水平力F 作用,沿水平面运动,板与平面间的动摩擦系数为f 。在板上放一质量为2m 的均质实心圆柱体,此圆柱体在板上只滚不滑动,试求板的加速度。
解:分别选板和圆柱体为研究对象,受力分析和运动分析如图所示。板作平动,由质心运动定理,有
·138·
C d s a m F F F 1=-- 01=--g m F F NC N 圆柱体作平面运动,由刚体平面运动微分方程,有 O s a m F 2'=
02'
=-g m F NC R F R m s '222
1
=ε
由运动学关系,可选C 点分动点,分析O 点加速度,由τOC n
OC C O a a a a ++=作O 点的加
速度合成图如图所示。由图可知
τ
OC C O a a a -=
其中:ετR a OC
=,N d fF F =,NC NC F F ='
,s s F F =',联立求解,可得板的加速度为 3
)(2
121m m g
m m f F a C +
+-=
NC C F
C NC F C a
N F
d F
s F g 1m
C a
图11.51
11-18 如图11.52所示结构中,重物A 、B 的质量分别为m 1和m 2,B 物体与水平面间摩擦系数为f ,鼓轮O 的质量为M ,半径为R 和r ,对O
轴的回转半径分别为ρ,求A 下降的加速度以及绳子两端的拉力。
A
g 1m
A a TA F
'F
B
g 2m
B a
NB F
TB F dB F
图11.52
解:分别选重物A 、B 和鼓轮O 为研究对象,受力分析和运动分析如图所示。分别列动
·139·
力学方程,有
重物A : A TA a m F g m 11=-
重物B : 02=-g m F NB B dB TB a m F F 2=- 其中:NB dB fF F =。
鼓轮O : R F r F M TB TA -=ερ2
由运动学关系,可知:εr a A =,εR a B =。联立求解可得A 下降的加速度为 gr M R m r m R fm r m a A 2
222121ρ++-=
绳子两端的拉力为
A TA a m g m F 11-=
A T
B a r
R
m g fm F 22+
= 11-19如图11.53所示均质杆AB 长为L ,重为Q ,杆上的D 点靠在光滑支撑上,杆与铅垂线的夹角为α,由静止将杆释放。求此时杆对支撑的压力以及杆重心C 的加速度(
设CD = a )。
F
图11.53
解:(1) 选杆AB 为研究对象,受力如图所示。列杆的平面运动微分方程
Cx a g
Q
Q =αcos
Cy N a g
Q
Q F =-αsin
a F L g
Q N =ε2121 (2) 以D 为基点,分析C 点的加速度。由τCD n
CD D Cy Cx a a a a a ++=+作C 点的加
速度合成图。列投影方程
τCD Cy a a -=
其中:ετ
a a CD
=。联立求解,可得 22212sin L a QL F N +=
α,αcos g a Cx =,2
2212sin 12L a g a a Cy +-=α
11-20如图11.54所示,曲柄OA 以匀角速度045rad s ./ω=绕O 轴沿顺时针转向在铅垂
·140·
面内转动。求当OA 处于水平位置时,细长杆AB 端部B 轮所受的反力。设杆AB 的质量为10kg ,长为1m ,各处摩擦力及OA 杆质量不计。
A
n A
图11.54
解:(1)选细长杆AB 为研究对象,受力分析和运动分析如图所示。列杆AB 的刚体平面运动微分方程,有
Cx Ax ma F = Cy NA Ay ma mg F F =-+
αααεcos 2
sin 2cos 21212l
F l F l F ml Ay Ax NA AB -+= (2)由A v 和B v 方向可知P 点为杆AB 的速度瞬心,杆AB 转动的角速度为
)/(36
.05
.44.00s rad PA OA PA v A AB =?=?==
ωω 以A 为基点分析B 点的加速度,由τ
BA n BA n A B a a a a ++=作B 点的加速度合成图。列PB 方
向的投影方程,有
αατsin cos 0n
BA BA a a +=
其中:22
/9s m AB a AB n BA
=?=ω,解得 2/123
4
9tan s m a a n
BA BA -=?
-=-=ατ 故杆AB 的角加速度为
2/12s rad AB
a BA
AB -==τε 再以A 为基点分析C 点的加速度,由τ
CA n CA n A Cy Cx
a a a a a ++=+作C 点的加速度合成图。
列投影方程,有
αατ
sin cos CA n CA n A Cx a a a a -+-=
αατcos sin CA n
CA Cy a a a +=
其中:220/1.8s m OA a n A =?=ω,22/5.4s m CA a AB n CA =?=ω,2
/6s m CA a AB CA -=?=ετ,代入上
式可得
2
/6.0sin cos s m a a a a CA n CA n A Cx -=-+-=αατ
0cos sin =+=αατCA n
CA Cy a a a
代入杆AB 的刚体平面运动微分方程,可解得细长杆AB 端部B 轮所受的反力为
)(33.36N F NA =
·141·
11-21 如图11.55所示,设均质杆O 1A 和O 2B 以及DAB ,各杆长均为L ,重均为
P ,在
A ,
B 处以铰链连接,O 1,O 2处于同一水平线上,且123
4
O O AB l ==,如图11.55所示,初
始时O 1A 与铅垂线的夹角为30?,由静止释放,试求此瞬时铰链O 1、O 2的约束反力。
O Ax
'By
Bx
O 2
图11.55
解:分别选杆O 1A 和O 2B 以及DAB 为研究对象,受力及运动分析如图所示。分别列三杆的
动力学方程:
杆O 1A : o 30cos 11τ
C x O Ax a g
P F F -
=+ o 30sin 11τ
C y O Ay a g
P P F F -
=-+
o o o o 230sin 2
30sin 230cos 230cos 212111l
F l F l F l F l g P Ay y O Ax x O -+-=ε 杆O 2B : o 30cos 22τ
C x O Bx a g
P F F -
=+ o 30sin 22τ
C y O By a g
P P F F -
=-+
o o o o 230sin 2
30sin 230cos 230cos 212122l
F l F l F l F l g P By y O Bx x O -+-=ε 杆DAB : o '
'30cos 3τ
C Bx Ax a g
P F F -
=--
·142·
o ''30sin 3τ
C By Ay a g
P P F F -
=--- 2
40''
l F l F By Ay
+-= 其中:ετ
τ2
2
1l a a C C ==,ετ
l a C =3
,联立求解,可得铰链O 1、O 2的约束反力为 P F F x O x O 516.021==,P F y O 434.11=,P F y O 164.12=
动量矩定理 12-1 质量为m 的点在平面Ox y内运动,其运动方程为: t b y t a x ωω2sin cos == 式中a 、b 和ω为常量。求质点对原点O的动量矩。 解:由运动方程对时间的一阶导数得原点的速度 t b t y v t a t x v y x ωωωω2cos 2d d sin d d ==-== 质点对点O 的动量矩为 t a t b m t b t a m x mv y mv m M m M L y x O O ωωωωωωcos 2cos 22sin )sin ()()(0??+?-?-=?+?-=+=y x v v ? t mab ωω3 cos 2= 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。轮子轴心为A ,质心为C,A C = e ;轮子半径为R,对轴心A 的转动惯量为JA ;C 、A、B 三点在同一铅直线上。(1)当轮子只滚不滑时,若v A已知,求轮子的动量和对地面上B 点的动量矩。(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对地面上B点的动量矩。 解:(1)当轮子只滚不滑时B 点为速度瞬心。 ? 轮子角速度R v A =ω? 质心C 的速度)(e R R v C B v A C += =ω? ?轮子的动量(A C mv R e R mv p += =?方向水平向右) ?对B点动量矩ω?=B B J L ? 由于? 2 22)( )( e R m me J e R m J J A C B ++-=++= 故[ ] R v e R m me J L A A B 2 2)( ++-=? (2)当轮子又滚又滑时由基点法求得C 点速度。 e v v v v A CA A C ω+=+= 轮子动量( )(e v m mv p A C ω+==?方向向右) 对B 点动量矩 ) ( )()()( )( 2e mR J e R mv me J e R e v m J BC mv L A A A A C C B +++=-+++=+=ωωωω 12-13 如图所示,有一轮子,轴的直径为50 m m,无初速地沿倾角?=20θ的轨道滚下,设只滚不滑,5秒内轮心滚动的距离为s = 3 m 。试求轮子对轮心的惯性半径。 解:取轮子为研究对象,轮子受力如图(a)所示,根据刚体平面运动微分方程有 ? F mg ma C -=θsin ? (1) J Cα = Fr ? ?(2) 因轮子只滚不滑,所以有 a C =αr (3)
第12章 动量矩定理 通过上一章的学习我们知道动量是表征物体机械运动的物理量。但是在某些情况下,一个物体的动量不足以反映它的运动特征。例如,开普勒在研究行星运动时发现,行星在轨道上各点的速度不同,因而动量也不同,但它的动量的大小与它到太阳中心的距离之乘积—称为行星对太阳中心的动量矩,总是保持为常量,可见,在这里,行星对太阳中心的动量矩比行星的动量更能反映行星运动的特征。 在另一些情况下,物体的动量则完全不能表征它的运动。例如,设刚体绕着通过质心C 的z 轴转动。因为不论刚体转动快慢如何,质 心速度C v 总是等于零,所以刚体的动量也总是零。但是,刚体上各质点的动量大小与其到z 轴的距离的乘积之和—即刚体对z 轴的动量矩却不等于零。可见,在这里,不能用动量而必须用动量矩来表征刚体的运动。 §12-1 质点动量矩定理 例2.人造地球卫星本来在位于离地面600km h =的圆形轨道上,如图所示,为使其进入410km r =的另一圆形轨道,须开动火箭,使卫星在A 点的速度于很短时间内增加0.646km/s ,然后令其沿椭圆轨道自由飞行到达远地点B ,再进入新的圆形轨道。问:(1)卫星在椭圆轨道的远地点B 处时的速度是多少?(2)为使卫星沿新的圆形轨道运行,当它到达远地点B 时,应如何调整其速度?大气阻力及其它星球的影响不计。地球半径6370km R =。 图12-5 解:首先求出卫星在第一个圆形轨道上的速度,可由质点动力学方程求出。卫星运行时只受地球引力的作用,即 2 2 () R F mg R x =+ 式中x 是卫星与地面的距离。当卫星沿第一圆形轨道运动时,有
22 2 ()()v R m mg R h R h =++ 即 2 2 () gR v R h =+ (b ) 将6370km R =,600km h =,9.8m/s g =代入上式,得卫星在第一个圆形轨道上运动的速度 17.553km/s v = 所以卫星在椭圆轨道上的A 点的速度为 7.5530.6468.199km/s A v =+= 卫星在椭圆轨道上运动时,仍然只受地球引力作用,而该引力始终指向地心O ,对地以O 的矩等于零,所以卫星对地心O 的动量矩应保持为常量。设卫星在远地点B 的速度为B v ,则有 A A B B r v r v = 所以 4 63706008.199 5.715km/s 10A B A B r v v r += ?=?= 设卫星沿新的圆形轨道运行时所需的速度为2v ,则 22 2 2 4 9.86370 6.306km/s 10gR v r ?=== 由此可见,为使卫星沿着第二个圆形轨道运行,当它沿椭圆轨道到达B 点时,应再开动火箭,使其速度增加一个值 20.591km/s B B v v v ?=-= 顺便指出,在(b )式中令0h →,就得到7.9km/s v =,这就是为使卫星在离地面不远处作圆周运动所需的速度,称为第一宇宙速度。 §12-2 质点系动量矩定理 例1.质量为1m 、半径为R 的均质圆轮绕定轴O 转动,如图所示。轮上缠绕细绳,绳端悬挂质量为2m 的物块,试求物块的加速度。均质圆 轮对于O 轴的转动惯量为211 2 O J m R =。
习 题 11-1 质量为m 的质点在平面Oxy 内运动,其运动方程为:t b y t a x ωω2sin ,cos ==。其中a 、b 和w 均为常量。试求质点对坐标原点O 的动量矩。 t a x v x ωωsin -== t b y v y ωω2cos 2== x mv y mv L y x O +-= )cos 2cos 22sin sin (t a t b t b t a m ωωωωωω?+?= )cos 2cos 22sin (sin t t t t mab ωωωωω?+?= )cos 2cos 2cos sin 2(sin t t t t t mab ωωωωωω?+?= )2cos (sin cos 22t t t mab ωωωω+= t mab ωω3cos 2= 11-2 C 、D 两球质量均为m ,用长为2 l 的杆连接,并将其中点固定在轴AB 上,杆CD 与轴AB 的交角为θ,如图11-25所示。如轴AB 以角速度w 转动,试求下列两种情况下,系统对AB 轴的动量矩。(1)杆重忽略不计;(2)杆为均质杆,质量为2m 。 图11-25 (1) θθ222sin 2)sin (2ml l m J z =?= θω22sin 2l m L z = (2) θθ220 2sin 3 2d )sin (2ml x x l m J l z ==?杆 θ22sin 3 8 ml J z = θ ω22sin 3 8 l m L z = 11-3 试求图11-26所示各均质物体对其转轴的动量矩。各物体质量均为m 。 图11-26 (a) ω23 1ml L O = (b) 22291)6(121ml l m ml J O =+= ω29 1ml L O -=
y x 第十一章 动量矩定理 习题解 [习题11-1] 刚体作平面运动。已知运动方程为:2 3t x C =,24t y C =,3 2 1t = ?,其中长度以m 计,角度以rad 计,时间以s 计。设刚体质量为kg 10,对于通过质心C 且垂直于图平面的惯性半径m 5.0=ρ,求s t 2=时刚体对坐标原点的动量矩。 解: )(1223|2 2m x t C =?== )(1624|22m y t C =?== t t dt d dt dx v C Cx 6)3(2=== )/(1226|2s m v t Cx =?== t t dt d dt dy v C Cy 8)4(2=== )/(1628|2s m v t Cy =?== 2323)21(t t dt d dt d === ?ω )/(622 3 |22s rad t =?==ω → →→+=k v m M J L C Z Cz O )]([ω → → -+=k y mv x mv m L C Cx C Cy O ][2 ωρ → =→ ?-?+??=k L t O ]1612121665.0[10|2 2 → =→ =k L t O 15|2 )/(2 s m kg ?,→ k 是z 轴正向的单位向量。 [习题11-2] 半径为R ,重为W 的均质圆盘固结在长l ,重为P 的均质水平直杆AB 的B 端,绕铅垂轴Oz 以角速度ω旋转,求系统对转轴的动量矩。 解: g Pl l g P J AB z 3312 2,=??=
平动 )(a O 转动 绕定轴C )( b 转动 绕定轴1 )(O c 1 O 在圆弧上作纯滚动 )(d g l R W l g W g J l z 4)4(R W 412222,+=?+??=圆盘 ωω?+?=圆盘,,z AB z z J J L ω4) 4(3[222g l R W g Pl L z ++= ω)4443( 2 2 2 g WR g Wl g Pl L z ++= ω)4333(2 22g WR g Wl g Pl L z ++= ω)433( 2 2R g W l g W P L z ++= [习题11-3] 已知均质圆盘质量为m ,半径为R ,当它作图示四种运动时,对固定点1O 的动量矩分别为多大?图中l C O =1。 解:)(a 因为圆盘作平动,所以 ωω211ml J L z O O == 解:)(b → →→→?+=p r L L C C O 1 其中,质心C 的动量为0 ωω22 1 1mR J L Cz O = = 解:)(c ωω)2 1 (2211ml mR J L z O O +== 解:)(d 因为圆盘作平面运动,所以: ) (11→ +=C Z O Cz O v m M J L ω
1 质点系对某轴的动量矩等于质点系中各质点的动量对同一轴之矩的代数和。 ( ) 2 刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体绕该轴转动时惯性大小的度量。 ( ) 3 刚体对某轴的回转半径等于其质心到该轴的距离。( ) 4 如果作用于质点系上的所有外力对固定点O 的主矩不为零,那么,质点系的动量矩一定不守恒。( ) 5 如果质点系所受的力对某点(或轴)的矩恒为零,则质点系对该点(或轴)的动量矩不变。( ) 6 图中所示已知两个均质圆柱,半径均为R ,质量分别为2m 和3m ,重物的质量为1m 。重物向下运动的速度为V ,圆柱C 在斜面上只滚不滑,圆柱O 与绳子之间无引对滑动,则系统 对O 轴的动量矩为vR m R m vR m H o 12 232 ++=ω。( ) 7 图中已知均质圆轮的半径为R ,质量为m ,在水平面上作纯滚动,质心速度为C v ,则轮子对速度瞬心I 的动量矩为R mv H c I =。( ) 1 已知刚体质心C 到相互平行的z z 、'轴的距离分别为b a 、,刚体的质量为m ,对z 轴的转动惯量为z J ,则' z J 的计算公式为__________________。
A .2)(b a m z z ++='J J ; B .)(2 2b a m z z -+=' J J ; C.)(2 2b a m z z --=' J J 。 2 两匀质圆盘A 、B ,质量相等,半径相同,放在光滑水平面上,分别受到F 和' F 的作用,由静止开始运动,若' F F =,则任一瞬间两圆盘的动量相比较是_____________________。 A.B A p p >; B.B A p p <; C.B A p p =。 3 在一重W 的车轮的轮轴上绕有软绳,绳的一端作用一水平力P ,已知车轮的半径为R ,轮轴的半径为r ,车轮及轮轴对中心O 的回转半径为ρ,以及车轮与地面间的滑动摩擦系数为f ,绳重和滚阻皆不计。当车轮沿地面作平动时,力P 的值为_________________。 A.ρ/fWR P =; B.r fWR P /=; C.r fW P /ρ=;④ fW P =。
第11章 动量矩定理 上一章我们学习了动量定理,它只是从一个侧面反映物体间机械运动传递时,动量的变化与作用在物体上力之间的关系。但当物体作定轴转动时,若质心在转轴上,则物体动量等于零,可见对于转动刚体而言,动量不再用来描述转动物体的物理量。在这一章里我们学习描述转动物体的物理量——动量矩,以及作用在物体上力之间的关系。 11.1 动量矩定理 11.1.1质点和质点系动量矩 1.质点的动量矩 如图11-1所示,设质点在图示瞬时A 点的动量为m v ,矢径为r ,与力F 对点O 之矩的矢量表示类似,定义质点对固定点O 的动量矩为 v r v M m ×=)(m o (11-1) 图11-1 图11-2 质点对固定点O 的动量矩是矢量,方向满足右手螺旋法则,如图11-1所示,大小为固 定点O 与动量AB 所围成的三角形面积的二倍,即 mvh =OAB =)(m M 0的面积Δ2v 其中,h 为固定点O 到AB 线段的垂直距离,称为动量臂。 单位为kg.m 2/s 。
质点的动量对固定轴z 的矩与力F 对固定轴z 的矩类似,如图11-2所示,质点的动量v m 在oxy 平面上的投影xy )m (v 对固定点O 的矩,定义质点对固定轴z 的矩,同时也等于质点对固定点O 的动量矩在固定轴z 上的投影。质点对z 轴的动量矩是代数量,即 z o xy o m =m M =m M Z )]([])[()(v M v v (11-2) 2.质点系的动量矩 质点系对固定点O 的动量矩等于质点系内各质点对固定点O 的动量矩的矢量和,即 ∑==n i i i o )(m 1v M L o (11-3) 质点系对固定轴z 的矩等于质点系内各质点对同一轴z 动量矩的代数和,即 Z o n i i i z z )(m =L ][L v M =∑=1 (11-4) 刚体作平移时动量矩的计算:将刚体的质量集中在刚体的质心上,按质点的动量矩计 算。 刚体作定轴转动时动量矩的计算: 设定轴转动刚体如图11-3所示,其上任一质点i 的质量为m i ,到转轴的垂直距离为i r ,某瞬时的角速度为ω,刚体对转轴z 的动量矩由式(11-4)得 图11-3 ω J =ω)r m (=) r ωr (m =)r v (m =)(m M =L z n i i i n i i i i n i i i i n i i i z ∑∑∑∑====1 21 1 1v z 即 ωJ =L z z (11-5)
动量矩定理 12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: x a cos t y bsin2 t 式中a 、b 和 为常量。求质点对原点 O 的动量矩。 解:由运动方程对时间的一阶导数得原点的速度 V x dx sin t dt a V y dy 2b cos2 t 质点对点 O 的动量矩为 L O M o (mV x ) M 0( mV y ) mv x y mv y x m ( a sin t) bsin2 t m 2b cos2 t acos t 2mab cos 3 t 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。 轮子轴心为A,质心为C, AC = e ;轮子半径为 R,对轴心A 的转动惯量为J A ; C 、A 、B 三点在同一铅直线上。(1 )当轮子只 滚不滑时,若 V A 已知,求轮子的动量和对地面上 B 点的动量矩。(2)当轮子又滚又滑时, 若V A 、 已知,求轮子的动量和对地面上 B 点的动量矩。 解:(1)当轮子只滚不滑时 B 点为速度瞬心。 轮子角速度 V A R 质心C 的速度V C BC R e 轮子的动量 p mv C mv A (方向水平向右) R 对B 点动量矩L B J B 2 2 2 由于 J B J C m (R e) J A me m (R e) 故 L B J A me 2 m (R e )2 食 (2)当轮子又滚又滑时由基点法求得 C 点速 度。 V C V A V CA V A e 轮子动量 p mv C m(v A e) (方向向右) 对B 点动量矩 L B mv C BC J C m(v A 2 e) (R e) (J A me) mv A (R e) (J A mRe) 12-13 如图所示,有一轮子,轴的直径为 50 mm 无初速地沿倾角 20的轨道滚下,设 只滚不滑,5秒内轮心滚动的距离为 s =3m 。试求轮子对轮心的惯性半径。 解:取轮子为研究对象,轮子受力如图( a )所示,根据刚体平面运动微分方程有 ma C mgsi n F ( 1) J C = Fr ( 2) 因轮子只滚不滑,所以有 a c = r ( 3) ? 12
y 第十一章 动量矩定理 习题解 [习题11-1] 刚体作平面运动。已知运动方程为:2 3t x C =,24t y C =,3 2 1t = ?,其中长度以m 计,角度以rad 计,时间以s 计。设刚体质量为kg 10,对于通过质心C 且垂直于图平面的惯性半径m 5.0=ρ,求s t 2=时刚体对坐标原点的动量矩。 解: )(1223|22m x t C =?== )(1624|2 2m y t C =?== t t dt d dt dx v C Cx 6)3(2=== )/(1226|2s m v t Cx =?== t t dt d dt dy v C Cy 8)4(2=== )/(1628|2s m v t Cy =?== 2323)21(t t dt d dt d === ?ω )/(622 3 |22s rad t =?==ω → →→+=k v m M J L C Z Cz O )]([ω → → -+=k y mv x mv m L C Cx C Cy O ][2 ωρ → =→ ?-?+??=k L t O ]1612121665.0[10|2 2 → =→ =k L t O 15|2 )/(2 s m kg ?,→ k 是z 轴正向的单位向量。 [习题11-2] 半径为R ,重为W 的均质圆盘固结在长l ,重为P 的均质水平直杆AB 的B 端,绕铅垂轴Oz 以角速度ω旋转,求系统对转轴的动量矩。 解: g Pl l g P J AB z 3312 2,=??=
平动 )(a O 转动 绕定轴C )( b 转动 绕定轴1 )(O c O 在圆弧上作纯滚动 )(d g l R W l g W g J l z 4)4(R W 412222,+=?+??=圆盘 ωω?+?=圆盘,,z AB z z J J L ω4) 4(3[222g l R W g Pl L z ++= ω)4443(2 22g WR g Wl g Pl L z ++= ω)4333(2 22g WR g Wl g Pl L z ++= ω)433( 2 2R g W l g W P L z ++= [习题11-3] 已知均质圆盘质量为m ,半径为R ,当它作图示四种运动时,对固定点1O 的动量矩分别为多大?图中l C O =1。 解:)(a 因为圆盘作平动,所以 ωω2 11ml J L z O O == 解:)(b → →→→?+=p r L L C C O 1 其中,质心C 的动量为0 ωω22 1 1mR J L Cz O = = 解:)(c ωω)2 1 (2211ml mR J L z O O +== 解:)(d 因为圆盘作平面运动,所以: )(11→ +=C Z O Cz O v m M J L ω
第十二章 动量矩定理 一、填空题 1.如下(1)图所示,在提升重为G的物体A时,可在半径为r的鼓轮上作用一力偶M。已知鼓轮对轴O的转动惯量为I,某瞬时鼓轮的角加速度为α,则该瞬时,系统对轴O的动量矩定理可写成______________。 2.如下(2)图所示,轮B由系杆AB带动在固定轮A上无滑动滚动,两圆的半径分别为R,r。若轮B的质量为m,系杆的角速度为ω,则轮B对固定轴A的动量矩大小是_______________。 3.图(3)中匀质圆盘在光滑水平面上作直线平动,图(4)中匀质圆盘沿水平直线作无滑动滚动。设两圆盘的质量皆为m,半径皆为r,轮心O速度皆为v,则图示瞬时,它们各自对轮心O和对与地面接触点D的动量矩分别为:(3)LO =___________ ;LD =_____________________; (4)LO =_____________;LD =_____________________。 二、选择题 1.如下图(1)所示,已知两个匀质圆轮对转轴转动惯量分别为I A,I B,半径分别为RA,RB,作用在A轮上的转矩为M,则系统中A轮角加速度的大小为( )。 2 2A 2 2B 2 A A B A A 222A D C I I M B A B A B A B A A B B R I R I MR I M R I R I MR +==+=+=αααα、;、;、;、 2.如下图(2)所示,两匀质细杆OA和BC的质量均为m = 8kg,长度均为l = 0.5m, 固连成图所示的T字型构件,可绕通过点O的水平轴转动。当杆OA处于图示水平位置时,该构件的角速度ω = 4rad/s。则该瞬时轴O处反力的铅垂分力NOy的大小为( )。 A.NO=24.5N;B.NO=32.3N;C.NO=73.8N;D.NO=156.8N 3.如果把下图(3)中重为G A 的物体换为图(4)所示的力G A ,在这两种情况下,若把匀质滑轮的角加速度ε1和ε2的大小比较,则有( )。 A . ε1 < ε; B . ε1 > ε; C . ε1 = ε2 (1) (2) (3) (4) (1) (2) (3) (4)
授课时间 第24课,第 2 周星期 4 第1、2 节课时 2 授课方式理论课√讨论课□习题课□实验课□上机课□技能课□其他□授课题目 第十二章动量矩定理§12-1 质点和质点系的动量矩 §12-2动量矩定理 目的与 要求 掌握质点和质点系的动量矩的概念,动量矩定理的应用。 重点与 难点 重点:动量矩定理的应用。 难点:动量矩定理的应用。 教学基本内容方法及手段§12-1 质点和质点系的动量矩 1.质点的动量矩 对点O的动量矩 对z 轴的动量矩 单位:kg·m2/s 2.质点系的动量矩 对点的动量矩 对轴的动量矩 电教 30分钟 () O M mv r mv =? r r r r () O M mv r mv =? r r r r [()]() O z z M mv M mv = r r r 1 () n O O i i i L M m v = =∑ r r r 1 () n z z i i i L M m v = =∑ r [] O z z L L = r O x y z L L i L j L k =++ r r r r 即
(1) 刚体平移.可将全部质量集中于质心,作为一个质点来计算. (2) 刚体绕定轴转动 转动惯量 §12-2 动量矩定理 1.质点的动量矩定理,设O 为定点,有 其中, 因此, 称为质点的动量矩定理:质点对某定点的 动量矩对时间的一阶导数,等于作用力对 同一点的矩. 投影式: 2. 质点系的动量矩定理 由于 20分钟 20分钟 10分钟 () z z C L M mv =r () O O C L M mv =r r r i i i i i z z r v m v m M L ∑=∑=)(2 i i i i i r m r r m ∑=∑=ωω2i i z r m J ∑=ω z z J L =d d ()()d d O M mv r mv t t =?r r r r d d ()d d r mv r mv t t =?+?r r r r d ()d mv F t =r r (O 为定点) d d r v t =r r 0v mv ?=r r d ()() d O O M mv M F t =r r r r d ()()d x x M mv M F t =r r d ()()d y y M mv M F t =r r d ()()d z z M mv M F t =r r ()()d ()()()d i e O i i O i O i M m v M F M F t =+r r r r r r ()()d ()()()d i e O i i O i O i M m v M F M F t ∑=∑+∑r r r s r r () ()0 i O i M F ∑=r r d d d ()()d d d O O i i O i i L M m v M m v t t t ∑=∑=r r r r r
习题 11-1质量为m的质点在平面Oxy内运动,其运动方程为: 。其中a、b和w均为常量。试求质点对坐标原点 O的动量矩。 11-2 C、D两球质量均为m,用长为2 l的杆连接,并将其中点固定在轴AB上,杆CD与轴AB的交角为,如图11-25所示。如轴AB以角速度w转动,试求下列两种情况下,系统对AB轴的动量矩。<1)杆重忽略不计;<2)杆为均质杆,质量为2m。b5E2RGbCAP 图11-25 (1> (2> 11-3 试求图11-26所示各均质物体对其转轴的动量矩。各物体质量均为m。 图11-26 (a>
(b> (c> (d> 11-4如图11-27所示,均质三角形薄板的质量为m,高为h,试求对底边的转动惯量Jx。 图11-27 面密度为 在y处 微小区域对于z轴的转动惯量 11-5 三根相同的均质杆,用光滑铰链联接,如图11-28所示。试求其对与ABC所在平面垂直的质心轴的转动惯量。p1EanqFDPw 图11-28 11-6 如图11-29所示,物体以角速度w绕O轴转动,试求物体对于O轴的动量矩。(1> 半径为R,质量为m的均质圆盘,在中央挖去一边长为R的正方形,如图11-32a所示。(2> 边长为4a,质量为
m的正方形钢板,在中央挖去一半径为a的圆,如图11-32b所示。DXDiTa9E3d 图11-29 (1> (2> 11-7如图11-30所示,质量为m的偏心轮在水平面上作平面运动。轮子轴心为A,质心为C,AC=e;轮子半径为R,对轴心A的转动惯量为JA;C、A、B三点在同一直线上。试求下列两种情况下轮子的动量和对地面上B点的动量矩:(1>当轮子只滚不滑时,已知vA;(2>当轮子又滚又滑时,已知vA、w。RTCrpUDGiT 图11-30 (1>
第12章 动量矩定理 12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: t b y t a x ωω2sin cos == 式中a 、b 和ω为常量。求质点对原点O 的动量矩。 解:由运动方程对时间的一阶导数得原点的速度 t b t y v t a t x v y x ωωωω2cos 2d d sin d d ==-== 质点对点O 的动量矩为 t a t b m t b t a m x mv y mv m M m M L y x O O ωωωωωωcos 2cos 22sin )sin ()()(0??+?-?-=?+?-=+=y x v v t mab ωω3cos 2= 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。轮子轴心为A ,质心为C ,AC = e ;轮子半径为R ,对轴心A 的转动惯量为J A ;C 、A 、B 三点在同一铅直线上。(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对地面上B 点的动量矩。(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对地面上B 点的动量矩。 解:(1)当轮子只滚不滑时B 点为速度瞬心。 轮子角速度 R v A =ω 质心C 的速度 )(e R R v C B v A C += =ω 轮子的动量 A C mv R e R mv p += =(方向水平向右) 对B 点动量矩 ω?=B B J L 由于 222)( )( e R m me J e R m J J A C B ++-=++= 故 [] R v e R m me J L A A B 22)( ++-= (2)当轮子又滚又滑时由基点法求得C 点速度。 e v v v v A CA A C ω+=+= 轮子动量 )(e v m mv p A C ω+== (方向向右) 对B 点动量矩 ) ( )()()( )( 2e mR J e R mv me J e R e v m J BC mv L A A A A C C B +++=-+++=+=ωωωω 12-5 图示水平圆板可绕z 轴转动。在圆板上有一质点M 作圆周运动,已知其速度的大小为常量,等于v 0,质点M 的质量为m ,圆的半径为r ,圆心到z 轴的距离为l ,M 点在圆板的位置由?角确定,如图所示。如圆板的转动惯量为J ,并且当点M 离z 轴最远在点M 0时,圆板的角速度为零。轴的摩擦和空气阻力略去不计,求圆板的角速度与?角的关系。 解:以圆板和质点M 为系统,因为系统所受外力(包括重力和约束反力),对z 轴的矩均为零,故系统对z 轴动量矩守恒。在任意时刻M 点的速度包含相对速度v 0和牵连速度v e 。其中ω?=OM v e 。设质点M 在M 0 位置为起始位置,该瞬时系统对z 轴的动量矩为
第十二章 动量矩定理 §12—1 质点和质点系的动量矩 一、质点的动量矩 质点Q 的动量对于点O 的矩,定义为质点对于点O 的动量矩 动量矩的单位:kgm 2/s 二、 质点系的动量矩 ()mv r mv M O ?=()OQA r mv mv M O ?=?=2sin ?() i i n i O O v m M L ∑==1 () i i n i z z v m M L ∑==1 ()A Q O mv M z ' '?±=2()[]() mv M mv M z z O =
绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角速度的乘积。 §12—2 动量矩定理 一、质点的动量矩定理 质点的动量矩定理: 质点对某定点的动量矩对时间的一阶导数,等于作用力对同一点的矩。 直角坐标投影式为 []z z O L L =()2 1 1 1 i n i i i n i i i i i n i z z r m r v m v m M L ∑∑∑====?==ω2 1 i n i i z r m J ∑==ω z z J L =()mv dt d r mv dt dr mv r dt d mv M dt d O ?+?=?=)()(()F r mv v mv M dt d O ?+?=()()F M mv M dt d O O =()()()()()()F M m v M dt d F M m v M dt d F M m v M dt d z z y y x x == =
特殊情形: 当质点受有心力F 的作用时,如图11-4所示,力矩0=)(o F M ,则质点对固定点O 的动量矩)(m o v M =恒矢量,质点的动量矩守恒。例如行星绕着恒星转,受恒星的引力作用,引力对恒星的矩0=)(o F M ,行星的动量矩 )(m o v M =恒矢量,此恒矢量的方向是不变的,因此行星作平面曲线运动;此 恒矢量的大小是不变的,即mvh =恒量,行星的速度v 与恒星到速度矢量的距离h 成反比。
动量矩定理 12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: t b y t a x ωω2sin cos == 式中a 、b 和ω为常量。求质点对原点O 的动量矩。 解:由运动方程对时间的一阶导数得原点的速度 t b t y v t a t x v y x ωωωω2cos 2d d sin d d ==-== 质点对点O 的动量矩为 t a t b m t b t a m x mv y mv m M m M L y x O O ωωωωωωcos 2cos 22sin )sin ()()(0??+?-?-=?+?-=+=y x v v t mab ωω3 cos 2= ? 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。轮子轴心为A ,质心为C ,AC = e ;轮子半径为R ,对轴心A 的转动惯量为J A ;C 、A 、B 三点在同一铅直线上。(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对地面上B 点的动量矩。(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对地面上B 点的动量矩。 解:(1)当轮子只滚不滑时B 点为速度瞬心。 轮子角速度 R v A = ω 质心C 的速度 )(e R R v C B v A C += =ω 轮子的动量 A C mv R e R mv p += =(方向水平向右) 对B 点动量矩 ω?=B B J L 由于 222)( )( e R m me J e R m J J A C B ++-=++= 故 [] R v e R m me J L A A B 22)( ++-= ` (2)当轮子又滚又滑时由基点法求得C 点速度。 e v v v v A CA A C ω+=+= 轮子动量 )(e v m mv p A C ω+== (方向向右) 对B 点动量矩 ) ( )()()( )( 2e mR J e R mv me J e R e v m J BC mv L A A A A C C B +++=-+++=+=ωωωω 12-13 如图所示,有一轮子,轴的直径为50 mm ,无初速地沿倾角?=20θ的轨道滚下,设只滚不滑,5秒内轮心滚动的距离为s = 3 m 。试求轮子对轮心的惯性半径。 解:取轮子为研究对象,轮子受力如图(a )所示,根据刚体平面运动微分方程有 F mg ma C -=θsin (1) — J C α = Fr (2) 因轮子只滚不滑,所以有 a C =αr (3)
梁坤京理论力学第十二章动量矩定理课后答案 案场各岗位服务流程 销售大厅服务岗: 1、销售大厅服务岗岗位职责: 1)为来访客户提供全程的休息区域及饮品; 2)保持销售区域台面整洁; 3)及时补足销售大厅物资,如糖果或杂志等; 4)收集客户意见、建议及现场问题点; 2、销售大厅服务岗工作及服务流程 阶段工作及服务流程 班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域 2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。 班中工作程序服务 流程 行为 规范 迎接 指引 递阅 资料 上饮品 (糕点) 添加茶水工作1)眼神关注客人,当客人距3米距离侯客迎询问客户送客户
注意事项 15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!” 3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人; 4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好 6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品); 7)在满座位的情况下,须先向客人致
待; 阶段工作及服务流程 班中工作程序工作 要求 注意 事项 饮料(糕点服务) 1)在所有饮料(糕点)服务中必须使用 托盘; 2)所有饮料服务均已“对不起,打扰一 下,请问您需要什么饮品”为起始; 3)服务方向:从客人的右面服务; 4)当客人的饮料杯中只剩三分之一时, 必须询问客人是否需要再添一杯,在二 次服务中特别注意瓶口绝对不可以与 客人使用的杯子接触; 5)在客人再次需要饮料时必须更换杯 子; 下班程 序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导; 2)填写物资领用申请表并整理客户意见;3)参加班后总结会; 4)积极配合销售人员的接待工作,如果下班
理论力学11章作业题解 11-3 已知均质圆盘的质量为m ,半径为R ,在图示位置时对O 1点的动量矩分别为多大?图中O 1C=l 。 解 (a) 2 1l m l mv L c O w == ,逆时针转动。 (b) w w 2 210||1mR J L v m r L c c c O =+=+′=r r ,逆时针转动。 (c ) )2(2 2 12 2 12 1l R m ml mR ml J J c O +=+=+= w w )2(2 2111l R m J L O O +==,逆时针转动。 (d) w w mR R l mv R l R v mR l mv J l mv L v m r L c c c c c c c O )5.0()5.0(/||2 2 11-=-=-=-=+′= r r ,顺时针转动 v c v c v c
11-5 均质杆AB 长l 、重为G 1,B 端刚连一重G 2的小球,弹簧系数为k ,使杆在水平位置保持平衡。设给小球B 一微小初位移0d 后无初速度释放,试求AB 杆的运动规律。 解 以平衡位置(水平)为0=j ,顺时针转为正。平衡时弹簧受力为: )5.0(312G G F s += 弹簧初始变形量: k G G k F s st /)5.0(3/12+==d 在j 角时弹簧的拉力为(小位移): 3/)5.0(3)3/(12l k G G l k F st s j j d ++=+=¢ 系统对A 点的动量矩: j j j &&&2 21233l g G G l l g G J L A A +=×+= 对点的动量矩定理)(/?=E i A A F M dt dL r : j j 9 3/5.0332 21221kl l F lG lG l g G G s -=¢-+=+&& 0)3(321=++j j G G gk &&,令) 3(3212G G gk p +=则有02=+j j p &&,其解为: )cos()sin(pt B pt A +=j 由初始条件0| ,/|000====t t l j d j &得l B A / ,00d ==。故运动方程为: )cos(0 pt l d j = G 1 G 2 F Ax F Ay F s
第十二章动量矩定理 一、填空题 1如下(1)图所示,在提升重为G 的物体A 时,可在半径为 r 的鼓轮上作用一力偶M 。已知鼓轮对轴O 的转动惯量为I,某瞬时鼓轮的角加速度为 G,则该瞬时,系统对轴O 的动量矩定理可写成 _____________________ 2.如下(2)图所示,轮E 由系杆AE 带动在固定轮A 上无滑动滚动,两圆的半径分别为R,r 。若轮E 的质量为m,系杆的角速度为 3,则轮E 对固定轴A 的动量矩大小是 ____________________ 3 .图(3)中匀质圆盘在光滑水平面上作直线平动,图( 4)中匀质圆盘沿水平直线作无滑动滚动。设两 圆盘的质量皆为m,半径皆为r,轮心O 速度皆为v,则图示瞬时,它们各自对轮心O 和对与地面接触点 D 的动量矩分另U 为: (3)L O = ___________ ; L D = _________________________ ; ( 4)L O = ________________ ; L D = _________________________ 。 2 .如下图(2)所示,两匀质细杆OA 和EC 的质量均为m = 8kg ,长度均为1 = 0.5m, 固连成图所示的T 字型构件,可绕通过点O 的水平轴转动。当杆OA 处于图示水平位置时,该构件的角速 度3 = 4rad/s 。则该瞬时轴O 处反力的铅垂分力NOy 的大小为( )。 A.N O =24.5N; B.N O =32.3N; C.N O = 73.8N; D.N O = 156.8N 3 .如果把下图(3)中重为G A 的物体换为图(4)所示的力 G A ,在这两种情况下,若把匀质滑轮的 A . &1 V $ B . e 1 > e ; C . e 1 = e 2 二、选择题 1.如下图(1)所示,已知两个匀质圆轮对转轴转动惯量分别为 在A 轮上的转矩为M,则系统中A 轮角加速度的大小为( I A , I B ,半径分别为R A ,R B ,作用 MR B A 、‘ A = I B R A I A R B ; B MR B I A D 、、心 A — 2 2 2 2 B A A B 角加速度 1和2的大小比较,则有( (1) (2) (1
·125· 第11章 动量矩定理 一、是非题(正确的在括号内打“√”、错误的打“×”) 1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。 (×) 2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。(√) 3. 质点系动量矩的变化与外力有关,与内力无关。 (√) 4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。 (√) 5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。 (×) 6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。 (×) 7. 质点系对某点的动量矩定理e 1d ()d n O O i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。 (√) 8. 如图11.23所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+ 221 3 ml mr =+,式中m 为AB 杆的质量。 (×) 9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1 d ()d n P P i i t ==∑L M F 的形式,而 不需附加任何条件。 (×) 10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。 (×) 图11.23 二、填空题 1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。 2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。 3. 质点系的质量与质心速度的乘积称为质点系的动量。 4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的内力无关。 5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零,质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数