
二次函数与四边形
一.二次函数与四边形的形状
例 1.(浙江义乌市 ) 如图,抛物线y x22x 3 与x轴交A、B两点(A点在B点左侧),直线 l 与抛物线交于A、C两点,其中C点的横坐标为2.
( 1)求 A、 B 两点的坐标及直线AC 的函数表达式;
( 2)P 是线段 AC 上的一个动点,过 P 点作 y 轴的平
行线交抛物线于 E 点,求线段 PE 长度的最大值;A ( 3)点 G 是抛物线上的动点,在x 轴上是否存在点 F,使 A 、C、 F、 G 这样的四
个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的 F 点坐标;如果不
存在,请说明理由.
练习 1.(河南省实验区) 23.如图,对称轴为直线x 7
的抛物线经过点
A(6,0)和B( 0, 4).2y7
x
( 1)求抛物线解析式及顶点坐标;2
( 2)设点 E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF
是以 OA 为对角线的平行四边形.求平行四边形OEAF 的面积 S 与x之间的函数B(0,4)
关系式,并写出自变量x 的取值范围;
①当平行四边形OEAF 的面积为24 时,请判断平行四边形OEAF 是否F
为菱形?
②是否存在点 E,使平行四边形OEAF 为正方形?若存在,求出点 E
A(6,0)x 的坐标;若不存在,请说明理由.
O
E
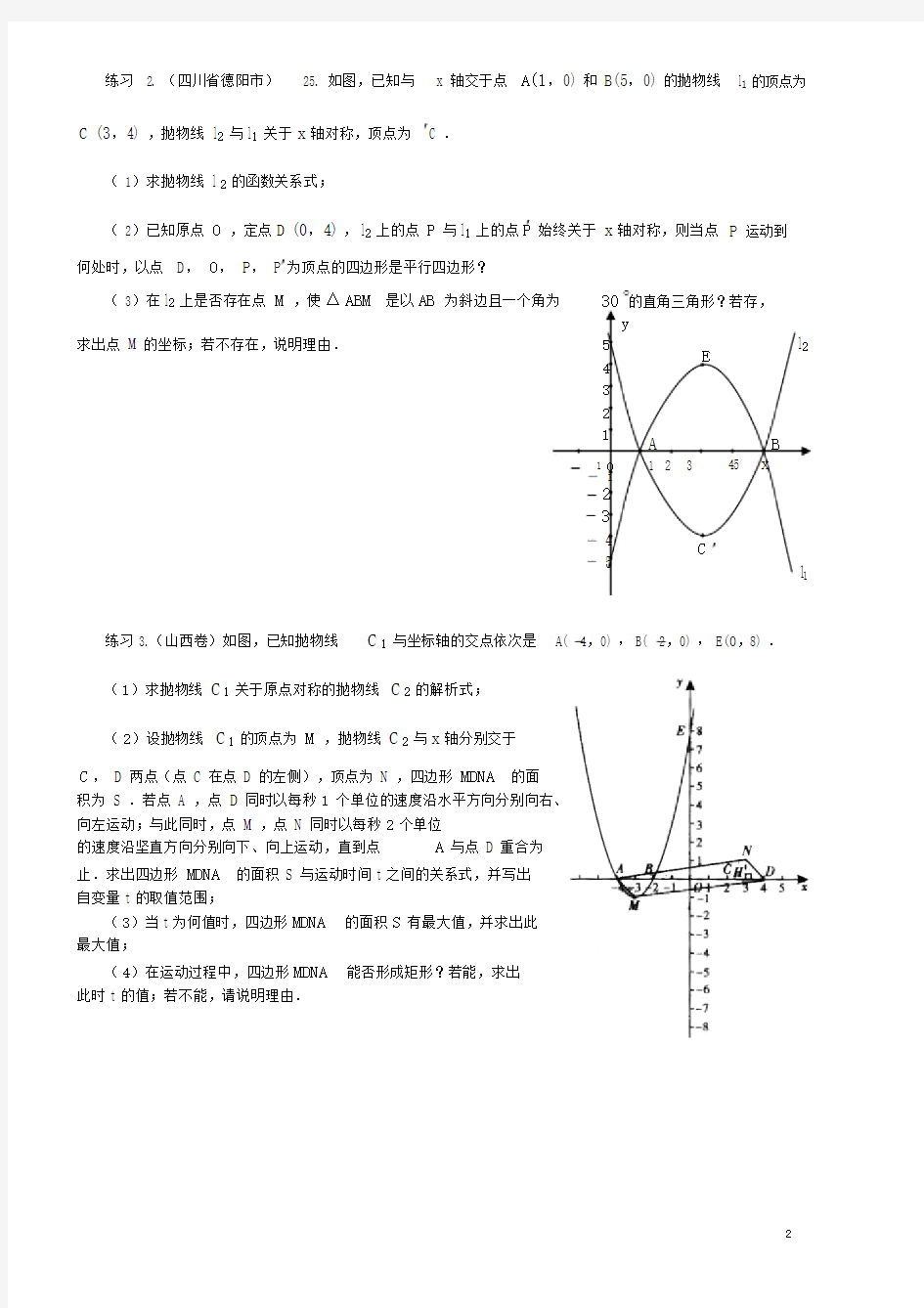
练习 2. (四川省德阳市)25. 如图,已知与x 轴交于点A(1,0) 和 B(5,0) 的抛物线l1的顶点为C (3,4) ,抛物线l2与l1关于x轴对称,顶点为 C .
( 1)求抛物线l2的函数关系式;
( 2)已知原点O,定点D (0,4),l2上的点P与l1上的点P始终关于x轴对称,则当点P 运动到何处时,以点 D, O, P, P 为顶点的四边形是平行四边形?
( 3)在l2上是否存在点M,使△ABM是以AB为斜边且一个角为30的直角三角形?若存,
求出点 M 的坐标;若不存在,说明理由.
y
l2 5
E
4
3
2
1A B
1 O 1
2 345 x
1
2
3
4C
5l
1
练习 3.(山西卷)如图,已知抛物线C1与坐标轴的交点依次是A( 4,0) , B( 2,0) , E(0,8) .(1)求抛物线C1关于原点对称的抛物线C2的解析式;
(2)设抛物线C1的顶点为M,抛物线C2与x轴分别交于
C, D 两点(点 C 在点 D 的左侧),顶点为 N ,四边形 MDNA 的面
积为 S .若点 A ,点 D 同时以每秒1个单位的速度沿水平方向分别向右、
向左运动;与此同时,点 M ,点 N 同时以每秒2个单位
的速度沿坚直方向分别向下、向上运动,直到点A与点 D 重合为
止.求出四边形 MDNA 的面积 S 与运动时间t之间的关系式,并写出
自变量 t 的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此
最大值;
(4)在运动过程中,四边形MDNA能否形成矩形?若能,求出
此时 t 的值;若不能,请说明理由.
二. 二次函数与四边形的面积
例 1. (资阳市) 25. 如图 10,已知抛物线
P : y=ax 2+bx+c(a ≠ 0) 与 x 轴交于 A 、B 两点 ( 点 A 在 x
轴的正半轴上 ) ,与 y 轴交于点 C ,矩形 DEFG 的一条边 DE 在线段 AB 上,顶点 F 、 G 分别在线段 BC 、 AC 上,抛物线 P 上部分点的横坐标对应的纵坐标如下:
x ? -3 -2 1 2 ? y
?
-
5
-4
-
5
?
2
2
(1) 求 A 、 B 、C 三点的坐标;
(2) 若点 D 的坐标为 (m ,0) ,矩形 DEFG 的面积为 S ,求 S 与 m 的函数关系,并指出 m 的取值范围;
(3) 当矩形 DEFG 的面积 S 取最大值时,连接 DF 并延长至点 M ,使 FM=k ·DF ,若点 M 不在抛物线 P 上,求 k 的取值范围 .
图 10
练习 1.(辽宁省十二市 2007 年第 26 题).如图,平面直角坐标系中有一直角梯形 OMNH ,点 H 的
坐标为(- 8, 0),点 N 的坐标为(- 6,- 4).
( 1)画出直角梯形 OMNH 绕点 O 旋转 180°的图形 OABC ,并写出顶点 A , B , C 的坐标(点 M 的对应点为 A , 点 N 的对应点为 B , 点 H 的对应点为 C );
( 2)求出过 A , B , C 三点的抛物线的表达式;
( 3)截取 CE =OF =AG =m ,且 E , F ,G 分别在线段 CO , OA , AB 上,求四边形 BEFG 的面积 S 与
m 之间的函数关系式,并写出自变量 m 的取值范围;面积 S 是否存在最小值 ?若存在,请求出这个最小值;若
不存在,请说明理由;
( 4)在(3)的情况下, 四边形 BEFG 是否存在邻边相等的情况, 若存在, 请直接写出此时 m 的值,并指出相等的邻边;若不存在,说明理由.
练习 3.(吉林课改卷)如图,正方形ABCD 的边长为 2cm ,在对称中心 O 处有一钉子.动点P ,Q同时从点 A出发,点P沿 A B C 方向以每秒 2cm 的速度运动,到点 C 停止,点 Q 沿 A D
方向以每秒 1cm 的速度运动,到点 D 停止. P , Q 两点用一条可伸缩的细橡皮B
C
P
O
筋联结,设 x 秒后橡皮筋扫过的面积为ycm2.
1y 与x之间的函数关系式;A Q D ()当 0 ≤ x ≤ 1时,求
B C
P ( 2)当橡皮筋刚好触及钉子时,求x 值;
O ( 3)当1≤x≤2时,求y与x之间的函数关系式,并写出橡皮筋从触及
钉子到运动停止时∠POQ 的变化范围;A Q D
y
3
( 4)当0≤x≤2时,请在给出的直角坐标系中画出y 与x之间的函数图
象.2
1
O1 2 x
练习 4.(四川资阳卷)如图,已知抛物线l1:y=x2-4 的图象与 x 轴相交于 A、C 两点, B 是抛物线l 1上的动点 (B 不与 A、 C 重合 ),抛物线 l2与 l1关于 x 轴对称,以 AC 为对角线的平行四边形ABCD 的第四个顶点为 D.
(1)求 l2的解析式;
(2)求证:点 D 一定在 l2上;
(3)□ ABCD能否为矩形?如果能为矩形,求这些矩形公共部分的面积
(若只有一个矩形符合条件,则求此矩形的面积 );如果不能为矩形,请说明理
由 . 注:计算结果不取近似值
.
三.二次函数与四边形的动态探究
例 1.(荆门市)28.如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知 O(0,0),A(4,0),
C(0,3),点 P 是 OA 边上的动点 (与点 O、A 不重合 ).现将△ PAB 沿 PB 翻折,得到△ PDB;再在 OC 边上选取适当的点 E,将△ POE 沿 PE 翻折,得到△ PFE ,并使直线 PD、 PF 重合.
(1) 设 P(x, 0),E(0, y),求 y 关于 x 的函数关系式,并求y 的最大值;
(2)如图 2,若翻折后点 D 落在 BC 边上,求过点 P、 B、 E 的抛物线的函数关系式;
(3)在 (2)的情况下,在该抛物线上是否存在点Q,使△ PEQ 是以 PE 为直角边的直角三角形?若不
存在,说明理由;若存在,求出点Q 的坐标.
y y
C B C
D B
F
E D
E F
O PA x O P A x
图 1图 2
例 2.(2010 年沈阳市第26 题)、已知抛物线y= ax2+bx+ c 与 x
轴交于 A、 B 两点,与 y 轴交于点 C,其中点 B 在 x 轴的正半轴上,点 C
在 y 轴的正半轴上,线段 OB、 OC 的长( OB 10x+ 16= 0 的两个根,且抛物线的对称轴是直线x=- 2. (1)求 A、B、 C 三点的坐标; (2)求此抛物线的表达式; ( 3)连接 AC、 BC,若点 E 是线段 AB 上的一个动点(与点 A、点 B 不重合),过点 E 作 EF ∥AC 交 BC 于点 F,连接 CE,设 AE 的 长为 m,△ CEF 的面积为 S,求 S 与 m 之间的函数关系式,并写出自 变量 m 的取值范围; ( 4)在( 3)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点 E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由. 例 3..(湖南省郴州 ) 27.如图,矩形ABCD 中, AB=3, BC= 4,将矩形 ABCD 沿对角线 A 平移, 平移后的矩形为EFGH ( A 、 E、 C、 G 始终在同一条直线上),当点 E 与 C 重时停止移动.平移中 EF 与 BC 交于点 N,GH 与 BC 的延长线交于点M, EH 与 DC 交于点 P, FG 与 DC 的延长线交于点Q.设 S 表示矩形 PCMH 的面积,S表示矩形 NFQC 的面积. ( 1) S 与S相等吗?请说明理由. ( 2)设 AE= x,写出 S 和 x 之间的函数关系式,并求出x 取何值时 S 有最大值,最大值是多少? ( 3)如图11,连结 BE,当 AE 为何值时,ABE 是等腰三角形. A D A D x P E H E P H B N C M B M N C F Q G F Q G 图 10 图 11 练习 1.(07 年河池市)如图 12,四边形 OABC 为直角梯形, A( 4,0),B( 3,4),C( 0,4).点 M 从O出发以每秒 2 个单位长度的速度向A运动;点N从B同时出发,以每秒 1 个单位长度的速度 向 C 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N 作 NP 垂直x轴于点P, 连结 AC 交 NP 于 Q,连结 MQ. ( 1)点(填 M 或 N)能到达终点; y C ( 2)求△ AQM 的面积 S 与运动时间 t 的函数关系式,并写出自 N B 变量 t 的取值范围,当 t 为何值时, S 的值最大; ( 3)是否存在点 M,使得△ AQM 为直角三角形?若存在,求出点M 的坐标, Q 若不存在,说明理由. M P A x O 图 12 练习 2..(江西省 ) 25.实验与探究 ( 1)在图 1,2,3 中,给出平行四边形ABCD 的顶点 A, B, D 的坐标(如图所示),写出图1,2, 3 中的顶点C的坐标,它们分别是(5,2) ,,; y y y B(12),B(c,d )B(c,d) C C C x x A( a, b) D (e,b) O (A)O (A) D (e,0)O x D (4,0) 图 1图 2图 3 ( 2)在图 4 中,给出平行四边形ABCD 的顶点 A, B, D 的坐标(如图所示),求出顶点 C 的坐标( C 点坐标用含 a, b, c, d, e, f 的代数式表示); y C B(c,d) D( e, f ) A( a, b) x O 图 4 归纳与发现 ( 3)通过对图1,2,3,4 的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD 处于直角坐标系中哪个位置,当其顶点坐标为A( a, b), B(c, d ), C (m, n), D (e, f ) (如图4)时, 则四个顶点的横坐标a, c, m, e ;纵坐标 b, d, n, f 之间的等量关之间的等量关系为 系为(不必证明); 运用与推广 ( 4)在同一直角坐标系中有抛物线y x2(5c3)x 1519 ,c 和三个点G c, c , S 2 c, c 222 H (2c,0) (其中 c0).问当 c 为何值时,该抛物线上存在点P ,使得以 G, S, H , P 为顶点的四边形是平行四边形?并求出所有符合条件的P 点坐标. 答案: 一. 二次函数与四边形的形状 例 1.解:( 1)令 y=0 ,解得 x 1 1或 x 2 3 ∴ A ( -1, 0)B ( 3, 0); 将 C 点的横坐标 x=2 代入 y x 2 2x 3 得 y=-3 ,∴C (2,-3)∴直线 AC 的函数解析式是 y=-x-1 ( 2)设 P 点的横坐标为 x ( -1≤ x ≤ 2)则 P 、 E 的坐标分别为: P (x , -x-1 ), E ( ( x, x 2 2x 3)∵ P 点在 E 点的上方, PE= ( x 1) ( x 2 2x 3) x 2 x 2 1 9 ∴当 x 时, PE 的最大值 = 2 4 ( 3)存在 4 个这样的点 F ,分别是 F 1(1,0), F 2 ( 3,0), F 3 (4 7,0), F 4 (4 7,0) 7 y 练 习 1. 解 : ( 1 ) 由 抛 物 线 的 对 称 轴 是 x ,可设解析式为 7) 2 x y a( x k .把 A 、 B 两点坐标代入上式,得 2 a(6 7 2 k 0, B(0,4) 2 ) 2 25 解之,得 a , k . a(0 7 ) 2 k 4. 3 6 2 故抛物线解析式为 y 2 7 2 25 7 25 ). O (x ) ,顶点为 ( , 3 2 6 2 6 E ( 2)∵点 E( x, y) 在抛物线上,位于第四象限,且坐标适合 y 2 (x 7)2 25 , 3 2 6 OEAF 的对角线, ∴ y<0,即 - y>0, - y 表示点 E 到 OA 的距离.∵ OA 是 ∴S 2S OAE 2 1 OA y 6y 4( 7) 2 25 . 2 2 因为抛物线与 x 轴的两个交点是( 1, 0)的( 6, 0),所以,自变量 x 的 取值范围是 1< x < 6. ① 根据题意,当 S = 24 时,即 4( x 7 ) 2 25 24. 7) 2 1 . 2 化简,得 ( x 解之,得 x 1 3, x 2 4. 2 4 故所求的点 E 有两个,分别为 E 1( 3,- 4), E 2( 4,- 4). 点 E 1 (3,- 4)满足 OE = AE ,所以 OEAF 是菱形; 点 E 2( 4,- 4)不满足 OE = AE ,所以 OEAF 不是菱形. ② 当 OA ⊥EF ,且 OA = EF 时, OEAF 是正方形,此时点 坐标只能是( 3,- 3). y 而坐标为( 3,- 3)的点不在抛物线上,故不存在这样的点 E , 5 使 OEAF 为正方形. 4 7 2 F A(6,0) x E 的 l 2 E 练习 2.解: ( 1)由题意知点 C 的坐标为 (3, 4) .设 l 2 的函数关系式为 y 3 a( x 3)2 4 . 2 又 点 A(10), 在抛物线 y a(x 3)2 4 上, (1 3)2 a 4 0 ,解得 a 1. 抛物线 l 2 的函数关系式为 y ( x 3)2 4 (或 y x 2 6x 5 ). ( 2) P 与 P 始终关于 x 轴对称, PP 与 y 轴平行. 设点 P 的横坐标为 m ,则其纵坐标为 m 2 6m 5 , OD 4, 2 m 2 6m 5 4 ,即 m 2 6m 5 2 . 当 m 2 6m 5 2时 , 解 得 m 3 6 . 当 m 2 6m 52时 , 解 得 m 3 2 . 当点 P 运动到 (3 6,2) 或 (3 6,2) 或 (3 2, 2)或 (3 2, 2) 时, P P ∥ OD ,以点 D , O , P , P 为顶点的四边形是平行四边形. ( 3)满足条件的点 M 不存在.理由如下:若存在满足条件的点 M 在 l 2 上,则 AMB 90 , BAM 30 (或 ABM 30 ), y BM 1 1 4 2 . 5 C l 2 AB 2 D 2 3 过点M 作ME AB 于点 E ,可得 BME BAM 30 . 2 1 1 1 E B EB 2 1,EM 3,OE 4. O x BM 2 1 1 2 3 4 5 2 1 4 A M 点 M 的坐标为 (4, 3) . 2 3 但是,当 x 4 时, y 4 2 6 4 5 16 24 5 3 3 . 5 C l 1 不存在这样的点 M 构成满足条件的直角三角形. 练习 3. [解 ] (1)点 A( 40), ,点 B( 20), ,点 E(08), 关于原点的对称点分别为 D (4,0) ,C (2,0) , F (0, 8) . 设抛物线 C 2 的解析式是 16a 4b c , a , 1 y ax 2 bx c(a 0) ,则 4a 2b c 0,解得 b 6, c 8. c 8. 所以所求抛物线的解析式是 y x 2 6x 8 . ( 2)由( 1)可计算得点 M ( 3, 1), N (31), . 过点N 作NH AD ,垂足为 H . 当运动到时刻 t 时, AD 2OD 8 2t , NH 1 2t . 根据中心对称的性质 OA OD , OM ON ,所以四边形 MDNA 是平行四边形. 所 以 2 △ .所以, 四 边 形 MDNA 的 面 积 S (8 2t )(1 2t ) 4t 214t 8 A 与点 D 重合为止,据题意可知 0≤ t 4. . 因为运动至点 所以,所求关系式是 S 4t 2 14t 8 , t 的取值范围是 0 ≤ t 4. (3)S 4 t 7 81 ,( 0 ≤ t 4 ). 4 4 所以 t 7 时, S 有最大值 81 . 4 4 提示:也可用顶点坐标公式来求. ( 4)在运动过程中四边形 MDNA 能形成矩形. 由( 2)知四边形 MDNA 是平行四边形, 对角线是 AD , MN ,所以当 AD MN 时四边形 MDNA 是矩形. 所以 OD ON .所以 OD 2 ON 2 OH 2 NH 2. 所以 t 2 4t 2 2 0 .解之得 t 16 2,t 2 6 2 (舍). 所以在运动过程中四边形 MDNA 可以形成矩形,此时 t 6 2 . [ 点评 ] 本题以二次函数为背景,结合动态问题、存在性问题、最值问题,是一道较传统的压轴题, 能力要求较高。 二. 二次函数与四边形的面积 例 1. 解:( 1)解法一:设 y ax 2 bx c(a 0) , 任取 x,y 的三组值代入,求出解析式 y = 1 x 2 + x - 4 , 2 令 y=0,求出 x 1 = - 4, x 2 = 2 ;令 x=0,得 y=-4 , ∴ A 、B 、 C 三点的坐标分别是 A(2 , 0) ,B(-4 , 0) , C(0, -4) .········· 解法二:由抛物线 P 过点 (1 , - 5 ),(-3 ,- 5 ) 可知, 2 2 抛物线 P 的对称轴方程为 x=-1 , 又∵ 抛物线 P 过 (2 , 0) 、 (-2 , -4) ,则由抛物线的对称性可知, 点 A 、B 、 C 的坐标分别为 A(2 , 0) , B(-4 , 0) , C(0, -4) . ( 2)由题意, AD = DG ,而 AO=2, OC=4, AD=2-m ,故 DG=4-2m , ········ AO OC 又 BE = EF , EF=DG ,得 BE=4-2m ,∴ DE=3m , BO OC ∴ s DEFG =DG · DE=(4-2m) 3m=12m-6m 2 (0 < m < 2) . 注:也可通过解 Rt △BOC 及 Rt △ AOC ,或依据△ BOC 是等腰直角三角形建立关系求解. 2 ,∴ m=1时,矩形的面积最大,且最大面积是6 . (3) ∵SDEFG=12m-6m(0 <m < 2) 当矩形面积最大时,其顶点为 D(1, 0) , G(1, -2) ,F(-2 , -2) , E(-2 ,0) , 设直线 DF 的解析式为 y=kx+b ,易知, k= 2 , b=- 2 ,∴ y = 2 x - 2 , 3 3 3 3 又可求得抛物线 P 的解析式为: 1 2 y = x + x - 4 , 2 令 2 x - 2 = 1 x 2 + x - 4 ,可求出 x 1 61 . 设射线 DF 与抛物线 P 相交于点 N , 3 3 2 3 则 N 的横坐标为 - 1- 61 ,过 N 作 x 轴的垂线交 x 轴于 H ,有 3 FN HE -2- -1- 3 61 - 5 + 61 = = , DF = 9 DE 3 点 M 不在抛物线 P 上,即点 M 不与 N 重合时,此时 k 的取值范围是 k ≠ - 5 + 61 且 k > 0. 9 说明:若以上两条件错漏一个,本步不得分 . 若选择另一问题: (2) ∵ AD = DG ,而 AD=1, AO=2, OC=4,则 DG=2, AO OC 又∵ FG = CP , 而 AB=6, CP=2, OC=4,则 FG=3, AB OC ∴ s DEFG =DG ·FG=6. 练习 1. 解:利用中心对称性质,画出梯形 OABC . ················· 1 分 ∵ , , C 三点与 , , H 分别关于点 O 中心对称, A B M N ∴ A (0, 4), B ( 6, 4), C ( 8, 0) ···················3 分 (写错一个点的坐标扣 1 分) ( 2)设过 A ,B , C 三点的抛物线关系式为 , ∵抛物线过点 A ( 0, 4), ∴ .则抛物线关系式为 . ·············· 4 分 将 B (6, 4), C ( 8, 0)两点坐标代入关系式,得 ···························· 5 AB ,垂足为 G ,则 sin ∠ FEG =sin ∠CAB = 分 解得 ····················· 6 分 所求抛物线关系式为: .········ 7 分 ( 3)∵ OA =4,OC =8,∴ AF =4- m , OE =8- m . ·········· 8 分 ∴ OA ( AB +OC ) AF · AG OE · OF CE ·OA ( 0 < < 4) ········ 10 分 ∵ . ∴当 时, S 的取最小值. 又∵ 0< < 4,∴不存在 值,使 S 的取得最小值. ······· 12 分 m m (4)当 时, GB =GF ,当 时, BE =BG . 14 分 练习 3.[解 ] ( 1)当 0 ≤ x ≤ 1时, AP 2x , AQ x , y 1 AQ AP x 2 , 2 即 y x 2 . ( 2)当 S 四边形 ABPQ 1 S 正方形 ABCD 时,橡皮筋刚好触及钉子, 2 BP 2x 2 , AQ x , 1 2 x 2 x 2 1 22 , x 4 . 2 2 3 ( 3)当 1≤ x ≤ 4 时, AB 2, 3 PB 2x 2 , AQ x , y AQ BP AB x 2x 2 2 3x 2, 2 2 即 y 3x 2 . 作 OE ⊥AB ,E 为垂足. 当 4 ≤ x ≤ 2 时, BP 2x 2 , AQ x , OE 1 , 3 yS S 梯形 3 y 3 2 1 即 y 3 x . 2 90 ≤∠ POQ ≤ 180 或 180 ≤∠ POQ ≤ 270 ( 4)如图所示: 练习 4.[解 ] (1) 设 l 2 的解析式为 y=ax 2+bx+c(a ≠ 0), ∵l 1 与 x 轴的交点为 A(- 2, 0), C(2,0) ,顶点坐标是 (0, - 4), l 2 与 l 1 关于 x 轴对称, ∴l 2 过 A(- 2,0),C(2,0),顶点坐标是 (0, 4), 4a 2b c 0 , ∴ 4a 2b c 0 , c 4. 2 ∴ a=- 1,b=0,c=4,即 l 2 的解析式为 y= - x +4 . (还可利用顶点式、对称性关系等方法解答 ) (2) 设点 B(m , n)为 l 1: y=x 2- 4 上任意一点,则 n= m 2- 4 (* ). ∵ 四边形 ABCD 是平行四边形,点 A 、 C 关于原点 O 对称, ∴ B 、D 关于原点 O 对称, ∴ 点 D 的坐标为 D(- m,- n) . 由 (* )式可知, - n=-( m 2- 4)= -(- m)2+4, 2 即点 D 的坐标满足 y= - x +4, ∴ 点 D 在 l 2 上 . (3) □ABCD 能为矩形 . 过点 B 作 BH ⊥x 轴于 H ,由点 B 在 l 1: y=x 2- 4 上,可设点 B 的坐标为 (x 0, x 02- 4), 则 OH=| x 0 |, BH =| x 0 2 -4|. 易知,当且仅当 BO= AO=2 时, □ ABCD 为矩形 . 在 Rt △OBH 中,由勾股定理得, | x 0|2+| x 0 2- 4|2=22, (x 0 2 - 4)( x 02 - 3)=0 ,∴x 0=±2(舍去 )、 x 0=± 3 . 所以,当点 B 坐标为 B( 3 , - 1)或 B ′(-3 , - 1)时, □ABCD 为矩形,此时,点 D 的坐标分别是 D(- 3 , 1)、D ′ ( 3 ,1). 因此,符合条件的矩形有且只有2 个,即矩形 ABCD 和矩形 AB ′CD ′. 设直线 AB 与 y 轴交于 E ,显然, △AOE ∽△AHB , ∴EO BH EO 1 AO =AH ,∴ 2 23 . ∴EO=4-2 3 . 由该图形的对称性知矩形 ABCD 与矩形 AB ′CD ′重合部分是菱形,其面积为 1 1 S=2S ACE =2× ×AC ×EO = 2 × ×4×(4- 2 3 )=16 - 8 3 . 2 2 三. 二次函数与四边形的动态探究 例 1.解: (1) 由已知 PB 平分∠ APD , PE 平分∠ OPF ,且 PD 、 PF 重合,则∠ BPE=90°.∴∠ OPE +∠ APB=90°.又∠ APB +∠ ABP=90°,∴∠ OPE=∠PBA . ∴ Rt △POE ∽ Rt △ BPA . ∴ PO BA x 3 .∴ y= 1 x( 4 x) 1 x 2 4 x (0< x < 4). .即 4 x OE AP y 3 3 3 且当 x=2 时, y 有最大值1.3 (2) 由已知,△ PAB 、△ POE 均为等腰三角形,可得P(1, 0), E(0,1),B(4, 3). a 1 , c1,2 3 , 设过此三点的抛物线为y=ax2+ bx+ c,则a b c0,∴ b 16a4b c 3. 2 c 1. y= 1 x2 3 x 1 .2 2 (3)由 (2)知∠ EPB =90 °,即点 Q 与点 B 重合时满足条件.直线 PB 为 y=x- 1,与 y 轴交于点 (0,- 1).将 PB 向上平移 2 个单位则过点 E(0, 1),∴ 该直线为 y=x+1. y x1, x 5, ∴ Q(5 ,6). 由 1x23得 y x 1,y 6. 22 故该抛物线上存在两点Q(4, 3)、 (5,6)满足条件. 例 2.解:( 1)解方程 x2- 10x+16= 0 得 x1= 2, x2=8 ???????? 1 分∵点 B 在 x 轴的正半轴上,点 C 在 y 轴的正半轴上,且 OB< OC ∴点 B 的坐标为( 2,0),点 C 的坐标为( 0,8) 又∵抛物线 y= ax2+ bx+c 的对称轴是直线 x=- 2 ∴由抛物线的对称性可得点 A 的坐标为(- 6, 0)??????? 4 分 (2)∵点 C( 0, 8)在抛物线 y= ax2+ bx+ c 的图象上 ∴ c= 8,将 A(- 6, 0)、 B( 2, 0)代入表达式,得 解得 ∴所求抛物线的表达式为y=x2x+ 8?????????7 分 (3)依题意, AE=m,则 BE= 8- m, ∵ OA=6, OC= 8,∴ AC= 10 ∵EF∥ AC ∴△ BEF ∽△ BAC ∴即 ∴ = ∴ FG = · = 8- m ∴ S =S △ BCE - S △ BFE = (8- m ) ×8- ( 8- m )( 8- m ) = ( 8- m )( 8- 8+ m )= ( 8-m ) m =- m2+ 4m ???? 10 分 自变量 m 的取值范围是 0< m < 8 ?????????? 11 分 ( 4)存在. 理由:∵ S =- m2+4m =- ( m - 4) 2+8 且- < 0, ∴当 m =4 时, S 有最大值, S 最大值= 8????????? 12 分 ∵ m = 4,∴点 E 的坐标为(- 2, 0) ∴△ BCE 为等腰三角形. ?????????? 14 分 (以上答案仅供参考,如有其它做法,可参照给分) 例 3 解: (1)相等 理由是:因为四边形 ABCD 、EFGH 是矩形, 所以 S EGH S EGF ,S ECN S ECP , S CGQ S CGM 所以 S EGH S ECP S CGM S EGF S ECN S CGQ , 即: S S ( 2)AB =3, BC = 4,AC =5,设 AE = x ,则 EC = 5- x , PC 3 (5 x), MC 4 x , 5 5 所以S PCMC 12 x(5 x) ,即 S 12 x 2 12 x (0 x 5) 25 25 5 配方得: S 12 (x 5)2 3,所以当 x 5 时, 25 2 2 S 有最大值 3 ( 3)当 AE= AB= 3 或 AE= BE=5 或 AE= 3.6 时,ABE 是等腰三角形2 练习 1.解:( 1)点 M 1 分( 2)经过 t 秒时,NB t , OM2t 则 CN3t , AM42t ∵ BCA =MAQ = 45∴ QN CN3t∴ PQ1t 1 AM PQ 1 (4t 21 2 9 ∴S △ AMQ2t )(1 t)t2∴ S t 2t2t 2224 ∵ 0≤ t ≤ 2 ∴当 t 1 时, S 的值最大.2 ( 3)存在.设经过 t 秒时, NB=t,OM= 2t则 CN3t , AM42t ∴BCA =MAQ = 45①若AQM90 ,则PQ是等腰Rt△MQA底边MA上的高 ∴ PQ 是底边MA的中线∴PQ AP 1 MA∴1t 1 (42t ) ∴ t1 222 ∴点 M 的坐标为(1,0) ②若QMA90 ,此时QM与QP重合∴QM QP MA ∴1t42t ∴ t1 ∴点 M 的坐标为(2,0) 练习 2.解:( 1)( e c, d ) , (c e a, d) . ( 2)分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1, 分别过 A,D 作AE BB1于E, DF CC1于点F. y C 在平行四边形ABCD中, CD BA ,又BB1∥ CC1, B (c, d )F D (e,f ) EBA ABC BCF ABC BCF FCD180 . O E A( a, b) x B 1 A 1 C 1 D 1 EBA FCD . 又BEA CFD90 , △BEA ≌△ CFD . AF DF a c , BE CF d b . 设 C (x, y) .由e x a c ,得 x e c a . 由 y f d b ,得 y f d b . C (e c a, f d b) . ( 3)m c e a, n d f b .或m a c e, n b d f . ( 4)若GS为平行四边形的对角线,由(3)可得P1(2c,7c) .要使 P1在抛物线上,则有 7c4c2(5c 3) ( 2c) c ,即c2c0 . c 1 0 (舍去), c21.此时 P1( 2,7) . 若 SH 为平行四边形的对角线,由(3)可得P2(3c,2c),同理可得c1,此时P2(3,2).若 GH 为平行四边形的对角线,由(3)可得(c,2c),同理可得c 1 ,此时P3(1,2).综上所述,当 c1时,抛物线上存在点 P ,使得以 G, S, H , P 为顶点的四边形是平行四边形.符合条件的点有P1 ( 2,7) , P2 (3,2), P3(1, 2). 练习 3.解:⑴由Rt△ AOB ≌ Rt △CDA得 OD=2+1=3,CD=1 ∴C 点坐标为 ( -3,1), ∵抛物线经过点C, ∴ 1= (-3) 2 a+(- 3)a- 2,∴a 1 。 2 ∴抛物线的解析式为 y 1 x2 1 x 2 . 22 ⑵在抛物线(对称轴的右侧)上存在点P、Q,使四边形 ABPQ 是正方形。 以AB 边在 AB 右侧作正方形 ABPQ 。过 P 作 PE⊥ OB 于 E, QG ⊥ x 轴于 G,可 证△ PBE≌△ AQG ≌△ BAO , ∴ PE= AG =BO= 2, BE =QG= AO = 1, ∴∴ P 点坐标为( 2,1), Q 点坐标为( 1,- 1)。 1 x 21x 2。 由( 1)抛物线y 2 2 当x=2 时, y= 1,当 x= ,1 时, y=- 1。 ∴ P、Q 在抛物线上。 故在抛物线(对称轴的右侧)上存在点P(2,1)、 Q( 1,- 1),使四边形ABPQ 是正方形。 ⑵另解:在抛物线(对称轴的右侧)上存在点P、 Q,使四边形ABPQ 是正方形。 延长 CA 交抛物线于Q,过 B 作 BP∥CA 交抛物线于P,连 PQ,设直线 CA 、BP 的解析式分别为y=k 1x+b1, y=k 2 x+b2 , ∵ A(- 1,0), C(- 3,1), ∴ CA 的解析式y 1 x1,同理 BP 的解析式为y 1 x1, 2222 y 1 x1 解方程组22得 Q 点坐标为( 1,-1),同理得 P 点坐标为( 2,1)。 1 x 2 1 x y2 22 由勾股定理得 AQ = BP = AB = 5 ,而∠ BAQ = 90°, ∴四边形 ABPQ 是正方形。故在抛物线(对称轴的右侧)上存在点 P (2,1)、 Q ( 1,- 1),使四 边形 ABPQ 是正方形。 ⑵另解:在抛物线(对称轴的右侧)上存在点 P 、 Q ,使四边形 ABPQ 是正方形。 如图,将线段 CA 沿 CA 方向平移至 AQ , ∵ C (- 3,1)的对应点是 A (- 1,0),∴ A (- 1,0)的对应点是 Q ( 1,- 1),再将线段 AQ 沿 AB 方向平移至 BP ,同理可得 P ( 2,1) ∵∠ BAC = 90°, AB =AC ∴四边形 ABPQ 是正方形。经验证 P ( 2,1)、 Q ( 1,-1)两点均在抛物线 y 1 x 2 1 x 2 上。 2 2 ⑶结论② BF BG 成立, AF AG 证明如下:连 EF ,过 F 作 FM ∥ BG 交 AB 的延长线于 M ,则△ AMF ∽△ ABG , ∴ MF BG 。由⑴知△ ABC 是等腰直角三角形, AF AG ∴∠ 1=∠ 2= 45°。∵ AF = AE ,∴∠ AEF =∠ 1= 45°。∴∠ EAF = 90°, EF 是⊙ O ′的直径。 ∴∠ EBF = 90°。∵ FM ∥BG ,∴∠ MFB =∠ EBF = 90°,∠ M =∠ 2= 45°, ∴ BF =MF , ∴ BF BG AF AG y x O 二次函数中的动点问题(二) 平行四边形的存在性问题 一、技巧提炼 1、二次函数y=ax 2 +bx+c 的图像和性质 a >0 a <0 图 象 开 口 对 称 轴 顶点坐标 最 值 当x = 时,y 有最 值是 当x = 时,y 有最 值是 增减 性 在对称轴左侧 y 随x 的增大而 y 随x 的增大而 在对称轴右侧 y 随x 的增大而 y 随x 的增大而 2、平行四边形模型探究 如图1,点A ()11,x y 、B ()22,x y 、C ()33,x y 是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D ,使得以A 、B 、C 、D 四点为顶点的四边形为平行四边形,如果存在,请求出点D 的坐标。 A B C x y 图1 图2 如图2,过A 、B 、C 分别作BC 、AC 、AB 的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。 由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。 3、平面直角坐标系中直线和直线l2: 当l1∥l2时k1= k2; 4、二次函数中平行四边形的存在性问题: 解题思路:(1)先分类(2)再画图(3)后计算 二、精讲精练 1、已知抛物线y=ax2+bx+c与x轴相交于A、B两点(A、B分别在原点的左右两侧),与y轴正半轴相交于C 点,且OA:OB:OC=1:3:3,△ABC的面积为6,(如图1) (1)求抛物线的解析式; (2)坐标平面内是否存在点M,使得以点M、A、B、C为顶点四边形是平行四边形若存在,请求出点M的坐标;若不存在,请说明理由; (3)如图2,在直线BC上方的抛物线上是否存在一动点P,△BCP面积最大如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由. 二次函数的动点问题 1.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒. (1)求正方形ABCD 的边长. (2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度. (3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标. (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =o ∠的点P 有 个. (抛物线()2 0y ax bx c a =++≠的顶点坐标是2424b ac b a a ?? -- ??? ,. [解] (1)作BF y ⊥轴于F . ()()01084A B Q ,,,, 86FB FA ∴==,. 10AB ∴=. (2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=Q ,. P Q ∴,两点的运动速度均为每秒1个单位. (3)方法一:作PG y ⊥轴于G ,则PG BF ∥. GA AP FA AB ∴ =,即610 GA t =. 35GA t ∴=. 3 105OG t ∴=-. 4OQ t =+Q , ()113410225S OQ OG t t ? ?∴= ??=+- ?? ?. 函数解题思路方法总结: ⑴求二次函数的图象与x轴的交点坐标,需转化为一元二次方程; ⑵求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶根据图象的位置判断二次函数ax2+bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断 图象的位置,要数形结合; ⑷二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸与二次函数有关的还有二次三项式,二次三项式ax2+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系: 动点问题题型方法归纳总结 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。 二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由. (3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标. 注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P 坐标----①C 为顶点时,以C 为圆心CM 为半径画弧,与对称轴交点即为所求点P ,②M 为顶点时,以M 为圆心MC 为半径画弧,与对称轴交点即为所求点P ,③P 为顶点时,线段MC 的垂直平分线与对称轴交点即为所求点P 。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC 平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。 共同点: 函数解题思路方法总结: ⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数ax 2+bx+c=0中a,b,c 的符号,或由二次函数中a,b,c 的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式ax 2+bx+c ﹙a ≠0﹚本身就是所含字母x 的二次函数;下面以a >0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系: 动点问题题型方法归纳总结 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。 二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x轴交于点M ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由. (3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标. 注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时,以C为圆心CM为半径画弧,与对称轴交点即为所求点P,②M为顶点时,以M为圆心MC为半径画弧,与对称轴交点即为所求点P,③P为顶点时,线段MC的垂直平分线与对称轴交点即为所求点P。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值);方法二,先求与BC平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。 函数解题思路方法总结: ⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数ax 2+bx+c=0中a,b,c 的符号,或由二次函数中a,b,c 的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求与已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标、 ⑸ 与二次函数有关的还有二次三项式,二次三项式ax 2+bx+c ﹙a ≠0﹚本身就就是所含字母x 的二次函数;下面以a >0时为例,揭示二次函数、二次三项式与一元二次方程之间的内在联系: 二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)与点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上就是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由. (3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标. 注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时,以C为圆心CM为半径画弧,与对称轴交点即为所求点P,②M为顶点时,以M为圆心MC为半径画弧,与对称轴交点即为所求点P,③P为顶点时,线段MC的垂直平分线与对称轴交点即为所求点P。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。 ①特殊四边形为背景; ②点动带线动得出动三角形; ③探究动三角形问题(相似、等腰三角形、面积函数关系式); ④求直线、抛物线解析式; ⑤探究存在性问题时,先画出图形,再根据图形性质探究答案。 二次函数的动态问题(动点) 中考二次函数动点问题(含答案) 1.如图①,正方形的顶点的坐标分别为,顶点在第一象限.点从点出发,沿正方形按逆时针方 向匀速运动,同时,点从点出发,沿轴正方向以相同速度运动.当点到达点时,两点同时停止 运动,设运动的时间为秒. (1)求正方形的边长. (2)当点在边上运动时,的面积(平方单位)与时间(秒)之间的函数图象为抛物线的一部分 (如图②所示),求两点的运动速度. (3)求(2)中面积(平方单位)与时间(秒)的函数关系式及面积取最大值时点的坐标.(4)若点ABCD保持(2)中的速度不变,则点ABCD沿着ABCD边运动时,ABCD的大小随着时间ABCD的增大而增大;沿着ABCD边运动时,ABCD的大小随着时间ABCD的增大而减小.当点ABCD沿着这两边运动时,使ABCD的点ABCD有个. (抛物线ABCD的顶点坐标是. [解] (1)作轴于. , . . (2)由图②可知,点从点运动到点用了10秒. 又. 两点的运动速度均为每秒1个单位. (3)方法一:作ABCD轴于ABCD,则ABCD. ABCD ,即 ABCD . ABCD .ABCD .ABCD, ABCD . 即 ABCD . ABCD ,且 ABCD , ABCD当 ABCD 时,ABCD有最大值. 此时 ABCD , ABCD点ABCD的坐标为 ABCD .(8分) 方法二:当ABCD时, ABCD . 设所求函数关系式为. 抛物线过点, . ,且, 当时,有最大值. 此时, 点的坐标为. (4). [点评]本题主要考查函数性质的简单运用和几何知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难。 . 2. 如图①,中,,.它的顶点的坐标为,顶点的坐标为,,点从点出发,沿的方向匀速运动,同时点从点出发,沿轴正方向以相同速度运动,当点到达点时,两点同时停止运动,设运动的时间为秒. (1)求的度数. (2)当点在上运动时,的面积(平方单位)与时间(秒)之间的函数图象为抛物线的一部分,(如图②),求点的运动速度. (3)求(2)中面积与时间之间的函数关系式及面积取最大值时点的坐标. (4)如果点ABCD保持(2)中的速度不变,那么点ABCD沿ABCD边运动时,ABCD的大小随着时间ABCD的增大而增大;沿着ABCD边运动时,ABCD的大小随着时间ABCD的增大而减小,当点ABCD沿这两边运动时,使ABCD的点ABCD有几个?请说明理由. 解: (1)ABCD. 函数性问题专题—动点问题 函数及其图象是初中数学中的主要内容之一,也是初中数学与高中数学相联系的纽带.它与代数、几何、三角函数等知识有着密切联系,中考命题中既重点考查函数及其图象的有关基础知识,同时以函数为背景的综合性问题也是命题热点之一,多数省市作压轴题.因此,在中考复习中,关注这一热点显得十分重要.以函数为背景的综合性问题往往都可归结为动点性问题,我们把它归纳为以下七种题型(附例题) 一、因动点而产生的面积问题 例1:如图10,已知抛物线P :y =ax 2 +bx +c (a ≠0 与x 轴交于A 、B 两点(点A 在x 轴的正半轴上,与y 轴交于点C ,矩形DEFG 的一条边DE 在线段AB 上,顶点F 、G 分别在线段BC 、AC 上,抛物线P 上部分点的横坐标对应的纵坐标如下: (1 求A 、B 、C 三点的坐标; (2 若点D 的坐标为(m ,0 ,矩形DEFG 的面积为S ,求S 与m 的函数关系,并指出m 的取值范围; (3 当矩形DEFG 的面积S 取最大值时,连接DF 并延长至点M ,使FM =k ·DF ,若点M 不在抛物线P 上,求k 的取值范围. 若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2、(3小题换为下列问题解答(已知条件及第(1小题与上相同,完全正确解答只能得到5分: (2 若点D 的坐标为(1,0 ,求矩形DEFG 的面积 . 例2:如图1,已知直线 12 y x =-与抛物线2 164 y x =- +交于A B ,两点. (1)求A B ,两点的坐标; (2)求线段A B 的垂直平分线的解析式; (3)如图2,取与线段A B 端点分别固定在A B ,两处.用铅笔拉着这根橡皮筋使笔尖P 在直线A B 动点P 将与A B ,构成无数个三角形,这些三角求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.图2 图1 图10 第-2-页共4页 例3:如图1,矩形ODEF 的一边落在矩形ABCO 的一边上,并且矩形ODE F ∽矩形ABCO ,其相似比为1 : 4,矩形ABCO 的边 AB=4,BC=4 二次函数与几何图形 模式1:平行四边形 分类标准:讨论对角线 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形,则可分成以下几种情况 (1)当边AB 是对角线时,那么有BC AP // (2)当边AC 是对角线时,那么有CP AB // (3)当边BC 是对角线时,那么有BP AC // 1、本题满分14分)在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标. 2、如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系. 模式2:梯形 分类标准:讨论上下底 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成梯形,则可分成以下几种情况 (1)当边AB 是底时,那么有PC AB // (2)当边AC 是底时,那么有BP AC // (3)当边BC 是底时,那么有AP BC // 3、已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 3 2 -=与边BC 相交于点D . (1)求点D 的坐标; (2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式; (3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由. (2)抛物线的对称轴与x轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点 精品资料欢迎下载 二次函数中的动点问题(一) 学习目标 1、熟悉掌握二次函数的概念及图像的特征。 2、掌握二次函数解析式的具体求法及二次函数的一些基本性质及利用二次函数的性质解决一些极值问题:如边长、面积、利润等。 3、解决二次函数中因动点产生不同图形的问题及其包含的一些几何问题 学习过程 一、因动点产生的相似三角形问题 例1:如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,D为OC的中点,直线AD交抛物线于点E(2,△6),且ABE与△ABC的面积之比为3∶2. (1)求直线AD和抛物线的解析式; ....的坐标. 专项练习: 直线y=- 1 3 x+1分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△COD,抛物线y =ax2+bx+c经过A、C、D三点. (1)写出点A、B、C、D的坐标; (2)求经过A、C、D三点的抛物线表达式,并求抛物线顶点G的坐标; (3)在直线BG上是否存在点Q,使得以点A、B、Q为顶点的三角形与△COD相似?若存在,请求出点Q的 坐标;若不存在,请说明理由. 二、因动点产生的等腰三角形问题 例2:如图1,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连 精品资料欢迎下载结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.(1)求y关于x的函数关系式; (2)若m=8,求x为何值时,y的值最大,最大值是多少? (3)若y 12 △,要使DEF为等腰三角形,m的值应为多少?m 图1 专项训练: 如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC 上一动点(C点除外),直线PM交AB的延长线于点D. (1)求点D的坐标(用含m的代数式表示); (2)当△APD是等腰三角形时,求m的值; (3)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2).当点P从O向C运动时,点H也随之运动.请直接写出点H所经过的路长(不必写解答过程). 图1图2 三、因动点产生的直角三角形问题 例3:如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),联结PP′、P′A、P′C.设点P的纵坐标为a. (1)当b=3时,①求直线AB的解析式; ②若点P′的坐标是(-1,m),求m的值; 2018年04月28日187****6232的初中数学组卷 一.解答题(共5小题) 1.如图,已知抛物线y=ax2+bx+c经过点A(﹣1,0),点B(3,0)和点C(0,3). (1)求抛物线的解析式和顶点E的坐标; (2)点C是否在以BE为直径的圆上?请说明理由; (3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R 的坐标,若不存在,请说明理由. 2.如图,已知抛物线y=ax2+bx+c过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D. (1)求抛物线的解析式; (2)设点M(1,m),当MB+MD的值最小时,求m的值; (3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E 作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由. 3.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(点A在点B的左侧),直线l与抛物线交于A,C两点,其中点C的横坐标为2. (1)求A,B两点的坐标及直线AC的函数表达式; (2)P是线段AC上的一个动点(P与A,C不重合),过P点作y轴的平行线交抛物线于点E,求△ACE面积的最大值; (3)若直线PE为抛物线的对称轴,抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点,则在x轴上是否存在一点N,使四边形DMNQ 的周长最小?若存在,求出这个最小值及点M,N的坐标;若不存在,请说明理由. (4)点H是抛物线上的动点,在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由. 4.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧). 二次函数动点问题的学习归纳 模式1:平行四边形 例题1:在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标. 练习:如图,抛物线 322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF//DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系. 例题2:如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次函数 y=ax2+bx+c的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2. (1)求二次函数y=ax2+bx+c的解析式; (2)设一次函数y=0.5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标. 练习:如图1,直线 4 3 4 + - =x y 和x轴、y轴的交点分别为B、C,点A的坐标是 (-2,0). (1)试说明△ABC是等腰三角形; (2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S. ①求S与t的函数关系式; ②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t 值;若不存在请说明理由; ③在运动过程中,当△MON为直角三角形时,求t的值. 二次函数的动态问题(动点) 1.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒. (1)求正方形ABCD 的边长. (2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度. (3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标. (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =∠的点P 有 个. [解] (1)作BF y ⊥轴于F . ()()01084A B ,,,, 86FB FA ∴==,. 10AB ∴=. (2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=,. P Q ∴,两点的运动速度均为每秒1个单位. 图① 图② (3)方法一:作PG y ⊥轴于G ,则PG BF ∥. GA AP FA AB ∴ =,即610 GA t =. 3 5 GA t ∴=. 3 105OG t ∴=-. 4OQ t =+, ()113410225S OQ OG t t ? ?∴= ??=+- ?? ?. 即2319 20105 S t t =- ++. 19195323 210b a -=-=???- ??? ,且190103≤≤, ∴当19 3t = 时,S 有最大值. 此时476331 1051555 GP t OG t ===-=,, ∴点P 的坐标为7631155?? ??? ,. (8分) 方法二:当5t =时,163 7922 OG OQ S OG OQ ==== ,,. 设所求函数关系式为220S at bt =++. 抛物线过点()63102852? ? ??? ,,,, 1001020286325520.2a b a b ++=??∴?++=??, 31019.5a b ?=-??∴??=?? , 二次函数的动点问题 1如图,已知抛物线经过原点O 和x 轴上另一点A ,它的对称轴x =2 与x 轴 交于点C ,直线y =-2x -1经过抛物线上一点B (-2,m ),且与y 轴、直线x =2分别交于点D 、E . (1)求m 的值及该抛物线对应的函数关系式; (2)求证:① CB =CE ;② D 是BE 的中点; (3)若P (x ,y )是该抛物线上的一个动点,是否存在这样的点P ,使得PB =PE ,若存在,试求出所有符合条件的点P 的坐标;若不存在,请说明理由 分析 (1)由点B (-2,m )在直线12--=x y 上,可求得m 的值及 点B 的坐标,进而求得抛物线的解析式; (2)通过分别求得CB 和CE 的长来说明CB =CE, 过点B 作BG ∥x 轴,与y 轴交于F 、直线x =2交于G ,过点E 作EH ∥x 轴,交y 轴于H ,由△DFB ≌△DHE,证得D 是BE 的中点; (3)若存在点P 使得PB=PE,则点P 必在线段BE 的中垂线CD 上, 动点P 又在抛物线上,通过解直线CD 和抛物线对应的函数关系式所联列的方程组,其解即为所求点的坐标. 解(1)∵ 点B (-2,m ) 在直线12--=x y 上, ∴ m =-2×(-2)-1=3. ∴ B (-2,3) ∵ 抛物线经过原点O 和点A ,对称轴为x =2, ∴ 点A 的坐标为(4,0) . 设所求的抛物线对应函数关系式为y =a (x -0)(x -4). 将点B (-2,3)代入上式,得3=a (-2-0)(-2-4),∴ 4 1=a . ∴ 所求的抛物线对应的函数关系式为)4(41-= x x y ,即x x y -=24 1 . (2)①直线y =-2x -1与y 轴、直线x =2的交点坐标分别为D (0,-1) E (2,-5). 二次函数综合(动点)问题——平行四边形存在问题 适用 学科 数学适用年级九年级授课教师叶祥教材 版本新人教版 课时时长 (分钟) 40分钟授课日期 2017年5月17日 (上午第4节) 知识点1、二次函数y=ax2+bx+c的图像和性质 2、平行四边形性质 3、平行四边形模型探究 教学目标一、知识与技能 1、掌握二次函数y=ax2+bx+c的图像和性质; 2、掌握平行四边形的性质; 3、会对平行四边形模型进行探究,分类讨论不同的情况。 二、过程与方法 1、首先要掌握二次函数y=ax2+bx+c的图像和性质,因为平行四边形存在问题是在二次函数的前提下进行的; 2、掌握平行四边形的性质,先脱离二次函数,再回到二次函数 的情景中研究; 3、先从简单入手探究平面直角坐标系中动点情况下平行四边形 的存在问题,然后回到二次函数前提下的平行四边形存在问题。 4、充分运用数形结合、转化、方程等数学思想来帮助解题。 三、情感、态度与价值观 1、培养学生的处理图像综合运用的能力; 2、让学生养成从特殊到一般,从简单到复杂的学习方法; 3、形成对图形的处理能力,形成解题技巧,树立对解决此类问 题的信心。 教学重 是否存在一点使得四边形是平行四边形,如果存在求出点的坐标点 教学难 是否存在一点使得四边形是平行四边形,如果存在求出点的坐标点 教学过程 一、课堂导入 如图,已知平面直角坐标系上的三点坐标分别为A(2,3)、B(6,3),C (4,0),现要找到一点D,使得这四个点构成的四边形是平行四边形,那 么点D的坐标_______________________________. A 专题九 二次函数与几何图形动点问题 中考目标: 1、 灵活运用二次函数、特殊三角形和四边形相关性质、判定、定理,确定二次函数,判定线与线关系、特殊三角形、四边形及相应的周长、面积、还有存在、最值等问题; 2、 能够通过数形结合,进行建构模型,联想、猜测,运用分类、转化、从特殊到一般归纳等数学思想解 决问题; 3、 运用“动中求静”,找到、运用不变的数、不变的量、不变的关系,建立函数关系及综合应用代数、 几何知识解决问题。 一.考点归纳:特殊图形的定义、性质、判定等,图形的变化:轴对称、平移、旋转(特殊的是中心对称) 二次函数部分的归纳: 1、二次函数的表达式:一般式 ,顶点( , ) 对称轴x= , 还有 式; 2、二次函数的图象是 ,二次函数的性质: 。 二、考点探究 活动一:二次函数与三角形 例1.已知抛物线y =ax 2+bx +c (a >0)的图象经过点B (12,0)和C (0,-6),对称轴为x =2. (1)求该抛物线的解析式; (2)点D 在线段AB 上且AD =AC ,若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同 时另一动点Q 以某一速度从C 出发沿线段CB 匀速运动,问是否存在某一时刻,使线段PQ 被直线CD 垂直 平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度;若不存在,请说明理由; (3)在(2)的结论下,直线x =1上是否存在点M 使,△MPQ 为等腰三角形?若存在,请求出所有点M 的 坐标,若不存在,请说明理由. 练习:如图,二次函数y = -x 2+ax +b 的图像与x 轴交于A (-2 1,0)、B (2,0)两点,且与y 轴交于点C ; (1) 求该拋物线的解析式,并判断△ABC 的形状; (2) 在x 轴上方的拋物线上有一点D ,且以A 、C 、D 、B 四点为顶点的四边形是等腰梯形,请直接写出D 点的坐标; (3) 在此拋物线上是否存在点P ,使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形?若存在,求出P 点的坐标;若不存在,说明理由。 跟踪练习:《题型专练》P56 T1;P58 T5 中考考点:二次函数与四边形 例1. 如图,抛物线2 23y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物 线交于A 、C 两点,其C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式; (2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最值; (3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶 点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由. 跟踪练习:《题型专练》P57 T3;P59 T7 中考考点:二次函数与三角形、四边形的面积 二次函数动点问题 1、如图,已知二次函数y=42 3 412++- x x 的图象与y 轴交于点A ,与x 轴交于B 、C 两点,其对称轴与x 轴交于点D ,连接AC . (1)点A 的坐标为_______ ,点C 的坐标为_______ ; (2)线段AC 上是否存在点E ,使得△EDC 为等腰三角形?若存在,求出所有符合条件的点E 的坐标;若不存在,请说明理由; (3)点P 为x 轴上方的抛物线上的一个动点,连接PA 、PC ,若所得△PAC 的面积为S ,则S 取何值时,相应的点P 有且只有2个? 2、已知抛物线 )0(2≠++=a c bx ax y 经过点B (2,0)和点C (0,8),且它的对称轴是直线2-=x 。 (1)求抛物线与x 轴的另一交点A 坐标; (2)求此抛物线的解析式; (3)连结AC 、BC ,若点E 是线段AB 上的一个动点(与点A 、点B )不重合,过点E 作EF ∥AC 交BC 于点F ,连结CE ,设AE 的长为m ,△CEF 的面积为S ,求S 与m 之间的函数关系式; (4)在(3)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点E 的 坐标,判断此时△BCE 的形状;若不存在,请说明理由。 3、如图,四边形ABCD 是平行四边形,AB=4,OB =2,抛物线过A 、B 、C 三点,与x 轴交于另一点D .一动点P 以每秒1个单位长度的速度从B 点出发沿BA 向点A 运动,运动到点A 停止,同时一动点Q 从点D 出发,以每秒3个单位长度的速度沿DC 向点C 运动,与点P 同时停止. (1)求抛物线的解析式; (2)若抛物线的对称轴与AB 交于点E ,与x 轴交于点F ,当点P 运动时间t 为何值时,四边形POQE 是等腰梯形? (3)当t 为何值时,以P 、B 、O 为顶点的三角形与以点Q 、B 、O 为顶点的三角形相似? 4、如图1,已知抛物线经过坐标原点O 和x 轴上另一点E ,顶点M 的坐标为 (2,4);矩形ABCD 的顶点A 与点O 重合,AD 、AB 分别在x 轴、y 轴上,且AD=2,AB=3. (1)求该抛物线的函数关系式; (2)将矩形ABCD 以每秒1个单位长度的速度从 图1所示的位置沿x 轴的正方向匀速平行移动,同时一动点P 也以相同的速度.....从点A 出发向B 匀速移动,设它们运动的时间为t 秒(0≤t ≤3),直线AB 与该抛物线的交点为N (如图2所示).① 当t= 时,判断点P 是否在直线ME 上,并说明理由; ② 设以P 、N 、C 、D 为顶点的多边形面积为S ,试问S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由. 2 5 二次函数压轴题 1.如图:抛物线经过A (-3,0)、B (0,4)、C (4,0)三点. (1) 求抛物线的解析式. (2)已知AD = AB (D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值; (3)在(2)的情况下,抛物线的对称轴上是否存在一点M ,使MQ+MC 的值最小若存在,请求出点M 的坐标;若不存在,请说明理由。 2.如图9,在平面直角坐标系中,二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点,与y 轴交于C 点,与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0), OB =OC ,tan∠ACO=3 1. (1)求这个二次函数的表达式. (2)经过C 、D 两点的直线,与x 轴交于点E ,在该抛物线上是否存在这样的点F ,使以点A 、C 、E 、F 为顶点的四边形为平行四边形若存在,请求出点F 的坐标;若不存在,请说明理由. (3)如图10,若点G (2,y )是该抛物线上一点,点P 是直线AG 下方的抛物线上一动点,当点P 运动到什么位置时,△APG 的面积最大求出此时P 点的坐标和△APG 的最大面积. 3.如图,已知抛物线与x 轴交于A (-1,0)、B (3,0)两点, 与y 轴交于点C (0,3)。 ⑴求抛物线的解析式; ⑵设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC 是等腰三角形若存在,求出符合条件的点P的坐标;若不存在,请说明理由; ⑶若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标。 4.已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB 第九讲——二次函数动点问题的学习归纳 模式1:平行四边形 例题1:在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标. 练习:如图,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧), 与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF//DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系. 例题2:如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次函数y=ax2+bx+c 的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2. (1)求二次函数y=ax2+bx+c的解析式; (2)设一次函数y=0.5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标. 练习:如图1,直线 4 3 4 + - =x y 和x轴、y轴的交点分别为B、C,点A的坐标是(-2, 0). (1)试说明△ABC是等腰三角形; (2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S. ①求S与t的函数关系式; ②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由; ③在运动过程中,当△MON为直角三角形时,求t的值. 二次函数与几何图形 模式1:平行四边形 分类标准:讨论对角线 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成平行四边形,则可分成以下几种情况 (1)当边AB 是对角线时,那么有BC AP // (2)当边AC 是对角线时,那么有CP AB // (3)当边BC 是对角线时,那么有BP AC // 1、本题满分14分)在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式; (2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标. 2、如图1,抛物线322 ++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系. 模式2:梯形 分类标准:讨论上下底 例如:请在抛物线上找一点p 使得P C B A 、、、四点构成梯形,则可分成以下几种情况 (1)当边AB 是底时,那么有PC AB // (2)当边AC 是底时,那么有BP AC // (3)当边BC 是底时,那么有AP BC // 3、已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 3 2-=与边BC 相交于点D . (1)求点D 的坐标; (2)抛物线c bx ax y ++=2 经过点A 、D 、O ,求此抛物线的表达式; (3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.专题:二次函数中的动点问题
最新最新中考二次函数动点问题(含答案)
二次函数动点问题解答方法技巧(含例解答案)
二次函数动点问题解答方法技巧(含例解答案)
二次函数动点问题解答方法技巧分析
中考二次函数动点问题(含答案)
初中数学二次函数动点问题
中考二次函数与几何图形动点问题--答案
二次函数动点问题(一)
二次函数中动点问题——平行四边形(练习)
二次函数动点问题的学习归纳
二次函数动点问题压轴题专题汇编(含答案)
中考数学压轴题 二次函数动点问题 专题练习
二次函数综合动点问题
二次函数与几何图形动点问题
初三二次函数动点问题(教师版)
中考数学压轴题二次函数动点问题一
(完整版)九年级--二次函数中的动点问题
中考二次函数与几何图形动点问题--答案