人教版八年级数学下册勾股定理第一课时公开课课件

B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中，∠C=90°,所以a2+b2=c2
D.在Rt△ABC中，∠B=90°,所以a2+b2=c2
2.图中阴影部分是一个正方形，则此正方形的面
积为 36 cm².
8 cm
最新人教版八年级下册数学精品课件设计
10 cm
3.在△ABC中，∠C=90°.
当AB为斜边时，如图，BC 42 32 7; 当BC为斜边时，如图，BC 42 32 5.
B 4
3
C 图 A
B
4
A
3
图
C
归纳 当直角三角形中所给的两条边没有指明是斜边或 直角边时，其中一较长边可能是直角边，也可能是斜
边，这种情况下一定要进行分类讨论，否则容易丢解.
最新人教版八年级下册数学精品课件设计
最新人教版八级下册数学精品课件设计
能力提升： 7.如图，以Rt△ABC的三边长为斜边分别向外作等腰直
角三角形．若斜边AB＝3，求△ABE及阴影部分的面积.
解：∵AE＝BE，
∴S△ABE＝
1 2
AE·BE＝12
AE2.
又∵AE2＋BE2＝AB2，
∴2AE2＝AB2，
∴S△ABE＝
1 4
AB2＝
9 4
最新人教版八年级下册数学精品课件设计
练一练
求下列图中未知数x、y的值：
81 x
144
解：由勾股定理可得 81+ 144=x2，
解得x=15.
最新人教版八年级下册数学精品课件设计
144 y
169
解：由勾股定理可得 y2+ 144=169，

A
勾股定理给出了直角三角形三边之间的 关系，即两直角边的平方和等于斜边的平方
c2=a2 + b2 b c
a c 2 b2
a2=c2－b2
b2 =c2-a2
b= c2-a2
C
a
B
c a b
2
2
例题讲解
例1、求下图中字母所代表的正方形的面积。
A 225 225 400
625
81 B
144
证法二：
现在我们一起来探 索“弦图”的奥妙吧！
c a
b
S大正方形＝c2 S小正方形＝（b-a）2
S大正方形＝4· S三角形＋S小正方形
1 即：c 2=4 ab+(b-a) 2 2 C2=2ab+a2-2ab+b2
弦图

2 2 a +b
=
2 c
它们的面积和 : a b
2
2
c
朱实
朱实 黄实 朱实
2002年国际数学家大会会标
它标志着我 国古代数学 的成就！
这个图形里 到底蕴涵了什 么样博大精深 的知识呢？
弦图
勾股定理
毕达哥拉斯(公元前572----前492年),古希腊著 名的哲学家、数学家、天文学家。
A
B
C
SA+SB=SC
SA+SB=SC C
B 图甲 图甲 A的面积 B的面积 C的面积 4 4 8 1.观察图甲，小方格 的边长为1. ⑴正方形A、B、C的 ⑵正方形 的 面积有什么关系？ 面积各为多少？
b
a b c
2 2
2
即：直角三角形两直角边的平方和等于 斜边的平方。
2 a 2 +b 2 =c

探究勾股定理——观察“地砖里的秘密”
相传2500年前,古希腊有一位 非常著名的数学家毕达哥拉斯,有 一次,他到朋友家做客,发现朋友 家的用砖铺成的地面中反映了直 角三角形三边的某种数量关系.
AB
C
探究勾股定理——观察“地砖里的秘密”
探究1（1）三个正方形A，B，C 的面积有什么关系？ （2）由这三个正方形A，B，C的围成的等腰 直角三角形三条边长度之间有怎样的特殊关系？
A a bB
c
C
SA SB SC
a2 b2 c2
进一步探究勾股定理
探究2：每个小方格的边长均为1.
（1）计算图中正方形A、B、C的面积.
A
B C
进一步探究勾股定理
探究2：每个小方格的边长均为1. （2）图中正方形A、B、C面积之间有何关系？
SA SB SC
A
B C
进一步探究勾股定理
思想方法？
课后作业
1、完成配套练习册（必做）。 2、做一棵奇妙的勾股树（选做）。
探究2：每个小方格的边长均为1.
（3）图中正方形A、B、C所围成的直角三角形
三边之间有什么关系？
A
SA SB SC
a2 b2 c2
a B bc
C
探究勾股定理——猜想
探究3： 猜一猜，直角三角形三边之间有什么数量关系？ 猜想：
直角三角形两直角边的平方和等于斜边的平方
已知：Rt△ABC中，∠C=90°
b
c
求证：a2 b2 c2
a
探究勾股定理——实验验证
探究4:(1)以小组为单位，用四个全等的直角三 角形拼成一个以c为边长的正方形 。注意拼出的 图形不能有重叠的部分。 (2) 你能用含a,b的式子表示它的面积吗？

是直角边，也可能是斜边，这种情况下一定要进行分类讨论，否则容易丢解.
新课讲解
例2 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解：由勾股定理可得
A
AB2=AC2+BC2=25， 即 AB=5.
D 3
根据三角形面积公式，
∴ ∴
C12DA=C1×2 B. C=
1 2
AB×CD.
C
内容 勾股定理
在Rt△ABC中， ∠C=90°,a,b
为直角边，c为斜边，则有 a2+b2=c2.
在直角三角形中
注意
看清哪个角是直角
已知两边没有指明是直角边 还是斜边时一定要分类讨论
当堂小练
1.下列说法中,正确的是
（C）
A.已知a,b,c是三角形的三边，则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
ac b
证明：
b ca
cb
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形 =4× 1 ab+c2
2
=c2+2ab，
a
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
新课讲解
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图，图中的三个三角形都是直角三角形，求证：a2 + b2 = c2.
，
c2
4
1
ab
b
a 2
a2
b2.
2
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智，它是我国古代数 学的骄傲.因为，这个图案被选为2002年在北京召开的国际数学大会的会徽.

图1
9
9 18
8
B 图1
C A
图2
A，B，C 面积关
系
44
SA+SB=SC
B 图2
（图中每个小方格代表一个单位面积）
直角三 角形三 边关系
两直角边的平方和 等于斜边的平方
即：两条直角边上的正方形面积之和等于
斜边上的正方形的面积
探究二：在一般 的直角三角形中， SA+SB=SC 还成立吗？
A
B C
A
B C
用了“补”的方法
用了“割”的方法
如图，小方格的边长为1.
(1)你能求出正方形C的面积吗？
观察所得到的各组数据，你有什么发现？
A
SA+SB=SC
a
Bb c
C
a2+b2=c2
猜想:两直角边a、b与斜边c 之间的关系？
观察所得到的各组数据，你有什么发现？
SA+SB=SC
a
bc
a2+b2=c2
猜想两直角边a、b与斜边c 之间的关系？
我们也来观察右图的地面， 你能发现A、B、C面积之间 有什么数量关系吗？
AB C
SA+SB=SC
每块砖都是等腰直角三角形哦
二、探究新知
探究一：你能发现图1中正方形A、B、C的面积之间有 什么数量关系吗？
C A
B 图1
（图中每个小方格是1个单位面积）
（1）观察图1-1
正方形A中含有 9 个
C
小方格，即A的面积是
A
9 个单位面积。
正方形B的面积是
B
C
9 个单位面积。
图1-1
A
正方形C的面积是

B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中，∠C=90°,所以a2+b2=c2
D.在Rt△ABC中，∠B=90°,所以a2+b2=c2
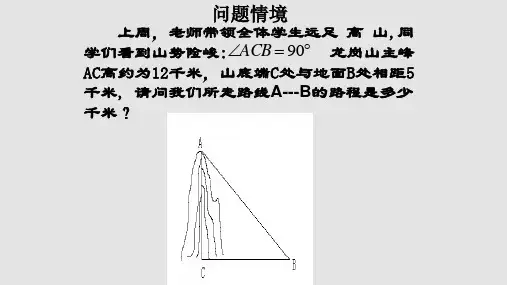
5.在△ABC中，∠C=90°. 在Rt△ABC中，两直角边长分别为3和 ，则斜边长为
.
【变式】 在Rt△ABC中，AB＝4，AC＝3，求BC的长.
（1）若a=6，b=8，则c=
.
（2）若a=1,c=2,求b.
别为a,b,斜边长为c,那么a2+b2=c2.
b 你知道在古代，人们如何称呼直角三角形的三边吗？
在Rt△ABC中，∠B=90°,所以a2+b2=c2
毕达哥拉斯在朋友家里做客时，从砖铺成的地面中发现了直角三角形三边的数量关系．
【变式】 在Rt△ABC中，AB＝4，AC＝3，求BC的长.
（2）若a=1,c=2,求b.
（
）
C
A
下通列过说 前法面中的,探正究确活的动是，你发现了直角（三角形三）边之间的关系规律了吗？
已（知1）∠若ACaB=b==950,°求,CcD; ⊥AB,AC=3,BC=4.
c a b 5 5 50 5 2; 等（在如腰2R果）t直 △直若A角角BaC三三=中1角角,c，形形=2∠三的,C求条两=b9边直.0°长角,所度边以之长a间分2+有别b2怎为=c样a22,b的,斜特边殊长关2为系c？,那么a2+b22=c2. 2
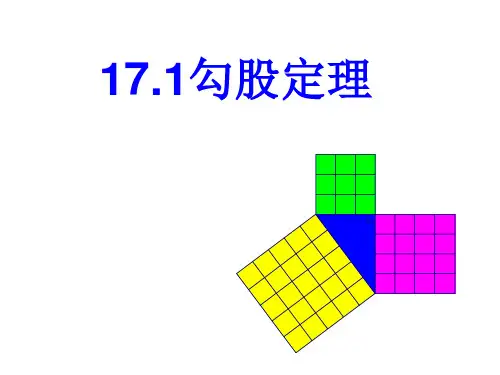
勾股定理的发现
毕达哥拉斯在朋友家里做客 时，从砖铺成的地面中发现了直 角三角形三边的数量关系．
三个正方形的面积有什么关系？
两个小正方形的面积之和等于大正方形的面积.
等腰直角三角形三条边长度 之间有怎样的特殊关系？

13 单位面 积.
勾命股题定1 理
如果直角三角形的两直角边 长分别为a，b，斜边长为c，那 么a2+b2=c2.
x
赵爽弦图
赵爽指出：按 弦图，又可以勾股 相乘为朱实二，倍 之为朱实四，以勾 股之差自相乘为中 黄实。加差实，亦 成弦实。
aB
c
a
b
C
c
朱实
b
朱实
A
朱实
朱实
学以致用
1、已知， Rt△ABC 中，a，b为的两条 直角边，c为斜边，求：
积. C的面积是 18 单位面
积.
好奇是人的本性! 观察图1-2，回答问题：
图1-1
图1-2
探索勾股定理
1.正方形A中 含有 4 个小 方格,即A的面 积是 4 单位 面积.
2.B的面积是 4 单位面
积. C的面积 是
8 单位面 积.
好奇是人的本性! 观察图1-3，填表：
图1-3
图1-4
探索勾股定理
1.正方形A中 含有 16 个小 方格,即A的面 积是 16 单位 面积.
2.B的面积是 9 单位面
积. C的面积是 25 单位面
积.
好奇是人的本性! 观察图1-4，填表：
图1-3
图1-4
探索勾股定理
1.正方形A中 含有 4 个小 方格,即A的面 积是 4 单位 面积.
2.B的面积是 9 单位面
积. C的面积 是
⑴已知： a＝3， b＝4，求c
⑵已知： c ＝10，a＝6，求b
2、已知： c ＝13，a＝5，
c
求阴影部分的面积。
ab
活学活用
探究1
一个门框尺寸如图所示，一
块长3m，宽2.2m的薄木板

同学们，我们也来观察下面图中的地面，看看你能 发现什么？是否也和大哲学家有同样的发现呢？
ａ2+b2=c2
A
B
ab
c
C
A、B、C的面积有什么关系？
SA+SB=SC 直角三角形三边有什么关系？ 两直角边的平方和等于斜边的平方。
在网格中一般的直角三角形，以它的三边为边长的三个正方 形A、B、C 是否也有类似的面积关系？(每个小正方形的面积为 单位1)：
毕达哥拉斯是古希腊著名的哲学家、数学家、天 文学家，相传2500多年前，一次，毕达哥拉斯去朋友 家作客．在宴席上，其他的宾客都在尽情欢乐，高谈 阔论，只有毕达哥拉斯却看着朋友家的方砖地而发起 呆来．原来，朋友家的地是用一块块直角三角形形状 的砖铺成的，黑白相间，非常美观大方．主人看到毕 达哥拉斯的样子非常奇怪，就想过去问他．谁知毕达 哥拉斯突然恍然大悟的样子，站起来，大笑着跑回家 去了．
问题情境
上周，老师带领全体学生远足 高 山,同
学们看到山势险峻:ACB 90 龙岗山主峰
AC高约为12千米，山底端C处与地面B处相距5 千米, 请问我们所走路线A---B的路程是多少 千米？
第十七章 勾股定理 17.1 勾股定理(一）
勾股世界
两千两千多多年年前前，古，希古腊有希个腊哥拉有个毕达哥拉斯 学斯学派派，，他他们首们先发发现现了了勾股勾定股理，定因此理，因此在国外 在人国们外人通们常通常称称勾勾股股定定理为理毕为达哥毕拉斯达哥拉斯定理。 定为理了。为纪了念纪念毕毕达达哥哥拉拉斯学斯派学，1派95，5 1955年希腊 年曾希经腊曾发经行发行了了一一枚枚纪纪念票念。邮票.
1
=4× 2ab+c2
cb
=c2+2ab，