小波去噪阈值的确定和分解层数的确定

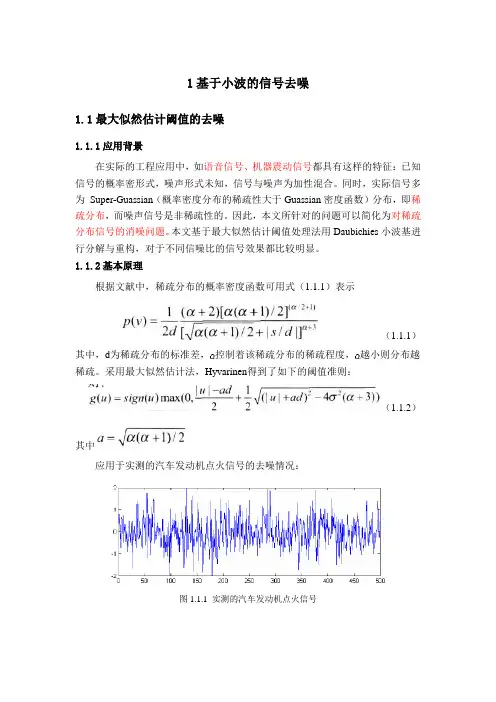
1基于小波的信号去噪1.1最大似然估计阈值的去噪1.1.1应用背景在实际的工程应用中，如语音信号、机器震动信号都具有这样的特征：已知信号的概率密形式，噪声形式未知，信号与噪声为加性混合。

同时，实际信号多为Super-Guassian（概率密度分布的稀疏性大于Guassian密度函数）分布，即稀疏分布，而噪声信号是非稀疏性的。

因此，本文所针对的问题可以简化为对稀疏分布信号的消噪问题。

本文基于最大似然估计阈值处理法用Daubichies小波基进行分解与重构，对于不同信噪比的信号效果都比较明显。

1.1.2基本原理根据文献中，稀疏分布的概率密度函数可用式（1.1.1）表示（1.1.1）其中，d为稀疏分布的标准差，控制着该稀疏分布的稀疏程度，越小则分布越稀疏。

采用最大似然估计法，Hyvarinen得到了如下的阈值准则：（1.1.2）其中应用于实测的汽车发动机点火信号的去噪情况：图1.1.1 实测的汽车发动机点火信号图1.1.2采用硬阈值、软阈值及最大似然估计阈值法消噪的比较1.1.3去噪效果优点：最大似然估计阈值去噪的方法，从概率密度的角度去看待信号，充分利用了脉冲信号概率密度的稀疏性，去噪的效果明显优于传统的小波消噪方法。

1.2人的脉搏信号小波去噪算法1.2.1应用背景用于去除脉搏信号中的基线漂移、工频干扰及肌电干扰噪声。

1.2.2基本原理对去噪后的脉搏信号进行小波分解，重构指定的细节分量，采用阈值法提取脉搏的P波波峰点。

依据P波波峰与其它特征点的位置关系，分别提取T波波峰点，D波波峰点，V波波谷和脉搏初始点A，实现了脉搏信号5个特征点的提取。

其典型的脉冲波形如下图：图1.2.1 典型的脉搏波形特征点提取的算法流程如下：图1.2.2 P 波波峰的提取 图1.2.3 脉搏波形特征点的识别1.2.3去噪效果图1.2.4 去噪后信号与重构后信号的能量值曲线图1.2.5 脉搏信号的5个特征点的提取表1.2.1 四种不同去噪法的信噪比、均方根误差与能量比优点：给定阈值法的RMSE明显小于前三种方法的RMSE，信噪比有很大的提高，且能量成分保持较好，失真度明显降低。

MATLAB小波变换信号去噪引言小波变换是一种多尺度分析方法，广泛应用于信号处理领域。

由于小波变换具有良好的时频局部性质，可以将信号分解为不同频率和时间分辨率的成分，因此被广泛应用于信号去噪领域。

本文将介绍如何使用MATLAB进行小波变换信号去噪的方法。

MATLAB中的小波变换在MATLAB中，可以使用Wavelet Toolbox中的wavedec函数进行小波分解，使用wrcoef函数进行重构。

具体步骤如下：1.导入待处理的信号数据。

2.选择适当的小波基函数和分解层数。

3.使用wavedec函数对信号进行小波分解，得到分解系数。

4.根据阈值方法对分解系数进行去噪处理。

5.使用wrcoef函数对去噪后的分解系数进行重构，得到去噪后的信号。

6.分析去噪效果并进行评估。

下面将逐步详细介绍这些步骤。

选择小波基函数和分解层数小波基函数的选择在小波分析中非常重要，不同的小波基函数适用于不同类型的信号。

常用的小波基函数有Daubechies小波、Haar小波、db2小波等。

根据信号的特点和分析需求，选择合适的小波基函数是非常重要的。

在MATLAB中，可以使用wname函数查看支持的小波基函数。

可以通过比较不同小波基函数的性能指标来选择合适的小波基函数。

常见的性能指标包括频率局部化、时频局部化和误差能量。

选择分解层数时，需要根据信号的特点和噪声的程度来决定。

一般而言，分解层数越高，分解的细节系数越多，信号的时间分辨率越高，但运算量也会增加。

小波分解使用wavedec函数对信号进行小波分解。

函数的输入参数包括待分解的信号、小波基函数名称和分解层数。

函数输出包括近似系数和细节系数。

[C, L] = wavedec(x, level, wname);其中，x是待分解的信号，level是分解层数，wname是小波基函数名称。

C是包含近似系数和细节系数的向量，L是分解的长度信息。

根据分解层数，可以将分解系数划分为不同频带的系数。

小波去噪小波分析是一种时频分析法，具有深刻的理论基础和广泛的应用范围两个特点，目前是应用数学和工程科学中一个发展迅速的领域，经过近三十年的探索研究，小波分析扎实的数学理论基础已经建立起来。

相比于傅里叶变换，小波变换有多分辨分析的能力，可以通过伸缩和平移运算对一个信号进行多尺度的精细化分析;此外小波变换在时频两域上同时都具有良好的局部化特性，也即是说在低频部分的频率分辨率高而时间分辨率低，在高频部分的时间分辨率高而频率分辨率低，这种优点使得小波变换能够有效地从信号中提取特征信息，并且小波变换可以经过适当的离散化形成标准的正交系，因此小波分析特别适用于突变信号。

由于小波分析的各种优良特性，现在小波分析己经广泛地用于应用数学、物理学、生物医学等学科以及语音合成、图像压缩、数据去噪、地震勘探、机械振动、故障诊断、计算机视觉和信号分析等许多领域。

图1小波变换三层分解1、信号分解与重构目前，小波去噪常用的方法可大致分为三类:第一类是基于信号和噪声在不同尺度下的特点，利用模极大值原理对测量信号进行去噪;第二类是根据对含噪信号进行小波分解后，信号和噪声表现出的不同的相关性而对其进行去噪处理的相关性去噪法;第三类是能够在最小均方误差意义下达到近似最优的小波闭值去噪法。

Donoho和Johnstone在1992年提出了基于正交离散小波变换的小波阈值(收缩)去噪法，并在众多领域得到广泛的研究和应用。

小的小波系数，噪声的能量便会分布在整个小波域中。

所以小波阂值去噪法的核心思想就是:将含噪信号进行小波分解后，保留大尺度低频部分的所有小波系数，对各尺度高频部分的小波系数设置阂值进行置零处理，然后利用处理完毕的全部小波系数来重构原始信号。

此类算法的优点在于该算法是计算量较小且最易实现的一种小波去噪方法，几乎能够完全抑制噪声，使用软闭值方法去噪还可以使去噪信号是原始信号的近似最优估计，且估计信号至少和原始信号同样光滑而不会产生附加振荡。

小波阈值去噪原理随着科技的不断发展，数字图像处理成为了一个重要的研究领域。

在数字图像处理中，噪声是一个令人头疼的问题，它会降低图像的质量和清晰度。

为了解决这个问题，人们提出了许多去噪算法，其中小波阈值去噪是一种常用且有效的方法。

小波阈值去噪主要基于小波分析的原理，小波分析是一种数学工具，可以将信号分解成不同频率的小波系数。

在小波阈值去噪中，首先将图像进行小波分解，得到不同频率的小波系数。

然后，通过对小波系数进行阈值处理，将小于某个阈值的系数置零，从而去除噪声。

小波阈值去噪的原理可以用以下几个步骤来概括：1. 小波分解：将原始图像进行小波分解，得到不同频率的小波系数。

小波分解可以通过多级分解来实现，每一级分解都会将图像的高频部分和低频部分分离出来。

2. 阈值处理：对小波系数进行阈值处理。

阈值可以根据具体的应用需求来确定，常见的阈值确定方法有全局阈值、局部阈值和自适应阈值等。

阈值处理的目的是将小于阈值的小波系数置零，从而去除噪声。

3. 小波重构：将经过阈值处理的小波系数进行重构，得到去噪后的图像。

小波重构是小波分解的逆过程，它将不同频率的小波系数进行合并，得到原始图像的近似重建。

小波阈值去噪作为一种基于小波分析的去噪方法，具有以下优点：1. 去噪效果好：小波阈值去噪可以有效地去除图像中的噪声，保留图像的细节和结构信息。

通过调整阈值的大小，可以控制去噪效果的好坏，使得去噪后的图像既能去除噪声，又能保持图像的清晰度。

2. 处理速度快：小波阈值去噪算法的计算复杂度相对较低，处理速度较快。

这使得它在实时图像处理和大规模图像处理中具有一定的优势。

3. 算法简单易实现：小波阈值去噪算法的原理相对简单，易于理解和实现。

这使得它成为了一种常用的去噪方法，广泛应用于各个领域。

虽然小波阈值去噪在去除噪声方面取得了一定的成果，但也存在一些局限性和挑战。

例如，阈值的选择是一个关键问题，不同的阈值选择方法会对去噪效果产生影响。

小波去噪的流程图小波去噪是一种基于小波变换的信号去噪方法，它通过对信号进行小波变换，将信号分解成多个频带，并通过对每个频带的小波系数进行去噪处理，最终重构信号以达到去噪的目的。

以下是小波去噪的流程图：1、选择小波基和分解层数首先，需要选择合适的小波基和分解层数。

小波基的选择应该根据信号的特性和去噪要求来确定，而分解层数则应该根据信号的复杂度和去噪要求来确定。

2、对信号进行小波变换将选定的小波基应用于输入信号，将其进行小波变换，将信号分解成多个频带。

小波变换可以将信号在不同频带上分解成不同的频率成分，从而将噪声和信号分离。

3、对小波系数进行去噪处理对每个频带的小波系数进行去噪处理，以消除噪声对信号的影响。

常用的去噪方法包括阈值去噪、模极大值去噪和相关性去噪等。

4、对去噪后的信号进行小波逆变换对每个频带去噪处理后的小波系数进行小波逆变换，将信号重构为原始信号。

5、对重构的信号进行后处理对重构的信号进行必要的后处理，如滤波、平滑等，以提高去噪效果和信号的质量。

综上所述，小波去噪的流程包括选择小波基和分解层数、对信号进行小波变换、对小波系数进行去噪处理、对去噪后的信号进行小波逆变换和对重构的信号进行后处理等步骤。

通过这些步骤，可以有效地去除信号中的噪声，提高信号的质量。

流程图4装修申请流程图装修申请流程图一、关键词1、装修申请2、流程图3、申请材料4、审核流程5、施工监管6、完成验收二、文章内容装修申请流程图详解在房屋装修过程中，申请装修是一个必不可少的环节。

本文将通过流程图的形式，详细介绍装修申请的整个过程，帮助您更好地了解这一流程。

首先，我们需要准备装修申请材料。

具体包括：房屋产权证明、身份证或营业执照、装修方案以及施工图纸等。

接下来，我们将进入审核流程。

在这一阶段，物业公司或相关部门将对您的装修申请材料进行审核。

审核内容主要包括装修方案是否符合规定，施工图纸是否完整等。

如果申请材料审核通过，您将进入施工监管环节。

小波阈值去噪算法小波阈值去噪算法（Wavelet threshold denoising algorithm）是一种常用的信号去噪方法。

它基于小波变换（Wavelet transform）和阈值处理（Thresholding），通过将信号分解为不同频率的子带，并对子带系数进行阈值处理，从而去除信号中的噪声。

小波变换是一种多尺度分析的方法，可以将信号在时间和频率上进行分解。

它将信号分解为低频和高频部分，低频部分反映了信号的整体趋势，而高频部分则反映了信号的细节信息。

小波变换的一个优点是可以通过改变小波基函数的选择来适应不同类型的信号。

阈值处理是指对信号中的小波系数进行幅值截断的操作。

假设子带系数为c，阈值处理函数定义为T(x)，则阈值处理的过程可以用以下公式表示：d=c*T(，c，)其中，c，表示系数的幅值，T(x)为阈值处理函数，d为处理后的系数。

阈值处理函数一般有硬阈值（Hard thresholding）和软阈值（Soft thresholding）两种形式。

硬阈值函数定义如下：T(x) = 0, if ，x，< λT(x) = x, if ，x，≥ λ其中，λ为阈值。

软阈值函数定义如下：T(x) = 0, if ，x，< λT(x) = sign(x)(，x，-λ), if ，x，≥ λ其中，sign(x)为x的符号。

1.对输入信号进行小波变换，将其分解为不同尺度的子带。

2.对每个子带的系数进行阈值处理，得到处理后的系数。

3.对处理后的系数进行逆小波变换，得到去噪后的信号。

在实际应用中，选择合适的小波基函数和阈值值对去噪效果有重要影响。

常用的小波基函数包括Daubechies小波、Haar小波、Symlets小波等。

阈值的选择可以通过交叉验证的方法进行，或者根据信噪比等指标来确定。

总之，小波阈值去噪算法是一种基于小波变换和阈值处理的信号去噪方法。

通过对信号进行小波变换和阈值处理，可以去除信号中的噪声，保留信号的重要信息。

小波去噪一、小波去噪中信号阈值的估算信号去噪是信号处理领域的经典问题之一。

传统的去噪方法主要包括线性滤波方法和非线性滤波方法，如中值滤波和wiener 滤波等。

传统去噪方法的不是在于使信号变换后的熵增高、无法刻画信号的非平稳特性并且无法得到信号的相关性。

为了克服上述缺点，人们开始使用小波变换解决信号去噪问题。

小波变换具有下列良好特性：(1) 低熵性：小波系数的稀疏分布，使信号变换后的熵降低；(2) 多分辨率特性：可以非常妤地刻画信号的非平稳特性，如边缘、尖峰、断点等；(3) 去相关性：可取出信号的相关性，且噪声在小波变换后有白化趋势，所以比时域更利于去噪；(4) 选基灵活性：由于小波变换可以灵活选择基函数，因此可根据信号特点和去噪要求选择适合小波。

小波在信号去噪领域已得到越来越广泛的应用。

阈值去噪方法是一种实现简单、效果较好的小波去噪方法。

阈值去噪方法的思想就是对小波分解后的各层系数中模大于和小于某阈值的系数分别处理，然后对处理完的小波系数再进行反变换，重构出经过去噪后的信号。

下面从阈值函数和阈值估计两方面对阈值去噪方法进行介绍。

1．阈值函数常用的阈值函数主要是硬阈值函数和软阈值函数。

(1)硬阈值函数。

表达式为)|(|)(T w wI w >=η，如图4.18所示，其中横坐标表示信号的原始小波系数，纵坐标表示阈值化后的小波系数。

(2)软阈值函数。

表达式为)|(|))sgn(()(T w I T w w w >-=η，如图4.19所示，其中横坐标表示信号的原始小波系数，纵坐标表示阈值化后的小波系数。

一般来说，硬阈值方法可以很好地保留信号边缘等局部特征，软阈值处理相对要平滑，但会造成边缘模糊等失真现象。

为了克服上述缺陷，最近提出了一种半软阈值函数，如图4.20所示。

它可以兼顾软阈值和硬阈值方法的优点，其表达式为)|(|)||()|(|)sgn()(2211212T w wI T w T I T T T w T w w >+<<--=η其中210T T <<。

小波去噪在GPS数据处理中的方法研究摘要：GPS技术在高精度工程测量中具有广泛的应用，GPS在采集数据的过程，受到外界环境的影响，数据结果往往很难达到预期的精度，小波去噪是根据信号中有用信号和噪声时频特性的不同，选择最佳小波基和尺度进行滤波，从而分离有用信号，为GPS技术的发展带来了新的突破口和切入点。

关键词：小波去噪小波分解阈值量化Matlab一、小波去噪原理小波去噪是根据信号中有用信号和噪声时频特性的不同，选择最佳小波基和尺度进行滤波，从而分离有用信号。

一个含噪声的一维信号的模型可表示为：式中，为真实信号，为噪声信号，为含噪信号。

这里以一个简单噪声模型加以说明，即为高斯白噪声N（0，1），噪声级为1，通常表现为高频信号，在实际工程中，有用信号通常表现为低频信号或较平稳的信号，所以消噪过程可按以下方法进行处理。

首先对实际信号进行小波分解，选择小波并确定分解层次为N，则噪声部分通常包含在高频中；然后对小波分解的高频系数进行门限阈值量化处理；最后根据小波分解的第N层低频系数和经过量化后的1～N层高频系数进行小波重构，达到消除噪声的目的，对信号降噪实质上是抑制信号的噪声，在实际信号中恢复真实信号的过程。

小波收缩去噪方法的关键步骤是如何选择阈值和如何进行门限阈值处理，在某种程度上，它关系到信号去噪的质量。

在对小波系数作门限阈值处理操作时，可以使用软阈值处理方法或硬阈值处理方法。

硬阈值是把信号的绝对值与指定的阈值进行比较，小于或等于阈值的点变为0，大于阈值的点保持不变。

软阈值是把信号的绝对值与指定的阈值进行比较，小于或等于阈值的点变为0，大于阈值的点变为该点值与阈值的差。

二、小波去噪基本步骤在小波分解中，小波基的选择没有统一的标准，目前主要结合小波基的特性，在考虑其正交性、消失矩、正则性、紧支性和对称性前提下，应用小波分析信号和理论分析结果的误差相结合判定小波基的好坏，并由此确定小波基。

而小波分解尺度取值越大就越利于信噪分离，但丢失的细节也就越多，信号失真就越大。

小波变换分解层数小波变换是一种信号分析和处理的方法，其基本思想是将信号分解为不同尺度和频率的成分，以便更好地理解和处理信号。

小波变换可以通过多层分解来实现对信号的细节和趋势的分离，这就需要确定小波变换的分解层数。

一、小波变换简介小波变换是一种时频分析方法，它将信号表示为一组基函数的线性组合，这些基函数被称为小波函数。

与傅里叶变换不同，小波函数是有限长度的，并且可以在时间和频率上进行局部化。

因此，小波变换可以提供更好的时域和频域信息。

二、小波变换分解层数在进行小波变换时，需要确定分解层数。

分解层数决定了信号被分解成多少个尺度和频率成分。

通常情况下，在进行小波变换时，会将信号进行多次迭代的低通滤波和高通滤波操作，并将每次滤波后得到的低频部分作为下一次迭代的输入。

因此，每次迭代会产生一个低频子带和一个高频子带。

根据迭代次数不同，可以得到不同层数的小波变换。

一般来说，小波变换的分解层数越高，分解得到的细节信息就越多，但是计算量也会增加。

因此，在实际应用中需要根据具体情况来确定分解层数。

三、如何确定小波变换的分解层数1. 根据信号特征确定在实际应用中，可以根据信号的特征来确定小波变换的分解层数。

例如，在处理语音信号时，通常只需要进行一次或两次分解即可得到有效的结果；而在处理图像信号时，则可能需要进行更多次分解才能得到满意的结果。

2. 根据应用需求确定另外，还可以根据具体应用需求来确定小波变换的分解层数。

例如，在进行压缩编码时，为了减少数据量和提高压缩比，可以选择较低的分解层数；而在进行信号恢复和滤波处理时，则可能需要选择较高的分解层数以获取更多细节信息。

3. 观察小波系数图像确定此外，在进行小波变换时，还可以观察小波系数图像来确定最适合的分解层数。

通常情况下，随着分解层数增加，小波系数图像会呈现出越来越多的细节信息，但是也会出现噪声等不必要的信息。

因此，在选择分解层数时，需要找到一个平衡点，既要保证分解得到足够的细节信息，又要避免过多的噪声。

V ol 39No.4Aug.2019噪声与振动控制NOISE AND VIBRATION CONTROL 第39卷第4期2019年8月文章编号：1006-1355(2019)04-0007-05汽车驾驶性评价中小波去噪分解层数的确定刘海江，张欣，李敏（同济大学机械与能源工程学院，上海201804）摘要：在汽车驾驶性评价试验过程中所采集的信号内通常混有诸多噪声信号，一般运用小波变换进行去噪，然而若小波去噪分解层数选择不当，则会影响去噪效果，从而影响驾驶性评价的准确性。

针对此问题，提出了一种通过信息熵法融合所采集的汽车驾驶性数据的均方根误差、信噪比以及平滑度等多指标来选择小波分解最佳层数的方法，从而取得较佳的去噪效果。

现对所采集的某一换挡工况下汽车振动加速度数据运用上述方法进行去噪，结果表明，基于此多指标融合的小波去噪方法在很好滤除初始信号中噪声的同时，能够有效保留数据中的有用成分，譬如驾驶过程中的冲击及振动等，从而保证了后续汽车驾驶性评价过程中所提取的指标的准确性。

关键词：声学；汽车驾驶性评价；小波去噪；信息熵法；多指标融合；分解层数中图分类号：U467.4+92文献标志码：A DOI 编码：10.3969/j.issn.1006-1355.2019.04.002Determination of the Number of Wavelet DenoisingDecomposition Layers in Vehicle Driving EvaluationLIU Haijiang ,ZHANG Xin ,LI Min（School of Mechanical Engineering,Tonggi University,Shanghai 201804,China ）Abstract :In the process of vehicle driving evaluation test,a lot of noise signals are usually mixed in the collected signals.And the wavelet transform is usually used for denoising.However,if the number of the wavelet denoising decomposition layers is not properly selected,it will reduce the denoising effect and lower the accuracy of the driving evaluation.For this reason,a multi-index fusion method based on root mean square error,signal-to-noise ratio and data smoothness,collected and combined by information entropy method,is proposed to select the optimal number of layers for wavelet decomposition,so as to obtain the best denoising effect.This method is performed for the acceleration data denoising of the car ’s vibration signals collected under a certain shifting condition.The results show that the wavelet denoising method based on this multi-index fusion can well filter the noise in the initial signal and retain the useful components such as various shocks and vibrations during driving so as to ensure the accuracy of the indicators extracted during the subsequent driving evaluation.Keywords :acoustics;vehicle driving evaluation;wavelet denoising;information entropy method;multiple indicator fusion;decomposition layer在汽车驾驶性评价过程中，由于测量过程中路面的不平坦、车身的振动、仪器本身及数据在传输过程中会受到诸多因素的影响，测量的数据中必然会存在噪声干扰，导致评价指标计算不准确，进而影响到驾驶性能的评价，因此在驾驶性评价之前需要进行含噪数据的处理[1–2]。