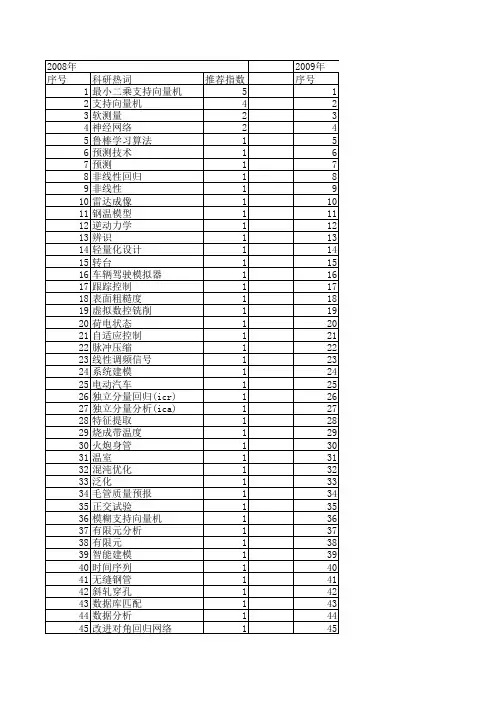
最小二乘支持向量机鲁棒回归算法研究

支持向量机（SVM ）原理及应用一、SVM 的产生与发展自1995年Vapnik(瓦普尼克)在统计学习理论的基础上提出SVM 作为模式识别的新方法之后，SVM 一直倍受关注。

同年，Vapnik 和Cortes 提出软间隔(soft margin)SVM ，通过引进松弛变量i ξ度量数据i x 的误分类(分类出现错误时i ξ大于0)，同时在目标函数中增加一个分量用来惩罚非零松弛变量(即代价函数)，SVM 的寻优过程即是大的分隔间距和小的误差补偿之间的平衡过程；1996年，Vapnik 等人又提出支持向量回归 (Support Vector Regression ，SVR)的方法用于解决拟合问题。

SVR 同SVM 的出发点都是寻找最优超平面(注：一维空间为点；二维空间为线；三维空间为面；高维空间为超平面。

)，但SVR 的目的不是找到两种数据的分割平面，而是找到能准确预测数据分布的平面，两者最终都转换为最优化问题的求解；1998年，Weston 等人根据SVM 原理提出了用于解决多类分类的SVM 方法(Multi-Class Support Vector Machines ，Multi-SVM)，通过将多类分类转化成二类分类，将SVM 应用于多分类问题的判断：此外，在SVM 算法的基本框架下，研究者针对不同的方面提出了很多相关的改进算法。

例如，Suykens 提出的最小二乘支持向量机 (Least Square Support Vector Machine ，LS —SVM)算法，Joachims 等人提出的SVM-1ight ，张学工提出的中心支持向量机 (Central Support Vector Machine ，CSVM)，Scholkoph 和Smola 基于二次规划提出的v-SVM 等。

此后，台湾大学林智仁(Lin Chih-Jen)教授等对SVM 的典型应用进行总结，并设计开发出较为完善的SVM 工具包，也就是LIBSVM(A Library for Support Vector Machines)。

支持向量回归模型,径向基函数1.引言1.1 概述概述支持向量回归模型是一种机器学习算法，用于解决回归问题。

它基于支持向量机（Support Vector Machine，简称SVM）算法发展而来，相比于传统的回归模型，支持向量回归模型具有更强的鲁棒性和泛化能力。

支持向量回归模型的核心思想是通过在训练数据中找到能够最好地拟合数据的超平面，以预测目标变量的值。

与传统的回归模型不同，支持向量回归模型不仅考虑样本点的位置关系，还引入了一个叫做“支持向量”的概念。

支持向量是在模型训练过程中起关键作用的样本点，它们离超平面的距离最近，决定了超平面的位置和形状。

径向基函数是支持向量回归模型中常用的核函数。

径向基函数通过将原始特征映射到高维空间，使得原本线性不可分的数据在新的空间中变得线性可分。

在支持向量回归模型中，径向基函数可以用于构建非线性的映射关系，从而提高模型的预测能力。

本文将围绕支持向量回归模型和径向基函数展开讨论。

首先，我们将详细介绍支持向量回归模型的原理和算法。

然后，我们将探讨径向基函数的概念和应用场景。

接下来，我们将设计实验来验证支持向量回归模型在不同数据集上的表现，并对实验结果进行分析。

最后，我们将对本文进行总结，并展望支持向量回归模型和径向基函数在未来的研究和应用中的潜力。

通过本文的阅读，读者将对支持向量回归模型和径向基函数有更深入的了解，并能够将其应用于实际问题中。

支持向量回归模型的引入和径向基函数的使用为解决回归问题提供了一种新的思路和方法，对于提高预测精度和模型的鲁棒性具有重要意义。

1.2文章结构文章结构部分可以描述整篇文章的组织和章节安排，使读者能够清楚地了解文章的框架和内容概要。

在本篇文章中，主要分为以下几个章节：1. 引言：- 1.1 概述：简要介绍支持向量回归模型和径向基函数的背景和概念。

- 1.2 文章结构：对整篇文章的章节和内容进行概述，让读者知道接下来会涉及到哪些内容。

- 1.3 目的：明确本文的研究目的和动机。

支持向量机与神经网络算法的对比分析1. 引言1.1 支持向量机与神经网络算法的对比分析支持向量机和神经网络是机器学习领域中两种常见的分类算法。

支持向量机（Support Vector Machine）是一种监督学习算法，其基本原理是找到一个最优的超平面来将不同类别的数据分隔开。

而神经网络（Neural Network）则是模仿人类神经系统构建的一种算法，通过多层神经元之间的连接来实现学习和分类。

在实际应用中，支持向量机通常表现出较好的泛化能力和高效性能。

它能够处理高维数据及非线性数据，并且在处理小样本数据上表现良好。

然而，神经网络在大规模数据集和复杂问题上具有更好的表现，能够学习复杂的模式和特征。

在优缺点对比方面，支持向量机在处理小数据集上表现较好，但对于大数据集可能会面临内存和计算资源消耗问题；而神经网络在大数据集上有优势，但对于小数据集可能会过拟合。

在应用领域上，支持向量机多用于文本分类、图像识别等领域；而神经网络则广泛应用于语音识别、自然语言处理等领域。

综上所述，支持向量机和神经网络在不同领域和问题上有各自的优势和劣势，需要根据具体情况选择合适的算法来解决问题。

在实际应用中，可以根据数据规模、问题复杂度等因素来进行选择，以达到更好的分类和预测效果。

2. 正文2.1 支持向量机算法原理支持向量机（Support Vector Machine，SVM）是一种常用的监督学习算法，主要用于分类和回归问题。

其基本原理是通过找到一个最优的超平面来对数据进行分类。

支持向量机的核心概念是最大化间隔，即在数据中找到最优的超平面，使得不同类别的样本离该超平面的距离最大化。

这个超平面可以用以下公式表示：w^T*x + b = 0，其中w是法向量，b是偏置。

SVM的目标是找到使得间隔最大化的超平面参数w和b。

支持向量机可以处理非线性问题，引入了核函数的概念。

通过将数据映射到高维空间，可以在新的空间中找到一个线性超平面来解决原始空间中的非线性问题。

用户定位算法的鲁棒性分析与改进方法摘要：随着移动互联网时代的到来，用户定位算法的准确性和稳定性变得越来越重要。

然而，在现实世界中，存在着许多挑战，如信号强度变化、多径效应和环境噪声等。

本文将对用户定位算法的鲁棒性进行分析，并提出了一些改进方法，以提高其定位精度和可靠性。

1. 引言用户定位是移动互联网和位置服务的基础，准确的用户定位对于提供个性化服务、资源管理和安全监控等方面至关重要。

然而，由于信号传播的复杂性和环境变化的影响，用户定位算法面临许多挑战，如信号衰减、阻塞、多径传播和噪声等。

2. 鲁棒性分析2.1 信号强度的变化移动设备接收到的信号强度受多种因素影响，如障碍物、遮挡和其他设备的干扰。

这种变化给用户定位算法带来了挑战。

为了提高算法的鲁棒性，可以采用滤波技术，例如卡尔曼滤波器和粒子滤波器，以消除噪声和平滑信号。

2.2 多径效应多径效应是信号在到达接收器之前经历多条路径的结果，从而引起了信号的干扰和延迟。

为了解决多径效应对用户定位算法的影响，可以采用信号处理技术，例如最小二乘法和波束形成算法，以消除干扰并提高定位精度。

2.3 环境噪声环境中存在的噪声，如电磁干扰和背景噪声，会干扰信号的接收和解码，从而降低用户定位算法的准确性。

为了应对环境噪声，可以采用信号处理和噪声抑制技术，例如自适应滤波和谱减法，以提高算法的鲁棒性。

3. 改进方法3.1 多传感器融合多传感器融合是一种改进用户定位算法的有效方法。

通过同时使用多个传感器（如GPS、Wi-Fi、蓝牙和惯性传感器）的信息，可以提高定位的准确性和可靠性。

例如，可以使用惯性传感器来补偿信号强度的不稳定性，以提高算法的鲁棒性。

3.2 机器学习算法机器学习算法是一种很有潜力的改进用户定位算法的方法。

通过使用大量的训练数据和先进的算法，可以构建准确的定位模型。

例如，可以使用支持向量机（SVM）、随机森林和深度学习等算法来提高定位的准确性和鲁棒性。

3.3 强化学习算法强化学习算法结合了传统的机器学习和决策理论，可以优化用户定位算法的决策流程。

分类与回归应用的主要算法分类与回归是机器学习中最普遍且重要的应用之一。

其目的是预测输出变量的值，考虑特征变量的影响。

机器学习中常用的分类算法有决策树、支持向量机、朴素贝叶斯和随机森林等，回归算法有线性回归、岭回归、LASSO回归和K-近邻回归等。

1.决策树决策树是一种基于树形结构进行决策的分类算法。

它通过判断特征变量的取值最为关键，根据特征值划分出不同的子节点，并根据节点之间的关系识别输出变量的值。

决策树有较高的解释性和可读性，处理小规模数据的效果非常出色，由于它的效率高、准确性好，近年来逐渐成为了分类问题中的主流方法。

2.支持向量机支持向量机(SVM)是一种基于间隔最大化原理进行分类的算法。

SVM通过选择最优的超平面来划分不同的类别，最终达到分类的目的。

该算法可以有效地解决高维数据的分类问题，广泛应用于文本分类、图像识别、生物信息学、金融和医学等领域。

3.朴素贝叶斯朴素贝叶斯算法是一种基于贝叶斯定理和特征条件独立假设进行分类的算法。

朴素贝叶斯算法可以对大规模样本进行有效的分类，广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。

4.随机森林随机森林(RF)是一种基于随机特征选择和决策树分类的算法。

RF可以在保证精确度的同时降低过拟合风险，不易受到噪声和异常点的影响，广泛应用于遥感影像分类、图像处理、文本分类等领域。

5.线性回归线性回归是一种基于线性模型进行回归分析的算法。

它可以通过变量之间线性关系进行预测，并给出输出变量的具体数值。

线性回归在数据量较大、特征空间较稀疏的情况下运行效果非常好，广泛应用于金融、医学和社会学等领域。

6.岭回归岭回归是一种基于线性回归进行优化的算法。

随着特征数量的增加，线性回归常常会发生过拟合的现象。

岭回归通过在原有的线性回归的模型中添加一个正则项(L2范数)来限制参数，降低模型的方差。

岭回归适用于处理多元线性回归并减少过拟合的问题。

SSO回归LASSO回归是一种基于线性回归进行优化的算法。

支持向量机的优缺点分析支持向量机（Support Vector Machine，简称SVM）是一种常用的机器学习算法，其在分类和回归问题中都有广泛的应用。

本文将对支持向量机的优缺点进行分析，以帮助读者更好地理解和应用这一算法。

一、优点1. 高效的非线性分类器：支持向量机在处理非线性分类问题时表现出色。

通过使用核函数将数据映射到高维空间，支持向量机可以构建非线性的决策边界，从而更好地分类数据。

2. 有效处理高维数据：支持向量机在高维空间中的表现较好，这使得它能够处理具有大量特征的数据集。

相比于其他机器学习算法，支持向量机在高维数据上的训练时间较短，且不易受到维度灾难的影响。

3. 可解释性强：支持向量机通过找到最佳的超平面来进行分类，因此其决策边界相对简单且易于解释。

这使得支持向量机在一些领域，如医学诊断和金融风险评估等，具有较高的可信度和可解释性。

4. 鲁棒性强：支持向量机对于训练数据中的噪声和异常值具有较好的鲁棒性。

由于支持向量机只关注距离决策边界最近的数据点，因此对于一些孤立的异常点不会过度拟合，从而提高了算法的泛化能力。

二、缺点1. 对大规模数据集的处理较慢：由于支持向量机在训练过程中需要计算每个样本点与决策边界的距离，因此对于大规模数据集，支持向量机的训练时间较长。

此外，支持向量机在处理大规模数据集时也需要较大的内存空间。

2. 参数选择敏感：支持向量机中的参数选择对算法的性能有很大影响。

例如，核函数的选择和参数的调整都需要经验和专业知识。

不合理的参数选择可能导致模型的欠拟合或过拟合，因此需要仔细调整参数以获得较好的性能。

3. 无法直接处理多类问题：支持向量机最初是为二分类问题设计的，对于多类问题需要进行一些扩展。

常用的方法是将多类问题转化为多个二分类问题，但这样会增加计算复杂度和内存消耗。

4. 对缺失数据敏感：支持向量机对于缺失数据比较敏感。

如果数据集中存在大量缺失值，或者缺失值的分布与其他特征相关，则支持向量机的性能可能会受到较大影响。

支持向量机与逻辑回归的比较在机器学习领域中，支持向量机（Support Vector Machine，SVM）和逻辑回归（Logistic Regression）是两种常用的分类算法。

它们各自具有独特的优势和适用范围，本文将对它们进行比较和分析。

一、原理与应用领域1. 支持向量机支持向量机是一种二分类模型，其基本思想是将样本空间通过超平面划分为两个子空间，使得不同类别的样本尽可能地分开。

在寻找最优超平面时，SVM主要关注支持向量，即距离超平面最近的样本点。

SVM通过使用核函数将样本映射到高维空间，从而能够处理非线性分类问题。

SVM在许多领域都有广泛的应用，如图像识别、文本分类、生物信息学等。

其在处理高维数据和小样本数据时表现出色，具有较强的泛化能力。

2. 逻辑回归逻辑回归是一种广义线性模型，主要用于解决二分类问题。

其基本思想是通过对输入特征进行线性组合，并通过一个逻辑函数（如sigmoid函数）将线性组合的结果映射到0-1之间的概率值，从而进行分类。

逻辑回归在实际应用中非常广泛，如医学疾病预测、金融风险评估等。

它具有简单易懂、计算效率高等优点，适用于处理大规模数据。

二、性能比较1. 模型复杂度逻辑回归是一种线性模型，其模型复杂度较低。

它的训练速度快，适用于处理大规模数据集。

而SVM则是一种非线性模型，其模型复杂度较高。

由于需要计算支持向量，SVM的训练速度相对较慢。

2. 数据要求逻辑回归对数据没有特殊要求，可以处理连续型数据和离散型数据。

而SVM对数据的要求较高，需要进行特征工程，将数据映射到高维空间。

此外，SVM对数据的分布和标签的平衡性也有一定要求。

3. 鲁棒性逻辑回归对异常值较为敏感，异常值的存在可能会影响模型的性能。

而SVM对异常值的鲁棒性较好，由于其关注支持向量，因此对于异常值的影响相对较小。

4. 泛化能力SVM在处理小样本数据时表现出较好的泛化能力，能够有效避免过拟合问题。

而逻辑回归在处理大规模数据时表现较好，但对于小样本数据容易出现欠拟合问题。

一种鲁棒性强的视频图像在线识别算法杨琼;王家全【摘要】Video image watermarking is a kind of technology to keep the security of video images.It is a hot spot in computer security field.On the problem of low accuracy of online recognition of video image watermarking,a robust video watermarking algorithm is proposed in this paper.Firstly,this paper analyzes the current status of video watermarking,and points out the shortcomings of the current video image watermarking algorithm.Then we use SVM to estimate the correlation between neighboring pixels.Based on the estimation results,we use support vector machine to estimate the relationship between neighbor-hood pixels.The experimental results on the Matlab 2012 platform show that the proposed algorithm is not only invisible,but also can be used in video image watermarking.%针对当前视频图像水印在线识别正确率低的问题，提出一种鲁棒强的视频水印在线识别算法。

数据建模常用的方法和模型数据建模是指根据不同的数据特征和业务需求，利用数学和统计方法对数据进行处理和分析的过程。

数据建模的结果可以用于预测、分类、聚类等任务。

以下是常用的数据建模方法和模型：1.线性回归模型：线性回归模型是一种通过拟合线性函数来建模目标变量与自变量之间关系的方法。

它假设目标变量与自变量之间存在线性关系，并且通过最小二乘法来估计模型参数。

2.逻辑回归模型：逻辑回归模型是一种广义线性模型，适用于二分类问题。

它通过拟合S形曲线来建模预测变量与目标变量之间的关系，并且使用最大似然估计来估计模型参数。

3.决策树模型：决策树模型是一种基于树形结构的分类模型。

它通过一系列的分裂条件来将数据分成不同的类别或者子集，最终得到一个预测模型。

决策树模型易于理解和解释，同时能够处理离散和连续特征。

4.随机森林模型：随机森林模型是一种集成学习方法，通过构建多个决策树模型并结合它们的预测结果来进行分类或回归。

它能够处理高维数据和具有不同尺度特征的数据，同时具有较高的预测准确性和稳定性。

5.支持向量机模型：支持向量机模型是一种非线性分类和回归方法。

它通过映射样本到高维特征空间，并在特征空间中找到一个最优超平面来进行分类或回归。

支持向量机模型具有较好的泛化能力和较强的鲁棒性。

6.贝叶斯网络模型：贝叶斯网络模型是一种基于贝叶斯定理的概率图模型，用于表示变量之间的依赖关系。

它通过学习样本数据中的条件概率分布来进行预测和推理。

贝叶斯网络模型可以解决不确定性问题，并且能够处理各种类型的变量。

7.神经网络模型：神经网络模型是一种模拟生物神经系统工作原理的计算模型。

它由多个节点和连接组成，通过调整节点之间的连接权重来学习和预测。

神经网络模型具有较强的非线性建模能力，适用于处理大规模和复杂的数据。

8. 聚类模型：聚类模型是一种无监督学习方法，用于将数据划分成不同的组别或簇。

聚类模型通过度量数据点之间的相似性来进行分组，并且可以帮助发现数据中的隐藏模式和规律。