第四章课后习题解答

第四章 光的衍射一、基本知识点光的衍射：当光遇到小孔、狭缝或其他的很小障碍物时，传播方向将发生偏转，而绕过障碍物继续前行，并在光屏上形成明暗相间的圆环或条纹。

光波的这种现象称为光的衍射。

菲涅耳衍射：光源、观察屏（或者是两者之一）到衍射屏的距离是有限的，这类衍射又称为近场衍射。

夫琅禾费衍射：光源、观察屏到衍射屏的距离均为无限远，这类衍射也称为远场衍射。

惠更斯－菲涅耳原理：光波在空间传播到的各点，都可以看作一个子波源，发出新的子波，在传播到空间某一点时，各个子波之间可以相互叠加。

这称为惠更斯－菲涅耳原理。

菲涅耳半波带法：将宽度为a 的缝AB 沿着与狭缝平行方向分成一系列宽度相等的窄条，1AA ，12A A ，…，k A B ，对于衍射角为θ的各条光线，相邻窄条对应点发出的光线到达观察屏的光程差为半个波长，这样等宽的窄条称为半波带。

这种分析方法称为菲涅耳半波带法。

单缝夫琅禾费衍射明纹条件：sin (21)(1,2,...)2a k k λθ=±+=单缝夫琅禾费衍射暗纹条件：sin (1,2,...)a k k θλ=±=在近轴条件下，θ很小，sin θθ≈, 则第一级暗纹的衍射角为 1aλθ±=±第一级暗纹离开中心轴的距离为 11x f faλθ±±==±, 式中f 为透镜的焦距。

中央明纹的角宽度为 112aλθθθ-∆=-=中央明纹的线宽度为 002tan 2l f f faλθθ=≈∆=衍射图样的特征：① 中央明纹的宽度是各级明纹的宽度的两倍，且绝大部分光能都落在中央明纹上。

② 暗条纹是等间隔的。

③ 当入射光为白光时，除中央明区为白色条纹外，两侧为由紫到红排列的彩色的衍射光谱。

④ 当波长一定时，狭缝的宽度愈小，衍射愈显著。

光栅: 具有周期性空间结构或光学性能（透射率，反射率和折射率等）的衍射屏，统称为光栅。

光栅常数: 每两条狭缝间距离d a b =+称为光栅常数。

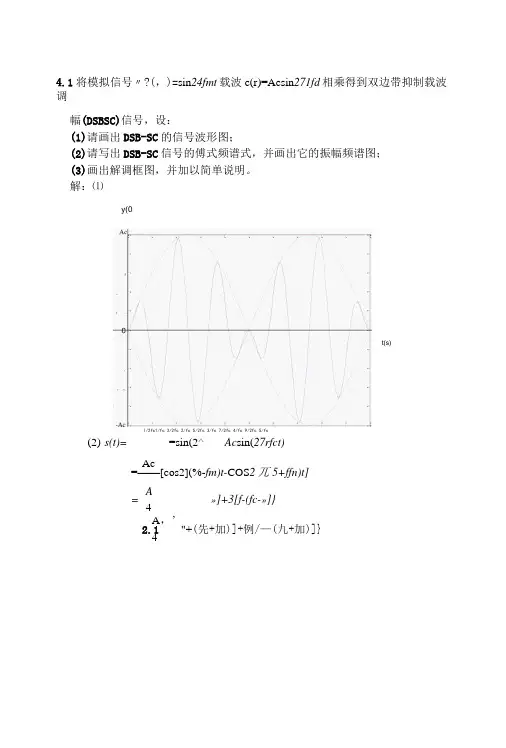
4.1将模拟信号〃?(，)=sin 24fmt 载波c(r)=Acsin 271fd 相乘得到双边带抑制载波调幅(DSBSC)信号，设：(1)请画出DSB-SC 的信号波形图；(2)请写出DSB-SC 信号的傅式频谱式，并画出它的振幅频谱图； (3)画出解调框图，并加以简单说明。

解：⑴(2) s(t)= =sin(2^ Ac sin(27rfct)Ac=——[cos2](%-fm)t-COS 2兀5+ffn)t] A = »]+3[f-(fc-»]} 4A ，’ 2.1 "+(先+加)]+例/—(九+加)]} 4y(0l/2fc1/fc 3/2fc 2/fc 5/2fc 3/fc 7/2fc 4/fc 9/2fc 5/fct(s)S ⑴八3Ac/4- Ac/2.Ac/4(3)相干解调Cos(Wct)与发端相干偏调相干解调：将接收信号与载波信号sin(2乙加)相乘，得至U A cr(t)sin(2^fct)=Acm(t)sin(2^fct)sin(2^fit)=--cos(44fct)]通过低通滤波器抑制载频的二倍频分量，得到解调信号为刈⑺=与机⑺ 2.2 已知某调幅波的展开式为：s(t)=cos(2/rxl()4r)+4COS (2TT xl.lxl040+cos(2万xl.2xl04r) (1)求调幅系数和调制信号频率；(2)写出该信号的傅式频谱式，画出它的振幅频谱图； (3)画出该信号的解调框图。

解：⑴sQ)=cos(24xl04r)+4cos(2乃xl.lxl04r)+cos(2万xl.2xl04r)=4cos(2%xl.lxl04r)[l+0.5cos(2万x0.1xl04r)] 调制系数是a=0.5;信号频率是f=1000Hz(2)S(/)=；U(/+104)+演f —i04)]+2[Mf+l.lxl()4)+5(/—1.1X104)]+-W+1.2X 104)+^(/-1.2X 104)]-fm-fc ・fc -fc+fm。

t k i，j 1 t k i，j t k i，j 1 t k i , j r r rj rj r 2 r 2 rj r
并简化，可以得出与上式完全一样相同的结果。
4-7、 一金属短圆柱在炉内受热厚被竖直地移植到空气中冷却， 底面可以认为是绝热的。为用数值法确定冷却过程中柱体温 度的变化， 取中心角为 1rad 的区域来研究 （如本题附图所示） 。 已知柱体表面发射率，自然对流表面传热系数，环境温度， 金属的热扩散率，试列出图中节点（1，1） ， （M,1）(M,n)及 （M,N） 的离散方程式。 在 r 及 z 方向上网格是各自均分的。 解：应用热平衡法来建立四个节点点离散方程。 节点（1，1） ：
， 离散方程的建立 4-5、试将直角坐标中的常物性无内热源的二维稳态导热微分方程化为显式差分格式，并指 出其稳定性条件（ x y) 。 解：常物性无内热源二维非稳态方程微分方程为
4.3636t 2 2.53t1 1.8336t f
t2
2.53t f 1.8336t f
2t 2t t a x 2 y 2
Bi=0.1,1,10 的三种情况计算下列特征方程的根
n (n 1,2,6) :
n a Fo 2 0.2 并用计算机查明，当 时用式（3-19）表示的级数的第一项代替整个级数（计
算中用前六项之和来替代）可能引起 的误差。 解： n Bi 0.1 1.0 10
tan n
第四章
复习题 1、 试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。 2、 试说明用热平衡法建立节点温度离散方程的基本思想。 3、 推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似， 为什么前者得到的是精确描述，而后者解出的确实近似解。 4、 第三类边界条件边界节点的离散那方程，也可用将第三类边界条件表达式中的一阶导数 用差分公式表示来建立。试比较这样建立起来的离散方程与用热平衡建立起来的离散方 程的异同与优劣。 5．对绝热边界条件的数值处理本章采用了哪些方法？试分析比较之． 6．什么是非稳态导热问题的显示格式？什么是显示格式计算中的稳定性问题？ 7．用高斯－塞德尔迭代法求解代数方程时是否一定可以得到收敛德解？不能得出收敛的解 时是否因为初场的假设不合适而造成？

第四章一、简述下列每对术语的区别：空串和空白串；串常量和串变量；主串和子串；静态分配的顺序串和动态分配的顺序串；目标串和模式串；有效位移和无效位移。

答：●空串是指不包含任何字符的串，它的长度为零。

空白串是指包含一个或多个空格的串，空格也是字符。

●串常量是指在程序中只可引用但不可改变其值的串。

串变量是可以在运行中改变其值的。

●主串和子串是相对的，一个串中任意个连续字符组成的串就是这个串的子串，而包含子串的串就称为主串。

●静态分配的顺序串是指串的存储空间是确定的，即串值空间的大小是静态的，在编译时刻就被确定。

动态分配的顺序串是在编译时不分配串值空间，在运行过程中用malloc和free等函数根据需要动态地分配和释放字符数组的空间(这个空间长度由分配时确定，也是顺序存储空间)。

●目标串和模式串:在串匹配运算过程中，将主串称为目标串，而将需要匹配的子串称为模式串，两者是相对的。

●有效位移和无效位移：在串定位运算中，模式串从目标的首位开始向右位移，每一次合法位移后如果模式串与目标中相应的字符相同，则这次位移就是有效位移(也就是从此位置开始的匹配成功)，反之，若有不相同的字符存在，则此次位移就是无效位移(也就是从此位置开始的匹配失败)。

二、假设有如下的串说明：char s1[30]="Stocktom,CA", s2[30]="March 5 1999", s3[30], *p;(1)在执行如下的每个语句后p的值是什么?p=stchr(s1,'t'); p=strchr(s2,'9'); p=strchr(s2,'6');(2)在执行下列语句后，s3的值是什么?strcpy(s3,s1); strcat(s3,","); strcat(s3,s2);(3)调用函数strcmp(s1,s2)的返回值是什么?(4)调用函数strcmp(&s1[5],"ton")的返回值是什么?(5)调用函数stlen(strcat(s1,s2))的返回值是什么?解：(1) stchr(*s,c)函数的功能是查找字符c在串s中的位置，若找到，则返回该位置，否则返回NULL。

第4章数据库安全性1 ．什么是数据库的安全性？答：数据库的安全性是指保护数据库以防止不合法的使用所造成的数据泄露、更改或破坏。

2 ．数据库安全性和计算机系统的安全性有什么关系？答：安全性问题不是数据库系统所独有的，所有计算机系统都有这个问题。

只是在数据库系统中大量数据集中存放，而且为许多最终用户直接共享，从而使安全性问题更为突出。

系统安全保护措施是否有效是数据库系统的主要指标之一。

数据库的安全性和计算机系统的安全性，包括操作系统、网络系统的安全性是紧密联系、相互支持的，3 ．试述可信计算机系统评测标准的情况，试述TDI / TCSEC 标准的基本内容。

答：各个国家在计算机安全技术方面都建立了一套可信标准。

目前各国引用或制定的一系列安全标准中，最重要的是美国国防部（DoD ）正式颁布的《DoD 可信计算机系统评估标准》（伽sted Co 哪uter system Evaluation criteria ，简称TcsEc ，又称桔皮书）。

（TDI / TCSEC 标准是将TcsEc 扩展到数据库管理系统，即《可信计算机系统评估标准关于可信数据库系统的解释》（Tmsted Database Interpretation 简称TDI , 又称紫皮书）。

在TDI 中定义了数据库管理系统的设计与实现中需满足和用以进行安全性级别评估的标准。

TDI 与TcsEc 一样，从安全策略、责任、保证和文档四个方面来描述安全性级别划分的指标。

每个方面又细分为若干项。

4 ．试述T csEC ( TDI ）将系统安全级别划分为4 组7 个等级的基本内容。

答：根据计算机系统对安全性各项指标的支持情况，TCSEC ( TDI ）将系统划分为四组（division ) 7 个等级，依次是D 、C ( CI , CZ ）、B ( BI , BZ , B3 ）、A ( AI ) ，按系统可靠或可信程度逐渐增高。

这些安全级别之间具有一种偏序向下兼容的关系，即较高安全性级别提供的安全保护包含较低级别的所有保护要求，同时提供更多或更完善的保护能力。

计算机网络课后习题答案（第四章2）(2009-12-14 18:26:17)转载▼标签：课程-计算机教育21某单位分配到一个B类IP地址，其net-id为129.250.0.0.该单位有4000台机器，分布在16个不同的地点。

如选用子网掩码为255.255.255.0，试给每一个地点分配一个子网掩码号，并算出每个地点主机号码的最小值和最大值4000/16=250，平均每个地点250台机器。

如选255.255.255.0为掩码，则每个网络所连主机数=28-2=254>250，共有子网数=28-2=254>16，能满足实际需求。

可给每个地点分配如下子网号码地点：子网号（subnet-id）子网网络号主机IP的最小值和最大值1： 00000001 129.250.1.0 129.250.1.1---129.250.1.2542： 00000010 129.250.2.0 129.250.2.1---129.250.2.2543： 00000011 129.250.3.0 129.250.3.1---129.250.3.2544： 00000100 129.250.4.0 129.250.4.1---129.250.4.2545： 00000101 129.250.5.0 129.250.5.1---129.250.5.2546： 00000110 129.250.6.0 129.250.6.1---129.250.6.2547： 00000111 129.250.7.0 129.250.7.1---129.250.7.2548： 00001000 129.250.8.0 129.250.8.1---129.250.8.2549： 00001001 129.250.9.0 129.250.9.1---129.250.9.25410： 00001010 129.250.10.0 129.250.10.1---129.250.10.25411： 00001011 129.250.11.0 129.250.11.1---129.250.11.25412： 00001100 129.250.12.0 129.250.12.1---129.250.12.25413： 00001101 129.250.13.0 129.250.13.1---129.250.13.25414： 00001110 129.250.14.0 129.250.14.1---129.250.14.25415： 00001111 129.250.15.0 129.250.15.1---129.250.15.25416： 00010000 129.250.16.0 129.250.16.1---129.250.16.25422..一个数据报长度为4000字节（固定首部长度）。

第四章
一、写出下列化合物的构造式或命名：
1、对二乙烯苯 2、对叔丁基甲苯 3、3-氯-4-硝基甲苯
CH2CH CH2
4、
5、
NO2CH2Br 6、 NhomakorabeaCH2CH CH2
O CH3
Cl
二、完成下列反应
CH2CH2 CH3
H3C CH CH3
1、
+
；
COOH
2、Cl2/光照； AlCl3 +
3、H2SO4/0～80℃； 165℃
CH3 Cl
NO2
CH3
Br2
CH3
3、
FeBr3
Br
Br
Br
4、
Br2
ClCOCH3
FeBr3
AlCl3
COCH3
CH3 KMnO4
7、
H+，△
COOH
HNO3 H2SO4 O2N
COOH NO2
八、指出下列化合物硝化时，导入的硝基在环上的位置：
CH3 CH3
CH3 OCH3
CH3
OH
SO3H
Cl
1、
＞
NO2
NO2
＞
＞
NO2
OH
2、
＞
COCH3 NO2
＞
＞
五、由苯或甲苯开始合成下列化合物：
CH3 HNO3
2、
H2SO4
CH3
Cl2
FeCl3
NO2
CH3 Cl
NO2
或：
CH3 浓H2SO4 100℃
CH3
Cl2
FeCl3
SO3H
CH3 Cl
H3O+ 150℃

asn2和fe3bcr2o72和sn2ccr3和sn4dcr2o72和fe3有一个原电池由两个氢电极组成其中有一个是标准氢电极为了得到最大的电动势另一个电极浸入的酸性溶液设ph2100kpa应为a01moldm3hclb01moldm3hac01moll1naacc01moldm3hacd01moldm3h3po4在下列电池反应中niscu2aqni210moldm3cus当该原电池的电动势为零时cu2浓度为a5051027moldm3b5711021moldm3c7101014moldm3d7561011moldm3阴极b阳极c任意一个极解
当pH=5.00,其他有关物质均处于标准条件时:
=1.033V
11.由镍电极和标准氢电极组成原电池。若c(Ni 2+=0.0100mol·dm -3时,原电池的电动势为0.315V ,其中镍为负极,计算镍电极的标准电极电势。
12.由两个氢电极H 2(101.325kPa|H +(0.10mol · dm -3|Pt和
(4计算c(I -=1.0×10-2mol·dm -3以及c(Fe 3+=c(Fe 2+/10时,原电池的电动势。
解:(1查阅教材附录10可知:32(Fe /Fe θφ++=0.771V ,
-
2(I /I θ
φ=0.5355 V
E θ=_θθφφ+-=32(Fe /Fe θφ++–-
2
(I
/I θφ=0.771 V – 0.5355 V=0.236 V
第四章电化学与金属腐蚀
1.是非题(对的在括号内填“+”,错的填“-”号
(1取两根铜棒,将一根插入盛有0.1mol·dm-3CuSO4溶液的烧杯中,另一根插入盛有1mol·dm-3CuSO4溶液的烧杯中,并用盐桥将两只烧杯中的溶液连结起来,可以组成一个浓差原电池。(

习题与思考题1. 简述S7-200 SMART 控制系统的基本构成答：一个最基本的S7-200 SMART PLC 控制系统由基本单元（S7-200 SMART CPU 模块）、个人计算机、STEP7-Micro/WIN 编程软件及通信网络设备构成。

2. S7-200 SMART 标准型CPU 有哪些型号？各型号之间有什么差异？答：标准型CPU 有SR20/ST20、SR30/ST30、SR40/ST40、SR60/ST60。

主要差异在于用户程序存储器容量、I/O （数字量与模拟量）数量、最大脉冲输出频率、脉冲捕获输入点数。

3. 画出CPU SR40 AC/DC/继电器模块的外部端子接线图。

答：见教材图4-3。

4. S7-200 SMART 数字量输出有哪两种类型？分别画出它们的外部端子接线图。

答：晶体管输出和继电器输出两种类型，外部端子接线图见教材图4-5。

5. S7-200 SMART 模拟量扩展模块的性能指标有哪些？画出模拟量输入与输出模块的外部端子接线图。

答：S7-200 SMART 模拟量扩展模块的性能指标包括输入/输出类型与端口数量、输入/输出的电压/电流范围、模拟量与数字量之间的转换时间、分辨率、对DC 5V 与传感器电源的消耗电流值等。

外部端子接线图见教材图4-14。

6. 用于测量温度（0~99℃）的变送器输出信号为4~20mA ，模拟量输入模块将0~20mA 转换为数字0~27648，试求当温度为40℃时，转换后得到的二进制数N ？ 答：14467553040099553027648=+×−−=N7. S7-200 SMART 的信号板有哪几种类型？答： SB DT04，SB AE01，SB AQ01，SB CM01，SB BA01。

8. S7-200 SMART 标准型CPU 扩展配置时，应考虑哪些因素？I/O 是如何编址的？答：要考虑主机能够扩展的模块数量、数字量输入/输出映像区的大小、模拟量输入/输出映像区的大小、内部电源的负载能力。

第四章 大数定律与中心极限定理习题4.11． 如果X X Pn →，且Y X Pn →．试证：P {X = Y } = 1．证：因 | X − Y | = | −(X n − X ) + (X n − Y )| ≤ | X n − X | + | X n − Y |，对任意的ε > 0，有⎭⎬⎫⎩⎨⎧≥−+⎭⎬⎫⎩⎨⎧≥−≤≥−≤2||2||}|{|0εεεY X P X X P Y X P n n ，又因X X Pn →，且Y X Pn →，有02||lim =⎭⎬⎫⎩⎨⎧≥−+∞→εX X P n n ，02||lim =⎭⎫⎩⎨⎧≥−+∞→εY X P n n ，则P {| X − Y | ≥ ε} = 0，取k 1=ε，有01||=⎭⎬⎫⎩⎨⎧≥−k Y X P ，即11||=⎭⎬⎫⎩⎨⎧<−k Y X P ， 故11||lim1||}{1=⎭⎬⎫⎩⎨⎧<−=⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧<−==+∞→+∞=k Y X P k Y X P Y X P k k I ． 2． 如果X X Pn →，Y Y Pn →．试证：（1）Y X Y X Pn n +→+； （2）XY Y X Pn n →．证：（1）因 | (X n + Y n ) − (X + Y ) | = | (X n − X ) + (Y n − Y )| ≤ | X n − X | + | Y n − Y |，对任意的ε > 0，有⎭⎫⎩⎨⎧≥−+⎭⎬⎫⎩⎨⎧≥−≤≥+−+≤2||2||}|)()({|0εεεY Y P X X P Y X Y X P n n n n ，又因X X P n →，Y Y P n →，有02||lim =⎭⎫⎩⎨⎧≥−+∞→εX X P n n ，02||lim =⎭⎬⎫⎩⎨⎧≥−+∞→εY Y P n n ，故0}|)()({|lim =≥+−++∞→εY X Y X P n n n ，即Y X Y X Pn n +→+；（2）因 | X n Y n − XY | = | (X n − X )Y n + X (Y n − Y ) | ≤ | X n − X | ⋅ | Y n | + | X | ⋅ | Y n − Y |，对任意的ε > 0，有⎭⎬⎫⎩⎨⎧≥−⋅+⎭⎬⎫⎩⎨⎧≥⋅−≤≥−≤2||||2||||}|{|0εεεY Y X P Y X X P XY Y X P n n n n n ，对任意的h > 0，存在M 1 > 0，使得4}|{|1h M X P <≥，存在M 2 > 0，使得8}|{|2hM Y P <≥， 存在N 1 > 0，当n > N 1时，8}1|{|h Y Y P n <≥−， 因| Y n | = | (Y n − Y ) + Y | ≤ | Y n − Y | + | Y |，有4}|{|}1|{|}1|{|22h M Y Y Y P M Y P n n <≥+≥−≤+≥， 存在N 2 > 0，当n > N 2时，4)1(2||2h M X X P n <⎭⎬⎫⎩⎨⎧+≥−ε，当n > max{N 1, N 2}时，有244}1|{|)1(2||2||||22h h h M Y P M X X P Y X X P n n n n =+<+≥+⎭⎬⎫⎩⎨⎧+≥−≤⎭⎬⎫⎩⎨⎧≥⋅−εε，存在N 3 > 0，当n > N 3时，42||1hM Y Y P n <⎭⎬⎫⎩⎨⎧≥−ε，有244}|{|2||2||||11h h h M X P M Y Y P X Y Y P n n =+<≥+⎭⎬⎫⎩⎨⎧≥−≤⎭⎬⎫⎩⎨⎧≥⋅−εε，则对任意的h > 0，当n > max{N 1, N 2, N 3} 时，有h h h Y Y X P Y X X P XY Y X P n n n n n =+<⎭⎬⎫⎩⎨⎧≥−⋅+⎭⎬⎫⎩⎨⎧≥⋅−≤≥−≤222||||2||||}|{|0εεε，故0}|{|lim =≥−+∞→εXY Y X P n n n ，即XY Y X Pn n →．3． 如果X X Pn →，g (x )是直线上的连续函数，试证：)()(X g X g Pn →． 证：对任意的h > 0，存在M > 0，使得4}|{|h M X P <≥， 存在N 1 > 0，当n > N 1时，4}1|{|h X X P n <≥−， 因| X n | = | (X n − X ) + X | ≤ | X n − X | + | X |，则244}|{|}1|{|}1|{|h h h M X P X X P M X P n n =+<≥+≥−≤+≥， 因g (x ) 是直线上的连续函数，有g (x ) 在闭区间 [− (M + 1), M + 1] 上连续，必一致连续， 对任意的ε > 0，存在δ > 0，当 | x − y | < δ 时，有 | g (x ) − g ( y ) | < ε ，存在N 2 > 0，当n > N 2时，4}|{|hX X P n <≥−δ，则对任意的h > 0，当n > max{N 1, N 2} 时，有{}}|{|}1|{|}|{|}|)()({|0M X M X X X P X g X g P n n n ≥+≥≥−≤≥−≤U U δεh hh h M X P M X P X X P n n =++<≥++≥+≥−≤424}|{|}1|{|}|{|δ， 故0}|)()({|lim =≥−+∞→εX g X g P n n ，即)()(X g X g Pn →．4． 如果a X P n →，则对任意常数c ，有ca cX Pn →． 证：当c = 0时，有c X n = 0，ca = 0，显然ca cX Pn →；当c ≠ 0时，对任意的ε > 0，有0||||lim =⎭⎬⎫⎩⎨⎧≥−+∞→c a X P n n ε， 故0}|{|lim =≥−+∞→εca cX P n n ，即ca cX Pn →．5． 试证：X X P n →的充要条件为：n → +∞ 时，有0||1||→⎟⎟⎠⎞⎜⎜⎝⎛−+−XX X X E n n ．证：以连续随机变量为例进行证明，设X n − X 的密度函数为p ( y )，必要性：设X X Pn →，对任意的ε > 0，都有0}|{|lim =≥−+∞→εX X P n n ，对012>+εε，存在N > 0，当n > N 时，εεε+<≥−1}|{|2X X P n ， 则∫∫∫≥<∞+∞−+++=+=⎟⎟⎠⎞⎜⎜⎝⎛−+−εε||||)(||1||)(||1||)(||1||||1||y y n n dy y p y y dy y p y y dy y p y y XX X X E εεεεεεεεεεεεε=+++<≥−+<−+=++≤∫∫≥<11}|{|}|{|1)()(12||||X X P X X P dy y p dy y p n n y y ，故n → +∞ 时，有0||1||→⎟⎟⎠⎞⎜⎜⎝⎛−+−XX X X E n n ； 充分性：设n → +∞ 时，有0||1||→⎟⎟⎠⎞⎜⎜⎝⎛−+−XX X X E n n ， 因∫∫∫≥≥≥++≤++==≥−εεεεεεεεεε||||||)(||1||1)(11)(}|{|y y y n dy y p y y dy y p dy y p X X P ⎟⎟⎠⎞⎜⎜⎝⎛−+−+=++≤∫∞+∞−||1||1)(||1||1X X X X E dy y p y y n n εεεε， 故0}|{|lim =≥−+∞→εX X P n n ，即X X Pn →．6． 设D (x )为退化分布：⎩⎨⎧≥<=.0,1;0,0)(x x x D试问下列分布函数列的极限函数是否仍是分布函数？（其中n = 1, 2, …．）（1）{D (x + n )}； （2）{D (x + 1/n )}； （3）{D (x − 1/n )}．解：（1）对任意实数x ，当n > −x 时，有x + n > 0，D (x + n ) = 1，即1)(lim =++∞→n x D n ，则 {D (x + n )} 的极限函数是常量函数f (x ) = 1，有f (−∞) = 1 ≠ 0，故 {D (x + n )} 的极限函数不是分布函数； （2）若x ≥ 0，有01>+n x ，11=⎟⎠⎞⎜⎝⎛+n x D ，即11lim =⎟⎠⎞⎜⎝⎛++∞→n x D n ，若x < 0，当x n 1−>时，有01<+n x ，01=⎟⎠⎞⎜⎝⎛+n x D ，即01lim =⎟⎠⎞⎜⎝⎛++∞→n x D n ，则⎩⎨⎧≥<=⎟⎠⎞⎜⎝⎛++∞→.0,1;0,01lim x x n x D n 这是在0点处单点分布的分布函数，满足分布函数的基本性质，故⎭⎬⎫⎩⎨⎧⎟⎠⎞⎜⎝⎛+n x D 1的极限函数是分布函数；（3）若x ≤ 0，有01<−n x ，01=⎟⎠⎞⎜⎝⎛−n x D ，即01lim =⎟⎠⎞⎜⎝⎛−+∞→n x D n ，若x > 0，当x n 1>时，有01>−n x ，11=⎟⎠⎞⎜⎝⎛−n x D ，即11lim =⎟⎠⎞⎜⎝⎛−+∞→n x D n ，则⎩⎨⎧>≤=⎟⎠⎞⎜⎝⎛−+∞→.0,1;0,01lim x x n x D n 在x = 0处不是右连续，故⎭⎬⎫⎩⎨⎧⎟⎠⎞⎜⎝⎛−n x D 1的极限函数不是分布函数．7． 设分布函数列 {F n (x )} 弱收敛于连续的分布函数F (x )，试证：{F n (x )} 在 (−∞, +∞) 上一致收敛于分布函数F (x )． 证：因F (x ) 为连续的分布函数，有F (−∞) = 0，F (+∞) = 1，对任意的ε > 0，取正整数ε2>k ，则存在分点x 1 < x 2 < … < x k −1，使得1,,2,1,)(−==k i kix F i L ，并取x 0 = −∞，x k = +∞， 可得k k i k x F x F i i ,1,,2,1,21)()(1−=<=−−L ε， 因 {F n (x )} 弱收敛于F (x )，且F (x ) 连续，有 {F n (x )} 在每一点处都收敛于F (x )，则存在N > 0，当n > N 时，1,,2,1,2|)()(|−=<−k i x F x F i i n L ε，且显然有20|)()(|00ε<=−x F x F n ，20|)()(|ε<=−k k n x F x F ，对任意实数x ，必存在j ，1 ≤ j ≤ k ，有x j −1 ≤ x < x j ，因2)()()()(2)(11εε+<≤≤<−−−j j n n j n j x F x F x F x F x F ，则εεεε−=−−>−−>−−222)()()()(1x F x F x F x F j n ，且εεεε=+<+−<−222)()()()(x F x F x F x F j n ，即对任意的ε > 0和任意实数x ，总存在N > 0，当n > N 时，都有 | F n (x ) − F (x ) | < ε ， 故 {F n (x )} 在 (−∞, +∞) 上一致收敛于分布函数F (x )．8． 如果X X Ln →，且数列a n → a ，b n → b ．试证：b aX b X a Ln n n +→+． 证：设y 0是F aX + b ( y ) 的任一连续点，则对任意的ε > 0，存在h > 0，当 | y − y 0 | < h 时，4|)()(|0ε<−++y F y F b aX b aX ，又设y 是满足 | y − y 0 | < h 的F aX + b ( y ) 的任一连续点，因⎟⎠⎞⎜⎝⎛−=⎭⎬⎫⎩⎨⎧−≤=≤+=+a b y F a b y X P y b aX P y F X b aX }{)(，有a b y x −=是F X (x )的连续点，且X X L n→， 有)()(lim x F x F X X n n =+∞→，存在N 1，当n > N 1时，4|)()(|ε<−x F x F X X n ，即4|)()(|ε<−++y F y F b aX b aX n ，则当n > N 1且 | y − y 0 | < h 时，2|)()(||)()(||)()(|00ε<−+−≤−++++++y F y F y F y F y F y F b aX b aX b aX b aX b aX b aX n n ， 因X 的分布函数F X (x ) 满足F X (−∞) = 0，F X (+∞) = 1，F X (x ) 单调不减且几乎处处连续， 存在M ，使得F X (x ) 在x = ± M 处连续，且41)(ε−>M F X ，4)(ε<−M F X ，因X X Ln →，有41)()(lim ε−>=+∞→M F M F X X n n ，4)()(lim ε<−=−+∞→M F M F X X n n ，则存在N 2，当n > N 2时，41)(ε−>M F n X ，4)(ε<−M F n X ，可得2)(1)(}|{|ε<−+−=>M F M F M X P n n X X n ，因数列a n → a ，b n → b ，存在N 3，当n > N 3时，M h a a n 4||<−，4||h b b n <−， 可得当n > max{N 2, N 3}时，⎭⎫⎩⎨⎧>−+−=⎭⎬⎫⎩⎨⎧>+−+2|)()(|2|)()(|h b b X a a P h b aX b X a P n n n n n n n2}|{|24||42||||||ε<>=⎭⎬⎫⎩⎨⎧>+⋅≤⎭⎬⎫⎩⎨⎧>−+⋅−≤M X P h h X M hP h b b X a a P nn n n n ， 则⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧>+−+⎭⎬⎫⎩⎨⎧+≤+≤≤+=+2|)()(|2}{)(000h b aX b X a h y b aX P y b X a P y F n n n n n n n n b X a n n n U222|)()(|200ε+⎟⎠⎞⎜⎝⎛+<⎭⎬⎫⎩⎨⎧>+−++⎭⎬⎫⎩⎨⎧+≤+≤+h y F h b aX b X a P h y b aX P b aX n n n n n n ， 且⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧>+−+≤+≤⎭⎬⎫⎩⎨⎧−≤+=⎟⎠⎞⎜⎝⎛−+2|)()(|}{22000h b aX b X a y b X a P h y b aX P h y F n n n n n n n n b aX n U2)(2|)()(|}{00ε+<⎭⎬⎫⎩⎨⎧>+−++≤+≤+y F h b aX b X a P y b X a P n n n b X a n n n n n n n ， 即22)(22000εε+⎟⎠⎞⎜⎝⎛+<<−⎟⎠⎞⎜⎝⎛−+++h y F y F h y F b aX b X a b aX n n n n n ，因当n > N 1且 | y − y 0 | < h 时，2)()(2)(00εε+<<−+++y F y F y F b aX b aX b aX n ，在区间⎟⎠⎞⎜⎝⎛++h y h y 00,2取F aX + b ( y ) 的任一连续点y 1，满足 | y 1 − y 0 | < h ，当n > max{N 1, N 2, N 3}时，εεε+<+≤+⎟⎠⎞⎜⎝⎛+<++++)(2)(22)(0100y F y F h y F y F b aX b aX b aX b X a n n n n n ，在区间⎟⎠⎞⎜⎝⎛−−2,00h y h y 取F aX + b ( y ) 的任一连续点y 2，满足 | y 2 − y 0 | < h ，当n > max{N 1, N 2, N 3}时，εεε−>−≥−⎟⎠⎞⎜⎝⎛−>++++)(2)(22)(0200y F y F h y F y F b aX b aX b aX b X a n n n n n ，即对于F aX + b ( y ) 的任一连续点y 0，当n > max{N 1, N 2, N 3}时，ε<−++|)()(|00y F y F b aX b X a n n n ， 故)()(y F y F b aX Wb X a n n n ++→，b aX b X a Ln n n +→+． 9． 如果X X Ln →，a Y Pn →，试证：a X Y X Ln n +→+． 证：设y 0是F X + a ( y ) 的任一连续点，则对任意的ε > 0，存在h > 0，当 | y − y 0 | < h 时，4|)()(|0ε<−++y F y F a X a X ，又设y 是满足 | y − y 0 | < h 的F X + a ( y )的任一连续点，因F X + a ( y ) = P {X + a ≤ y } = P {X ≤ y − a } = F X ( y − a )，有x = y − a 是F X (x )的连续点，且X X Ln →， 有)()(lim x F x F X X n n =+∞→，存在N 1，当n > N 1时，4|)()(|ε<−x F x F X X n ，即4|)()(|ε<−++y F y F a X a X n ， 则当n > N 1且 | y − y 0 | < h 时，2|)()(||)()(||)()(|00ε<−+−≤−++++++y F y F y F y F y F y F a X a X a X a X a X a X n n ，因a Y Pn →，有02||lim =⎭⎫⎩⎨⎧>−+∞→h a Y P n n ，存在N 2，当n > N 2时，22||ε<⎭⎬⎫⎩⎨⎧>−h a Y P n ， 则⎭⎬⎫⎩⎨⎧⎭⎫⎩⎨⎧>−⎭⎬⎫⎩⎨⎧+≤+≤≤+=+2||2}{)(000h a Y h y a X P y Y X P y F n n n n Y X n n U222||200ε+⎟⎠⎞⎜⎝⎛+<⎭⎬⎫⎩⎨⎧>−+⎭⎬⎫⎩⎨⎧+≤+≤+h y F h a Y P h y a X P a X n n n ， 且⎭⎬⎫⎩⎨⎧⎭⎫⎩⎨⎧>−≤+≤⎭⎬⎫⎩⎨⎧−≤+=⎟⎠⎞⎜⎝⎛−+2||}{22000h a Y y Y X P h y a X P h y F n n n n a X n U2)(2||}{00ε+<⎭⎬⎫⎩⎨⎧>−+≤+≤+y F h a Y P y Y X P n n Y X n n n ， 即22)(22000εε+⎟⎠⎞⎜⎝⎛+<<−⎟⎠⎞⎜⎝⎛−+++h y F y F h y F a X Y X a X n n n n ，因当n > N 1且 | y − y 0 | < h 时，2)()(2)(00εε+<<−+++y F y F y F a X a X a X n ，在区间⎟⎠⎞⎜⎝⎛++h y h y 00,2取F X + a ( y ) 的任一连续点y 1，满足 | y 1 − y 0 | < h ，当n > max{N 1, N 2}时，εεε+<+≤+⎟⎠⎞⎜⎝⎛+<++++)(2)(22)(0100y F y F h y F y F a X a X a X Y X n n n n ，在区间⎟⎠⎞⎜⎝⎛−−2,00h y h y 取F X + a ( y ) 的任一连续点y 2，满足 | y 2 − y 0 | < h ，当n > max{N 1, N 2}时，εεε−>−≥−⎟⎠⎞⎜⎝⎛−>++++)(2)(22)(0200y F y F h y F y F a X a X a X Y X n n n n ，即对于F X + a ( y ) 的任一连续点y 0，当n > max{N 1, N 2}时，ε<−++|)()(|00y F y F a X Y X n n ， 故)()(y F y F a X WY X n n ++→，a X Y X Ln n +→+． 10．如果X X Ln →，0Pn Y →，试证：0Pn n Y X →．证：因X 的分布函数F X (x ) 满足F X (−∞) = 0，F X (+∞) = 1，F X (x ) 单调不减且几乎处处连续，则对任意的h > 0，存在M ，使得F X (x ) 在x = ± M 处连续，且41)(h M F X −>，4)(hM F X <−， 因X X L n →，有41)()(lim h M F M F X X n n −>=+∞→，4)()(lim h M F M F X X n n <−=−+∞→，则存在N 1，当n > N 1时，41)(h M F n X −>，4)(hM F n X <−，可得2)(1)(}|{|hM F M F M X P n n X X n <−+−=>，因0Pn Y →，对任意的ε > 0，有0||lim =⎭⎬⎫⎩⎨⎧>+∞→M Y P n n ε，存在N 2，当n > N 2时，2||h M Y P n <⎭⎬⎫⎩⎨⎧>ε， 则当n > max{N 1, N 2}时，有h M Y P M X P M Y M X P Y X P n n n n n n <⎭⎬⎫⎩⎨⎧>+>≤⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧>>≤>εεε||}|{|||}|{|}|{|U ，故0}|{|lim =>+∞→εn n n Y X P ，即0Pn n Y X →．11．如果X X Ln →，a Y Pn →，且Y n ≠ 0，常数a ≠ 0，试证：aXY X L n n →． 证：设y 0是F X / a ( y ) 的任一连续点，则对任意的ε > 0，存在h > 0，当 | y − y 0 | < h 时，4|)()(|0//ε<−y F y F a X a X ，又设y 是满足 | y − y 0 | < h 的F X / a ( y ) 的任一连续点，因)(}{)(/ay F ay X P y a X P y F X a X =≤=⎭⎬⎫⎩⎨⎧≤=，有x = ay 是F X (x )的连续点，且X X Ln →，有)()(lim x F x F X X n n =+∞→，存在N 1，当n > N 1时，4|)()(|ε<−x F x F X X n ，即4|)()(|//ε<−y F y F a X a X n ，则当n > N 1且 | y − y 0 | < h 时，2|)()(||)()(||)()(|0////0//ε<−+−≤−y F y F y F y F y F y F a X a X a X a X a X a X n n ，因X 的分布函数F X (x )满足F X (−∞) = 0，F X (+∞) = 1，F X (x )单调不减且几乎处处连续，存在M ，使得F X (x ) 在x = ± M 处连续，且121)(ε−>M F X ，12)(ε<−M F X ，因X X Ln →，有121)()(lim ε−>=+∞→M F M F X X n n ，12)()(lim ε<−=−+∞→M F M F X X n n ，则存在N 2，当n > N 2时，121)(ε−>M F n X ，12)(ε<−M F n X ，可得6)(1)(}|{|ε<−+−=>M F M F M X P n n X X n ，因0≠→a Y Pn ，有02||lim =⎭⎬⎫⎩⎨⎧>−+∞→h a Y P n n ，存在N 3 > 0，当n > N 3时，62||||ε<⎭⎬⎫⎩⎨⎧>−a a Y P n ，有62||||ε<⎭⎬⎫⎩⎨⎧<a Y P n ，且64||2ε<⎭⎬⎫⎩⎨⎧>−M h a a Y P n ， 可得当n > max{N 1, N 2, N 3}时，⎭⎬⎫⎩⎨⎧>⋅−⋅=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−2||||||||2)(2h Y a a Y X P h aY Y a X P h a X Y X P n n n n n n n n n ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎭⎬⎫⎩⎨⎧<⎭⎬⎫⎩⎨⎧>−>≤2||||4||}|{|2a Y M h a a Y M X P n n n U U22||||4||}|{|2ε<⎭⎬⎫⎩⎨⎧<+⎭⎬⎫⎩⎨⎧>−+>≤a Y P M h a a Y P M X P n n n ，则⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎫⎪⎩⎪⎨⎧>−⎭⎬⎫⎩⎨⎧+≤≤⎭⎬⎫⎩⎨⎧≤=22)(000/h a X Y X h y a XP y Y X P y F n n n n n n Y X n n U22220/0ε+⎟⎠⎞⎜⎝⎛+<⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−+⎭⎬⎫⎩⎨⎧+≤≤h y F h a X Y X P h y a X P a X n n n n n ，且⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−⎭⎬⎫⎩⎨⎧≤≤⎭⎬⎫⎩⎨⎧−≤=⎟⎠⎞⎜⎝⎛−222000/h a X Y X y Y X P h y a X P h y F n n n nn n a X n U2)(20/0ε+<⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−+⎭⎬⎫⎩⎨⎧≤≤y F h a X Y X P y Y X P n n Y X n n n n n ，即22)(220/0/0/εε+⎟⎠⎞⎜⎝⎛+<<−⎟⎠⎞⎜⎝⎛−h y F y F h y F a X Y X a X n n n n ，因当n > N 1且 | y − y 0 | < h 时，2)()(2)(0//0/εε+<<−y F y F y F a X a X a X n ，在区间⎟⎠⎞⎜⎝⎛++h y h y 00,2取F X / a ( y ) 的任一连续点y 1，满足 | y 1 − y 0 | < h ，当n > max{N 1, N 2, N 3}时，εεε+<+≤+⎟⎠⎞⎜⎝⎛+<)(2)(22)(0/1/0/0/y F y F h y F y F a X a X a X Y X n n n n ，在区间⎟⎠⎞⎜⎝⎛−−2,00h y h y 取F X / a ( y ) 的任一连续点y 2，满足 | y 2 − y 0 | < h ，当n > max{N 1, N 2, N 3}时，εεε−>−≥−⎟⎠⎞⎜⎝⎛−>)(2)(22)(0/2/0/0/y F y F h y F y F a X a X a X Y X n n n n ，即对于F X / a ( y ) 的任一连续点y 0，当n > max{N 1, N 2, N 3}时，ε<−|)()(|0/0/y F y F a X Y X n n ，故)()(//y F y F a X WY X n n →，aX Y X L n n →． 12．设随机变量X n 服从柯西分布，其密度函数为+∞<<∞−+=x x n nx p n ,)1π()(22．试证：0Pn X →．证：对任意的ε > 0，)arctan(π2)arctan(π1)1π(}|{|22εεεεεεn nx dx x n n X P n ==+=<−−∫， 则12ππ2)arctan(lim π2}|0{|lim =⋅==<−+∞→+∞→εεn X P n n n ， 故0Pn X →．13．设随机变量序列{X n }独立同分布，其密度函数为⎪⎩⎪⎨⎧<<=.,0;0,1)(其他ββx x p其中常数β > 0，令Y n = max{X 1, X 2, …, X n }，试证：βPn Y →．证：对任意的ε > 0，P {| Y n − β | < ε} = P {β − ε < Y n < β + ε} = P {max{X 1, X 2, …, X n } > β − ε}= 1 − P {max{X 1, X 2, …, X n } ≤ β − ε} = 1 − P {X 1 ≤ β − ε} P {X 2 ≤ β − ε} … P {X n ≤ β − ε}n⎟⎟⎠⎞⎜⎜⎝⎛−−=βεβ1， 则11lim }|{|lim =⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−=<−+∞→+∞→nn n n Y P βεβεβ， 故βPn Y →．14．设随机变量序列{X n }独立同分布，其密度函数为⎩⎨⎧<≥=−−.,0;,e )()(a x a x x p a x 其中Y n = min{X 1, X 2, …, X n }，试证：a Y Pn →．证：对任意的ε > 0，P {| Y n − a | < ε} = P {a − ε < Y n < a + ε} = P {min{X 1, X 2, …, X n } < a + ε}= 1 − P {min{X 1, X 2, …, X n } ≥ a + ε} = 1 − P {X 1 ≥ a + ε} P {X 2 ≥ a + ε} … P {X n ≥ a + ε}εεεn na a x n a a x dx −∞++−−∞++−−−=⎟⎠⎞⎜⎝⎛−−=⎟⎠⎞⎜⎝⎛−=∫e 1e 1e 1)()(， 则1)e 1(lim }|{|lim =−=<−−+∞→+∞→εεn n n n a Y P ，故a Y Pn →．15．设随机变量序列{X n }独立同分布，且X i ~ U(0, 1)．令nni i n X Y 11⎟⎟⎠⎞⎜⎜⎝⎛=∏=，试证明：c Y P n →，其中c 为常数，并求出c ．证：设∑∏===⎟⎟⎠⎞⎜⎜⎝⎛==n i i n i i n n X n X n Y Z 11ln 1ln 1ln ，因X i ~ U (0, 1)， 则1)ln (ln )(ln 101−=−==∫x x x xdx X E i ，2)2ln 2ln (ln )(ln 12122=+−==∫x x x x x xdx X E i ，1)](ln [)(ln )Var(ln 22=−=i i i X E X E X ， 可得1)(ln 1)(1−==∑=n i i n X E n Z E ，n X nZ ni in 1)Var(ln 1)Var(12==∑=，由切比雪夫不等式，可得对任意的ε > 0，221)Var(}|)({|εεεn Z Z E Z P n n n =≤≥−，则01lim }|)({|lim 02=≤≥−≤+∞→+∞→εεn Z E Z P n n n n ，即0}|)({|lim =≥−+∞→εn n n Z E Z P ，1)(−=→n P n Z E Z ，因n Z n Y e =，且函数e x 是直线上的连续函数，根据本节第3题的结论，可得1e e −→=PZ n n Y ， 故c Y Pn →，其中1e −=c 为常数．16．设分布函数列{F n (x )}弱收敛于分布函数F (x )，且F n (x ) 和F (x ) 都是连续、严格单调函数，又设 ξ 服从(0, 1)上的均匀分布，试证：)()(11ξξ−−→F F Pn． 证：因F (x ) 为连续的分布函数，有F (−∞) = 0，F (+∞) = 1，则对任意的h > 0，存在M > 0，使得21)(h M F −>，2)(h M F <−， 因F (x ) 是连续、严格单调函数，有F −1( y ) 也是连续、严格单调函数， 可得F −1( y ) 在区间 [F (− M − 1), F (M + 1)] 上一致连续， 对任意的ε > 0，存在δ > 0，当y , y * ∈ [F (− M − 1), F (M + 1)] 且 | y − y * | < δ 时，| F −1( y ) − F −1( y *) | < ε， 设y * 是 [F (−M ), F (M )] 中任一点，记x * = F −1( y *)，有x * ∈ [−M , M ]，不妨设0 < ε < 1， 则对任意的x 若满足 ε≥−|*|x x ，就有 δ≥−|*)(|y x F ，根据本节第7题的结论知，{F n (x )} 在 (−∞, +∞) 上一致收敛于分布函数F (x )， 则对δ > 0和任意实数x ，总存在N > 0，当n > N 时，都有 | F n (x ) − F (x ) | < δ， 因当n > N 时，δ<−|)()(|x F x F n 且δ≥−|*(|y x F ，有*)(y x F n ≠，即*)(1y F x n −≠， 则对任意的0 < ε < 1，当n > N 时，*)(1y F n −满足ε<−=−−−−|*)(*)(||**)(|111y F y F x y F n n ， 可得对任意的0 < ε < 1，当n > N 时，h M F M F P F F P n −>−∈≥<−−−1)]}(),([{}|)()({|11ξεξξ由h 的任意性可知1}|)()({|lim 11=<−−−+∞→εξξF F P n n ，故)()(11ξξ−−→F F Pn．17．设随机变量序列{X n }独立同分布，数学期望、方差均存在，且E (X n ) = µ，试证：µP n k k X k n n →⋅+∑=1)1(2．证：令∑=⋅+=nk k n X k n n Y 1)1(2，并设Var (X n ) = σ 2， 因µµµ=+⋅+=+=∑=)1(21)1(2)1(2)(1n n n n k n n Y E nk n ， 且222212222)1(324)12)(1(61)1(4)1(4)Var(σσσ++=++⋅+=+=∑=n n n n n n n n k n n Y nk n ， 则由切比雪夫不等式可得，对任意的ε > 0，222)1(3241)Var(1}|{|1σεεεµ++−=−≥<−≥n n n Y Y P n n ， 因1)1(3241lim 22=⎥⎦⎤⎢⎣⎡++−+∞→σεn n n n ，由夹逼准则可得1}|{|lim =<−+∞→εµn n Y P ， 故µP n k kn X k n n Y →⋅+=∑=1)1(2． 18．设随机变量序列{X n }独立同分布，数学期望、方差均存在，且E (X n ) = 0，Var (X n ) = σ 2．试证：E (X n ) = 0，Var (X n ) = σ 2．试证：2121σP n k k X n →∑=． 注：此题与第19题应放在习题4.3中，需用到4.3节介绍的辛钦大数定律．证：因随机变量序列}{2n X 独立同分布，且222)]([)Var()(σ=+=n n n X E X X E 存在，故}{2nX 满足辛钦大数定律条件，}{2nX 服从大数定律，即2121σP n k k X n →∑=．19．设随机变量序列{X n }独立同分布，且Var (X n ) = σ 2存在，令∑==n i i X n X 11，∑=−=n i i n X X n S 122)(1．试证：22σPnS →．证：2122112122122121)2(1)(1X X n X n X X X n X X X X n X X n S n i i ni i n i i n i i i n i i n−=⎟⎟⎠⎞⎜⎜⎝⎛+−=+−=−=∑∑∑∑∑=====，设E(X n ) = µ，{X n }满足辛钦大数定律条件，{X n }服从大数定律，即µP nk k X n X →=∑=11，则根据本节第2题第（2）小问的结论知，22µPX →，因随机变量序列}{2n X 独立同分布，且2222)]([)Var()(µσ+=+=n n n X E X X E 存在，则}{2nX 满足辛钦大数定律条件，}{2nX 服从大数定律，即22121µσ+→∑=P n k k X n ，故根据本节第2题第（1）小问的结论知，22222122)(1σµµσ=−+→−=∑=P n i i nX X n S ．20．将n 个编号为1至n 的球放入n 个编号为1至n 的盒子中，每个盒子只能放一个球，记⎩⎨⎧=.,0;,1反之的盒子的球放入编号为编号为i i X i 且∑==ni i n X S 1，试证明：0)(Pn n n S E S →−． 证：因n X P i 1}1{==，nX P i 11}0{−==，且i ≠ j 时，)1(1}1{−==n n X X P j i ，)1(11}0{−−==n n X X P j i ， 则n X E i 1)(=，⎟⎠⎞⎜⎝⎛−=n n X i 111)Var(， 且i ≠ j 时，)1(1)(−=n n X X E j i ，)1(11)1(1)()()(),Cov(22−=−−=−=n n n n n X E X E X X E X X j i j i j i ， 有1)()(1==∑=ni i n X E S E ，1)1(1)1(11),Cov(2)Var()Var(211=−⋅−+−=+=∑∑≤<≤=n n n n n X X X S nj i j i ni i n ， 可得0)]()([1)(=−=⎥⎦⎤⎢⎣⎡−n n n n S E S E n n S E S E ，221)Var(1)(Var n S n n S E S n n n ==⎥⎦⎤⎢⎣⎡−， 由切比雪夫不等式，可得对任意的ε > 0，2221)(Var 1)()(εεεn n S E S n S E S E n S E S P n n n n n n =⎥⎦⎤⎢⎣⎡−≤⎭⎬⎫⎩⎨⎧≥⎥⎦⎤⎢⎣⎡−−−， 则01lim )()(lim 022=≤⎭⎬⎫⎩⎨⎧≥⎥⎦⎤⎢⎣⎡−−−≤+∞→+∞→εεn n S E S E n S E S P n n n n n n ， 故0)(Pn n nS E S →−．习题4.21． 设离散随机变量X 的分布列如下，试求X 的特征函数．1.02.03.04.03210PX解：特征函数ϕ (t ) = e it ⋅ 0 × 0.4 + e it ⋅ 1 × 0.3 + e it ⋅ 2 × 0.2 + e it ⋅ 3 × 0.1 = 0.4 + 0.3 e it + 0.2 e 2it + 0.1 e 3it ．2． 设离散随机变量X 服从几何分布P {X = k } = (1 − p ) k − 1 p ， k = 1, 2, … ．试求X 的特征函数．并以此求E (X ) 和Var (X )． 解：特征函数ititk k ititk k itk p p p p p p t e)1(1e )]1([ee)1(e )(1111−−=−=−⋅=∑∑+∞=−+∞=−ϕ； 因22]e )1(1[e ]e )1(1[]e )1([e ]e )1(1[e )(it it it it it it it p ip p i p p p i p t −−=−−⋅−−⋅−−−⋅⋅=′ϕ，有)()0(2X iE pip ip ===′ϕ，故pX E 1)(=； 因332]e )1(1[]e )1(1[e ]e )1([]e )1(1[e 2]e )1(1[e )(it it it itit itit itp p p i p p ip p i ip t −−−+−=⋅−−⋅−−−−−⋅⋅=′′−−ϕ， 有)(2)2()0(2223X E i pp p p p =−−=−−=′′ϕ，可得222)(p p X E −=， 故222112)Var(p pp p p X −=⎟⎟⎠⎞⎜⎜⎝⎛−−=． 3． 设离散随机变量X 服从巴斯卡分布rk r p p r k k X P −−⎟⎟⎠⎞⎜⎜⎝⎛−−==)1(11}{，k = r , r + 1, …试求X 的特征函数．解：特征函数∑∑+∞=−−+∞=−−+−−−=−⎟⎟⎠⎞⎜⎜⎝⎛−−⋅=r k r k it r k itr r r k r k r itkp r k k r p p p r k t )(e)1)(1()1()!1(e )1(11e )(L ϕ ∑∑+∞=−=−−−+∞=−=−−=+−−−=r k p x r k r r it rk p x r k r it ititdx x d r p x r k k r p e )1(111e )1()()!1()e ()1()1()!1()e (L itit it p x r r it p x r r r it p x k k r r r it x r r p x dx d r p x dx d r p e )1(e )1(11e )1(1111)1()!1()!1()e (11)!1()e ()!1()e (−=−=−−−=+∞=−−−−−⋅−=⎟⎠⎞⎜⎝⎛−⋅−=⎟⎟⎠⎞⎜⎜⎝⎛⋅−=∑rit itr it r it p p p p ⎥⎦⎤⎢⎣⎡−−=−−=e )1(1e ]e )1(1[)e (． 4． 求下列分布函数的特征函数，并由特征函数求其数学期望和方差．（1）)0(,e 2)(||1>=∫∞−−a dt a x F x t a ； （2）)0(,1π)(222>+=∫∞−a dt at a x F x ． 解：（1）因密度函数||11e 2)()(x a ax F x p −=′=，故⎥⎥⎦⎤⎢⎢⎣⎡−++=⎥⎦⎤⎢⎣⎡+=⋅=+∞−∞−+∞+−∞−+∞+∞−−∫∫∫0)(0)(0)(0)(||1e e 2e e 2ee 2)(ait a it a dx dx a dx a t x a it x a it x a it x a it x a itx ϕ 222112at a a it a it a +=⎟⎠⎞⎜⎝⎛−−+=； 因222222221)(22)()(a t ta t a t a t +−=⋅+−=′ϕ，有)(0)0(1X iE ==′ϕ， 故E (X ) = 0；因32242242222222221)(26)(2)(22)(2)(a t a t a a t t a t t a a t a t +−=+⋅+⋅−+⋅−=′′ϕ， 有)(22)0(222641X E i a a a =−=−=′′ϕ，可得222)(a X E =， 故222202)Var(aa X =−=；（2）因密度函数22221π)()(ax a x F x p +⋅=′=， 则∫+∞∞−+⋅=dx a x a t itx 2221e π)(ϕ， 由第（1）小题的结论知∫∞+∞−=+=dx x p a t a t itx )(e )(12221ϕ，根据逆转公式，可得∫∫∞+∞−−∞+∞−−−+⋅===dt at a dt t a x p itx itx x a 2221||1e π21)(e π21e 2)(ϕ， 可得||||222e πe 2π21e y a y a itya a a dt a t −−−+∞∞−=⋅=+⋅∫， 故||||222e e ππ1e π)(t a t a itx a a dx ax a t −−+∞∞−=⋅=+⋅=∫ϕ； 因⎩⎨⎧>−<=′−,0,e ,0,e )(2t a t a t atat ϕ 有a a −=+′≠=−′)00()00(22ϕϕ，即)0(2ϕ′不存在， 故E (X ) 不存在，Var (X ) 也不存在．5． 设X ~ N (µ, σ 2)，试用特征函数的方法求X 的3阶及4阶中心矩． 解：因X ~ N (µ, σ 2)，有X 的特征函数是222e)(t t i t σµϕ−=，则)(e)(2222t i t t t i σµϕσµ−⋅=′−，)(e)(e )(222222222σσµϕσµσµ−⋅+−⋅=′′−−t t i t t i t i t ，因)()(3e)(e)(2223222222σσµσµϕσµσµ−⋅−⋅+−⋅=′′′−−t i t i t t t i t t i ，有ϕ″′(0) = e 0 ⋅ (i µ )3 + e 0 ⋅ 3i µ ⋅ (−σ 2) = − i µ 3 − 3i µσ 2 = i 3E (X 3) = − i E (X 3)， 故E (X 3) = µ 3 + 3µσ 2； 又因2222222422)4()(3e)()(6e)(e)(222222σσσµσµϕσµσµσµ−⋅+−⋅−⋅+−⋅=−−−t t i t t i t t i t i t i t ，有ϕ (4)(0) = e 0 ⋅ (i µ )4 + e 0 ⋅ 6(i µ)2 ⋅ (−σ 2) + e 0 ⋅ 3σ 4 = µ 4 + 6µ 2σ 2 + 3σ 4 = i 4E (X 4) = E (X 4)， 故E (X 4) = µ 4 + 6µ 2σ 2 + 3σ 4．6． 试用特征函数的方法证明二项分布的可加性：若X ~ b (n , p )，Y ~ b (m , p )，且X 与Y 独立，则X + Y ~ b (n + m , p )．证：因X ~ b (n , p )，Y ~ b (m , p )，且X 与Y 独立，有X 与Y 的特征函数分别为ϕ X (t ) = ( p e it + 1 − p ) n ，ϕ Y (t ) = ( p e it + 1 − p ) m ， 则X + Y 的特征函数为ϕ X + Y (t ) = ϕ X (t ) ⋅ϕ Y (t ) = ( p e it + 1 − p ) n + m ，这是二项分布b (n + m , p )的特征函数， 故根据特征函数的唯一性定理知X + Y ~ b (n + m , p )．7． 试用特征函数的方法证明泊松分布的可加性：若X ~ P (λ1)，Y ~ P (λ2)，且X 与Y 独立，则X + Y ~ P (λ1 + λ2)．证：因X ~ P (λ1)，Y ~ P (λ2)，且X 与Y 独立，有X 与Y 的特征函数分别为)1(e1e )(−=itt X λϕ，)1(e2e )(−=itt Y λϕ，则X + Y 的特征函数为)1)(e(21e )()()(−++==itt t t Y X Y X λλϕϕϕ，这是泊松分布P (λ1 + λ2)的特征函数，故根据特征函数的唯一性定理知X + Y ~ P (λ1 + λ2)．8． 试用特征函数的方法证明伽马分布的可加性：若X ~ Ga (α1, λ)，Y ~ Ga (α2, λ)，且X 与Y 独立，则X + Y ~ Ga (α1 + α2 , λ)．证：因X ~ Ga (α1, λ)，Y ~ Ga (α2, λ)，且X 与Y 独立，有X 与Y 的特征函数分别为11)(αλϕ−⎟⎠⎞⎜⎝⎛−=it t X ，21)(αλϕ−⎟⎠⎞⎜⎝⎛−=it t Y ，则X + Y 的特征函数为)(211)()()(ααλϕϕϕ+−+⎟⎠⎞⎜⎝⎛−==it t t t Y X Y X ，这是伽马分布Ga (α1 + α2 , λ)的特征函数，故根据特征函数的唯一性定理知X + Y ~ Ga (α1 + α2 , λ)．9． 试用特征函数的方法证明χ 2分布的可加性：若X ~ χ 2 (n )，Y ~ χ 2 (m )，且X 与Y 独立，则X + Y ~ χ 2 (n + m )．证：因X ~ χ 2 (n )，Y ~ χ 2 (m )，且X 与Y 独立，有X 与Y 的特征函数分别为2)21()(n X it t −−=ϕ，2)21()(m Y it t −−=ϕ，则X + Y 的特征函数为2)21()()()(m n Y X Y X it t t t +−+−==ϕϕϕ，这是χ 2分布χ 2 (n + m )的特征函数，故根据特征函数的唯一性定理知X + Y ~ χ 2 (n + m )．10．设X i 独立同分布，且X i ~ Exp(λ)，i = 1, 2, …, n ．试用特征函数的方法证明：),(~1λn Ga X Y ni i n ∑==．证：因X i ~ Exp (λ)，i = 1, 2, …, n ，且X i 相互独立，有X i 的特征函数为11)(−⎟⎠⎞⎜⎝⎛−=−=λλλϕit it t i X ，则∑==ni i n X Y 1的特征函数为nni X Y it t t i n −=⎟⎠⎞⎜⎝⎛−==∏λϕϕ1)()(1，这是伽马分布Ga (n , λ)的特征函数，故根据特征函数的唯一性定理知Y n ~ Ga (n , λ)．11．设连续随机变量X 的密度函数如下：+∞<<∞−−+⋅=x x x p ,)(π1)(22µλλ， 其中参数λ > 0, −∞ < µ < +∞，常记为X ~ Ch (λ, µ )．（1）试证X 的特征函数为exp{i µ t − λ | t |}，且利用此结果证明柯西分布的可加性； （2）当µ = 0, λ = 1时，记Y = X ，试证ϕ X + Y (t ) = ϕ X (t ) ⋅ϕ Y (t )，但是X 与Y 不独立；（3）若X 1, X 2, …, X n 相互独立，且服从同一柯西分布，试证：)(121n X X X n+++L 与X 1同分布． 证：（1）根据第4题第（2）小题的结论知：若X *的密度函数为22π1)(*xx p +⋅=λλ，即X * ~ Ch (λ, 0)， 则X *的特征函数为ϕ * (t ) = e −λ | t |，且X = X * + µ 的密度函数为22)(π1)(µλλ−+⋅=x x p ， 故X 的特征函数为ϕ X (t ) = e i µ t ϕ * (t ) = e i µ t ⋅ e −λ | t | = e i µ t −λ | t |； 若X 1 ~ Ch (λ1, µ1)，X 2 ~ Ch (λ2, µ2)，且相互独立，有X 1与X 2的特征函数分别为||111e )(t t i X t λµϕ−=，||222e )(t t i X t λµϕ−=， 则X 1 + X 2的特征函数为||)()(21212121e )()()(t t i X X X X t t t λλµµϕϕϕ+−++==，这是柯西分布Ch (λ1 + λ2, µ1 + µ2)的特征函数，故根据特征函数的唯一性定理知X 1 + X 2 ~ Ch (λ1 + λ2, µ1 + µ2)； （2）当µ = 0, λ = 1时，X ~ Ch (1, 0)，有X 的特征函数为ϕ X (t ) = e −| t |，又因Y = X ，有Y 的特征函数为ϕ Y (t ) = e −| t |，且X + Y = 2X ，故X + Y 的特征函数为ϕ X + Y (t ) = ϕ 2X (t ) = ϕ X (2t ) = e −| 2t | = e −| t | ⋅ e −| t | =ϕ X (t ) ⋅ϕ Y (t )； 但Y = X ，显然有X 与Y 不独立；（3）因X i ~ Ch (λ, µ )，i = 1, 2, …, n ，且X i 相互独立，有X i 的特征函数为||e )(t t i X t i λµϕ−=， 则)(121n n X X X nY +++=L 的特征函数为 )(e e )()(1||111t n t t t X t t i n t n ti n ni X ni X nY i in ϕϕϕϕλµλµ===⎟⎠⎞⎜⎝⎛==−⎟⎟⎠⎞⎜⎜⎝⎛⋅−⋅==∏∏，故根据特征函数的唯一性定理知)(121n X X X n+++L 与X 1同分布． 12．设连续随机变量X 的密度函数为p (x )，试证：p (x ) 关于原点对称的充要条件是它的特征函数是实的偶函数．证：方法一：根据随机变量X 与−X 的关系充分性：设X 的特征函数ϕ X (t )是实的偶函数，有ϕ X (t ) = ϕ X (−t )，则−X 的特征函数ϕ −X (t ) = ϕ X (−t ) = ϕ X (t )，根据特征函数的唯一性定理知−X 与X 同分布，因X 的密度函数为p (x )，有−X 的密度函数为p (−x )，故由−X 与X 同分布可知p (−x ) = p (x )，即p (x ) 关于原点对称； 必要性：设X 的密度函数p (x ) 关于原点对称，有p (−x ) = p (x )， 因−X 的密度函数为p (−x )，即−X 与X 同分布，则−X 的特征函数ϕ −X (t ) = ϕ X (−t ) = ϕ X (t )，且)(][e ][e ][e )()()(t E E E t t X itX itX X it X X ϕϕϕ=====−−−， 故X 的特征函数ϕ X (t )是实的偶函数． 方法二：根据密度函数与特征函数的关系充分性：设连续随机变量X 的特征函数ϕ X (t )是实的偶函数，有ϕ X (t ) = ϕ X (−t )，因∫+∞∞−−=dt t x p itx )(e π21)(ϕ，有∫∫+∞∞−+∞∞−−−==−dt t dt t x p itxx it )(e π21)(e π21)()(ϕϕ， 令t = −u ，有dt = −du ，且当t → −∞时，u → +∞；当t → +∞时，u → −∞，则)()(e π21)(e π21))((e π21)()(x p du u du u du u x p iuxiux x u i ==−=−−=−∫∫∫+∞∞−−+∞∞−−−∞∞+−ϕϕϕ， 故p (x ) 关于原点对称；必要性：设X 的密度函数p (x ) 关于原点对称，有p (−x ) = p (x )，因∫+∞∞−−==dx x p E t itxitX)(e )(e)(ϕ，有∫∫+∞∞−−+∞∞−−==−dx x p dx x p t itx xt i )(e )(e)()(ϕ，令x = −y ，有dx = −dy ，且当x → −∞时，y → +∞；当x → +∞时，y → −∞， 则)()(e )(e ))((e )()(t dy y p dy y p dy y p t X ity ity y it X ϕϕ==−=−−=−∫∫∫+∞∞−+∞∞−−∞∞+−−，且)(][e ][e ][e )()()(t E E E t t X itX itX X t i X X ϕϕϕ====−=−−， 故X 的特征函数ϕ X (t )是实的偶函数．13．设X 1, X 2, …, X n 独立同分布，且都服从N(µ , σ 2)分布，试求∑==ni i X n X 11的分布．证：因X i ~ N (µ , σ 2)，i = 1, 2, …, n ，且X i 相互独立，有X i 的特征函数为222e)(t t i X t i σµϕ−=，则∑==n i i X n X 11的特征函数为nt t i n t n t i n ni X n i X n X n t t t i i 2211112222ee)()(σµσµϕϕϕ−⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⋅====⎟⎠⎞⎜⎝⎛==∏∏，这是正态分布⎟⎟⎠⎞⎜⎜⎝⎛n N 2,σµ的特征函数，故根据特征函数的唯一性定理知⎟⎟⎠⎞⎜⎜⎝⎛=∑=n N X n X ni i 21,~1σµ． 14．利用特征函数方法证明如下的泊松定理：设有一列二项分布{b (k , n , p n )}，若λ=→∞n n np lim ，则L ,2,1,0,e !),,(lim ==−∞→k k p n k b kn n λλ．证：二项分布b (n , p n )的特征函数为ϕ n (t ) = ( p n e it + 1 − p n ) n = [1 + p n (e it − 1)] n ，且n → ∞时，p n → 0，因)1(e)1(e )1(e 1e )]1(e 1[lim )]1(e 1[lim )(lim −−⋅−→→∞→∞=−+=−+=itit n it n n np p itn p n it n n n n p p t λϕ，。

第四章 理想气体的热力过程
第四章 理想气体的热力过程
4—1 有 2.3 千克的 CO， 初态 T1 = 477K，p1 = 0.32MPa ， 经可逆定容加热， 终温 T2 = 600K ， 设 CO 为理想气体，求 ∆U 、 ∆H 、 ∆S ，过程功及过程热量。 （1）设比热容为定值； （2）变 值比热容，按气体性质表。 解： （1）定值比热容
4—3 试由 w = 算式。 解： 可逆过程的过程功 w =
2 2
∫
1
pdv，wt = − ∫ vdp 导出理想气体进行可逆绝热过程时过程功和技术功的计
1
∫
2
1
pdv ，由绝热过程方式可知 p1v1κ = pvκ ， p =
p1v1κ vκ
所以
w = p1v1κ ∫
v2
v1
dv 1 1 = ( p1v1 − p2 v2 ) = Rg (T − T ) κ v κ −1 κ −1 1 2
60.08K = 13546.39J/mol 100K
1 ( H m,1 − H m,2 ) M 1 (9123.608 − 13546.39)J/(mol ⋅ K) = −138.21× 103 J/kg = −3 32.0 × 10 kg/mol
4—6 3kg 空气， p1 = 1MPa，T1 = 900K ，绝热膨胀到 p2 = 0.1MPa 。设比热容为定
Rg =
R 8.3145J/(mol ⋅ K) = = 0.260J/(kg ⋅ K) T1 = t1 + 273 = 40 + 273 = 313K M 32.0 × 10−3 kg/mol
p1 0.1MPa = 0.260J/(kg ⋅ K) × 313K ln = −112.82J/kg p2 4MPa

第四章社会主义改造理论一、填空题：1、新中国的成立，标志着我国新民主主义革命阶段的基本结束和阶段的开始。

答：社会主义革命2、我国新民主主义社会是属于社会主义体系的，是逐步过渡到社会主义的性质的社会。

答：过渡3、党的七届二中全会提出“两个转变”同时并举的思想，即使中国稳步地由转变为，由转变为。

答：农业国，工业国，新民主主义国家，社会主义国家4、党在过渡时期的总路线实行社会主义和社会主义同时并举。

答：建设，改造5、党对农业的社会主义改造，是通过互助合作的方式，把农民对生产资料的个体所有改造成。

答：集体所有二、单项选择题：1、过渡时期的总路线的主体是（ A ）A、实现社会主义工业化B、对个体农业的社会主义改造C、对个体手工业的社会主义改造D、对资本主义工商业的社会主义改造2、党的过渡时期总路线所指的过渡时期是（C ）A、从中华人民共和国成立到国民经济恢复B、从国民经济恢复到社会主义改造基本完成C、从中华人民共和国成立到社会主义改造基本完成D、从中华人民共和国成立到党的十一届三中全会召开3、新民主主义社会是（ B ）A、固定不变的社会B、过渡性的社会C、独立的社会形态D、从属于新民主主义革命的社会4、我国对农业的社会主义改造采取的过渡形式是（ D ）A、初级社、互助组、高级社B、高级社、初级社、互助组C、互助组、高级社、初级社D、互助组、初级社、高级社5、在资本主义工商业的社会主义改造中，实行个别企业的公私合营是（ B ）A、初级形式的国家资本主义B、高级形式的国家资本主义C、合作化的最初表现形式D、合作化的最高表现形式6、我国新民主主义革命阶段的基本结束和社会主义革命阶段开始的标志是（ A ）A、新中国的成立B、土地改革的完成C、社会主义改造的完成D、过渡时期的结束7、在新民主主义社会中存在多种经济成分，其中掌握了国家主要经济命脉的是（ A ）A、国营经济B、合作社经济C、个体经济D、私人资本主义经济8、党提出过渡时期总路线的物质基础是（ A ）A、相对强大的国营经济的建立B、土改的完成和农业互助合作组织的建立C、以国家资本主义形式对工商业的调整D、强大的社会主义阵营的支持和援助9、我国对资本主义工商业的社会主义改造基本完成的标志是（ D ）A、个别企业的公私合营B、实行初级形式的国家资本主义C、把私营工商业的生产经营纳入国家计划的轨道D、全行业的公私合营10、社会主义革命的目的是为了（ B ）A、改变生产关系，建立公有制B、解放生产力、发展生产力C、实现工业化D、消灭资本家11、我国农业社会主义改造基本完成的标志是（ C ）A、土地改革的完成B、初级农业合作社的建立C、高级农业合作社的建立D、人民公社的建立12、我国在资本主义工商业的社会主义改造中，对资本家实行（ C ）A、利用、限制、改造的方针B、斗争、限制、改造的方针C、团结、教育、改造的方针D、团结、教育、利用的方针13、社会主义制度的确立，为中国现代化建设创造了（ C ）A、政治条件B、经济条件C、制度条件D、思想条件14、社会主义改造完成后，我国社会的主要矛盾是（ D ）A、生产力与生产关系之间的矛盾B、工人阶级与资产阶级的矛盾C、经济基础与上层建筑之间的矛盾D、人民群众对于经济文化迅速发展的需要同当前经济文化发展不能满足人民需要的矛盾参考答案1、A2、C3、B4、D5、B6、A7、A8、A9、D 10、B 11、C 12、C 13、C 14、D三、多项选择题：1、新民主主义社会主要的经济成分有（ACD ）A、社会主义经济B、合作社经济C、个体经济D、资本主义经济E、外资经济2、中国民族资产阶级在社会主义改造时期具有的两面性是指（BE ）A、革命性B、剥削工人获取利润C、动摇性D、妥协性E、拥护宪法，愿意接受社会主义改造3、关于过渡时期总路线的表述正确的是（ ABCDE ）A、过渡时期总路线实行社会主义建设和社会主义改造同时并举B、过渡时期总路线体现了社会主义工业化和社会主义改造的紧密结合C、过渡时期总路线体现了解放生产力与发展生产力的有机统一D、过渡时期总路线体现了变革生产关系与发展生产力的有机统一E、过渡时期总路线的主要内容被概括为“一化三改”4、下面对资本主义工商业的社会主义改造经历的步骤表述正确的是（ ADE ）A、第一步主要是实行初级形式的国家资本主义B、第一步主要是实行委托加工C、第二步主要是实行统购包销和经销代销D、第二步主要实行个别企业的公私合营E、第三步是实行全行业的公私合营5、对农业的社会主义改造坚持的基本原则有（ ACD ）A、自愿互利B、听从上级安排C、典型示范D、国家帮助E、少数服从多数6、关于社会主义改造说法正确的是（ ABD ）A、社会主义改造的基本完成，使我国社会经济结构发生了根本变化B、社会主义改造的基本完成，使我国社会的阶级关系发生了根本变化C、社会主义改造的基本完成，表明我国的一切剥削现象都已经被消灭D、社会主义改造的基本完成，表明社会主义制度已经基本确立E、社会主义改造的基本完成，表明我国的所有矛盾都得到解决7、新民主主义时期我国基本的阶级力量包括（ ABCD ）A、工人阶级B、贫下中农C、民族资产阶级D、城市小资产阶级E、富农阶级8、对于工人阶级和社会主义革命来说，民族资产阶级是（ ABCD ）A、剥削阶级B、被消灭对象C、团结对象D、改造对象E、革命对象9、在新民主主义社会中，社会主义因素与资本主义因素之间不可避免地存在着（ ABC ）A、社会主义和资本主义的发展方向的斗争B、限制和反限制的斗争C、改造和被改造的斗争D、革命和反革命的斗争E、守法和违法的斗争10、在资本主义工商业改造中，初级形式的国家资本主义包括了以下形式（ ABCD ）A、委托加工B、统购包销C、计划订货D、经销代销E、公私合营11、在资本主义工商业改造中，高级形式的国家资本主义包括了以下形式（ CD ）A、委托加工、计划订货B、统购包销和代购代销C、个别企业的公私合营D、全行业的公私合营E、把私营企业的生产经营纳入国家计划的轨道参考答案1、ACD2、BE3、ABCDE4、ADE5、ACD6、ABD7、ABCD 8、ABCD 9、ABC 10、ABCD 11、CD四、辨析题：1、社会主义改造取得了伟大胜利，所以没有留下任何问题。

精选文档第四章动态数列一﹑单项选择题以下动向数列中属于时点数列的是A.历年在校学生数动向数列B.历年毕业生人数动向数列C.某厂各年工业总产值数列D.某厂各年劳动生产率数列组成动向数列的两个基本因素是A. 主词和宾词B. 变量和次数C. 分组和次数D. 现象所属的时间及其指标值动向数列中各项指标数值能够相加的是A.相对数动向数列B.均匀数动向数列C. 期间数列D. 时点数列最基本的动向数列是A.指数数列B.相对数动向数列C. 均匀数动向数列D. 绝对数动向数列动向数列中，指标数值的大小与其时间长短没有直接关系的是A. 期间数列B. 时点数列C. 相对数动向数列D. 均匀数动向数列动向数列中，指标数值是经过连续不停登记获得的数列是A.期间数列B.时点数列C. 相对数动向数列D. 均匀数动向数列以下动向数列中属于期间数列的是A.公司历年员工人数数列B.公司历年劳动生产率数列C.公司历年利税额数列D.公司历年单位产品成本数列动向数列中，各项指标数值不可以够相加的是A. 相对数动向数列B. 绝对数动向数列C. 期间数列D. 时点数列动向数列中，指标数值大小与其时间长短相关的是A.相对数动向数列B.绝对数动向数列C. 期间数列D. 时点数列动向数列中，指标数值是经过一次登记获得的数列是A.相对数动向数列B.绝对数动向数列C. 期间数列D. 时点数列编制动向数列的最基来源则是保证数列中各项指标一定拥有A. 可加性B. 可比性C. 连续性D. 一致性基期为某一固准期间水平的增添量是A.累计增添量B.逐期增添量C.均匀增添量D. 年距增添量基期为先期水平的增添量是A.累计增添量B.逐期增添量C.均匀增添量D. 年距增添量累计增添量与逐期增添量之间的关系是A.累计增添量等于相应的各个逐期增添量之和.A.精选文档B.C.累计增添量等于相应的各个逐期增添量之差D.累计增添量等于相应的各个逐期增添量之商E.累计增添量等于相应的各个逐期增添量之积F.均匀增添量等于G. A.累计增添量 B. 逐期增添量H. C.逐期增添量之和除以逐期增添量的项 D. 以上均不对I.动向数列中的发展水平是指J. A.总量指标B.相对指标K. C.均匀指标 D. 以上指标均可L.进行动向剖析的基础指标是M. A.发展水平B.均匀发展水平N. C. 增添量 D. 均匀增添量O.动向数列的剖析指标主要包含两个类型，即P.发展水平易发展速度B.水平指标和速度指标Q. C.均匀发展水平易均匀发展速度D.增添量和增添速度R.序时均匀数和一般均匀数的共同点在于二者S.都是依据动向数列计算B.都是依据变量数列计算T.都是反应现象的一般水平D.均能够除去现象颠簸的影响U.依据期间数列计算序时均匀数应采纳V. A.简单算术均匀法B.加权算术均匀法W. C.简单序时均匀法 D. 加权序时均匀法X.依据间隔相等连续时点数列计算序时均匀数应采纳Y.简单算术均匀法B.加权算术均匀法Z.简单序时均匀法D.加权序时均匀法AA.依据间隔不相等连续时点数列计算序时均匀数应采纳BB.简单算术均匀法B.加权算术均匀法CC.简单序时均匀法D.加权序时均匀法DD.依据间隔相等中断时点数列计算序时均匀数应采纳EE.简单算术均匀法B.加权算术均匀法FF. C.简单序时均匀法 D. 加权序时均匀法GG.依据间隔不相等中断时点数列计算序时均匀数应采纳HH. A.简单算术均匀法B.加权算术均匀法II. C. 简单序时均匀法 D. 加权序时均匀法JJ.序时均匀数计算中，“首未折半法”运用于KK. A.期间数列的资料B.间隔相等的时点数列资料LL.间隔不等的时点数列资料MM. D.由两个时点数列组成的相对数动向数列NN.将研究对象在不一样时间上的数目差异抽象化，从动向上说明现象在某一期间内发展的一般水平的方法是OO. A.一般均匀数B.序时均匀数PP. C. 均匀发展速度 D. 均匀增添速度QQ.间隔不相等的中断时点数列计算均匀发展水平，应采纳RR.以每次改动连续的时间长度对各时点水平加权均匀SS.用各间隔长度对各间隔的均匀水平加权均匀.精选文档对各时点水平简单算术均匀以数列的总速度按几何均匀法计算依据采纳的对照基期不一样发展速度有环比发展速度与定基发展速度环比发展速度与环比增添速度C.定基发展速度与定基增添速度环比增添速度与定基增添速度发展速度的计算方法能够表述为报告期水平与基期水平之差B.增添量与基期水平之差C.报告期水平与基期水平之比D. 增添量与基期水平之比基期为前一期水平的发展速度是A.定基发展速度B.环比发展速度C.年距发展速度D. 均匀发展速度基期为某一固按期水平的发展速度是A.定基发展速度B.环比发展速度C.年距发展速度D. 均匀发展速度定基发展速度和环比发展速度的关系是两个相邻期间的定基发展速度之商等于相应的环比发展速度之差等于相应的环比发展速度C.之和等于相应的环比发展速度D.之积等于相应的环比发展速度增添速度是A.动向数列水平之差B.动向数列水平之比增添量同发展速度之比增添量同作为比较基准的数列水平之比定基增添速度与环比增添速度的关系表现为定基增添速度等于各环比增添速度的连乘积B.定基增添速度等于各环比增添速度的连乘积的n次方根各环比增添速度连乘积加一等于定基增添速度加一定基增添速度等于各环比增添速度加一后的连乘积减一既然总速度是环比发展速度的连乘积,那么均匀发展速度就应按A. 简单算术均匀数计算B. 加权算术均匀数计算C.几何均匀数计算D. 调解均匀数计算发展速度与增添速度的关系是定基发展速度等于环比增添速度加一环比增添速度等于环比发展速度减一C.定基增添速度的连乘积等于定基发展速度D.环比增添速度的连乘积等于环比发展速度动向数列中的均匀增添速度是各个期间环比增添速度的算术均匀数各个期间环比增添速度的调解均匀数C.各个期间环比增添速度的几何均匀数.精选文档D.各个期间环比增添速度的序时均匀数采纳几何均匀法计算均匀发展速度的原因是各期环比发展速度之积等于总速度各期环比发展速度之和等于总速度各期环比增添速度之积等于总速度各期环比增添速度之和等于总速度已知各期定基发展速度和期间数,而不知道各期水平要计算均匀发展速度A.只好用水平法计算B.只好用累计法计算C. 两种方法皆能计算D. 两种方法都没法计算已知各期间发展水平之和与最先水平实期间数,要计算均匀发展速度A.只好用水平法计算B.只好用累计法计算C. 两种方法皆能计算D. 两种方法都没法计算当动向数列剖析目的是重视于观察期未发展水平,则均匀发展速度A.应采纳算术均匀法计算B.应采纳调解均匀法计算C. 应采纳几何均匀法计算D. 应采纳方程式法计算当动向数列剖析目的是重视于观察整个期间中各年发展水平的总和,则均匀发展速度A.应采纳算术均匀法计算B.应采纳调解均匀法计算应采纳几何均匀法计算D.应采纳方程式法计算动向数列中的均匀发展速度等于各期间定基发展速度的序时均匀数各期间环比发展速度的序时均匀数各期间环比发展速度的算术均匀数D.各期间定基发展速度的算术均匀数几何均匀数所计算的均匀发展速度的数值大小不受最先水平易最未水平的影响只受中间各期发展水平的影响只受最先水平易最未水平的影响既受最先水平易最未水平的影响,又受中间各期发展水平的影响累计法计算均匀发展速度的本质是从最先水平出发按均匀增添量增添,经过n期,正好达到最未水平B.按均匀发展速度发展,经过n期,正好达到第n期本质水平按均匀发展速度计算获得的各期理论水平之和正好等于各期的本质水平总和按均匀发展速度发展获得的各期理论水平之和正好等于最未期的本质水平直线趋向方程YC=a＋bx中a和b的意义是是截距,b表示X=0的趋向值表示最先发展水平的趋向值,b表示均匀发展水平表示最先发展水平的趋向值,b表示均匀发展速度.是直线的截距,表示最先发展水平的趋向值;b是直线的斜率,表示按最小平方法计算的均匀增添量47. 用最小平方法配合趋向直线方程Y C=a＋bx在什么条件下,a=Y;b=ΣXY/ΣX2A.ΣX=0B.Σ(Y-Y)=0C.ΣY=0D.Σ(Y-Y)2=最小值二﹑多项选择题组成动向数列的两个基本因素是A.变量B.次数C.现象所属的时间D.现象所属的范围E.反应现象的统计指标数值动向数列按研究任务不一样能够分为A.绝对数动向数列B.均匀数动向数列C.相对数动向数列D.期间数列E.时点数列动向数列的作用表此刻A.描绘现象变化的过程B.说明现象发展的速度和趋向探究现象发展变化的规律性对现象的发展进行展望反应现象整体的散布特色期间数列的特色数列中各个指标数值能够相加数列中指标数值大小与其期间长短无直接关系数列中各个指标数值不可以相加数列中指标数值大小与其期间长短有直接关系数列中指标数值往常是经过连续不停登记而获得的时点数列的特色数列中各个指标数值能够相加数列中指标数值大小与此间隔长短无直接关系数列中各个指标数值不可以相加数列中指标数值大小与此间隔长短有直接关系E.数列中指标数值往常是经过中断登记而获得的以下动向数列中,各项指标数值不可以相加的有A.绝对数动向数列B.相对数动向数列B.均匀数动向数列 D.期间数列时点数列以下数列中,属于两个期间对照组成的相对数动向数列有A.全员劳动生产率动向数列B.百元产值收益率动向数列C.员工人数动向数列D.计划达成程度动向数列出勤率动向数列以下数列中属于期间数列的有A.历年年未人口总数B.历年出生人数B.历年工业增添值 D.各月商品库存量各月未银行存款余额以下数列中属于时点数列的有A.高校每年毕业生人数B.高校每年在校学生数C.银行每个月未银行存款余额D.商铺各月商品库存额.我国历年外汇贮备量编制动向数列应依照的原则有期间长短应当相等B.指标的经济内容应当同样C.整体范围应当一致D.指标的计算方法应当一致E.指标的计算价钱和计量单位应当一致动向数列中的水平剖析指标有A.发展水平B.均匀发展水平C.增添量D.均匀增添量E.均匀发展速度动向数列中的速度剖析指标有A.均匀发展水平B.增添速度C.均匀发展速度D.均匀增添速度E.发展速度以下指标中属于序时均匀数的有A.均匀发展水平B.均匀增添量C.均匀发展速度D.均匀增添速度E.均匀指标动向数列中的发展水平包含A.期初水平B.期未水平C.中间水平D.报告期水平E.基期水平将不一样期间的发展水平加以均匀所获得的均匀数称为A.一般均匀数B.算术均匀数C.序时均匀数D.动向均匀数E.均匀发展水平均匀增添量的计算公式是逐期增添量之和/逐期增添量项数逐期增添量的序时均匀数C.累计增添量/动向数列项数-1D.累计增添量/动向数列项数累计增添量/动向数列项数+1定基发展速度与环比发展速度之间的关系表现为A.两个相邻期间的定基发展速度之商等于相应的环比发展速度定基发展速度等于相应的各个环比发展速度的连乘积C.定基发展速度等于环比发展速度加一D.定基发展速度等于环比增添速度加一后的连乘积环比发展速度乘积等于总速度增添速度和发展速度的关系为A.仅差一个基数B.发展速度=增添速度+1C.定基增添速度=各环比增添速度的连乘积C.定基发展速度=定基增添速度+1定基增添速度=各环比发展速度的连乘积-1定基增添速度等于A.累计增添量除以基期发展水平B.定基发展速度减去一C.总速度减去一D.环比增添速度的连乘积逐期增添量除从先期发展水平环比增添速度等于A累计增添量除以基期发展水平 B.环比发展速度减去一.精选文档C.定基发展速度减去一D.环比增添速度的连乘积逐期增添量除从先期发展水平动向数列中的发展水平能够是A.总量指标B.相对指标C.均匀指标D.变异指标E.样本指标增添1%的绝对值等于累计增添量除以定基发展速度逐期增添量除以环比发展速度C.逐期增添量除以环比增添速度×100D.累计增添量除以定基增添速度×100E. 固按期水平除以100计算均匀发展速度的方法有A.几何均匀法B.水平法C.方程式法D.累计法E.序时均匀法均匀发展速度从广义上讲属于A.静态均匀数B.动向均匀数C.序时均匀数D.几何均匀数E.调解均匀数计算均匀发展速度的几何均匀法和方程式法的差异是A.数理依照不一样B.重视点不一样C.合用条件不一样D.合用范围不一样E.对资料要求不一样常用的长久趋向测定的方法有A.时距扩大法B.挪动均匀法C.分段均匀法D.最小平方法E.季节比率法直线趋向方程Y c=a+bx的参数b是表示A.趋向值B.趋向线的截距C.趋向线的斜率D.当X=0时的Y c的数值当X每改动一个单位时Y c均匀增减的数值三﹑填空题1.动向数列一般由两个基本因素组成，即和。

分析化学（高教第五版）课后习题第四章答案（整理排版20页）第四章习题习题4-14.1 下列各种弱酸的p K a 已在括号内注明，求它们的共轭碱的pKb ；(1)HCN(9.21)；(2)HCOOH(3.74)；(3)苯酚(9.95)；(4)苯甲酸(4.21)。

解： (1) HCN p K b =14-9.25=4.79 (2) HCOOH p K b =14-3.74=10.26 (3) 苯酚pK b =14-9.95=4.05 (4) 苯甲酸pK b =14-4.21=9.794.2. 已知H 3PO 4的p K a =2.12，p K a =7.20，p K a =12.36。

求其共轭碱PO 43-的pK b1，HPO 42-的pK b2．和H 2PO 4- 的p K b3。

解：PO 43- pK b =14-12.36=1.64 HPO 42- pK b =2．14-7.20=6.80H 2PO 4- pK b =14-2.12=11.884.3 已知琥珀酸(CH 2COOH)2(以H 2A 表示)的p K al =4.19，p K b1=5.57。

试计算在pH4.88和5．0时H 2A 、HA -和A 2-的分布系数δ2、δ1和δ0。

若该酸的总浓度为0.01mol ·L -1，求pH ＝4.88时的三种形式的平衡浓度。

解： pH=4.88 〔H +〕=1.32×10-55655252521046.61069.21032.11046.6)1032.1()1032.1()(------2++??=A H δ=0.1455655255511046.61069.21032.11046.6)1032.1(1046.61032.1)(--------++?=HA δ =0.71056552565201046.61069.21032.11046.6)1032.1(1096.21046.6)(--------++?=A δ=0.145 pH=55655252521046.61069.2100.11046.6)100.1()100.1()(------2++??=A H δ =0.1095655255511046.61069.2100.11046.6)100.1(1046.6100.1)(--------++?=HA δ =0.70256552565201046.61069.2100.11046.6)100.1(1096.21046.6)(--------++?=A δ =0.189pH=4.88 c (H 2A)=0.01mol·L -1 c (H 2A)=0.145×0.01=1.45×10-3mol·L c (HA -)=0.710×0.01=7.10×10-3mol·Lc (A 2-)=0.145×0.01=1.45×10-3mol·L -14.4 分别计算H 2CO 3(p K a1=6.38，pK a2=10.25)在pH=7.10，8.32及9.50时，H 2CO 3，HCO 3-和CO 32-的分布系数δ2` δ1和δ0。

x 轴正方向运动，代表此简谐振动的旋转矢量图为
（）
[答案：B]
（2）两个同周期简谐振动曲线如图所示，振动曲线 1 的相位比振动曲线 2
的相位 （
）
（A）落后
2
（B）超前
2
（C）落后
（D）超前
[答案： B]
习题 4.1（2）图
（3）一质点作简谐振动的周期是 T,当由平衡位置向 x 轴正方向运动时，从
E
1 2
mvm2
3.16 102 J
E p E k 1 E 1.58102 J 2
当 Ek E p 时，有 E 2E p ，
即
1 kx 2 1 ( 1 kA2 )
2
22
∴
x 2 A 2m
2
20
(3)
(t2 t1 ) 8 (5 1) 32
4.4 一个沿 x 轴作简谐振动的弹簧振子，振幅为 A ，周期为T ，其振动 方程用余弦函数表示．如果 t 0 时质点的状态分别是：
的单位是 s，则 （A）波长为 5m
向传播 [答案：C]
（B）波速为 10ms-1
（C）周期为 1 s 3
（D）波沿 x 正方
（8）如图所示，两列波长为 的相干波在 p 点相遇。波在 S1 点的振动初相是 1 ，点 S1 到点 p 的距离是 r1。波在 S2 点的振动初相是2 ，点 S2 到点 p 的距离是
（A）它的动能转化为势能. （B）它的势能转化为动能. （C）它从相邻的一段质元获得能量其能量逐渐增大. （D）它把自己的能量传给相邻的一段质元，其能量逐渐减小.
[答案：D]
4.2 填空题 （1）一质点在 X 轴上作简谐振动，振幅 A＝4cm，周期 T＝2s，其平衡位置

第四章随机变量的数字特征4.1 数学期望习题1设随机变量X服从参数为p的0-1分布，求E(X).解答：依题意，X的分布律为X01P1-p p由E(X)=∑i=1∞xipi,有E(X)=0⋅(1-p)+1⋅p=p.习题2袋中有n张卡片，记有号码1,2,…,n.现从中有放回抽出k张卡片来，求号码之和X的期望.分析：.解答：设Xi表示第i次取得的号码，则X=∑i=1kXi,且P{Xi=m}=1n,其中m=1,2,⋯,n,i=1,2,⋯,k,故E(Xi)=1n(1+2+⋯+n)=n+12,i=1,2,⋯,k,从而E(X)=∑i=1kE(Xi)=k(n+1)2.习题3某产品的次品率为0.1,检验员每天检验4次. 每次随机地抽取10件产品进行检验，如发现其中的次品数多于1，就去调整设备. 以X表示一天中调整设备的次数，试求E(X)(设诸产品是否为次品是相互独立的).解答：X的可能取值为0,1,2,3,4,且知X∼b(4,p),其中p=P{调整设备}=1-C101×0.1×0.99-0.910≈0.2639,所以E(X)=4×p=4×0.2639=1.0556.习题4据统计，一位60岁的健康(一般体检未发生病症)者，在5年之内仍然活着和自杀死亡的概率为p(0<p<1,p为已知),在5年之内非自杀死亡的概率为1-p,保险公司开办5年人寿保险，条件是参加者需交纳人寿保险费a元(a已知),若5年内非自杀死亡，公司赔偿b元(b>a),应如何确定b才能使公司可期望获益，若有m人参加保险，公司可期望从中收益多少？解答：令X=“从一个参保人身上所得的收益”，由X的概率分布为+32×0.1+22×0.0+12×0.1+42×0.0+32×0.3+22×0.1=5.也可以利用期望的性质求E(Z), 得E[(X-Y)2]=E(X2-2XY+Y2)=E(X2)-2E(XY)+E(Y2)=(12×0.4+22×0.2+32×0.4)-2[-1×0.2 +1×0.1+(-2)×0.1+2×0.1+(-3)×0.0+3×0.1] +(-1)2×0.3+12×0.3 =5.习题12设(X,Y)的概率密度为f(x,y)={12y2,0≤y≤x≤10,其它,求E(X),E(Y),E(XY),E(X2+Y2). 解答： 如右图所示.E(X)=∫-∞+∞∫-∞+∞xf(x,y)dxdy=∫01dx∫0xx ⋅12y2dy=45,E(Y)=∫-∞+∞∫-∞+∞yf(x,y)dxdy=∫01dx∫0xy ⋅12y2dy=35,E(XY)=∫-∞+∞∫-∞+∞xyf(x,y)dxdy=∫01dx∫0xxy ⋅12y2dy=12,E(X2+Y2)=∫-∞+∞∫-∞+∞(x2+y2)f(x,y)dxdy=∫01dx∫0x(x2+y2)⋅12y2dy=23+615=1615. 习题13设X 和Y 相互独立，概率密度分别为ϕ1(x)={2x,0≤x≤10,其它,ϕ2(y)={e-(y-5),y>50,其它,求E(XY). 解答：解法一 由独立性.E(XY)=E(X)⋅E(Y)=∫01x ⋅2xdx∫0+∞ye -(y-5)dy=23×6=4.解法二 令z=y-5, 则E(XY)=E(X)⋅E(Y)=∫01x ⋅2xdx ⋅E(z+5)=23×(1+5)=4.4.2 方差习题1设随机变量X 服从泊松分布，且P(X=1)=P(X=2), 求E(X),D(X). 解答：由题设知，X 的分布律为P{X=k}=λkk!e -λ(λ>0)λ=0(舍去),λ=2.所以E(X)=2,D(X)=2.习题2下列命题中错误的是().(A)若X∼p(λ),则E(X)=D(X)=λ;(B)若X服从参数为λ的指数分布，则E(X)=D(X)=1λ; Array (C)若X∼b(1,θ),则E(X)=θ,D(X)=θ(1-θ);(D)若X服从区间[a,b]上的均匀分布，则E(X2)=a2+ab+b23.解答：应选(B).E(X)=1λ,D(X)=1λ2.习题3设X1,X2,⋯,Xn是相互独立的随机变量，且都服从正态分布N(μ,σ2)(σ>0),则ξ¯=1n∑i=1nξi服从的分布是¯.解答：由多维随机变量函数的分布知：有限个相互独立的正态随机变量的线性组合仍然服从正态分布，且E(X¯)=μ,D(X¯)=σ2n.习题4若Xi∼N(μi,σi2)(i=1,2,⋯,n),且X1,X2,⋯,Xn相互独立，则Y=∑i=1n(aiXi+bi)服从的分布是 .解答：应填N(∑i=1n(aiμi+bi),∑i=1nai2σi2).由多维随机变量函数的分布知：有限个相互独立的正态随机变量的线性组合仍然服从正态分布，且E(Y)=∑i=1n(aiμi+bi),D(Y)=∑i=1nai2σi2.习题5设随机变量X服从泊松分布，且3P{X=1}+2P{X=2}=4P{X=0},求X的期望与方差.解答：X的分布律为P{X=k}=λkk!e-λ,k=0,1,2,⋯,于是由已知条件得3×λ11!e-λ+2×λ22!e-λ=4×λ00!e-λ,\becauseD(XY)=E(XY)2-E2(XY)=E(X2Y2)-E2(X)2 (Y),又\becauseE(X2Y2)=∫-∞+∞∫-∞+∞x2y2f(x,y)dxdy=∫-∞+∞x2fX(x)dx∫-∞+∞y2fY(y)dy=E(X2)E(Y2),∴D(XY)=E(X2)E(Y2)-E2(X)E2(Y)=[D(X)+E2(X)][D(Y)+E2(Y)]-E2(X)E2(Y)=D(X)D(Y)+D(X)E2(Y)+D(Y)E2(X)=2×3+2×32+3×12=27.习题9设随机变量X1,X2,X3,X4相互独立，且有E(Xi)=i,D(Xi)=5-i,i=1,2,3,4,又设Y=2X1-X2+3X3-12X4,求E(Y),D(Y).解答：E(Y)=E(2X1-X2+3X3-12X4)=2E(X1)-E(X2)+3E(X 3)-12E(X4)=2×1-2+3×3-12×4=7,D(Y)=4D(X1)+D(X2)+9D(X3)+14D(X4)=4×4+3+9×2+14×1=37.25.习题105家商店联营，它们每两周售出的某种农产品的数量(以kg计)分别为X1,X2,X3,X4,X5.已知X1∼N(200,225),X2∼N(240,240),X3∼N(180,225),X4∼N(260,265),X5∼N(320,270),X1,X2,X3,X4,X5相互独立.(1)求5家商店两周的总销售量的均值和方差；(2)商店每隔两周进货一次，为了使新的供货到达前商店不会脱销的概率大于0.99，问商店的仓库应至少储存该产品多少千克？解答：(1)设总销售量为X,由题设条件知X=X1+X2+X3+X4+X5,于是E(X)=∑i=15E(Xi)=200+240+180+260+320=1200, D(X)=∑i=15D(X i)=225+240+225+265+270=1225 .(2)设商店的仓库应至少储存y千克该产品，为使P{X≤y}>0.99,求y.由(1)易知，X∼N(1200,1225),P{X≤y}=P{X-12001225≤y-12001225=Φ(y-12001225)>0.99.查标准正态分布表得y-12001225=2.33,y=2.33×1225+1200≈1282(kg).习题11设随机变量X1,X2,⋯,Xn相互独立，且都服从数学期望为1的指数分布，求Z=min{X1,X2,⋯,Xn}的数学期望和方差.解答：Xi(i=1,2,⋯,n)的分布函数为F(x)={1-e-x,x>00,其它,Z=min{X1,X2,⋯,Xn}的分布函数为FZ(z)=1-[1-F(z)]n={1-e-nz,z>00,其它,于是E(Z)=∫0∞zne-nzdz=-ze-nz∣0∞+e-nzdz=1n,而E(Z2)=∫0∞z2ne-nzdz=2n2,于是D(Z)=E(Z2)-(E(Z))2=1n2.4.3 协方差与相关系数习题1设(X,Y)服从二维正态分布，则下列条件中不是X,Y相互独立的充分必要条件是().(A)X,Y不相关；(B)E(XY)=E(X)E(Y);(C)cov(X,Y)=0;(D)E(X)=E(Y)=0.解答：应选（D）。

第四章习题及答案1. 300K时，Ge的本征电阻率为47Ωcm，如电子和空穴迁移率分别为3900cm2/( V.S)和1900cm2/( V.S)。

试求Ge 的载流子浓度。

解：在本征情况下，n=p=ni,由ρ=1/σ=47⨯1.602⨯10-191nqun+pqu=p1niq(un+up)cm-3知ni=ρq(un+up)=⨯(3900+1900)=2.29⨯10132. 试计算本征Si在室温时的电导率，设电子和空穴迁移率分别为1350cm2/( V.S)和500cm2/( V.S)。

当掺入百万分之一的As后，设杂质全部电离，试计算其电导率。

比本征Si的电导率增大了多少倍？解：300K时，un=1350cm2/(V⋅S),up=500cm2/(V⋅S)，查表3-2或图3-7可知，室温下Si的本征载流子浓度约为ni=1.0⨯1010cm-3。

本征情况下，σ=nqun+pqup=niq(un+up)=1⨯1010⨯1.602⨯1018-19⨯(1350+500)=3.0⨯1012-6S/cm金钢石结构一个原胞内的等效原子个数为8⨯+6⨯的晶格常数为0.543102nm，则其原子密度为+4=8个，查看附录B知Si。

8(0.543102⨯1011000000-7)3=5⨯1022cm-3掺入百万分之一的As,杂质的浓度为ND=5⨯1022⨯=5⨯1016cm-3，杂质全2ND>>ni，部电离后，这种情况下，查图4-14（a）可知其多子的迁移率为800 cm/( V.S)σ≈NDqun=5⨯10''16⨯1.602⨯10-19⨯800=6.4S/cm比本征情况下增大了σσ'=6.43⨯10-6=2.1⨯10倍63. 电阻率为10Ω.m的p型Si样品，试计算室温时多数载流子和少数载流子浓度。

解：查表4-15(b)可知，室温下，10Ω.m的p型Si样品的掺杂浓度NA约为1.5⨯1015cm-3,查表3-2或图3-7可知，室温下Si的本征载流子浓度约为ni=1.0⨯1010cm-3,NA>>nip≈NA=1.5⨯1015cm-3n=ni2p=(1.0⨯101015)21.5⨯10=6.7⨯10cm4-34. 0.1kg的Ge单晶，掺有3.2⨯10-9kg的Sb，设杂质全部电离，试求该材料的电阻率[μn=0.38m/( V.S),Ge的单晶密度为5.32g/cm,Sb原子量为121.8]。